 Open Access Article
Open Access ArticleControlled deposition of nanoparticles with critical Casimir forces†
Emanuele
Marino
 ab,
Oleg A.
Vasilyev
ab,
Oleg A.
Vasilyev
 cd,
Bas B.
Kluft
b,
Milo J. B.
Stroink
b,
Svyatoslav
Kondrat
cd,
Bas B.
Kluft
b,
Milo J. B.
Stroink
b,
Svyatoslav
Kondrat
 *cde and
Peter
Schall
*b
*cde and
Peter
Schall
*b
aDepartment of Chemistry, University of Pennsylvania, Philadelphia, Pennsylvania 19104, USA
bvan der Waals-Zeeman Institute, University of Amsterdam, Amsterdam, The Netherlands. E-mail: p.schall@uva.nl
cMax-Planck-Institut für Intelligente Systeme, Heisenbergstraße 3, D-70569 Stuttgart, Germany. E-mail: svyatoslav.kondrat@gmail.com; skondrat@ichf.edu.pl
dIV. Institut für Theoretische Physik, Universität Stuttgart, Pfaffenwaldring 57, D-70569 Stuttgart, Germany
eInstitute of Physical Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warsaw, Poland
First published on 28th May 2021
Abstract
Nanocrystal assembly represents the key fabrication step to develop next-generation optoelectronic devices with properties defined from the bottom-up. Despite numerous efforts, our limited understanding of nanoscale interactions has so far delayed the establishment of assembly conditions leading to reproducible superstructure morphologies, therefore hampering integration with large-scale, industrial processes. In this work, we demonstrate the deposition of a layer of semiconductor nanocrystals on a flat and unpatterned silicon substrate as mediated by the interplay of critical Casimir attraction and electrostatic repulsion. We show experimentally and rationalize with Monte Carlo and molecular dynamics simulations how this assembly process can be biased towards the formation of 2D layers or 3D islands and how the morphology of the deposited superstructure can be tuned from crystalline to amorphous. Our findings demonstrate the potential of the critical Casimir interaction to direct the growth of future artificial solids based on nanocrystals as the ultimate building blocks.
New conceptsTraditional assembly methods for nanoparticles rely on fast solvent drying, resulting in superstructure morphologies that are difficult to reproduce. In this paper, we take advantage of attractive critical Casimir interactions to get a direct grip on the nanoscale assembly and steer the growth of specific nanoparticle morphologies with external temperature control. Such direct control is so far lacking at the nanometer scale. We demonstrate the flexibility of our method by growing crystalline, amorphous, and spinodal superstructures, as well 2D layers and 3D islands. As the superstructures grow on a silicon substrate, the resulting nanocrystal films may be directly processed into a device structure for applications. In addition, our approach allows new insights into the nature of fluctuations and inter-particle interactions by visualization of the nanoscale footprint of the critical Casimir interactions through the spinodal nanoparticle tiling. |
Semiconductor nanocrystals, quantum dots (QDs), reside at the 1–10 nm length scale separating atoms and colloids and have the potential of becoming the ultimate building blocks of future artificial solids1 by promoting material properties fundamentally defined from the bottom-up.2,3 The assembly of QDs into crystalline solids, or supercrystals, is of key importance as it represents the main fabrication step of these complex materials. Of the several assembly techniques investigated,4,5 controlled solvent evaporation at the air/liquid interface has led to the largest crystalline domain size of 2D supercrystals of QDs;6 this approach is versatile and compatible with 3D assembly,7 although the transfer of the crystalline QD layer to a solid substrate can lead to film cracking,8 hampering scalability. There is, therefore, the need to improve the integration of QD supercrystals onto planar substrates. An ideal solution would be controlling both QD–QD and QD-substrate interactions to drive the growth of QD supercrystals directly onto a desired substrate.
Critical Casimir interactions have attracted much attention recently as a means to steer the assembly of micro-scaled colloids and nanoparticles dissolved in a binary solvent close to its critical point.9–15 The confinement of solvent fluctuations between particles causes a net attractive force driving the assembly process.15–17 Changing the distance from the critical point regulates the size and composition of these fluctuations, thereby controlling the magnitude and the range of the Casimir interaction. Consequently, the temperature of the near-critical solvent represents a physical knob to finely tune the particle interactions, favoring interaction-dependent superstructure morphologies.14 Similarly, the confinement of solvent fluctuations between particles and a substrate also leads to particle–substrate interactions that can ultimately result in controllable adsorption of particles on a substrate.18–22 In the case of nanoparticles, this can allow for controlled nanocrystal deposition analogous to atomic deposition techniques such as chemical vapor deposition, with the advantage that the nanocrystal interactions can be directly controlled by temperature. While for typically-used micrometer-sized colloidal particles the temperature needs to be inconveniently close to the critical temperature, Tc, by several tens of millikelvin to reach interaction ranges comparable to the colloid size, for nanoparticles the temperature range widens up to ten Kelvin below Tc, making this technique more easily applicable.12
Herein, we demonstrate the controlled deposition of QDs onto a silicon substrate driven by critical Casimir forces. By tuning the interplay between the critical Casimir attraction and electrostatic repulsion, we direct the growth of patches of a crystalline monolayer of QDs on a substrate. We show how the morphology of deposited QD superstructures can be varied from crystalline to amorphous and from layer-by-layer to island growth by navigating through the multidimensional parameter space of Debye screening length, substrate wetting properties and solvent correlation length. To gain physical insights into the assembly process, we perform 3D Monte Carlo (MC) simulations of the Ising model, which mimics a binary liquid mixture close to criticality. To connect simulations and experiments, we measure the size of the solvent fluctuations in situ and compute the critical Casimir interaction potentials for the experimentally relevant configurations. Our results open up new directions for the assembly and deposition control of QDs at nanometer length scales, demonstrating conveniently tunable nanoparticle interactions.
We prepare cadmium selenide (CdSe) QDs with average diameter dQD = 5.5 nm and passivated by hydrophilic 2,3-dimercapto-1-propanesulfonate (DMPS) ligands, and disperse them in a binary mixture of lutidine and water with lutidine mass fraction cL = 0.3, just above the critical concentration cc = 0.286. Since the presence of QDs and free ligands in solution influences the binary liquid phase diagram slightly, we experimentally measure the phase diagram of the nanocrystal-containing binary mixture. To induce attractive critical Casimir interactions at a substrate, we heat the substrate to the desired temperature below Tc, T = Tc − ΔT. The heated substrate is submerged into the solution from above to avoid particle clusters assembling in the bulk of the solvent from sedimenting onto it and to minimize convection, see Fig. 1a. The solution is in thermal contact with a bath at room temperature, establishing a temperature gradient away from the heated substrate (see Fig. S2 (ESI†) for the calculated temperature distribution). We measure the temperature-dependent solvent correlation length ξ directly using dynamic light scattering by aligning the laser beam of a light scattering setup (ALV-6000/60X0) close to the substrate so that scattering results from the solvent fluctuations near the surface. This allows us to directly measure the crucial parameter determining the attraction, ξ.13 Due to the slightly off-critical composition, ξ does not diverge upon approaching the critical temperature, but increases strongly to correlation lengths substantially larger than the molecular dimension.13
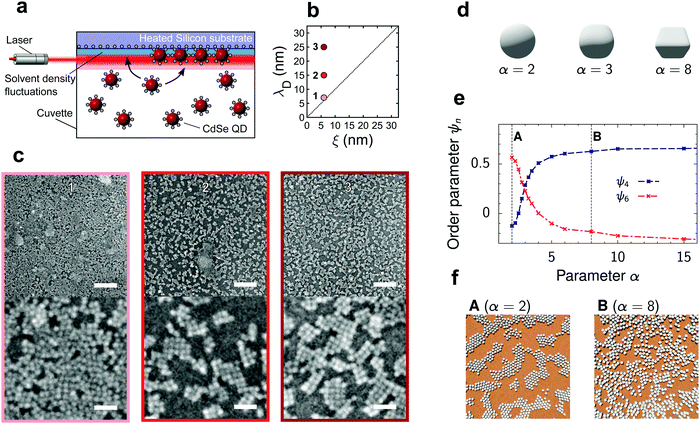 | ||
| Fig. 1 Deposition of quantum dots onto a silicon substrate driven by critical Casimir forces. (a) Schematic of the experimental deposition setup. The heated silicon substrate is submerged in a dispersion of quantum dots in binary solvent. The solvent fluctuations near the substrate are probed by the laser of a dynamic light scattering setup. The resulting vertical temperature gradient drives the assembly close to the substrate. (b) Experimental parameter space controlling the interaction potential is spanned by the Debye screening length, λD, and solvent correlation length, ξ. (c) Representative scanning electron micrographs of QD structures deposited on a hydrophilic silicon substrate for λD ≳ ξ with ξ = 6 nm. Numbers refer to the state points in (b). Top and bottom scale bars indicate 125 nm and 25 nm, respectively. (d) Examples of cubo-spherical particles (eqn (1)) used to model quadratic ordering of the deposited quantum dots. (e) Order parameters ψ4 and ψ6 (eqn (S10), ESI†) describing square and hexagonal ordering as obtained from 2D molecular dynamics (MD) simulations. The critical Casimir and electrostatic interactions, used in the MD code, were pre-computed for a spherical particle inscribed in the cubo-sphere with given α. The critical Casimir potential between QDs was computed in the presence of a hydrophilic substrate for the reduced temperature τ = (T − Tc)/Tc = 0.007 and bulk magnetic field of the Ising model h = 0.01. The Debye length λD ≈ 5.5 nm. (f) Snapshots from the MD simulations demonstrating (A) hexagonal and (B) quadratic ordering, corresponding to α = 2 and α = 8. See also videos (ESI†). | ||
While the magnitude and range of the critical Casimir attraction depend on the size of the solvent composition fluctuations, ξ(ΔT),9,15,16,18 the magnitude and extent of the electrostatic repulsion depend on the Debye screening length λD, set by the concentration of free ions in solution.23 Since the dielectric constant of the QDs and silicon substrate (ε ≈ 5–6.25, see ref. 24 and 25) is comparable to the dielectric constant of the near-critical water-lutidine (ε ≈ 7, see ref. 26), the van der Waals interactions are weak and hence the behaviour of the QDs at a substrate is mostly determined by the interplay of the electrostatic and critical Casimir interactions. The corresponding experimental parameter space of ξ and λD is shown in Fig. 1b.
With increasing exposure time in the QD suspension, the silicon substrate exhibits an increasing amount of deposited material (Fig. S3, ESI†), suggesting the continuous deposition of a QD film. The assembly also appears general yet sensitive to the choice of substrate, as exemplified by depositions on a gold substrate (Fig. S4, ESI†). We focus on short deposition times of 1 hour on silicon and investigate the structure and morphology of the deposits. At sufficiently low attraction, λD > ξ, the substrate after drying contains ordered crystalline patches of QDs (Fig. 1c). Drawing an analogy with atomic deposition processes,27 the deposition of planar structures suggests that the attraction between a QD and the substrate is larger than that between the QDs; furthermore, the overall low attraction magnitude allows the particles to form an equilibrium crystalline phase. Surprisingly, the crystalline patches exhibit square packing featuring four nearest neighbors, instead of six neighbors characterizing the hexagonal packing. The square packing may arise due to QD facets, relating to their zinc blende atomic lattice, emphasized by passivation with short DMPS ligands.
To assess whether such cubic-like shapes could lead to the formation of square lattices, we model the deposited particles as rounded cubes described by
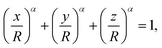 | (1) |
When decreasing the Debye screening length to reduce the repulsive component to λD ∼ ξ, the crystalline structure dissolves in favor of amorphous deposits (Fig. 1c). A similar loss of crystallinity is observed when we increase the attractive length scale while keeping the repulsion fixed: The initially crystalline deposits become increasingly amorphous as shown in Fig. 2. In both cases, we increase the attractive character of the effective particle–particle and particle–substrate interactions that result from the superposition of the screened electrostatic repulsion and the critical Casimir attraction. We conclude that the structure can no longer rearrange to reach the lowest-energy configuration. We can thus tune the structure of the deposit by either adjusting the salt concentration or temperature to modulate the QD-substrate interaction. Furthermore, controlling the wetting properties of the substrate offers an orthogonal handle over the assembly behaviour, as we will show below. We note that our 2D multiscale simulations28 do not show this loss of crystalline order with decreasing λD but rather the opposite trend; we therefore associate it with ligand or surface friction effects that slow down the particle dynamics at increasing attraction.
 | ||
| Fig. 2 QD deposition on a hydrophilic silicon substrate for fixed Debye screening length. (a) Schematic of the available parameter space and the values of the measured correlation length, ξ, and Debye screening length, λD, used in (b). (b) Representative scanning electron micrographs for the states indicated in (a). Top and bottom scale bars indicate 125 nm and 25 nm, respectively. Dashed circles indicate two times the correlation length for orientation. (c) Attractive critical Casimir potential between a QD and the substrate obtained by Monte Carlo (MC) simulations of the Ising model. D is the surface-to-surface distance and λCas ≈ ξ is the decay length of the Casimir potential obtained by fitting it to the exponentially decaying function of D (Section S3A, ESI†). The grey area shows the region of steric exclusion. | ||
The increasing solvent correlation length also leads to a key morphological feature: As the size of the solvent fluctuations increases, the QD aggregates coarsen and assume a well-defined morphology, reminiscent of spinodal patterns. Such spinodal morphologies are characteristic of two-component mixtures subjected to rapid demixing.29 Indeed, the size of the observed structures is of the order of 2ξ (dashed circles in Fig. 2b) and increases with increasing ξ (from left to right in Fig. 2b). Similar spinodal structures are also obtained in our multi-scale molecular dynamics simulations of deposited nanoparticles.28
As opposed to micrometer-sized colloidal particles, the solvent fluctuations can reach sizes comparable to or larger than the QD diameter even at temperatures far below Tc. By increasing the solvent correlation length from ξ = 5 nm < dQD to ξ ≥ 15 nm > dQD, we invert the ratio of ξ to the particle diameter dQD. The case ξ/dQD < 1 is typical for micron-sized colloids and has been extensively studied in the literature.10,11,13,15,18,30,31 For ξ/dQD > 1, many-body interactions between the QDs likely play a dominant role.32,33Fig. 2b suggest that, in this case, the QDs adsorbed onto the substrate follow the specific patterns of the solvent fluctuations. Thus, besides nanoparticle deposition, our experimental approach can be used to deepen the fundamental understanding of colloidal interactions by using nanoparticles as spatial probes.
The increasing correlation length also leads to a nontrivial change of the amount of deposited material, namely, with increasing ξ the surface coverage changes in a non-monotonic way (Fig. 2b). The critical Casimir potential UCas shown in Fig. 2c cannot explain this surprising behaviour because its magnitude increases with increasing decay length λCas ≈ ξ. The reduced surface coverage in Fig. 2 suggests that the increasing correlation length enhances the surface charge density due to the increased water content at the substrate, hence amplifying the QD-substrate electrostatic repulsion. For the larger correlation lengths (ξ ≳ 18 nm in Fig. 2b), the critical Casimir forces eventually start to dominate the interactions, leading to an increase in surface coverage. While microscopic theories and complementary experiments are needed to assess this hypothesis, we note that such unusual effects have been previously reported for other types of surfaces. For equally-charged surfaces with unlike preferences for the fluid component (e.g., hydrophobic substrates and hydrophilic particles), there is a temperature-induced crossover between attractive and repulsive forces34 that arises due to the subtle interplay between the electrostatic and critical Casimir forces.35–37 Similarly, oppositely-charged hydrophobic surfaces can repel each other, even though separately both the critical Casimir and electrostatic forces are attractive.38
When we increase the range of the attraction and repulsion simultaneously, keeping their ratio constant, we observe a substantial decrease in the surface coverage (Fig. 3a and b). The strength of the electrostatic repulsion increases quadratically with the Debye screening length (Section S2B, eqn (S6), ESI†), while the magnitude of the critical Casimir attraction varies only weakly with the correlation length (Fig. 2c). This leads to an energy barrier for QDs approaching the substrate when λD = ξ increases (Fig. 3c), which reduces the surface coverage. A similar effect has been reported for the assembly of micro-scale colloids, which yields the aggregation line well below the λD = ξ line.39
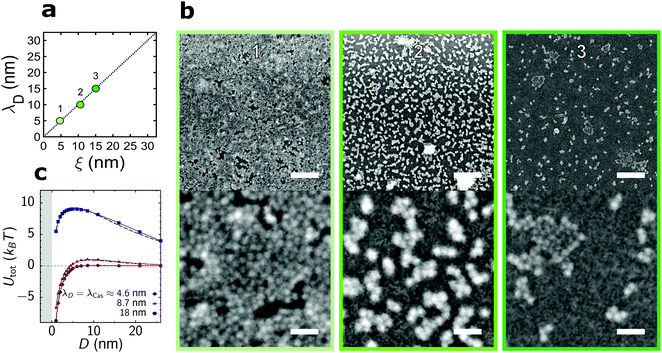 | ||
| Fig. 3 QD deposition on a hydrophilic substrate in the regime λD ≈ ξ. (a) Available parameter space and the values of the correlation length, ξ, and Debye screening length, λD, used in (b). (b) Representative scanning electron micrographs for the parameters indicated in (a). Top and bottom scale bars indicate 125 nm and 25 nm, respectively. (c) Total interaction potential Utot between a QD and the substrate as a sum of the critical Casimir attractive (Fig. 2c) and electrostatic repulsive (Section S2B, ESI†) potentials. The critical Casimir potential was calculated from Monte Carlo (MC) simulations of the Ising model and its decay length λCas ≈ ξ was obtained by fitting the MC data to an exponentially decaying function of separation. | ||
We finally bias the assembly process to selectively drive QD island growth. Atomic deposition methods describe island growth as characterized by interparticle interactions stronger than particle–substrate interactions. We achieve these conditions by engineering the surface affinity of the silicon substrate from hydrophilic to hydrophobic by treating the substrate with 3-mercaptopropyl trimethoxysilane,40 resulting in a contact angle of 74° with water, see Fig. S1 (ESI†). The resulting deposits indeed exhibit island morphology, as shown in Fig. 4b.
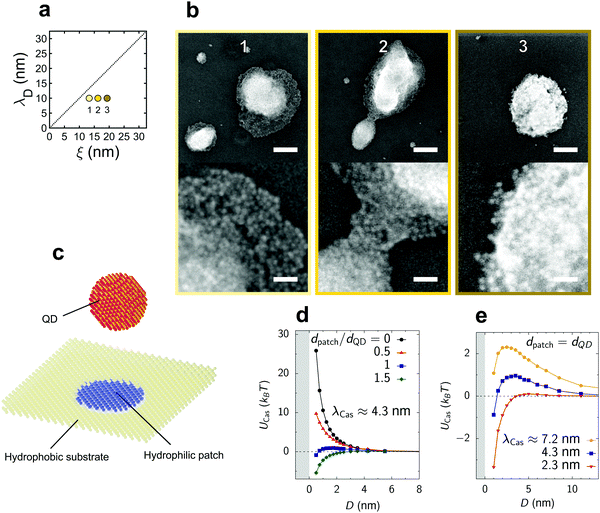 | ||
| Fig. 4 QD deposition on a hydrophobic silicon substrate. (a) Schematic of the available parameter space. (b) Representative scanning electron micrographs of the deposited QD islands. Top and bottom scale bars indicate 125 nm and 25 nm, respectively. (c) Schematic of the model used in Monte Carlo (MC) simulations of the Ising model. A spherical nanoparticle of diameter dQD, modelling a QD, approaches an overall hydrophobic surface (yellow) with a circular hydrophilic defect (blue patch) of diameter dpatch (Section S3, ESI†). (d) Critical Casimir potential UCas between a QD and the patched substrate as a function of the surface-to-surface distance D obtained from MC simulations. The QD is located above the patch so that their centers form a vector normal to the substrate. The decay length of the critical Casimir potential, λCas ≈ 4.3 nm, was determined from the decay of UCas for dpatch = 0 (Section S3A, ESI†). An energy barrier for a QD to deposit on the substrate decreases quickly with increasing the patch size, allowing island growth at the location of the patch. (e) Critical Casimir potential for a few values of the decay length λCas. An energy barrier for the QD deposition decreases for decreasing λCas, enabling more deposition islands to form on the substrate. | ||
We thus tuned the deposition of 2D QD layers towards 3D island growth, with island sizes between 50 and 500 nm. Yet, it is surprising that we observe any superstructure growth at all as the critical Casimir force becomes repulsive in the presence of asymmetric boundary conditions, namely hydrophobic substrate and hydrophilic particles.18 Such islands may grow on locations of the substrate where the hydrophobic surface coverage is defective, therefore exposing hydrophilic patches (Fig. 4c). To understand how the presence of such patches affects the critical Casimir interactions between a QD and the substrate, we performed MC simulations for various patch sizes dpatch. Fig. 4d shows that the energy barrier for QD deposition decreases rapidly with increasing dpatch and practically vanishes when the patch size becomes comparable to the QD size. Hence, deposition of a single QD may result in a cascade reaction that will quickly lead to the formation of an island. Our simulations also reveal that the energy barrier decreases for decreasing decay length of the critical Casimir interactions (Fig. 4e). The decreasing range of interactions weakens the effect of the hydrophobic substrate on a QD that is located exactly above the hydrophilic patch, thus weakening the repulsion. This explains why more islands form for smaller correlation lengths. Such island formation due to hydrophilic patches demonstrates the potential of our method for fabricating complex nanoparticle structures via substrate patterning.
In conclusion, our experiments and simulations demonstrate that via direct particle interaction control at the nanoscale, the critical Casimir effect allows the deposition of QDs on a substrate in an administering manner. Application of this effect to nanometer-size particles offers convenient tuning of their interactions in a temperature window of more than 10 K, a range much larger than in previous studies on micron-scale colloids.10,11,15,18,30 By varying the Casimir attraction and the electrostatic repulsion, we obtain various morphologies ranging from crystalline to spinodal. We expect this effect to be general to any nanoparticle that can be charge stabilised in the binary mixture; the magnitude of the repulsive and attractive components will then be set by the surface charges of particles and substrate, and their lutidine/water affinities, respectively. Furthermore, by changing the substrate wetting properties, we direct the growth from 2D layers to 3D islands (Fig. 1,4, respectively). Our experiments also uncover physically unexpected results such as the formation of quadratic, rather than hexagonal, lattices (Fig. 1) and a surprising non-monotonic behavior of surface coverage with the solvent correlation length (Fig. 2).
We envision that our method may lead to faster and cheaper fabrication techniques for optoelectronic devices based on nanocrystal self-assembly. Combined with chemical substrate patterning, the critical Casimir-driven nanoparticle deposition can produce desired structures, challenging to fabricate otherwise. These well-defined morphologies can find a broad range of applications, such as light-emitting diode displays with nanocrystal-sized pixels. Our approach may also serve as the testing ground to deepen our knowledge of fluctuation phenomena and critical Casimir forces at the nanoscale to experimentally assess the effects predicted by theory.15,28,33,41–45
Methods
Experiments
We have synthesized CdSe QDs by following a procedure reported in the literature.46 The hydrophobic, oleate-capped, QDs were ligand-exchanged for hydrophilic DMPS ligands by using an equal volume hexane/N-methyl formamide two-phase system featuring an excess of 1000 ligands per QD. After washing with acetonitrile, the ligand-exchanged QDs were re-dispersed in the binary mixture of 2,6-lutidine in water.The QD dispersion was then transferred to a custom-made glass cuvette for light-scattering which was placed in the sample holder for a standard dynamic light scattering system (ALV-6000/60X0 Multiple Tau Digital Real Correlator), a decaline bath at room temperature. A silicon substrate, made either hydrophilic through plasma-cleaning or hydrophobic through silanization (see ref. 40, method 2), was placed in contact with the QD dispersion by immersion. The silicon substrate was in thermal contact with a steel block. The steel block was then heated to the desired temperature by means of an embedded thermistor.
The solvent correlation length ξ was directly measured by using dynamic light scattering after aligning the He–Ne laser beam (wavelength 632.8 nm, power 22 mW) parallel and close to the submerged substrate. Specifically, we carefully lowered the cuvette containing the nanocrystal dispersion in the binary mixture in contact with the heating block until the laser beam just cleared of the substrate. The single exponential decay time τ of the scattered intensity correlation curve is related to the hydrodynamic diameter dH of the scattering objects undergoing diffusion by ξ: = dH = (kBT/3πη)q2τ, where kB Boltzmann's constant, T the temperature, η is the solvent viscosity, and q is the scattering wavevector. The Debye screening length λD of the binary mixture was controlled by adjusting the concentration of NaCl according to 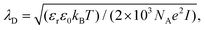 where εr is the volume-averaged dielectric constant of the solvent mixture, ε0 the permittivity of free space, NA Avogadro's number, e the elementary charge, and I the molar concentration of NaCl. The depositions shown in the main text lasted one hour. A more extensive description of these procedures can be found in Section S1 (ESI†).
where εr is the volume-averaged dielectric constant of the solvent mixture, ε0 the permittivity of free space, NA Avogadro's number, e the elementary charge, and I the molar concentration of NaCl. The depositions shown in the main text lasted one hour. A more extensive description of these procedures can be found in Section S1 (ESI†).
Monte Carlo simulations
We have used 3D Monte Carlo (MC) simulations of the Ising model, which mimics a near-critical binary solvent, to compute critical Casimir interaction potentials between a QD and a substrate and between two QDs at a substrate. QDs were modeled as spherical particles on a lattice using the method developed by Vasilyev47 (Section S3A, ESI†). To mimic the experimental conditions, where an off-critical concentration was kept fixed, we varied the values of the reduced temperature and external magnetic field in the Ising model such as to have a constant non-zero magnetization in the bulk (Section S3B, ESI†).Molecular dynamics simulations
We performed 2D molecular dynamics simulations of deposited cubo-spherical particles with the shape defined by eqn (1). The shape was taken into account only on the level of short-range repulsive interactions (Section S4, ESI†). The electrostatic and critical Casimir forces were calculated for a sphere inscribed in the corresponding cubo-spherical particle. For electrostatic interactions, we used the DLVO theory (Section S2A, ESI†) and the critical Casimir potentials were computed by Monte Carlo simulations of the Ising model, as described above.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is part of the research programme “Nanoarchitectures: Smart Assembly, Quantum Electronics and Soft Mechanics” with project number 680.47.615, which is financed by the Dutch Research Council (NWO). P. S. acknowledges financial support from NWO through personal Vici grant. The authors acknowledge Dr Yingying Tang for carrying out the contact angle measurements.References
- T. Hanrath, Colloidal nanocrystal quantum dot assemblies as artificial solids, J. Vac. Sci. Technol., A, 2012, 30, 030802 CrossRef.
- M. Cargnello, A. C. Johnston-Peck, B. T. Diroll, E. Wong, B. Datta, D. Damodhar, V. V. T. Doan-Nguyen, A. A. Herzing, C. R. Kagan and C. B. Murray, Substitutional doping in nanocrystal superlattices, Nature, 2015, 524, 450 CrossRef CAS PubMed.
- E. Marino, A. Sciortino, A. Berkhout, K. E. MacArthur, M. Heggen, T. Gregorkiewicz, T. E. Kodger, A. Capretti, C. B. Murray, A. F. Koenderink, F. Messina and P. Schall, Simultaneous Photonic and Excitonic Coupling in Spherical Quantum Dot Supercrystals, ACS Nano, 2020, 14(10), 13806–13815 CrossRef CAS PubMed.
- K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Nanoscale Forces and Their Uses in Self-Assembly, Small, 2009, 5, 1600–1630 CrossRef CAS PubMed.
- M. A. Boles, M. Engel and D. V. Talapin, Self-Assembly of Colloidal Nanocrystals: From Intricate Structures to Functional Materials, Chem. Rev., 2016, 116, 11220–11289 CrossRef CAS PubMed.
- A. Dong, J. Chen, P. M. Vora, J. M. Kikkawa and C. B. Murray, Binary nanocrystal superlattice membranes self-assembled at the liquid-air interface, Nature, 2010, 466, 474–477 CrossRef CAS PubMed.
- E. Marino, T. E. Kodger, G. H. Wegdam and P. Schall, Revealing Driving Forces in Quantum Dot Supercrystal Assembly, Adv. Mater., 2018, 30, 1803433 CrossRef PubMed.
- B. T. Diroll, X. Ma, Y. Wu and C. B. Murray, Anisotropic Cracking of Nanocrystal Superlattices, Nano Lett., 2017, 17, 6501–6506 CrossRef CAS PubMed.
- D. Bonn, J. Otwinowski, S. Sacanna, H. Guo, G. Wegdam and P. Schall, Direct observation of colloidal aggregation by critical Casimir forces, Phys. Rev. Lett., 2009, 103, 156101 CrossRef PubMed.
- V. D. Nguyen, S. Faber, Z. Hu, G. H. Wegdam and P. Schall, Controlling colloidal phase transitions with critical Casimir forces, Nat. Commun., 2013, 4, 1584 CrossRef PubMed.
- P. B. Shelke, V. Nguyen, A. Limaye and P. Schall, Controlling colloidal morphologies by critical Casimir forces, Adv. Mater., 2013, 25, 1499–1503 CrossRef CAS PubMed.
- E. Marino, T. E. Kodger, J. B. ten Hove, A. H. Velders and P. Schall, Assembling quantum dots via critical Casimir forces, Sol. Energy Mater. Sol. Cells, 2016, 158, 154–159 CrossRef CAS.
- S. G. Stuij, M. Labbé-Laurent, T. E. Kodger, A. Maciołek and P. Schall, Critical Casimir interactions between colloids around the critical point of binary solvents, Soft Matter, 2017, 13, 5233–5249 RSC.
- E. Marino, D. M. Balazs, R. W. Crisp, D. Hermida-Merino, M. A. Loi, T. E. Kodger and P. Schall, Controlling Superstructure-Property Relationships via Critical Casimir Assembly of Quantum Dots, J. Phys. Chem. C, 2019, 123, 13451–13457 CrossRef CAS PubMed.
- A. Maciołek and S. Dietrich, Collective behavior of colloids due to critical Casimir interactions, Rev. Mod. Phys., 2018, 90, 045001 CrossRef.
- M. E. Fisher and P.-G. de Gennes, Phénomènes aux parois dans un mélange binaire critique, CR Acad. Sci. Ser. B, 1978, 287, 207–209 CAS.
- A. Gambassi, The Casimir effect: From quantum to critical fluctuations, J. Phys.: Conf. Ser., 2009, 161, 012037 CrossRef.
- C. Hertlein, L. Helden, A. Gambassi, S. Dietrich and C. Bechinger, Direct measurement of critical Casimir forces, Nature, 2008, 451, 172–175 CrossRef CAS PubMed.
- M. Tröndle, S. Kondrat, A. Gambassi, L. Harnau and S. Dietrich, Normal and lateral critical Casimir forces between colloids and patterned substrates, EPL, 2009, 88, 40004 CrossRef.
- M. Tröndle, S. Kondrat, A. Gambassi, L. Harnau and S. Dietrich, Critical Casimir effect for colloids close to chemically patterned substrates, J. Chem. Phys., 2010, 133, 074702 CrossRef PubMed.
- M. Tröndle, O. Zvyagolskaya, A. Gambassi, D. Vogt, L. Harnau, C. Bechinger and S. Dietrich, Trapping colloids near chemical stripes via critical Casimir forces, Mol. Phys., 2011, 109, 1169–1185 CrossRef.
- A. Gambassi and S. Dietrich, Critical Casimir forces steered by patterned substrates, Soft Matter, 2011, 7, 1247–1253 RSC.
- J. N. Israelachvili, Intermolecular and surface forces, Academic press, 2011 Search PubMed.
- U. Pal, D. Samanta, S. Ghorai and A. K. Chaudhuri, Optical constants of vacuum-evaporated polycrystalline cadmium selenide thin films, J. Appl. Phys., 1993, 74, 6368–6374 CrossRef CAS.
- T. Wakaoka, K. Hirai, K. Murayama, Y. Takano, H. Takagi, S. Furukawa and S. Kitagawa, Confined synthesis of CdSe quantum dots in the pores of metal–organic frameworks, J. Mater. Chem. C, 2014, 2, 7173–7175 RSC.
- F. Pousaneh, O. Edholm and A. Maciołek, Molecular dynamics simulation of a binary mixture near the lower critical point, J. Chem. Phys., 2016, 145, 014501 CrossRef PubMed.
- I. V. Markov, Crystal Growth for Beginners, World Scientific, 2018, p. 632 Search PubMed.
- O. A. Vasilyev, E. Marino, B. B. Kluft, P. Schall and S. Kondrat, Debye vs. Casimir: controlling the structure of charged nanoparticles deposited on a substrate, Nanoscale, 2021, 13, 6475–6488 RSC.
- E. M. Herzig, K. A. White, A. B. Schofield, W. C. K. Poon and P. S. Clegg, Bicontinuous emulsions stabilized solely by colloidal particles, Nat. Mater., 2007, 6, 966 CrossRef CAS PubMed.
- D. Beysens and D. Estève, Adsorption Phenomena at the Surface of Silica Spheres in a Binary Liquid Mixture, Phys. Rev. Lett., 1985, 54, 2123–2126 CrossRef CAS PubMed.
- A. Magazzù, A. Callegari, J. P. Staforelli, A. Gambassi, S. Dietrich and G. Volpe, Controlling the dynamics of colloidal particles by critical Casimir forces, Soft Matter, 2019, 15, 2152–2162 RSC.
- S. Paladugu, A. Callegari, Y. Tuna, L. Barth, S. Dietrich, A. Gambassi and G. Volpe, Nonadditivity of critical Casimir forces, Nat. Commun., 2016, 7, 11403 CrossRef CAS PubMed.
- O. A. Vasilyev, S. Dietrich and S. Kondrat, Nonadditive interactions and phase transitions in strongly confined colloidal systems, Soft Matter, 2018, 14, 586–596 RSC.
- U. Nellen, J. Dietrich, L. Helden, S. Chodankar, K. Nygård, J. F. van der Veen and C. Bechinger, Salt-induced changes of colloidal interactions in critical mixtures, Soft Matter, 2011, 7, 5360 RSC.
- F. Pousaneh and A. Ciach, The origin of the attraction between like charged hydrophobic and hydrophilic walls confining a near-critical binary aqueous mixture with ions, J. Phys.: Condens. Matter, 2011, 23, 412101 CrossRef PubMed.
- M. Bier, A. Gambassi, M. Oettel and S. Dietrich, Electrostatic interactions in critical solvents, EPL, 2011, 95, 60001 CrossRef.
- F. Pousaneh, A. Ciach and A. Maciołek, Effect of ions on confined near-critical binary aqueous mixture, Soft Matter, 2012, 8, 7567 RSC.
- F. Pousaneh, A. Ciach and A. Maciołek, How ions in solution can change the sign of the critical Casimir potential, Soft Matter, 2014, 10, 470–483 RSC.
- A. Gambassi and S. Dietrich, Colloidal Aggregation and Critical Casimir Forces, Phys. Rev. Lett., 2010, 105, 059601 CrossRef PubMed.
- J. Cras, C. Rowe-Taitt, D. Nivens and F. Ligler, Comparison of chemical cleaning methods of glass in preparation for silanization, Biosens. Bioelectron., 1999, 14, 683–688 CrossRef CAS.
- T. F. Mohry, S. Kondrat, A. Maciołek and S. Dietrich, Critical Casimir interactions around the consolute point of a binary solvent, Soft Matter, 2014, 10, 5510–5522 RSC.
- S. Kondrat, O. A. Vasilyev and S. Dietrich, Probing interface localization–delocalization transitions by colloids, J. Phys.: Condens. Matter, 2018, 30, 414002 CrossRef PubMed.
- K. Marolt, M. Zimmermann and R. Roth, Microphase separation in a two-dimensional colloidal system with competing attractive critical Casimir and repulsive magnetic dipole interactions, Phys. Rev. E, 2019, 100, 052602 CrossRef CAS PubMed.
- O. A. Vasilyev, M. Labbé-Laurent, S. Dietrich and S. Kondrat, Bridging transitions and capillary forces for colloids in a slit, J. Chem. Phys., 2020, 153, 014901 CrossRef CAS PubMed.
- N. F. Bafi, P. Nowakowski and S. Dietrich, Effective pair interaction of patchy particles in critical fluids, J. Chem. Phys., 2020, 152, 114902 CrossRef PubMed.
- B. D. Chernomordik, A. R. Marshall, G. F. Pach, J. M. Luther and M. C. Beard, Quantum Dot Solar Cell Fabrication Protocols, Chem. Mater., 2017, 29, 189–198 CrossRef CAS.
- O. A. Vasilyev, Critical Casimir interactions between spherical particles in the presence of bulk ordering fields, Phys. Rev. E, 2014, 90, 012138 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: A detailed description of experimental and modeling procedures. See DOI: 10.1039/d0nh00670j |
| This journal is © The Royal Society of Chemistry 2021 |
