Simulated annealing fitting: a global optimization method for quantitatively analyzing growth kinetics of colloidal Ag nanoparticles†
Siyu
Wu‡
 ,
Qinwei
An‡
and
Yugang
Sun
,
Qinwei
An‡
and
Yugang
Sun
 *
*
Department of Chemistry, Temple University, 1901 North 13th Street, Philadelphia, Pennsylvania 19122, USA. E-mail: ygsun@temple.edu
First published on 30th April 2021
Abstract
The involvement of heterogeneous solid/liquid reactions in growing colloidal nanoparticles makes it challenging to quantitatively understand the fundamental steps that determine nanoparticles' growth kinetics. A global optimization protocol relying on simulated annealing fitting and the LSW growth model is developed to analyze the evolution data of colloidal silver nanoparticles synthesized from a microwave-assisted polyol reduction reaction. Fitting all data points of the entire growth process determines with high fidelity the diffusion coefficient of precursor species and the heterogeneous reduction reaction rate parameters on growing silver nanoparticles, which represent the principal functions to determine the growth kinetics of colloidal nanoparticles. The availability of quantitative results is critical to understanding the fundamentals of heterogeneous solid/liquid reactions, such as identifying reactive species and reaction activation energy barriers.
New conceptsReal-time probing of colloidal nanoparticles' evolution kinetics in liquid solutions represents an emerging research area to understand the fundamental steps determining nanoparticle growth. The heterogeneous solid/liquid interfacial reactions responsible for growing nanoparticles in a closed system usually involve two primary interdependent functions, i.e., diffusion of reactive precursor species and surface reactions of the precursor species on the growing nanoparticles. Many attempts have been made to develop in situ techniques for measuring nanoparticle evolution. It is still challenging to quantitatively determine the intrinsic parameters (i.e., the diffusion coefficient of the precursor and the surface reaction rate constant) of the two intertwined functions. We apply the LSW model to describe nanoparticle growth with an autonomous ordinary differential equation that is challenging to fit to in situ measurements of low/moderate-density data points. A new concept of a global optimization protocol based on simulated annealing fitting is proposed to fit all data points of the entire growth process numerically. The fitting determines diffusion coefficients and surface reaction rate constants with high fidelity. The availability of intrinsic parameters' values offers the unprecedented opportunity to quantitatively understand the heterogeneous solid/liquid interfacial reactions of growing nanoparticles and rationally design the synthesis of colloidal nanoparticles. |
We reported the measurement of growth kinetics of colloidal silver (Ag) nanoparticles in a microwave reactor using in situ high-energy X-ray diffraction (HEXRD), which was published in Nano Letters in 2016.1 The availability of high-quality time-resolved HEXRD patterns offered the promise of quantifying the evolution kinetics of colloidal Ag nanoparticles in the course of reducing silver nitrate (AgNO3) at elevated temperatures. The time-dependent mass evolution of the crystalline Ag nanoparticles exhibited sigmoidal shapes, and we mathematically fitted the data with a sigmoidal function, i.e.,
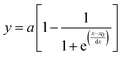 . The data fitting determined the constant parameters of a, x0, and dx, which allowed us to conveniently compare the evolution kinetics under various reaction conditions (e.g., different temperatures and different concentrations of AgNO3). However, the condition-dependent constants derived from the pure mathematical fitting lacked physical meaning to represent the fundamental functions that determine the growth kinetics of colloidal nanoparticles. Professor Özkar and Professor Finke criticized this issue later in a paper published in The Journal of Physical Chemistry C,2 in which they digitized our data and fitted the data with the Finke–Watzky (FW) two-step mechanism proposed by Professor Finke and Professor Watzky back in 1997.3 The FW two-step mechanism consists of slow, continuous nucleation with a reaction rate constant of k1 and autocatalytic surface growth with a reaction rate constant of k2. The mechanism is generally described in the format of serial (homogeneous) reactions as eqn (1):
. The data fitting determined the constant parameters of a, x0, and dx, which allowed us to conveniently compare the evolution kinetics under various reaction conditions (e.g., different temperatures and different concentrations of AgNO3). However, the condition-dependent constants derived from the pure mathematical fitting lacked physical meaning to represent the fundamental functions that determine the growth kinetics of colloidal nanoparticles. Professor Özkar and Professor Finke criticized this issue later in a paper published in The Journal of Physical Chemistry C,2 in which they digitized our data and fitted the data with the Finke–Watzky (FW) two-step mechanism proposed by Professor Finke and Professor Watzky back in 1997.3 The FW two-step mechanism consists of slow, continuous nucleation with a reaction rate constant of k1 and autocatalytic surface growth with a reaction rate constant of k2. The mechanism is generally described in the format of serial (homogeneous) reactions as eqn (1):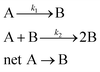 | (1) |
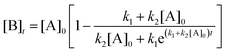 | (2) |
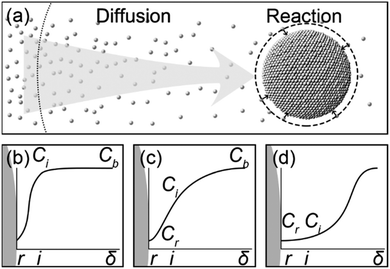
The models reported in the literature (including the FW two-step mechanism) describe the growth of colloidal nanoparticles as autocatalytic surface reactions.2–6 Therefore, we believe that the mathematical equations describing the growth kinetics of colloidal nanoparticles should include the parameter of the surface area (equivalent to r2) of the growing nanoparticles. For example, the model proposed by Lifshitz, Slyozov, and Wagner (LSW model) is well known to describe the growth of colloidal particles after nucleation.5,6 In such a multiple-phase system, growing solid particles dispersed in a liquid solution containing precursor species depends on two consecutive processes, i.e., the diffusion of precursor species to the surface of growing particles and the reaction of precursor species on the particles' surface (Fig. 1a).7,8 When one of the two processes plays the decisive role in the growth kinetics of colloidal nanoparticles, the LSW model can be simplified to an asymptotic format, i.e., either a surface reaction-limited model (Fig. 1b) or a diffusion-limited model (Fig. 1d).6,9 The asymptotic models enable the feasibility to fit the in situ kinetic data of growing colloidal nanoparticles under well-controlled synthesis conditions, leading to the determination of fundamental parameters such as the diffusion coefficient (D) of precursor species in the reaction solution and the reaction rate constant (k) of the precursor species on the growing nanoparticles' surface.10–14 In most cases of colloidal nanoparticle synthesis, neither of the asymptotic models can accurately reflect the growth kinetics since both the diffusion of precursor species and surface reactions contribute comparably to determine the growth kinetics (Fig. 1c).9 The full-version LSW model including the contributions of both diffusion and surface reactions has to be applied to fit the in situ measurement data to simultaneously determine D and k with acceptable fidelity. Because of the complexity of the kinetic equation, accurate determination of D and k from fitting the in situ data is still challenging.
In this Communication, we report the use of simulated annealing (SA) fitting to analyze in situ data throughout the entire growth of colloidal nanoparticles using the full-version LSW model and determine the values of both D and k with high fidelity. We use in situ data of synthesizing Ag nanoparticles in microwave-assisted polyol reduction of AgNO3 (reported in our 2016 Nano Letters paper; ESI,† Section I) as an example to highlight the feasibility and accuracy of the SA fitting. In the synthesis, microwave heating was used to control the temperature of ethylene glycol (EG) solutions. Poly(vinyl pyrrolidone) (PVP) was added to serve as capping ligands to stabilize Ag nanoparticles. Successful determination of the values of fundamental kinetic parameters is promising to understand the thermodynamics and the active precursor species responsible for growing Ag nanoparticles. According to the LSW model shown in Fig. 1a (see the ESI,† Section II), the growth rate of the Ag nanoparticles is described as
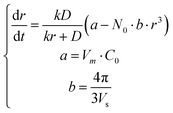 | (3) |
The autonomous ordinary differential equation (eqn (3)) can be solved numerically using the classic fourth-order Runge–Kutta method (RK4)15 to give the nanoparticle growth trajectory r(t) when the values of k and D are available, and an initial condition r(t0) is provided. On the other hand, when the nanoparticle growth trajectory r(t) can be measured from in situ experiments, the values of k and D can be, in principle, determined by fitting the r(t) ∼ t data with eqn (3). In our 2016 paper the nanoparticle growth trajectory can be obtained from the total volume of Ag nanoparticles (Vtot), where 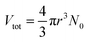 (see the ESI,† Section II, Fig. S2c). The average size of the as-synthesized Ag nanoparticles (rmax) after the complete reduction of AgNO3 was determined using transmission electron microscopy (TEM) imaging. The complete reduction of AgNO3 generated the maximum total volume of Ag nanoparticles (Vmaxtot), which was calculated from the amount of AgNO3 added to the reaction solution. The number of growing Ag nanoparticles (N0) could be calculated accordingly. The values of a and b were defined for a given reaction system. Fitting eqn (3) to the experimental data is reduced to a three-parameter estimation problem about k, D, and r(t0). To avoid the uncertainty of the initial condition r(t0) that is close to zero, we applied the two-way RK4 method in which the initial condition r(t0) was set to the midpoint of the growth curve where the first derivative (i.e., dVtot/dt) reaches the maximum. Since the size at the midpoint r(tmid) of stable growing nanoparticles is a fixed non-zero number in a given synthesis, the actual freedom of the numerical fitting becomes two. We have developed an extreme-condition model to determine k and D using the simplified asymptotic LSW models by focusing on the growth at the very early stage (reaction-limited model) and the very late stage (diffusion-limited model).16 Because of the low density and small variation of experimental data points at the very early and the very late growth stages, the fidelity and accuracy of the fitted (k, D) values may be questionable. However, they can be used as the references as well as the initial guess for SA fitting to fit more experimental data points throughout the entire growth process, leading to improved fitting efficiency and saving computational time.
(see the ESI,† Section II, Fig. S2c). The average size of the as-synthesized Ag nanoparticles (rmax) after the complete reduction of AgNO3 was determined using transmission electron microscopy (TEM) imaging. The complete reduction of AgNO3 generated the maximum total volume of Ag nanoparticles (Vmaxtot), which was calculated from the amount of AgNO3 added to the reaction solution. The number of growing Ag nanoparticles (N0) could be calculated accordingly. The values of a and b were defined for a given reaction system. Fitting eqn (3) to the experimental data is reduced to a three-parameter estimation problem about k, D, and r(t0). To avoid the uncertainty of the initial condition r(t0) that is close to zero, we applied the two-way RK4 method in which the initial condition r(t0) was set to the midpoint of the growth curve where the first derivative (i.e., dVtot/dt) reaches the maximum. Since the size at the midpoint r(tmid) of stable growing nanoparticles is a fixed non-zero number in a given synthesis, the actual freedom of the numerical fitting becomes two. We have developed an extreme-condition model to determine k and D using the simplified asymptotic LSW models by focusing on the growth at the very early stage (reaction-limited model) and the very late stage (diffusion-limited model).16 Because of the low density and small variation of experimental data points at the very early and the very late growth stages, the fidelity and accuracy of the fitted (k, D) values may be questionable. However, they can be used as the references as well as the initial guess for SA fitting to fit more experimental data points throughout the entire growth process, leading to improved fitting efficiency and saving computational time.
Since both k and D influence the growth rate of Ag nanoparticles, many different pairs of (k, D) can generate similar growth rates according to eqn (3) during the focused time periods, which results in a challenge to simultaneously determine the values of k and D with high fidelity from data fitting. We report the development of a global optimization fitting protocol that allows fitting all data points of the entire growth process to minimize the possible errors. Specifically, a SA method17 allows a random search of the mathematically valid (k, D) pairs to determine the physically accurate (k, D) pair through statistical analysis. A C-program based on the SA algorithm is developed to determine the optimum (k, D) pairs that give the least sum of squared residuals (SSR) of Vtot between the theoretical fitting predictions (Vfit) and experimental curve (Vexp) at each data point measured at different time ti (see the ESI,† Section III):
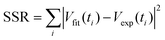 | (4) |
At the beginning of the algorithm, a random (k, D) pair is chosen as the starting point. The program will jump randomly to a new (k, D) pair in a neighboring region and check whether the SSR of the new iteration (n + 1) becomes smaller than the available record to give a better fit to the experimental data. The possibility of acceptance (P) of the new (k, D) pair relies on the Metropolis jumping rule.18 A smaller SSR will be accepted immediately (P = 1), and a larger SSR will be accepted with the condition:
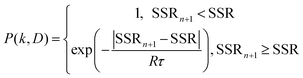 | (5) |
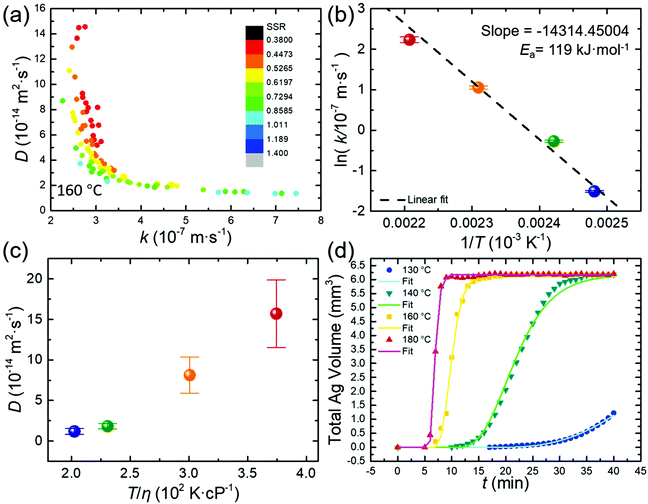
Fig. 2(a) presents the (k, D) results from fitting the experimental data of growing Ag nanoparticles at 160 °C by repeating the SA program for 100 cycles. The (k, D) pair determined with the extreme-condition model was used as the starting point for the SA fitting. The likely optimized (k, D) pairs scatter around one of the branches of the rectangular hyperbola, i.e., H = kD/(kri + D) with both ri and H constants, in the k (horizontal)–D (vertical) plane. The (k, D) pairs with the smallest SSRs (red dots, Fig. 2a) cluster in a confined region, highlighting the feasibility to determine high-fidelity values of k and D. The distribution of k is very narrow (i.e., 2.5–3.1 × 10−7 m s−1) while the values of D scatter in a wider range (i.e., 5–10 × 10−14 m2 s−1), suggesting that k can be more accurately determined than D. Such a difference indicates that the contribution of surface reactions to the growth kinetics of Ag nanoparticles at 160 °C is more determining than the contribution of precursor diffusion. Considering that the SA algorithm suggests the uncertainty of the fitting results, we use the averages of the top 10% results from 100 cycles of SA fitting to improve the accuracy. The statistical accuracy of k evaluated from the clustered (k, D) pairs with the smallest SSRs is higher than that of D, i.e., (2.87 ± 0.052) × 10−7 m s−1 for k with a statistical deviation of 18% versus (8.13 ± 2.24) × 10−14 m2 s−1 for D with a statistical deviation of 28%. It is worth pointing out that the (k, D) pairs with the smallest SSRs derived from the SA fitting cluster at the upper arm of the half hyperbola to highlight the more reaction-limited growth of Ag nanoparticles. Such a conclusion is consistent with krmax/D < 1, which is calculated using the fitted (k, D) values (see the ESI,† Table S2).
The growth kinetics of Ag nanoparticles accelerates significantly with the reaction temperature. SA fitting reveals that increasing temperature leads to the increase of both the diffusion of the Ag(I) precursor and the surface reduction of Ag(I) precursor species on growing Ag nanoparticles. The values of k and D of the syntheses at varying temperatures, e.g., 130 °C, 140 °C, 160 °C, and 180 °C, are presented in Table S2 (see the ESI†). When the temperature increases from 130 °C to 180 °C, k increases by 42.4 times from 0.22 × 10−7 m s−1 to 9.33 × 10−7 m s−1. The logarithm of the temperature-dependent reaction rate constant (i.e., ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k) exhibits a linear relationship with the reciprocal of the thermodynamic temperature (1/T) (Fig. 2b). According to the Arrhenius equation k = Ae−Ea/RT (R and A represent the universal gas constant and the frequency factor), the activation energy (Ea) of reducing the Ag(I) precursor on growing Ag nanoparticles in EG is calculated to be 119.0 kJ mol−1.
k) exhibits a linear relationship with the reciprocal of the thermodynamic temperature (1/T) (Fig. 2b). According to the Arrhenius equation k = Ae−Ea/RT (R and A represent the universal gas constant and the frequency factor), the activation energy (Ea) of reducing the Ag(I) precursor on growing Ag nanoparticles in EG is calculated to be 119.0 kJ mol−1.
The clustering center of the D values increases by 13.2 times from 1.19 × 10−14 m2 s−1 to 1.57 × 10−13 m2 s−1 as the temperature increases from 130 °C to 180 °C (Fig. 2c, Table S2, see the ESI†). According to the Stokes–Einstein equation, 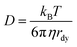 , the diffusion coefficient (D) of a dynamic spherical molecule is proportional to temperature (T) and inversely proportional to the viscosity (η) of the solvent and the dynamic radius of the diffusive molecule (rdy). Fig. 2c shows the dependence of D derived from the SA fitting on T/η, in which the temperature-dependent viscosity of a PVP–EG solution is adjusted according to the reported data.19 The plot is linear despite the first data point being collected at 130 °C, where the growth curve is incomplete and may not represent the true D value. The accuracy of the values of k and D determined from the SA fitting can be evaluated by comparing the theoretical growth kinetics calculated from eqn (3) with the experimental growth kinetics. The good agreement is shown in Fig. 2d, highlighting the high fidelity of the SA fitting in determining k and D.
, the diffusion coefficient (D) of a dynamic spherical molecule is proportional to temperature (T) and inversely proportional to the viscosity (η) of the solvent and the dynamic radius of the diffusive molecule (rdy). Fig. 2c shows the dependence of D derived from the SA fitting on T/η, in which the temperature-dependent viscosity of a PVP–EG solution is adjusted according to the reported data.19 The plot is linear despite the first data point being collected at 130 °C, where the growth curve is incomplete and may not represent the true D value. The accuracy of the values of k and D determined from the SA fitting can be evaluated by comparing the theoretical growth kinetics calculated from eqn (3) with the experimental growth kinetics. The good agreement is shown in Fig. 2d, highlighting the high fidelity of the SA fitting in determining k and D.
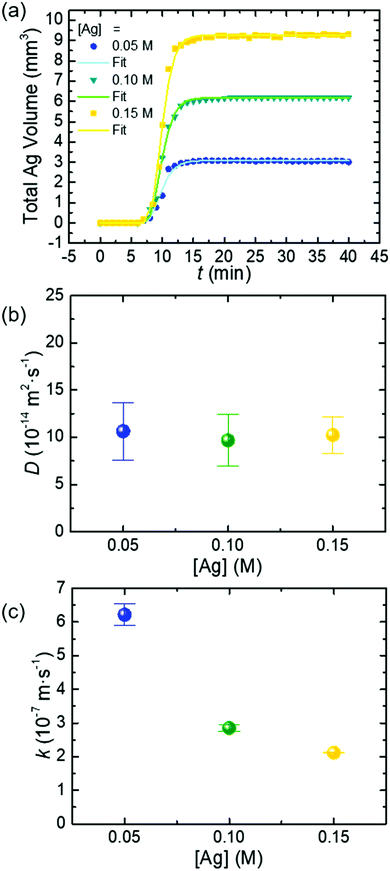
The SA fitting is also applied to analyze the growth kinetics of colloidal Ag nanoparticles synthesized with different concentrations (C0 = 0.05 M, 0.10 M, and 0.15 M) of AgNO3 at a constant temperature of 160 °C and a constant concentration of PVP (0.15 M) (Fig. 3a). The values of k and D determined from these syntheses are presented in Table S3 (see the ESI†). The diffusion coefficient of reactive precursor species, D, remains essentially constant around ∼10 × 10−14 m2 s−1 (Fig. 3b), which is consistent with the Stokes–Einstein equation. In contrast, the fitted surface reaction rate constant, k, decreases from 6.21 × 10−7 m s−1 to 2.12 × 10−7 m s−1 as the concentration of AgNO3 increases from 0.05 M to 0.15 M (Fig. 3c). According to the Arrhenius equation, the surface reaction rate constant should not vary with the precursor concentration at a constant temperature. The deviation of the fitted k and the expected k implies that the actual precursor involved in the surface reduction for growing Ag nanoparticles is not AgNO3 (or Ag+).
We have performed basic density functional theory (DFT) calculations on the interactions between Ag+ ions (or Ag0 atoms) and the vinylpyrrolidone (VP) repeat unit (see the ESI,† Section IV). The calculation results show that the linear coordination of Ag ions to the carbonyl groups of VP units is thermodynamically favorable (see the ESI,† Fig. S7), which is consistent with claims proposed in a previous report.20 The formation of the Ag+–O–VP complex enriches the electron densities on the Ag+ ions due to electron donation of the pyrrolidone ring, benefiting the reduction of Ag(I) to metallic Ag.21 Therefore, the actual precursor species involved in the surface reaction is the Ag+–O–VP complex rather than all Ag(I) species that are used in the SA fitting. According to the LSW model, the consumption rate of Ag(I) species due to the surface reaction on growing Ag nanoparticles is described as (eqn (S2), see the ESI†):
| Jrxn = 4πr2k(Ci − Cr) ≈ 4πr2k·Ci | (6) |
 | (7) |
The left term represents the fraction of Ag+ coordinated with PVP. When the concentration of PVP is constant, a higher concentration of AgNO3 gives a lower 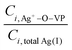 at constant temperature. Since the principle kactual is constant at a given temperature, the value of kfit determined from the SA fitting is smaller at a higher concentration of AgNO3, which is observed in Fig. 3c.
at constant temperature. Since the principle kactual is constant at a given temperature, the value of kfit determined from the SA fitting is smaller at a higher concentration of AgNO3, which is observed in Fig. 3c.
Conclusions
In summary, a global fitting method based on the SA algorithm has been developed to fit the experimentally measured growth kinetics of colloidal nanoparticles using the full-version LSW model. The fitting applies to all data points throughout the entire growth process determined by both the surface reaction and diffusion of precursor species, resulting in the extraction of reliable k and D. According to the principle of the LSW model, the presented fitting protocol readily applies to the synthesis of colloidal nanoparticles, in which continuous growth of colloidal nanoparticles is supported by the surface reaction after burst nucleation. Availability of the fundamental kinetic parameters, k and D, is crucial to understand the insightful details of nanoparticle growth. For example, the precursor species involved in the surface reaction on growing Ag nanoparticles is suggested as the Ag+–O–VP complex. The activation energy of the surface reduction of the Ag+–O–VP complex on growing Ag nanoparticles is 119.0 kJ mol−1. The global fitting and quantitative understanding of the growth kinetics of colloidal nanoparticles provide a promising strategy for understanding the in-depth mechanism of surface reactions on growing nanoparticles.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation under NSF award 1946912. We thank Prof. Spiridoula Matsika for the tutoring and guidance on the DFT calculations.References
- Q. Liu, M. R. Gao, Y. Liu, J. S. Okasinski, Y. Ren and Y. Sun, Nano Lett., 2016, 16, 715–720 CrossRef CAS.
- S. Özkar and R. G. Finke, J. Phys. Chem. C, 2017, 121, 27643–27654 CrossRef.
- M. A. Watzky and R. G. Finke, J. Am. Chem. Soc., 1997, 119, 10382–10400 CrossRef CAS.
- J. D. Martin, Chem. Mater., 2020, 32, 3651–3656 CrossRef CAS.
- I. M. Lifshitz and V. V. Slyozov, J. Phys. Chem. Solids, 1961, 19, 35–50 CrossRef.
- C. Wagner, Ber. Bunsen-Ges. Phys. Chem., 1961, 65, 581–591 CAS.
- T. Sugimoto, Monodispersed Particles, Elsevier, Amsterdam, NL, 2001 Search PubMed.
- N. T. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610–7630 CrossRef CAS PubMed.
- R. Viswanatha, P. K. Santra, C. Dasgupta and D. D. Sarma, Phys. Rev. Lett., 2007, 98, 255501 CrossRef PubMed.
- H. Zheng, R. K. Smith, Y. W. Jun, C. Kisielowski, U. Dahmen and A. P. Alivisatos, Science, 2009, 324, 1309–1312 CrossRef CAS.
- J. M. Yuk, J. Park, P. Ercius, K. Kim, D. J. Hellebusch, M. F. Crommie, J. Y. Lee, A. Zettl and A. P. Alivisatos, Science, 2012, 336, 61–64 CrossRef CAS PubMed.
- J. Lee, J. Yang, S. G. Kwon and T. Hyeon, Nat. Rev. Mater., 2016, 1, 16034 CrossRef CAS.
- H. G. Liao, D. Zherebetskyy, H. Xin, C. Czarnik, P. Ercius, H. Elmlund, M. Pan, L. W. Wang and H. Zheng, Science, 2014, 345, 916–919 CrossRef CAS PubMed.
- Y. Sun, X. Zuo, S. Sankaranarayanan, S. Peng, B. Narayanan and G. Kamath, Science, 2017, 356, 303–307 CrossRef CAS PubMed.
- C. Runge, Math. Ann., 1895, 46, 167–178 CrossRef.
- S. Wu and Y. Sun, Nano Res., 2019, 12, 1339–1345 CrossRef CAS.
- T. J. P. Penna, Comput. Phys., 1995, 9, 341–343 CrossRef.
- B. Gidas, in Topics in Contemporary Probability and Its Applications, ed. J. L. Snell, CRC, Boca Raton, FL, 1995, ch. 7, 159–232 Search PubMed.
- W. Yu, H. Xie, L. Chen and Y. Li, Powder Technol., 2010, 197, 218–221 CrossRef CAS.
- X. Xia, J. Zeng, L. K. Oetjen, Q. Li and Y. Xia, J. Am. Chem. Soc., 2012, 134, 1793–1801 CrossRef CAS PubMed.
- C. Wu, B. P. Mosher, K. Lyons and T. Zeng, J. Nanosci. Nanotechnol., 2010, 10, 2342–2347 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experiment details on the in situ experiment; full-version LSW model describing the growth kinetics of colloidal Ag nanoparticles; data processing and simulated annealing fitting of in situ experimental data; density functional theory calculations on Ag–PVP complexes. See DOI: 10.1039/d1nh00152c |
| ‡ S. W. and Q. A. made equal contributions. |
| This journal is © The Royal Society of Chemistry 2021 |