Mechano-ferroelectric coupling: stabilization enhancement and polarization switching in bent AgBiP₂Se₆ monolayers

Abstract

Two-dimensional (2D) van der Waals (vdW) ferroelectrics are core candidates for the development of next-generation non-volatile storage devices, which rely highly on ferroelectric stability and feasible approaches to manipulate the ferroelectric polarization and domain. Here, based on density functional theory calculations, we demonstrate that the bending deformation can not only manipulate the polarization direction and domain size of AgBiP₂Se₆ monolayers but also significantly improve the ferroelectric stability. The ordered polarization in the bent AgBiP₂Se₆ monolayers can be well maintained at a temperature of 200 K in molecular dynamics simulations; by contrast, it is broken at only 100 K for their freestanding counterparts. These phenomena can be attributed to synergic effects from the asymmetric strain energy induced by a strain gradient and a reduced migration barrier of Ag ions from convex to concave surfaces. More interestingly, a ferroelectric bubble can be induced in the monolayer under biaxial compression strain. This mechano-ferroelectric coupling represents a new mechanism and feasible route towards stabilization and polarization flip in 2D ferroelectrics.

---

New concepts

Two-dimensional (2D) intrinsic ferroelectrics are promising for use in novel non-volatile high-density storage technologies such as ferroelectric random-access memories and non-volatile storage devices, which are, however, hindered by a low ferroelectric stability and the absence of feasible approaches for manipulating the ferroelectric polarization. Technologies that can stabilize and manipulate the ferroelectric polarization states are thus urgently needed. In our work, three novel aspects and new concepts are developed to address the issues as follows. 1. Different from traditional approaches like using the electric field or mechanical compressive strain to tune the ferroelectric polarization, we clarified the underlying relationship between mechanical bending and ferroelectricity in AgBiP₂Se₆ monolayers. Since 2D materials tend to have an out-of-plane ripple under compressive strain, our research provides practical guidance for the experimental demonstration. 2. For the first time, we proposed the new concept of “mechano-ferroelectric coupling” based on our findings of the enhanced ferroelectric stability and ferroelectric manipulations in AgBiP₂Se₆ monolayers (from 100 to 200 K) via the bending strain. 3. We, for the first time, revealed the ferroelectric bubble as a result of biaxial compressive bending in AgBiP₂Se₆ monolayers, which will provide a new pathway toward the novel phenomena of ferroelectric topology.

1. Introduction

Ferroelectricity, caused by the spontaneous ordering of electric dipoles, has attracted extensive research attention in the past few decades due to its promising applications in non-volatile electronic devices and ultra-high-density data storage.^1,2 The bistable and reversible polarization states of ferroelectrics can be used for information storage with the advantages of fast access speed, low power consumption, extended read/write endurance, and non-volatility. For example, ferroelectric random-access memories have been designed based on ultrathin perovskite films, such as BaTiO₃ and PbTiO₃,^3,4 with an ON/OFF ratio of 10²–10³. However, their practical application has been hindered by their severe depolarization and weak ferroelectric stability when the thickness of the non-vdW films reaches a critical value,⁵ due to electron screening and surface reconstructions.^3,6 It is thus urgent to search for new ferroelectric materials with high structural and ferroelectric stabilities or to develop feasible approaches to improve the ferroelectric performance.

The recently emerged 2D van der Waals (vdW) ferroelectric materials are promising candidates for achieving these goals due to their clean surface without any dangling bonds,⁷ and their intrinsic ferroelectricity, which originates from simultaneously broken inversion symmetries that are generally robust against the depolarization field, as seen in α-In₂Se₃^8,9 and ABP₂X₆ (A = Ag, Cu; B = Bi, In; and X = S, Se) monolayers from theoretical predictions^10,11 and experimental demonstrations.¹² Taking advantage of their intrinsic ferroelectric order and unique polarization reorietantions,¹³ ferroelectric semiconducting field effect transistors have been built for non-volatile data storage, where the conducting channel can be switched on/off upon ferroelectric switching.^14,15 The atomic thickness of 2D ferroelectric materials not only satisfactorily meets the requirements of ultra-high-density storage for next-generation devices, but also introduces the era of ferroelectric nanoelectronics. Due to the different electrostatic potential and surface chemical activity upon polarization flipping, 2D ferroelectrics have also been used for chemical reactions and physical adsorption in some cases, such as controllable photocatalytic water splitting,^16–18 gas sensing,¹⁹ H₂ evolution²⁰ as well as magnetoelectric coupling.²¹ However, their promising applications rely highly on two prerequisites, namely the robust ferroelectric stability and effective polarization manipulation, which must not be significantly affected by external fluctuations. Unfortunately, these two prerequisites, which need to be urgently solved, are not always met in 2D ferroelectrics, although they have been experimentally synthesized/demonstrated. For example, the ground states of 2D ferroelectric CuInP₂S₆ layers and the family of ferroelectrics ABP₂X₆ (A = Cu, Ag; B = In, Bi, and X = S, Se) are antiferroelectric (AFE),^11,22 whose overall polarization is cancelled out by the off-centring anti-parallel displacements of the Cu⁺ (A⁺) and In³⁺ (B³⁺) ions. Although the ferroelectric AgBiP₂Se₆ bulk was synthesized experimentally in 2005,²³ its ferroelectricity at the atomic-layer thickness has rarely been detected due to the weak polarization (∼0.2 μC cm⁻¹) and low energy barrier (6 meV)¹⁰ of the polarization flip. Recently, it has been proposed that compressive strain can induce the transition from antiferroelectricity to ferroelectricity in the CuInP₂S₆ monolayer,²² effectively tuning the electronic properties of 2D nanomaterials^24,25 and increasing the energy barrier of the polarization switching in AgBiP₂Se₆;¹⁰ however, the feasibility of this is questionable under practical conditions since 2D materials tend to crumple naturally under compression, which can lower the strain energy and stabilize the structure according to the Mermin–Wagner theorem.^26–31

In this paper, for the first time, we reveal the intriguing phenomena of bending-induced polarization manipulation and ferroelectric-stabilization enhancement in AgBiP₂Se₆ monolayers using density functional theory (DFT) simulations. Due to the synergic effects from the bending-induced strain gradient, Ag⁺ ions prefer to diffuse to the stretched sides because of the lower strain energy and decreased diffusion barrier, leading to polarization upwards (downward) at the convex (concave) bending area. The working mechanism is explicitly confirmed in uniaxial compression-induced bending monolayers from structural relaxation and electron distribution. The enhanced ferroelectric stability is supported by ab initio molecular dynamics simulations, where the ferroelectric domains of the 8% bent AgBiP₂Se₆ monolayers can be well preserved at 200 K, which is a two-fold increase compared with that of the free-standing counterparts. When the biaxial strain is applied, novel ferroelectric bubbles can be induced, where the concave (convex) area has the polarization pointing downwards (upwards). This bending-induced ferroelectric stabilization and polarization manipulation open a new and feasible route towards stabilizing and reversing the ferroelectricity in 2D ferroelectrics, which will lay a solid foundation for its future applications in non-volatile storage devices.

2. Computational methods and models

All the DFT calculations were performed using the PAW approach and the Vienna ab initio simulation package (VASP)^32,33 code with generalized gradient approximation (GGA) in the form of the Perdew–Burke–Ernzerhof (PBE)³⁴ function. The energy cut-off of the plane wave was set to 400 eV. Gaussian smearing with a smearing width of 0.1 meV was used in the Brillouin zone integration. The structures were relaxed until the energy differences are converged within 10⁻⁵ eV with a force convergence threshold of 10⁻³ eV Å⁻¹ for all the calculations. The Brillouin zone was represented by a gamma k-point mesh of 1 × 5 × 1 for all tube, ribbon and 2D structures. The energy barriers between the FE phases were calculated using the climbing-image nudged elastic band (CI-NEB) method.³⁵ A vacuum layer of at least 20 Å was included in the non-periodic orientations. Four non-zero second-order elastic constants were calculated in the 2D system, i.e., C₁₁, C₁₂, C₂₂ and C₆₆, which satisfied the rules of C₁₁ = C₁₂ and C₆₆ = (C₁₁ – C₁₂)/2. According to the relationship between the in-plane stiffness Y and the elastic constant of the hexagonal 2D system,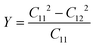 , the stiffness Y could be obtained.

3. Results and discussion

Mechanism of ferroelectric switching in AgBiP₂Se₆

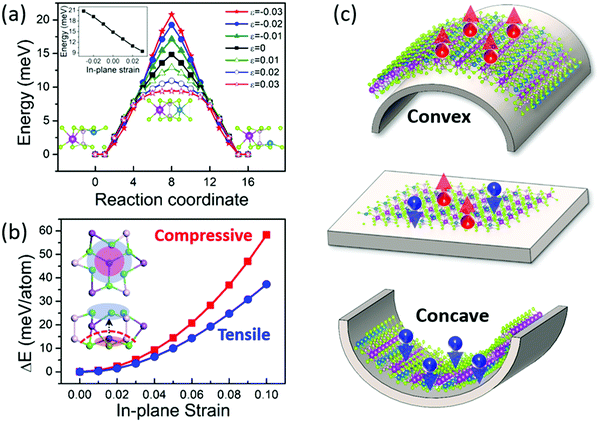
The ferroelectric family of ABP₂X₆ (A = Cu, Ag; B = In, Bi; and X = S, Se) shares the same mechanism of intrinsic ferroelectricity, namely the offset/displacement of the A⁺ ions from the centre positions, leading to an asymmetric electron distribution and spontaneous polarization. Therefore, the ABP₂X₆ monolayers are in the paraelectric phase when the A⁺ ions are located at the symmetric middle positions, and in the ferroelectric phase when they are shifted to bottom or top surfaces. Ferroelectric switching can be achieved by the shifts of the off-centred A⁺ ions to the opposite directions along the out-of-plane direction, see the insets of Fig. 1a. Therefore, the relative positions of the Ag⁺ ions in AgBiP₂Se₆ monolayers along the out-of-plane direction can be approximately regarded as the index of the polarization direction; ferroelectric switching can be presented with the position shift from the top to the bottom surfaces. For example, the polarization is pointing upwards (P↑) when the Ag⁺ ions are located on the top surface, but downwards (P↓) when the Ag⁺ ions are located on the bottom surface. The mechanism is crucial for the understanding of bending-induced polarization manipulation and enhanced stability.

Fig. 1 (a) Energy pathways of the P↑–PE–P↓ transition in AgBiP₂Se₆ monolayers with various strains from −3% to +3%. Inset: the energy barrier as a function of the in-plane uniaxial strain for the AgBiP₂Se₆ monolayer unit cell. (b) Strain energies (ΔE) under the external compressive and tensile strains. The inset illustrates the mechanism of the displacement of the Ag⁺ ion when it is under a bending deformation; blue (red) circle indicates the area with the tensile (compressive) deformation due to the strain gradient from the bending deformation of the AgBiP₂Se₆ monolayer. (c) Schematic diagram of polarization regulation in the AgBiP₂Se₆ monolayer under convex and concave bending deformations. The red and blue arrows represent the polarization directions.

Barriers of FE switching and the effects of uniaxial strain

As a benchmark, we first calculate the energy barrier of polarization reversal (namely, the Ag⁺ ion moving from the top to the bottom surfaces) using the NEB method (see Fig. 1a). The diffusion barrier of 14 meV per unit cell in the AgBiP₂Se₆ monolayer is obtained, which is slightly larger than but qualitatively consistent with a previous report.¹⁰ The small diffusion barrier renders the polarization flip easy, but this is also the main reason for the ferroelectric instability in AgBiP₂Se₆ monolayers. From ab initio molecular dynamics (AIMD) simulations, the ordered ferroelectric phases can be broken under a 100 K environment for 5 ps (see the following discussion) since the estimated thermal energy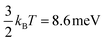 is comparable with the energy barrier of FE switching. When the uniaxial strain (−3% to +3%) is applied, the flip barriers can be effectively decreased (increased) by the stretched (compressed) deformation, which is also consistent with the previous report.¹⁰ It is thus reasonable to conclude that Ag⁺ ions will be easier (more difficult) to move upwards or downwards in ferroelectric AgBiP₂Se₆ monolayers under tensile (compressive) strain. In addition, it is worth pointing out that the strain energies of ferroelectric AgBiP₂Se₆ monolayers have asymmetric responses to tensile and compressive strains, as shown in Fig. 1(b): the strain energy clearly rises faster under a compressive deformation than under a tensile deformation, implying that the Ag⁺ ions prefer to locate at the tensile area due to the lower strain energy if both the tensile and compression strains coexist (see the insets of Fig. 1b). Based on the findings in uniaxially strained ferroelectric AgBiP₂Se₆ monolayers, we can hypothesize that the Ag⁺ ions can move upwards spontaneously to the tensile side due to the synergetic effects of the decreased diffusion barrier and lower strain energies when it is convexly bent but move oppositely when concavely bent, as shown in Fig. 1c. The polarization, determined by the relative position of Ag⁺ ions as discussed above, is therefore reversible by the convex–concave bending deformation. The back-migration of Ag⁺ ions will be remarkably prevented due to the larger energy barrier and higher strain energies at the compressed strain area, as shown in Fig. 1a and b, and, therefore, the ferroelectric stability is enhanced.

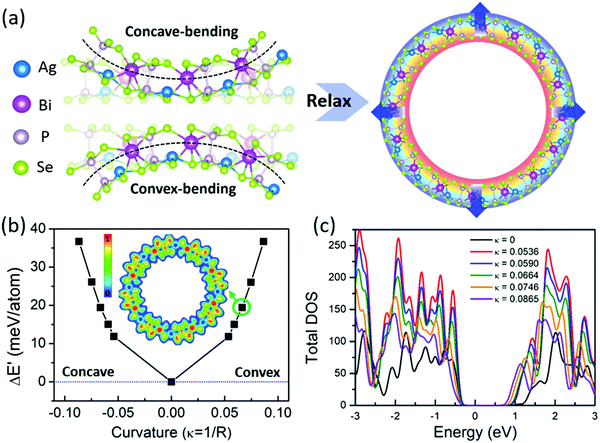
Bending–polarization coupling in AgBiP₂Se₆ nanotubes

To confirm the hypothesis and provide an intuitive understanding of the effects of the bending deformation on the polarization directions and stabilities, we start the discussion using AgBiP₂Se₆ nanotubes due to their intrinsic pure bending deformations and the absence of dangling bonds. The calculated in-plane stiffness Y of the AgBiP₂Se₆ monolayer is 21.51 N m⁻¹ based on the independent elastic constants C₁₁ and C₁₂ (30.87 and 16.99 N m⁻¹, respectively, which show good consistency with the previous results (31.76 and 16.36 N m⁻¹)³⁶). The value of Y is much smaller than that of graphene (356.9 N m⁻¹), h-BN (267 N m⁻¹) or MoS₂ (123 N m⁻¹),³⁷ indicating that the AgBiP₂Se₆ monolayer is softer and much easier to bend and roll into a tube. Structural models of the nanotubes with different radii (9.8–20.44 Å) are created to simulate the bending deformation, which can be defined with the curvature κ = 1/R (R is the bending radius). Similar to carbon nanotubes, we roll up the ferroelectric layers with Ag⁺ ions locating at the bottom surface (see blue balls in Fig. 2(a)) to build the AgBiP₂Se₆ nanotubes. For either of the convex- or concave-bending, the bending energy (defined as the energy difference between the nanotube and the monolayer with the same number of atoms) is smaller than 40 meV per atom and increases with the bending curvature. Interestingly, regardless of the convex or concave bending, the Ag⁺ ions spontaneously move to the outer surface of the tubes after the structural relaxations for all the models considered in the present work. For example, the positions of the Ag⁺ ions remain unchanged for the nanotubes with negative curvatures (κ = −0.1 to 0), where the Ag⁺ ions initially stay on the outside of the tubes. By contrast, the Ag⁺ ions, which are originally located at the inside of the tube, spontaneously move to the outside after the structural relaxation for the positive curvatures (κ = 0 to 0.1). This phenomenon can be easily understood using the developed theory from uniaxial strained AgBiP₂Se₆ monolayers as shown in Fig. 1. Due to the strain gradient as a result of the bending deformation, the strain energy is more quickly increased for the convex bent layer with the Ag⁺ ions located in the compressive area, which needs to be lowered via the diffusion of Ag⁺ ions into the tensile area (outside of the tube wall), as shown in Fig. 1c; meanwhile, the increased (decreased) energy barrier of the Ag⁺ ion diffusion under compressive (tensile) strain further facilitates the displacement of Ag⁺ ions from the inside to outside surfaces. Due to the structural symmetry of the nanotubes, there is no overall polarization; however, the ordered polarization can be reflected by the bonding character and electron redistribution. We plot the electron localization function (ELF) map for the AgBiP₂Se₆ nanotube with κ = 0.066, as shown in the inset of Fig. 2(b). In general, high ELF values (∼1, red regions) imply a high degree of electron localization and accumulation, while the values near 0 (blue regions) denote electron depletion and a very low charge density. For the AgBiP₂Se₆ nanotube with κ = 0.066, localized electrons are widely distributed in the outside area of the tube, implying a strong charge accumulation. By contrast, the electron deficiency can be seen on the inside of the tube. The different electron distribution indicates the presence of ordered polarization. Due to the larger diffusion barriers under compressive strain, the Ag⁺ ions are prevented from moving back inside, thus increasing the ferroelectric stability. A similar conclusion can be obtained in bent AgBiP₂Se₆ nanoribbons, where a critical bending curvature (0.02) can be obtained for FE switching (see Fig. S1 (ESI†)) and in bent FE In₂Se₃ monolayers (see Fig. S2 in the ESI.†) For their practical application in electronics, it is critical to keep the semiconductive state of the FE materials so as to avoid the depolarization. Compared with the 2D monolayer without any bending (Fig. 2c), both the conduction band minimum and the valence band maximum are shifted to higher energy levels by the bending deformation. The band gap values are thus decreased due to the larger shifts of the VBM, but the semiconductive properties are well reserved in ABP₂X₆ tubes with various bending curvatures.

Fig. 2 (a) Schematic of nanotubes with convex- and concave-bending in the AgBiP₂Se₆ monolayer. The blue, purple, pink and green balls represent the Ag, Bi, P and Se atoms, respectively. After relaxation for both convex- and concave-bending tubes, the direction of ferroelectric polarization points outwards. The blue and red colours indicate the tensile and compressive areas, respectively. The blue arrows point in the direction of the ferroelectric polarization. (b) Energy differences (ΔE′) between nanotubes with various curvatures and periodic flat AgBiP₂Se₆ monolayers. The inset is the ELF map sliced along the a–c plane of the nanotube of κ = 0.066 pointed to by the green circle. The colours blue (0) and red (1) indicate electron depletion and accumulation, respectively. (c) DOS of AgBiP₂Se₆ flat monolayer (κ = 0) and nanotubes with various curvatures.

Manipulation of the polarization domain and ferroelectric stability in bent AgBiP₂Se₆ monolayers

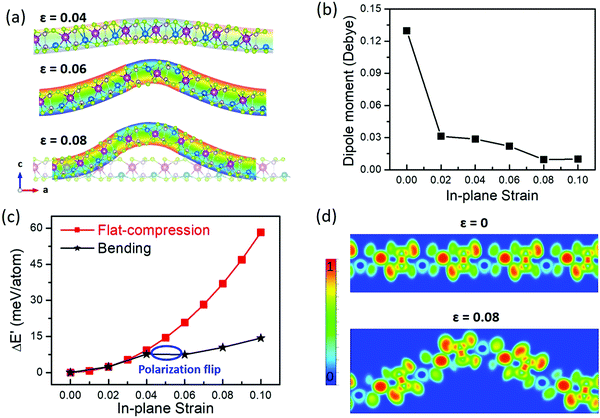
Like graphene and MoS₂ layers, the complex coexistence of convex and concave bending can be commonly seen when the ferroelectric layers are placed on rough substrates or under external local disturbance. To simulate the complicated deformation and investigate the influence on the ferroelectric properties, bent 2D AgBiP₂Se₆ monolayers with Ag ions initially locating at the bottom surface (namely, P↓-AgBiP₂Se₆) are studied. Due to the periodic requirement, the bending deformation is simulated with a cosine or a sine shape. The uniaxial strain is applied along the a direction by compressing the corresponding lattice constant by the amount of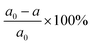 , where a₀ and a are the lattice constants of the free and strained states, and an initial small out-of-plane ripple is preset for the compressed models. After full structural relaxation, it is found that when the bending strain is less than 0.04, the Ag⁺ ions keep locating at the bottom surface although the part of them are clearly shifted upwards compared with the freestanding ferroelectric monolayer (Fig. 3a). When the compressive strain reaches 0.06, a quarter of the Ag⁺ ions locating at the wave crest move to the top surface, while the positions of those at the wave trough stay at the bottom, leading to the ferroelectric domain with the coexistence of polarization upwards and downwards which are located in the areas of the concave- and convex-bending deformation, respectively. The electron localization in the ELF maps (Fig. 3d) for the bent 2D AgBiP₂Se₆ monolayers confirms the FE switch. As a result, the overall dipole moment along the out-of-plane direction decreases with the increasing compression strain, as shown in Fig. 3b since part of the upwards dipole is cancelled out by the reversed polarization at the concave bending area. The spatial distribution of the ferroelectric domain perfectly matches up with that of the strain gradient – see the bending structure at a strain of 0.06 – indicating the internal correlations between the bending deformation and the polarization reversal. As a result of the polarization reversal, when the strain is larger than 0.04, the strain energy increment becomes flat compared with the corresponding compressed structure without bending (Fig. 3c) since part of energy is lowered by the diffusion of Ag⁺ from the compressive to the tensile side.

Fig. 3 (a) Stable (after relaxation) 8-unit cells of AgBiP₂Se₆ with convex compressive strains of 0.04, 0.06 and 0.08. The blue and red areas indicate tensile and compressive areas, respectively. (b) Change in dipole moment along the out-of-plane direction with compressive strain. (c) Energy difference (ΔE′) between bent and periodic flat 2D AgBiP₂Se₆ monolayers as a function of in-plane compressive strain (black curve) and the strain energy (ΔE′ has the same meaning as the previous ΔE) under an external compressive strain (red curve). (d) ELF maps for the AgBiP₂Se₆ monolayer with a compressive strain of 0 and 0.08, respectively.

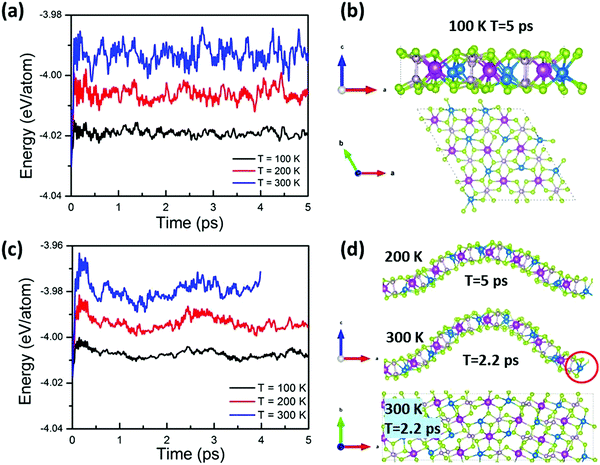
In addition to the ferroelectric switching and domain, bending can also stabilize the ferroelectric states. As obtained from NEB calculations (Fig. 1), the energy barrier of the polarization flip is only 14 meV, and the ferroelectric phase is easily destroyed by external thermal fluctuations, leading to ferroelectric instability (see Fig. 4a). The ordered polarization of freestanding ferroelectric AgBiP₂Se₆ is broken even when the environmental temperature is as low as 100 K. By contrast, the ferroelectric stability in bent AgBiP₂Se₆ monolayers can be significantly improved due to the asymmetric energy changes induced by the strain gradient (Fig. 1b) and the larger energy barrier of Ag⁺ diffusion from tensile to compressive surfaces. Taking the 8% bent AgBiP₂Se₆ monolayer as an example, we performed AIMD simulations under 100, 200 and 300 K for 5 ps. It is found that the Ag⁺ ions stay on the top (bottom) surface at the convex (concave) bending area at 100 K and 200 K environments (see Fig. 4b and top of 4d), indicating that the stability of the ferroelectric domains is remarkably enhanced, which can remain stable at 200 K. The slightly larger energy fluctuations (see Fig. 4a and c) in the bent monolayer can be attributed to the fact that the atoms/bonding at the convex (concave) area are under tensile (compressive) strain after bending deformation, which are in higher energy states (see Fig. 3c) and therefore more sensitive to the thermal disturbance. However, the ordered polarization structure is broken at a temperature of 300 K, as seen from the randomly distributed Ag⁺ ions after 2.2 ps simulations. It can be seen that the tuned ferroelectric polarization is the result of a competition effect between the temperature and the bending load, as clearly demonstrated by the AIMD results in Fig. 4 and the energy variation in Fig. 3. At the lower temperatures (such as 100 and 200 K), the ferroelectric polarization is dominated by the bending deformation. However, at the higher temperature, the thermal fluctuation-induced distortion will dominate, leading to a clear structural distortion at 300 K, as shown in Fig. 4d.

Fig. 4 Energies (eV per atom) of flat (a) and bent (c) AgBiP₂Se₆ monolayers from AIMD simulations. The corresponding structures at different temperatures and strain deformations are shown in (b and d).

Ferroelectric bubble in the biaxially strained AgBiP₂Se₆

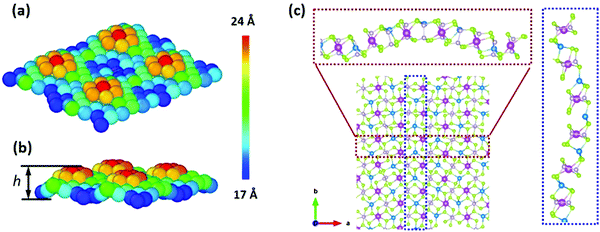
Due to local heating or deformation, nanobubbles are also commonly seen in 2D materials,³⁸ which can change the thermal conductivity and chemical reactivity. Ferroelectric skyrmions, or polarization vortices, have recently been found in ferroelectric PbZr_0.2Ti_0.8O₃ (PZT) sandwich heterostructures.³⁹ Here, we apply the biaxial compression strain to the AgBiP₂Se₆ monolayer to examine the possible ferroelectric topological structures. The 6 × 6 AgBiP₂Se₆ monolayer supercell (containing 360 atoms) with less than 8% biaxial strain is used as the model to investigate the effects on the ferroelectric domain (see Fig. 5). After full structural relaxation, a bubble forms where the middle area has a convex ripple while the surrounding area has a concave ripple, and the bubble height (measured from the Ag⁺ ions on the top to the bottom surface) is around 9.91 Å (see Fig. 5a and b). From the section diagram in Fig. 5c, it is clear that the Ag⁺ ions locate on the top (bottom) surface of the convex (concave) area, leading to the local polarization pointing upwards (downwards) at the bubble crest (trough). The polarization will gradually switch from upwards to downwards from the bubble crest to the trough, leading to the ferroelectric skyrmions or polarization vortices of the ferroelectric PZT structure.³⁹ The ferroelectric bubble is also observed in different sized models, and the height (h) is sensitive to the cell size, as seen in Fig. S3 in the ESI.† Therefore, it is worth pointing out that similar experimental findings have been found in the strained ferroelectric polymer, poly(vinylidene fluoride-ran-trifluoroethylene) [P(VDF-TrFE)].⁴⁰

Fig. 5 Ferroelectric bubble in the biaxially rippled AgBiP₂Se₆ monolayer. (a and b) Spatial elevation distribution of Ag⁺ ions; (c) horizontal and vertical section figures of the nanobubble of the AgBiP₂Se₆ monolayer.

4. Conclusions

In summary, FE switching and stabilization in bent AgBiP₂Se₆ monolayers has been investigated based on DFT calculations. It is found that the polarization of AgBiP₂Se₆ monolayers can be switched and stabilized by convex- and concave-bending deformations. These bending-stabilized polarization states and ferroelectric switching are mainly contributed by the synergic effects from the asymmetric energy barrier of Ag⁺ ion displacement and the strain energy differences from a strain gradient, where the Ag⁺ ions are pushed to the stretched region. Under biaxial strain, a ferroelectric bubble can be induced with the polarization vortex. The present results offer a new and feasible route towards stabilizing and reversing the ferroelectricity in 2D ferroelectrics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the granting of high-performance computer time from the computing facility at the Queensland University of Technology, the Pawsey Supercomputing Centre and the Australian National Computational Infrastructure (NCI). Y. G. gratefully acknowledges financial support by the ARC Discovery Project (DP200102546).

References

1. D. Lee, H. Lu, Y. Gu, S.-Y. Choi, S.-D. Li, S. Ryu, T. R. Paudel, K. Song, E. Mikheev, S. Lee, S. Stemmer, D. A. Tenne, S. H. Oh, E. Y. Tsymbal, X. Wu, L.-Q. Chen, A. Gruverman and C. B. Eom, Emergence of room-temperature ferroelectricity at reduced dimensions, Science, 2015, 349, 6254.
2. X. Tang and L. Kou, Two-dimensional ferroics and multiferroics: platforms for new physics and applications, J. Phys. Chem. Lett., 2019, 10(21), 6634–6649.
3. C. H. Ahn, K. M. Rabe and J.-M. Triscone, Ferroelectricity at the nanoscale: local polarization in oxide thin films and heterostructures, Science, 2004, 303, 488–491.
4. V. Garcia and M. Bibes, Ferroelectric tunnel junctions for information storage and processing, Nat. Commun., 2014, 5, 4289.
5. M. Trieloff, E. K. Jessberger, I. Herrwerth, J. Hopp, C. Fieni, M. Ghelis, M. Bourot-Denise and P. Pellas, Structure and thermal history of the H-chondrite parent asteroid revealed by thermochronometry, Nature, 2003, 422(6931), 502–506.
6. D. D. Fong, S. K. Streiffer, J. A. Eastman, O. Auciello, P. H. Fuoss and C. Thompson, Ferroelectricity in ultrathin perovskite films, Science, 2004, 304, 1650–1653.
7. Z. Guan, H. Hu, X. Shen, P. Xiang, N. Zhong, J. Chu and C. Duan, Recent progress in two-dimensional ferroelectric materials, Adv. Electron. Mater., 2019, 6, 1.
8. W. Ding, J. Zhu, Z. Wang, Y. Gao, D. Xiao, Y. Gu, Z. Zhang and W. Zhu, Prediction of intrinsic two-dimensional ferroelectrics in In₂Se₃ and other III₂–VI₃ van der Waals materials, Nat. Commun., 2017, 8, 14956.
9. Y. Zhou, D. Wu, Y. Zhu, Y. Cho, Q. He, X. Yang, K. Herrera, Z. Chu, Y. Han, M. C. Downer, H. Peng and K. Lai, Out-of-plane piezoelectricity and ferroelectricity in layered alpha-In₂Se₃ nanoflakes, Nano Lett., 2017, 17(9), 5508–5513.
10. B. Xu, H. Xiang, Y. Xia, K. Jiang, X. Wan, J. He, J. Yin and Z. Liu, Monolayer AgBiP₂Se₆: an atomically thin ferroelectric semiconductor with out-plane polarization, Nanoscale, 2017, 9(24), 8427–8434.
11. W. Song, R. Fei and L. Yang, Off-plane polarization ordering in metal chalcogen diphosphates from bulk to monolayer, Phys. Rev. B, 2017, 96, 23.
12. F. Liu, L. You, K. L. Seyler, X. Li, P. Yu, J. Lin, X. Wang, J. Zhou, H. Wang, H. He, S. T. Pantelides, W. Zhou, P. Sharma, X. Xu, P. M. Ajayan, J. Wang and Z. Liu, Room-temperature ferroelectricity in CuInP₂S₆ ultrathin flakes, Nat. Commun., 2016, 7, 12357.
13. J. Shang, X. Tang and L. Kou, Two dimensional ferroelectrics: candidate for controllable physical and chemical applications, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1496.
14. X. Lin, W. Yang, K. L. Wang and W. Zhao, Two-dimensional spintronics for low-power electronics, Nat. Electron., 2019, 2(7), 274–283.
15. M. Dai, K. Li, F. Wang, Y. Hu, J. Zhang, T. Zhai, B. Yang, Y. Fu, W. Cao, D. Jia, Y. Zhou and P. Hu, Intrinsic dipole coupling in 2D van der Waals ferroelectrics for gate-controlled switchable rectifier, Adv. Electron. Mater., 2019, 6, 2.
16. L. Ju, J. Shang, X. Tang and L. Kou, Tunable photocatalytic water splitting by the ferroelectric switch in a 2D AgBiP₂Se₆ monolayer, J. Am. Chem. Soc., 2020, 142(3), 1492–1500.
17. C. F. Fu, J. Sun, Q. Luo, X. Li, W. Hu and J. Yang, Intrinsic electric fields in two-dimensional materials boost the solar-to-hydrogen efficiency for photocatalytic water splitting, Nano Lett., 2018, 18(10), 6312–6317.
18. Y. Tian, L. Wei, Q. Zhang, H. Huang, Y. Zhang, H. Zhou, F. Ma, L. Gu, S. Meng, L. Q. Chen, C. W. Nan and J. Zhang, Water printing of ferroelectric polarization, Nat. Commun., 2018, 9(1), 3809.
19. X. Tang, J. Shang, Y. Gu, A. Du and L. Kou, Reversible gas capture using a ferroelectric switch and 2D molecule multiferroics on the In₂Se₃ monolayer, J. Mater. Chem. A, 2020, 8(15), 7331–7338.
20. B. Lin, A. Chaturvedi, J. Di, L. You, C. Lai, R. Duan, J. Zhou, B. Xu, Z. Chen, P. Song, J. Peng, B. Ma, H. Liu, P. Meng, G. Yang, H. Zhang, Z. Liu and F. Liu, Ferroelectric-field accelerated charge transfer in 2D CuInP₂S₆ heterostructure for enhanced photocatalytic H₂ evolution, Nano Energy, 2020, 76, 104972.
21. X. Tang, J. Shang, Y. Ma, Y. Gu, C. Chen and L. Kou, Tuning magnetism of metal porphyrazine molecules by a ferroelectric In₂Se₃ monolayer, ACS Appl. Mater. Interfaces, 2020, 12(35), 39561–39566.
22. Z.-Z. Sun, W. Xun, L. Jiang, J.-L. Zhong and Y.-Z. Wu, Strain engineering to facilitate the occurrence of 2D ferroelectricity in CuInP₂S₆ monolayer, J. Phys. D: Appl. Phys., 2019, 52, 46.
23. M. A. Gave, D. Bilc, S. D. Mahanti, J. D. Breshears and M. G. Kanatzidis, On the lamellar compounds CuBiP₂Se₆, AgBiP₂Se₆ and AgBiP₂S₆ antiferroelectric phase transitions due to cooperative Cu⁺ and Bi³⁺ ion motion, Inorg. Chem., 2005, 44, 5293–5303.
24. A. J. Lu, R. Q. Zhang and S. T. Lee, Stress-induced band gap tuning in 〈112〉 silicon nanowires, Appl. Phys. Lett., 2007, 91, 26.
25. C. Zhang, A. De Sarkar and R.-Q. Zhang, Strain induced band dispersion engineering in Si nanosheets, J. Phys. Chem. C, 2011, 115(48), 23682–23687.
26. L. Yu, A. Ruzsinszky and J. P. Perdew, Bending two-dimensional materials to control charge localization and Fermi-level shift, Nano Lett., 2016, 16(4), 2444–2449.
27. M. E. P. Tweedie, Y. Sheng, S. G. Sarwat, W. Xu, H. Bhaskaran and J. H. Warner, Inhomogeneous strain release during bending of WS₂ on flexible substrates, ACS Appl. Mater. Interfaces, 2018, 10(45), 39177–39186.
28. Y. Guo, J. Qiu and W. Guo, Tunable bending stiffness of MoSe₂/WSe₂ heterobilayers from flexural wrinkling, Nanotechnology, 2017, 28(19), 195701.
29. T. Shimada, X. Wang, Y. Kondo and T. Kitamura, Absence of ferroelectric critical size in ultrathin PbTiO₃ nanotubes: a density-functional theory study, Phys. Rev. Lett., 2012, 108(6), 067601.
30. J. Wang, T. Xu, T. Shimada, X. Wang, T.-Y. Zhang and T. Kitamura, Chiral selectivity of improper ferroelectricity in single-wall PbTiO₃ nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 14.
31. H. F. Li, G. H. Zhang, Y. Zheng, B. Wang and W. J. Chen, Ab initio study on mechanical-bending-induced ferroelectric phase transition in ultrathin perovskite nanobelts, Acta Mater., 2014, 76, 472–481.
32. G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
33. G. Kresse, Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16.
34. P. P. John, B. Kieron and E. Matthias, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
35. H. Graeme, P. U. Blas and J. Hannes, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901.
36. S. Jiang, H. Yin, J. Li, L. Liu, X. Shi, Y. Yan, C. Liu, G.-P. Zheng and P.-F. Liu, Multidirectional intrinsic piezoelectricity of 2D metal chalcogen–diphosphate ABP2X6 monolayers, Phys. Status Solidi RRL, 2020, 14, 10.
37. Q. Yue, J. Kang, Z. Shao, X. Zhang, S. Chang, G. Wang, S. Qin and J. Li, Mechanical and electronic properties of monolayer MoS₂ under elastic strain, Phys. Lett. A, 2012, 376(12–13), 1166–1170.
38. Y. Huang, X. Wang, X. Zhang, X. Chen, B. Li, B. Wang, M. Huang, C. Zhu, X. Zhang, W. S. Bacsa, F. Ding and R. S. Ruoff, Raman spectral band oscillations in large graphene bubbles, Phys. Rev. Lett., 2018, 120(18), 186104.
39. Q. Zhang, S. Prokhorenko, Y. Nahas, L. Xie, L. Bellaiche, A. Gruverman and N. Valanoor, Deterministic switching of ferroelectric bubble nanodomains, Adv. Funct. Mater., 2019, 29, 28.
40. M. Guo, C. Guo, J. Han, S. Chen, S. He, T. Tang, Q. Li, J. Strzalka, J. Ma and D. Yi, et al., Toroidal polar topology in strained ferroelectric polymer, Science, 2021, 371(6533), 1050–1056.

---

Footnote

† Electronic supplementary information (ESI) available: The phase transition from P↓ to P↑ in bent AgBiP₂Se₆ ribbon. The energy difference (ΔE′) between bent and flat AgBiP₂Se₆ ribbons. The dipole moment for the bent AgBiP₂Se₆ ribbons with various bending curvatures. Structures with and without bending in the In₂Se₃ monolayer. Ferroelectric bubble with heights (h) in biaxially rippled AgBiP₂Se₆ monolayers. See DOI: 10.1039/d1nh00402f

---