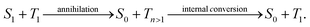Open Access Article
Open Access ArticleAll-optical manipulation of singlet exciton transport in individual supramolecular nanostructures by triplet gating†
Bernd
Wittmann
a,
Till
Biskup‡
 b,
Klaus
Kreger
b,
Klaus
Kreger
 cd,
Jürgen
Köhler
cd,
Jürgen
Köhler
 ade,
Hans-Werner
Schmidt
ade,
Hans-Werner
Schmidt
 cd and
Richard
Hildner
cd and
Richard
Hildner
 *af
*af
aSpectroscopy of Soft Matter, University of Bayreuth, Universitätsstraße 30, 95447 Bayreuth, Germany
bInstitute of Physical Chemistry, University of Freiburg, Albertstraße 21, 79104 Freiburg, Germany
cMacromolecular Chemistry I, University of Bayreuth, Universitätsstraße 30, 95447 Bayreuth, Germany
dBavarian Polymer Institute, Universitätsstraße 30, 95447 Bayreuth, Germany
eBayreuth Institute of Macromolecular Research (BIMF), University of Bayreuth, Universitätsstraße 30, 95447 Bayreuth, Germany
fZernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands. E-mail: r.m.hildner@rug.nl
First published on 28th October 2021
Abstract
Directed transport of singlet excitation energy is a key process in natural light-harvesting systems and a desired feature in assemblies of functional organic molecules for organic electronics and nanotechnology applications. However, progress in this direction is hampered by the lack of concepts and model systems. Here we demonstrate an all-optical approach to manipulate singlet exciton transport pathways within supramolecular nanostructures via singlet–triplet annihilation, i.e., to enforce an effective motion of singlet excitons along a predefined direction. For this proof-of-concept, we locally photo-generate a long-lived triplet exciton population and subsequently a singlet exciton population on single bundles of H-type supramolecular nanofibres using two temporally and spatially separated laser pulses. The local triplet exciton population operates as a gate for the singlet exciton transport since singlet–triplet annihilation hinders singlet exciton motion across the triplet population. We visualize this manipulation of singlet exciton transport via the fluorescence signal from the singlet excitons, using a detection-beam scanning approach combined with time-correlated single-photon counting. Our reversible, all-optical manipulation of singlet exciton transport can pave the way to realising new design principles for functional photonic nanodevices.
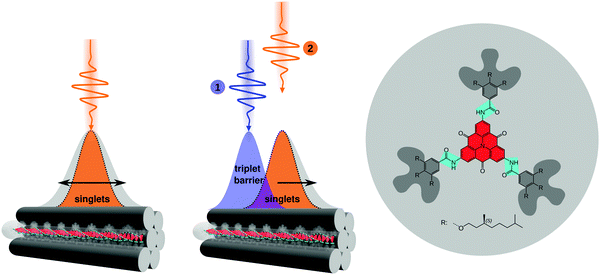
New conceptsThe directed transport of excitation energy (excitons) is a key step in the initial light-driven steps of photosynthesis and is critically important to advance applications of organic photoactive materials towards novel photonic nanodevices. Current approaches to manipulate exciton migration make use of pre-structured substrates or (permanent) local defects imprinted into the organic materials. Here we introduce a novel all-optical concept to effectively steer excitons within assemblies of functional organic molecules: the transport of photogenerated singlet excitons within supramolecular nanostructures is controlled by a precisely positioned, optically created local triplet exciton population acting as a gate. Since this gate is optically prepared and decays with the long triplet lifetime it can be re-written at any position within the molecular assembly rendering our approach non-invasive, fully reversible and flexible. To highlight the suitability of our concept for nanotechnology, we specifically demonstrate it on individual one-dimensional supramolecular nanostructures. Our results illustrate the feasibility of this all-optical method for manipulation and control of singlet exciton transport and allow for new approaches in the design of functional photonic nanodevices exploiting directed exciton motion. |
Introduction
Manipulating the flow of excitation energy (excitons) within supramolecular assemblies of functional organic materials is a key feature to expand their applicability in various fields including sustainable energy conversion1–3 and (quantum) information technology.4,5 While important design principles for long-range energy transport2,6–12 and the manipulation of energy transport between nanoparticles and molecules13 are emerging, there is a lack of approaches to manipulate the transport of excitation energy within supramolecular structures in a reliable and reversible manner. In this context, the photosynthetic apparatus in nature provides an intriguing example:3,14,15 sophisticated pigment-protein complexes direct excitation energy towards a reaction centre via a built-in energy funnel using only one or two species of pigment molecules. This funnel is created by a precise spatial organisation of the pigments as well as by carefully tuned interactions between the pigments and the protein scaffold. Although this energy funnel is not reversible, it inspired synthetic approaches. For instance, appending several chemically distinct chromophores to a DNA scaffold16,17 or doping one-dimensional supramolecular nanostructures with acceptor molecules18,19 predefines the direction for energy transfer. Control of energy transport by external stimuli was shown in organic single crystals20 and hybrid systems21 by applying an electric field or by introducing a local strain gradient with an atomic force microscope tip that creates local topological quenchers.22 However, all those approaches are based on structuring samples and/or substrates in advance, i.e., the direction of transport cannot be reversed, or irreversible changes are introduced into the system, which inhibits full control over exciton transport. Hence, there is a lack of suitable model systems and concepts to enable room-temperature manipulation of exciton transport.Ideally, manipulation of exciton transport in supramolecular nanostructures must be flexible, reversible and non-invasive. We propose here an all-optical concept based on independently photo-generated singlet and triplet exciton populations to effectively steer an exciton population into a predefined direction (Fig. 1). Singlet–triplet annihilation can then be exploited to gate the (long-range) transport of singlet excitons by a local triplet exciton population. This approach exploits three intrinsic properties of singlet and triplet excitons in organic assemblies:23,24 first, the excited-state lifetime of singlet excitons is in the nanosecond range, while triplet excitons typically have micro- to millisecond lifetimes.24,25 Second, while singlet exciton transport is mediated predominantly by long-range Coulomb interactions, triplet exciton transport is driven by short-range exchange interactions.24,26 Therefore, experimentally observed diffusivities of singlet excitons are typically two to three orders of magnitude greater than those of triplet excitons,10,27–35i.e., triplet excitons are essentially immobile on time scales of the short (nanosecond) singlet exciton lifetime. Finally, contrary to singlet–singlet or triplet–triplet annihilation, after singlet–triplet annihilation an excited triplet state survives due to spin conservation:24
Here, we demonstrate this all-optical approach by manipulating singlet exciton transport pathways via singlet–triplet annihilation in individual one-dimensional supramolecular nanostructures. Using a two-pulse excitation scheme, we effectively generate an initial triplet exciton population via inter-system crossing of photo-generated singlet excitons, and subsequently we create mobile singlet excitons with a spatial offset (Fig. 1). The presence of a local triplet exciton population effectively steers singlet excitons away from the triplet population, i.e., the net effect is the transport of singlet excitons away from the triplet excitons. The singlet exciton transport within a single nanostructure is monitored with time-resolved detection-beam scanning.10,31 The supramolecular nanostructures are based on a carbonyl-bridged triarylamine trisamide, CBT,10,36,37 as shown in Fig. 1. Its structure formation is mainly driven by three directed hydrogen bonds between the amide groups. Consequently, this molecular design gives rise to a cofacial H-type arrangement of the CBT cores (see Fig. S1, ESI†) that supports singlet exciton transport up to several micrometres as we have shown recently.10,11 We specifically study individual bundles of supramolecular nanofibres.10 Since each bundle comprises more than 1000 H-type nanofibres, the fluorescence signal from singlet excitons features a high signal-to-noise ratio to detect small changes in time- and spatially resolved measurements (see the Materials and Methods section, ESI,† for a detailed justification for the choice of the system).
Results and discussion
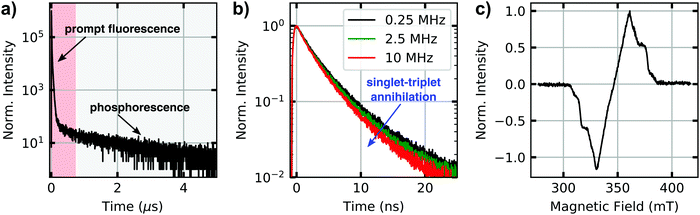
Lifetimes of singlet and triplet excited states of bulk dispersions both of molecularly dissolved CBT (in THF) and of bundles of nanofibres (in anisole) were determined using time-correlated single-photon counting after pulsed excitation of singlet states at room temperature (Fig. 2a and Fig. S2c, ESI†). The excited-state decay curves of both samples feature a rapid initial decay on nanosecond time scales, associated with the prompt fluorescence from the singlet excited states. Moreover, a much weaker delayed signal on microsecond time scales is present. We attribute this long-lived signal to phosphorescence from triplet states that are populated via intersystem crossing from initially excited singlet states. For molecularly dissolved CBT the singlet lifetime is 2.7 ns,10 while for bundles of nanofibres we find a longer singlet exciton lifetime of 4.1 ns due to the H-type aggregation of CBT cores10 (both are amplitude-weighted lifetimes, see Fig. S3, ESI†). This trend is also seen in the microsecond lifetime component: for molecularly dissolved CBT this lifetime is 766 ns (Fig. S2, ESI†), while for the bundles we find 1320 ns (Fig. 2a). These numbers are in agreement with triplet lifetimes of other small carbonyl-bridged triarylamines in their crystalline solid state.25Further indirect evidence for the presence of long-lived triplet excitons in bundles of nanofibres in anisole dispersion is provided by fluence and laser repetition rate dependent fluorescence lifetime measurements.23,24,38Fig. 2b shows an example, where the excitation fluence per pulse was kept constant at 8.6 × 1015 photons (pulse cm2)−1, while the laser repetition rate was increased from 0.25 MHz to 2.5 MHz and finally 10 MHz, corresponding to pulse-to-pulse times of 4 μs, 0.4 μs and 0.1 μs. We find a decrease in the amplitude-weighted fluorescence lifetime from 4 ns to 3.3 ns. This characteristic trend indicates annihilation between singlet excitons and a species with μs lifetime,23,38 here the triplet excitons within bundles of nanofibres. This effect is particularly pronounced at high fluences and at laser repetition rates higher than the inverse triplet lifetime (Fig. S3, ESI†). In this situation, the triplet population does not fully decay between subsequent laser pulses and accumulates. Mobile singlet excitons thus encounter an increasing number of triplet excitons for annihilation, which creates an additional decay channel for singlet excitons and reduces the singlet exciton lifetime (see Fig. S3–S5, ESI†).
In addition to this indirect evidence, the detection of the time-resolved electron paramagnetic resonance (EPR) signal following pulsed laser excitation at 80 K39 provides direct evidence for the presence of long-lived excited triplet states in our supramolecular CBT building block (in THF) as well as in bundles of nanofibres (in anisole dispersion, Fig. 2c, see also Materials and Methods in the ESI,† and Fig. S2a). The laser excitation occurs resonantly into the singlet exciton absorption at 465 nm10 and triplet excitons are thus generated via intersystem crossing, as in the optical experiments. The EPR signal can be unequivocally assigned to originating from a spin-polarised (i.e., non-thermal) triplet state due to its spectral shape.39 Stable paramagnetic species would not be detectable with this particular experiment, and charge-transfer states (i.e., spin-correlated radical pairs) as well as polarisation transfer from an excited state to a stable radical can be excluded as well, as they would result in much narrower EPR spectra. Since the EPR spectra in Fig. 2c and Fig. S2a (ESI†) were retrieved, respectively, at 900 ns (molecularly dissolved) and at 1300 ns (bundles) after laser excitation, this proves that the microsecond lifetime component in Fig. 2a stems from phosphorescence from triplet states. Note that the decay of the EPR signal measures the decay of the spin-polarisation, which is not related to the triplet lifetime. Comparing the EPR data measured at 80 K and the lifetime decays recorded at room temperature, respectively, we emphasise that intersystem crossing rates typically do not change much as function of temperature.24 Hence, triplet states will be populated in both experiments via intersystem crossing from initially photo-excited singlet states, although absolute triplet population densities might be different.
The data in Fig. 2 demonstrate that long-lived triplet excitons are present in bundles of nanofibres and that the dynamics of singlet excitons is strongly influenced by singlet–triplet annihilation. The combination of long-range singlet exciton transport,10 the one-dimensional nature of our bundles of nanofibres (Fig. 1), and the presence of long-lived triplet states that enable singlet–triplet annihilation (see Fig. 2b and Fig. S3, S4, ESI†) make this system perfectly suited for a proof of concept to show manipulation of singlet exciton transport by spatio-temporal control of local triplet exciton populations.
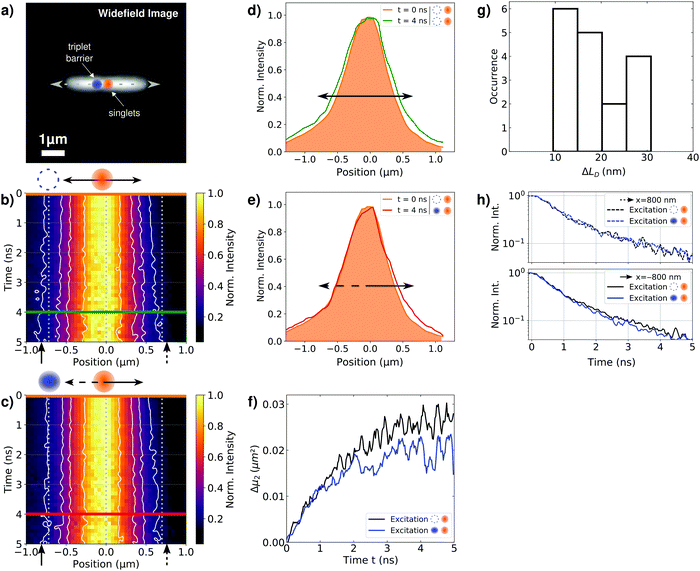
To demonstrate this manipulation of singlet exciton motion in individual bundles of nanofibres, we spin-coated bundles from a 40 μM anisole dispersion onto microscopy cover slips. Fig. 3a displays a representative widefield image of an isolated bundle (this image represents predominantly the prompt fluorescence from singlet excitons, see Fig. 2a). This bundle possesses a length of several micrometres, in agreement with atomic force microscopy data from bundles (Fig. S1, ESI†), see also our recent work.10 We excite this bundle confocally by two distinct pulsed lasers (both resonant with the singlet exciton absorption between 400 nm and 520 nm, see Fig. S2b, ESI†): first, a 420 nm laser (‘triplet laser’) is used to create a singlet exciton population 800 nm to the left of the centre of the bundle (at x = −800 nm, blue circle, Fig. 3a). Second, a 450 nm laser (‘singlet laser’) is used to create a singlet exciton population in the centre of the bundle (at x = 0 nm, orange circle, Fig. 3a). This ‘singlet laser’ hits the sample 120 ns after the arrival of the ‘triplet laser’. The naming of the two lasers reflects that 120 ns after the arrival of the ‘triplet laser’ all (short-lived) photo-generated singlet excitons already decayed and only triplet excitons generated by intersystem crossing are present. The ‘singlet laser’ excitation thus creates a spatially separated and temporally delayed singlet exciton population. If those singlet excitons diffuse to the left, they will interact with triplet excitons via singlet–triplet annihilation, whereas singlet excitons migrating to the right along the bundle will not encounter this triplet population and transport is unperturbed (see also Fig. S5a, ESI†).
We visualise the spatio-temporal dynamics of singlet excitons, created by the ‘singlet laser’, as well as their manipulation by the triplet population using a detection-beam scanning approach combined with time-correlated single-photon counting of the prompt fluorescence signal.10,28,31 We measure fluorescence decay curves at fixed positions of the laser foci, while scanning the detection position along the long (x-) axis of the bundle (centred around the ‘singlet laser’ focus). We thus create a time-dependent distribution of the prompt fluorescence of singlet excitons, I(x,t), as a function of the distance x relative to the centre of the ‘singlet laser’ and time t after its arrival on the sample (see Materials and methods, ESI†). To exclude artefacts (defocusing, bleaching etc., for example see Fig. S7, ESI†) we record two fluorescence decay curves for each detection position before moving to the next. The first fluorescence decay is measured only with the ‘singlet laser’ as the excitation source, while for the second decay curve both the ‘triplet laser’ and the ‘singlet laser’ hit the sample with time ordering as explained above. This interleaved experiment allows to unambiguously assign changes in the singlet exciton dynamics to the presence or absence of the triplet population, since the measurement with only the ‘singlet laser’ serves as a reference for the unperturbed singlet exciton dynamics. Finally, we normalize the spatial intensity distributions at each point in time to emphasize the fluorescence broadening along the bundle's long axis. We note again that the measurement with only ‘singlet laser’ excitation serves as a direct control experiment to exclude irreversible effects.
Fig. 3b shows the resulting spatio-temporal fluorescence distribution I(x,t) of our reference experiment, generated only by ‘singlet laser’ excitation. As in our recent work,10 the fluorescence intensity distribution shows a broadening in both directions of the bundle's long axis on a (sub-)nanosecond time scale. This temporal broadening reflects unperturbed long-range singlet exciton transport in our bundles.10 For the measurement with both lasers active, the resulting fluorescence distribution I(x,t) is shown in Fig. 3c. A careful inspection of this distribution and a comparison with the reference experiment indicates a modified transport dynamics of singlet excitons. In particular towards the left side (x < 0 μm), where the triplet exciton population is now present on the bundle, broadening seems to be suppressed (compare the vertical dashed lines with the solid contour lines).
We further extracted intensity profiles from the fluorescence distributions shown in Fig. 3b and c at different times ti after singlet exciton generation. The profiles of our reference experiment reveal a symmetric broadening, i.e., the initial profile (orange line, at t = 0 ns) broadens in both directions of the bundle's long axis (green line, at t = 4 ns, Fig. 3d). For the measurement with both lasers active, we observe a different behaviour (Fig. 3e): for positions in the direction of the triplet population (x < 0 μm) the initial and delayed profiles overlap (orange and red lines), i.e., no spatial broadening of the initial singlet exciton population occurs. In contrast, to the right (x > 0 μm) singlet exciton diffusion is unperturbed, since the initial profile does not overlap with the profile at t = 4 ns (orange and red lines, compare also with the reference experiment in Fig. 3d). Although the changes in singlet transport to the left are small, these are meaningful and robust, since a control experiment on a sample without long-range energy transport yields exactly overlapping profiles at all times (Fig. S9, ESI†).
To quantitatively evaluate the altered transport dynamics in the presence of the triplet exciton population, we analyse the changes of the second moments μ2(t) of the spatial intensity profiles,10 with respect to the second moment of the initial profile μ2(0), i.e.,
| Δμ2(t) = μ2(t) − μ2(0). |
The Δμ2(t) curves retrieved from the data in Fig. 3b and c are shown in Fig. 3f. For both curves we observe a pronounced and sub-diffusive broadening in our bundles of nanofibers, which is characteristic of long-range exciton transport in a disordered excited-state energy landscape.10,40 In our reference experiment we find at t = 5 ns an exciton diffusion length of 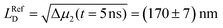 (Fig. 3f, black line). However, for times t > 1 ns and both lasers active, the Δμ2(t) values (Fig. 3f, blue line) are significantly and consistently smaller compared to those with only the ‘singlet laser’ active, i.e., without the triplet population on the bundle (Fig. 3f, black line). This behaviour clearly underpins the restricted singlet exciton diffusion in the presence of the triplet exciton population. To evaluate the influence of the triplet population on the singlet exciton diffusion, we fitted a power law to the Δμ2(t) curves in the presence and absence of the triplet population for times t > 1 ns. From the differences in the singlet exciton diffusion lengths from our fit at time t = 5 ns, we calculated the overall reduction of the diffusion length ΔLD due to the triplet population: ΔLD = LRefD − LD (see also Materials and methods, ESI†). For in total 17 individual bundles this difference in diffusion length is greater than the corresponding error, and for those bundles we find a significant average reduction of
(Fig. 3f, black line). However, for times t > 1 ns and both lasers active, the Δμ2(t) values (Fig. 3f, blue line) are significantly and consistently smaller compared to those with only the ‘singlet laser’ active, i.e., without the triplet population on the bundle (Fig. 3f, black line). This behaviour clearly underpins the restricted singlet exciton diffusion in the presence of the triplet exciton population. To evaluate the influence of the triplet population on the singlet exciton diffusion, we fitted a power law to the Δμ2(t) curves in the presence and absence of the triplet population for times t > 1 ns. From the differences in the singlet exciton diffusion lengths from our fit at time t = 5 ns, we calculated the overall reduction of the diffusion length ΔLD due to the triplet population: ΔLD = LRefD − LD (see also Materials and methods, ESI†). For in total 17 individual bundles this difference in diffusion length is greater than the corresponding error, and for those bundles we find a significant average reduction of 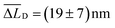 (Fig. 3g). We emphasise here that this reduction of ΔLD in our bundles is exclusively caused by the presence of a locally positioned triplet exciton population with concomitant singlet–triplet annihilation (e.g. to the left of the singlet exciton population in Fig. 3). Those data include also measurements with different distances between the local triplet and singlet exciton populations (between ∼500 nm and 800 nm, see e.g. Fig. S7, ESI†).
(Fig. 3g). We emphasise here that this reduction of ΔLD in our bundles is exclusively caused by the presence of a locally positioned triplet exciton population with concomitant singlet–triplet annihilation (e.g. to the left of the singlet exciton population in Fig. 3). Those data include also measurements with different distances between the local triplet and singlet exciton populations (between ∼500 nm and 800 nm, see e.g. Fig. S7, ESI†).
To confirm that this hindered singlet exciton diffusion is caused by singlet–triplet annihilation, we extracted the fluorescence lifetimes as a function of the position relative to the centre (x = 0 μm) of the ‘singlet laser’ from the fluorescence intensity distributions in Fig. 3b and c. While the fluorescence lifetimes retrieved at x = 800 nm to the right of the ‘singlet laser’ do not differ from each other (Fig. 3h, top), the lifetimes at x = −800 nm to the left side are slightly shorter for the measurement where both lasers excite the bundle (Fig. 3h, bottom). This change in lifetimes is not as pronounced as in the measurement on the bulk dispersion in Fig. 2b and Fig. S3 (ESI†), and it is not as pronounced as in a single-molecule experiment, where ‘on–off’ blinking events can be observed in the photoluminescence signal due to transitions into triplet states.41,42 Here we work in an intermediate regime between bulk and single molecule, since one bundle comprises 1000 nanofibres and each nanofibre contains about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules. Nevertheless, the decay curves in Fig. 3h indicate that singlet–triplet annihilation processes take place in a single bundle, and that this process only occurs locally at the position of the triplet exciton population.
000 molecules. Nevertheless, the decay curves in Fig. 3h indicate that singlet–triplet annihilation processes take place in a single bundle, and that this process only occurs locally at the position of the triplet exciton population.
The presence of a triplet exciton population creates a barrier, which is responsible for the hindered singlet exciton dynamics within the bundle of nanofibres towards the position of the ‘triplet laser’ excitation. Thus, we designed a controllable gate for singlet excitons with their motion being effectively steered by a local triplet exciton population (Fig. S5, ESI†). This gate can be written at any position of the supramolecular bundle, as we have demonstrated on 17 individual bundles with arbitrary orientation and different distances (∼500–800 nm) between the triplet and singlet populations (for further examples see Fig. S7 and S8, ESI†). The ‘triplet laser’ serves as a user input for our gate. When this input is active, diffusion in one direction is suppressed by singlet–triplet annihilation: such a triplet barrier causes singlet–triplet annihilation when a singlet exciton approaches, leaving behind a triplet exciton. Thus, a self-sustaining barrier is established, which serves as a drain for singlet excitons. This behaviour is reproduced by numerical simulations of a simple diffusion equation (eqn (4), ESI†) with an effective position-dependent annihilation rate γeff = γT420, which is the product of the (constant) singlet–triplet annihilation rate γ and the position-dependent triplet population density T420 created by the 420 nm ‘triplet laser’. The effective annihilation rate is approximately constant over time during the (short) singlet exciton lifetime. For instance, the data in Fig. 3 can be accurately reproduced with γeff = 0.29 ns−1 (see Fig. S5, ESI†), using γ = 0.013 μm ns−1 as determined from fits to repetition-rate-dependent measurements (Fig. S4, ESI†), and T420 = 23 μm−1 per nanofibre determined from the laser intensity and photophysical parameters of our system (Table S2, ESI†). The gate remains closed until the user input is deactivated, i.e., the ‘triplet laser’ is turned off, the triplet excitons return to the ground state, and the annihilation rate becomes zero.
Further numerical simulations were performed, in which we systematically varied parameters, starting from the values determined from the data in Fig. 3, see above. We find that the effective annihilation rate γeff has a strong effect on the average reduction in diffusion length ΔLD and can thus be tuned to achieve the desired effect (Fig. S6, ESI†). The singlet–triplet annihilation rate γ and the position-dependent triplet population T420 are strongly determined by photophysical parameters of the system under investigation, e.g. the absorption cross section, the intersystem crossing rates and the singlet exciton diffusion constant (see Section 2 and Fig. S6, ESI†). However, since also the intensity of the ‘triplet laser’ plays a strong role for the achievable triplet population density T420 and thus for γeff, this intensity can be exploited as a ‘control knob’ to compensate for potentially unfavourable photophysical parameters that cannot be controlled externally. We believe therefore that our approach can be applied to a wide range of systems with very different photophysical parameters.
Based on our proof of concept a key aspect that can be improved in future work is related to the broad singlet and triplet populations photo-generated by the diffraction-limited excitation. Both populations overlap even at distances of 800 nm, due to singlet diffusion prior to intersystem crossing leading to a broadened triplet exciton population (Fig. S5, ESI†). Hence, the precise distance between the populations has, compared to enhancing γeff, a less pronounced effect on the achievable reduction in singlet exciton diffusion length ΔLD (Fig. S6, ESI†). Moreover, the diffraction-limited excitation gives rise to a distribution of singlet and triplet excitons over a wide range on each nanofiber within a bundle. Annihilation does therefore not necessarily take place on each nanofibre and singlet excitons can partially diffuse into the region of the triplet gate reducing the overall effect. These drawbacks can be overcome by using near-field techniques or plasmonic nanoparticles, that create substantially more localised triplet population densities. In combination with high triplet densities, i.e., with more than one triplet exciton per nanofibre created by e.g. high laser intensities, each singlet exciton travelling towards this triplet population will be annihilated at a defined position. This will result in fully deterministic gating of singlet exciton motion.
Conclusion and outlook
In conclusion, we have presented a novel concept based on an all-optical approach to manipulate singlet exciton transport in assemblies of functional organic molecules. As a model system for this proof of concept we exploit bundles of supramolecular H-type nanofibres. Using two spatially and temporally separated laser pulses we photo-excite two independent exciton populations within a single bundle of nanofibres. The first pulse generates a triplet exciton population via intersystem crossing of initially photo-generated singlet excitons. This triplet population acts as a barrier for the subsequently generated singlet exciton population, because singlet–triplet annihilation hinders singlet exciton diffusion across the triplet exciton population within the bundle. The effective singlet–triplet annihilation rate is position-dependent and can be controlled by the spatial separation of the singlet and triplet exciton populations. In this way, a fully reversible, optically switchable triplet exciton gate for the control of singlet exciton motion is created in our one-dimensional bundles of nanofibers that does not require restructuring the sample. We emphasise that our all-optical gating approach is not limited to one-dimensional nanostructures. We believe that it can be extended to (supramolecular) systems of higher dimensionality and complexity if those systems carry mobile excitons that interact and annihilate with other elementary excitations of sufficiently long lifetime. This long-lived excitation is not necessarily a triplet, but can be any species, such as charge-transfer states, that can be photo-generated and suitably positioned to suppress diffusion of the mobile excitons along desired direction(s), e.g. by using illumination masks. Our approach opens new opportunities for design principles for new photonic nanodevices and paves the way towards tailored, all-optical control of singlet exciton energy transport.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from the German Research Foundation (DFG) through the research training group GRK1640 and from the Bavarian State Ministry of Science and the Arts through the Collaborative Research Network ‘Solar Technologies go Hybrid’. We also acknowledge support by the Elite Network of Bavaria (ENB) through the study program “Biological Physics” (J. K., R. H.). We are grateful to Felix Wenzel, Doris Hanft and Sandra Ganzleben (Macromolecular Chemistry, University of Bayreuth) for their help with synthesis and self-assembly.References
- O. Dumele, J. Chen, J. V. Passarelli and S. I. Stupp, Adv. Mater., 2020, 32, 1907247 CrossRef CAS PubMed.
- J. L. Brédas, E. H. Sargent and G. D. Scholes, Nat. Mater., 2016, 16, 35–44 CrossRef PubMed.
- G. D. Scholes, G. R. Fleming, A. Olaya-Castro and R. van Grondelle, Nat. Chem., 2011, 3, 763–774 CrossRef CAS PubMed.
- J. H. Reina, C. E. Susa and R. Hildner, Phys. Rev. A: At., Mol., Opt. Phys., 2018, 97, 63422 CrossRef CAS.
- M. A. Castellanos, A. Dodin and A. P. Willard, Phys. Chem. Chem. Phys., 2020, 22, 3048–3057 RSC.
- T. Zhu, Y. Wan and L. Huang, Acc. Chem. Res., 2017, 50, 1725–1733 CrossRef CAS PubMed.
- G. D. Scholes, Chem. Phys., 2002, 275, 373–386 CrossRef CAS.
- J. R. Caram, S. Doria, D. M. Eisele, F. S. Freyria, T. S. Sinclair, P. Rebentrost, S. Lloyd and M. G. Bawendi, Nano Lett., 2016, 16, 6808–6815 CrossRef CAS PubMed.
- A. K. Topczak, T. Roller, B. Engels, W. Brütting and J. Pflaum, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 201203 CrossRef.
- B. Wittmann, F. A. Wenzel, S. Wiesneth, A. T. Haedler, M. Drechsler, K. Kreger, J. Köhler, E. W. Meijer, H.-W. Schmidt and R. Hildner, J. Am. Chem. Soc., 2020, 142, 8323–8330 CrossRef CAS PubMed.
- A. T. Haedler, K. Kreger, A. Issac, B. Wittmann, M. Kivala, N. Hammer, J. Köhler, H.-W. Schmidt and R. Hildner, Nature, 2015, 523, 196–199 CrossRef CAS PubMed.
- K. Kreger, H.-W. Schmidt and R. Hildner, Electron. Struct., 2021, 3, 23001 CrossRef CAS.
- Ł. Bujak, T. Ishii, D. K. Sharma, S. Hirata and M. Vacha, Nanoscale, 2017, 9, 1511–1519 RSC.
- R. J. Cogdell, A. Gall and J. Köhler, Q. Rev. Biophys., 2006, 39, 227–324 CrossRef CAS PubMed.
- T. Mirkovic, E. E. Ostroumov, J. M. Anna, R. van Grondelle, Govindjee and G. D. Scholes, Chem. Rev., 2017, 117, 249–293 CrossRef CAS PubMed.
- E. Boulais, N. P. D. Sawaya, R. Veneziano, A. Andreoni, J. L. Banal, T. Kondo, S. Mandal, S. Lin, G. S. Schlau-Cohen, N. W. Woodbury, H. Yan, A. Aspuru-Guzik and M. Bathe, Nat. Mater., 2018, 17, 159–166 CrossRef CAS PubMed.
- M. Heilemann, P. Tinnefeld, G. Sanchez Mosteiro, M. Garcia Parajo, N. F. van Hulst and M. Sauer, J. Am. Chem. Soc., 2004, 126, 6514–6515 CrossRef CAS PubMed.
- J. Jevric, S. M. Langenegger and R. Häner, Eur. J. Org. Chem., 2020, 4677–4680 CrossRef CAS.
- J. Gierschner, Phys. Chem. Chem. Phys., 2012, 14, 13146–13153 RSC.
- Q. H. Cui, Q. Peng, Y. Luo, Y. Jiang, Y. Yan, C. Wei, Z. Shuai, C. Sun, J. Yao and Y. S. Zhao, Sci. Adv., 2018, 4, 1–8 Search PubMed.
- K. Becker, J. M. Lupton, J. Müller, A. L. Rogach, D. V. Talapin, H. Weller and J. Feldmann, Nat. Mater., 2006, 5, 777–781 CrossRef CAS PubMed.
- D. Chaudhuri, D. Li, Y. Che, E. Shafran, J. M. Gerton, L. Zang and J. M. Lupton, Nano Lett., 2011, 11, 488–492 CrossRef CAS PubMed.
- H. van Amerongen, R. van Grondelle and L. Valkunas, Photosynthetic Excitons, World Scientific, 2000 Search PubMed.
- A. Köhler and H. Bässler, Electronic processes in organic semiconductors: An introduction, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2015.
- E. Hamzehpoor and D. F. Perepichka, Angew. Chem., Int. Ed., 2020, 59, 9977–9981 CrossRef CAS PubMed.
- A. Köhler and H. Bässler, J. Mater. Chem., 2011, 21, 4003–4011 RSC.
- O. V. Mikhnenko, P. W. M. Blom and T. Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867–1888 RSC.
- G. M. Akselrod, P. B. Deotare, N. J. Thompson, J. Lee, W. A. Tisdale, M. A. Baldo, V. M. Menon and V. Bulovic, Nat. Commun., 2014, 5, 3646 CrossRef CAS PubMed.
- Y. Wan, A. Stradomska, J. Knoester and L. Huang, J. Am. Chem. Soc., 2017, 139, 7287–7293 CrossRef CAS PubMed.
- T. Kim, S. Ham, S. H. Lee, Y. Hong and D. Kim, Nanoscale, 2018, 10, 16438–16446 RSC.
- B. Wittmann, S. Wiesneth, S. Motamen, L. Simon, F. Serein-Spirau, G. Reiter and R. Hildner, J. Chem. Phys., 2020, 153, 144202 CrossRef CAS PubMed.
- K. A. Clark, E. L. Krueger and D. A. Vanden Bout, J. Phys. Chem. Lett., 2014, 5, 2274–2282 CrossRef CAS PubMed.
- T. Zhu, Y. Wan, Z. Guo, J. Johnson and L. Huang, Adv. Mater., 2016, 28, 7539–7547 CrossRef CAS PubMed.
- Y. Wan, Z. Guo, T. Zhu, S. Yan, J. Johnson and L. Huang, Nat. Chem., 2015, 7, 785–792 CrossRef CAS PubMed.
- S. R. Yost, E. Hontz, S. Yeganeh and T. Van Voorhis, J. Phys. Chem. C, 2012, 116, 17369–17377 CrossRef CAS.
- A. T. Haedler, S. C. J. Meskers, R. H. Zha, M. Kivala, H. W. Schmidt and E. W. Meijer, J. Am. Chem. Soc., 2016, 138, 10539–10545 CrossRef CAS PubMed.
- J. S. Valera, R. Gómez and L. Sánchez, Small, 2018, 14, 1702437 CrossRef PubMed.
- T. J. Pflock, S. Oellerich, J. Southall, R. J. Cogdell, G. M. Ullmann and J. Köhler, J. Phys. Chem. B, 2011, 115, 8813–8820 CrossRef CAS PubMed.
- T. Biskup, Front. Chem., 2019, 7, 10 CrossRef CAS PubMed.
- S. M. Vlaming, V. A. Malyshev, A. Eisfeld and J. Knoester, J. Chem. Phys., 2013, 138, 214316 CrossRef CAS PubMed.
- J. Hofkens, M. Cotlet, T. Vosch, P. Tinnefeld, K. D. Weston, C. Ego, A. Grimsdale, K. Müllen, D. Beljonne, J. L. Brédas, S. Jordens, G. Schweitzer, M. Sauer and F. De Schryver, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 13146–13151 CrossRef CAS PubMed.
- D. A. Vanden Bout, W. T. Yip, D. Hu, D. K. Fu, T. M. Swager and P. F. Barbara, Science, 1997, 277, 1074–1077 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nh00514f |
| ‡ Current address: Chair of Physical Chemistry and Chemical Education, University of Saarland, Campus B2 2, 66123 Saarbrücken, Germany. |
| This journal is © The Royal Society of Chemistry 2021 |