Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Substrate adhesion evolves non-monotonically with processing time in millimeter-scale aligned carbon nanotube arrays†
Ashley L.
Kaiser
 *a,
Dale L.
Lidston
b,
Sophie C.
Peterson
bc,
Luiz H.
Acauan
*a,
Dale L.
Lidston
b,
Sophie C.
Peterson
bc,
Luiz H.
Acauan
 b,
Stephen A.
Steiner
III
b,
Roberto
Guzman de Villoria‡
b,
Stephen A.
Steiner
III
b,
Roberto
Guzman de Villoria‡
 b,
Amy R.
Vanderhout
b,
Amy R.
Vanderhout
 b,
Itai Y.
Stein§
b,
Itai Y.
Stein§
 *b and
Brian L.
Wardle
*b and
Brian L.
Wardle
 *bc
*bc
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: alkaiser@alum.mit.edu
bDepartment of Aeronautics and Astronautics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: iys@alum.mit.edu; wardle@mit.edu
cDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 25th November 2020
Abstract
The advantageous intrinsic and scale-dependent properties of aligned nanofibers (NFs) and their assembly into 3D architectures motivate their use as dry adhesives and shape-engineerable materials. While controlling NF–substrate adhesion is critical for scaled manufacturing and application-specific performance, current understanding of how this property evolves with processing conditions is limited. In this report, we introduce substrate adhesion predictive capabilities by using an exemplary array of NFs, aligned carbon nanotubes (CNTs), studied as a function of their processing. Substrate adhesion is found to scale non-monotonically with process time in a hydrocarbon environment and is investigated via the tensile pull-off of mm-scale CNT arrays from their growth substrate. CNT synthesis follows two regimes: Mode I (‘Growth’) and Mode II (‘Post-Growth’), separated by growth termination. Within 10 minutes of post-growth, experiments and modeling indicate an order-of-magnitude increase in CNT array–substrate adhesion strength (∼40 to 285 kPa) and effective elastic array modulus (∼6 to 47 MPa), and a two-orders-of-magnitude increase in the single CNT–substrate adhesion force (∼0.190 to 12.3 nN) and work of adhesion (∼0.07 to 1.5 J m−2), where the iron catalyst is found to remain on the substrate. Growth number decay in Mode I and carbon accumulation in Mode II contribute to the mechanical response, which may imply a change in the deformation mechanism. Predictive capabilities of the model are assessed for previously studied NF arrays, suggesting that the current framework can enable the future design and manufacture of high-value NF array applications.
Recent progress towards the development of one-dimensional nanoscale systems, such as aligned nanofibers (NFs), nanotubes, and nanowires,1–3 provides key opportunities for the design and manufacture of high-performance nano-engineered architectures and devices.4–6 In particular, the advantageous intrinsic, scale-dependent, and mass-specific thermal, electrical, and mechanical properties of aligned carbon nanotubes (CNTs)7–10 make these materials promising for commercial applications where robust and tunable interfacial performance is essential. Controlling the adhesion strength of a vertically aligned CNT array to its growth substrate (σa–s) is therefore necessary for shape-engineerable CNT array manufacturing and application-specific performance.7,11,12 Tailoring adhesion strength both up and down is important; for example, CNT-based field emitters require large σa–s to remain adhered to the substrate during operation,11,13,14 and high quality CNT yarns and sheets made from CNT arrays benefit from small σa–s, as their fabrication often requires facile CNT spinnability from the growth substrate.7,15 Other NF systems requiring tunable adhesion strength include NF arrays for gecko-inspired fibrillar adhesives and MEMS devices,16,17 contact printing,18–20 energy harvesting and storage,4,21,22 and thermal interface materials.7,23 Models that can guide NF processing towards these applications are a clear gap in the current understanding.
Issues in CNT synthesis are often marked by a limited knowledge of how σa–s scales with processing parameters, such as the CNT process time (tp) during chemical vapor deposition (CVD), an easily controllable and critical parameter governing array properties24,25 such as (primarily) CNT array height (h) tied to the CNT radius and wall thickness (see Fig. 1). This can make the fabrication of multi-scale CNT arrays with tunable adhesion strength challenging when a specific σa–s is required, particularly in continuous manufacturing, where the residence time of CNTs in the reactor affects both h and σa–s.1,26 To address these challenges and expand opportunities for shape-engineerable NF patterning and applications,12,27 it is necessary to develop an experimentally validated analytical model that can accurately describe and predict σa–s based on tp while considering the evolving array morphology, CNT–substrate interface, and mechanical behavior based on growth parameters. In this work, σa–s is quantified via tensile testing and modeled via contact mechanics, and we find that the non-monotonic evolution of σa–s with tp, particularly post-growth, is driven by the bimodal scaling of CNT geometry, CNT root density (i.e. number density, n), effective elastic array modulus (E), and interfacial work of adhesion (γ) for the CNT–substrate interface.
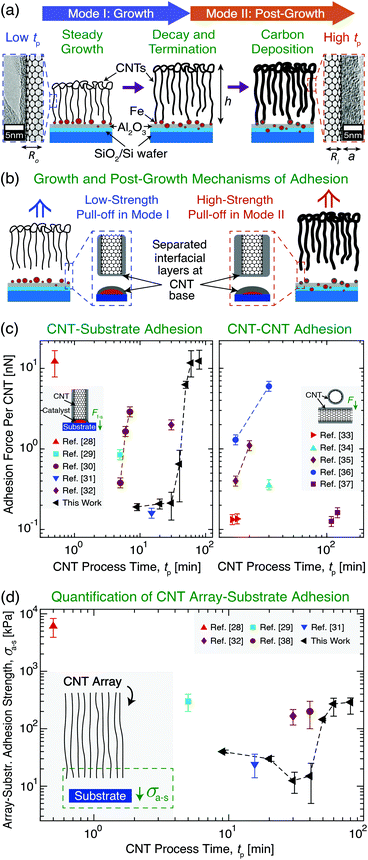 | ||
| Fig. 1 Overview of vertically aligned multiwall carbon nanotube (CNT) array growth and CNT adhesion to a Si wafer growth substrate with an Fe catalyst layer. (a) Illustration and transmission electron microscopy images showing CNT array evolution after growth initiation through two Modes as a function of CNT process time (tp): Mode I (‘Growth’) and Mode II (‘Post-Growth’), separated by CNT root density decay towards growth termination and a plateau in array height (h) at the end of Mode I. Carbon deposition in Mode II increases CNT wall thickness (a) and outer radius (Ro) at constant inner radius (Ri), increasing (b) CNT–substrate adhesion (i.e. ultimate tensile stress) measured via tensile pull-off. Illustrations and plots show previously reported (c) adhesion force (F) between a vertical CNT and its growth substrate (Ff–s)28–32 and between two CNTs33–37 and (d) CNT array–substrate adhesion strength (σa–s) between the array and its growth substrate28,29,31,32,38 as a function of tp. | ||
Due to the importance of tp in governing process–structure–property relations, many previous studies24,39–41 have evaluated CNT growth as a function of tp and noted that CNT synthesis follows two modes after growth initiation: Mode I, ‘Growth’, and Mode II, ‘Post-Growth’. These are separated by growth termination, which is preceded by CNT root density decay in Mode I, and is followed (post-termination) by a plateau in h and carbon deposition onto the array in Mode II (see Fig. 1a).24,39–41 To link the effects of tp with ongoing efforts to understand the origins of CNT adhesion, Fig. 1c and d show the results of prior studies that quantified, for a variety of CNT systems and tp values, the individual CNT–substrate adhesion force (Ff–s) via single CNT pull-off/lift-off,28–32 the CNT–CNT adhesion force,33–37 and σa–s, which was measured by the pull-off of vertically aligned CNT arrays from their growth substrates.28,29,32,38Fig. 1c shows that these CNT adhesion forces vary only over two orders of magnitude. Along with σa–s shown in Fig. 1d, different adhesion values can be achieved due to the unique CNT sizes, number densities, moduli, and work of adhesion values that result from each study's CVD growth conditions and catalysts. Our work with a single system covers this entire range of CNT adhesion forces just from varying tp. Unfortunately, predictive scaling relations for Ff–s and σa–s do not yet exist, and these are needed to quantify the substrate adhesion and γ evolution of both individual CNTs and arrays containing ∼109–1011 aligned CNTs,7,42 which are commonly used in applications. Therefore, to address this gap, we present an experimentally validated model and mechanisms to describe adhesion at the CNT–substrate interface. Several of the interfacial effects, array mechanics, and physiochemical mechanisms that could be responsible for the origin of non-monotonic σa–s scaling with tp are discussed, and future studies to support the manufacturing of NF systems with predictable and application-specific substrate interactions are proposed.
Results
Nanofiber–substrate adhesion theoretical framework
To provide mechanistic insight into the origin and scaling of σa–s, E, and γ with processing, a model is developed based on the following assumptions (see derivation in section S1 of the ESI†). The bulk NF array, here an exemplary CNT array as shown in Fig. 2a, is composed of vertically aligned, hollow, and cylindrical multiwall CNTs, where CNT–CNT interactions43–45 and waviness effects42,46 are implicitly captured by the volume-averaged effective elastic array modulus E, and only the annular CNT bases contact the growth substrate (Fe catalyst particles on an Al2O3/SiO2/Si wafer). Fig. 2a shows that the CNT–substrate contact area is between n annular CNT bases and the CNT-catalyst growth front interface, following hollow cylinder geometry.47,48 The CNT–substrate interaction is assumed to occur via dispersive adhesion attraction based on the intermolecular van der Waals (VDW) forces acting between the contacting materials,49–51 where each CNT has its own adhesion force (Ff–s). σa–s (i.e. the array mean ultimate tensile stress) is derived based on the Johnson–Kendall–Roberts (JKR) contact mechanics theory for relatively compliant elastic solids,49,50,52 where σa–s represents the detachment of all CNT bases from the substrate via the minimization of elastic and surface energy, assuming no energy dissipation outside of the separation region following previous work for similar fibrillar systems.52–55γ is assumed to be constant within each mode and signifies twice the surface free energy of the contacting surfaces in Kendall's framework.28,50,56,57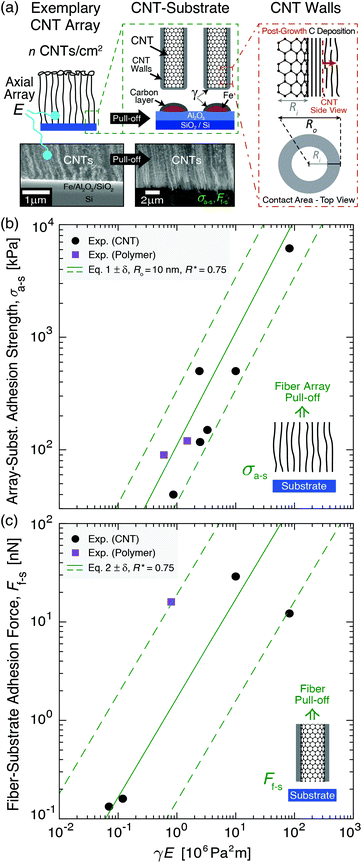 | ||
| Fig. 2 System geometry and corresponding adhesion modeling applied to previously reported experimental results of bulk fiber array–substrate adhesion strength (σa–s) and single fiber–substrate adhesion force (Ff–s). Adhesion is plotted versus the product of the work of adhesion between the separating fiber–substrate interfaces (γ) and the effective elastic array modulus (E) in eqn (1). (a) Illustrations and scanning electron microscopy images of an exemplary CNT array showing its tensile pull-off from the growth substrate and adhesion modeled via hollow cylinder geometry. (b) σa–sversus γE showing experiment-model agreement (eqn (1)) for Ro = 10 nm, R* = (Ro2 − Ri2)/Ro2 = 0.75, n = 2 × 109–2 × 1010 fibers per cm2 (solid line→6.5 × 109 fibers per cm2), and β = 0.4 for aligned CNT28,38,55,58,59 and polymer60,61 fiber arrays. (c) Ff–sversus γE showing experiment-model agreement (eqn (2)) for R* = 0.75, Ro = 2–50 nm (solid line→10 nm), and β = 0.4 for aligned CNT28,31,33,58 and polymer62 fiber arrays. | ||
Here, we consider the CNT array–substrate adhesion strength (σa–s) to be Ff–s scaled by n, where σa–s(tp) can be calculated viaeqn (1) (see Fig. 2b for experiment-model agreement of previously reported vertically aligned CNT and polymer NF arrays). The prefactor β ∼ 0.4 accounts for variations in the contact region,48 such as geometric irregularities, defects, and surface roughness reducing the true contact area in fibrillar systems.57,63,64Ff–s(tp) is then estimated viaeqn (2) (see Fig. 2c), where synchronous CNT separation from the substrate is assumed for simplicity, and failure occurs at a deterministic mean stress28,29,52 based on bulk adhesion scaling with the number of contacts,65 such as for gecko-inspired microfibrillar dry adhesives20,47,52 and recently for micron-tall vertically aligned CNT arrays.28,29 Finally, linear elastic behavior for the CNT array is assumed during tensile pull-off testing,29,42 with increases in E proportional to the increasing adhesion force and CNT outer radius (Ro) at a constant CNT inner radius (Ri) with tp. Shear/lateral adhesion force contributions from CNT sections lying parallel to the substrate are neglected due to the vertical CNT growth direction during synthesis and minimal compressive preload during testing.64,66Fig. 2b and c show the key drivers in this theoretical framework and illustrate the experiment-model agreement for exemplary values of n, Ro, and R* = (Ro2 − Ri2)/Ro2. These are plotted versus characteristic γE values for CNT and polymer NF systems, representing 0.05 J m−2 ≲ γ ≲ 5 J m−2 and 0.2 MPa ≲ E ≲ 200 MPa.
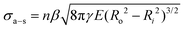 | (1) |
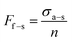 | (2) |
CNT–substrate adhesion: experimental and modeling results
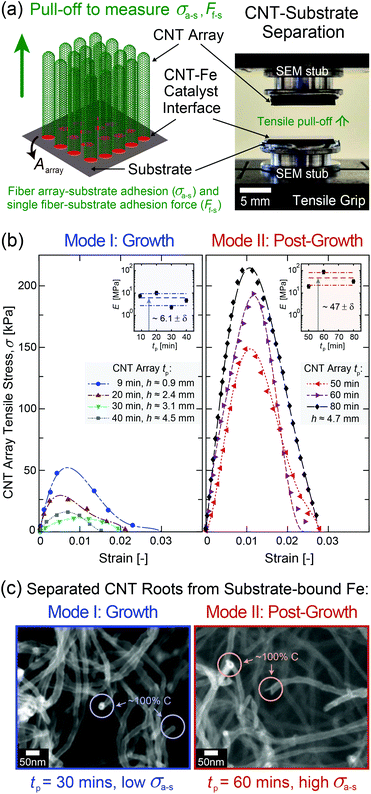
To experimentally quantify σa–s as a function of tp up to 80 min, mm-scale vertically aligned CNT arrays were synthesized via base-growth CVD and are categorized as Mode I: ‘Growth’, tp = 9–40 min, and Mode II: ‘Post-Growth’, tp = 40–80 min, following abrupt vertical growth termination observed at 40 min in this system. It is important to note that the process conditions, including the hydrocarbon flow, are part of the post-growth process. CNT arrays were then separated from their Fe catalyst/Al2O3/Si wafer substrates via the direct tensile testing procedure illustrated in Fig. 3, after which their structure and morphology were characterized as inputs into the adhesion model (see additional details in Methods and sections S2–S4 in the ESI†). TEM images of individual CNTs show that Ri(tp) remains constant at ∼3 nm, while the average wall thickness increases from ∼1.5 to 7.0 nm for tp = 9 to 80 min. The wall thickness is observed to follow a quadratic scaling with tp due to carbon deposition on the outer CNT walls, which increases the CNT diameter, stiffens the array, and decreases the averaged sp2 carbon character during growth41,67,68 and post-growth69–72 (Fig. S6–S8†). The number density of CNTs attached to the substrate (n, see Fig. S2†) was calculated as ∼2.1 × 1010 CNTs per cm2 at the start of Mode I (tp = 9 min) based on the ∼1% CNT volume fraction (Vf) for a ∼1 mm-tall CNT array.73–75In adhesion testing, the CNT array–substrate sample is glued to two scanning electron microscopy (SEM) stubs and pulled upwards until full wafer detachment from the array. This mechanical test is well-suited to the vertically aligned CNT array morphology28,29,76 to accurately measure the CNT–substrate adhesion force, Fa–s, defined as the maximum tensile force necessary to separate the two array–substrate interfaces.76 This gives σa–s, the array mean ultimate tensile stress, representing the CNT–substrate adhesion strength. For each measured strain, σ is obtained by dividing F by the apparent CNT array area, Aarray ∼ 1 cm2. Representative stress–strain curves are plotted for the range of tested tp values shown in Fig. 3b, and the average σa–s(tp) values are plotted in Fig. 4a. E is measured from the initial linear slope of the stress–strain curves and is observed to increase by nearly 10× from ∼6.14 ± 1.7 MPa in Mode I to ∼47.1 ± 21 MPa in Mode II.
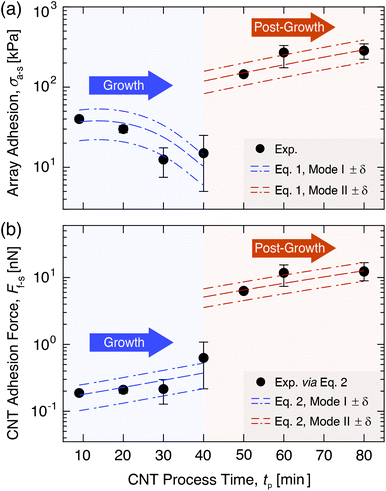 | ||
| Fig. 4 Experimental quantification and modeling of the CNT array–substrate adhesion strength (σa–s) and individual CNT–substrate adhesion force (Ff–s) as a function of CNT process time (tp) in Mode I (‘Growth’) and Mode II (‘Post-Growth’). (a) Plot showing that the experimental and model-predicted σa–s values (eqn (1)) evolve non-monotonically with tp, decreasing in Mode I due to reduced n, and increasing in Mode II due to higher γ, E, and Ro from carbon deposition within the CNT array. Continuity is not enforced at tp = 40 min to show the Mode I to Mode II shift at growth termination, and δ represents standard error. (b) Plot showing that the experimental and predicted Ff–s values (eqn (2)) scale with tp and increase by an order of magnitude from Mode I to Mode II due to increases in γ, E, and Ro with tp. | ||
From Fig. 3b and 4a, σa–s scales non-monotonically with tp, decreasing from 40.0 ± 2.5 kPa at tp = 9 min (start of Mode I) to 12.5 ± 5.0 kPa at 30 min, then 15.0 ± 5.0 kPa at 40 min (end of Mode I), and then increases by an order of magnitude to 145 ± 5.0 kPa at 50 min (after the onset of Mode II), finally reaching 285 ± 41 kPa at 80 min. This signifies that the adhesive response is governed by the evolving CNT geometry and total CNT–substrate contact area (via Ro and n), the array mechanics (via E), and the work of adhesion between the separating interfaces (via γ) due to the evolving carbon character with increasing tp. Fig. S4† shows SEM images of the wafer surface post-separation at each tp, where the absence of catalyst pits28,41 suggests that the iron catalyst particles that nucleated CNTs remained on the substrate after tensile testing.19,77,78 Similarly, representative SEM images with energy-dispersive X-ray spectroscopy (EDS) analysis for element mapping in Fig. 3c show open ended, iron-free, and carbon-covered CNT roots in the array after separation in both Modes, showing that the CNTs separate from the substrate–bound Fe catalyst particles during pull-off. No iron is found attached to the CNT roots (Fig. S5 and section S2 in the ESI†), similar to previous work at moderate tp.18,79–82 This suggests that the breaking interface is the same for both modes, and is likely between the relatively low surface energy C–C layers at the CNT base resulting from carbon accumulation during the CVD process. Therefore, σa–s is associated with the separation of the crystalline CNT base from the carbon on the catalyst surface, as shown in Fig. 2a.
With inputs of experimental values of σa–s, Ro, Ri, and E, and estimated values of β and n, eqn (1) is used to calculate γ as a function of tp to provide theoretical insight into CNT–substrate adhesion. The evolution of n with tp was estimated as follows for use in eqn (1) and (2). During Mode I for tp > 9 min, n is set to follow a cubic decay to reach ∼11% of its original value at growth termination, in agreement with previously reported measurements of n decay to ∼11% of the original n at termination due to CNT–substrate debonding during growth, and the subsequent loss of a self-supporting array structure.40,83 Incorporating this scaling into eqn (1) is consistent with the experimental Mode I E values (∼6.14 ± 1.7 MPa) in the expected range of 1–10 MPa based on prior work for similar CVD-grown aligned CNT arrays.30,42,46,84,85 In Mode I, significant moduli variations are not expected due to the minimal changes in carbon character. It is noted that this effective array modulus, not the orders-of-magnitude higher intrinsic CNT axial elastic modulus of 1 TPa,86 governs the bulk CNT array's interfacial behavior, similar to the mechanics governing the capillary densification of CNT arrays, for which CNT–substrate adhesion is an important consideration.27,87,88 Mode I n(tp) is therefore quantified by a cubic fit, as detailed in section S1 of the ESI.† The ∼11% lower n value at growth termination (calculated as ∼2.3 × 109 CNTs per cm2 at tp = 40 min) is kept constant in Mode II, since CNT growth in the vertical direction has stopped, and further information about n scaling after growth termination is not currently available. Quantification of n could be incorporated into this model in future studies. In addition, while we do observe additional growth attempts by several short, small-diameter CNTs in Mode II (Fig. S4†), consistent with prior work, these CNTs are not incorporated into the n scaling, since they are not pulled off of the substrate during tensile testing and therefore are not expected to contribute significantly to the bulk-scale adhesion response.28 Finally, continuity in σa–s, Ff–s, E, and γ between Mode I and Mode II is not enforced at tp = 40 min (see Fig. 4), since more data supplemented by stochastic simulations are required to accurately characterize the scaling of this transition. Additional details concerning γ, n, and E scaling with tp, including all experimentally measured and calculated values, are shown in Table S1 in section S1 of the ESI.†
With n(tp) established, γ is calculated viaeqn (1) to be 0.07 ± 0.02 J m−2 in Mode I and 1.5 ± 0.2 J m−2 in Mode II. These average values are then input into eqn (1) and (2) with the average E values, Ro scaling, and n scaling to plot continuous functions of σa–s(tp) and Ff–s(tp) in each Mode (Fig. 4). These γ values, which equate to surface energies of ∼0.033 J m−2 in Mode I and ∼0.75 J m−2 in Mode II, are in the range of intermolecular VDW forces for the separation of carbon layers that are proposed to be governing σa–s in this system.89–92 They are also consistent with previously reported surface energy values of graphitic C–C interfaces (i.e. CNTs, graphene, and graphite) in the range of 0.029–0.875 J m−2.66,89,91–96 Higher γ is attributed to carbon deposition in the array with a higher sp3 carbon character, exhibiting further interactions in addition to the ideal peeling of smooth, well-ordered sp2 graphitic surfaces with correspondingly lower surface energies.54,56,96 The calculated γ values also support experimental observations, as Raman spectroscopy analysis69,97–99 of the CNT base after array pull-off (see section S4 of the ESI†) shows that the CNTs exhibit a well-ordered, sp2 graphitic wall structure in Mode I, and a more defective, turbostratic sp3 carbon structure in Mode II as carbon deposits on the outer CNT walls at long tp.100 Since the wafer surface (Fig. S4†) is expected to have a broader distribution of carbon character as compared to the CNT roots (i.e. having carbon that encapsulates the activated catalysts, covers larger iron particles and the alumina surface, and comprises residual short CNTs),40,76,83 analysis of the CNT array roots after pull-off can provide more instructive characterization of the deposited carbon that gives rise to the adhesion evolution. Therefore, increases in σa–s in Mode II are likely attributed to higher Ro, E, and γ based on the sp2-to-sp3-dominated carbon evolution and deposition with tp,54,56,96 where significant changes in E and γ may be especially responsible for the rapid adhesion evolution following growth termination. In sum, the application of this adhesion model to our aligned CNT arrays shows that σa–s evolves non-monotonically with tp and increases by an order of magnitude after growth termination, which is attributed to n decay during growth and a subsequent order-of-magnitude increase in E and γ due to carbon deposition in Mode II.
Discussion
Mechanistic insights into CNT–substrate adhesion
The CNT–substrate adhesion model is used to predict γ, σa–s, and Ff–s, which corroborates experimental results of iron-free CNT roots and C–C layer separation during CNT array pull-off. Since γ for CNTs with VDW-dominated adhesion is approximately constant for CNTs with more than 3 walls,101 and γ is assumed to be higher in Mode II only due to the increased turbostratic/disordered carbon character, γ is kept constant throughout Mode I and Mode II to represent the VDW-dominated CNT–C layer interaction as the weakest interface governing CNT–substrate separation. This carbon layer may form during the cooling process due to carbon precipitation from the iron catalyst,81,102,103 and it may also increase in thickness after growth termination due to catalyst deactivation39,104,105 and deposition of additional carbon during Mode II. Furthermore, since the interaction energy between C–Fe is higher (yielding γ ∼ 1.84 J m−2 or greater)19,39,106,107 and this is inconsistent with our σa–s and γ calculations, it is proposed that the separated carbon layer at the CNT root remains on the Fe catalyst after CNT pull-off.108 Still higher are the Fe–alumina interaction energies19,82 as well as iron oxide109,110 and iron carbide,111,112 which would all yield γ > 2 J m−2, exceeding the γ values here of 0.07 and 1.5 J m−2 in Mode I and Mode II, respectively. Therefore, in contrast to previous work at short tp (on the order of seconds, where the Fe catalyst was observed to stay attached to the CNT roots during the tensile pull-off of a microscale CNT array),28 only the C–C interfaces are observed to separate in this system at moderate to long tp, yielding a maximum σa–s of ∼285 kPa after 80 min of processing. Based on these results, it is plausible that additional increases in σa–s may be obtained via extended carbon deposition at longer tp to further engineer the substrate adhesion strength of aligned NF arrays.Next, the mechanisms governing CNT array deformation and substrate adhesion are investigated as a function of tp. Comparing the average experimental E values for Mode I and Mode II (6.14 ± 1.7 MPa and 47.1 ± 21 MPa, respectively) to the mechanical properties of carbon systems reveals a connection to two elastic constants for carbon materials: C44 ≈ 0.35 GPa for turbostratic graphite, the inter-layer shear modulus,113 and C33 ≈ 37 GPa, the inter-layer cleavage modulus.113 These E values can be obtained by scaling the two governing elastic constants by the CNT Vf (here 1 vol%), since CNT arrays are nanoporous materials, and the elastic axial moduli in self-assembled nanoporous films can exhibit a linear, foam-like scaling with density due to two-dimensional effects.45,46 Therefore, E in Mode I and Mode II can be estimated as 1% of 0.35 GPa (C44) and 37 GPa (C33), with an additional reduction of C33 by 11% due to reduced n and effective stiffness at growth termination for Mode II. This yields ∼3.5 MPa for Mode I and ∼41 MPa for Mode II, which matches closely with experimental values and prior work obtaining CNT array moduli in the MPa range.27,42,45,113 Therefore, it is proposed that in the transition from Mode I to Mode II, carbon deposition in the array (i.e. carbon deposited conformally onto the CNTs in the array) causes a change in deformation mechanism from C44 to C33, consistent with the directionally dependent elastic constants of turbostratic graphitic crystallites and the relative importance of C33 as the bending stiffness of an individual CNT, which increases nonlinearly (R4) by the carbon deposition versus a linear increase for C44. To support this trend, E has previously been observed to scale with NF diameter,79 the number of CNT walls and contact area,40,114 carbon deposition on the array,45 and CNT Vf.42,45,114,115
Applicability to previously reported CNT–substrate adhesion
Modeling results that are developed and experimentally-validated here are compared to past work to assess the model's consistency with previously characterized CNT arrays. Fig. 1c shows that CNT–CNT and CNT–substrate adhesion forces versus tp are of similar magnitude, showing that the weakest interface between CNTs and their growth substrate can be between the CNT roots and the carbon layer as observed here, which has not previously been modeled at the bulk scale. This result agrees with our experiments, modeling, and prior experimental evidence that Fe particles can remain on the substrate after CNT array separation,79,80,108 as measured via SEM and X-ray photoelectron spectroscopy for aligned CNT arrays.18,81,82 Specifically, previously reported Ff–s values of ∼0.133–0.28 nN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31,33,65,79 are in the same range as the calculated results of ∼0.204 ± 0.007 nN on average in Mode I (before growth termination), as well as at the start of Mode I: ∼0.190 ± 0.011 nN for a ∼1 mm-tall CNT array (tp ≈ 9 min, ∼9 nm outer CNT diameter, and 3–7 CNT walls). This agrees closely with the force output of Ff–s ∼ 0.16 nN presented in ref. 31 for CNTs having an outer diameter of 9 nm and 5 walls. Additionally, prior work demonstrating individual CNTs breaking at 300 nN due to vertical tensile loading116 supports the argument that even at long tp, CNT failure within the nanotube is likely not the main mechanism governing σa–s, since Ff–s only reaches up to ∼12 nN at the longest tp. Therefore, it is reasonable that CNT array–substrate separation is attributed to C–C layer cleavage at the CNT base. Since σa–s values shown in Fig. 4a (∼40–285 kPa) are of the same magnitude as σa–s previously reported to range from tens to hundreds of kPa for similar CNT array areas, E, and n,29,32,76 prior systems may also be described via this theoretical framework to enable tunable substrate adhesion.
31,33,65,79 are in the same range as the calculated results of ∼0.204 ± 0.007 nN on average in Mode I (before growth termination), as well as at the start of Mode I: ∼0.190 ± 0.011 nN for a ∼1 mm-tall CNT array (tp ≈ 9 min, ∼9 nm outer CNT diameter, and 3–7 CNT walls). This agrees closely with the force output of Ff–s ∼ 0.16 nN presented in ref. 31 for CNTs having an outer diameter of 9 nm and 5 walls. Additionally, prior work demonstrating individual CNTs breaking at 300 nN due to vertical tensile loading116 supports the argument that even at long tp, CNT failure within the nanotube is likely not the main mechanism governing σa–s, since Ff–s only reaches up to ∼12 nN at the longest tp. Therefore, it is reasonable that CNT array–substrate separation is attributed to C–C layer cleavage at the CNT base. Since σa–s values shown in Fig. 4a (∼40–285 kPa) are of the same magnitude as σa–s previously reported to range from tens to hundreds of kPa for similar CNT array areas, E, and n,29,32,76 prior systems may also be described via this theoretical framework to enable tunable substrate adhesion.
Finally, the utility of this model to describe and accurately predict the substrate adhesion of other CNT arrays is demonstrated by the experimental-modeling agreement in Fig. 2b and c, and by applying this framework to the exemplary CNT arrays in ref. 28, where agreement between their Ff–s ≈ 12 nN per CNT and σa–s ≈ 6.1 MPa is achieved when eqn (1) and (2) are used with their reported Ro = 5.5 nm, Ri = 3.6 nm, n = 5 × 1010 CNTs cm−2, γ ≈ 4.1 J m−2 (signifying the suggested Fe–alumina separating interface),19,82β = 1 (assuming ideal CNT–substrate contact due to the early stage of growth and small array size), and E ≈ 20 MPa, which was not reported but is assumed to be reasonable due to their higher n compared to our system, which can yield a greater number of inter-CNT connections to reinforce the array.28,42 The ability of this model to accurately reflect the breaking Fe–alumina interface that was proposed in ref. 28, and its agreement with the previously reported NF–substrate adhesion values plotted in Fig. 2, show that this model may be extensible to different NF arrays given that the appropriate parameters are known or can be estimated. This work thereby offers an experimental–theoretical framework that may be broadly applied and supports the general trends in the literature, which report an increased adhesion strength with the surface energy and total VDW interaction energy51,79 attributed to increases in NF diameter,79,101,117 chemical and structural evolution at the adhesive interface,54,56 and contact area.59
Conclusions
In this work, we present experimental evidence and model-informed mechanistic insight for the non-monotonic substrate adhesion evolution for aligned carbon nanotube (CNT) arrays, an exemplary nanofiber (NF) array system. We experimentally quantify the CNT array–substrate adhesion strength (σa–s) for CNT process times (tp) ranging from 9–80 min for mm-tall, cm-wide CNT arrays via uniform tensile CNT array separation from a flat growth substrate. Here, σa–s(tp) is modeled via contact mechanics to better understand and predict CNT–substrate adhesion during CVD processing. We report that the evolution of σa–s with tp is driven by the bimodal scaling of CNT geometry, number density (n), effective elastic array modulus (E), and C–C interfacial work of adhesion (γ) during two regimes, termed Mode I (‘Growth’) and Mode II (‘Post-Growth’) separated by growth termination. Between Mode I and Mode II, experiments and modeling indicate an order-of-magnitude increase in σa–s (∼40→285 kPa) and E (∼6→47 MPa), a two-orders-of-magnitude increase in the adhesion force per CNT (∼0.190→12.3 nN) and γ (∼0.07→1.5 J m−2), and an order-of-magnitude decrease in n (∼2.10 × 1010→2.3 × 109 CNTs per cm2).In this work, the observed increase in CNT wall thickness and sp3 bond character with tp shows that the accumulation of carbon species in the CNT array strongly affects the mechanical response, which may be indicative of a change in deformation mechanism, i.e. a shift in the dominating carbon elastic constant from C44 to C33. These results indicate that the CNTs are not breaking in tension, as experiments and modeling show that the CNT roots separate from their carbon-covered Fe catalyst particles at a C–C interface during tensile pull-off, leaving the Fe particles completely on the substrate in each mode. Finally, the utility of this model to accurately describe the substrate adhesion of previously synthesized aligned NF arrays is demonstrated, establishing a theoretical framework to help inform process design and enhance NF–substrate adhesion tunability for a wide range of commercial applications. In the future, additional characterization via in situ high-resolution SEM imaging during pull-off tests, TEM imaging of the CNT–substrate interfaces with tp, and in situ X-ray analysis of the CNT-catalyst evolution during CNT nucleation at short tp, steady growth, growth termination, and extended tp values would help to elucidate catalytic phase transformations, diffusion, and the structural evolution of the CNT–substrate interface. Using this approach, these results could enable versatile NF–substrate adhesion for better control over NF post-processing techniques, such as capillary densification, the spinning of NF yarns from forests, and post-growth NF array transfer for composite reinforcement, as well as for the design of high-value applications such as thermal interface materials, sensors, interconnects, field emitters, and dry adhesives, where interfacial bonding and morphology are critical for application-specific performance.
Methods
Carbon nanotube growth via chemical vapor deposition
Vertically aligned multiwall CNT arrays were grown by a base-growth mechanism in a 22 mm internal diameter quartz tube furnace at atmospheric pressure via a previously described thermal catalytic CVD process using ethylene as the carbon source and 600 ppm of water vapor added to inert helium gas.73,118 The CNTs were grown on a catalytic layer composed of 1 nm Fe on 10 nm Al2O3 deposited via electron beam physical vapor deposition on 1 cm × 1 cm SiO2/Si substrates.27 The growing CNTs self-assembled into aligned arrays of h up to ∼4.7 mm for tp from 9–80 min, where tp is the CNT process time (i.e. duration of ethylene gas flow during the CVD growth process). For this range of tp, the vertical arrays were comprised of multiwalled CNTs with an average outer diameter of ∼8–18 nm (3–16 walls with ∼6 nm inner diameter and intrinsic CNT density of ≈1.6 g cm−3),119 and an inter-CNT spacing of ∼60–80 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 and CNT volume fraction of ∼1%73–75 (for a nominal ∼10 min growth period yielding 1 mm-tall CNTs). A minimum of four samples were grown for each tp, and the resulting CNT array heights (h) were measured via optical microscopy using a Carl Zeiss Axiotech 30 HD optical microscope.76
75 and CNT volume fraction of ∼1%73–75 (for a nominal ∼10 min growth period yielding 1 mm-tall CNTs). A minimum of four samples were grown for each tp, and the resulting CNT array heights (h) were measured via optical microscopy using a Carl Zeiss Axiotech 30 HD optical microscope.76
Carbon nanotube–substrate adhesion testing
To measure the normal CNT array–substrate adhesion force (Fa–s) via vertical CNT array–substrate separation/pull-off, aluminum SEM stubs with silver epoxy were used to mount the CNT–substrate samples in the grips of a Zwick Roell mechanical tester operating in the tensile testing configuration, following the procedure first reported in ref. 76. A ∼1 mm-thick layer of a viscous two-part silver epoxy was applied to the face of an SEM stub, on top of which a CNT array–Si wafer sample was placed (wafer side contacting epoxy) and cured for 4 h at room temperature. The stub was inserted into the lower grip of the mechanical tester. Then, a ∼1 mm-thick layer of epoxy was applied to the face of a second SEM stub, which was inserted into the upper grip and lowered until it contacted and covered the top of the CNT array, experiencing a load of ∼0.1 N. The load returned to zero as the epoxy relaxed <30 microns into the stub–CNT interface, after which it was cured. ∼4–5 samples for each tp were then tested following ASTM D5179-02 (crosshead speed of 5 cm min−1, 500 N load cell), recording the load and displacement until the CNT array–Si wafer interfaces were ultimately separated. See section S2 in the ESI† for additional details.CNT morphology characterization via electron microscopy
SEM was performed using a Zeiss Merlin High-resolution SEM with an acceleration voltage of 1 kV and an InLens detector. TEM samples were prepared via the ultrasonication of CNT array sections in isopropyl alcohol for five minutes. These CNTs were then dropcast onto a copper TEM grid, and the solvent was evaporated. The sample preparation of the TEM specimens was not limited to a specific location in the CNT array, and so the measured CNT wall thickness (a) values represent an average throughout the array for each tp.76 The TEM analysis was performed using a JEOL 2100 TEM at an acceleration voltage of 200 kV.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by Airbus, Boeing, ANSYS, Embraer, Lockheed Martin, Saab AB, Saertex, and Teijin Carbon America through MIT's Nano-Engineered Composite aerospace STructures (NECST) Consortium, the U. S. Army Research Office through the Institute for Soldier Nanotechnologies at MIT, under Contract Number W911NF-13-D-0001 and W911NF-07-D-0004, and the National Aeronautics and Space Administration (NASA) Space Technology Research Institute (STRI) for Ultra-Strong Composites by Computational Design (US-COMP), grant number NNX17AJ32G. This work was performed in part at: the MIT MRSEC Shared Experimental Facilities supported by the National Science Foundation under award number DMR-0819762, facilities supported by the U. S. Army Research Office through the Institute for Soldier Nanotechnologies at MIT, under Collaborative Agreement Number W911NF-18-2-0048, and in part through the use of MIT's Microsystems Technology Laboratories and the Center for Nanoscale Systems (CNS) at Harvard University, a member of the National Nanotechnology Infrastructure Network (NNIN), which is supported by the National Science Foundation under award no. ECS-0335765. A. Kaiser was supported by the Department of Defense through the National Defense Science and Engineering Graduate Fellowship (NDSEG) Program. At MIT, the authors thank the members of necstlab for technical support and advice, and Prof. C. Thompson and Prof. M. Cima for helpful discussions.References
- R. Rao, C. L. Pint, A. E. Islam, R. S. Weatherup, S. Hofmann, E. R. Meshot, F. Wu, C. Zhou, N. Dee, P. B. Amama, J. Carpena-Nunez, W. Shi, D. L. Plata, E. S. Penev, B. I. Yakobson, P. B. Balbuena, C. Bichara, D. N. Futaba, S. Noda, H. Shin, K. S. Kim, B. Simard, F. Mirri, M. Pasquali, F. Fornasiero, E. I. Kauppinen, M. Arnold, B. A. Cola, P. Nikolaev, S. Arepalli, H.-M. Cheng, D. N. Zakharov, E. A. Stach, J. Zhang, F. Wei, M. Terrones, D. B. Geohegan, B. Maruyama, S. Maruyama, Y. Li, W. W. Adams and A. J. Hart, ACS Nano, 2018, 12, 11756–11784 CrossRef CAS PubMed.
- W. Wu, Nanoscale, 2017, 9, 7342–7372 RSC.
- K. Kenry and C. T. Lim, Prog. Polym. Sci., 2017, 70, 1–17 CrossRef.
- H. Sun, Y. Zhang, J. Zhang, X. Sun and H. Peng, Nat. Rev. Mater., 2017, 2, 17023 CrossRef CAS.
- M. M. Shulaker, G. Hills, R. S. Park, R. T. Howe, K. Saraswat, H.-S. P. Wong and S. Mitra, Nature, 2017, 547, 74 CrossRef CAS PubMed.
- D. Zhong, Z. Zhang, L. Ding, J. Han, M. Xiao, J. Si, L. Xu, C. Qiu and L.-M. Peng, Nat. Electron., 2018, 1, 40–45 CrossRef CAS.
- M. F. L. De Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Science, 2013, 339, 535–539 CrossRef CAS PubMed.
- J. Di, X. Wang, Y. Xing, Y. Zhang, X. Zhang, W. Lu, Q. Li and Y. T. Zhu, Small, 2014, 10, 4606–4625 CrossRef CAS PubMed.
- Y. Bai, R. Zhang, X. Ye, Z. Zhu, H. Xie, B. Shen, D. Cai, B. Liu, C. Zhang, Z. Jia, S. Zhang, X. Li and F. Wei, Nat. Nanotechnol., 2018, 13, 589–595 CrossRef CAS PubMed.
- L. Zhang, G. Zhang, C. Liu and S. Fan, Nano Lett., 2012, 12, 4848–4852 CrossRef CAS PubMed.
- S. J. Kim, S. A. Park, Y.-C. Kim and B.-K. Ju, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2017, 35, 011802 Search PubMed.
- S. H. Tawfick, J. Bico and S. Barcelo, MRS Bull., 2016, 41, 108–114 CrossRef CAS.
- I. Lahiri, D. Lahiri, S. Jin, A. Agarwal and W. Choi, ACS Nano, 2011, 5, 780–787 CrossRef CAS PubMed.
- A. C. Ferrari, F. Bonaccorso, V. Fal'ko, K. S. Novoselov, S. Roche, P. Bøggild, S. Borini, F. H. L. Koppens, V. Palermo, N. Pugno, J. A. Garrido, R. Sordan, A. Bianco, L. Ballerini, M. Prato, E. Lidorikis, J. Kivioja, C. Marinelli, T. Ryhanen, A. Morpurgo, J. N. Coleman, V. Nicolosi, L. Colombo, A. Fert, M. Garcia-Hernandez, A. Bachtold, G. F. Schneider, F. Guinea, C. Dekker, M. Barbone, Z. Sun, C. Galiotis, A. N. Grigorenko, G. Konstantatos, A. Kis, M. Katsnelson, L. Vandersypen, A. Loiseau, V. Morandi, D. Neumaier, E. Treossi, V. Pellegrini, M. Polini, A. Tredicucci, G. M. Williams, B. Hee Hong, J.-H. Ahn, J. Min Kim, H. Zirath, B. J. van Wees, H. van der Zant, L. Occhipinti, A. Di Matteo, I. A. Kinloch, T. Seyller, E. Quesnel, X. Feng, K. Teo, N. Rupesinghe, P. Hakonen, S. R. T. Neil, Q. Tannock, T. Lofwander and J. Kinaret, Nanoscale, 2015, 7, 4598–4810 RSC.
- Y. Zhang, E. Suhir, Y. Xu and C. Gu, J. Mater. Res., 2006, 21, 2922–2926 CrossRef CAS.
- B. Chen, G. Zhong, P. Goldberg Oppenheimer, C. Zhang, H. Tornatzky, S. Esconjauregui, S. Hofmann and J. Robertson, ACS Appl. Mater. Interfaces, 2015, 7, 3626–3632 CrossRef CAS PubMed.
- B. Hu, H. Ago, N. Yoshihara and M. Tsuji, J. Phys. Chem. C, 2010, 114, 3850–3856 CrossRef CAS.
- C. L. Pint, Y.-Q. Xu, S. Moghazy, T. Cherukuri, N. T. Alvarez, E. H. Haroz, S. Mahzooni, S. K. Doorn, J. Kono, M. Pasquali and R. H. Hauge, ACS Nano, 2010, 4, 1131–1145 CrossRef CAS PubMed.
- L. Ping, P.-X. Hou, H. Wang, M. Chen, Y. Zhao, H. Cong, C. Liu and H.-M. Cheng, Carbon, 2018, 133, 275–282 CrossRef CAS.
- Y. Hwang, S. Yoo, N. Lim, S. M. Kang, H. Yoo, J. Kim, Y. Hyun, G. Y. Jung and H. C. Ko, ACS Nano, 2020, 14, 118–128 CrossRef CAS PubMed.
- J. Ni and Y. Li, Adv. Energy Mater., 2016, 6, 1600278 CrossRef.
- L. Mai, X. Tian, X. Xu, L. Chang and L. Xu, Chem. Rev., 2014, 114, 11828–11862 CrossRef CAS PubMed.
- Y. Zhang, Y.-J. Heo, Y.-R. Son, I. In, K.-H. An, B.-J. Kim and S.-J. Park, Carbon, 2019, 142, 445–460 CrossRef CAS.
- E. S. Avraham, A. S. Westover, A. Itzhak, L. Shani, V. Mor, O. Girshevitz, C. L. Pint and G. D. Nessim, Carbon, 2018, 130, 273–280 CrossRef.
- E. R. Meshot, M. Bedewy, K. M. Lyons, A. R. Woll, K. A. Juggernauth, S. Tawfick and A. J. Hart, Nanoscale, 2010, 2, 896–900 RSC.
- R. Guzman de Villoria, A. J. Hart and B. L. Wardle, ACS Nano, 2011, 5, 4850–4857 CrossRef CAS PubMed.
- A. L. Kaiser, I. Y. Stein, K. Cui and B. L. Wardle, Phys. Chem. Chem. Phys., 2018, 20, 3876–3881 RSC.
- J. Brown, T. Hajilounezhad, N. T. Dee, S. Kim, A. J. Hart and M. R. Maschmann, ACS Appl. Mater. Interfaces, 2019, 38(11), 35221–35227 CrossRef PubMed.
- P. Pour Shahid Saeed Abadi, S. B. Hutchens, J. R. Greer, B. A. Cola and S. Graham, Appl. Phys. Lett., 2013, 102, 223103 CrossRef.
- Y. Gao, T. Kodama, Y. Won, S. Dogbe, L. Pan and K. E. Goodson, Carbon, 2012, 50, 3789–3798 CrossRef CAS.
- A. J. Hart and A. H. Slocum, Nano Lett., 2006, 6, 1254–1260 CrossRef CAS PubMed.
- P. Pour Shahid Saeed Abadi, S. B. Hutchens, J. R. Greer, B. A. Cola and S. Graham, Nanoscale, 2012, 4, 3373–3380 RSC.
- J. Choi, Y. Eun and J. Kim, ACS Appl. Mater. Interfaces, 2014, 6, 6598–6605 CrossRef CAS PubMed.
- B. Chen, M. Gao, J. M. Zuo, S. Qu, B. Liu and Y. Huang, Appl. Phys. Lett., 2003, 83, 3570–3571 CrossRef CAS.
- B. Bhushan, X. Ling, A. Jungen and C. Hierold, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165428 CrossRef.
- B. Bhushan and X. Ling, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045429 CrossRef.
- C. Ke, M. Zheng, G. Zhou, W. Cui, N. Pugno and R. N. Miles, Small, 2010, 6, 438–445 CrossRef CAS PubMed.
- A. Cao, V. P. Veedu, X. Li, Z. Yao, M. N. Ghasemi-Nejhad and P. M. Ajayan, Nat. Mater., 2005, 4, 540 CrossRef CAS PubMed.
- M. Stadermann, S. P. Sherlock, J.-B. In, F. Fornasiero, H. G. Park, A. B. Artyukhin, Y. Wang, J. J. De Yoreo, C. P. Grigoropoulos, O. Bakajin, A. A. Chernov and A. Noy, Nano Lett., 2009, 9, 738–744 CrossRef CAS PubMed.
- M. Bedewy, E. R. Meshot, H. Guo, E. A. Verploegen, W. Lu and A. J. Hart, J. Phys. Chem. C, 2009, 113, 20576–20582 CrossRef CAS.
- X. Cui, W. Wei, C. Harrower and W. Chen, Carbon, 2009, 47, 3441–3451 CrossRef CAS.
- I. Y. Stein, D. J. Lewis and B. L. Wardle, Nanoscale, 2015, 7, 19426–19431 RSC.
- S. Cranford, H. Yao, C. Ortiz and M. J. Buehler, J. Mech. Phys. Solids, 2010, 58, 409–427 CrossRef CAS.
- M. R. Maschmann, Carbon, 2015, 86, 26–37 CrossRef CAS.
- Y. Won, Y. Gao, M. A. Panzer, R. Xiang, S. Maruyama, T. W. Kenny, W. Cai and K. E. Goodson, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20426–20430 CrossRef CAS PubMed.
- H. Cebeci, I. Y. Stein and B. L. Wardle, Appl. Phys. Lett., 2014, 104, 023117 CrossRef.
- V. L. Popov, R. Pohrt and Q. Li, Friction, 2017, 5, 308–325 CrossRef.
- V. Popov, M. Heß and E. Willert, Handbook of Contact Mechanics: Exact Solutions of Axisymmetric Contact Problems, Springer Berlin Heidelberg, 2019 Search PubMed.
- D. Tabor, J. Colloid Interface Sci., 1977, 58, 2–13 CrossRef CAS.
- K. Kendall, J. Phys. D: Appl. Phys., 1971, 4, 1186 CrossRef.
- R. S. Ruoff, J. Tersoff, D. C. Lorents, S. Subramoney and B. Chan, Nature, 1993, 364, 514–516 CrossRef CAS.
- R. Spolenak, G. Stanislav, G. Huajian and A. Eduard, Proc. R. Soc. A, 2005, 461, 305–319 CrossRef.
- H. Gao, X. Wang, H. Yao, S. Gorb and E. Arzt, Mech. Mater., 2005, 37, 275–285 CrossRef.
- M. R. Roenbeck, X. Wei, A. M. Beese, M. Naraghi, A. Furmanchuk, J. T. Paci, G. C. Schatz and H. D. Espinosa, ACS Nano, 2014, 8, 124–138 CrossRef CAS PubMed.
- C. T. Wirth, S. Hofmann and J. Robertson, Diamond Relat. Mater., 2008, 17, 1518–1524 CrossRef CAS.
- M. R. Roenbeck, A. Furmanchuk, Z. An, J. T. Paci, X. Wei, S. T. Nguyen, G. C. Schatz and H. D. Espinosa, Nano Lett., 2015, 15, 4504–4516 CrossRef CAS PubMed.
- Y. Chen, D. Ding, C. Zhu, J. Zhao and T. Rabczuk, Compos. Struct., 2019, 208, 150–167 CrossRef.
- M. R. Maschmann, Q. Zhang, R. Wheeler, F. Du, L. Dai and J. Baur, ACS Appl. Mater. Interfaces, 2011, 3, 648–653 CrossRef CAS.
- L. Qu, L. Dai, M. Stone, Z. Xia and Z. L. Wang, Science, 2008, 322, 238–242 CrossRef CAS PubMed.
- B. Aksak, M. P. Murphy and M. Sitti, IEEE International Conference on Robotics and Automation, 2008, pp. 3058–3063 Search PubMed.
- D. Sameoto and C. Menon, J. Micromech. Microeng., 2009, 19, 115002 CrossRef.
- Y. Tian, N. Pesika, H. Zeng, K. Rosenberg, B. Zhao, P. McGuiggan, K. Autumn and J. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19320–19325 CrossRef CAS PubMed.
- Y. P. Zhao, L. S. Wang and T. X. Yu, J. Adhes. Sci. Technol., 2003, 17, 519–546 CrossRef CAS.
- V. Tinnemann, L. Hernandez, S. C. L. Fischer, E. Arzt, R. Bennewitz and R. Hensel, Adv. Funct. Mater., 2019, 29, 1807713 CrossRef.
- M. Bedewy, E. R. Meshot and A. J. Hart, Carbon, 2012, 50, 5106–5116 CrossRef CAS.
- Y. Zhao, T. Tong, L. Delzeit, A. Kashani, M. Meyyappan and A. Majumdar, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 2006, 24, 331–335 CrossRef CAS.
- X. Li, X. Zhang, L. Ci, R. Shah, C. Wolfe, S. Kar, S. Talapatra and P. M. Ajayan, Nanotechnology, 2008, 19, 455609 CrossRef PubMed.
- S. Yasuda, T. Hiraoka, D. N. Futaba, T. Yamada, M. Yumura and K. Hata, Nano Lett., 2009, 9, 769–773 CrossRef CAS PubMed.
- S. Santangelo, M. Lanza and C. Milone, J. Phys. Chem. C, 2013, 117, 4815–4823 CrossRef CAS.
- V. Thiagarajan, X. Wang, P. Bradford, Y. Zhu and F. Yuan, Compos. Sci. Technol., 2014, 90, 82–87 CrossRef CAS.
- A. A. Puretzky, D. B. Geohegan, S. Jesse, I. N. Ivanov and G. Eres, Appl. Phys. A, 2005, 81, 223–240 CrossRef CAS.
- C. Singh, M. S. Shaffer and A. H. Windle, Carbon, 2003, 41, 359–368 CrossRef CAS.
- J. Lee, I. Y. Stein, M. E. Devoe, D. J. Lewis, N. Lachman, S. S. Kessler, S. T. Buschhorn and B. L. Wardle, Appl. Phys. Lett., 2015, 106, 053110 CrossRef.
- I. Y. Stein and B. L. Wardle, Phys. Chem. Chem. Phys., 2016, 18, 694 RSC.
- I. Y. Stein and B. L. Wardle, Phys. Chem. Chem. Phys., 2013, 15, 4033–4040 RSC.
- D. L. Lidston, M.Sc. thesis, Massachusetts Institute of Technology, 2017.
- D. N. Futaba, K. Hata, T. Namai, T. Yamada, K. Mizuno, Y. Hayamizu, M. Yumura and S. Iijima, J. Phys. Chem. B, 2006, 110, 8035–8038 CrossRef CAS PubMed.
- L. Zhu, Y. Xiu, D. W. Hess and C.-P. Wong, Nano Lett., 2005, 5, 2641–2645 CrossRef CAS PubMed.
- J.-H. Han, R. A. Graff, B. Welch, C. P. Marsh, R. Franks and M. S. Strano, ACS Nano, 2008, 2, 53–60 CrossRef CAS PubMed.
- D.-M. Tang, C. Liu, W.-J. Yu, L.-L. Zhang, P.-X. Hou, J.-C. Li, F. Li, Y. Bando, D. Golberg and H.-M. Cheng, ACS Nano, 2014, 8, 292–301 CrossRef CAS PubMed.
- C. L. Pint, Y.-Q. Xu, M. Pasquali and R. H. Hauge, ACS Nano, 2008, 2, 1871–1878 CrossRef CAS PubMed.
- C. Mattevi, C. T. Wirth, S. Hofmann, R. Blume, M. Cantoro, C. Ducati, C. Cepek, A. Knop-Gericke, S. Milne, C. Castellarin-Cudia, S. Dolafi, A. Goldoni, R. Schloegl and J. Robertson, J. Phys. Chem. C, 2008, 112, 12207–12213 CrossRef CAS.
- M. Bedewy, E. R. Meshot, M. J. Reinker and A. J. Hart, ACS Nano, 2011, 5, 8974–8989 CrossRef CAS PubMed.
- X. Liang, J. Shin, D. Magagnosc, Y. Jiang, S. J. Park, A. J. Hart, K. Turner, D. S. Gianola and P. K. Purohit, Int. J. Solids Struct., 2017, 122–123, 196–209 CrossRef CAS.
- C.-C. Su, T.-X. Chen and S.-H. Chang, Materials, 2017, 10, 206 CrossRef PubMed.
- J.-P. Salvetat, J.-M. Bonard, N. H. Thomson, A. J. Kulik, L. Forro, W. Benoit and L. Zuppiroli, Appl. Phys. A, 1999, 69, 255–260 CrossRef CAS.
- X. Lim, H. W. G. Foo, G. H. Chia and C.-H. Sow, ACS Nano, 2010, 4, 1067–1075 CrossRef CAS PubMed.
- A. L. Kaiser, I. Y. Stein, K. Cui and B. L. Wardle, Nano Futures, 2019, 3, 011003 CrossRef CAS.
- S. C. Roh, E. Y. Choi, Y. S. Choi and C. Kim, Polymer, 2014, 55, 1527–1536 CrossRef CAS.
- A. Zebda, H. Sabbah, S. Ababou-Girard, F. Solal and C. Godet, Appl. Surf. Sci., 2008, 254, 4980–4991 CrossRef CAS.
- X. Yuan, J. Yang, J. He, H. H. Tan and C. Jagadish, J. Phys. D: Appl. Phys., 2018, 51, 283002 CrossRef.
- W. Li, Y. Li, M. Sheng, S. Cui, Z. Wang, X. Zhang, C. Yang, Z. Yu, Y. Zhang, S. Tian, Z. Dai and Q. Xu, Langmuir, 2019, 35, 4527–4533 CrossRef CAS.
- L. S. Kocherlakota, B. A. Krajina and R. M. Overney, J. Chem. Phys., 2015, 143, 241105 CrossRef.
- R. J. Cartwright, S. Esconjauregui, R. S. Weatherup, D. Hardeman, Y. Guo, E. Wright, D. Oakes, S. Hofmann and J. Robertson, Carbon, 2014, 75, 327–334 CrossRef CAS.
- M. Xia, C. Liang, Z. Cheng, R. Hu and S. Liu, Phys. Chem. Chem. Phys., 2019, 21, 1217–1223 RSC.
- R. Zacharia, H. Ulbricht and T. Hertel, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155406 CrossRef.
- M. S. Dresselhaus, A. Jorio, M. Hofmann, G. Dresselhaus and R. Saito, Nano Lett., 2010, 10, 751–758 CrossRef CAS PubMed.
- A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 14095–14107 CrossRef CAS.
- L. G. Cancado, A. Jorio, E. H. M. Ferreira, F. Stavale, C. A. Achete, R. B. Capaz, M. V. O. Moutinho, A. Lombardo, T. S. Kulmala and A. C. Ferrari, Nano Lett., 2011, 11, 3190–3196 CrossRef CAS PubMed.
- A. L. Kaiser, M.Sc. thesis, Massachusetts Institute of Technology, 2019.
- X. Yuan and Y. Wang, J. Phys. D: Appl. Phys., 2017, 50, 395303 CrossRef.
- M. De Volder, S. H. Tawfick, S. J. Park, D. Copic, Z. Zhao, W. Lu and A. J. Hart, Adv. Mater., 2010, 22, 4384–4389 CrossRef CAS PubMed.
- M. Bedewy, J. Mater. Res., 2017, 32, 153–165 CrossRef CAS.
- V. Balakrishnan, M. Bedewy, E. R. Meshot, S. W. Pattinson, E. S. Polsen, F. Laye, D. N. Zakharov, E. A. Stach and A. J. Hart, ACS Nano, 2016, 10, 11496–11504 CrossRef CAS PubMed.
- S. Jeong, J. Lee, H.-C. Kim, J. Y. Hwang, B.-C. Ku, D. N. Zakharov, B. Maruyama, E. A. Stach and S. M. Kim, Nanoscale, 2016, 8, 2055–2062 RSC.
- M. He, Y. Magnin, H. Amara, H. Jiang, H. Cui, F. Fossard, A. Castan, E. Kauppinen, A. Loiseau and C. Bichara, Carbon, 2017, 113, 231–236 CrossRef CAS.
- C. Zhang, A. C. van Duin, J. W. Seo and D. Seveno, Carbon, 2017, 115, 589–599 CrossRef CAS.
- J.-Q. Huang, Q. Zhang, M.-Q. Zhao and F. Wei, Carbon, 2010, 48, 1441–1450 CrossRef CAS.
- D. Tromans and J. Meech, Miner. Eng., 2002, 15, 1027–1041 CrossRef CAS.
- A. Schron and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 165112 CrossRef.
- S. Zhao, X.-W. Liu, C.-F. Huo, Y.-W. Li, J. Wang and H. Jiao, J. Catal., 2012, 294, 47–53 CrossRef CAS.
- H. Hugosson, O. Eriksson, U. Jansson, A. Ruban, P. Souvatzis and I. Abrikosov, Surf. Sci., 2004, 557, 243–254 CrossRef CAS.
- G. Savini, Y. Dappe, S. Oberg, J.-C. Charlier, M. Katsnelson and A. Fasolino, Carbon, 2011, 49, 62–69 CrossRef CAS.
- G. Guhados, W. Wan, X. Sun and J. L. Hutter, J. Appl. Phys., 2007, 101, 033514 CrossRef.
- N. Dee, M. Bedewy, A. Rao, J. Beroz, B. Lee, E. R. Meshot, C. A. Chazot, P. R. Kidambi, H. Zhao, T. Serbowicz, K. Teichert, P. K. Purohit and A. J. Hart, Chem. Mater., 2019, 31, 407–418 CrossRef CAS.
- K. Liew, C. Wong and M. Tan, Acta Mater., 2006, 54, 225–231 CrossRef CAS.
- J. Liu, X. Tang, Y. Li, Z. Dai, F. Chen, H. Huang, H. Li, H. Liu and D. Chen, Mater. Chem. Phys., 2017, 196, 160–169 CrossRef CAS.
- I. Y. Stein, A. L. Kaiser, A. J. Constable, L. Acauan and B. L. Wardle, J. Mater. Sci., 2017, 52, 13799–13811 CrossRef CAS.
- I. Y. Stein, N. Lachman, M. E. Devoe and B. L. Wardle, ACS Nano, 2014, 8, 4591–4599 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: CNT–substrate adhesion modeling details (Fig. S1–S2, Table S1, eqn (S1)–(S10)), adhesion testing and post-separation characterization (Fig. S3–S5), CNT array morphology as a function of the CNT process time (Fig. S6–S7, eqn (S11)), and structural CNT evolution via Raman spectroscopy (Fig. S8, eqn (S12)–(S13)). See DOI: 10.1039/D0NR05469K |
| ‡ Current affiliation: Department of Mechanical Engineering, Escuela Politécnica Superior de Zamora, University of Salamanca, Avenida Requejo, 33, 49022 Zamora, Spain. |
| § Current affiliation: Cross-cutting Urgent Innovation Cell, The MITRE Corporation, Bedford, MA 01730, USA. The author's affiliation with the MITRE Corporation is provided for identification purposes only, and is not intended to convey or imply MITRE's concurrence with, or support for, the positions, opinions or viewpoints expressed by the author. Approved for Public Release; Distribution Unlimited. Public Release Case Number 20-1511. |
| This journal is © The Royal Society of Chemistry 2021 |