Solvent manipulation of the pre-reduction metal–ligand complex and particle-ligand binding for controlled synthesis of Pd nanoparticles†
Wenhui
Li
a,
Michael G.
Taylor
b,
Dylan
Bayerl
b,
Saeed
Mozaffari
a,
Mudit
Dixit
 b,
Sergei
Ivanov
b,
Sergei
Ivanov
 c,
Soenke
Seifert
d,
Byeongdu
Lee
c,
Soenke
Seifert
d,
Byeongdu
Lee
 e,
Narasimhamurthy
Shanaiah
a,
Yubing
Lu
e,
Narasimhamurthy
Shanaiah
a,
Yubing
Lu
 a,
Libor
Kovarik
a,
Libor
Kovarik
 f,
Giannis
Mpourmpakis
f,
Giannis
Mpourmpakis
 *b and
Ayman M.
Karim
*b and
Ayman M.
Karim
 *a
*a
aDepartment of Chemical Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 24060, USA. E-mail: amkarim@vt.edu
bDepartment of Chemical Engineering, University of Pittsburgh, Pittsburgh, PA 15261, USA. E-mail: gmpourmp@pitt.edu
cCenter for Integrated Nanotechnologies, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
dAdvanced Photon Source, Argonne National Laboratory, Argonne, IL 60439, USA
eX-ray Science Division, Argonne National Laboratory, Argonne, IL 60439, USA
fInstitute for Integrated Catalysis, and Physical and Computational Science Directorate, Pacific Northwest National Laboratory, P.O. Box 999, Richland, Washington 99352, USA
First published on 30th November 2020
Abstract
Understanding how to control the nucleation and growth rates is crucial for designing nanoparticles with specific sizes and shapes. In this study, we show that the nucleation and growth rates are correlated with the thermodynamics of metal–ligand/solvent binding for the pre-reduction complex and the surface of the nanoparticle, respectively. To obtain these correlations, we measured the nucleation and growth rates by in situ small angle X-ray scattering during the synthesis of colloidal Pd nanoparticles in the presence of trioctylphosphine in solvents of varying coordinating ability. The results show that the nucleation rate decreased, while the growth rate increased in the following order, toluene, piperidine, 3,4-lutidine and pyridine, leading to a large increase in the final nanoparticle size (from 1.4 nm in toluene to 5.0 nm in pyridine). Using density functional theory (DFT), complemented by 31P nuclear magnetic resonance and X-ray absorption spectroscopy, we calculated the reduction Gibbs free energies of the solvent-dependent dominant pre-reduction complex and the solvent-nanoparticle binding energy. The results indicate that lower nucleation rates originate from solvent coordination which stabilizes the pre-reduction complex and increases its reduction free energy. At the same time, DFT calculations suggest that the solvent coordination affects the effective capping of the surface where stronger binding solvents slow the nanoparticle growth by lowering the number of active sites (not already bound by trioctylphosphine). The findings represent a promising advancement towards understanding the microscopic connection between the metal–ligand thermodynamic interactions and the kinetics of nucleation and growth to control the size of colloidal metal nanoparticles.
Introduction
Strategies for predictably controlling the synthesis of colloidal metal nanoparticles are of extreme importance because their properties (catalytic, thermal, optical) vary with size, shape, and composition.1–6 Many studies have focused on controlling the size and shape of colloidal nanoparticles by changing synthesis reagents such as the precursors,7–10 ligands11–17 or solvents,18–20 or by changing the synthesis conditions21,22 such as precursor/ligand concentrations23–30 and reaction temperature.31–33 Among these factors, ligands have gained significant attention due to their wide variety in terms of steric effect and binding strength with the metal precursor and nanoparticle surface. It has been demonstrated that the nanoparticle size and shape can be affected by the ligand type11,13,16,34,35 and concentration,12,29,36 which have been attributed to differences in the precursor reactivity, or the ligand capping (strength or density) on the nanoparticle surface. These differences in sizes and shapes which are largely dependent on the nature of metal–ligand interactions (binding), give evidences that ligands play an important role in controlling the nucleation and growth rates. We have recently shown37–40 that the ligand–metal interaction could be responsible for the synthesis mechanism of colloidal metal nanoparticles (e.g. Pd,37,38 Au,41 Rh42 and Ir43) not following the LaMer44 nucleation and growth model. Specifically, instead of a short burst of nucleation followed by diffusion controlled growth (temporal separation), slow nucleation and temporal overlap of growth have been reported by several groups12,37,38,42,43 and alternative mechanisms/models have been proposed.37,43,45–48 Depending on whether the ligand has a higher affinity to the metal monomers or to the nanoparticle surface, it could either inhibit the nucleation resulting in fast growth and large sizes of nanoparticles, or block the surface sites for growth resulting in a continuous nucleation and smaller sizes.49–51Organic solvents have been investigated to vary the size and shape of colloidal nanoparticles.18–20,34,52,53 The large amount of solvent molecules in the synthetic phase may modify the ligand binding strength on the nanoparticle surface through van der Waals interaction with the ligand carbon chains.20,52 This steric interaction has been proposed to change the ligand capping density through different mechanisms, i.e., either occupying space between the surface ligands,52 or modifying the electronic property of the ligand binding functional group/atom.20 Additionally, solvents can also act as ligands if they have considerable direct interactions with the metal complex or the nanoparticle surface. Solvent's binding to the metal center can lower the precursor reactivity16,35 while binding to the nanoparticle surface can inhibit surface growth and the ability to bind to both can affect the nucleation and growth rates.54 Therefore, the solvent can serve as a promising variable for controlling the size and shape of colloidal metal nanoparticles. We note that the effects of ligands, solvents, and other synthesis parameters on kinetics have been mostly shown indirectly, for example, by correlating known or calculated trend of metal–ligand/solvent binding energies/affinities with only the final size of the nanoparticles. However, the final nanoparticle size is the result of an interplay between nucleation and growth rates and the solvents and ligands can affect both. Therefore, without in situ kinetics measurements the effects of solvents and ligands on kinetics and size are difficult to predict.
In this work, we investigated the effect of different solvents, i.e., toluene, and nitrogen coordinating (N-coordinating) solvents, piperidine, 3,4-lutidine and pyridine on the synthesis kinetics of Pd nanoparticles in the presence of trioctylphosphine (TOP). We directly correlate the metal–solvent interactions (structure and reducibility of the pre-reduction complexes, and solvent binding with the nanoparticle surface) with the nucleation and growth rates using in situ small angle X-ray scattering (SAXS), 31P nuclear magnetic resonance (31P NMR), X-ray absorption fine structure (XAFS) and density functional theory (DFT) calculations. We directly measure the nucleation and growth rates to determine the effect of solvent properties on metal–ligand/solvent interactions and kinetics of metal colloidal nanoparticle synthesis. The results show that the nucleation and growth rates are correlated with the stability/reducibility of the TOP-Pd pre-reduction complexes and binding strength of the solvent/TOP-nanoparticle surface, respectively. The findings provide a promising route to systematically identify ligands/solvents to tune the synthesis kinetics and final nanoparticle size.
Experimental section
Colloidal Pd nanoparticle synthesis and characterization
The heat-up method84 was used in the colloidal Pd nanoparticle synthesis. Palladium(II) acetate (Aldrich 99.9%) was used after recrystallization. Trioctylphosphine (Aldrich 97%) was used after further purification (distillation) and stored in a nitrogen (N2) glovebox. The procedures for recrystallization and distillation have been reported in our previous study.48,55 Anhydrous toluene (Sial 99.8%), 3,4-lutidine (Aldrich, 98%), piperidine (Aldrich, redistilled 99.5%) and pyridine (EMD Millipore 99.8%) were used as solvents. Anhydrous hexanol (Sial 99%) was used as the reducing agent. All the solvents and reducing agents were degassed using nitrogen (99.999% from liquid N2 boil off) at a flow rate of 10 mL min−1 for 30 min before use. 10 mM recrystallized Pd acetate was dissolved in solvent![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hexanol = 1
hexanol = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solution, with TOP
1 solution, with TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd = 1 or 2 (molar), and heated to 100 °C under 300 rpm stirring. All the agents were mixed in an inert gas (N2) glove box with both moisture and oxygen levels below 1.0 ppm. The syntheses have been repeated multiple times with 2 mL solution in 7 mL glass vials and 6 mL solution in 25 mL round bottom glass flask under 0–1000 rpm stirring, and the sizes were similar.
Pd = 1 or 2 (molar), and heated to 100 °C under 300 rpm stirring. All the agents were mixed in an inert gas (N2) glove box with both moisture and oxygen levels below 1.0 ppm. The syntheses have been repeated multiple times with 2 mL solution in 7 mL glass vials and 6 mL solution in 25 mL round bottom glass flask under 0–1000 rpm stirring, and the sizes were similar.
In situ and ex situ small-angle X-ray scattering (SAXS) data acquisition and analysis
The in situ SAXS experiments were conducted at Argonne National Laboratory's Advanced Photon Source at beamline 12-ID-C. The incident X-ray energy is 18 keV. All the agents were mixed in the glove box at wet labs in sectors 16 and sector 20 and transferred immediately to the beamline under inert gas atmosphere. The reaction was conducted in a 25 mL round bottom flask (with 6 mL solution) with 300 rpm stirring. The synthesis setup is similar to the one used by Kwon, et al.,85 which minimizes possible reactions triggered by the X-ray beam. A syringe needle was punched through the capping septum to avoid pressure build-up from the solvent evaporation during the synthesis. In each measurement, 300 μL was taken out of 6 mL solution into a quartz capillary for SAXS data acquisition using a syringe pump, and then returned into the flask. The pumping process took 7 s, and the fastest time resolution was set as 8 s. Each SAXS measurement was done when the solution flowed slowly through the capillary, with 0.1 s exposure time. The two-dimensional scattering pattern was averaged and normalized to get the curve of differential scattering cross section I(q) to the scattering vector q. The pure mixture of solvent and reducing agent at 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 volume ratio was used as background. To get the absolute scale intensity so that the nanoparticle concentration can be obtained, water was used as a primary standard due to its well-studied differential scattering cross section.86 The ex situ SAXS was conducted on N8 Horizon (Bruker AXS Gmbh, Germany) equipped with Cu (Kα radiation, λ = 1.54 Å) source, 2-dimensional VÅNTEC-500 TM detector and SCATEX TM scatter-free pinholes. The colloidal nanoparticle solution samples were loaded and measured in a sealed in quartz capillaries (d = 1.5 mm or 2.0 mm) at room temperature in vacuum. Water was used as the standard for absolute calibration.
50 volume ratio was used as background. To get the absolute scale intensity so that the nanoparticle concentration can be obtained, water was used as a primary standard due to its well-studied differential scattering cross section.86 The ex situ SAXS was conducted on N8 Horizon (Bruker AXS Gmbh, Germany) equipped with Cu (Kα radiation, λ = 1.54 Å) source, 2-dimensional VÅNTEC-500 TM detector and SCATEX TM scatter-free pinholes. The colloidal nanoparticle solution samples were loaded and measured in a sealed in quartz capillaries (d = 1.5 mm or 2.0 mm) at room temperature in vacuum. Water was used as the standard for absolute calibration.
Data analysis was done using IGOR pro,87 Bruker SAXS software and simSAXSLee package88 on Matlab. The scattering curves were fitted using Schultz polydisperse spherical nanoparticles model, based on the assumption of spherical nanoparticle shape (justified from TEM images, see below), dilute solution and homogeneous electron density. The Schulz–Zimm distribution function is:
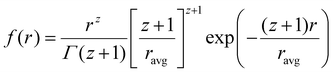 | (1) |
If I(q) is in absolute intensity, it is related to both of the size and number of nanoparticles in the solution:
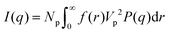 | (2) |
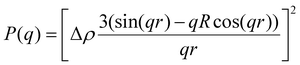 | (3) |
P(q) is the form factor of a specific size of particles. For spherical particles, at q = 0, P(q) = Δρ2. Np is the number of particles, Vp is the particle volume (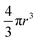 , and r is the radius), Δρ is the scattering length density difference between palladium and solvent. At q = 0, a relation can be used to calculate the number of particles:
, and r is the radius), Δρ is the scattering length density difference between palladium and solvent. At q = 0, a relation can be used to calculate the number of particles:
| I(0) = Np〈Vp〉2(Δρ)2 | (4) |
From eqn (4) the number of particles Np, and further the extent of reaction (i.e. conversion of precursor into nanoparticles) can be calculated (see further details in ESI†).
Transmission electron microscopy (TEM)
TEM images of synthesized nanoparticles were taken to confirm the nanoparticle size and shape. Images for the toluene, piperidine and 3,4-lutidine samples were acquired in scanning transmission electron microscopy (STEM) mode on FEI TITAN 80-300, equipped with the CEOS GmbH double-hexapole aberration corrector. The images were taken in high angle annular dark field (HAADF) mode. Images for pyridine samples were taken on JEOL 2100 TEM operated at 200 kV, which is equipped with a thermionic emission source and possesses a high-resolution objective pole piece. The resolution can reach 0.1 nm on both microscopes. The reaction solution was diluted 10 times with the respective anhydrous solvent. One drop of the solution was added on the lacey carbon copper grid and dried on top of a hotplate set up at 50 °C. The image analysis was performed with ImageJ.89 At least 300 nanoparticles were measured to calculate the number-average diameter and the polydispersity.Nuclear magnetic resonance
Deuterated solvents, toluene-d8 (Alfa Aesar, 99.6%) and pyridine-d5 (Alfa Aesar, 99.5%) were used for NMR measurements. All the NMR measurements were taken at room temperature. The deuterated solvents were degassed with nitrogen at 10 mL min−1 before dissolving any agents. For each sample, 0.6 mL 20 mM freshly made palladium acetate solution was loaded in NMR tubes in the nitrogen glovebox, and sealed with rubber septa. All the measurements were taken immediately after the appropriate amount of ligand was added and mixed well in the NMR tube. One-dimensional 31P NMR spectra with proton decoupling were acquired at 25 °C on a Bruker Avance II 500 MHz system equipped with a 5 mm broad band prodigy cryo probe. 31P NMR parameters included a total of 256 transients, 64K data points, spectral width of 59.5 kHz and a relaxation delay of 5.0 s between the transients. Apodization corresponding to a line broadening of 1.0 Hz was applied before Fourier transformation. Resonances were assigned based on the chemical shift position of external standard 85% H3PO4 singlet at 0 ppm.XAFS data collection and analysis
XAFS experiments were performed at beamline BL 2-2 at the Stanford synchrotron radiation light source at SLAC National Accelerator Laboratory. 25 mM and 20 mM Pd acetate were dissolved in toluene and pyridine in 20 mL capped glass vial in an inert atmosphere glovebox and transferred to the synchrotron. The beam size was 200 μm vertical by 3 mm horizontal. The spectra were collected at the Pd K-edge in transmission mode. Four scans (20 minutes each) were collected then merged and aligned using a Pd foil spectrum collected simultaneously for each scan. All the measurements were taken at room temperature. Both XANES and EXAFS data processing and analysis were performed using Athena and Artemis programs of the IFEFFIT data analysis package.90,91 After the normalization of the absorption coefficient, the smooth atomic background was subtracted using the AUTOBKG code Athena to obtain χ(k) (where k is the photoelectron wavenumber). FEFF6 code was used for constructing the theoretical EXAFS signal for Pd–Pd, Pd–P, Pd–C, and Pd–O scattering paths. For the scattering paths, structure of Pd acetate trimer (Pd–O and long Pd–C) was used in toluene, and Pd acetate monomer with terminal acetate (Pd–O and short Pd–C) was used in pyridine. The theoretical EXAFS signals fitting was conducted using Artemis in r-space. The spectra were fitted by changing the following parameters for the scattering paths of Pd–Pd, Pd–O, Pd–C: bond length disorder, σ2Pd–Pd, σ2Pd–O, σ2Pd–C; coordination numbers of the single scattering paths, NPd–Pd, NPd–O, NPd–C; the effective scattering lengths (RPd–Pd, RPd–O, RPd–C); and the correction to the threshold energy, ΔE0 (ΔE0 for metallic Pd–Pd was assumed to be the same as other paths in the model to limit the number of parameters). The best fit of the passive electron reduction factor (0.83), S20, was fixed during the fitting based on analyzing the Pd foil spectrum. The k-range for Fourier transform of the χ(k) and the r-range for the fitting were 2.5–12.5 Å−1 and 1.1–3.1 Å, respectively.Density functional theory (DFT) calculations
DFT calculations were performed to capture the complexation of Pd species using the BP-8692,93 functional combined with the def2-SV(P) basis set94 and the resolution of identities (RI) approximation95 as implemented in the Turbomole package.96 To capture dispersion interactions between carbon chains we used the Grimme D3 dispersion correction.97 Similar DFT methods have previously been used to study palladium complexes and nanoparticles, showing reasonable accuracy.98,99 Implicit solvation effects (Fig. S17†) were accounted for using the conductor-like screening model (COSMO)100 with dielectric constants taken, when available, from the Minnesota Solvent Descriptor Database101 or from other102,103 databases. Different initial configurations were tested for each precursor complex and the lowest-energy fully relaxed structure is reported. Geometry relaxations were carried out using the quasi-Newton–Raphson method without any symmetry constraints. Multiple spin states were tested for each Pd-containing complex and the lowest-energy electron configuration always corresponded to the lowest possible spin state of the complex (i.e. singlet or doublet spin states). Vibrational analysis was performed to verify the relaxed structures as local minima and structures exhibiting imaginary frequencies were displaced (along the imaginary mode) and re-relaxed until no imaginary frequencies remained. Gibbs free energies were calculated (at 298.15 K) using the ideal gas rigid rotator harmonic oscillator approach applied to the vibrational modes for each system.67,104 For each complex at least two initial configurations were tested and we report the values and structures of the lowest-energy configurations. Periodic DFT calculations were performed using the CP2K package to simulate adsorption on nanoparticle surface.105 The PBE functional106 was used with Grimme's D3 dispersion corrections. DZVP basis sets with the Goedecker, Teter, and Hutter (GTH) pseudopotentials were used with a kinetic energy cutoff of 500 Ry. To obtain the bulk unitcell parameters of Pd, a 2 × 2 × 2 supercell of the conventional unitcell (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) was fully relaxed. The periodic geometries were optimized using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization algorithm with convergence criteria of 4.0 × 10−4Eh per Bohr and 10−7 au for force and energy, respectively. To model the (111) surface facet of Pd, a p5 × 5 supercell (representing 1.649 nm2 of surface area) was created using the primitive unitcell (of the relaxed unitcell) with four atomic layers and a vacuum of 12 Å was added for the construction of slab models. For surface calculations, the atoms of two bottom layers were kept frozen at their bulk positions and two top layers were allowed to relax. To reduce the computational cost of periodic DFT calculations, triethylphosphine (TEP) was used as a model to represent the TOP ligand. We note that four TEP molecules sufficiently cover the full supercell of Pd (111) (Fig. S22†) leaving no space for further ligands to adsorb on the surface. The adsorption binding energy of ligands (TEP or solvent) at Nlig/4 monolayer coverage (Fig. 5a) is defined as:
m) was fully relaxed. The periodic geometries were optimized using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization algorithm with convergence criteria of 4.0 × 10−4Eh per Bohr and 10−7 au for force and energy, respectively. To model the (111) surface facet of Pd, a p5 × 5 supercell (representing 1.649 nm2 of surface area) was created using the primitive unitcell (of the relaxed unitcell) with four atomic layers and a vacuum of 12 Å was added for the construction of slab models. For surface calculations, the atoms of two bottom layers were kept frozen at their bulk positions and two top layers were allowed to relax. To reduce the computational cost of periodic DFT calculations, triethylphosphine (TEP) was used as a model to represent the TOP ligand. We note that four TEP molecules sufficiently cover the full supercell of Pd (111) (Fig. S22†) leaving no space for further ligands to adsorb on the surface. The adsorption binding energy of ligands (TEP or solvent) at Nlig/4 monolayer coverage (Fig. 5a) is defined as: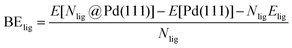 | (5) |
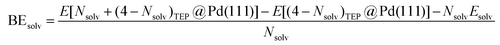 | (6) |
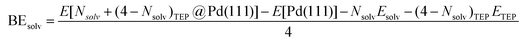 | (7) |
Results and discussion
Solvent coordination effects on synthesis kinetics using in situ SAXS
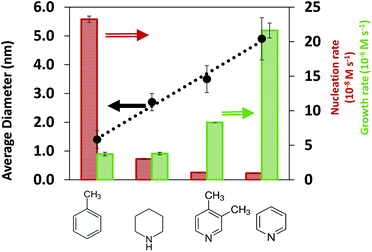
To provide insights on the effect of the solvents on the synthesis kinetics and final nanoparticle size, we conducted in situ SAXS measurements in all solvents. The first observation is that the final Pd nanoparticle size increased in the order of toluene < piperidine < 3,4-lutidine < pyridine for both TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd = 1 and 2 as shown in Fig. 1 and S1,† respectively (see representative SAXS spectra in Fig. S2 and S3† for TOP
Pd = 1 and 2 as shown in Fig. 1 and S1,† respectively (see representative SAXS spectra in Fig. S2 and S3† for TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd = 1, TEM images and SAXS spectra in Fig. S4 and S5† for TOP
Pd = 1, TEM images and SAXS spectra in Fig. S4 and S5† for TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd = 2 in ESI†). We note that the effect of exposure to the X-ray beam was negligible since no reaction was triggered under beam exposure (see Fig. S6†), and the final nanoparticle size from in situ and ex situ SAXS measurements was similar (see Fig. S7†). The results in Fig. 1 show that the nanoparticle size in toluene (1.4 nm) was much smaller than in N-coordinating solvents, piperidine (2.7 nm), 3,4-lutidine (3.5 nm) and pyridine (4.8 nm), indicating that the solvents have a strong effect on the nucleation and growth rates.
Pd = 2 in ESI†). We note that the effect of exposure to the X-ray beam was negligible since no reaction was triggered under beam exposure (see Fig. S6†), and the final nanoparticle size from in situ and ex situ SAXS measurements was similar (see Fig. S7†). The results in Fig. 1 show that the nanoparticle size in toluene (1.4 nm) was much smaller than in N-coordinating solvents, piperidine (2.7 nm), 3,4-lutidine (3.5 nm) and pyridine (4.8 nm), indicating that the solvents have a strong effect on the nucleation and growth rates.
An advantage of the in situ SAXS measurements is the ability to capture the time evolutions of both, the number of nanoparticles and the nanoparticle size (Fig. S8†), which allows the extraction of both nucleation and growth rates (Fig. S9, see details in ESI† and previous studies48,55). We note that based on our estimation of the rates of reaction and diffusion (see details in ESI† and our previous studies56), the nanoparticle synthesis reactions in our specific system are kinetically controlled rather than diffusion controlled. To directly identify the effect of solvents on the synthesis kinetics, it is important to compare the nucleation and growth rates in the kinetic regime at similar extent of reaction (i.e. low conversion of Pd acetate into nanoparticles, see Methods for details on how conversion is calculated) instead of at the same reaction time. At 5% and 10% extents of reaction (Fig. S10† and Fig. 1, respectively), the nucleation rate decreases and the growth rate increases in the following order: toluene, piperidine, 3,4-lutidine and pyridine which is consistent with the increasing trend of the final nanoparticle size.
The results in Fig. 1 indicate that in the order of toluene < piperidine < 3,4-lutidine < pyridine, growth on the existing nanoparticles becomes more preferred compared with forming new nuclei. This can be better seen in Fig. S11† where the ratio of growth-to-nucleation rates increases in the same solvent order of toluene < piperidine < 3,4-lutidine < pyridine up to 40% extent of reaction (highest conversion for reliable extraction of rates, in particular nucleation). The inhibited nucleation, and enhanced growth (likely autocatalytic as shown previously for toluene and pyridine48,55) can be due to solvent-dependent precursor reactivity and/or surface properties of the nanoparticles (including coverage of TOP and/or solvent). To determine the possible role(s) of the solvent, we investigated the interactions of coordinating species (TOP and solvents) with Pd acetate and Pd nanoparticle surface under different solvent environments as discussed below.
Pd pre-reduction complexes in different solvents: 31P NMR and XAFS
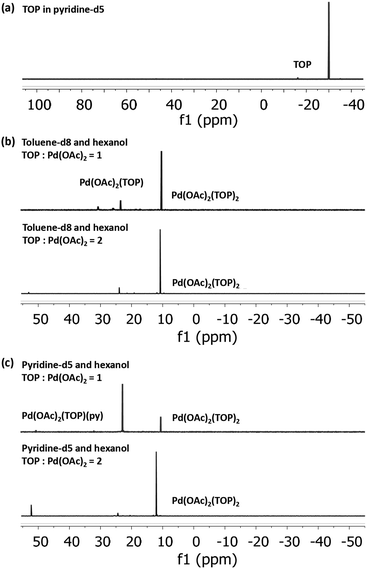
To determine the initial Pd-acetate-TOP pre-reduction complex formed in the different solvents, we characterized Pd acetate in toluene and pyridine (without hexanol due to the instability of Pd acetate in hexanol without TOP), and the binding complexes of Pd(OAc)2 with TOP in solvent-hexanol mixtures using 31P NMR and EXAFS. The TOP-Pd acetate binding complexes identified from the NMR and EXAFS experiments are representative of the initial pre-reduction precursor present during the synthesis, since the solutions (for all characterizations and synthesis) were freshly prepared and used within minutes. Modeling of the EXAFS spectra of Pd acetate dissolved in pyridine show that Pd is present, on average, as Pd(OAc)2(py)2, while in toluene it is present as trimers, Pd3(OAc)6 (see EXAFS results in Fig. S12 and Table S1†).
31P NMR spectra of Pd(OAc)2 dissolved in toluene-d8 and pyridine-d5, each with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hexanol at TOP
1 hexanol at TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd molar ratio of 1 and 2 (Fig. 2), indicate that all the added TOP is bound with Pd(OAc)2 or is converted to other species as evidenced by the absence of a free TOP peak (Fig. 2a). At TOP
Pd molar ratio of 1 and 2 (Fig. 2), indicate that all the added TOP is bound with Pd(OAc)2 or is converted to other species as evidenced by the absence of a free TOP peak (Fig. 2a). At TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd molar ratio of 2, the major peaks in toluene-d8-hexanol at 10.4 ppm and pyridine-d5-hexanol at 10.6 ppm can be assigned to the trans-Pd(OAc)2(TOP)2 complex as we previously reported for Pd(OAc)2 dissolved in toluene-d8 (peak at 10.3 ppm).57 The small shift is due to the different solvents as previously reported for the divalent trans-Pd(OAc)2(PPh3)2 complex in THF (14.48 ppm)58 and in DMF (15.08 ppm).59 At TOP
Pd molar ratio of 2, the major peaks in toluene-d8-hexanol at 10.4 ppm and pyridine-d5-hexanol at 10.6 ppm can be assigned to the trans-Pd(OAc)2(TOP)2 complex as we previously reported for Pd(OAc)2 dissolved in toluene-d8 (peak at 10.3 ppm).57 The small shift is due to the different solvents as previously reported for the divalent trans-Pd(OAc)2(PPh3)2 complex in THF (14.48 ppm)58 and in DMF (15.08 ppm).59 At TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd molar ratio of 1, the major peak in pyridine-d5-hexanol is at 22.9 ppm while in toluene-d8-hexanol the major peak remains at 10.4 ppm with a small peak at 23.5 ppm. Moschetta et al.60 reported that, in the same solvent, the peak for trans-PdCl2(PPh3)(solv) was at ca. 8–10 ppm higher (downfield) than the peak for the divalent trans-PdCl2(PPh3)2 (e.g. in acetonitrile, 31.2 ppm for PdCl2(PPh3)(MeCN) vs. 23.4 ppm for PdCl2(PPh3)2). Similarly, our 31P NMR spectra (Fig. S13†) of the binding of TOP with PdCl2 in pyridine-d5 at TOP
Pd molar ratio of 1, the major peak in pyridine-d5-hexanol is at 22.9 ppm while in toluene-d8-hexanol the major peak remains at 10.4 ppm with a small peak at 23.5 ppm. Moschetta et al.60 reported that, in the same solvent, the peak for trans-PdCl2(PPh3)(solv) was at ca. 8–10 ppm higher (downfield) than the peak for the divalent trans-PdCl2(PPh3)2 (e.g. in acetonitrile, 31.2 ppm for PdCl2(PPh3)(MeCN) vs. 23.4 ppm for PdCl2(PPh3)2). Similarly, our 31P NMR spectra (Fig. S13†) of the binding of TOP with PdCl2 in pyridine-d5 at TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd ratio of 1 and 2 showed peaks at 29.0 ppm and 11.8 ppm corresponding to trans-PdCl2(TOP)(py) and trans-PdCl2(TOP)2, respectively. Therefore, we assign the peak at 22.9 ppm in pyridine-d5-hexanol to the trans-Pd(OAc)2(TOP)(py) complex and the peak at 23.5 ppm in toluene-d8-hexanol tentatively to Pd(OAc)2(TOP)(Tol). Our EXAFS modeling results of the coordination of Pd(OAc)2 to TOP in pyridine and toluene (Fig. S14–S16 and Table S2†) are consistent with the 31P NMR results. In pyridine, Pd was found to be coordinated, on average, with 1 and 2 TOP molecules at TOP
Pd ratio of 1 and 2 showed peaks at 29.0 ppm and 11.8 ppm corresponding to trans-PdCl2(TOP)(py) and trans-PdCl2(TOP)2, respectively. Therefore, we assign the peak at 22.9 ppm in pyridine-d5-hexanol to the trans-Pd(OAc)2(TOP)(py) complex and the peak at 23.5 ppm in toluene-d8-hexanol tentatively to Pd(OAc)2(TOP)(Tol). Our EXAFS modeling results of the coordination of Pd(OAc)2 to TOP in pyridine and toluene (Fig. S14–S16 and Table S2†) are consistent with the 31P NMR results. In pyridine, Pd was found to be coordinated, on average, with 1 and 2 TOP molecules at TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd molar ratios of 1 and 2 respectively. In toluene, Pd was coordinated to 2 TOP molecules (on average) at TOP
Pd molar ratios of 1 and 2 respectively. In toluene, Pd was coordinated to 2 TOP molecules (on average) at TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd molar ratio of 2.
Pd molar ratio of 2.
Our 31P NMR results indicate that the major Pd complex in pyridine changes from trans-Pd(OAc)2(TOP)(py) to trans-Pd(OAc)2(TOP)2 as the TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd ratio increases from 1 to 2. On the other hand, the major complex in toluene is trans-Pd(OAc)2(TOP)2 at both TOP
Pd ratio increases from 1 to 2. On the other hand, the major complex in toluene is trans-Pd(OAc)2(TOP)2 at both TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd ratios. The difference in the relative amounts of the complexes formed in toluene compared with pyridine is because Pd acetate is present as monomers in pyridine while it is present mostly as trimers in toluene as shown by our EXAFS results (see Fig. S12 and Table S1†) and previous work.57 In toluene each Pd3(OAc)6 trimer requires 6 TOP molecules per trimer (2 TOP per Pd center) to break into monomers at room temperature as we previously reported57 (see also Tables S1 and 2†). However, dissociation of a TOP ligand from trans-Pd(OAc)2(TOP)2 is energetically unfavorable57 which is why trans-Pd(OAc)2(TOP)2 is the major complex in toluene–hexanol at TOP
Pd ratios. The difference in the relative amounts of the complexes formed in toluene compared with pyridine is because Pd acetate is present as monomers in pyridine while it is present mostly as trimers in toluene as shown by our EXAFS results (see Fig. S12 and Table S1†) and previous work.57 In toluene each Pd3(OAc)6 trimer requires 6 TOP molecules per trimer (2 TOP per Pd center) to break into monomers at room temperature as we previously reported57 (see also Tables S1 and 2†). However, dissociation of a TOP ligand from trans-Pd(OAc)2(TOP)2 is energetically unfavorable57 which is why trans-Pd(OAc)2(TOP)2 is the major complex in toluene–hexanol at TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd ratio = 1. The results indicate that at TOP
Pd ratio = 1. The results indicate that at TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd molar ratio of 1, TOP would bind to ca. half the Pd acetate forming trans-Pd(OAc)2(TOP)2 while the remaining Pd acetate trimers are not bound to TOP and do not appear as phosphine bonded complexes in the 31P NMR spectrum. However, we note that once the temperature increases during the nanoparticle synthesis experiments, the remaining trimers in toluene would dissociate into monomers and all the Pd acetate would be available for TOP binding.
Pd molar ratio of 1, TOP would bind to ca. half the Pd acetate forming trans-Pd(OAc)2(TOP)2 while the remaining Pd acetate trimers are not bound to TOP and do not appear as phosphine bonded complexes in the 31P NMR spectrum. However, we note that once the temperature increases during the nanoparticle synthesis experiments, the remaining trimers in toluene would dissociate into monomers and all the Pd acetate would be available for TOP binding.
In summary, the NMR and EXAFS results indicate that in toluene, pyridine and by extension the other solvents, a mixture of complexes are present in solution and their relative amounts depend on the thermodynamic equilibrium (dictated by concentrations and temperature in each solvent). Based on the EXAFS and NMR results, we anticipate that at the nanoparticles synthesis conditions, the major pre-reduction Pd complexes present in solution are Pd(OAc)2(TOP)(solv) and Pd(OAc)2(TOP)2 at TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd molar ratio of 1 and 2 respectively, while Pd(OAc)2(solv)2 is a minority species (solv represents a solvent molecule).
Pd molar ratio of 1 and 2 respectively, while Pd(OAc)2(solv)2 is a minority species (solv represents a solvent molecule).
Solvent effect on speciation and reducibility of Pd complexes using DFT
The NMR and EXAFS results show that N-coordinating solvents act as ligands and bind to Pd acetate. The coordination of the solvents with Pd acetate could modify the reactivity of the resulting complexes depending on the solvent electron donating ability61 and binding stoichiometry.58,62,63 Such complexes, which are discrete molecular precursors different from both the initial reagents and final nanoparticles, can affect the nanoparticle formation mechanisms.64–66 Therefore, we performed density functional theory calculations to provide details on the Pd complexes formed in the different solvents, their concentrations at equilibrium, as well as reducibility. Below we list the possible initial binding, solvent-TOP exchange and reduction reactions, where solv represents the solvent molecule:| Pd(OAc)2 + 2solv → Pd(OAc)2(solv)2 | (8) |
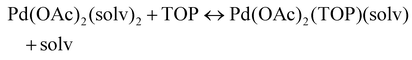 | (9) |
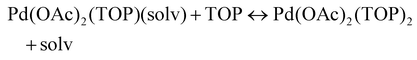 | (10) |
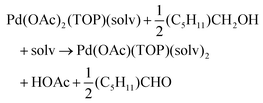 | (11) |
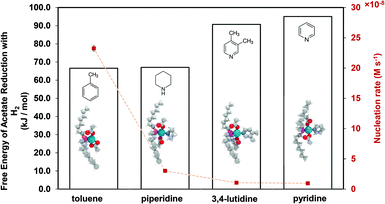
The equations represent: eqn (8), solvent binding to Pd(OAc)2 (i.e. Pd(OAc)2 dissolving in each solvent); eqn (9), first TOP ligand substituting solv in Pd(OAc)2(solv)2; eqn (10), second (subsequent) TOP substituting solv in Pd(OAc)2(solv)(TOP); eqn (11), potential initial reduction reaction by hexanol of the Pd Pd(OAc)2(solv)(TOP) complexes through acetate dissociation. First, to investigate the complex stability and speciation, we calculated the Gibbs free energy for the formation of all the possible unreduced Pd complexes before the addition of hexanol (Fig. 3). Compared with Pd(OAc)2, the Gibbs free energies of Pd complexes are in the following order (lowest to highest free energy): Pd(OAc)2(TOP)2 < Pd(OAc)2(solv)(TOP) < Pd(OAc)2(solv)2 < Pd(OAc)2(solv) < Pd(OAc)2. The complex is readily bound by the solvents (reacts exothermically) except for toluene (consistent with the stability of Pd acetate trimers in toluene)57 and the solvents are favorably displaced with the addition of TOP. Although the Gibbs free energies reported in Fig. 3 are all calculated from gas phase calculations, we note that when implicit solvent is included the trends in binding strength do not change as seen in Fig. S17.† Further, a recent benchmark study on Pd-phosphine complexes found ideal gas rigid rotator harmonic oscillator approach with solvent effects yielded accurate free energies of reaction.67 Overall, this shows our gas-phase free energy calculations should at least trend with the equivalent solvent-phase reactions.
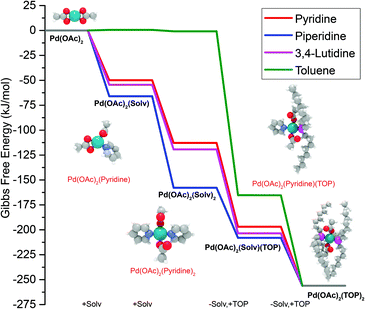 | ||
| Fig. 3 Gibbs free energy of different Pd complexes from DFT calculations. Example pyridine-containing precursor structures are shown as insets. Color code of atoms: Pd – teal, N – light blue, H – white, O – red, P – magenta, and C – gray. All Pd complex images are in Fig. S18.† | ||
The nucleation is dependent on the reduction rate which is affected by the reducibility of the Pd pre-reduction complexes in solution. Thus, to estimate the major pre-reduction complex, we performed DFT calculations on the free energies of solvent coordination of eqn (8), as well as equilibrium thermodynamics of eqn (9) and (10). From the DFT-based thermodynamic equilibrium results presented in Table 1 for TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd = 1 (see Table S3† for equilibrium calculation details and results for TOP
Pd = 1 (see Table S3† for equilibrium calculation details and results for TOP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd = 2), the most abundant complex in all solvents is trans-Pd(OAc)2(TOP)(solv) (and cis-Pd(OAc)2(TOP) in toluene).
Pd = 2), the most abundant complex in all solvents is trans-Pd(OAc)2(TOP)(solv) (and cis-Pd(OAc)2(TOP) in toluene).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pd = 1, T = 293.15 K
Pd = 1, T = 293.15 K
| Solvent | mol% Pd(OAc)2(TOP)(solv) | mol% Pd(OAc)2(TOP)2 | mol% Pd(OAc)2(solv)2 |
|---|---|---|---|
| Toluene | 96.00 | 2.00 | 2.00 |
| Pyridine | 98.70 | 0.65 | 0.65 |
| 3,4-Lutidine | 99.70 | 0.15 | 0.15 |
| Piperidine | 47.31 | 26.35 | 26.35 |
Therefore, our next step was to address the reducibility of the most abundant complexes by calculating their reduction Gibbs free energies, 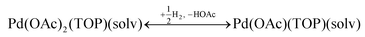 . Our analysis ignores hexoxy formation or hexanol displacement of ligands, since hexoxy displacement of acetate and hexanol displacement of ligands were both found to be endothermic (see Tables S4 and S5†). We used H2 as the reference reducing agent as the exact reduction byproducts (potential reduction reaction in eqn (11)) are unknown and using H2 as a common reference allows us to calculate consistent trends in reduction affinity. The results in Fig. 4 show that without the solvent coordination in toluene, the Gibbs free energy of Pd(OAc)2(TOP) reduction is the most favorable. Addition, as Fig. 4 demonstrates, the binding of more basic N-coordinating solvents makes the reduction affinity of the complexes more endothermic (piperidine < 3,4-lutidine < pyridine). For reactions in the gas phase, liquid phase and onsurfaces, the activation energies for a series of reactions have been shown to be linearly correlated to the reaction enthalpies (or free energies) through Brønsted–Evans–Polanyi (BEP) relationship.68–72 Therefore, an increase in the reduction free energy (more endothermic) is expected to increase the activation energy of reduction and consequently result in lower reduction and nucleation rates. Consistent with this argument, the DFT calculated trend of thermodynamic reducibility presented in Fig. 4, toluene (lowest reduction free energy, highest reducibility) > piperidine > 3,4-lutidine > pyridine (highest reduction free energy, lowest reducibility), appears to be correlated with the trend in nucleation rates measured experimentally (Fig. 1 and also shown in Fig. 4). Furthermore, we observed that the same trends in reduction free energy with different solvents also hold for the partially-reduced precursors (i.e. further reduction of Pd(OAc)(TOP)(solv)2, Fig. S19†). Beyond the reducibility preference of the predominant precursor complex in Fig. 4, the weak binding (non-coordination) of toluene to the precursor complexes likely contributes to faster (less-inhibited) nucleation rates. Thus, the weak binding of toluene to the precursor complexes may have a dual impact on the nucleation rates of Pd nanoparticles, resulting in the especially high nucleation rate observed experimentally.
. Our analysis ignores hexoxy formation or hexanol displacement of ligands, since hexoxy displacement of acetate and hexanol displacement of ligands were both found to be endothermic (see Tables S4 and S5†). We used H2 as the reference reducing agent as the exact reduction byproducts (potential reduction reaction in eqn (11)) are unknown and using H2 as a common reference allows us to calculate consistent trends in reduction affinity. The results in Fig. 4 show that without the solvent coordination in toluene, the Gibbs free energy of Pd(OAc)2(TOP) reduction is the most favorable. Addition, as Fig. 4 demonstrates, the binding of more basic N-coordinating solvents makes the reduction affinity of the complexes more endothermic (piperidine < 3,4-lutidine < pyridine). For reactions in the gas phase, liquid phase and onsurfaces, the activation energies for a series of reactions have been shown to be linearly correlated to the reaction enthalpies (or free energies) through Brønsted–Evans–Polanyi (BEP) relationship.68–72 Therefore, an increase in the reduction free energy (more endothermic) is expected to increase the activation energy of reduction and consequently result in lower reduction and nucleation rates. Consistent with this argument, the DFT calculated trend of thermodynamic reducibility presented in Fig. 4, toluene (lowest reduction free energy, highest reducibility) > piperidine > 3,4-lutidine > pyridine (highest reduction free energy, lowest reducibility), appears to be correlated with the trend in nucleation rates measured experimentally (Fig. 1 and also shown in Fig. 4). Furthermore, we observed that the same trends in reduction free energy with different solvents also hold for the partially-reduced precursors (i.e. further reduction of Pd(OAc)(TOP)(solv)2, Fig. S19†). Beyond the reducibility preference of the predominant precursor complex in Fig. 4, the weak binding (non-coordination) of toluene to the precursor complexes likely contributes to faster (less-inhibited) nucleation rates. Thus, the weak binding of toluene to the precursor complexes may have a dual impact on the nucleation rates of Pd nanoparticles, resulting in the especially high nucleation rate observed experimentally.
Solvent effect on Pd nanoparticle surface growth
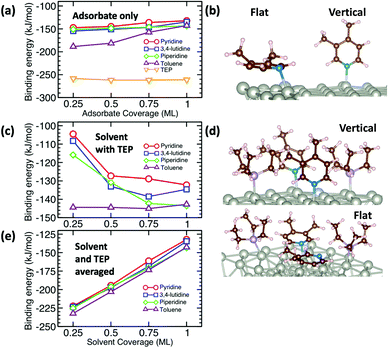
The growth rate is affected by the binding and coverage of ligands on the nanoparticle surface. As the ligand coverage increases, the number of available sites for growth becomes limited, and the growth rate on the nanoparticle would decrease. The relative coverage of the solvent and TOP on the surface of nanoparticles is dynamic throughout a nanoparticle synthesis and depends on several factors including their respective concentrations and binding energies. Thus, periodic DFT calculations were conducted to compare binding energies of the solvent molecules to Pd(111) surface partially covered by triethylphosphine (TEP, as an approximation of TOP to reduce computational cost). The Pd(111) facet was selected as it is one of the most abundant facets in previous calculations73 (even for small nanoparticle sizes, 1.8–3.0 nm)74 and experiments75 as also seen from our high resolution TEM images in Fig. S20.†We calculated the binding energies of all solvents in both vertical and flat configurations with and without TEP competing for binding sites as a function of solvent monolayer fraction (Fig. 5 and S21, S22, S24, S25†). Flat binding (Fig. S24†) is in general more exothermic than vertical binding (Fig. S25†), though vertical-bound solvents better protect the nanoparticle surface by allowing more adsorbates per unit surface area whilst exhibiting comparable binding energies. However, considering either vertical or flat configurations in isolation does not capture the full physical picture. Dynamic fluctuation between both configurations is possible on the nanoparticle surface. To account for the collective solvent configurational variation, we present in Fig. 5a and c the average binding energy of both vertical and flat configurations at each solvent coverage fraction. The results in Fig. 5a show that TEP has the most negative binding energy, indicating the strongest binding affinity and consequently the tendency toward high surface coverage at equilibrium, see discussion below. Similarly, if we consider the combined molar binding energy of all adsorbates (averaged over TEP and solvent as a function of solvent coverage), we observe a monotonic increase in binding strength (more negative binding energy) as TEP replaces solvent on the Pd surface as shown in Fig. 5e. What is remarkable is that the configurationally-averaged solvent binding energies when co-adsorbed with TEP (Fig. 5c and e) follow the same order as the experimental growth rate: toluene (strongest binding, slowest growth) > piperidine > 3,4-lutidine > pyridine (weakest binding, fastest growth) as shown in Fig. 6 (with one exception for the case of 0.5 ML solvent, 0.5 ML TEP where the order of piperidine and 3,4-lutidine is reversed). We note in Fig. S23† that overall similar binding trends between the ligand/solvents on Pd(111) appear to hold on the surface of a small 13-atom Pd nanoparticle, which indicates similar ligand-dependent binding trends may occur on different facets of the Pd nanoparticles present during growth.
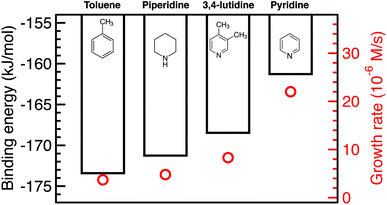 | ||
| Fig. 6 Combined binding energies of 0.25 ML TEP with 0.75 ML of toluene, piperidine, 3,4-lutidine, or pyridine on Pd(111) as also shown in Fig. 5e (black bars) and the growth rates at 10% Pd conversion (red circles). | ||
Our results show that in the presence of solvents, despite their less exothermic binding energy compared with TOP (Fig. 5), the nanoparticle surface will be covered by both the solvents and TOP. This is due to the much higher concentration of the solvents and their less bulky structures compared with TOP allowing co-adsorption, especially for N-coordinating solvents through vertical binding. Therefore, regardless of whether the coverage of TOP on the surface of the nanoparticles is at equilibrium (high coverage), or if the coverage of TOP is low at early times and increases with time (as shown from our previous in situ EXAFS and kinetic modeling37,48 studies and reports by other groups76–78), the solvent will act as a second ligand that helps passivate the surface. Since the solvents bind significantly weaker than TOP (more labile than TOP) as shown in Fig. 5 and S21, 22,† the sites occupied by the solvent will be less effectively passivated and allow adsorption of Pd adatoms and growth of the nanoparticle (the weaker the binding of the solvent, the less effective passivation and faster growth). This can be also explained in terms of adsorption/desorption rates of the solvents. Assuming a Brønsted–Evans–Polanyi (BEP) relationship between the solvent binding energy and its desorption/adsorption rates at the nanoparticle surface, weaker binding solvents (e.g. pyridine) would show higher rates of desorption, which creates open sites at the nanoparticle surface leading to faster nanoparticle growth. This is consistent with the increase in the growth rate in the same order as the decrease in solvent binding energy shown in Fig. 6 (weaker binding energy, i.e. less negative, of solvent or combined solvent-TEP results in less effective passivation and faster growth).
Insights on deconvoluting the effects of solvents on nucleation and growth rates
The final size of the nanoparticles is controlled by the relative nucleation and growth rates which are affected by the precursor reactivity and ligand capping on the nanoparticle surface, respectively. For example, introducing stronger binding ligands was used to stabilize the ligated-metal complex and inhibit the nucleation, leading to larger nanoparticle size.8,12,13,16 Other studies showed that a stronger capping ligand or higher ligand to metal ratio lead to smaller nanoparticle size which was attributed to slower surface growth (e.g. Au,49 Pd,25,37,48 Pt,79,80 and quantum dots51). However, the reported trends were mostly qualitative and relied on correlations with the final nanoparticle size. Additionally, since the ligand and/or solvent can play more than one role81 by binding to both, the metal precursor and nanoparticle surface, the deconvolution of these two factors is necessary to understand the effects on nucleation and growth kinetics. In this study, we used solvents of different coordinating abilities to investigate the effects on the reducibility of Pd precursors, ligand capping on the nanoparticle surface and provide mechanistic details on the synthesis kinetics of Pd colloidal nanoparticles. We directly correlate the ligated-metal complex reduction and ligand-surface binding thermodynamics (free energy of reduction and binding energies, respectively) calculated using DFT to the nucleation and growth rates measured using in situ SAXS. The results show that solvents (and ligands in general) can be used to tune the reactivity of the metal–ligand pre-reduction complexes. More importantly, the reduction free energy of the metal–ligand pre-reduction complex in each solvent was found to correlate with the measured nucleation rates (Fig. 4). Furthermore, the solvent is shown to affect the effective capping on the nanoparticle surface (and possibly the reactivity of surface atoms) which was reflected in a correlation between the solvent/ligand surface binding energy and the measured growth rates (Fig. 6). The results show the importance of understanding the distinct roles ligands and solvents play in affecting the nucleation and growth rates during the synthesis of colloidal nanoparticles. Additionally, the results suggest that general correlations, i.e. Brønsted–Evans–Polanyi relationships, likely exist between thermodynamics of metal–ligand binding and the kinetics of nucleation and growth. We note that although microkinetic models have been attempted in other works studying nanoparticle growth,82,83 such studies necessarily require heavy assumptions due to the complex chemical environment present during growth. Rather than focusing effort on addressing the complex chemical environment during growth and get accurate nanoparticle growth kinetics from our theoretical predictions, here, we identify simple theory-derived quantities that correlate with the experimental kinetics as a means of understanding factors dictating nanoparticle nucleation and growth. Our future efforts will focus on investigating other ligands and metals to determine if they follow similar correlation between the metal–ligand thermodynamic interactions and nucleation and growth rates. Such correlations would enable the selection of ligands and/or solvents, a priori, to synthesize nanoparticles with specific sizes.Conclusions
We investigated the effect of solvent coordinating ability on the final size of colloidal Pd nanoparticles and provide a direct correlation between the metal–ligand–solvent interactions and the synthesis kinetics using in situ SAXS, XAFS, NMR and DFT calculations. The nanoparticle size can be tuned from 1.4–5.0 nm with narrow size distribution solely through changing the solvent coordinating ability (toluene vs. N-coordinating solvents). Our in situ kinetic measurements indicate slower nucleation and faster growth in N-coordinating solvents compared with toluene. Through 31P NMR characterization and theoretical calculations of the Pd pre-reduction complexes, we show that the reduction free energy of the most abundant complexes increases with the solvent electron donating ability. The trend in the DFT calculated free energy of reduction is shown to correlate with the nucleation rates measured experimentally (increase in reduction free energy corresponds to lower nucleation rate), which is consistent with a Brønsted–Evans–Polanyi relationship. Similarly, the experimental growth rates are correlated with the solvent-surface binding energies (weaker binding corresponds to faster growth). Our study demonstrates the importance of solvents in colloidal synthesis of nanoparticles and their role in affecting the synthesis kinetics. The results provide insights on the microscopic relationship between the metal–ligand–solvent interactions and nucleation and growth rates and introduces a promising method for tuning the size of colloidal metal nanoparticles.Conflicts of interest
The authors have no conflict of interest to report.Acknowledgements
The work was supported by the National Science Foundation, Chemistry Division, award number CHE-1507370. AMK would like to acknowledge support by 3M Non-Tenured Faculty Award. W. Li would like to thank Wanluo Wang for the work on the graphical abstract. This research used resources of the Stanford Synchrotron Radiation Lightsource (beamline 2-2, user proposal N036A), SLAC National Accelerator Laboratory, supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515, Synchrotron Catalysis Consortium, US Department of Energy Grant No. DE-SC0012335. This research used resources of the Advanced Photon Source (beamline 12-ID-C, user proposal GUP-45774), a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. TEM imaging was performed at the Environmental Molecular Science Laboratory (EMSL) sponsored by the U.S. DOE Office of Biological and Environmental Research located at Pacific Northwest National Laboratory (PNNL) under a science theme proposal 49326. The authors would like to thank Dr C. Winkler for help with TEM imaging performed at the Nanoscale Characterization and Fabrication Laboratory facility operated by the Institute for Critical Technology and Applied Science at Virginia Tech. This work was performed, in part, at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science. Los Alamos National Laboratory, an affirmative action equal opportunity employer, is operated by Los Alamos National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy under contract DE-AC52-06NA25396. G. M. acknowledges support by the National Science Foundation (CBET-CAREER program) under Grant No. 1652694. M. G. T. acknowledges support by the National Science Foundation Graduate Research Fellowship under Grant No. 1247842. Computational support was provided by the Center for Research Computing at the University of Pittsburgh, and the Extreme Science and Engineering Discovery.Notes and references
- K. M. Bratlie, H. Lee, K. Komvopoulos, P. Yang and G. A. Somorjai, Nano Lett., 2007, 7, 3097–3101 CrossRef PubMed.
- K. Sugawa, H. Tahara, A. Yamashita, J. Otsuki, T. Sagara, T. Harumoto and S. Yanagida, ACS Nano, 2015, 9, 1895–1904 CrossRef PubMed.
- R. Narayanan and M. A. El-Sayed, J. Phys. Chem. B, 2005, 109, 12663–12676 CrossRef PubMed.
- L. Zhang, H. Jing, G. Boisvert, J. Z. He and H. Wang, ACS Nano, 2012, 6, 3514–3527 CrossRef PubMed.
- J. D. Aiken and R. G. Finke, J. Mol. Catal. A: Chem., 1999, 145, 1–44 CrossRef.
- Z. Zhou, X. Liu, L. Yue and I. Willner, ACS Nano, 2018, 12, 10725–10735 CrossRef PubMed.
- Y. Wang, S. Xie, J. Liu, J. Park, C. Z. Huang and Y. Xia, Nano Lett., 2013, 13, 2276–2281 CrossRef PubMed.
- L. Lian, Y. Xia, C. Zhang, B. Xu, L. Yang, H. Liu, D. Zhang, K. Wang, J. Gao and J. Zhang, Chem. Mater., 2018, 30, 982–989 CrossRef.
- L. Wu, H. Lian, J. J. Willis, E. D. Goodman, I. S. McKay, J. Qin, C. J. Tassone and M. Cargnello, Chem. Mater., 2018, 30, 1127–1135 CrossRef.
- N. Zheng, J. Fan and G. D. Stucky, J. Am. Chem. Soc., 2006, 128, 6550–6551 CrossRef PubMed.
- A. J. Biacchi and R. E. Schaak, ACS Nano, 2015, 9, 1707–1720 CrossRef.
- N. Ortiz and S. E. Skrabalak, Angew. Chem., Int. Ed., 2012, 51, 11757–11761 CrossRef PubMed.
- W. W. Yu, Y. A. Wang and X. Peng, Chem. Mater., 2003, 15, 4300–4308 CrossRef.
- B. Hu, K. Ding, T. Wu, X. Zhou, H. Fan, T. Jiang, Q. Wang and B. Han, Chem. Commun., 2010, 46, 8552–8554 RSC.
- H. Qian, Y. Zhu and R. Jin, ACS Nano, 2009, 3, 3795–3803 CrossRef PubMed.
- Z. Q. Yang and K. J. Klabunde, J. Organomet. Chem., 2009, 694, 1016–1021 CrossRef.
- Y. Xia, X. Xia and H. C. Peng, J. Am. Chem. Soc., 2015, 137, 7947–7966 CrossRef.
- A. J. Biacchi and R. E. Schaak, ACS Nano, 2011, 5, 8089–8099 CrossRef.
- J. Song, D. Kim and D. Lee, Langmuir, 2011, 27, 13854–13860 CrossRef PubMed.
- Y. Jiang, Y. Y. Huang, H. Cheng, Q. H. Liu, Z. Xie, T. Yao, Z. Jiang, Y. Y. Huang, Q. Bian, G. Q. Pan, Z. H. Sun and S. Q. Wei, J. Phys. Chem. C, 2014, 118, 714–719 CrossRef.
- W. Yu, W. Tu and H. Liu, Langmuir, 1999, 15, 6–9 CrossRef.
- W. Yu, M. Liu, H. Liu and J. Zheng, J. Colloid Interface Sci., 1999, 210, 218–221 CrossRef CAS.
- C. B. Williamson, D. R. Nevers, T. Hanrath and R. D. Robinson, J. Am. Chem. Soc., 2015, 137, 15843–15851 CrossRef CAS PubMed.
- S.-W. Kim, J. Park, Y. Jang, Y. Chung, S. Hwang, T. Hyeon and Y. W. Kim, Nano Lett., 2003, 3, 1289–1291 CrossRef CAS.
- T. Teranishi and M. Miyake, Chem. Mater., 1998, 10, 594–600 CrossRef CAS.
- A. P. LaGrow, B. Ingham, M. F. Toney and R. D. Tilley, J. Phys. Chem. C, 2013, 117, 16709–16718 CrossRef CAS.
- A. Henglein and M. Giersig, J. Phys. Chem. B, 1999, 103, 9533–9539 CrossRef CAS.
- D. D. Vaughn, S.-I. In and R. E. Schaak, ACS Nano, 2011, 5, 8852–8860 CrossRef CAS PubMed.
- M. J. Hostetler, J. E. Wingate, C.-J. Zhong, J. E. Harris, R. W. Vachet, M. R. Clark, J. D. Londono, S. J. Green, J. J. Stokes, G. D. Wignall, G. L. Glish, M. D. Porter, N. D. Evans and R. W. Murray, Langmuir, 1998, 14, 17–30 CrossRef CAS.
- C. Evangelisti, N. Panziera, A. D'Alessio, L. Bertinetti, M. Botavina and G. Vitulli, J. Catal., 2010, 272, 246–252 CrossRef CAS.
- H. P. Choo, K. Y. Liew and H. Liu, J. Mater. Chem., 2002, 12, 934–937 RSC.
- N. Sakamoto, M. Harada and T. Hashimoto, Macromolecules, 2006, 39, 1116–1124 CrossRef CAS.
- J. Wang, R. E. Winans, S. L. Anderson, S. Seifert, B. Lee, P. J. Chupas, Y. Ren, S. Lee and Y. Liu, J. Phys. Chem. C, 2013, 117, 22627–22635 CrossRef CAS.
- J. Park, K. An, Y. Hwang, J. G. Park, H. J. Noh, J. Y. Kim, J. H. Park, N. M. Hwang and T. Hyeon, Nat. Mater., 2004, 3, 891–895 CrossRef CAS.
- X. Yin, M. Shi, J. Wu, Y.-T. Pan, D. L. Gray, J. A. Bertke and H. Yang, Nano Lett., 2017, 17, 6146–6150 CrossRef CAS.
- L. Scarabelli, M. Coronado-Puchau, J. J. Giner-Casares, J. Langer and L. M. Liz-Marzán, ACS Nano, 2014, 8, 5833–5842 CrossRef CAS.
- A. M. Karim, N. Al Hasan, S. Ivanov, S. Siefert, R. T. Kelly, N. G. Hallfors, A. Benavidez, L. Kovarik, A. Jenkins, R. E. Winans and A. K. Datye, J. Phys. Chem. C, 2015, 119, 13257–13267 CrossRef.
- P. Abellan, L. R. Parent, N. Al Hasan, C. Park, I. Arslan, A. M. Karim, J. E. Evans and N. D. Browning, Langmuir, 2016, 32, 1468–1477 CrossRef CAS.
- S. Mozaffari, W. Li, C. Thompson, S. Ivanov, S. Seifert, B. Lee, L. Kovarik and A. M. Karim, Nanoscale, 2017, 9, 13772–13785 RSC.
- S. Mozaffari, W. Li, C. Thompson, S. Ivanov, S. Seifert, B. Lee, L. Kovarik and A. M. Karim, J. Visualized Exp., 2018, e57667, DOI:10.3791/57667.
- J. Polte, T. T. Ahner, F. Delissen, S. Sokolov, F. Emmerling, A. F. Thünemann and R. Kraehnert, J. Am. Chem. Soc., 2010, 132, 1296–1301 CrossRef CAS.
- M. Harada, N. Tamura and M. Takenaka, J. Phys. Chem. C, 2011, 115, 14081–14092 CrossRef CAS.
- M. A. Watzky and R. G. Finke, J. Am. Chem. Soc., 1997, 119, 10382–10400 CrossRef CAS.
- V. K. LaMer and R. H. Dinegar, J. Am. Chem. Soc., 1950, 72, 4847–4854 CrossRef CAS.
- C. Besson, E. E. Finney and R. G. Finke, Chem. Mater., 2005, 17, 4925–4938 CrossRef CAS.
- S. R. K. Perala and S. Kumar, Langmuir, 2013, 29, 9863–9873 CrossRef CAS.
- M. Harada and R. Ikegami, Cryst. Growth Des., 2016, 16, 2860–2873 CrossRef CAS.
- S. Mozaffari, W. Li, C. Thompson, S. Ivanov, S. Seifert, B. Lee, L. Kovarik and A. M. Karim, Nanoscale, 2017, 9, 13772–13785 RSC.
- A. E. Saunders, M. B. Sigman and B. A. Korgel, J. Phys. Chem. B, 2004, 108, 193–199 CrossRef CAS.
- C. R. Bullen and P. Mulvaney, Nano Lett., 2004, 4, 2303–2307 CrossRef CAS.
- J. van Embden and P. Mulvaney, Langmuir, 2005, 21, 10226–10233 CrossRef CAS.
- B. H. Wu, H. Y. Yang, H. Q. Huang, G. X. Chen and N. F. Zheng, Chin. Chem. Lett., 2013, 24, 457–462 CrossRef CAS.
- E. Redel, P. Mirtchev, C. Huai, S. Petrov and G. A. Ozin, ACS Nano, 2011, 5, 2861–2869 CrossRef CAS.
- M. L. Personick and C. A. Mirkin, J. Am. Chem. Soc., 2013, 135, 18238–18247 CrossRef CAS.
- S. Mozaffari, W. Li, C. Thompson, S. Ivanov, S. Seifert, B. Lee, L. Kovarik and A. M. Karim, J. Visualized Exp., 2018,(136), e57667 Search PubMed.
- S. Mozaffari, W. Li, M. Dixit, S. Seifert, B. Lee, L. Kovarik, G. Mpourmpakis and A. M. Karim, Nanoscale Adv., 2019, 1, 4052–4066 RSC.
- W. Li, S. Ivanov, S. Mozaffari, N. Shanaiah and A. M. Karim, Organometallics, 2019, 38, 451–460 CrossRef CAS.
- C. Amatore, A. Jutand and M. A. M'Barki, Organometallics, 1992, 11, 3009–3013 CrossRef CAS.
- J. A. Goodfellow, T. A. Stephenson and M. C. Cornock, J. Chem. Soc., Dalton Trans., 1978, 1195–1200, 10.1039/DT9780001195.
- E. G. Moschetta, K. M. Gans and R. M. Rioux, J. Catal., 2013, 302, 1–9 CrossRef CAS.
- P. R. Vashi and H. M. Marques, J. Inorg. Biochem., 2004, 98, 1471–1482 CrossRef CAS.
- C. Amatore and A. Jutand, Acc. Chem. Res., 2000, 33, 314–321 CrossRef CAS PubMed.
- C. Amatore, A. Jutand and A. Thuilliez, Organometallics, 2001, 20, 3241–3249 CrossRef CAS.
- L. E. Marbella, D. M. Chevrier, P. D. Tancini, O. Shobayo, A. M. Smith, K. A. Johnston, C. M. Andolina, P. Zhang, G. Mpourmpakis and J. E. Millstone, J. Am. Chem. Soc., 2015, 137, 15852–15858 CrossRef CAS.
- G. Mpourmpakis, S. Caratzoulas and D. G. Vlachos, Nano Lett., 2010, 10, 3408–3413 CrossRef CAS.
- X. Yin, X. Liu, Y.-T. Pan, K. A. Walsh and H. Yang, Nano Lett., 2014, 14, 7188–7194 CrossRef CAS PubMed.
- M. Besora, P. Vidossich, A. Lledós, G. Ujaque and F. Maseras, J. Phys. Chem. A, 2018, 122, 1392–1399 CrossRef CAS.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1936, 32, 1333–1360 RSC.
- T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217 CrossRef CAS.
- J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937 CrossRef PubMed.
- F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Nat. Chem., 2015, 7, 403 CrossRef CAS PubMed.
- M. Dixit, X. Peng, M. D. Porosoff, H. D. Willauer and G. Mpourmpakis, Catal. Sci. Technol., 2017, 7, 5521–5529 RSC.
- M. Crespo-Quesada, A. Yarulin, M. Jin, Y. Xia and L. Kiwi-Minsker, J. Am. Chem. Soc., 2011, 133, 12787–12794 CrossRef CAS.
- H. Ramezani-Dakhel, P. A. Mirau, R. R. Naik, M. R. Knecht and H. Heinz, Phys. Chem. Chem. Phys., 2013, 15, 5488–5492 RSC.
- J. M. Petroski, Z. L. Wang, T. C. Green and M. A. El-Sayed, J. Phys. Chem. B, 1998, 102, 3316–3320 CrossRef CAS.
- S. R. K. Perala and S. Kumar, Langmuir, 2013, 29, 9863–9873 CrossRef CAS PubMed.
- S. R. K. Perala and S. Kumar, Langmuir, 2014, 30, 12703–12711 CrossRef CAS PubMed.
- S. Lazzari, P. M. Theiler, Y. Shen, C. W. Coley, A. Stemmer and K. F. Jensen, Langmuir, 2018, 34, 3307–3315 CrossRef CAS PubMed.
- K. Wikander, C. Petit, K. Holmberg and M.-P. Pileni, Langmuir, 2006, 22, 4863–4868 CrossRef CAS.
- M. Osmić, J. Kolny-Olesiak and K. Al-Shamery, CrystEngComm, 2014, 16, 9907–9914 RSC.
- N. Ortiz and S. E. Skrabalak, Langmuir, 2014, 30, 6649–6659 CrossRef CAS PubMed.
- C. H. Turner, Y. Lei and Y. Bao, Nanoscale, 2016, 8, 9354–9365 RSC.
- X.-Y. Li, B. Zhu, R. Qi and Y. Gao, Adv. Theory Simul., 2019, 2, 1800127 CrossRef.
- J. van Embden, A. S. R. Chesman and J. J. Jasieniak, Chem. Mater., 2015, 27, 2246–2285 CrossRef CAS.
- S. G. Kwon, G. Krylova, P. J. Phillips, R. F. Klie, S. Chattopadhyay, T. Shibata, E. E. Bunel, Y. Liu, V. B. Prakapenka, B. Lee and E. V. Shevchenko, Nat. Mater., 2015, 14, 215–223 CrossRef CAS.
- C. A. Dreiss, K. S. Jack and A. P. Parker, J. Appl. Crystallogr., 2006, 39, 32–38 CrossRef CAS.
- Igor Pro, Wavemetrics, Lake Oswego, OR, USA, https://www.wavemetrics.com/ Search PubMed.
- T. Li, A. J. Senesi and B. Lee, Chem. Rev., 2016 DOI:10.1021/acs.chemrev.5b00690.
- M. D. Abràmoff, P. J. Magalhães and S. J. Ram, Biophotonics Int., 2004, 11, 36–42 Search PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- M. Newville, J. Synchrotron Radiat., 2001, 8, 96–100 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- F. Weigend and M. Häser, Theor. Chem. Acc., 1997, 97, 331–340 Search PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- C. Popa, T. Zhu, I. Tranca, P. Kaghazchi, T. Jacob and E. J. M. Hensen, Phys. Chem. Chem. Phys., 2015, 17, 2268–2273 RSC.
- M. Steinmetz and S. Grimme, ChemistryOpen, 2013, 2, 115–124 CrossRef CAS.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805, 10.1039/P29930000799.
- P. Winget, D. M. Dolney, D. J. Giesen, C. J. Cramer and D. G. Truhlar, Minnesota solvent descriptor database, https://comp.chem.umn.edu/solvation/ Search PubMed.
- A. Douidah, P. Marecot, S. Szabo and J. Barbier, Appl. Catal., A, 2002, 225, 21–31 CrossRef CAS.
- Dielectric Constants of Common Materials, https://www.kabusa.com/Dilectric-Constants.pdf.
- J. W. Ochterski, Thermochemistry in Gaussian, Gaussian, Inc., Wallingford, CT, 2000 Search PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Estimations of the number of nanoparticles and extent of reaction, extracting the rates of nucleation and growth from experimental data, precursor speciation calculations from density functional theory (DFT), representative SAXS spectra, TEM images of nanoparticles, in situ SAXS measurement fitting results, kinetics extracted from in situ SAXS, XANES and XAFS results, 31P NMR spectra, mole fraction of different precursor complexes from DFT calculations, rendered images of all precursors, Gibbs free energy of H2 reduction of Pd(OAc)(TOP)(solv)2, DFT calculation results and images for solvent-nanoparticle/Pd(111) surface binding. See DOI: 10.1039/d0nr06078j |
| This journal is © The Royal Society of Chemistry 2021 |