Open Access Article
Open Access ArticlePolarized emission of CdSe nanocrystals in magnetic field: the role of phonon-assisted recombination of the dark exciton†
Gang
Qiang‡
 *a,
Aleksandr A.
Golovatenko‡
*a,
Aleksandr A.
Golovatenko‡
 *b,
Elena V.
Shornikova
*b,
Elena V.
Shornikova
 a,
Dmitri R.
Yakovlev
a,
Dmitri R.
Yakovlev
 *ab,
Anna V.
Rodina
b,
Evgeny A.
Zhukov
ab,
Ina V.
Kalitukha
b,
Victor F.
Sapega
b,
Vadim Kh.
Kaibyshev
*ab,
Anna V.
Rodina
b,
Evgeny A.
Zhukov
ab,
Ina V.
Kalitukha
b,
Victor F.
Sapega
b,
Vadim Kh.
Kaibyshev
 b,
Mikhail A.
Prosnikov
c,
Peter C. M.
Christianen
c,
Aleksei A.
Onushchenko
d and
Manfred
Bayer
b,
Mikhail A.
Prosnikov
c,
Peter C. M.
Christianen
c,
Aleksei A.
Onushchenko
d and
Manfred
Bayer
 ab
ab
aExperimentelle Physik 2, Technische Universität Dortmund, 44227 Dortmund, Germany. E-mail: gang.qiang@tu-dortmund.de; dmitri.yakovlev@tu-dortmund.de
bIoffe Institute, Russian Academy of Sciences, 194021 St. Petersburg, Russia. E-mail: sasha.pti@mail.ioffe.ru
cHigh Field Magnet Laboratory (HFML-EMFL), Radboud University, 6525 ED Nijmegen, The Netherlands
dITMO University, 199034 St Petersburg, Russia
First published on 7th December 2020
Abstract
The recombination dynamics and spin polarization of excitons in CdSe nanocrystals synthesized in a glass matrix are investigated using polarized photoluminescence in high magnetic fields up to 30 Tesla. The dynamics are accelerated by increasing temperature and magnetic field, confirming the dark exciton nature of low-temperature photoluminescence (PL). The circularly polarized PL in magnetic fields reveals several unusual appearances: (i) a spectral dependence of the polarization degree, (ii) its low saturation value, and (iii) a stronger intensity of the Zeeman component which is higher in energy. The latter feature is the most surprising being in contradiction with the thermal population of the exciton spin sublevels. The same contradiction was previously observed in the ensemble of wet-chemically synthesized CdSe nanocrystals but was not understood. We present a theory which explains all the observed features and shows that the inverted ordering of the circularly polarized PL maxima from the ensemble of nanocrystals is a result of competition between the zero phonon (ZPL) and one optical phonon-assisted (1PL) emission of the dark excitons. The essential aspects of the theoretical model are different polarization properties of the dark exciton emission via ZPL and 1PL recombination channels and the inhomogeneous broadening of the PL spectrum from the ensemble of nanocrystals exceeding the optical phonon energy.
1. Introduction
For a few decades, colloidal semiconductor nanocrystals (NCs) have been the focus of intensive research. Due to the continuous progress in technology, nanocrystals with different sizes, shapes, compositions, and surface properties have been synthesized.1–8 Understanding their optical, electrical and chemical properties has led to applications in various fields, such as light-emitting diodes,9,10 laser technology,11 field-effect transistors,12 solar cells,13,14 biological labels,15,16etc.For direct bandgap semiconductor NCs, e.g. made up of CdSe, CdTe or InP, most of the optical properties can be explained within the exciton fine structure model.17–20 In ideal spherical NCs, the band-edge exciton state 1S3/21Se is eight-fold degenerate. 1S3/2 is the lowest quantum size level of the holes and is four-fold degenerate with respect to its total angular momentum components. 1Se is the lowest quantum size level of the electrons, which is doubly degenerate with respect to its spin components. However, due to the NC shape asymmetry, the intrinsic crystal field, and the electron–hole exchange interaction, the degeneracy is lifted resulting in the formation of five exciton states. In the case of wurtzite CdSe NCs, the two lowest states are a typically optically forbidden (dark) exciton state |F〉 (angular momentum projection along the NC quantization axis ±2) and a higher-lying optically allowed (bright) exciton state |A〉 (momentum projection ±1).19 The presence of the bright and dark excitons allows one to explain the recombination dynamics, spin dynamics, and magneto-optical properties, taking into account also the Zeeman effect.17,21–27
CdSe NCs are a test bed for investigation of colloidal NCs; therefore, their optical properties have been extensively studied. External magnetic fields have been used as a powerful tool not only to address magneto-optical properties and spin-dependent phenomena, but also to identify the exciton energy, spin structure and mechanisms responsible for recombination of the dark excitons. In particular, the following magneto-optical properties in external magnetic fields of wet-chemically synthesized colloidal CdSe NCs were reported: shortening of the dark exciton lifetime,17,28 circular polarization of photoluminescence (PL),21,22,29,30 exciton fine structure splitting including the Zeeman effect in single NCs,25,31 anisotropic exchange interaction,32,33 and electron spin coherence.34,35 All these make the colloidal NCs promising for spintronics and quantum information applications based on the spin-dependent phenomena. No magneto-optical study has been performed so far on CdSe in the glass matrix.
Studies on the circularly polarized PL of CdSe-based NCs in the magnetic field22,29 revealed a puzzling behavior: with increasing field the σ− polarized PL, which is stronger in intensity compared to the σ+ component, shifts to higher energy than the σ+ polarized emission. This contradicts with the expectation for the thermal population of the exciton spin sublevels split in the magnetic field. Later, the same contradiction was reported for colloidal CdTe NCs.24 This contradiction, however, is absent in fluorescence line narrowing (FLN) experiments and in measurements of single NCs, i.e. for the experimental conditions when the inhomogeneous broadening of the PL due to NC size dispersion in the ensemble is suppressed.25,29 In the FLN experiments, pronounced optical phonon-assisted recombination of the dark exciton was observed.17,28,29,36–38 Under nonresonant excitation, the low-temperature PL of the NC ensemble is contributed by zero phonon and optical phonon-assisted exciton emission, which form overlapping bands due to NCs of different sizes.17,37 In ref. 22 and 29, the contradiction with respect to the energy shift was tentatively assigned to the interplay between different emission channels of the dark exciton. However, a corresponding theoretical model has not been proposed so far.
For the present magneto-optical study, we choose CdSe NCs which are synthesized in a glass matrix. One of the motivations is to compare their magneto-optical properties with those of the wet-chemically synthesized CdSe NCs. Further reasons are based on the simpler experimental situation, namely the simpler surface conditions due to the absence of organic ligand passivation, long-term stability due to the matrix encapsulation, and the ideally random orientation of the NC quantization axis in the glass-based NC ensemble which allow us to make an easier model description. The wet-chemically grown and glass-based NCs differ by their surface conditions. In the first case, a NC is passivated using organic ligands, in the second case is surrounded by a glass matrix. Our study shows that the magneto-optical properties of the dark excitons in both cases are similar and not affected by the difference in the NC surrounding media.
In this paper, we study CdSe NCs in glass with diameters varying from 3.3 nm up to 6.1 nm and investigate the recombination dynamics and spin polarization properties of excitons in strong magnetic fields up to 30 T. We find experimentally the same contradiction between intensities and energies of the circularly polarized PL as reported for wet-chemically prepared CdSe NCs, and a strong spectral dependence of the circular polarization degree. We develop a theoretical model accounting for the contributions of both zero phonon emission (ZPL) and first optical phonon-assisted emission (1PL) of the dark excitons, which allows us to describe all experimental signatures.
2. Experimental results and modeling
2.1. Time-integrated and time-resolved photoluminescence
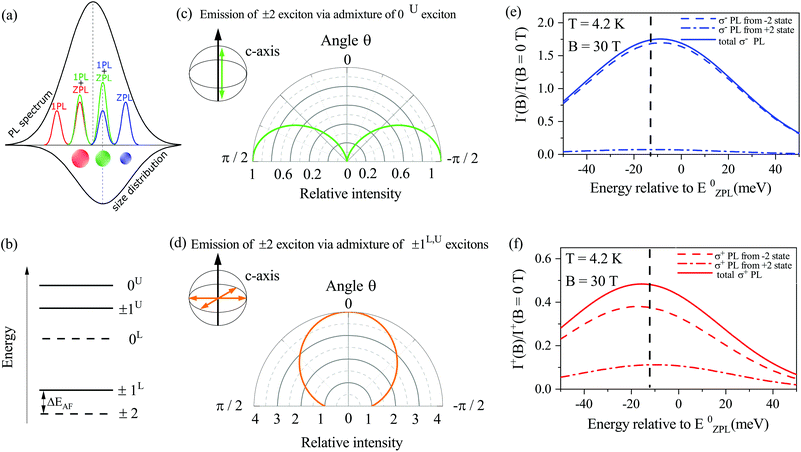
We studied four samples with CdSe NCs synthesized in a silicate glass matrix (see Methods). The sample parameters are given in Table 1. Their photoluminescence (PL) spectra measured at T = 4.2 K are shown in Fig. 1a. The quantum confinement enhancement with reducing NC diameter shifts the emission band to higher energies from 2.017 eV for D6.1 up to 2.366 eV for D3.3. The full width at half maximum (FWHM) of the PL spectra is about 100 meV, which is caused by the dispersion of NC sizes. Absorption spectra are shown and compared with the PL in Fig. S1.† The Stokes shift between the exciton resonance in absorption and PL maximum is also size-dependent, it is larger in smaller NCs, e.g. 89 meV in D3.3 and only 22 meV in D6.1.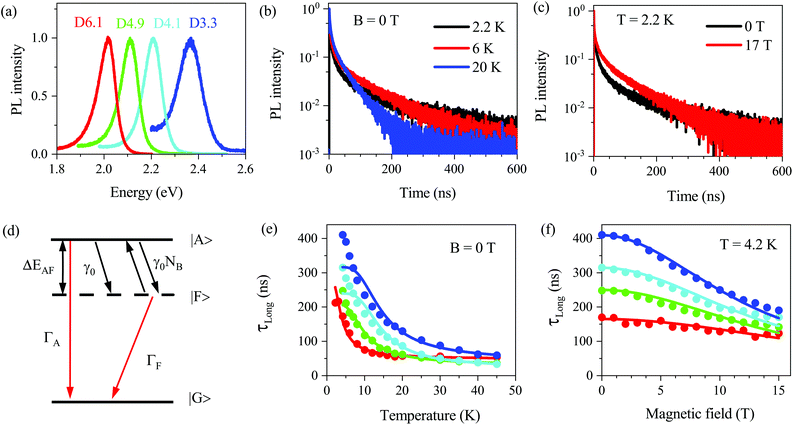 | ||
| Fig. 1 Photoluminescence and recombination dynamics. (a) PL spectra of the studied CdSe NCs measured at T = 4.2 K. (b) Recombination dynamics measured for sample D6.1 at various temperatures, B = 0 T. (c) Recombination dynamics measured for sample D6.1 at B = 0 and 17 T, T = 2.2 K. (d) Scheme of exciton energy levels. |A〉, |F〉, and |G〉 denote the bright and dark exciton states, and crystal ground state, respectively. ΔEAF is the bright–dark splitting. γ0 is the zero-temperature relaxation rate from the bright to the dark exciton state. γ0NB is the thermal activation rate of the reverse process. ΓA and ΓF are the recombination rates of the bright and dark excitons. (e) Temperature dependence of the long component of the PL decay, τLong, for all samples at B = 0 T. The lines are fits with eqn (S5†). (f) Magnetic field dependence of τLong at T = 4.2 K for all samples. The lines show the averaged lifetime of the dark exciton calculated with eqn (S23†) in a randomly oriented ensemble of NCs as described in ESI section S4.2.† The color codes in panels (e and f) are same as in panel (a). | ||
| Sample | D3.3 | D4.1 | D4.9 | D6.1 |
|---|---|---|---|---|
| NC diameter (nm) | 3.30 ± 0.17 | 4.10 ± 0.21 | 4.9 ± 0.25 | 6.1 ± 0.31 |
| PL FWHM (meV) | 120 | 99 | 96 | 101 |
| PL peak energy (eV) | 2.366 | 2.210 | 2.111 | 2.017 |
| Absorption peak energy (eV) | 2.455 | 2.267 | 2.160 | 2.039 |
| Stokes shift (meV) | 89 | 57 | 49 | 22 |
| Bright–dark splitting from PL decay (meV) | 3.9 | 4.3 | 2.6 | 0.9 |
| Bright–dark splitting from FLN (meV) | — | 8.4 | 7.5 | 3.5 |
The low-temperature PL in the studied samples is dominated by exciton recombination, which has a characteristic decay variation with temperature and magnetic field. This allows one to distinguish neutral and charged excitons in the NCs.40–42 Taking sample D6.1 as a representative example, we show in Fig. 1b the recombination dynamics at various temperatures. With increasing temperature from 2.2 to 20 K, the decay time of the long component, τLong, shortens from 212 ns down to 58 ns. The temperature dependence of τLong for all the studied samples is given in Fig. 1e. One can see that the decay times shorten with increasing temperature as a result of thermal activation from the dark exciton to the bright exciton state. A similar behavior is observed when external magnetic field is applied; in Fig. 1c, the long component measured at T = 2.2 K shortens from 212 ns down to 119 ns with increasing field up to B = 17 T. The magnetic field dependence of τLong for all studied samples is given in Fig. 1f.
This is the typical behavior for exciton emission in CdSe NCs and can be well explained with the diagram as shown in Fig. 1d (a detailed scheme of the exciton levels is given in Fig. S13a†). The optically forbidden dark state |F〉 with angular momentum projection ±2 is the exciton ground state. The closest optically allowed bright state |A〉 with angular momentum projection ±1 is shifted to higher energy by the bright–dark splitting ΔEAF.17 The fast component of the PL decay is provided by the recombination of bright excitons with rate ΓA and their rapid thermalization to the dark state with rate γ0(1 + NB), where γ0 is the spin–flip rate, NB = 1/[exp(ΔEAF/kBT) − 1] is the Bose–Einstein phonon occupation at temperature T. The long component corresponds to the dark exciton recombination with rate ΓF. With an increase in temperature, the dark excitons are activated to the bright state. In the case of a one-phonon process, the activation rate is given by γ0NB. The shortening of the long component in a magnetic field is due to the mixing of bright and dark exciton states by the field component perpendicular to the NC quantization axis.17,40 These properties allow us to uniquely assign the long decay component τLong to the recombination of the dark excitons. More information about the PL decay fitting is given in ESI section S2.†
The analysis of the τLong temperature dependence allows us to evaluate the bright–dark splitting ΔEAF (see ESI section S2†). The corresponding fits are shown by the solid lines in Fig. 1e, and the evaluated ΔEAF values are given in Table 1. In Fig. S6c,† we compare the ΔEAF values with the literature data17,37–39 and a good consistency is found. However, ΔEAF in D3.3 is deviating from the general trend, which may point toward a slightly prolate shape of the CdSe NCs.43 The ΔEAF values determined from fluorescence line narrowing (see ESI section S2.3†) are found to be larger compared to the values determined from the τLong temperature dependence. Two explanations for this discrepancy were proposed: (i) The ΔEAF values determined from the τLong temperature dependence correspond to the true values of the bright–dark splitting, while the ΔEAF values from FLN can show an additional energy shift due to polaron formation,44 (ii) The ΔEAF values determined from the τLong temperature dependence correspond to the energy of confined acoustic phonons, which provide thermal activation to the bright excitons.45
2.2. Polarized exciton emission in strong magnetic fields
Let us turn to the main focus of this paper, i.e. the polarized exciton emission in strong magnetic fields. Fig. 2a (left axis) shows circularly polarized PL spectra of the sample D6.1 measured at T = 4.2 K and B = 30 T. One can see that compared to the black spectrum at B = 0 T, the intensity of the σ− component (blue) is increased, while it is decreased for the σ+ component (red). The green line in Fig. 2a (right axis) shows the spectral dependence of Pintc, which is larger at the high energy side (−0.63), decreases around the PL peak energy, and remains nearly constant (−0.53) at the low energy side. This is quite unusual as one does not expect to have a considerable spectral dependence of the dark exciton g-factor, gF, within the emission line. In fact, as shown below (Table S3†), gF is about constant for all studied NCs covering a much larger spectral range.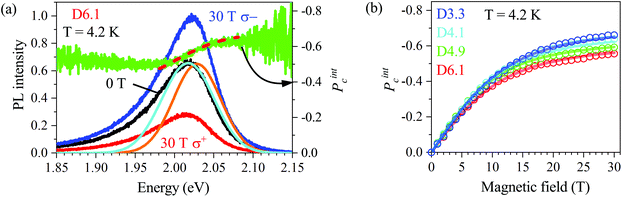 | ||
| Fig. 2 Polarized photoluminescence in magnetic field. (a) (left axis) σ− (blue) and σ+ (red) circularly polarized emission, measured at B = 30 T for sample D6.1. The black spectrum at B = 0 T is shown for comparison. (right axis) Green and red-dashed curves show the experimental and calculated spectral dependence of the time-integrated DCP, respectively. The orange curve is the function fZPL(E) and the cyan curve is the calculated PL spectrum at B = 0 T, which accounts for the ZPL and 1PL contributions. (b) Magnetic field dependences of Pintc (B) measured at the PL maximum in all samples. Lines are fits with eqn (1) and (3). | ||
Fig. 2b shows the magnetic field dependence of the time-integrated degree of circular polarization (DCP), Pintc, measured at the PL maximum. It is expected that in the ensemble of NCs with randomly oriented c-axis (the case for NCs in glass), the DCP saturation value should reach −0.75.21 However, as one can see in Fig. 2b, this is obviously not the case, Pintc does not reach −0.75 and has a clear size-dependence. At B = 30 T, Pintc = −0.56 in D6.1 and −0.66 in D3.3.
Fig. 3a–d show the magnetic field dependence of the polarized PL intensity. The σ− polarized component increases monotonously with the magnetic field and the σ+ polarized component remains almost constant after an initial decrease. Most surprising are the spectral shifts of the σ+ and σ− polarized components (Fig. 3e and f). For neutral excitons, it is expected that the PL maximum of the stronger component, i.e. σ−, shifts in the magnetic field to lower energy, as the lower energy spin state of the exciton has the higher thermal population. This expectation is shown by the dashed lines for the sample D6.1 in Fig. 3e (more details will be given below), but the experimental shift of the PL maximum demonstrates a very different behavior. First, for the D6.1, D4.9 and D4.1 samples, the σ+ component shifts to lower energy and second, the splitting between σ+ and σ− is several times larger than expected (Fig. 3e–g). In the sample D3.3, both components shift initially to higher energy and the σ+ component lowers its energy for fields above 15 T (Fig. 3h).
 | ||
| Fig. 3 Photoluminescence intensity and spectral shifts in magnetic fields. (a–d) PL intensity of the σ+ (red) and σ− (blue) polarized PL as functions of the magnetic field in the CdSe NCs. (e–h) Magnetic field dependences of the corresponding PL peak energies. For all panels, the symbols correspond to the experimental data, and the lines show the modeling results. Dashed lines in panel (e) show the Zeeman splitting of the dark exciton spin sublevels −2 (blue) and +2 (red) in a nanocrystal with the c-axis parallel to the magnetic field direction. We note that the energy of ±2 states at B = 0 T is taken the same as the PL maxima position for the sake of demonstrativeness. Relative positions of ±2 energy state distribution maxima and polarized PL maxima in the applied magnetic field are shown in Fig. S15.† | ||
2.3. Model description
In order to resolve the contradiction between intensities and energies of the polarized PL, we extend the theoretical model for the circular polarized emission from an ensemble of randomly oriented nanocrystals first developed in ref. 21. The extension accounts for the linearly polarized contribution coming from the dark exciton recombination assisted by optical phonons. For the spectrally broad PL bands in CdSe NCs of about 100 meV width, which is four times the optical phonon energy in CdSe (26 meV in bulk), the PL is composed of the ZPL emission of the dark excitons from NCs of one size and optical phonon-assisted emission of the dark excitons from smaller NCs, as illustrated in Fig. 4a. The contribution of acoustic phonon-assisted recombination of the dark excitons cannot be resolved within the ZPL line; however, it is can be seen by single nanocrystal spectroscopy.46 The ZPL emission usually has properties of a two-dimensional dipole, indicating the activation of the ±2 dark exciton through an admixture with the ±1L,U bright excitons (see Fig. 4d).47 However, the specific mechanism of the ZPL recombination is still under debate.48–50 It was shown in ref. 48 that the dark exciton recombination with the assistance of optical or acoustic phonons results in predominantly linearly polarized emission, corresponding to the admixture of the 0U bright exciton (Fig. 4c). Thus, the ZPL and phonon-assisted emission have different spatial distribution profiles of the emission, which are determined by the relative orientation between the direction of the light propagation and the direction of the anisotropic c-axis of wurtzite CdSe nanocrystals.17,47,48 In the case of a randomly oriented ensemble of nanocrystals, all these factors modify the magnetic field and spectral dependences of Pintc.The modeling results presented in Fig. 2 and 3 are based on the consideration of the ZPL and one optical phonon-assisted line (1PL) contributions to the PL. The contribution of the linearly polarized recombination of the dark exciton with assistance of acoustic phonons is considered in ESI section S4.† Our task is to calculate the σ+ and σ− polarized PL spectra and the spectral dependence of Pintc. For this purpose, we sum the ZPL and 1PL contributions, which have different spectral distributions, and average them over the random orientation of the hexagonal c-axis in an ensemble of NCs:
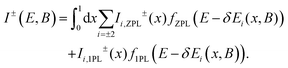 | (1) |
Here, E is the spectral energy, δE±2(x, B) = ±gFμBBx/2 are the Zeeman shifts of the ±2 dark exciton states, x = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ with θ being the angle between the c-axis of the nanocrystal and the magnetic field applied in the Faraday geometry. The explicit forms of Ii,ZPL±(x) and Ii,1PL±(x) are given in ESI section S4.† Functions fZPL(E) and f1PL(E) describing the inhomogeneous broadening of ZPL and 1PL emission due to size dispersion of NCs are determined as follows:
θ with θ being the angle between the c-axis of the nanocrystal and the magnetic field applied in the Faraday geometry. The explicit forms of Ii,ZPL±(x) and Ii,1PL±(x) are given in ESI section S4.† Functions fZPL(E) and f1PL(E) describing the inhomogeneous broadening of ZPL and 1PL emission due to size dispersion of NCs are determined as follows:
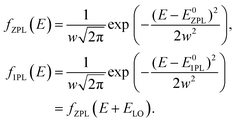 | (2) |
Here, E0ZPL corresponds to the energy of the ZPL in QDs at the maximum of the size distribution, ELO = 26 meV is the energy of the optical phonon in CdSe, and w is the standard deviation. The function fZPL(E) used for the fitting of the experimental data for the D6.1 sample is shown in Fig. 2a by the orange line. The cyan line in Fig. 2a models the PL spectrum at B = 0 T with accounting for the 1PL contribution.
Using eqn (1), we calculate the DCP spectral dependence as:
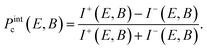 | (3) |
The fit parameters are: the dark exciton g-factor gF, the characteristic energy of interaction ε which results in the admixture of the dark and ±1L bright exciton states in the zero magnetic field, the ratio of the 1PL and ZPL recombination rates at zero magnetic field χ0, and a phenomenological parameter c1PL, which determines an increase in the 1PL recombination rate in the magnetic field, while an increase in the ZPL recombination rate in the magnetic field is described within second order perturbation theory.17,48 The parameter χ0 can be estimated independently from the ratio of the 1PL to ZPL intensities measured in fluorescence line narrowing experiments. Typically, this ratio is of the order of unity.17,28,29,36–38 The FLN spectra for samples D4.1, D4.9 and D6.1 are shown in Fig. S7.† Fitting of the magnetic field dependence of the long decay time (Fig. 1f) imposes a restriction on the χ0, ε and c1PL values. Finally, the linked sets of parameters χ0, ε and c1PL together with gF are used for joint fitting of the magnetic field dependences of Pintc, the intensities and maxima positions of the σ− and σ+ polarized PL.
2.4. Modeling of experimental results
Results of modeling for magnetic field dependences of Pintc at the energy of zero magnetic field PL maximum are shown by the lines in Fig. 2b. We find that low values of Pintc at B = 30 T are caused by the contribution of the predominantly linearly polarized 1PL emission of dark excitons. This contribution is found to be stronger in large nanocrystals (Table S3†), resulting in a smaller saturation value of the DCP, and is consistent with the relative intensities of the 1PL and ZPL emission determined from FLN (see Fig. S7†).Besides the saturation of the DCP in high magnetic fields, the 1PL emission causes the DCP spectral dependence (calculation is shown by the orange dashed curve in Fig. 2a). The reason is the weaker relative intensity of the 1PL emission at the high-energy side of the PL spectrum due to the small number of NCs that can provide this contribution. The pronounced spectral dependence of the DCP in large NCs correlates with its low saturation level, i.e. with the strong 1PL emission (Fig. S18†).
We turn now to the modeling of the intensities and maxima positions of the σ+ and σ− polarized PL. The calculated magnetic field dependences of the PL intensities (Fig. 3a–d) are in good agreement with the experimental data for all the studied samples. In a randomly oriented ensemble of NCs, the emission of σ+ polarized photons from the predominantly populated −2 dark exciton state results in the saturation of the σ+ PL intensity at a level of 0.4 of the zero-field intensity. This is observed for all the studied samples (Fig. 3a–d).
The ability of the dark exciton states to emit both σ− and σ+ polarized light also explains the energy shifts of the polarized PL maxima in a magnetic field. The spectral maximum of σ− polarized PL (solid line in Fig. 4e) is determined by the relationship between the σ− polarized emission from the −2 (dashed line) and +2 (dash-dotted line) states. In a magnetic field, the ZPL emission from the −2 state dominates, and the PL maximum shifts toward higher energy. This behavior is observed in all the studied samples (Fig. 3e and h). Similarly (Fig. 4f), the spectral maximum of σ+ polarized PL is determined by the emission from the −2 and +2 states. In high magnetic fields, the 1PL emission from the −2 state dominates, and the PL maximum shifts to lower energy. Thus, positions of polarized PL maxima to a large extent are controlled by the emission of the −2 state: ZPL in the case of σ−, and 1PL in the case of σ+.
For comparison, the Zeeman splitting of the dark exciton spin sublevels −2 (blue) and +2 (red) in a nanocrystal with the c-axis parallel to the magnetic field direction is presented in Fig. 3e by the dash lines. One can see that it is much smaller than the difference of PL maxima energies and also results in reversed order (see also Fig. S15†).
The developed model allows us to describe all unusual features of the polarized PL in CdSe NCs by accounting for the superposition of the ZPL and 1PL emission of the dark excitons. It is important to note that the model is universal and can be readily applied to describe the properties of the wet-chemically grown NCs. Their magneto-optical properties are very similar to what we have found in CdSe NCs in glass.22,29 This allows us to conclude that the spectral shifts of the polarized emission in magnetic fields are controlled by the mechanism suggested in this paper and are weakly dependent on the surface conditions. However, the surface can be strongly modified by the growth conditions and post-growth treatment in the wet-chemically grown NCs. Furthermore, in this case, the splitting of the PL lines in magnetic fields can be additionally contributed by the surface states.
3 Discussion
From the fitting of the magnetic field dependences of the DCP, we find that the g-factor of the dark exciton gF ≈ 1.7 is almost independent of the NC diameter. For colloidal CdSe nanocrystals with a diameter of 5.7 nm, gF = 1.7 was determined in ref. 21. gF = 1.3 was estimated in ref. 30 for CdSe NCs with diameters of 3.5–5 nm. This value is smaller than gF ≈ 4 obtained from theoretical estimations17 and gF = 2.7 from a single CdSe/ZnS nanocrystal study.25 In ESI section S4.5,† we demonstrate the results of fitting with the assumption of an additional linearly polarized contribution to the ZPL emission, which can be associated with acoustic phonon-assisted recombination of the dark exciton. In this case, we extract gF ≈ 2.5, almost independent of the NC diameter. Accounting for the 2PL and 3PL, emission can further improve the agreement of experiment and theory for gF and for the energy positions of the σ+ polarized PL maximum in the sample D3.3 (Fig. 3h) in low magnetic fields.The dark exciton g-factor comprises the electron, ge, and hole, gh, g-factors as17gF = ge − 3gh. The size dependence of ge is well known for CdSe NCs34,35,51 (Fig. S26†). This allows us to evaluate the hole g-factor as gh = (ge − gF)/3. Using the gF values determined from the fitting with the linearly polarized contribution to the ZPL, we find gh ≈ −0.45 and without it gh ≈ −0.15 for NCs with diameters of 4–6 nm (Fig. S27†). It is smaller than the theoretically estimated value of gh ≈ −1 from ref. 17 and 52. However, the first value is close to gh ≈ −0.56 measured in giant shell CdSe/CdS colloidal nanocrystals from the polarized PL of negative trions.40
The values of the dark exciton g-factor used for the modeling of experimental data in Fig. 2 and 3 are obtained in the assumption of thermal equilibrium between the ±2 states. However, the spin relaxation between these states requires a change in the exciton total spin projection by ΔF = 4. If the rate of this process is much slower than the dark exciton lifetime, the populations of the ±2 states are determined by the relaxation from the bright ±1 exciton states. As shown in ESI section S4.7–8,† the fitting of the experimental dependences in this case results in larger values of the dark exciton g-factor, which are close to the theoretical estimations. The spin relaxation time, or spin dynamics, is often evaluated from the rise of the degree of circular polarization in the magnetic field.21,22 However, such evaluation might be complicated in the case of an ensemble with a nonmonoexponential PL decay.53 We have presented the analysis of the DCP dynamics in ESI section S3,† showing that in any case it is faster than the dark exciton recombination and there is not much of a difference between the time-integrated and saturated DCP values. However, as this time is of the order of the relaxation time from the bright to the dark exciton state (the first time component in the PL decay), it is not possible to conclude whether the DCP rise and the population of the dark exciton sublevels is determined by the spin relaxation between ±1 and ±2 states. Further clarification of this question is beyond the scope of this paper.
In previous publications, a saturation value of the DCP in high magnetic fields lower than −0.75 was associated with nonradiative recombination of the dark excitons,21 partial activation of the dark exciton recombination via an admixture of the 0U bright exciton resulting in linearly polarized ZPL emission,54 or the presence of prolate and oblate nanocrystals in the same ensemble.24 Accounting for the linearly polarized dark exciton emission assisted by optical phonons is in line with the first two explanations. Here, we show that consideration of the 1PL emission of the dark excitons besides the saturation of the DCP in high magnetic fields determines the DCP spectral dependence. Similar to the samples studied in the present paper, the DCP increase towards the high energy part of the PL spectrum was previously observed for CdSe/CdS dot-in-rods54 and CdTe NCs.24 Recently, it was also reported for InP NCs,26 where also the strong phonon-assisted emission of dark excitons was observed. We suggest that the developed theory of the circular polarized PL with account of the phonon-assisted recombination of dark excitons can explain these and other experimental observations for different ensembles of colloidal nanocrystals.
We introduce a phenomenological magnetic field-induced increase of the 1PL recombination rate. This increase is required for the modeling of the experimentally observed σ− and σ+ polarized PL maxima positions. Note that within our model, the σ− and σ+ polarized PL maxima from the ensemble have the inverted ordering with respect to the exciton Zeeman splitting; however, both shift to higher energies if the 1PL recombination rate is constant in the external magnetic field. Within the second-order perturbation theory, the external magnetic field results only in an increase in the ZPL recombination rate.17,48 An increase in the 1PL recombination rate in the external magnetic field, as well as in the recombination rate with the assistance of two or three optical phonons, requires consideration of higher-order corrections to the recombination rate and will be presented elsewhere. It should be noted that some additional influence on the shift of the polarized PL maxima can come from the Förster energy transfer between NCs in dense ensembles.22,24 It results in spectral diffusion towards lower energy due to the exciton transfer from smaller to larger NCs. These remarks indicate that the analysis of the polarized PL of dark excitons in ensembles of CdSe nanocrystals is a complicated task due to multiple recombination channels with different energy and polarization properties of the emitted light.
4 Conclusions
In summary, the spin polarization of excitons in CdSe NCs embedded in a glass matrix has been studied experimentally in strong magnetic fields up to 30 T. Several unusual features in circularly polarized emission spectra have been found: a low saturation of the degree of circular polarization combined with a pronounced spectral dependence and large and inverted spectral shifts between the oppositely polarized PL components. This puzzling behavior is similar to those of earlier reports on wet-chemically grown CdSe NCs. We have developed a model that takes into account the cumulative contribution of the zero phonon and one optical phonon-assisted emission of dark excitons to the emission spectra of the NC ensemble. This model describes well all unusual experimental findings and can be readily extended to other colloidal nanocrystals, whose inhomogeneous broadening exceeds the optical phonon energy.5. Methods
5.1. Samples
The CdSe NCs embedded in glass were synthesized by the following method, which allows considerable reduction of the size dispersion of NCs. The batch composition of 61.5SiO2, 15.0Na2O, 10.0ZnO, 2.5Al2O3, 3.0CdO, 4.1Se, 2.6NaF, and 1.3C (mol%) was used to synthesize the initial glass suitable for the precipitation of the cadmium selenide crystalline phase. The given amount of activated carbon was introduced directly into the batch in order to provide the required redox conditions of the synthesis. The glass batch was melted in a laboratory electric furnace at 1400–1450 °C for 3 hours with stirring for 1 hour at the last stage of melting. The glass melt was poured into graphite molds and annealed in an inertial cooling mode. The initial glass was slightly yellowish in color and optically transparent down to light wavelengths in the near ultraviolet. To isolate the nanostructured CdSe phase, small pieces of the initial glass were heat-treated under isothermal conditions in a two-stage treatment mode, which allows preparation of high quality samples with very low size dispersion of the CdSe nanocrystals (standard deviation <5% as shown in ref. 55). Precipitation of wurtzite modification of the CdSe phase was also evidenced there. Using the data on the kinetics of CdSe crystallite growth given in ref. 55, we determined the heat treatment condition to prepare CdSe nanocrystals with different diameters in the range from 3.3 nm up to 6.1 nm. We label the samples with names starting with D followed by their diameter in nanometers. Four samples were studied, whose parameters are given in Table 1.The prepared glass samples with CdSe NCs were examined by small angle X-ray scattering (SAXS) with an infinitely high primary beam using Ni-filtered CuKα radiation. We processed the scattering curves, namely the angular dependence of the scattered X-ray intensity, using the Guinier plot56 to obtain the radius of gyration, Rg, of the CdSe crystallites and evaluate the NC diameters with D = 2.58Rg.
5.2. Absorption measurements
Low temperature absorption spectra were recorded with an Agilent Cary 6000i UV-Visible-NIR spectrophotometer combined with a helium flow cryostat. The spectra recorded at T = 4.2 K are shown in Fig. S1.†5.3. Polarized photoluminescence
The samples were placed in the variable temperature insert (2.2 K to 70 K) of a cryostat so that they come into contact with helium exchange gas. External magnetic fields up to 17 T were generated by a superconducting solenoid and applied in the Faraday geometry, i.e. parallel to the direction of photoexcitation and PL collection. The PL was excited with a continuous wave (cw) diode laser (wavelength 405 nm, photon energy 3.06 eV). In all PL experiments, the samples were excited nonresonantly, i.e. well above the exciton emission energy. Low excitation densities not exceeding 1 W cm−2 were used to exclude effects caused by exciton–exciton interactions. The PL was detected in backscattering geometry, dispersed with a 0.5 m spectrometer, and measured with a liquid nitrogen-cooled charge-coupled-device camera.5.4. Time-resolved photoluminescence
A pulsed diode laser (wavelength 405 nm, photon energy 3.06 eV, pulse duration 50 ps, and pulse repetition rate 1 MHz) was used for excitation. The PL was dispersed with a 0.5 m spectrometer and its decay was measured with a Si avalanche photodiode connected to a conventional time-correlated single-photon counting module with an overall temporal resolution of 200 ps.5.5. Polarization-resolved photoluminescence
The PL circular polarization degree was analyzed by a combination of a quarter-wave plate and a linear polarizer. Both the magnetic field and spectral dependences of the circular polarization were measured. The degree of circular polarization (DCP) of the PL, Pc, is defined by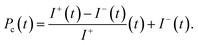 | (4) |
Here, I+(t) and I−(t) are the intensity of the σ+ and σ− polarized PL, respectively, measured at time delay t after pulsed excitation. For cw laser excitation, the measured polarization degree corresponds to the time-integrated DCP, Pintc, which is calculated as
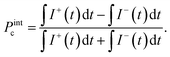 | (5) |
5.6. Photoluminescence in magnetic fields up to 30 T
The experiments were performed in the High Magnetic Field Lab, Nijmegen. The samples were mounted inside a liquid helium bath cryostat (T = 4.2 K), which was inserted in a 50 mm bore Florida–Bitter magnet with a maximum dc magnetic field of 32 T. The emission of a 405 nm cw diode laser was focused onto the sample using a lens (10 mm focal length), and the same lens was used to collect the PL. The polarized PL was dispersed with a 0.5 m spectrometer and measured with a liquid nitrogen-cooled charge-coupled-device camera.Author contributions
AAO prepared the samples. GQ, EVS and MAP performed the magneto-optical measurements under the guidance of DRY, PCMC and MB. AAG and AVR developed the theory and modeled the data. GQ and EAZ performed the absorption measurements. VKK performed the PLE measurements. IVK and VFS performed the FLN measurements. GQ, AAG and DRY wrote the paper with the assistance of all co-authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Al. L. Efros for valuable discussions and T. V. Shubina for the help with the PLE measurements. This work was funded by the Deutsche Forschungsgemeinschaft (DFG) in the frame of the International Collaborative Research Centre TRR 160 (Project B1) and the Russian Science Foundation (Grant No. 20-42-01008). IVK and VFS acknowledge partial support from the DFG, TRR 160 (Project B2) and RFBR (Project 19-52-12064) for FLN measurements. VKK acknowledges partial support from the DFG, TRR 160 (Project C1) and RFBR (Project 19-52-12057) for PLE measurements. AAG acknowledges support from the Grants Council of the President of the Russian Federation. Experiments in strong magnetic fields up to 30 T were supported by HFML-RU/NWO-I, a member of the European Magnetic Field Laboratory (EMFL).References
- A. I. Ekimov and A. A. Onushchenko, Quantum size effect in three-dimensional microscopic semiconductor crystals, JETP Lett., 1981, 34, 345–349 Search PubMed.
- C. B. Murray, D. J. Norris and M. G. Bawendi, Synthesis and characterization of nearly monodisperse CdE (E=S, Se, Te) semiconductor nanocrystallites, J. Am. Chem. Soc., 1993, 115, 8706–8715 CrossRef CAS.
- O. I. Micic, C. J. Curtis, K. M. Jones, J. R. Sprague and A. J. Nozik, Synthesis and characterization of InP quantum dots, J. Phys. Chem., 1994, 98, 4966–4969 CrossRef CAS.
- X. Peng, L. Manna, W. Yang, J. Wickham, E. Scher, A. Kadavanich and A. P. Alivisatos, Shape control of CdSe nanocrystals, Nature, 2001, 404, 59–61 CrossRef.
- M. V. Kovalenko, L. Manna, A. Cabot, Z. Hens, D. V. Talapin, C. R. Kagan, V. I. Klimov, A. L. Rogach, P. Reiss, D. J. Milliron, P. Guyot-Sionnnest, G. Konstantatos, W. J. Parak, T. Hyeon, B. A. Korgel, C. B. Murray and W. Heiss, Prospects of nanoscience with nanocrystals, ACS Nano, 2015, 9, 1012–1057 CrossRef CAS.
- S. Ithurria and B. Dubertret, Quasi 2d colloidal CdSe platelets with thicknesses controlled at the atomic level, J. Am. Chem. Soc., 2008, 130, 16504–16505 CrossRef CAS.
- V. Lesnyak, N. Gaponik and A. Eychmüller, Colloidal semiconductor nanocrystals: the aqueous approach, Chem. Soc. Rev., 2013, 42, 2905–2929 RSC.
- I. Fedin and D. V. Talapin, Colloidal CdSe quantum rings, J. Am. Chem. Soc., 2016, 138, 9771–9774 CrossRef CAS.
- V. L. Colvin, M. C. Schlamp and A. P. Alivisatos, Light-emitting diodes made from cadmium selenide nanocrystals and a semiconducting polymer, Nature, 1994, 370, 354–357 CrossRef CAS.
- T.-H. Kim, K.-S. Cho, E. K. Lee, S. J. Lee, J. Chae, J. W. Kim, D. H. Kim, J.-Y. Kwon, G. Amaratunga, S. Y. Lee, B. L. Choi, Y. Kuk, J. M. Kim and K. Kim, Full-colour quantum dot displays fabricated by transfer printing, Nat. Photonics, 2011, 5, 176–182 CrossRef CAS.
- V. I. Klimov, A. A. Mikhailovsky, S. Xu, A. Malko, J. A. Hollingsworth, C. A. Leatherdale, H.-J. Eisler and M. G. Bawendi, Optical gain and stimulated emission in nanocrystal quantum dots, Science, 2000, 290, 314–317 CrossRef CAS.
- D. V. Talapin and C. B. Murray, PbSe nanocrystal solids for n- and p-channel thin film field-effect transistors, Science, 2005, 310, 86–89 CrossRef CAS.
- G. H. Carey, A. L. Abdelhady, Z. Ning, S. M. Thon, O. M. Bakr and E. H. Sargent, Colloidal quantum dot solar cells, Chem. Rev., 2015, 115, 12732–12763 CrossRef CAS.
- J. M. Pietryga, Y.-S. Park, J. Lim, A. F. Fidler, W. K. Bae, S. Brovelli and V. I. Klimov, Spectroscopic and device aspects of nanocrystal quantum dots, Chem. Rev., 2016, 116, 10513–10622 CrossRef CAS.
- M. Bruchez Jr., M. Moronne, P. Gin, S. Weiss and A. P. Alivisatos, Semiconductor nanocrystals as fluorescent biological labels, Science, 1998, 281, 2013–2016 CrossRef CAS.
- A. L. Efros, J. B. Delehanty, A. L. Huston, I. L. Medintz, M. Barbic and T. D. Harris, Evaluating the potential of using quantum dots for monitoring electrical signals in neurons, Nat. Nanotechnol., 2018, 13, 278–288 CrossRef CAS.
- A. L. Efros, M. Rosen, M. Kuno, M. Nirmal, D. J. Norris and M. Bawendi, Band-edge exciton in quantum dots of semiconductors with a degenerate valence band: Dark and bright exciton states, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 4843–4856 CrossRef CAS.
- S. V. Goupalov and E. L. Ivchenko, The fine structure of excitonic levels in CdSe nanocrystals, Phys. Solid State, 2000, 42, 2030–2038 CrossRef.
- Al. L. Efros, Chapter 3 on Fine structure and polarization properties of band-edge excitons in semiconductor nanocrystals, in Semiconductor and Metal Nanocrystals: Synthesis and Electronic and Optical Properties, ed. V. I. Klimov, Marcel Dekker, New York, 2003, pp. 97–132 Search PubMed.
- P. C. Sercel and A. L. L. Efros, Band-Edge Exciton in CdSe and Other II–VI and III–V Compound Semiconductor Nanocrystals - Revisited, Nano Lett., 2018, 18, 4061–4068 CrossRef CAS.
- E. Johnston-Halperin, D. D. Awschalom, S. A. Crooker, A. L. Efros, M. Rosen, X. Peng and A. P. Alivisatos, Spin spectroscopy of dark excitons in CdSe quantum dots to 60 T, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 205309 CrossRef.
- M. Furis, J. A. Hollingsworth, V. I. Klimov and S. A. Crooker, Time- and polarization-resolved optical spectroscopy of colloidal CdSe nanocrystal quantum dots in high magnetic fields, J. Phys. Chem. B, 2005, 109, 15332–15338 CrossRef CAS.
- O. Labeau, P. Tamarat and B. Lounis, Temperature dependence of the luminescence lifetime of single CdSe/ZnS quantum dots, Phys. Rev. Lett., 2003, 90, 257404 CrossRef.
- F. Liu, A. V. Rodina, D. R. Yakovlev, A. Greilich, A. A. Golovatenko, A. S. Susha, A. L. Rogach, Y. G. Kusrayev and M. Bayer, Exciton spin dynamics of colloidal CdTe nanocrystals in magnetic fields, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 115306 CrossRef.
- L. Biadala, Y. Louyer, P. Tamarat and B. Lounis, Band-edge exciton fine structure of single CdSe/ZnS nanocrystals in external magnetic fields, Phys. Rev. Lett., 2010, 105, 157402 CrossRef CAS.
- A. Brodu, M. D. Tessier, D. Canneson, D. Dupont, M. V. Ballottin, P. C. M. Christianen, C. De Mello Donega, Z. Hens, D. R. Yakovlev, M. Bayer, D. Vanmaekelbergh and L. Biadala, Hyperfine Interactions and Slow Spin Dynamics in Quasi-isotropic InP-based Core/Shell Colloidal Nanocrystals, ACS Nano, 2019, 13, 10201–10209 CrossRef CAS.
- A. Brodu, V. Chandrasekaran, L. Scarpelli, J. Buhot, F. Masia, M. V. Ballottin, M. Severijnen, M. D. Tessier, D. Dupont, F. T. Rabouw, P. C. M. Christianen, C. De Mello Donega, D. Vanmaekelbergh, W. Langbein and Z. Hens, Hyperfine Interactions and Slow Spin Dynamics in Quasi-isotropic InP-based Core/Shell Colloidal Nanocrystals, J. Phys. Chem. Lett., 2019, 10, 5468–5475 CrossRef CAS.
- M. Nirmal, D. J. Norris, M. Kuno, M. G. Bawendi, A. L. Efros and M. Rosen, Observation of the “dark exciton” in CdSe quantum dots, Phys. Rev. Lett., 1995, 75, 3728–3731 CrossRef CAS.
- F. J. P. Wijnen, J. H. Blokland, P. T. K. Chin, P. C. M. Christianen and J. C. Maan, Competition between zero-phonon and phonon-assisted luminescence in colloidal CdSe quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235318 CrossRef.
- A. G. Del Águila, G. Pettinari, E. Groeneveld, C. De Mello Donegá, D. Vanmaekelbergh, J. C. Maan and P. C. M. Christianen, Optical spectroscopy of dark and bright excitons in CdSe nanocrystals in high magnetic fields, J. Phys. Chem. C, 2017, 121, 23693–23704 CrossRef.
- M. J. Fernee, C. Sinito, P. Tamarat and B. Lounis, State selective pumping reveals spin-relaxation pathways in CdSe quantum dots, Nano Lett., 2014, 14, 4480–4485 CrossRef CAS.
- M. Furis, H. Htoon, M. A. Petruska, V. I. Klimov, T. Barrick and S. A. Crooker, Bright-exciton fine structure and anisotropic exchange in CdSe nanocrystal quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 241313 CrossRef.
- H. Htoon, S. A. Crooker, M. Furis, S. Jeong, A. L. Efros and V. I. Klimov, Anomalous circular polarization of photoluminescence spectra of individual CdSe nanocrystals in an applied magnetic field, Phys. Rev. Lett., 2009, 102, 017402 CrossRef CAS.
- J. A. Gupta, D. D. Awschalom, A. L. Efros and A. V. Rodina, Spin dynamics in semiconductor nanocrystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 125307 CrossRef.
- R. Hu, D. R. Yakovlev, P. Liang, G. Qiang, C. Chen, T. Jia, Z. Sun, M. Bayer and D. Feng, Origin of two larmor frequencies in the coherent spin dynamics of colloidal CdSe quantum dots revealed by controlled charging, J. Phys. Chem. Lett., 2019, 10, 3681–3687 CrossRef CAS.
- M. Nirmal, C. B. Murray and M. G. Bawendi, Fluorescence-line narrowing in CdSe quantum dots: Surface localization of the photogenerated exciton, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 2293 CrossRef CAS.
- D. J. Norris, A. L. Efros, M. Rosen and M. G. Bawendi, Size dependence of exciton fine structure in CdSe quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 16347–16354 CrossRef CAS.
- U. Woggon, F. Gindele, O. Wind and C. Klingshirn, Exchange interaction and phonon confinement in CdSe quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1506–1509 CrossRef CAS.
- M. Chamarro, C. Gourdon, P. Lavallard, O. Lublinskaya and A. I. Ekimov, Enhancement of electron-hole exchange interaction in CdSe nanocrystals: A quantum confinement effect, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 1336–1342 CrossRef CAS.
- F. Liu, L. Biadala, A. V. Rodina, D. R. Yakovlev, D. Dunker, C. Javaux, J.-P. Hermier, A. L. Efros, B. Dubertret and M. Bayer, Spin dynamics of negatively charged excitons in CdSe/CdS colloidal nanocrystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 035302 CrossRef.
- E. V. Shornikova, L. Biadala, D. R. Yakovlev, V. F. Sapega, Y. G. Kusrayev, A. A. Mitioglu, M. V. Ballottin, P. C. M. Christianen, V. V. Belykh, M. V. Kochiev, N. N. Sibeldin, A. A. Golovatenko, A. V. Rodina, N. A. Gippius, A. Kuntzmann, Y. Jiang, M. Nasilowski, B. Dubertret and M. Bayer, Addressing the exciton fine structure in colloidal nanocrystals: the case of CdSe nanoplatelets, Nanoscale, 2018, 10, 646–656 RSC.
- E. V. Shornikova, D. R. Yakovlev, L. Biadala, S. A. Crooker, V. V. Belykh, M. V. Kochiev, A. Kuntzmann, M. Nasilowski, B. Dubertret and M. Bayer, Negatively charged excitons in CdSe nanoplatelets, Nano Lett., 2020, 20, 1370–1377 CrossRef CAS.
- A. V. Rodina, A. A. Golovatenko, E. V. Shornikova and D. R. Yakovlev, Spin physics of excitons in colloidal nanocrystals, Phys. Solid State, 2018, 60, 1537–1553 CrossRef CAS.
- L. Biadala, E. V. Shornikova, A. V. Rodina, D. R. Yakovlev, B. Siebers, T. Aubert, M. Nasilowski, Z. Hens, B. Dubertret, A. L. Efros and M. Bayer, Magnetic polaron on dangling-bond spins in CdSe colloidal nanocrystals, Nat. Nanotechnol., 2017, 12, 569–574 CrossRef CAS.
- D. Oron, A. Aharoni, C. De Mello Donega, J. Van Rijssel, A. Meijerink and U. Banin, Universal role of discrete acoustic phonons in the low-temperature optical emission of colloidal quantum dots, Phys. Rev. Lett., 2009, 102, 177402 CrossRef.
- M. J. Fernée, B. N. Littleton, S. Cooper, H. Rubinsztein-Dunlop, D. E. Gómez and P. Mulvaney, Acoustic phonon contributions to the emission spectrum of single CdSe nanocrystals, J. Phys. Chem. C, 2008, 112, 1878–1884 CrossRef.
- S. A. Empedocles, R. Neuhauser, K. Shimizu and M. G. Bawendi, Photoluminescence from single semiconductor nanostructures, Adv. Mater., 1999, 11, 1243–1256 CrossRef CAS.
- A. V. Rodina and A. L. Efros, Radiative recombination from dark excitons in nanocrystals: Activation mechanisms and polarization properties, Phys. Rev. B, 2016, 93, 155427 CrossRef.
- K. Leung, S. Pokrant and K. B. Whaley, Exciton fine structure in CdSe nanoclusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 12291–12301 CrossRef CAS.
- M. Califano, A. Franceschetti and A. Zunger, Temperature dependence of excitonic radiative decay in CdSe quantum dots: the role of surface hole traps, Nano Lett., 2005, 5, 2360–2364 CrossRef CAS.
- A. Tadjine, Y.-M. Niquet and C. Delerue, Universal behavior of electron g-factors in semiconductor nanostructures, Phys. Rev. B, 2017, 95, 235437 CrossRef.
- M. A. Semina, A. A. Golovatenko and A. V. Rodina, Ground state of the holes localized in II-VI quantum dots with gaussian potential profiles, Phys. Rev. B, 2016, 93, 045409 CrossRef.
- E. V. Shornikova, A. A. Golovatenko, D. R. Yakovlev, A. V. Rodina, L. Biadala, G. Qiang, A. Kuntzmann, M. Nasilowski, B. Dubertret, A. Polovitsyn, I. Moreels and M. Bayer, Surface spin magnetism controls the polarized exciton emission from CdSe nanoplatelets, Nat. Nanotechnol., 2020, 15, 277–282 CrossRef CAS.
- B. Siebers, L. Biadala, D. R. Yakovlev, A. V. Rodina, T. Aubert, Z. Hens and M. Bayer, Exciton spin dynamics and photoluminescence polarization of CdSe/CdS dot-in-rod nanocrystals in high magnetic fields, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155304 CrossRef.
- V. V. Golubkov, P. A. Onushchenko and A. A. Onushchenko, The kinetics of the formation of CdSe nanocrystals in sodium–zinc–silica glass, Glass Phys. Chem., 2014, 40, 291–297 CrossRef CAS.
- A. Guinier, La diffraction des rayons x aux très petits angles: application à l’étude de phénomènes ultramicroscopiques, Ann. Phys., 1939, 11, 161–237 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Absorption spectra, bright–dark splitting of excitons in CdSe NCs in glass, degree of circular polarization (DCP) dynamics, model description. See DOI: 10.1039/D0NR07117J |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |