Open Access Article
Open Access ArticleSingle-layer polymeric tetraoxa[8]circulene modified by s-block metals: toward stable spin qubits and novel superconductors†
Lyudmila V.
Begunovich
a,
Artem V.
Kuklin
 *ab,
Gleb V.
Baryshnikov
bc,
Rashid R.
Valiev
de and
Hans
Ågren
*ab,
Gleb V.
Baryshnikov
bc,
Rashid R.
Valiev
de and
Hans
Ågren
 bf
bf
aInternational Research Center of Spectroscopy and Quantum Chemistry (IRC SQC), Siberian Federal University, 26 Kirensky st., 660074, Krasnoyarsk, Russia. E-mail: artem.icm@gmail.com
bDepartment of Physics and Astronomy, Uppsala University, Box 516, SE-751 20 Uppsala, Sweden
cDepartment of Chemistry and Nanomaterials Science, Bohdan Khmelnytsky National University, 18031, Cherkasy, Ukraine
dResearch School of Chemistry & Applied Biomedical Sciences, National Research Tomsk Polytechnic University, Lenin Avenue 30, Tomsk 634050, Russia
eDepartment of Chemistry, Faculty of Science, University of Helsinki, FIN-00014, Helsinki, Finland
fCollege of Chemistry and Chemical Engineering, Henan University, Kaifeng, Henan 475004, P.R. China
First published on 4th February 2021
Abstract
Tunable electronic properties of low-dimensional materials have been the object of extensive research, as such properties are highly desirable in order to provide flexibility in the design and optimization of functional devices. In this study, we account for the fact that such properties can be tuned by embedding diverse metal atoms and theoretically study a series of new organometallic porous sheets based on two-dimensional tetraoxa[8]circulene (TOC) polymers doped with alkali or alkaline-earth metals. The results reveal that the metal-decorated sheets change their electronic structure from semiconducting to metallic behaviour due to n-doping. Complete active space self-consistent field (CASSCF) calculations reveal a unique open-shell singlet ground state in the TOC–Ca complex, which is formed by two closed-shell species. Moreover, Ca becomes a doublet state, which is promising for magnetic quantum bit applications due to the long spin coherence time. Ca-doped TOC also demonstrates a high density of states in the vicinity of the Fermi level and induced superconductivity. Using the ab initio Eliashberg formalism, we find that the TOC–Ca polymers are phonon-mediated superconductors with a critical temperature TC = 14.5 K, which is within the range of typical carbon based superconducting materials. Therefore, combining the proved superconductivity and the long spin lifetime in doublet Ca, such materials could be an ideal platform for the realization of quantum bits.
Introduction
Great effort is being devoted to the design and fabrication of new materials that meet the requirements of modern devices. Among many promising materials recently proposed, two-dimensional (2D) single atomic sheets have attracted particular interest due to their unique properties and the possibility of high scaling and minimization of devices.1,2 The utilization of organic moieties as initial building blocks in the formation of 2D materials (covalent organic frameworks – COFs) makes it possible to tune the properties of such systems. These properties depend on the selected moiety, on the type of fusing between the moieties3 and on the size of the obtained nanomaterials.4 Typical examples of such COFs are tetraoxa[8]circulene (TOC) based nanosheets, which are planar 2D porous sheets with the space group symmetry P4/mmm. These nanosheets are predicted to be thermodynamically and kinetically stable5 and are found to be nonmagnetic direct band gap semiconductors or semimetals3,5 with the HOMO–LUMO gap of the TOC-based nanosheets being much smaller than that of the parent tetraoxa[8]circulene molecule.6 Moreover, the band gap decreases significantly as the number of moieties in the structure increases. This feature is very useful for a purposeful design of semiconducting materials with tunnable band gaps (band gap engineering).7,8 In addition, these compounds have considerable mechanical strength5 and can strongly adsorb visible light,4,5,9 thus they can be promising candidates for solar and thermoelectric applications.The ability of metal ions to be embedded regularly and separately to porous sheets provides promising new features and expands the applications of such materials. The perspective organometallic porous sheets with a wide range of potential applications in semiconductor industry, spintronics,10,11 optoelectronics, catalysis,12 gas13,14 and magnetic storage devices15 have been reported. All of the above data give hope that such intriguing structures will be synthesized in the near future. Abel et al. synthesized a 2D Fe-phthalocyanine single layer with magnetic metal atoms regularly embedded in the polymer lattice.16 It can be expected that their flexible synthesis method can be applied to the synthesis of other metal-based 2D organometallic porous sheets. Indeed, a polymeric step-by-step mechanism of Mn-phthalocyanines has been demonstrated.17 Recently, a number of transition metals (Cr, Fe, Co, Ni and Cu) as well as metal-free (H2) phthalocyanines were also synthesized with a temperature-dependent mechanism of polymerization.18
Although doping with d-block metals brings many new advantages, s-block metals could also be utilized to modify the electronic properties of 2D COFs. Actually, alkali metal decoration is a widely applied scheme to modify 2D material properties. For example, lithiation could introduce electrons into MoS2 and trigger phase transition.19,20 Doping by alkali and alkaline-earth metals results in enhanced conductivity and emergence of superconducting states. Superconducting states have been discovered in Ca-doped graphite with a critical transition temperature (TC) of 11.5 K21–23 and also in large-scale graphene films24 with a similar TC. To expand this behaviour, graphene-based superconducting fibers have been produced and intercalated with Ca, which led to a superconducting transition at ∼11 K.25 Besides, superconductivity has also been found in carbon materials doped with alkaline metals such as Li, Na and K.22,26–30
Recently, some hydrocarbons doped with alkali metals demonstrated superconducting behaviour with critical temperatures similar to or higher than that of graphite and graphene.31–35 In particular, superconductivity up to 33 K was discovered in K-doped dibenzopentacene (C30H18).36 Despite the significant interest in carbon and hydrocarbon based superconductors, only a couple of reports can be found on similar properties in coordination polymers,37,38 which also represent a remarkable part of modern 2D science. In the case of 2D covalent organic frameworks, no superconductors have been discovered at all.
Inspired by previous works, we here propose 2D COFs based on planar heterocyclic molecules, namely two types of tetraoxa[8]circulene organometallic porous sheets (TOC–Me) decorated by some alkali and alkaline-earth metals. The atomic and electronic structures of TOC–Me sheets (Me = Li, Na and Ca) were studied using first-principles calculations. Alkali and alkaline-earth metal complexes with tetraoxa[8]circulene molecules have been studied recently.39 However, in that work metal atoms were initially in the charged (cationic) state, while in the present paper we consider TOC-based complexes with electroneutral alkali and alkaline-earth metal atoms. We demonstrate effective interactions of Me atoms with TOC that change the electronic structure of the latter from semiconductor to metallic by an n-doping mechanism. We propose that the superconducting state could be realized in TOC–Ca monolayers with TC = 14.5 K caused by the high density of states in the vicinity of the Fermi level, as estimated by the Eliashberg theory. Employing the complete active space self-consistent field (CASSCF) and broken symmetry density functional theory (DFT) methods, a unique open-shell singlet in TOC–Ca is determined as a ground state, where the Ca species are in the S = 1/2 state, proposing promising application as magnetic quantum bits for quantum computing nodes.
Computational details
The density functional theory40,41 calculations were performed using the Open source package for Material eXplorer software package (OpenMX)42 based on a linear combination of pseudo-atomic orbitals (PAO)43–46 method and norm-conserving pseudopotentials.47–51 The cutoff energy value was equal to 150 Ry. The pseudo-atomic orbital basis sets, s3p3d2 for Ca, s3p2 for Na and Li, s2p2d2 for C, s2p2d2f1 for O with cutoff radii 9.0 a.u. for Ca and Na, 8.0 a.u. for Li, and 5.0 a.u. for C and O, were converged and found to be good enough to describe the studied nanostructures. The gradient exchange-correlation functional in the form proposed by Perdew–Burke–Ernzerhof (PBE)52 was employed. Empirical D3 Grimme correction was included to take into account van der Waals interactions.53,54 All structures were relaxed until forces acting on the atoms and translation vectors became less than 1 × 10−5 Hartree per Bohr. The convergence condition for the energy minimization was equal to 1 × 10−7 Hartree. To simulate the 2D structures using Periodic Boundary Conditions (PBCs), the periodic replicas were separated by a vacuum spacing of at least 15 Å along the c axis. The first Brillouin zone (1BZ) was sampled on a grid of 20 × 20 × 1 k-points generated according to the Monkhorst–Pack method.55 The band structure calculations were carried out along the high symmetry Γ(0,0,0)–X(0,1/2,0)–M(1/2,1/2,0)–Γ(0,0,0) directions in 1BZ. The charges on atoms were obtained by integrating electron and spin densities in the Voronoi polyhedra constructed from smeared surfaces which are defined by a Fuzzy cell partitioning method.56 The Visualization for Electronic and STructural Analysis (VESTA) software57 was used for the visualization of atomic structures.The binding energies (Ebind) of metal atoms with TOC sheets were calculated using the following equation:
| Ebind = Etot − ETOC – EMe, | (1) |
To calculate the spectral function and critical temperature (TC), we employed the EPW code,58–60 where the electronic wave functions required for the Wannier–Fourier interpolation61 were obtained using the Quantum-ESPRESSO package.62,63 The structure was initially optimized and a non-self-consistent calculation was then performed using 64 k-points in the first Brillouin zone and an energy cut-off of 40 Ry for the wavefunction and 160 Ry for the charge density. Phonon calculations were carried out using a 4 × 4 × 1 q-point grid. No imaginary phonon frequencies were observed, suggesting that the proposed material is in the dynamically stable phase. The standard PBE–PAW pseudopotentials64 were employed. The interpolated grid of 20 × 20 × 1 k and q points were utilized in the Migdal–Eliashberg equation.
The energies of ground singlet (S0) and the first singlet excited state (S1) of the [TOC–Ca] complex were calculated by the extended multi-configuration quasi-degenerate perturbation theory at the second-order (XMC-QDPT2)65 level of theory. The CASSCF was chosen as 10 electrons in 10 molecular orbitals (MOs). The stage-average procedure was performed over the first lowest electronic states. The effective Hamiltonian included 30 states. The 6-31G(d) basis set was used. The calculations were performed using the Firefly software.66
“Broken symmetry”67,68 DFT calculations were performed for the [TOC–Ca] complexes using the Gaussian 16 software69 to confirm the open-shell singlet (OSS) ground state of the [TOC–Ca] complex. We have used Becke′s three-parameter hybrid exchange functional combined with the Lee–Yang–Parr (B3LYP)70,71 hybrid exchange-correlation functional with the extended 6-31+G(d) basis set72–74 and Grimme's D3 empirical dispersion correction.53 The search for the OSS solution was arranged as follows. A self-consistent field (SCF) calculation was first performed for the closed-shell singlet state (hereinafter called the CSS state). Next, a SCF calculation of the “broken symmetry” state was performed for the antiparallel orientation of the unpaired electrons on the Ca center and TOC ligand (the OSS state).
An analysis of the electron density distribution function by using Bader's “atoms in molecules” formalism75 was additionally performed for the [TOC–Me] (Me = Li, Na, Ca) complexes in order to explain the binding mechanism between the Me atom and the TOC ligand. Quantum Theory of Atoms In Molecules (QTAIM) calculations have been carried out for that purpose using the AIMAll software.76
Results and discussion
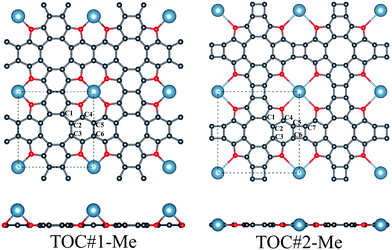
In this work, the interaction between Li, Na and Ca atoms and two types of TOC porous sheets were investigated. The positions of the metal atoms in and above the TOC plane were considered for both types of TOC polymers. Our calculations reveal that the TOC#1–Me systems prefer the configuration with the metal atom above the plane (Fig. 1) with relative energies compared to the structures with a metal atom located in the plane equal to −0.06, −0.25 and −0.58 eV for the TOC#1–Li, TOC#1–Na and TOC#1–Ca organometallic sheets, respectively. The details of the atomic structures of the fully relaxed TOC#1–Me polymers are listed in Table 1 and Tables S1–S6 (in ESI†). The translation vectors of all TOC#1–Me organometallic sheets are slightly increased as compared to the metal-free sheet. The distance between the metal atom and the surrounding oxygen atoms decreases from 2.648 Å (TOC#1–Ca) to 2.059 Å (TOC#1–Li), which is in good agreement with previous results for the Ca2+ and Li+ complexes with tetraoxa[8]circulene.39 The oxygen atoms are slightly displaced towards the metal atoms resulting in longer C–O bonds. A Voronoi charge analysis (Table 2) indicates that 0.51, 0.72 and 0.94 electrons are transferred from the Li, Na and Ca atoms to the TOC sheet, respectively. This means that the TOC sheet prefers to snatch electrons from the alkali and alkaline-earth metals to form a more stable state. In the case of TOC#2–Me organometallic sheets, Me atoms are embedded in the center of the pores due to their large size (Fig. 1). The changes of the structural parameters of TOC#2–Me relative to the metal-free TOC#2 sheet are almost similar to those in TOC#1–Me (Table 1); the translation vectors are slightly increased and the oxygen atoms are shifted towards the metal atom. The distance between the Me atom and the neighboring oxygen atoms is almost the same for all TOC#2–Me organometallic sheets and equals to ∼3 Å. In this type of organometallic sheets, more electrons are transferred from the Me atom to the TOC#2 polymer. The Voronoi analysis indicates that the positive charges on the Li, Na and Ca atoms are equal to 0.85, 0.87 and 1.13 ē, respectively.| Structure | Binding energy, eV | Lattice parameter a = b, Å | Bond length, Å | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Me⋯O | C–O | C1–C2 | C2–C3 | C2–C4 | C4–C5 | C5–C6 | C5–C7 | |||
| TOC#1–Li | −3.02 | 8.416 | 2.059 | 1.408 | 1.419 | 1.424 | 1.397 | 1.402 | 1.479 | — |
| TOC#1–Na | −1.71 | 8.429 | 2.272 | 1.402 | 1.418 | 1.421 | 1.397 | 1.408 | 1.480 | — |
| TOC#1–Ca | −1.29 | 8.457 | 2.648 | 1.417 | 1.426 | 1.424 | 1.404 | 1.412 | 1.477 | — |
| TOC#1 | — | 8.412 | — | 1.394 | 1.428 | 1.410 | 1.402 | 1.416 | 1.460 | — |
| TOC#2–Li | −2.14 | 9.762 | 2.962 | 1.399 | 1.426 | 1.415 | 1.429 | 1.361 | 1.454 | 1.463 |
| TOC#2–Na | −1.96 | 9.765 | 2.966 | 1.399 | 1.426 | 1.415 | 1.428 | 1.362 | 1.454 | 1.464 |
| TOC#2–Ca | −1.34 | 9.748 | 2.952 | 1.402 | 1.424 | 1.415 | 1.427 | 1.358 | 1.454 | 1.458 |
| TOC#2 | — | 9.743 | — | 1.379 | 1.426 | 1.405 | 1.428 | 1.366 | 1.439 | 1.473 |
| Atom | Voronoi charges, ē | |||||||
|---|---|---|---|---|---|---|---|---|
| TOC#1 | TOC#1–Li | TOC#1–Na | TOC#1–Ca | TOC#2 | TOC#2–Li | TOC#2–Na | TOC#2–Ca | |
| C2 | −0.01 | −0.02 | −0.03 | −0.01 | −0.01 | −0.03 | −0.03 | −0.02 |
| C4 | 0.16 | 0.14 | 0.13 | 0.13 | 0.17 | 0.15 | 0.15 | 0.15 |
| C5 | 0.01 | −0.03 | −0.03 | −0.02 | −0.01 | −0.04 | −0.04 | −0.04 |
| O | −0.30 | −0.32 | −0.36 | −0.43 | −0.30 | −0.37 | −0.38 | −0.44 |
| Me | 0.51 | 0.72 | 0.94 | 0.85 | 0.87 | 1.13 | ||
To compare the energetic stability of the organometallic sheets, the binding energies (Ebind) were calculated with the corresponding values of −3.02, −1.71, −1.29, −2.14, −1.96 and −1.34 eV for TOC#1–Li, TOC#1–Na, TOC#1–Ca, TOC#2–Li, TOC#2–Na and TOC#2–Ca sheets, respectively (Table 1). Negative binding energies for all the studied organometallic sheets reveal that their formation is energetically feasible. The binding energies of TOC decorated by Ca atoms are comparable to those reported for Ca deposited on graphene nanoribbons (∼0.7–1.1 eV).77 The energies found are in the order of chemical bonding energies.
One can understand that the chemical potential of the dopant strongly depends on the host material and therefore that additional calculations of the formation energy with respect to the metals in their bulk phase is required. The calculated binding energy in the TOC#1–Ca system with respect to the energy of one Ca atom in the face centered cubic bulk structure was found to be positive (1.01 eV). This is because a much higher energy is required to eliminate the Ca atom from the bulk compared to the energy release upon TOC#1–Ca formation. The formation energies estimated in a similar manner for TOC#1–Li and TOC#1–Na are −0.06 and 0.43 eV, respectively. However, to have a meaningful reference, we also address the binding energy in the graphene/Ca system. To calculate the binding energy of the Ca atom with graphene, we used the optimized supercell containing 72 carbon atoms. The Ca atom was placed above a hexagon (which is the most favorable position) and then the supercell was relaxed. The binding energy of the isolated Ca with graphene is found to be negative (−0.38 eV), while it is significantly positive with respect to the energy of the atom in the bulk phase (1.93 eV). Though the formation energy of Ca with graphene is almost twice more positive compared to TOC#1–Ca, obviously such materials can be produced experimentally.78,79 The stability of Ca-decorated carbon nanostructures has also been confirmed theoretically with high-level approaches80 and the binding energies found are close to those found in our calculations. Actually, the atomization energy of the bulk Ca is positive and much higher by absolute value than the complexing energy of the Ca atom and the TOC sheet. It means that if we start from the bulk Ca as a source of Ca atoms, we need to apply some energy to extract the Ca atom from the metal lattice and then the Ca atom forms the TOC–Ca complex, accompanied by an energy release. The complex is not metastable in itself, while some energy should be applied during the real synthesis procedure in order to get free Ca atoms (it could be evaporation of the bulk Ca or the electrochemical reduction of Ca2+ ions). Therefore, we believe that the formation energy with respect to bulk metals cannot be a true indicator of practical realization. This is the significant evidence of the possibility of experimental realization of the proposed nanomaterials. One should also admit, as diamond can be formed from graphite, that some metastable materials also can be realized under specific conditions.
The binding energies of organometallic sheets with s-block metals depend on the nanopore size and metal radius. The small radius of the Li atom allows it to be closer to the TOC#1 plane, something that leads to a stronger interaction between the Li atom and the TOC#1 polymer than between Na/Ca and TOC#1. The larger pore size of the TOC#2 structure facilitates the atom localization in the plane of the polymer, resulting in a stronger interaction between Na/Ca and the polymer compared to those in TOC#1–Na and TOC#1–Ca. Thus, TOC#2–Na and TOC#2–Ca sheets are more energetically stable than TOC#1–Na and TOC#1–Ca. In the case of the TOC#2–Li polymer, the large distances between the Li and O atoms and the small radius of the Li atom reduce the mutual interaction of the counterparts compared to that in TOC#1–Li.
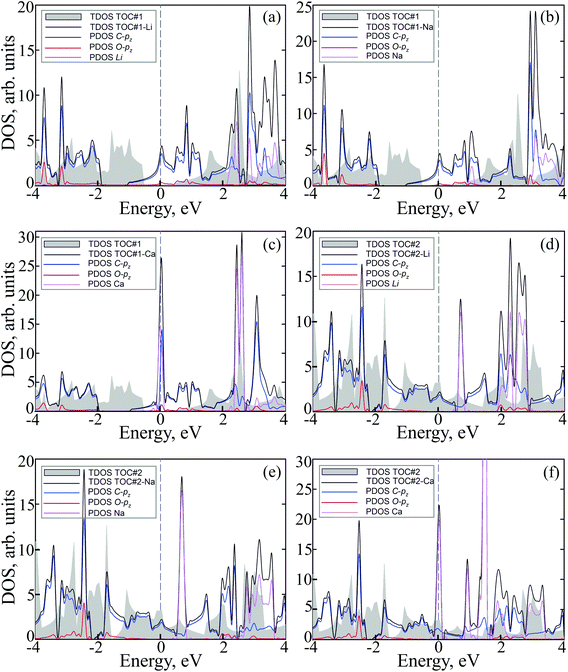
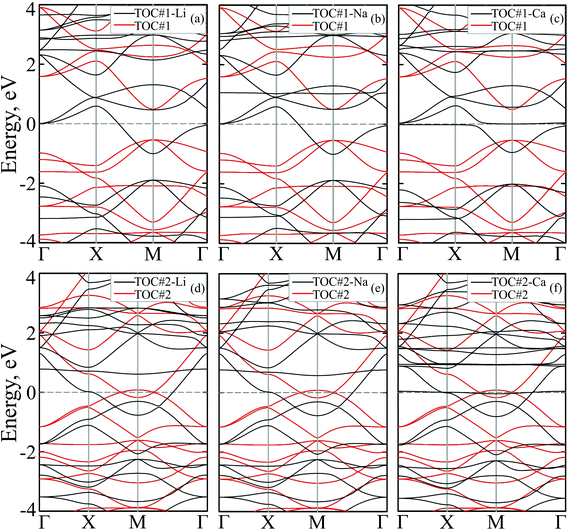
To study how the modification affects the electronic properties of the TOC sheets, the densities of states (DOS) and the corresponding electronic band structures were calculated and plotted in Fig. 2 and 3, respectively. The metal-free TOC#1 polymer exhibits nonmagnetic semiconducting properties with a band gap width of 0.96 eV. The band gap found is close to the recently reported data calculated within the plane-wave basis set3 and the same level of theory (0.87 eV). The modification of TOC#1 by s-block metals leads to the emergence of metallic character caused by charge transfer from the metal atom to the circulene sheet. Decoration by Li and Na atoms has a similar effect on the electronic structure of TOC (Fig. 2(a and b) and 3(a and b)). Compared to the bare TOC, the vacant and occupied states are shifted by 1.52 and by 1.36 eV to lower energies for TOC#1–Li and TOC#1–Na systems, respectively, without the direct contribution of the Li and Na states in the vicinity of the Fermi level. However, both of them affect the vacant states and have contributions starting from 2.13 eV (Li) and 0.80 eV (Na) that coincide with the recent data on Li intercalation to the carbon nanostructures.81
States at the Fermi level are formed by C-pz and O-pz orbitals, which are shifted down inducing semiconductor–metal transition after accepting the charge transferred from the s-metal. The top valence band crosses the Fermi level in the X–M interval and at the Γ point (Fig. 3(a and b)), forming quite a large amount of electron density in the vicinity of the Fermi level that should result in enhanced conductivity. Doping of TOC#1 by Ca atoms (TOC#1–Ca) induces the shift of electronic states by 1.44 eV to lower energies as compared to the metal-free polymer (Fig. 2(c)). An interesting fact in this case is that the electron density at the Fermi level is represented not only by C-pz and O-pz states, but also by Ca states simultaneously, greatly enhancing the states of the circulene sheet due to the larger amount of transferred charge (Table 2). As in the Li and Na doped TOC#1, the shifted conduction band crosses the Fermi level in the X–M interval and at the Γ point (Fig. 3(c)), forming the metallic features. However, the additional band caused by Ca doping locates exactly at the Fermi level, demonstrating a flat distribution along the k-vector (Fig. 3(c) and Fig. S1 and S2 in the ESI†) like the bands formed in the twisted bilayer graphene82–85 and the doped graphene.30,86,87 The presence of these flat bands at the Fermi level is caused by the formation of covalent bonds between Ca and the TOC monolayer with its following electron doping that should result in great enhancement of conductivity and that could induce a superconducting state in the tetraoxa[8]circulene polymer. Many theoretical reports reveal a phonon-mediated scenario of superconductivity in Ca-doped carbon materials,88–90 where the perpendicular C lattice vibrations couple with the parallel Ca vibrations.
Next, we calculated the superconducting properties employing the PW, Phonon and EPW codes as implemented in the Quantum-ESPRESSO package. The calculated equilibrium lattice constant, a = 8.459 Å, is in excellent agreement with the previous calculation. Though the densities of states (Fig. S3†) demonstrate a slightly different distribution caused by the different basis type used, the main peaks are located at similar energies. One can clearly see a similar large peak located at the vicinity of the Fermi level. The temperature of the transition to the superconducting state (TC) can be estimated by the approximation of the Eliashberg equation using the McMillan formula91 as modified by Allen and Dynes:92
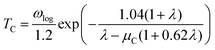 | (2) |
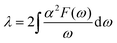 | (3) |
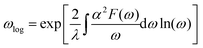 | (4) |
Fig. 4 shows the Eliashberg spectral function, α2F(ω), and the cumulative total electron–phonon coupling (EPC), λ(ω). One can see that the major part of the coupling recieves contributins from the low-energy modes, while the contribution from other branches is negligible. The calculated total e–p coupling, λ(ω), is 1.1. Such a large value of λ is likely to be assigned to the high density of states at the vicinity of the Fermi level where Ca provides the main contribution from both s and pz orbitals. We used the Interactive phonon visualizer93 to analyse the vibrational properties. One can clearly see that the main contribution to EPC is below 30 meV, where λ(ω) reaches about 75% of the total coupling strength associated with the Caz and Caxy vibrations at ∼8 meV and ∼20–30 meV, respectively, coupled with the out-of-plane collective vibrations of the tetraene core and vibrations of oxygen.
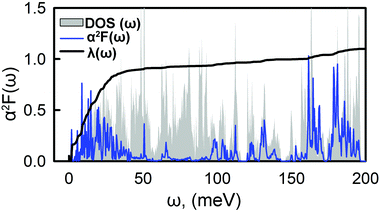 | ||
| Fig. 4 Frequency-dependent phonon DOS, electron–phonon spectral function, α2F(ω), and integrated electron–phonon coupling strength, λ(ω). | ||
Another significant contribution, approximately 10% of the EPC, origins from the in-plane Cxy vibrations in the range of 170–190 meV. Using the typical empirical value of μC = 0.1, the critical temperature, TC, is 14.5 K. This value is within the range of typical carbon based superconducting materials.21–24
It has been demonstrated that the diffusion barriers of s-block metals between 5, 6, and 8 coordinated carbon rings amount up to 0.8 eV (ref. 94 and 95), while the binding energies listed in Table 1 are considerably lower (∼from −1.3 to −3.0 eV), which clearly show that the pores are global energy minimum positions. For instance, if an initially deposited s-block metal atom drops at a 5, 6, or 8 carbon ring of TOC it is expected to migrate to the pore position and can be trapped there by the covalent bonds, therefore, filling those sites. If an atom will be initially placed at a pore site, its escape would be hampered inhibiting segregation. Moreover, the use of modern techniques like the atomic layer deposition method96 allows a precise control of the atomic concentration up to the submonolayer level and the speed of deposition, providing isolated single atoms to be deposited onto the substrate surface and preventing their segregation. While hard doping is usually required to induce superconducting behaviour in molecular structures, the present polymers require only one Ca atom per monomer to induce a high density of states in the vicinity of the Fermi level and superconducting properties. In contrast to traditional 2D materials like graphene, TOC monolayers can strongly adsorb s-metals in pores, therefore effectively creating a stable composite.
The doped TOC#2–Me sheets reveal metallic features in contrast to the semimetallic metal-free TOC#2, which was highlighted as a candidate of the spin–orbit coupling induced topological materials with the gap of ∼87 meV.3 However, in contrast to TOC#1–Me, the DOS of circulene at the Fermi level is reduced compared to those in the metal-free TOC#2 polymer (Fig. 2(d, e and f)) due to the shift of the energy levels to the lower energy region. It was determined that O-pz states are not represented at the Fermi level. Similar to TOC#1, Ca-doped TOC#2 reveals significantly enhanced DOS at the Fermi level. The increase in density results from the doping-induced conduction band minimum (CBM) splitting and the formation of new states in the vicinity of the Fermi level. The bands of TOC#2–Me systems cross the Fermi level in the vicinity of the X–M–Γ intervals. In general, for TOC#2–Me we reveal similar features to TOC#1–Me with the exception of the Me position, which tends to occupy an in-plane state due to the larger pore size.
Next, we performed molecular structure simulations at the B3LYP/6-31+G(d) level of theory to elucidate how intercalation affects the energy level positions in the tetraoxa[8]circulene monolayers. The used oligomer models composed of 4 TOC monomers were terminated with hydrogen atoms as if they are in the original TOC molecules. The LUMO state of the bare TOC in these complexes acts as an electron acceptor. The HOMO level in the metal-free TOC#1 changes to HOMO−1 upon doping while keeping almost the same energy. Intercalation of Li and Na into the TOC lattices leads to splitting of the LUMO into a single occupied molecular orbital (SOMO) and single unoccupied molecular orbital (SUMO) with a gap of 0.58 eV between them. The SOMO wavefunction is similar to the LUMO one of the metal-free molecule. The adsorption of Ca atoms leads to a LUMO splitting by two states: HOMO and LUMO having the same nodes but a different sign of the wavefunction with the main contribution from the Ca s-states. The newly formed HOMO–LUMO gap becomes much smaller and equal to 0.64 eV. In contrast, there are no contributions from s1 metals to the HOMO and LUMO levels. The unoccupied LUMO+1 states preserve the doubly degenerate pattern as in the metal–free TOC (Fig. 5). Since both models (polymer and oligomer) exhibit similar TOC–Me distances and charge transfer, we believe that the results obtained are mutually transferable. We also should note that in the discussed 2D polymers the band gaps vanish because of the quantum confinement effect. At the same time, one can clearly observe the new band caused by Ca doping and great enhancement in the density of states at the Fermi level of TOC–Ca (Fig. 2c and f), which should lead to much better conductivity and to the emergence of a superconducting state.
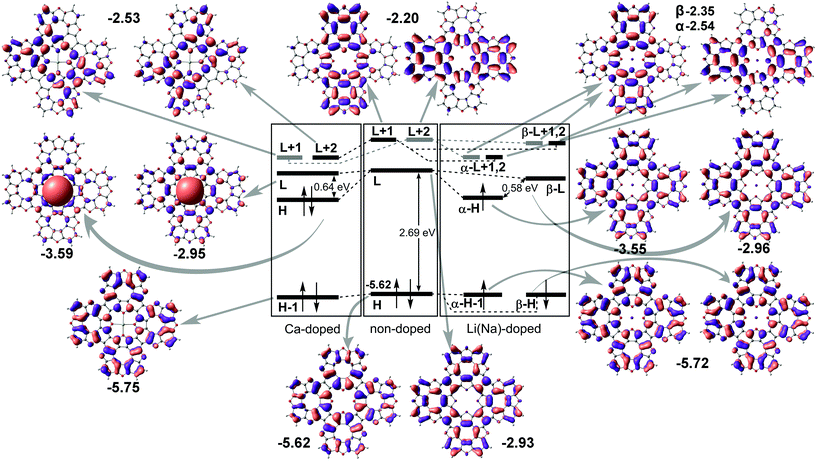 | ||
| Fig. 5 Energy molecular orbital diagram of tetraoxa[8]circulene doped by s-metals. “H” and “L” denote HOMO and LUMO terms, respectively; the numbers correspond to orbital energies (in eV). | ||
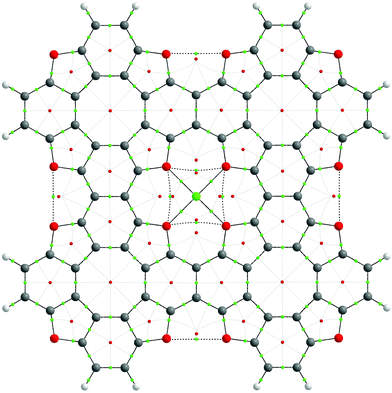
To explore the bonding features of the TOC–Me structures, Bader's electron density distribution analysis was performed within the Quantum Theory of Atoms In Molecules (QTAIM) approach. The graph structure of the TOC#1–Me complexes and the most important electronic characteristics of the coordination Me–O bonds and non-covalent interactions are presented in Fig. 6 and Table 3, respectively. One can see that for all the considered cases (Me = Li, Na, Ca), the Me–O bonds can be assigned to the closed-shell type interactions in terms of Bader's classification (electron density Laplacian in the bond critical point ∇2ρ(r) > 0 as well as the electron energy density he(r) > 0 (he(r) = g(r) + ν(r)), meaning a predominant localization of the electron density in atomic basins and domination of the kinetic energy density, g(r), over the potential energy density, ν(r). Indeed, the delocalization indices (DI) for the Me–O bonds are quite small (0.06, 0.08 and 0.14 for Li–O, Na–O and Ca–O bonds, respectively), and they expectedly increase in the order Li, Na, Ca, implying an increase in the covalence degree with an increase in the metal atom size. The ellipticity parameter (ε) of the Me–O bonds is quite small (less than 0.1), meaning a slight deviation from the cylindrical bond symmetry as well as the dynamic stability of these bonds. Indeed, the Me–O bond critical points (BCP) (3,−1) are placed far from any ring critical points (RCP) (3,+1) indicating a low probability of RCP-with-BCP bifurcation upon the vibrational atomic motions. In contrast, O⋯O and O′⋯O′ interactions are characterized by quite high ellipticity and a close interposition of RCP-BCP, indicating a potential dynamic instability.
| Complex | Bond | d, Å | ρ(r), e Å−3 | ∇2ρ(r), e Å−5 | ν(r), a.u. | h e(r), a.u. | ε | DI |
|---|---|---|---|---|---|---|---|---|
| TOC#1–Li | Li⋯O | 2.038 | 0.0213 | 0.1354 | −0.0211 | 0.0064 | 0.013 | 0.06 |
| O⋯O | 2.882 | 0.0101 | 0.0364 | −0.0083 | 0.0004 | 0.768 | 0.04 | |
| O′⋯O′ | 2.919 | 0.0077 | 0.0308 | −0.0066 | 0.0006 | 0.395 | 0.04 | |
| TOC#1–Na | Na⋯O | 2.270 | 0.0223 | 0.1440 | −0.0230 | 0.0065 | 0.075 | 0.08 |
| O⋯O | 2.918 | 0.0090 | 0.0328 | −0.0077 | 0.0003 | 0.327 | 0.04 | |
| O′⋯O′ | 2.923 | 0.0077 | 0.0306 | −0.0065 | 0.0005 | 0.405 | 0.04 | |
| TOC#1–Ca | Ca⋯O | 2.478 | 0.0261 | 0.1284 | −0.0251 | 0.0035 | 0.095 | 0.14 |
| O⋯O | 2.908 | 0.0097 | 0.0339 | −0.0081 | 0.0002 | 1.121 | 0.04 | |
| O′⋯O′ | 2.924 | 0.0077 | 0.0306 | −0.0065 | 0.0006 | 0.417 | 0.04 |
Due to the charge redistribution, the TOC–Ca sheets can be good candidates for the construction of computing nodes of qubits. Alkaline and alkaline-earth metals are of particular interest toward scalable quantum computing architectures.97–99 Though the approach proposed in the above papers to trap neutral atoms is quite challenging to achieve, there is also the alternative approach based on electron spin manipulation.100,101 One of the key parameters in the construction of magnetic qubits is the spin coherence time, which is related to the lifetime of a quantum superposition of states and which strictly depends on the spin state. Materials with active centers in the S = 1/2 spin state have been highlighted as most promising in terms of spin coherence time, and therefore practical realization of qubit architecture,102 due to the reduced spin–phonon coupling.103
As follows from atomic charge calculations (Table 1) for the TOC#1–Ca complex, a strong charge polarization within the Ca–O bonds takes place. Actually, one can speculate about a 4s electron transfer from the Ca atom to the TOC ligand upon complexation. Since only one electron transfers from the Ca atom to the TOC sheet, one can also predict the appearance of spin-polarization in this system. Therefore, a unique situation can be realized: the complexation of a TOC ligand, which is a closed-shell singlet (CSS) ground electronic state, with a Ca atom, which is also a CSS ground electronic state, may lead to a spin-polarized open-sell singlet (OSS) state of theTOC#1–Ca complex (Fig. 7), i.e. the entire spin state of the complex is singlet, while the Ca atom and TOC ligand both are doublets. Such a state is promising for obtaining building blocks for logical processes in quantum technology. The doublet spin state is characterized by a long spin coherence time and could therefore be of interest for applications in quantum information processing. Thus, the proved S = 1/2 ground state of Ca implemented in TOC could make TOC–Ca monolayers attractive materials for quantum computing purposes.
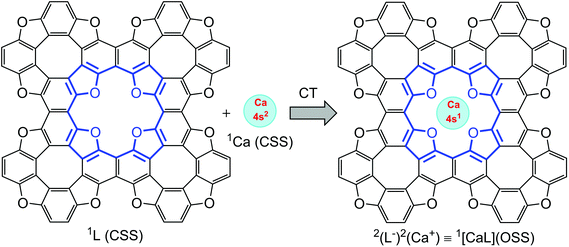 | ||
| Fig. 7 Schematic representation of open-shell singlet formation, where Ca and the ligand are in a doublet state. | ||
In order to prove our idea, we carried out broken symmetry (BS) DFT and CASSCF simulations to reveal the true ground state of Ca-intercalated TOC. A CASSCF calculation involving 10 electrons in 10 orbitals and an effective Hamiltonian in a multi-configuration quasi-degenerate second-order perturbation theory (XMC-QDPT2) confirms this assumption (Fig. 7). The result shows that the ground electronic state is a singlet with an open shell with the contribution of two determinants (−0.6 and 0.4 CI coefficients). The broken symmetry approximation at the UB3LYP/6-31+G(d,p) level with the consideration of GD3 empirical dispersion correction also confirms the open-shell singlet state is the ground state of the studied complex, while the closed-shell singlet state wavefunction demonstrates the Restricted to Unrestricted Hartree–Fock (RHF-UHF) instability.
It is found that the open-shell singlet state is of multi-configurational nature, while the current DFT methods coupled with the PBC model do not allow one to carry out such kind of calculations and therefore to reveal a true spin state. It should be also noted that the transferred spin spreads on the infinite organic part in the PBC approximation and that we did not find any sizable spin-polarization there, while the Ca atoms in the spin-polarized calculations reveal a minor magnetic moment of ∼0.03 μB. Therefore, the infinite organic part has no spin polarization and can so be considered as only electron-doped. Generally, magnetism is harmful for superconductivity and superconductors expel the magnetic field. However, magnetic impurities can interact with superconductors inducing Yu–Shiba–Rusinov (YSR) states.104,105 The existence of superconducting states in superconductor/ferromagnet heterostructures has also been recently experimentally confirmed in terms of topological superconductivity.106,107
In the case of molecular magnets having the desired spin state, it is necessary to couple them to the superconducting resonator in a precise well-ordered manner, which is also a challenging task. However, the present TOC–Ca material possesses intrinsic superconducting properties along with the S = 1/2 spin state of Ca simultaneously, which, therefore, makes this material a promising platform for quantum information processing. Though the doping-induced superconducting states have been widely proved in carbon-based superlattices, this work is probably the first report of superconductivity in Ca-doped molecular-based polymer structures and 2D covalent organic frameworks. We expect that superconductivity may be realized in other COFs through the doping mechanism.
Conclusions
In this work the structure and properties of the new organometallic porous sheets formed by 2D TOC polymers and alkali (Li, Na) or alkaline-earth (Ca) metals have been studied using first-principles methods. Two types of TOC polymers with different fusing of the TOC moieties were considered to design the TOC–Me sheets. The results show that the localization of metal atoms depends on the pore size: polymers with larger pores (TOC#2) promote the in-plane localization of the metal atoms, while the metal atoms are located above the plane in TOC#1. Voronoi charges indicate that the TOC polymers accept electrons from the alkali and alkaline-earth metals to form a more stable state. All organometallic structures are energetically stable. It was revealed that Me atoms have a significant influence on the TOC polymers, resulting in changes in the electronic structure from semiconductor to metallic. Using CASSCF calculations of a model of the TOC–Ca polymer, we determined a unique open-shell singlet ground state formed by two closed-shell singlets. Both the ligand and the Ca atom becomes a doublet, which is favorable for the construction of quantum nodes consisting of magnetic active centers with S = 1/2 as qubits. We found superconducting behaviour in the TOC–Ca polymers with TC = 14.5 K. Therefore, this material could be an ideal platform for quantum information processing. The idea of the possibility to use the proposed materials as a platform for quantum qubits is additionally supported by the recent experimental observations of an ultralong spin lifetime in light alkali atom doped graphene.108Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Russian Science Foundation (Project 19-73-10015). The authors thank the Information Technology Center, Novosibirsk State University, Institute of Computational Modelling of SB RAS, Krasnoyarsk and the Swedish National Infrastructure for Computing (SNIC 2020-3-29) at the High Performance Computing Center North (HPC2N) partially funded by the Swedish Research Council through the grant agreement no. 2018-05973 for providing the access to supercomputer facilities. G. V. B. and H. A. are thankful for the support from the Olle Engkvist Byggmästare Foundation (contract no. 189-0223). G. V. B. is also thankful for the financial support from the Ministry of Education and Science of Ukraine (project no. 0117U003908). R. R. V. thanks the Tomsk Polytechnic University Competitiveness Enhancement Program.Notes and references
- K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453 CrossRef CAS.
- J. Zhou, J. Lin, X. Huang, Y. Zhou, Y. Chen, J. Xia, H. Wang, Y. Xie, H. Yu, J. Lei, D. Wu, F. Liu, Q. Fu, Q. Zeng, C.-H. Hsu, C. Yang, L. Lu, T. Yu, Z. Shen, H. Lin, B. I. Yakobson, Q. Liu, K. Suenaga, G. Liu and Z. Liu, Nature, 2018, 556, 355–359 CrossRef CAS.
- A. V. Kuklin, G. V. Baryshnikov, B. F. Minaev, N. Ignatova and H. Ågren, J. Phys. Chem. C, 2018, 122, 22216–22222 CrossRef CAS.
- G. V. Baryshnikov, B. F. Minaev, N. N. Karaush and V. A. Minaeva, RSC Adv., 2014, 4, 25843–25851 RSC.
- J. Yu, Q. Sun, Y. Kawazoe and P. Jena, Nanoscale, 2014, 6, 14962–14970 RSC.
- B. F. Minaev, G. V. Baryshnikov and V. A. Minaeva, Comput. Theor. Chem., 2011, 972, 68–74 CrossRef CAS.
- L. Liu and Z. Shen, Appl. Phys. Lett., 2009, 95, 252104 CrossRef.
- H. J. Conley, B. Wang, J. I. Ziegler, R. F. Haglund Jr., S. T. Pantelides and K. I. Bolotin, Nano Lett., 2013, 13, 3626–3630 CrossRef CAS.
- G. V. Baryshnikov, B. F. Minaev, N. N. Karaush and V. A. Minaeva, Phys. Chem. Chem. Phys., 2014, 16, 6555–6559 RSC.
- J. Zhou and Q. Sun, J. Am. Chem. Soc., 2011, 133, 15113–15119 CrossRef CAS.
- J. Tan, W. Li, X. He and M. Zhao, RSC Adv., 2013, 3, 7016–7022 RSC.
- Y. Li and Q. Sun, Sci. Rep., 2014, 4, 4098 CrossRef.
- K. Lü, J. Zhou, L. Zhou, Q. Wang, Q. Sun and P. Jena, Appl. Phys. Lett., 2011, 99, 163104 CrossRef.
- K. Lü, J. Zhou, L. Zhou, X. S. Chen, S. H. Chan and Q. Sun, J. Chem. Phys., 2012, 136, 234703 CrossRef.
- P. Wang, X. Jiang, J. Hu, X. Huang and J. Zhao, J. Mater. Chem. C, 2016, 4, 2147–2154 RSC.
- M. Abel, S. Clair, O. Ourdjini, M. Mossoyan and L. Porte, J. Am. Ceram. Soc., 2011, 133, 1203–1205 CAS.
- M. Koudia and M. Abel, Chem. Commun., 2014, 50, 8565–8567 RSC.
- D. M. Sedlovets, V. T. Volkov, I. I. Khodos, A. V. Zotov and V. I. Korepanov, J. Phys. D: Appl. Phys., 2019, 52, 245303 CrossRef.
- M. Kan, J. Y. Wang, X. W. Li, S. H. Zhang, Y. W. Li, Y. Kawazoe, Q. Sun and P. Jena, J. Phys. Chem. C, 2014, 118, 1515–1522 CrossRef CAS.
- Y. Li, K. A. N. Duerloo, K. Wauson and E. J. Reed, Nat. Commun., 2016, 7, 10671 CrossRef CAS.
- T. E. Weller, M. Ellerb, S. S. Saxena, R. P. Smith and N. T. Skipper, Nat. Phys., 2005, 1, 39–41 Search PubMed.
- G. Csányi, P. B. Littlewood, A. H. Nevidomskyy, C. J. Pickard and B. D. Simons, Nat. Phys., 2005, 1, 42–45 Search PubMed.
- N. Emery, C. Hérold, M. D'Astuto, V. Garcia, C. Bellin, J. F. Marêché, P. Lagrange and G. Loupias, Phys. Rev. Lett., 2005, 95, 087003 CrossRef CAS.
- H. Liang, X. Zang, Y. Liu, D. Chen, Z. Xu, W. Gao, X. Wang, C. Gao, G. Chen and M. Xue, Carbon, 2019, 152, 527–531 CrossRef CAS.
- Y. Liu, H. Liang, Z. Xu, J. Xi, G. Chen, W. Gao, M. Xue and C. Gao, ACS Nano, 2017, 11, 4301–4306 CrossRef CAS.
- B. M. Ludbrook, G. Levy, P. Nigge, M. Zonno, M. Schneider, D. J. Dvorak, C. N. Veenstra, S. Zhdanovich, D. Wong, P. Dosanjh, C. Straßer, A. Stöhr, S. Forti, C. R. Ast, U. Starke and A. Damascelli, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11795–11799 CrossRef CAS.
- M. Xue, G. Chen, H. Yang, Y. Zhu, D. Wang, J. He and T. Cao, J. Am. Chem. Soc., 2012, 134, 6536–6539 CrossRef CAS.
- I. T. Belash, A. D. Bronnikov, O. V. Zharikov and A. V. Palnichenko, Solid State Commun., 1987, 64, 1445–1447 CrossRef CAS.
- R. A. Jishi and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 12465 CrossRef.
- S. Ichinokura, K. Sugawara, A. Takayama, T. Takahashi and S. Hasegawa, ACS Nano, 2016, 10, 2761–2765 CrossRef CAS.
- R. Mitsuhashi, Y. Suzuki, Y. Yamanari, H. Mitamura, T. Kambe, N. Ikeda, H. Okamoto, A. Fujiwara, M. Yamaji, N. Kawasaki, Y. Maniwa and Y. Kubozono, Nature, 2010, 464, 76–79 CrossRef CAS.
- G. H. Zhong, D. Y. Yang, K. Zhang, R. S. Wang, C. Zhang, H. Q. Lin and X. J. Chen, Phys. Chem. Chem. Phys., 2018, 20, 25217–25223 RSC.
- J. F. Yan, G. H. Zhong, R. S. Wang, K. Zhang, H. Q. Lin and X. J. Chen, J. Phys. Chem. Lett., 2019, 10, 40–47 CrossRef CAS.
- X. W. Yan, C. Zhang, G. Zhong, D. Ma and M. Gao, J. Mater. Chem. C, 2016, 4, 11566–11571 RSC.
- X. Wu, C. Xu, K. Wang and X. Xiao, J. Phys. Chem. C, 2016, 120, 15446–15552 CrossRef CAS.
- M. Xue, T. Cao, D. Wang, Y. Wu, H. Yang, X. Dong, J. He, F. Li and G. F. Chen, Sci. Rep., 2012, 2, 389 CrossRef.
- X. Huang, S. Zhang, L. Liu, L. Yu, G. Chen, W. Xu and D. Zhu, Angew. Chem., Int. Ed., 2018, 57, 146–150 CrossRef CAS.
- X. Zhang, Y. Zhou, B. Cui, M. Zhao and F. Liu, Nano Lett., 2017, 17, 6166–6170 CrossRef CAS.
- N. N. Karaush, G. V. Baryshnikov and B. F. Minaev, RSC Adv., 2015, 5, 24299–24305 RSC.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864–871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133 CrossRef.
- S. Boker, M. Neale, H. Maes, M. Wilde, M. Spiegel, T. Brick, J. Spies, R. Estabrook, S. Kenny, T. Bates, P. Mehta and J. Fox, Psychometrika, 2011, 76, 306–317 CrossRef.
- T. Ozaki and H. Kino, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 195113 CrossRef.
- T. Ozaki, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155108 CrossRef.
- T. Ozaki and H. Kino, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045121 CrossRef.
- K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. Dal Corso, S. De Gironcoli, T. Deutsch, J. K. Dewhurst, I. Di Marco, C. Draxl, M. Dułak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Grånäs, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iuşan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Küçükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G. M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. Van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G. X. Zhang and S. Cottenier, Science, 2016, 351, aad3000 CrossRef.
- G. B. Bachelet, D. R. Hamann and M. Schlüter, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 4199–4228 CrossRef CAS.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS.
- L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425–1428 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 5414–5416 CrossRef.
- I. Morrison, D. M. Bylander and L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 6728–6731 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- A. D. Becke and R. M. Dickson, J. Chem. Phys., 1988, 89, 2993–2997 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- F. Giustino, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 165108 CrossRef.
- E. R. Margine and F. Giustino, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 024505 CrossRef.
- S. Poncé, E. R. Margine, C. Verdi and F. Giustino, Comput. Phys. Commun., 2016, 209, 116–133 CrossRef.
- A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685–699 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. De Gironcoli, P. Delugas, R. A. Distasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Kücükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-De-La-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef.
- A. A. Granovsky, Firefly version 8.2 [Electronic resource]. Available at: http://classic.chem.msu.su/gran/gamess/index.html Search PubMed.
- E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 131391 CrossRef.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. S. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, P. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. E. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Rev. A. 03, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Clarendon Press, Oxford, 1990 Search PubMed.
- T. A. Keith, AIMAll (Version 10.07.25), TK Gristmill Software, Overland Park KS, USA, 2010, http://www.aim.tkgristmill.com Search PubMed.
- H. Lee, J. Ihm, M. L. Cohen and S. G. Louie, Nano Lett., 2010, 10(3), 793–798 CrossRef CAS.
- B. M. Ludbrook, G. Levy, P. Nigge, M. Zonno, M. Schneider, D. J. Dvorak, C. N. Veenstra, S. Zhdanovich, D. Wong, P. Dosanjh, C. Straßer, A. Stöhr, S. Forti, C. R. Ast, U. Starke and A. Damascelli, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11795–11799 CrossRef CAS.
- J. Chapman, Y. Su, C. A. Howard, D. Kundys, A. N. Grigorenko, F. Guinea, A. K. Geim, I. V. Grigorieva and R. R. Nair, Sci. Rep., 2016, 6, 1–6 CrossRef.
- C. Cazorla, S. A. Shevlin and Z. X. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155454 CrossRef.
- Y. Yamada, A. V. Kuklin, S. Sato, F. Esaka, N. Sumi, C. Zhang, M. Sasaki, E. Kwon, Y. Kasama, P. V. Avramov and S. Sakai, Carbon, 2018, 133, 23–30 CrossRef CAS.
- K. Kim, A. DaSilva, S. Huang, B. Fallahazad, S. Larentis, T. Taniguchi, K. Watanabe, B. J. LeRoy, A. H. MacDonald and E. Tutuc, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3364–3369 CrossRef CAS.
- D. Marchenko, D. V. Evtushinsky, E. Golias, A. Varykhalov, T. Seyller and O. Rader, Sci. Adv., 2018, 4, eaau0059 CrossRef CAS.
- Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50 CrossRef CAS.
- E. Suárez Morell, J. D. Correa, P. Vargas, M. Pacheco and Z. Barticevic, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 121407(R) CrossRef.
- J. L. McChesney, A. Bostwick, T. Ohta, T. Seyller, K. Horn, J. González and E. Rotenberg, Phys. Rev. Lett., 2010, 104, 136803 CrossRef CAS.
- N. Ehlen, M. Hell, G. Marini, E. H. Hasdeo, R. Saito, Y. Falke, M. O. Goerbig, G. Di Santo, L. Petaccia, G. Profeta and A. Grüneis, ACS Nano, 2020, 14, 1055–1069 CrossRef CAS.
- A. P. Durajski, K. M. Skoczylas and R. Szcześniak, Phys. Chem. Chem. Phys., 2019, 21, 5925–5931 RSC.
- E. R. Margine, H. Lambert and F. Giustino, Sci. Rep., 2016, 6, 21414 CrossRef CAS.
- M. Calandra and F. Mauri, Phys. Status Solidi, 2006, 243, 3458 CrossRef CAS.
- W. L. McMillan, Phys. Rev., 1968, 167, 331 CrossRef CAS.
- P. B. Allen and R. C. Dynes, Phys. Rev. B: Solid State, 1975, 12, 905 CrossRef CAS.
- https://www.materialscloud.org/work/tools/interactivephonon .
- X. Fan, W. T. Zheng and J. L. Kuo, ACS Appl. Mater. Interfaces, 2012, 4, 2432 CrossRef CAS.
- C. Cazorla, S. A. Shevlin and Z. X. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155454 CrossRef.
- S. M. George, Chem. Rev., 2010, 110, 111–131 CrossRef CAS.
- A. J. Daley, M. M. Boyd, J. Ye and P. Zoller, Phys. Rev. Lett., 2008, 101, 170504 CrossRef.
- I. S. Madjarov, J. P. Covey, A. L. Shaw, J. Choi, A. Kale, A. Cooper, H. Pichler, V. Schkolnik, J. R. Williams and M. Endres, Nat. Phys., 2020, 16, 857–861 Search PubMed.
- A. V. Gorshkov, A. M. Rey, A. J. Daley, M. M. Boyd, J. Ye, P. Zoller and M. D. Lukin, Phys. Rev. Lett., 2009, 102, 110503 CrossRef CAS.
- M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793 CrossRef CAS.
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS.
- M. D. Jenkins, D. Zueco, O. Roubeau, G. Aromí, J. Majer and F. Luis, Dalton Trans., 2016, 45, 16682–16693 RSC.
- A. Albino, S. Benci, L. Tesi, M. Atzori, R. Torre, S. Sanvito, R. Sessoli and A. Lunghi, Inorg. Chem., 2019, 58, 10260–10268 CrossRef CAS.
- X. Yang, Y. Yuan, Y. Peng, E. Minamitani, L. Peng, J. J. Xian, W. H. Zhang and Y. S. Fu, Nanoscale, 2020, 12, 8174–8179 RSC.
- B. W. Heinrich, J. I. Pascual and K. J. Franke, Prog. Surf. Sci., 2018, 93, 1–19 CrossRef CAS.
- S. Kezilebieke, M. N. Huda, P. Dreher, I. Manninen, Y. Zhou, J. Sainio, R. Mansell, M. M. Ugeda, S. van Dijken, H. P. Komsa and P. Liljeroth, Commun. Phys., 2020, 3, 1–8 CrossRef.
- S. Kezilebieke, M. N. Huda, V. Vaňo, M. Aapro, S. C. Ganguli, O. J. Silveira, S. Głodzik, A. S. Foster, T. Ojanen and P. Liljeroth, Nature, 2020, 588, 424–428 CrossRef CAS.
- B. G. Márkus, P. Szirmai, K. F. Edelthalhammer, P. Eckerlein, A. Hirsch, F. Hauke, N. M. Nemes, J. C. Chacón-Torres, B. Náfrádi, L. Forró, T. Pichler and F. Simon, ACS Nano, 2020, 14, 7492–7501 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Structural parameters, the orbital decomposed band structure and DOS of TOC-Ca, the comparative total density of states calculated within different codes, and the spatial distribution of charge density. See DOI: 10.1039/d0nr08554e |
| This journal is © The Royal Society of Chemistry 2021 |