Open Access Article
Open Access ArticleConformation-dependent charge transport through short peptides†
Davide
Stefani‡
 a,
Cunlan
Guo‡§
a,
Cunlan
Guo‡§
 *b,
Luca
Ornago
*b,
Luca
Ornago
 a,
Damien
Cabosart
a,
Maria
El Abbassi
a,
Damien
Cabosart
a,
Maria
El Abbassi
 a,
Mordechai
Sheves
a,
Mordechai
Sheves
 b,
David
Cahen
b,
David
Cahen
 b and
Herre S. J.
van der Zant
b and
Herre S. J.
van der Zant
 *a
*a
aKavli Institute of Nanoscience, Delft University of Technology, Delft, The Netherlands. E-mail: h.s.j.vanderzant@tudelft.nl
bMaterials and Interfaces, Weizmann Institute of Science, Rehovot, Israel. E-mail: cunlanguo@whu.edu.cn
First published on 26th December 2020
Abstract
We report on charge transport across single short peptides using the Mechanically Controlled Break Junction (MCBJ) method. We record thousands of electron transport events across single-molecule junctions and with an unsupervised machine learning algorithm, we identify several classes of traces with multifarious conductance values that may correspond to different peptide conformations. Data analysis shows that very short peptides, which are more rigid, show conductance plateaus at low conductance values of about 10−3G0 and below, with G0 being the conductance quantum, whereas slightly longer, more flexible peptides also show plateaus at higher values. Fully stretched peptide chains exhibit conductance values that are of the same order as that of alkane chains of similar length. The measurements show that in the case of short peptides, different compositions and molecular lengths offer a wide range of junction conformations. Such information is crucial to understand mechanism(s) of charge transport in and across peptide-based biomolecules.
Introduction
Electronic charge transport through a peptide matrix is crucial for proteins to perform their function in processes such as respiration, photosynthesis, and cellular signaling.1 Their remarkably good electrical conductance, diverse and programmable structure, and unique bio-recognition ability make proteins suitable candidates for functional molecular electronic devices.2 Peptides are common building blocks of biomolecules, but in order to implement them in solid-state devices, the relationship between electron transport, peptide structure and amino acid composition needs to be understood. Amino acid composition, i.e., the side chains present in the peptide, influences the electronic structure of the peptide, impacting its energy levels and coupling to the electrodes.3–5Tunnelling is the dominant charge transport mechanism observed in solid-state junctions of linear peptide chains, with conductance exponentially decreasing with molecular length.5–7 However, the electronic properties of peptides significantly change once they form secondary structures, generally resulting in an increase in length-normalized conductance and variable length-conductance dependence for both linear and helical peptides,5,8–12 or because of the functional groups at the amino acid that modify the interaction with the electrodes.13,14 All these variables multiply the possible behaviors of peptide molecular junctions, information which is usually averaged out by measurements in bulk and, although to a lesser extent, also in self-assembled monolayers. Investigating the intrinsic properties of single peptides is thus crucial to understand electron transport via peptide junctions and to separate intrinsic properties from cooperative effects.
The conductance of single peptides was measured in a mechanically controlled break junction (MCBJ) at a fixed distance for recognition purposes15 and in the STM-BJ as a function of electrode separation.16–18 In the later experiments, the weak effect of the amino-acid composition on the peptide conductance was confirmed. Typically, the analysis only involves the study of the most prominent conductance peak and stretched peptide chains were found to be poor conductors. In this work, we study the electron transport properties of single peptides using the MCBJ technique (Fig. 1a) while stretching the junction. The mechanical stability of this technique allows one to study in detail the evolution of junction conduction with electrode separation. Several conductance plateaus at different electrode separations are observed and analyzed using a machine learning clustering method; the multiple plateaus may correspond to different configurations of the peptide in the junction.
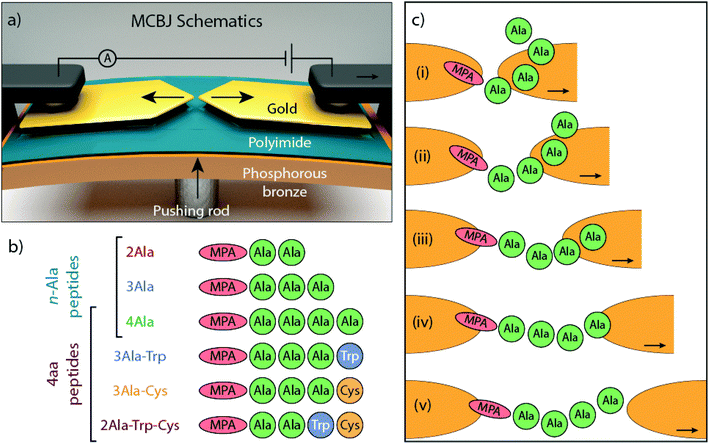
In the MCBJ technique, a flexible substrate is coated with an insulating polyimide layer. A 100 nm wide constriction is lithographically defined in a gold wire and then suspended by reactive ion etching. By bending the substrate with a pushing rod, the suspended gold wire is stretched until it ruptures, forming two atomically sharp electrodes (Fig. 1a). This process can be reverted by reducing the deformation of the substrate, fusing back the wire. When a bias voltage is applied, current flows through the junction and a trace of conductance versus electrode displacement is recorded (Fig. S1†). The conductance recorded while the junction is broken constitutes the so-called breaking trace. By repeatedly breaking and fusing the wire, statistical information about the junction's conductance is collected.
The molecules under investigation are a series of linear peptides composed of typical amino acids: alanine (Ala), tryptophan (Trp), and cysteine (Cys), which have, respectively, methyl, methyl-indole and thiomethyl as side chains. Mercaptopropionic acid (MPA) is added to the N-terminus of the peptides to introduce a thiol group that acts as an anchoring unit to one of the gold electrodes of the MCBJ device. The dependence of electron transport on chain length is studied with poly-Ala peptides (Fig. 1b), whereas the influence of side chain composition is investigated in a series of 4-amino-acid long peptides with different amino acid combinations. The roles of different electrode-anchoring groups at the C-terminus (–COOH and –SH) are explored by introducing a terminal Cys element (Fig. 1b). Because of the important role that aromatic groups play in molecular conductance,19–23 Trp, an aromatic amino acid, is introduced into the peptide to investigate its effect on electron transport. Trp has a low ionization potential (IP) as natural amino acid and its indole ring provides delocalized electrons that can contribute to transport.4,24 In the following sections, the peptides will be denoted without the MPA and we will use common abbreviations for the amino acids (Ala, Cys and Trp).
Experimental results
The MCBJ charge transport measurements across single peptides are performed in a vacuum.25–27 After electrical characterization of a bare gold device, 2 μM solution of the target peptide in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ACN
3 ACN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
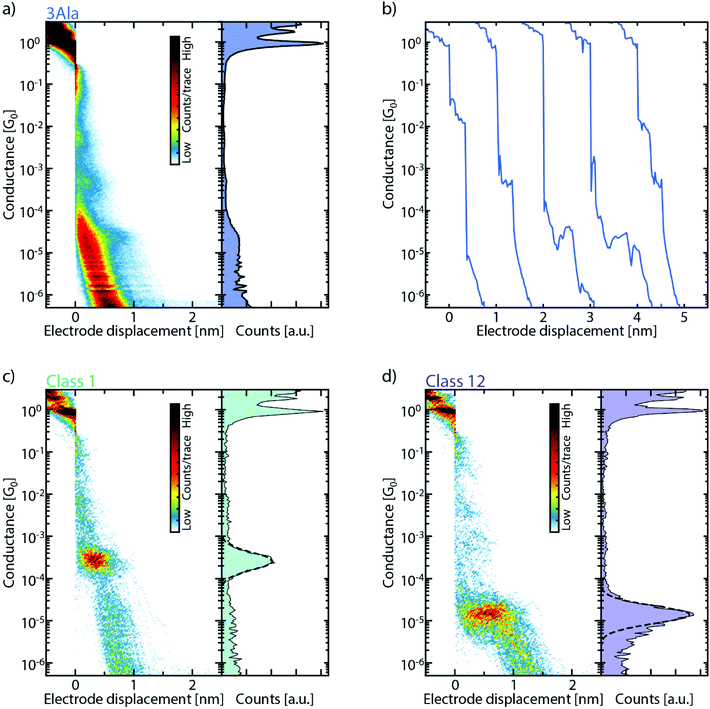
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O is drop-cast on the MCBJ sample. After evacuating the sample chamber and the solvent has evaporated, thousands of consecutive breaking traces are collected and combined into one- and two-dimensional conductance histograms (Fig. 2a, S2, and S3†). One-dimensional histograms (right panel of Fig. 2a) are usually employed to extract the most probable conductance of the molecule. However, for all peptides, no unique conductance peak is found in these histograms. However, the data show longer traces and clustering of counts at particular conductance values absent before drop-casting of the molecular solution, revealing a signature of the molecule. Specifically, when examining individual breaking traces, short plateaus are observed as the molecule is stretched across the junction (Fig. 2b). These short plateaus are found for all peptide junctions studied (Fig. S2b, d, f and S3b, d, f†). Interestingly, they are distributed over a wide conductance range, which indicates the formation of several metastable molecular junction configurations at different conductance values and electrode separations. It is important to note that these plateaus are absent in the same bare gold junctions, characterized before deposition (see Fig. S1 and S4†).
H2O is drop-cast on the MCBJ sample. After evacuating the sample chamber and the solvent has evaporated, thousands of consecutive breaking traces are collected and combined into one- and two-dimensional conductance histograms (Fig. 2a, S2, and S3†). One-dimensional histograms (right panel of Fig. 2a) are usually employed to extract the most probable conductance of the molecule. However, for all peptides, no unique conductance peak is found in these histograms. However, the data show longer traces and clustering of counts at particular conductance values absent before drop-casting of the molecular solution, revealing a signature of the molecule. Specifically, when examining individual breaking traces, short plateaus are observed as the molecule is stretched across the junction (Fig. 2b). These short plateaus are found for all peptide junctions studied (Fig. S2b, d, f and S3b, d, f†). Interestingly, they are distributed over a wide conductance range, which indicates the formation of several metastable molecular junction configurations at different conductance values and electrode separations. It is important to note that these plateaus are absent in the same bare gold junctions, characterized before deposition (see Fig. S1 and S4†).
To help sorting the plateaus, we employ a reference-free classification algorithm based on clustering of the data with the K-means++ method.28 The algorithm groups traces that have similar one- and two-dimensional histograms, thus highlighting their most prominent features. Fig. 2c and d show two of these classes which clearly exhibit distinct features around a particular conductance value both in the one- and two-dimensional histograms. In the algorithm, from each trace, a 28-by-28 two-dimensional histogram and a 100-bin one-dimensional histogram are extracted. These are then combined to form the 884-dimensional feature space over which the clustering algorithm operates; the inclusion of the 1D histograms gives more weight to the short plateaus in the traces and thus helps with their classification.29 More details can be found in the ESI (section IV†).
An important parameter to be set in the classification algorithm is the number of clusters. In order to account for the behavior of the high diversity of traces, the default number of clusters is chosen to be 15 (more details can be found in the following paragraph). It is important to realize that the number of clusters does not correspond to the number of possible plateau groups in the measurement (see Fig. S5†). One reason is that not all classes contain molecular, plateau-like features; a few of the clusters contain tunnelling-like curves without clear features. Additionally, in some cases, multiple clusters represent similar features, which are split because the K-means algorithm has the tendency to create clusters of equal size.30
For each cluster, the conductance value, length, and position of the plateaus are extracted and compared between the different peptide series (more details can be found in the ESI, section V†). For conductance values below 10−1G0, the three parameters are obtained in the following way: a log–normal fit of the one-dimensional histogram of each cluster yields the conductance value associated with that cluster as illustrated in Fig. 3a. The fit also defines the interval used for the calculation of the plateau length and position. To do so, a conductance interval centered around the peak of the fit is defined with a width equal 3 times its standard deviation (Fig. 3a). Then, the length is calculated as the portion of each trace that falls in this interval (see Fig. S6†) and the plateau position as the displacement at the middle of this length interval. With these conductance values and position of the clusters, we construct graphs (Fig. 3c and d) which show where the various plateaus appear in the breaking traces. Fig. 3b shows this for 3Ala when considering different numbers of clusters in the classification algorithm and Fig. 3c shows the comparison of the results for (n)Ala with n = 2, 3 and 4. We find that the conductance peaks decay approximately exponentially with the plateau position over several orders of magnitude. We define a parameter γ corresponding to the decay rate of this exponential curve. When considering 15 clusters, we find γ = (15.3 ± 3.3) nm−1 for 3Ala. Importantly, the inset of Fig. 3b shows that this value is approximately the same when considering different cluster numbers as input in the classification algorithm. The green dashed line in Fig. 3c yields γ = (13.5 ± 1.3) nm−1 for the 4Ala measurement.
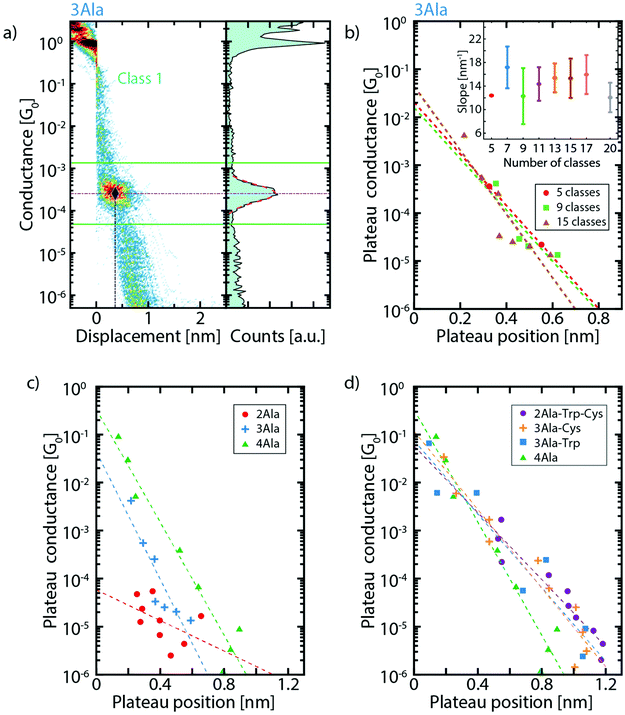 | ||
| Fig. 3 (a) Exemplification of the method for defining the plateau position: the dash-dotted horizontal purple line corresponds to the conductance of the plateau extracted from the fit. The solid green lines define the limits of the 3σ interval around it; the dash-dotted vertical blue line indicates the plateau position so that the crossing of the two dash-dotted lines defines the point shown in the plateau conductance vs. plateau position plots (same data as in Fig. 2c). (b) Dependence of the plateau conductance vs. position plot on the number of classes for 3Ala. The panel reports the results for 5, 9 and 15 classes. Each dot corresponds to the plateau position and conductance of a molecular cluster. The dashed lines are the corresponding fits. The inset displays the slope of the fit for 5, 7, 9, 11, 13, 15, 17 and 20 classes (the error bar is the standard deviation on the slope. Note that for 5 clusters there is no error bar, as the clustering yielded only 2 molecular classes. (c) Extracted conductance value vs. plateau position for increasing peptide length, and (d) for different peptide composition. In both panels, the results corresponding to 15 clusters are reported, and the dashed lines (best fit) illustrate the exponential decay (γ) of conductance on plateau position. γ4Ala = 13.5 ± 1.3 nm−1, γ3Ala-Cys = 9.4 ± 0.9 nm−1, γ3Ala-Trp = 8.8 ± 1.3 nm−1, and γ2Ala-Trp-Cys = 8.0 ± 0.9 nm−1. | ||
A decay rate is commonly used to study the conductance of a series of molecules with the same repeating subunit (G = Ae−βL with A being a constant, L the length of the molecule and β the decay parameter). β-values of peptide chains found in the literature are deduced from measurements performed with scanning tunnelling microscopy (STM) break junctions: for cysteamine-(n)glycinecysteine chains, β = 8.7 ± 7.0 nm−1,31 for tri-alanine, β = 9.3 ± 0.4 nm−1 and for tri-glycine, β = 9.7 ± 0.1 nm−1.33 These STM break-junction-derived values are in the same range as the γ-values in our MCBJ measurements and indicate low tunnelling efficiency. Furthermore, the low tunnelling efficiency is close to that of other non-conjugated molecules like alkanes (β ≈ 7.5–10.0 nm−1),32–35 implying that short peptides are not particularly good conductors, in agreement with recent calculations.36 We want to stress that, while β is usually determined by separately measuring molecules with systematically changing lengths, we estimate the tunnelling decay from a series of successive measurements done on a single molecule of a given type. More details about this method can be found in the ESI (section VI†).
As shown in Fig. 3c, the extracted conductance peaks for 3Ala and 4Ala show a similar distribution across a large conductance range; however, they are found across different displacement values (ranging both from <0.05 nm to around 0.6 nm for 3Ala and 0.9 nm for 4Ala) in agreement with their respective total length. The conductance peak distribution of 2Ala does not have a clear correspondence with those of 3- and 4Ala, but the most striking difference is that the peaks at high conductance (>10−4G0) are absent in 2Ala. The high-conductance peaks are also significantly less prominent in 3Ala than in 4Ala. Furthermore, by systematically changing the number of clusters from 5 to 20, we demonstrate that the number of clusters does not affect these observations (Fig. 3b).
The role of peptide composition in its electron transport was studied by comparing the clustering results of 4Ala, 3Ala-Trp, 3Ala-Cys, and 2Ala-Trp-Cys (Fig. 3d). The extracted conductance peaks are found across the whole conductance range and at displacement values ranging from 0.05 to 1.2 nm. This matches well with the estimated length of the 4-amino-acid peptides of 1.7 nm after we take into account the 0.5 nm snap back distance of the electrodes which occurs as the last gold atom connection breaks.37,38 The conductance peaks of these four peptides all show exponential decays with the plateau position. The steepness follows the order 4Ala > 3Ala-Cys ≈ 3Ala-Trp ≈ 2Ala-Trp-Cys, indicating that the precise amino acid composition has only a marginal effect on molecular conductance.
Discussion
The plateau-like features observed in the measurements are likely associated with various metastable junction configurations probed during the breaking process. The configurations can vary depending on the binding sites involved, the local geometries of the Au atoms, the electrode surface and the conformation of the molecule. Possible binding groups in the peptides are the thiol (–SH), carboxyl/carboxylic (–COOH/–COO–) and indole (–C8NH7) groups.13,14 Common combinations of these binding sites can be found in the different peptides studied, which suggests that there should be some similarity between the conductance values and the positions of the peaks for the different peptides. Indeed, there are similarities between the extracted conductance peak distributions for different peptides (peaks overlay for different peptides in Fig. 3c and d). Furthermore, mechanical stabilization involving van der Waals forces between the metallic electrode and molecule may also lead to metastable junction configurations.39 It is thus not straightforward to associate a conductance peak with a specific electron path because of the complexity of the peak distribution. To be able to identify the metastable peptide conformation corresponding to each extracted conductance, complementary electronic structure computations will be required.The plateau distribution of 4Ala shows exponential decay over a wider distance range compared to that of the shorter 3Ala and 2Ala. Classes at high conductance and short distance are present in 3Ala and 4Ala and are absent in the shorter 2Ala one. This may be related to the increasing flexibility of 3Ala and 4Ala, compared to the shorter one. When a polymer is close to or shorter than its persistence length, it behaves like a relatively rigid rod. From atomic force spectroscopy, the persistence length of unfolded peptides was found to be approximately 0.4 nm.40–43 This value is close to the distance of two adjacent α-carbons in the peptide backbone (approximately the length of an amide group), even though the persistence length of peptides is affected by the amino acid composition, pH, ionic strength in the solution, and other environmental factors. Therefore, it is possible to imagine a peptide as composed of rigid rods (the amide groups) that can rotate around their connection points (the α-carbons). Peptide flexibility and the possible conformations it can have3 thus increase with the number of amino acids. Even in a vacuum, linear (unfolded) 4Ala likely has several conformations and there will be additional ones in our experiments, considering the presence of multiple binding sites to Au. However, estimating such conformations is significantly more cumbersome than doing so in the gas phase. Molecular dynamics simulations could help in this regard, but they are out of the scope of this work.
Some information can still be gained from considering the persistence length and the carbon–carbon bonds (see the ESI, section VII†). The α-carbon has sp3 hybridization, which means that the angles of two adjacent bonds via α-carbons are around 110°. Since the length of the stretched peptides (2Ala, 3Ala, and 4Ala) is approximately 2, 3, and 4 times the persistence length, the flexibility of the peptides should follow 4Ala > 3Ala > 2Ala (Fig. S7†). Based on this information, it is possible that 3Ala and 4Ala have the ability to fold and form a molecular junction with non-linear configurations somewhat akin to the random coil of a peptide. If electrons flow via these metastable peptide junctions, they need not flow along the peptide backbone but across charge pathways shorter than the length of the stretched molecule. This can result in higher conductance plateaus at the initial stages of the breaking sequence, which will be absent for 2Ala and less prominent in 3Ala because the associated configurations are not available to them due to their reduced flexibility. Thus, long and flexible enough peptides that are pulled across the gap between the electrodes may be able to bridge this gap in different configurations while preserving a non-linear structure, as illustrated in Fig. 1c. Moreover, since all of the 4-amino-acid peptides have a similar length, they are also expected to have a flexibility similar to that of 4Ala. This is consistent with the experiments, which show that all of them exhibit conductance plateaus above 10−4G0 at short displacement. Finally, we note that at the largest electrode spacing, the peptides are extended in the junction and are expected to approach a linear structure, which would be consistent with the low conductance observed in this regime.
The conductance of a flexible molecule under stretching between electrodes, before/without breaking the junction, has been studied, with an eye towards the contribution of molecular conformations44 and contact geometry.45,46 Here, we classified the conductance plateaus which represent the breaking of peptide junctions in the metastable conformations. The exponential decay of plateau conductance with position is similar to that computed for stretched molecules (∼10 nm−1)44 and consistent with tunneling,47 which responds to the change of peptide conformations. Specific models, like the pathway (through bond and space segments) and single energy level (consider the junction as a whole) ones, have been developed. While our results indicate differences between peptides, they do not allow, at this stage, the singling out of a more specific model than that of tunneling through the peptide. Further studies including molecular simulations are required to draw more specific conclusions.
Conclusions
In this work, we used the MCBJ technique to measure the conductance of six different peptides, investigating the influence of the chain length and composition on electronic transport across them. The MCBJ results were classified by a reference-free algorithm based on K-means++ clustering. The multitude of conductance plateaus observed at various displacements suggests that peptides establish various metastable conformations when forming a single-molecule junction. The overall low tunnelling efficiency found for these peptides suggests that stretched peptides are not good conductors. However, short plateaus at high conductance values are found for the peptides composed of 4 amino acids, suggesting that their increased flexibility allows them to fold into non-linear configurations which might be beneficial for electron transport. These results are helpful for understanding electron transport mechanism(s) in peptides and proteins and in future works, molecular dynamics simulations may help to identify preferred molecular junction conformations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
DS, M. El Abbassi and HSJZ acknowledge financial support by the EU through the H2020 FET QuIET project (no. 767187). Device fabrication was done at the Kavli Nanolab at Delft. CG thanks the Weizmann Inst. for partial support as a sr. PD fellow and the NSFC (21974102) for financial support. DC, MS and CG thank the Israel Science Foundation for partial support.References
- Biological Inorganic Chemistry, ed. I. Bertini, H. B. Gray, E. I. Stiefel and J. S. Valentine, 2007 Search PubMed.
- P. Facci, Biomolecular electronics: bioelectronics and the electrical control of biological systems and reactions, William Andrew Inc., 2014, pp. 1–240 Search PubMed.
- C. Guo, S. Sarkar, S. Refaely-Abramson, D. A. Egger, T. Bendikov, K. Yonezawa, Y. Suda, T. Yamaguchi, I. Pecht, S. Kera, N. Ueno, M. Sheves, L. Kronik and D. Cahen, Electronic structure of dipeptides in the gas-phase and as an adsorbed monolayer, Phys. Chem. Chem. Phys., 2018, 20, 6860–6867 RSC.
- C. Guo, X. Yu, S. Refaely-Abramson, L. Sepunaru, T. Bendikov, I. Pecht, L. Kronik, A. Vilan, M. Sheves and D. Cahen, Tuning electronic transport via hepta-alanine peptides junction by tryptophan doping, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10785–10790 CrossRef CAS PubMed.
- L. Sepunaru, S. Refaely-Abramson, R. Lovrincic, Y. Gavrilov, P. Agrawal, Y. Levy, L. Kronik, I. Pecht, M. Sheves and D. Cahen, Electronic transport via homopeptides: the role of side chains and secondary structure, J. Am. Chem. Soc., 2015, 137, 9617–9626 CrossRef CAS PubMed.
- M. Baghbanzadeh, C. M. Bowers, D. Rappoport, T. Zaba, M. Gonidec, M. H. Al-Sayah, P. Cyganik, A. Aspuru-Guzik and G. M. Whitesides, Charge tunnelling along short oligoglycine chains, Angew. Chem., Int. Ed., 2015, 54, 14743–14747 CrossRef CAS PubMed.
- J. Juhaniewicz, J. Pawlowski and S. Sek, Electron transport mediated by peptides immobilized on surfaces, Isr. J. Chem., 2015, 55, 645–660 CrossRef CAS.
- N. Amdursky, Electron Transfer across Helical Peptides, ChemPlusChem, 2015, 80, 1075–1095 CrossRef CAS PubMed.
- R. A. Malak, Z. N. Gao, J. F. Wishart and S. S. Isied, Long-range electron transfer across peptide bridges: The transition from electron superexchange to hopping, J. Am. Chem. Soc., 2004, 126, 13888–13889 CrossRef CAS PubMed.
- H. S. Mandal and H.-B. Kraatz, Electron Transfer Mechanism in Helical Peptides, J. Phys. Chem. Lett., 2012, 3, 709–713 CrossRef CAS PubMed.
- A. Shah, B. Adhikari, S. Martic, A. Munir, S. Shahzad, K. Ahmad and H. B. Kraatz, Electron transfer in peptides, Chem. Soc. Rev., 2015, 44, 1015–1027 RSC.
- J. R. Horsley, J. Yu, K. E. Moore, J. G. Shapter and A. D. Abell, Unraveling the Interplay of Backbone Rigidity and Electron Rich Side-Chains on Electron Transfer in Peptides: The Realization of Tunable Molecular Wires, J. Am. Chem. Soc., 2014, 136, 12479–12488 CrossRef CAS PubMed.
- J. Feng, R. B. Pandey, R. J. Berry, B. L. Farmer, R. R. Naik and H. Heinz, Adsorption mechanism of single amino acid and surfactant molecules to Au {111} surfaces in aqueous solution: design rules for metal-binding molecules, Soft Matter, 2011, 7, 2113–2120 RSC.
- F. Iori, R. Di Felice, E. Molinari and S. Corni, GolP: An atomistic force-field to describe the interaction of proteins with Au(111) surfaces in water, J. Comput. Chem., 2009, 30, 1465–1476 CrossRef CAS PubMed.
- T. Ohshiro, M. Tsutsui, K. Yokota, M. Furuhashi, M. Taniguchi and T. Kawai, Detection of post-translational modifications in single peptides using electron tunnelling currents, Nat. Nanotechnol., 2014, 9, 835–840 CrossRef CAS PubMed.
- X. Xiao, B. Xu and N. Tao, Changes in the Conductance of Single Peptide Molecules upon Metal-Ion Binding, Angew. Chem., Int. Ed., 2004, 43, 6148–6152 CrossRef CAS PubMed.
- J. M. Brisendine, S. Refaely-Abramson, Z.-F. Liu, J. Cui, F. Ng, J. B. Neaton, R. L. Koder and L. Venkataraman, Probing Charge Transport through Peptide Bonds, J. Phys. Chem. Lett., 2018, 9, 763–767 CrossRef CAS PubMed.
- F. Zheng, F. Jiang, R. He, Y. Yang, J. Shi and W. Hong, Charge Transport through Peptides in Single–Molecule Electrical Measurements, Chin. J. Chem., 2019, 37, 1083–1096 CrossRef.
- R. Frisenda, V. A. E. C. Janssen, F. C. Grozema, H. S. J. van der Zant and N. Renaud, Mechanically controlled quantum interference in individual π-stacked dimers, Nat. Chem., 2016, 8, 1099–1104 CrossRef CAS PubMed.
- D. Nozaki, A. Lücke and W. G. Schmidt, Molecular Orbital Rule for Quantum Interference in Weakly Coupled Dimers: Low-Energy Giant Conductivity Switching Induced by Orbital Level Crossing, J. Phys. Chem. Lett., 2017, 8, 727–732 CrossRef CAS PubMed.
- S. T. Schneebeli, M. Kamenetska, Z. L. Cheng, R. Skouta, R. A. Friesner, L. Venkataraman and R. Breslow, Single-Molecule Conductance through Multiple pi-pi-Stacked Benzene Rings Determined with Direct Electrode-to-Benzene Ring Connections, J. Am. Chem. Soc., 2011, 133, 2136–2139 CrossRef CAS PubMed.
- G. C. Solomon, J. Vura-Weis, C. Herrmann, M. R. Wasielewski and M. A. Ratner, Understanding Coherent Transport through π-Stacked Systems upon Spatial Dislocation, J. Phys. Chem. B, 2010, 114, 14735–14744 CrossRef CAS PubMed.
- S. Wu, M. T. González, R. Huber, S. Grunder, M. Mayor, C. Schönenberger and M. Calame, Molecular junctions based on aromatic coupling, Nat. Nanotechnol., 2008, 3, 569–574 CrossRef CAS PubMed.
- E. W. Schlag, S.-Y. Sheu, D.-Y. Yang, H. L. Selzle and S. H. Lin, Distal charge transport in peptides, Angew. Chem., Int. Ed., 2007, 46, 3196–3210 CrossRef CAS PubMed.
- R. Frisenda, D. Stefani and H. S. J. van der Zant, Quantum Transport through a Single Conjugated Rigid Molecule, a Mechanical Break Junction Study, Acc. Chem. Res., 2018, 51, 1359–1367 CrossRef CAS PubMed.
- C. A. Martin, D. Ding, J. K. Sorensen, T. Bjornholm, J. M. van Ruitenbeek and H. S. J. van der Zant, Fullerene-based anchoring groups for molecular electronics, J. Am. Chem. Soc., 2008, 130, 13198–13199 CrossRef CAS PubMed.
- C. A. Martin, R. H. M. Smit, R. V. Egmond, H. S. J. van der Zant and J. M. van Ruitenbeek, A versatile low-temperature setup for the electrical characterization of single-molecule junctions, Rev. Sci. Instrum., 2011, 82, 053907 CrossRef PubMed.
- D. Cabosart, M. El Abbassi, D. Stefani, R. Frisenda, M. Calame, H. S. J. van der Zant and M. L. Perrin, A reference-free clustering method for the analysis of molecular break-junction measurements, Appl. Phys. Lett., 2019, 114, 143102 CrossRef.
- L. A. Zotti, B. Bednarz, J. Hurtado-Gallego, D. Cabosart, G. Rubio-Bollinger, N. Agrait and H. S. J. van der Zant, Can One Define the Conductance of Amino Acids?, Biomolecules, 2019, 9, 580 CrossRef CAS PubMed.
- V. Y. Kiselev, T. S. Andrews and M. Hemberg, Challenges in unsupervised clustering of single-cell RNA-seq data, Nat. Rev. Genet., 2019, 20, 273–282 CrossRef CAS PubMed.
- X. Y. Xiao, B. Q. Xu and N. J. Tao, Conductance titration of single-peptide molecules, J. Am. Chem. Soc., 2004, 126, 5370–5371 CrossRef CAS PubMed.
- F. Chen, X. L. Li, J. Hihath, Z. F. Huang and N. J. Tao, Effect of anchoring groups on single-molecule conductance: Comparative study of thiol-, amine-, and carboxylic-acid-terminated molecules, J. Am. Chem. Soc., 2006, 128, 15874–15881 CrossRef CAS PubMed.
- Y. S. Park, A. C. Whalley, M. Kamenetska, M. L. Steigerwald, M. S. Hybertsen, C. Nuckolls and L. Venkataraman, Contact chemistry and single-molecule conductance: A comparison of phosphines, methyl sulfides, and amines, J. Am. Chem. Soc., 2007, 129, 15768–15769 CrossRef CAS PubMed.
- A. Salomon, D. Cahen, S. Lindsay, J. Tomfohr, V. B. Engelkes and C. D. Frisbie, Comparison of electronic transport measurements on organic molecules, Adv. Mater., 2003, 15, 1881–1890 CrossRef CAS.
- B. Q. Xu and N. J. Tao, Measurement of single-molecule resistance by repeated formation of molecular junctions, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- L. A. Zotti and J. C. Cuevas, Electron Transport Through Homopeptides: Are They Really Good Conductors?, ACS Omega, 2018, 3, 3778–3785 CrossRef CAS PubMed.
- M. Kamenetska, M. Koentopp, A. C. Whalley, Y. S. Park, M. L. Steigerwald, C. Nuckolls, M. S. Hybertsen and L. Venkataraman, Formation and evolution of single-molecule junctions, Phys. Rev. Lett., 2009, 102, 126803 CrossRef CAS PubMed.
- A. I. Yanson, G. R. Bollinger, H. E. van den Brom, N. Agraït and J. M. van Ruitenbeek, Formation and manipulation of a metallic wire of single gold atoms, Nature, 1998, 395, 783 CrossRef CAS.
- M. El Abbassi, P. Zwick, A. Rates, D. Stefani, A. Prescimone, M. Mayor, H. S. J. van der Zant and D. Dulic, Unravelling the conductance path through single-porphyrin junctions, Chem. Sci., 2019, 10, 8299–8305 RSC.
- H. Dietz, F. Berkemeier, M. Bertz and M. Rief, Anisotropic deformation response of single protein molecules, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12724–12728 CrossRef CAS PubMed.
- M. Rief, M. Gautel, F. Oesterhelt, J. M. Fernandez and H. E. Gaub, Reversible unfolding of individual titin immunoglobulin domains by AFM, Science, 1997, 276, 1109–1112 CrossRef CAS PubMed.
- G. Stirnemann, D. Giganti, J. M. Fernandez and B. J. Berne, Elasticity, structure, and relaxation of extended proteins under force, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3847–3852 CrossRef CAS PubMed.
- K. A. Walther, F. Grater, L. Dougan, C. L. Badilla, B. J. Berne and J. M. Fernandez, Signatures of hydrophobic collapse in extended proteins captured with force spectroscopy, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 7916–7921 CrossRef CAS PubMed.
- J. Lin and D. N. Beratan, Tunneling while pulling: the dependence of tunneling current on end-to-end distance in a flexible molecule, J. Phys. Chem. A, 2004, 108, 5655–5661 CrossRef CAS.
- S. Y. Quek, M. Kamenetska, M. L. Steigerwald, H. J. Choi, S. G. Louie, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, Mechanically controlled binary conductance switching of a single-molecule junction, Nat. Nanotechnol., 2009, 4, 230–234 CrossRef CAS PubMed.
- I. Diez-Perez, J. Hihath, T. Hines, Z. S. Wang, G. Zhou, K. Müllen and N. Tao, Controlling single-molecule conductance through lateral coupling of π orbitals, Nat. Nanotechnol., 2011, 6, 226–231 CrossRef CAS PubMed.
- D. N. Beratan, J. N. Betts and J. N. Onuchic, Protein electron transfer rates set by the bridging secondary and tertiary structure, Science, 1991, 252, 1285–1288 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nr08556a |
| ‡ These two authors contributed equally to this work. |
| § Current address: College of Chemistry and Molecular Sciences, Wuhan University, No. 299 Bayi Road, Wuhan, Hubei, 430072, P.R. China. |
| This journal is © The Royal Society of Chemistry 2021 |