Open Access Article
Open Access ArticleQuantitative mapping of magnetic properties at the nanoscale with bimodal AFM†
Victor G.
Gisbert
 a,
Carlos A.
Amo
a,
Miriam
Jaafar
a,
Carlos A.
Amo
a,
Miriam
Jaafar
 b,
Agustina
Asenjo
b,
Agustina
Asenjo
 a and
Ricardo
Garcia
a and
Ricardo
Garcia
 *a
*a
aInstituto de Ciencia de Materiales de Madrid, CSIC, c/Sor Juana Inés de la Cruz 3, 28049 Madrid, Spain
bDepartamento de Física de la Materia Condensada and Condensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, 28049 Madrid, Spain. E-mail: r.garcia@csic.es
First published on 15th January 2021
Abstract
We demonstrate that a force microscope operated in a bimodal configuration enables the mapping of magnetic interactions with high quantitative accuracy and high-spatial resolution (∼30 nm). Bimodal AFM operation doubles the number of observables with respect to conventional magnetic force microscopy methods which enables to determine quantitatively in a single processing step several magnetic properties. The theory of bimodal AFM provides analytical expressions for different magnetic force models, in particular those characterized by power-law and exponential distance dependences. Bimodal AFM provides a self-evaluation protocol to test the accuracy of the measurements. The agreement obtained between the experiments and theory for two different magnetic samples support the application of bimodal AFM to map quantitatively long-range magnetic interactions.
1. Introduction
The emergence of hybrid materials that integrate different types of functionalities such as mechanical, electrical, magnetic, chemical or biological requires the development of quantitative, high-spatial resolution and efficient methods to map quantitatively spatial variations in the functionality or functionalities of interest. Atomic force microscopy has provided a variety of methods to map interfacial properties,1–8 among them, bimodal AFM offers a flexible platform for fast, quantitative and high-spatial resolution mapping of surfaces.9–11Bimodal AFM is based on the simultaneous excitation and detection of two cantilever modes, commonly, the first and the second modes (Fig. 1a). General descriptions about bimodal AFM operation might be found elsewhere.8,10,11 The first bimodal AFM experiments exploited the observables associated with the 2nd mode to enhance compositional contrast.12–18 A theoretical framework based on decomposing the equation of motion of the whole cantilever into the equations of motion of the excited modes19 enabled to transform the observables into mechanical properties such as the elastic modulus20,21 or viscoelastic coefficients.22,23 Thus, bimodal AFM provided high-spatial resolution and accurate nanomechanical property maps of a large variety of materials and interfaces such as proteins,11,21,24,25 DNA,26–28 cells,29,30 bone microconstituents,31 lipid bilayers,32,33 liposomes loaded with nanoparticles,34 self-assembled monolayers,35 virus,36 2D materials,37 organic crystals,38,39 solid–liquid interfaces40 and a variety of polymer surfaces.22,23,41,42
Bimodal AFM was also applied to generate material contrast images on heterogeneous samples made of regions with different electrical43–49 or magnetic properties.50–54 However, in those experiments and in particular in magnetic samples, it was not possible to determine the magnetic moment or the magnetic field of the material. The protocol and the theory to transform the bimodal observables under the interaction of a long-range electromagnetic force was not available.
Magnetic force microscopy (MFM) has been extensively applied to image magnetic nanostructures.6,55–58 The technique has experienced significant advances since the first implementations.59,60 However, the capability to combine quantitative information and high spatial resolution maps about magnetic properties remains very challenging.6
Here we demonstrate that bimodal AFM provides high-spatial resolution quantitative maps of magnetic properties. The magnetic properties of a high-density disk and a FePd film were determined with a spatial resolution of about 30 nm. Bimodal AFM provides also a self-evaluation protocol to determine the accuracy of the magnetic property maps.
The first section of the paper is devoted to introduce the theory that enables to transform the bimodal observables into magnetic properties. The generality of the theory is illustrated by proving analytical expressions for power-law and exponential magnetic interactions. The second section illustrates the capabilities of bimodal AFM to map a variety of properties such as the magnetic moment or the magnetic field. High spatial resolution (∼30 nm) maps of the magnetic properties of a hard disk drive and a FePd thin film are presented. The third section shows a self-evaluation criterion coming directly from the bimodal data to determine the accuracy of the measurement.
2 Theory of bimodal AFM for long-range magnetic interactions
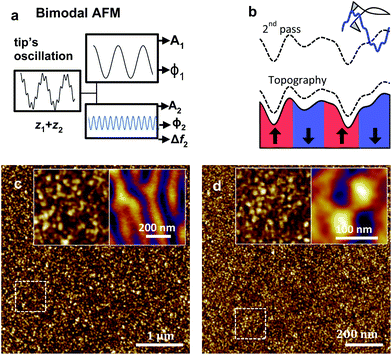
The analytical expressions that relate the magnetic parameters of a material to bimodal AFM observables are deduced by recording the changes of the amplitude A1 and phase shift ϕ1 of the first mode and the amplitude and either the phase shift ϕ2 or frequency shift Δf2 of the 2nd mode (Fig. 1a). The frequency shift Δf2 represents the shift in the resonant frequency of the second mode with respect to its free (absence of tip–sample interaction forces) resonant frequency f02. The measurements were performed with a two-pass approach (Fig. 1b), therefore, feedback controls were not applied during the recording of the observables.To relate the bimodal AFM observables with the magnetic parameters of a sample requires (i) a model of the tip–sample magnetic interaction and (ii) to solve the virial equations for the first and second mode of the cantilever. We assume that the tip–sample force dependence on the distance is known. In particular, we present the theory for two different magnetic models, a dipole (tip)-dipole (sample) model and a tip–sample transfer function model.55,56
For a dipole–dipole interaction model we assume that the dipoles are oriented perpendicular to the sample surface (Fig. 1b), then the force acting on a magnetized tip is approximated by57
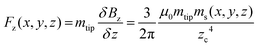 | (1) |
For a tip–sample magnetic interaction deduced by using the tip transfer-function theory55,56
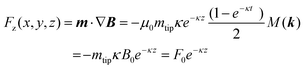 | (2) |
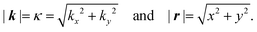 | (3) |
The second step in the development of the theory involved to apply the virial theorem to the tip's motion.61 We approximated the motion of the cantilever-tip system by the elastic beam equation of a rectangular cantilever62 and subsequently we projected the motion into the components of the excited modes by ref.63
Fts(t) + F1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πf1t) = k1/(2πf1)2 cos(2πf1t) = k1/(2πf1)2![[z with combining umlaut]](https://www.rsc.org/images/entities/i_char_007a_0308.gif) 1 + (k1/(Q12πf01))ż1 + k1z1 1 + (k1/(Q12πf01))ż1 + k1z1 | (4) |
Fts(t) + F2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πf2t) = k2/(2πf2)2 cos(2πf2t) = k2/(2πf2)2![[z with combining umlaut]](https://www.rsc.org/images/entities/i_char_007a_0308.gif) 2 + (k2/(Q22πf02))ż2 + k2z2 2 + (k2/(Q22πf02))ż2 + k2z2 | (5) |
z(t) = z0 + z1(t) + z2(t) ≈ A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πf1t − ϕ1) + A2 cos(2πf1t − ϕ1) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πf2t − ϕ2) cos(2πf2t − ϕ2) | (6) |
The amplitude of the first mode A1 is set to a fixed value Asp (set-point amplitude) which is lower than the free amplitude A01 during the measurement of the topography. To facilitate the deduction of analytical expressions, we assume that the value of A2 is much smaller than the value of A1 and z0 is negligible with respect to both A1 and A2.
To relate the observables with the tip–sample force we applied the virial Vi equations19,21 to the excited modes
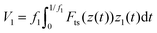 | (7) |
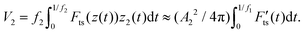 | (8) |
The above equations can be resolved in terms of the observables without knowing the explicit expression of the interaction force. This was accomplished by integrating the equation of motion of the modes over a period.19,21
For a bimodal AFM configuration characterized by a single amplitude modulation feedback loop acting on the 1st mode, the virials V1 and V2 are determined by
V1 = −((k1A1A01)/(2Q1))cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ1 ϕ1 | (9) |
V2 = −((k2A2A02)/(2Q2))cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ2. ϕ2. | (10) |
For a bimodal AFM configuration that incorporates two feedback loops; an amplitude modulation feedback loop acting on the 1st mode and a phase-locked loop to track the shift of the resonant frequency of the second mode (ϕ2 = π/2)64, V2 is obtained by
| V2 = −k2A22Δf2/f02. | (11) |
By combining eqn (1), (9) and (11), the sample magnetic moment (dipole–dipole interaction) is given by
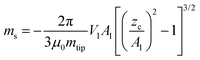 | (12) |
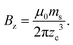 | (13) |
The mean distance zc might be determined from the bimodal AFM observables as
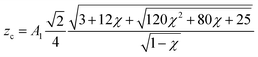 | (14) |
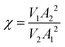 | (15) |
For the tip transfer-function model (eqn (2)), the virials Vi are given by
| V1(zc) = −F0e−κzcA1I1(κA1)I0(κA2) | (16) |
| V2(zc) = −F0e−κzcA2I1(κA2)I0(κA1) | (17) |
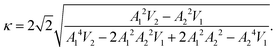 | (18) |
Once the magnetization wave number is known, the magnetic field at a given distance from the surface is obtained by
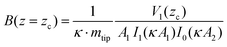 | (19) |
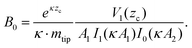 | (20) |
3 Materials and methods
3.1 Bimodal AFM set-up and magnetic property mapping
We developed a custom-made code to process the bimodal AFM data. The code was incorporated into a commercial AFM (Cypher S, Asylum Research-Oxford Instruments). To separate the magnetic interactions from the topography of the samples, we applied a two-pass method65 (the so called lift-mode). In first pass the topography of the sample along a given line was obtained. Immediately afterwards, the tip was lifted some distance from the surface and displaced over the same line by following the topography profile (2nd pass) (Fig. 1b). The lift height was about 2 nm on the HDD and 20 nm on the FePd film. Those values were chosen to maximize the magnetic contrast of the observables of the 2nd mode.In bimodal AFM, the first and second mode of the cantilever are excited and detected at the same time. The amplitudes of A1 and A2 used here were, respectively, in the 7–42 nm and 1–10 nm ranges (see figure captions for specific details). To detect frequency shifts associated with the 2nd mode requires the use of a phase-locked loop to keep at 90° the phase shift between the excitation signal and the cantilever-tip response.
The two-pass method did not suppress completely the influence of non-magnetic long-range interactions such as van der Waals or electrostatic forces. In fact, in our experiments those long-range interactions were comparable to the magnetic interaction. Several procedures have been developed in MFM to remove non-magnetic effects from the data.50,66,67 Here we developed a method to separate the magnetic force from non-magnetic long-range forces especially suited for bimodal AFM operation. The method is based on the additive character of the forces and the virials. It has three main steps.
First, in the case that the force acting on the tip has different origins, for example, Fm (magnetic) and Fnm (non-magnetic), the virial of mode i satisfies
| Vi = Vim + Vinm. | (21) |
Second, we proceed to determine the contribution of the non-magnetic forces in the virials. This was achieved by calculating the average value of the virial in the map,
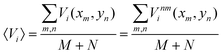 | (22) |
| 〈Vim〉 = 0. | (23) |
Over a large region of the HDD, the virials of the up domains are cancelled by the virials of the down domains. The FePd film was measured on the demagnetized state, therefore the number of up regions coincide with the number of down regions.
Third, a new set of virial maps is generated by using
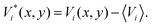 | (24) |
Finally, the new virials are introduced into the eqn (9), (10), (11), (16) and (17).
3.2 Magnetic samples
Two different magnetic samples were used in this work. A commercial high-density disk (HDD) from Toshiba (Japan) made of a CoCrPt alloy with perpendicular anisotropy. The HDD was pre-patterned with 50 nm bits. The other sample was a FePd thin film (40 nm) grown by sputtering on a MgO substrate at room temperature. The FePd sample, demagnetized before the experiments, presented a stripe domain configuration.68 The magnetic moment of the stripes was aligned perpendicular to the surface. The comparison with the topographic images (Fig. 1c and d) illustrates the absence of any correlation between topography images and magnetic property maps.3.3 Cantilever type and calibration
SSS-MFMR (Nanosensors, Germany) cantilevers with f1 = 75 kHz, k1 = 2.8 N m−1, Q1 = 160, f2 = 400 kHz, k2 = 90 Nm−1, Q2 = 400, were used to image the magnetic samples. The tip had a hard magnetic coating and a radius of curvature <15 nm. The coating is characterized by magnetization of mtip ≈ 2.5 × 10−14 emu and a coercivity ≈125 Oe. Before performing the bimodal AFM experiments, the tip was magnetized by using of a strong permanent magnet.Quantitative property mapping by bimodal AFM operation required to calibrate the force constant of the excited modes.69 The force constant of the first mode was calibrated using the multiple reference calibration method.70 This method avoided the mechanical contact between the tip and the sample during the calibration. The second mode of the cantilever was calibrated by using the stiffness-frequency power law relationship, k2 = k1(f2/f1)ζ2, where ζ2 is an experimental calibration parameter.71
3.4 Definition of material contrast
The material contrast of a given observable was defined as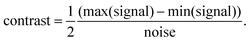 | (25) |
The signal was measured as the peak-to-peak difference over two consecutive magnetic domains. The noise was measured by calculating the standard deviation on an area of the map that has a constant value of the magnetic field.
4. Results and discussion
The accuracy and the spatial resolution capabilities of bimodal AFM were tested on the HDD and the FePd film. A quick comparison between the AFM topographic and the magnetic images (Fig. 1c and d) revealed the absence of any correlation. To determine the magnetic properties of the sample required a model of the probe magnetization. Here, the tip is considered to have a net magnetic moment mtip. The tip–sample magnetic interaction transfer function model proposed by Hug et al. is considered the most suitable theoretical framework to describe MFM experiments at the nanoscale.55,56 Therefore, the experiments are explained by using the theory of bimodal AFM for interactions characterized by an exponential dependence on the tip–sample distance. In this model, the force exerted by the sample's stray magnetic field in the perpendicular direction is determined in the Fourier space by introducing magnetization wave number k(x,y).4.1 Bimodal AFM mapping of magnetic properties
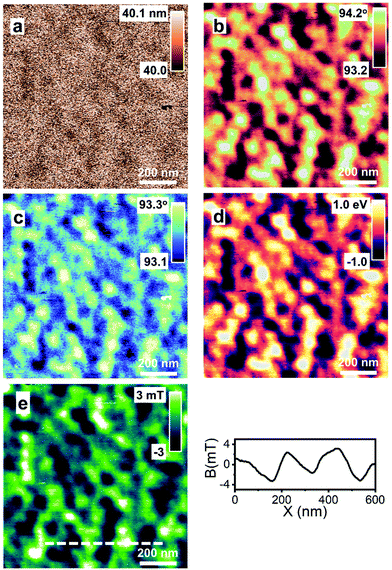
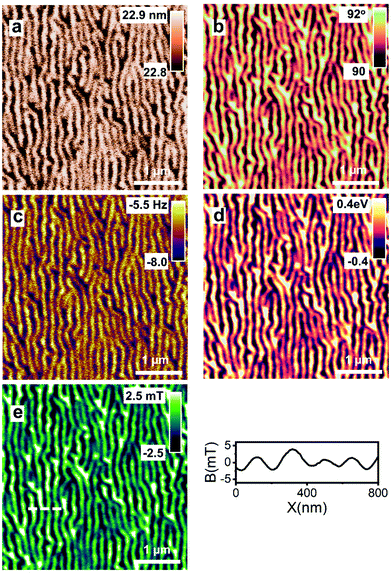
Fig. 2a–d shows the maps of the A1, ϕ1, ϕ2 and V1 obtained on the HDD sample at zc = 45 nm. The maps revealed the same magnetic domain structure. The magnetic contrast depended on the observable. The contrast for A1 and ϕ1 was, respectively, 1.8 and 4.3 while Δf2 and V1 gave a contrast of 1.3 and 4.5. A map of the magnetic field is shown in Fig. 2e. The cross-section showed the variations of the magnetic field along the dashed line. It oscillated between −3.7 and 3.8 mT.Fig. 3 shows the maps of the A1, ϕ1 and Δf2 and V1 obtained on the FePd film at zc = 42 nm. The maps revealed the longitudinal character of the magnetic domains. The contrast obtained in the ϕ1(x,y) and V1(x,y) maps was, respectively, of 9.8; V2(x,y) and Δf2(x, y) have a contrast of 3. However, the magnetic domain structure seems identical. The map of the stray magnetic field (zc = 42 nm) varied between −3 and 3 mT (Fig. 3e). By changing the lift value, it is possible to determine the maps at other distances.
4.2 Self-evaluation criterion
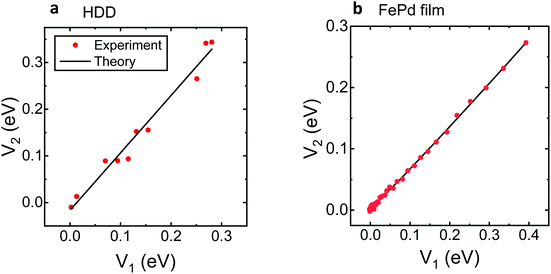
Bimodal AFM offers a self-evaluation criterion to verify whether the quantitative data obtained on the sample's magnetic properties do represent the real properties of the sample. The criterion comes from the bimodal AFM equations (see section 2). The theory shows the cross-representation of the virials V1 and V2 should follow a straight line if the magnetic interaction is dominated by an exponentially decaying force. Therefore, the accuracy of the magnetic field maps might be determined by plotting the experimental dependence of V2versus V1. If the cross-representation of the virials departs significantly from a straight line, it should be concluded that the model applied in bimodal to transform the observables into magnetic properties was not appropriate.Fig. 4 shows the cross-representations of the virials of the excited modes for the HDD and FePd film samples. Both samples, and in particular the FePd film, follow a straight line as predicted by the theory. These results underlined that the approximations used to develop the bimodal AFM theory are fully consistent with the experimental data.
5 Conclusions
Bimodal AFM has expanded the quantitative characterization of materials at the nanoscale by providing high resolution maps of magnetic parameters. Bimodal AFM generates quantitative 2D maps of the magnetic moment and the magnetic field created by a magnetized sample with high quantitative accuracy. We have developed the theory of bimodal AFM to transform the observables into magnetic parameters in terms of the tip transfer function model. This theory enables the mapping of the sample's magnetic properties at different tip–sample distances. The accuracy and spatial resolution has been tested on a hard disk drive and FePd thin film samples. In both cases, the bimodal AFM observables provided high-spatial resolution maps of the magnetic domain structure.The bimodal AFM has two key features that are not found in any other magnetic force microscopy method. First, it is efficient. It just requires the recording of four data points per pixel to generate several magnetic property maps. Second, it provides a criterion to determine whether the measured magnetic property map gives a faithful characterization of the sample. To our best knowledge, this self-evaluation criterion is unique to bimodal AFM.
In summary, this contribution expands the quantitative characterization capabilities of bimodal force microscopy by providing a robust, reliable and high spatial resolution method to measure magnetic properties.
Author contributions
VGG performed the experiments and developed the bimodal AFM code. CAA developed the bimodal AFM theory. VGG and RG adapted the theory for magnetic property mapping and developed the self-evaluation criterion. AA and MJ provided the magnetic samples and performed additional macroscopic magnetic property measurements. RG conceived the project and wrote the manuscript. All the authors discussed the data and revised the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support from the Ministerio de Ciencia, Innovación y Universidades (PID2019-106801GB-I00; PID2019-108075RB-C31; MAT2016-76507-R) and Comunidad de Madrid (SI1/PJI/2019-00055) are acknowledged.References
- R. Garcia and E. T. Herruzo, Nat. Nanotechnol., 2012, 7, 217–226 CrossRef CAS.
- S. Zhang, H. Aslan, F. Besenbacher and M. Dong, Chem. Soc. Rev., 2014, 43, 7412–7429 RSC.
- Y. F. Dufrêne, T. Ando, R. Garcia, D. Alsteens, D. Martinez-Martin, A. Engel, C. Gerber and D. J. Muller, Nat. Nanotechnol., 2017, 12, 295–307 CrossRef.
- L. Collins, J. I. Kilpatrick, S. V. Kalinin and B. J. Rodriguez, Rep. Prog. Phys., 2018, 81, 086101 CrossRef.
- D. Wang and T. P. Russell, Macromolecules, 2018, 51, 3–24 CrossRef CAS.
- O. Kazakova, R. Puttock, C. Barton, H. Corte-León, M. Jaafar, V. Neu and A. Asenjo, J. Appl. Phys., 2019, 125, 060901 CrossRef.
- G. Stan and S. W. King, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2020, 38, 060801 CAS.
- R. Garcia, Chem. Soc. Rev., 2020, 49, 5850–5884 RSC.
- T. R. Rodriguez and R. Garcia, Appl. Phys. Lett., 2004, 84, 449–451 CrossRef CAS.
- R. Garcia and R. Proksch, Eur. Polym. J., 2013, 49, 1897–1906 CrossRef CAS.
- S. Benaglia, V. G. Gisbert, A. P. Perrino, C. A. Amo and R. Garcia, Nat. Protoc., 2018, 13, 2890–2907 CrossRef CAS.
- R. Proksch, Appl. Phys. Lett., 2006, 89, 113121 CrossRef.
- N. F. Martinez, S. Patil, J. R. Lozano and R. Garcia, Appl. Phys. Lett., 2006, 89, 153115 CrossRef.
- S. Patil, N. F. Martinez, J. R. Lozano and R. Garcia, J. Mol. Recognit., 2007, 20, 516–523 CrossRef CAS.
- S. D. Solares and G. Chawla, Meas. Sci. Technol., 2010, 21, 125502 CrossRef.
- D. Ebeling, B. Eslami and S. D. J. Solares, ACS Nano, 2013, 7, 10387–10396 CrossRef CAS.
- S. An, S. D. Solares, S. Santos and D. Ebeling, Nanotechnology, 2014, 25, 475701 CrossRef.
- S. Santos, C. Y. Lai, T. Olukan and M. Chiesa, Nanoscale, 2017, 9, 5038–5043 RSC.
- J. R. Lozano and R. Garcia, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 014110 CrossRef.
- A. Labuda, M. Kocuń, W. Meinhold, D. Walters and R. Proksch, Beilstein J. Nanotechnol., 2016, 7, 970–982 CrossRef CAS.
- C. A. Amo, A. P. Perrino, A. F. Payam and R. Garcia, ACS Nano, 2017, 11, 8650–8659 CrossRef CAS.
- E. T. Herruzo, A. P. Perrino and R. Garcia, Nat. Commun., 2014, 5, 1–8 Search PubMed.
- S. Benaglia, C. A. Amo and R. Garcia, Nanoscale, 2019, 11, 15289–15297 RSC.
- D. Martinez-Martin, E. T. Herruzo, C. Dietz, J. Gomez-Herrero and R. Garcia, Phys. Rev. Lett., 2011, 106, 198101 CrossRef CAS.
- G. Lamour, C. K. Yip, H. Li and J. Gsponer, ACS Nano, 2014, 8, 3851–3861 CrossRef CAS.
- C. Y. Lai, S. Santos and M. Chiesa, ACS Nano, 2016, 10, 6265–6272 CrossRef CAS.
- C.-Y. Y. Lai, S. Perri, S. Santos, R. Garcia and M. Chiesa, Nanoscale, 2016, 8, 9688–9694 RSC.
- M. Kocun, A. Labuda, W. Meinhold, I. Revenko and R. Proksch, ACS Nano, 2017, 11, 10097–10105 CrossRef CAS.
- A. X. Cartagena-Rivera, W. H. Wang, R. L. Geahlen and A. Raman, Sci. Rep., 2015, 5, 11692 CrossRef CAS.
- D. Guan, E. Charlaix, R. Z. Qi and P. Tong, Phys. Rev. Appl., 2017, 8, 044010 CrossRef.
- Y. Sun, L. H. Vu, N. Chew, Z. Puthucheary, M. E. Cove and K. Zeng, ACS Biomater. Sci. Eng., 2019, 5, 478–486 CrossRef CAS.
- Z. Al-Rekabi and S. Contera, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2658–2663 CrossRef CAS.
- W. Trewby, J. Faraudo and K. Voïtchovsky, Nanoscale, 2019, 11, 4376–4384 RSC.
- M. E. F. Brollo, A. Domínguez-Bajo, A. Tabero, V. Domínguez-Arca, V. Gisbert, G. Prieto, C. Johansson, R. Garcia, A. Villanueva, M. C. Serrano and M. del P. Morales, ACS Appl. Mater. Interfaces, 2020, 12, 4295–4307 CrossRef.
- E. N. Athanasopoulou, N. Nianias, Q. K. Ong and F. Stellacci, Nanoscale, 2018, 10, 23027–23036 RSC.
- I. González-Domínguez, S. Gutiérrez-Granados, L. Cervera, F. Gòdia and N. Domingo, Biophys. J., 2016, 111, 1173–1179 CrossRef.
- Y. Li, C. Yu, Y. Gan, P. Jiang, J. Yu, Y. Ou, D.-F. Zou, C. Huang, J. Wang, T. Jia, Q. Luo, X.-F. Yu, H. Zhao, C.-F. Gao and J. Li, npj Comput. Mater., 2018, 4, 49 CrossRef.
- R. Giridharagopal, L. Q. Flagg, J. S. Harrison, M. E. Ziffer, J. Onorato, C. K. Luscombe and D. S. Ginger, Nat. Mater., 2017, 16, 737–742 CrossRef CAS.
- M. F. Dupont, A. Elbourne, E. Mayes and K. Latham, Phys. Chem. Chem. Phys., 2019, 21, 20219–20224 RSC.
- E. T. Herruzo, H. Asakawa, T. Fukuma and R. Garcia, Nanoscale, 2013, 5, 2678–2685 RSC.
- H. K. Nguyen, M. Ito and K. Nakajima, Jpn. J. Appl. Phys., 2016, 55, 08NB06 CrossRef.
- A. Bubendorf, S. Walheim, T. Schimmel and E. Meyer, Beilstein J. Nanotechnol., 2018, 9, 1–10 CrossRef CAS.
- R. W. Stark, N. Naujoks and A. Stemmer, Nanotechnology, 2007, 18, 065502 CrossRef.
- U. Bostanci, M. K. Abak, O. Aktaş and A. Dâna, Appl. Phys. Lett., 2008, 92, 093108 CrossRef.
- X. D. Ding, J. An, J. B. Xu, C. Li and R. Y. Zeng, Appl. Phys. Lett., 2009, 94, 223109 CrossRef.
- H. T. Thompson, F. Barroso-Bujans, J. G. Herrero, R. Reifenberger and A. Raman, Nanotechnology, 2013, 24, 135701 CrossRef.
- S. Kawai, F. F. Canova, T. Glatzel, T. Hynninen, E. Meyer and A. S. Foster, Phys. Rev. Lett., 2012, 109, 146101 CrossRef.
- N. Liu, R. Dittmer, R. W. Stark and C. Dietz, Nanoscale, 2015, 7, 11787–11796 RSC.
- J. L. Garrett, M. S. Leite and J. N. Munday, ACS Appl. Mater. Interfaces, 2018, 10, 28850–28859 CrossRef CAS.
- J. W. Li, J. P. Cleveland and R. Proksch, Appl. Phys. Lett., 2009, 94, 163118 CrossRef.
- C. Dietz, E. T. Herruzo, J. R. Lozano and R. Garcia, Nanotechnology, 2011, 22, 125708 CrossRef.
- J. Schwenk, M. Marioni, S. Romer, N. R. Joshi and H. J. Hug, Appl. Phys. Lett., 2014, 104, 112412 CrossRef.
- J. Schwenk, X. Zhao, M. Bacani, M. A. Marioni, S. Romer and H. J. Hug, Appl. Phys. Lett., 2015, 107, 132407 CrossRef.
- L. Stühn, J. Auernhammer and C. Dietz, Sci. Rep., 2019, 9, 17755 CrossRef.
- H. J. Hug, B. Stiefel, P. J. A. Van Schendel, A. Moser, R. Hofer, S. Martin, H. J. Güntherodt, S. Porthun, L. Abelmann, J. C. Lodder, G. Bochi and R. C. O'Handley, J. Appl. Phys., 1998, 83, 5609–5620 CrossRef CAS.
- E. Meyer, H. J. Hug and R. Bennewitz, Scanning Probe Microscopy: Lab on a tip, Springer-Verlag, Berlin, 2004 Search PubMed.
- U. Hartmann, Annu. Rev. Mater. Sci., 1999, 29, 53–87 CrossRef CAS.
- A. Schwarz and R. Wiesendanger, Nano Today, 2008, 3, 28–39 CrossRef CAS.
- Y. Martin and H. K. Wickramasinghe, Appl. Phys. Lett., 1987, 50, 1455–1457 CrossRef.
- J. J. Sáenz, N. Garcia, P. Grütter, E. Meyer, H. Heinzelmann, R. Wiesendanger, L. Rosenthaler, H. R. Hidber and H. J. Güntherodt, J. Appl. Phys., 1987, 62, 4293–4295 CrossRef.
- A. San Paulo and R. Garcia, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 193411 CrossRef.
- T. R. Rodriguez and R. Garcia, Appl. Phys. Lett., 2002, 80, 1646–1648 CrossRef CAS.
- J. R. Lozano and R. Garcia, Phys. Rev. Lett., 2008, 100, 076102 CrossRef.
- S. Kawai, T. Glatzel, S. Koch, B. Such, A. Baratoff and E. Meyer, Phys. Rev. Lett., 2009, 103, 220801 CrossRef.
- S. Hosaka, A. Kikukawa, Y. Honda, H. Koyanagi and S. Tanaka, Jpn. J. Appl. Phys., 1992, 31, L904–L907 CrossRef CAS.
- M. Jaafar, O. Iglesias-Freire, L. Serrano-Ramón, M. R. Ibarra, J. M. de Teresa and A. Asenjo, Beilstein J. Nanotechnol., 2011, 2, 552–560 CrossRef CAS.
- X. Zhao, J. Schwenk, A. O. Mandru, M. Penedo, M. Baćani, M. A. Marioni and H. J. Hug, New J. Phys., 2018, 20, 013018 CrossRef.
- A. Asenjo, J. M. García, D. García, A. Hernando, M. Vázquez, P. A. Caro, D. Ravelosona, A. Cebollada and F. Briones, J. Magn. Magn. Mater., 1999, 196–197, 23–25 CrossRef CAS.
- J. R. Lozano, D. Kiracofe, J. Melcher, R. Garcia and A. Raman, Nanotechnology, 2010, 21, 465502 CrossRef.
- J. E. Sader, R. Borgani, C. T. Gibson, D. B. Haviland, M. J. Higgins, J. I. Kilpatrick, J. Lu, P. Mulvaney, C. J. Shearer, A. D. Slattery, P.-A. Thorén, J. Tran, H. Zhang, H. Zhang and T. Zheng, Rev. Sci. Instrum., 2016, 87, 093711 CrossRef.
- A. Labuda, M. Kocun, M. Lysy, T. Walsh, J. Meinhold, T. Proksch, W. Meinhold, C. Anderson and R. Proksch, Rev. Sci. Instrum., 2016, 87, 073705 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Data to illustrate the self-evaluation protocol. See DOI: 10.1039/d0nr08662b |
| This journal is © The Royal Society of Chemistry 2021 |