Open Access Article
Open Access ArticleMachine learning and materials modelling interpretation of in vivo toxicological response to TiO2 nanoparticles library (UV and non-UV exposure)†
Susana I. L.
Gomes‡
 a,
Mónica J. B.
Amorim‡
a,
Mónica J. B.
Amorim‡
 *a,
Suman
Pokhrel
*a,
Suman
Pokhrel
 bc,
Lutz
Mädler
bc,
Lutz
Mädler
 bc,
Matteo
Fasano
bc,
Matteo
Fasano
 d,
Eliodoro
Chiavazzo
d,
Eliodoro
Chiavazzo
 d,
Pietro
Asinari
d,
Pietro
Asinari
 de,
Jaak
Jänes
f,
Kaido
Tämm
de,
Jaak
Jänes
f,
Kaido
Tämm
 f,
Jaanus
Burk
f and
Janeck J.
Scott-Fordsmand
g
f,
Jaanus
Burk
f and
Janeck J.
Scott-Fordsmand
g
aDepartment of Biology & CESAM, University of Aveiro, 3810-193 Aveiro, Portugal. E-mail: mjamorim@ua.pt
bDepartment of Production Engineering, University of Bremen, Badgasteiner Str. 1, 28359 Bremen, Germany
cLeibniz Institute for Materials Engineering IWT, Badgasteiner Str. 3, 28359 Bremen, Germany
dEnergy Department, Politecnico di Torino, Corso Duca degli Abruzzi 24, Torino 10129, Italy
eINRIM, Istituto Nazionale di Ricerca Metrologica, Strada delle Cacce 91, Torino 10135, Italy
fDepartment of Chemistry, University of Tartu, Ravila 14a, Tartu 50411, Estonia
gDepartment of Bioscience, Aarhus University, Vejlsovej 25, PO BOX 314, DK-8600 Silkeborg, Denmark
First published on 19th August 2021
Abstract
Assessing the risks of nanomaterials/nanoparticles (NMs/NPs) under various environmental conditions requires a more systematic approach, including the comparison of effects across many NMs with identified different but related characters/descriptors. Hence, there is an urgent need to provide coherent (eco)toxicological datasets containing comprehensive toxicity information relating to a diverse spectra of NPs characters. These datasets are test benches for developing holistic methodologies with broader applicability. In the present study we assessed the effects of a custom design Fe-doped TiO2 NPs library, using the soil invertebrate Enchytraeus crypticus (Oligochaeta), via a 5-day pulse via aqueous exposure followed by a 21-days recovery period in soil (survival, reproduction assessment). Obviously, when testing TiO2, realistic conditions should include UV exposure. The 11 Fe–TiO2 library contains NPs of size range between 5–27 nm with varying %Fe (enabling the photoactivation of TiO2 at energy wavelengths in the visible-light range). The NPs were each described by 122 descriptors, being a mixture of measured and atomistic model descriptors. The data were explored using single and univariate statistical methods, combined with machine learning and multiscale modelling techniques. An iterative pruning process was adopted for identifying automatically the most significant descriptors. TiO2 NPs toxicity decreased when combined with UV. Notably, the short-term water exposure induced lasting biological responses even after longer-term recovery in clean exposure. The correspondence with Fe-content correlated with the band-gap hence the reduction of UV oxidative stress. The inclusion of both measured and modelled materials data benefitted the explanation of the results, when combined with machine learning.
1. Introduction
Ecotoxicological studies with nanomaterials (NMs)/nanoparticles (NPs) are still mostly focused on testing one or few NMs at a time, with the few studies testing a range of materials dealing almost exclusively with in vitro embedded cells.1–3 Obviously, this shows the need to explore a more systematic approach where advanced toxicity measures are compared across many NMs with highly identified characters/descriptors. Attempts have been made to apply various Quantitative Structure–Activity Relationship (QSAR) models to nanotoxicology data, i.e., to relate a set of descriptors characterizing the NMs/NPs with their measured biological effects (e.g. ref. 4–7). Most of these studies deal with cells or unicellular organisms, although some studies deal with higher organisms.8–13 Collectively, the trans-material studies that have been performed confirm the logic that NMs specific characters indeed are important for NM toxicity (e.g. ref. 14). The trans-material studies are mainly (with few exceptions) based on correlating toxicity measures to a few commonly measurable descriptors, i.e. size (TEM/DLS based), zeta potential (usually in pure water), surface charge (few studies), and dissolution rate (for specific metal based materials). However, there is a wealth of other characters (or descriptors) available for the NM, i.e. either from directly measurable (e.g. energy bands), from simply calculable (e.g. particle number), or from more advance atomistic modelling (e.g. atomic bond length) (e.g. ref. 6 and 15).The novel descriptors can obviously enable a better explanation of the biological effects, however they will also require the use of more advanced data-analytical methods including atomistic and multiscale modelling, possibly supported by machine learning techniques to identify patterns otherwise hidden (e.g. ref. 16–19). To study the integration of more advanced NM descriptors with biological measures, the best approach (i.e. balancing between material diversity and explainable variation) would be to use materials that somehow have similar but yet distinct traits. A custom designed NM library offers this opportunity, to test the hypothesis relating effects to particles characters’. Among this, the TiO2 NPs library (containing pure and Fe doped NPs) is a candidate which covers a wide spectrum of properties (e.g., size, crystal structure, %Fe, band gap energy), while keeping others constant. That is done by doping the TiO2 NPs with Fe, the band gap energy decreases, which enables the photoactivation of the TiO2 at wavelength close to the visible light range, thus allowing a more effective use of TiO2 photocatalytic properties (i.e., under solar light). We here employ a library of such doped TiO2 materials that have been extensively characterized. The characterizations include crystal structure (XRD), specific surface area (BET), transmission electron microscopic (TEM) imaging, NPs band gap energy (UV-visible spectroscopy), photo-oxidation capability (fluorimetric analysis) and reactive oxygen species (ROS) generation, hydroxyl radical generation (electron paramagnetic resonance (EPR)), hydrodynamic size and zeta potential measurements (DLS). Further, a similar Fe doped TiO2 NPs library was tested in vitro (mammalian cell model, RAW 264.7 and leukemic HL60) and in unicellular models.20–22 George et al.20 observed an increase in cytotoxicity, accompanied by increased mitochondrial superoxide generation and decrease in mitochondrial membrane potential, under near-visible light, dependent on the increase in Fe content (1 to 10%). Huang et al.22 showed that the effect was dependent on %Fe increase under light (light emitting diodes (LED) light). Yadav et al.21 investigated, at a fluorescent light (with 10 times lower intensity in comparison to ref. 22), Fe–TiO2 NPs, which enhanced photocatalytic inactivation of the bacteria Escherichia coli and Staphylococcus aureus.21 As mentioned, similar studies in vivo whole organism are absent (i.e. multicellular).
In the present study, we investigate the in vivo toxicity across this Fe-doped TiO2 NPs library using 11 TiO2 materials. Since band-gap is a prominent feature for these TiO2 materials, the effects of TiO2 NPs were assessed under UV and non-UV (fluorescent) light. These materials were tested using an important soil representative model worm species, Enchytraeus crypticus (Oligochaeta),23,24 assessing survival and reproductive output. Enchytraeids are the most important organisms in many habitats, dominant both in biomass and abundance,25 ranging between 102–105 individuals per m2. The testing resulted in 22 in vivo concentration-response experiments, leading to 44 population measures. In addition, besides the material descriptors (also measured in this study) we include both simply calculable and advanced atomistic modelled material descriptors, reaching 122 NP related characters/descriptors for each NP.
2. Results
2.1. Materials characterisation
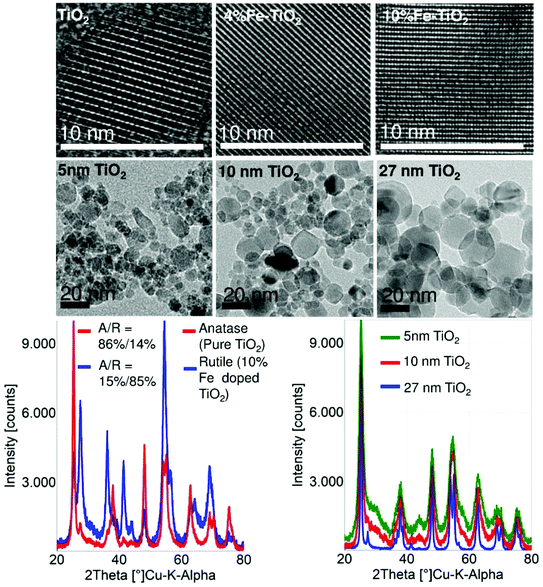
TEM results confirmed the indistinguishable crystalline morphology of the pure and Fe-doped TiO2 particles in the range of 9–20 nm, i.e., Fe is homogeneously distributed within the crystalline TiO2 matrix. The highly crystalline nature of these particles was also confirmed by HRTEM and XRD (Fig. 1, for further details see ref. 20).Fe doping of TiO2 has additional effects besides the anticipated band gap engineering: (1) the equivalent primary particle size (dBET) and the crystallite size (dXRD) decrease and (2) the anatase to rutile ratio decreases with an increase in Fe loading (0–10%), see Table 2. UV-visible spectra were recorded for pure and Fe-doped TiO2 nanoparticles in order to demonstrate the lowering of the band gap energy after Fe doping. The band gap energy (Eg) values for undoped and Fe-doped TiO2 nanoparticles range from 3.3 to 2.8 eV (Table 2). DLS results showed a decrease of agglomerate size with the increasing Fe content (Table 2). The ζ-potential measurement showed an increase in the negative surface charge in Fe-doped TiO2 (Table 2). This indicates that the electrostatic repulsive force contributes to the reduction in the agglomeration size of Fe-doped TiO2.
2.2. Materials modelling
The calculated 86 all-atom full-particle nanodescriptors (Table S1†) describe the core and surface regions of the NPs. These descriptors cover total number of atoms (both Ti and Fe), NP size, surface area and volume of the particles, potential energy of the atoms in various regions, coordination numbers, lattice energies, length of force vectors and dipole moments.2.3. Exposure characterization
The exposure characterisation via DLS (Table S1†) shows that there is a high degree of agglomeration in the system, but it was not possible to identify a clear relationship between the particle descriptors and the hydrodynamic size distribution (DLS measure).The zeta potential showed that with increasing concentrations there was an increase in stability i.e. a lower zeta potential. There was generally lower zeta potential for non-UV exposure samples than for UV exposed samples.
2.4. Biological measures (survival and reproduction)
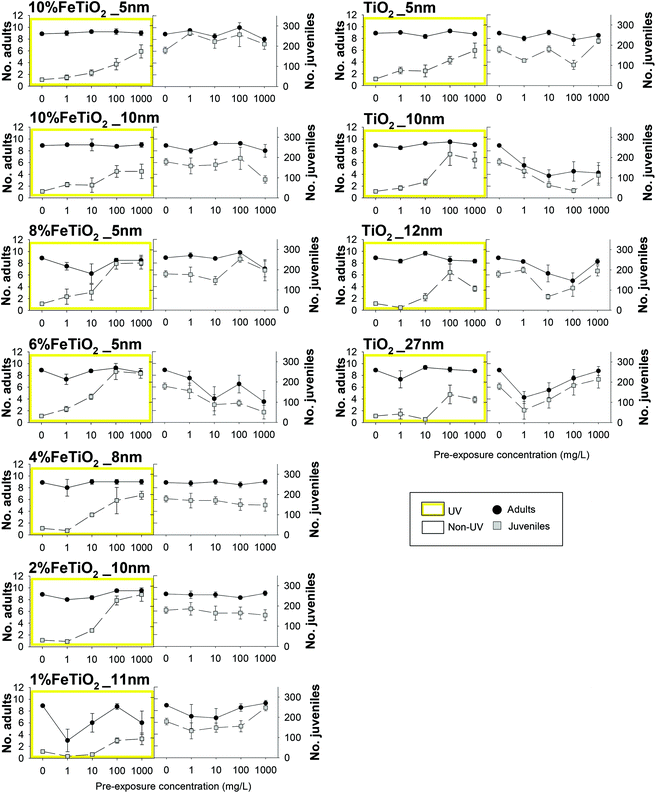
The exposure in ISO water in controls had a survival >80% (controls non-UV and UV). The pH of the test media was 6.7 ± 0.1 in all treatments, without significant change over the test duration.Survival was not affected during the 5 days of exposure in ISO water for all treatments. For the subsequent 21 days in clean LUFA 2.2 soil, survival and reproduction varied with material and UV exposure (Fig. 2), from no apparent impact (e.g. non-UV 4%FeTiO2_8 nm) to clear dose–response (e.g. non-UV 6%FeTiO2_5 nm). When under UV exposure it showed several cases where the impact was reduced with increasing concentration.
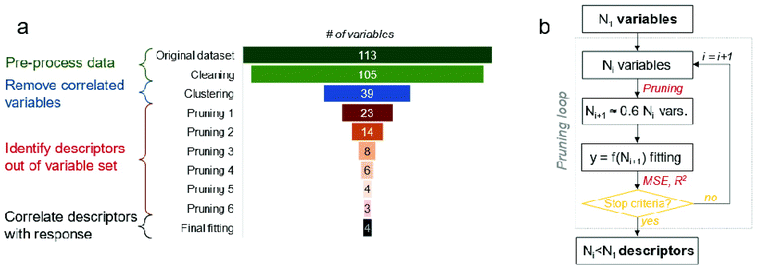
Starting from the initial amount of N = 113 variables (x1, x2, …, x113), the data cleaning process reduced this number to N = 105 for both datasets. After that, the hierarchical clustering algorithm identified the variables showing the highest similarity in terms of Spearman's correlation coefficient (see Fig. S4 and S5† for the non-UV and UV case, respectively), grouping them into clusters according to a pair-wise rationale. This algorithm has highlighted the presence of 39 clusters of similar (i.e., correlated) variables for the non-UV experiments, while 40 for the UV ones. The clustering of variables operated by the algorithm is both quantitatively and qualitatively robust. From one side, the obtained high value of cophenetic correlation coefficient (0.72 for the non-UV and 0.74 for the UV case) and Spearman's correlation coefficients between the pairs of variables within each cluster (0.63 or above for both non-UV and UV case, see Fig. S6 and S7,† respectively) are indicators of good clustering accuracy. From the other side, the clusters of variables listed in Tables S2 and S3† are also reasonable from a qualitative perspective, for instance: cluster #1 includes both the percent concentration of iron and titanium, which are complementary between each other; cluster #11 groups all the modelling variables related to the number of Ti and O atoms in the core and shell of particles, which clearly depend on the unit cell of crystal; cluster #14 groups the computed lattice energy of particles normalized by their radius, surface, or volume. Interestingly, the only different clusters in the two datasets are due to the Polydispersity Index (PDI) and average size of particle aggregates from DLS measures, whose values appear to be correlated between each other when solutions are not exposed to UV whereas they become uncorrelated under UV light.
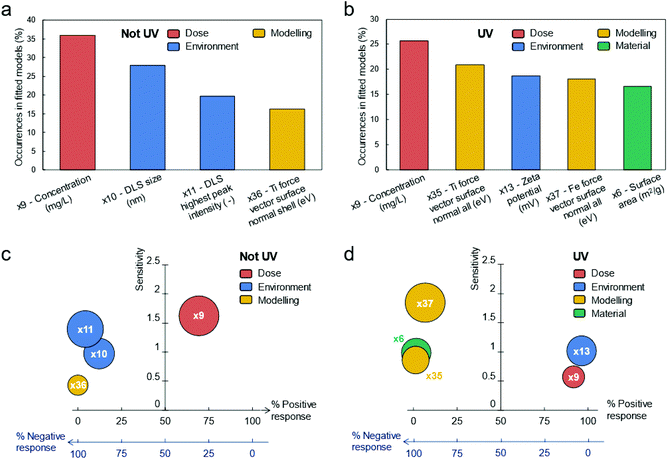
The representative variables nominated per each cluster are listed in Tables S4 and S5.† Then, those variables (39 for the non-UV and 40 for the UV case) have been pruned iteratively following the algorithm depicted in Fig. 5b. Several rounds of pruning were carried out, until one of the chosen stopping criteria was met (see Fig. S8 and ESI Movies S1 and S2† for a dynamic overview of the process). This was achieved at the 7th round for the experiments without UV exposure and at the 6th round for the experiments with UV exposure. The variables remaining after the pruning process can be considered as significant descriptors of the biological mechanism to the tested TiO2 particles. Notice that the descriptors of the toxicological responses for TiO2 particles have been analysed separately for UV and non-UV exposure, since they can be governed by different biological pathways (due to interaction between UV and TiO2); however, multi-output model fitting27–32 could be also used when more homogeneous mechanisms underlying the toxicological response are present in the dataset analysed. As reported in Fig. 3a, the four descriptors identified in case of no exposure to UV are (sorted by per cent occurrence in the best fitting functions found by the symbolic regressor): concentration; average size of particle aggregates from DLS measures; highest peak intensity from DLS measures; normal surface force vector of Ti atoms in the particle shell. The five descriptors of biological response experiments under the UV lights are listed instead in Fig. 3b, being: concentration; normal surface force vector of Ti atoms in the whole particle; zeta potential; normal surface force vector of Fe atoms in the whole particle; surface area of the suspension. Notably, the effect of chemical composition of particles on biological response is better described by variables obtained from numerical computations rather than experimental ones, thus justifying the need for hybrid characterization/modelling datasets for describing biological mechanisms in a more comprehensive way.
As expected, Fig. 3a and b remark that the dose of particles is a common descriptor in both experimental conditions. Furthermore, the surface-to-volume of particles appears as an important aspect in both cases, with the important difference that the descriptors found for the non-UV case (i.e., average size and highest peak intensity of particle aggregates by DLS measure) are affected by the surrounding environment (e.g., pH, temperature, dissolved ions), while the one for the UV case (i.e., surface area of dry particles by BET measure) is not.
The chemical composition of particles is also found to be another important descriptor in both experimental conditions, with only slight differences (normal surface force vector of Ti atoms in the particle shell vs. normal surface force vectors of Fe and Ti atoms in the whole particle). Instead, the zeta potential seems to affect the biological response only when UV light irradiates particles.
In Fig. 3c (non-UV) and 3d (UV), we report also the “sensitivity” and “% positive response” of descriptors on the biological response: the former quantifies the average relative impact within the identified fitting functions that a descriptor has on biological responses; the latter describes the likelihood that increasing a descriptor will increase the biological response as well. Again, the observed direct proportionality between concentration and biological response agrees with typical results in the literature. However, here the dose of particles has the highest sensitivity on biological response only for experiments without UV, while other descriptors seem to have a bigger impact in case of UV exposition. In this latter case, the response is more sensitive to chemical composition of particles, instead. Other interesting evidence from Fig. 3c and d are the inverse proportionality between the descriptors related to the surface-to-volume and chemical composition of particles and the biological response, and the direct proportionality between the zeta potential and biological response (UV case).
Finally, considering only the last extended fitting by the symbolic regressor, Fig. 4a shows that the best correlation between the descriptors and the biological response for non-UV exposure achieves a remarkable R2 = 0.82 with the following function:
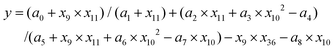 | (1) |
| y = b0 + b1 × x9 + b2/(x10 − b3 − x9) − x9 × x36 − b4 × x11 − b5 × x10 | (2) |
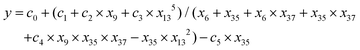 | (3) |
| y = (d0 + d1 × x9 + x134)/(x35 + x37 + x6 × x13) | (4) |
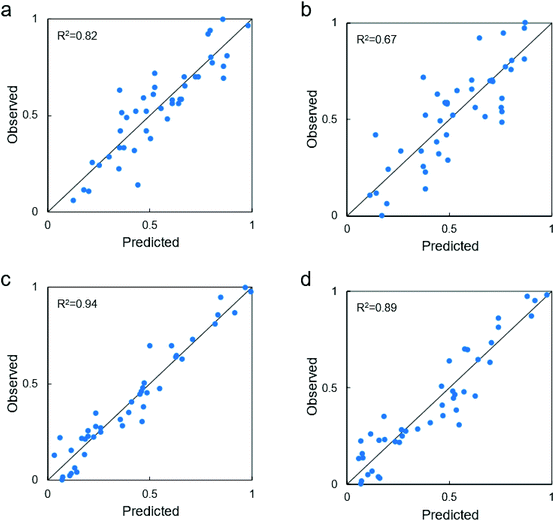 | ||
| Fig. 4 Best model correlations with the identified descriptors: experimental observations vs. model predictions (values are normalized by min–max approach, each dot represent one tested configuration). (a) Fitting performance of the most complex, most accurate function for TiO2 particles not exposed to UV (see eqn (1)). (b) Fitting performance of the best compromise (i.e., elbow of Pareto front) between model complexity and accuracy for TiO2 particles not exposed to UV (see eqn (2)). (c) Fitting performance of the most complex, most accurate function for TiO2 particles exposed to UV (see eqn (3)). (d) Fitting performance of the best compromise (i.e., elbow of Pareto front) between model complexity and accuracy for TiO2 particles exposed to UV (see eqn (4)). The definitions of the reported variables x1, …, x39 are reported in the Tables S4 (no exposure to UV) and S5 (exposure to UV).† | ||
3. Discussion
The study shows that the biological response of TiO2 depends on the Fe doping when under UV light exposure, even though the organisms recovered after a longer-term period in clean soil without UV. We saw a clear advantage of including both measured and modelled materials related descriptors when performing extensive (90 in vivo exposure concentrations (460 replicates) of 26 days) ecotoxicological experiments with nanomaterials, as both contributed to describe the results. However, including a high number (113 descriptors in this case) of material descriptors generates a high number of linked data, which requires a structured multi-step data analytical approach, e.g. through machine learning as done here. This results in a pruning process, hence the selected descriptors represent other correlated descriptors which also explain the observed biological responses. Notably, the effect of chemical composition of particles on biological response was better described by variables obtained from numerical computations rather than experimental ones, thus justifying the need for hybrid characterization/modelling datasets for describing biological mechanisms in a more comprehensive way.For nanomaterials the primary core size has commonly been observed as important for toxicity.33,34 However, this was not the case here but instead the hydrodynamic diameter correlated with biological impact (the primary size did not correlate with hydrodynamic size) which is in line with previous studies by Roohi et al.35 who also showed that smaller hydrodynamic size related to higher bio-distribution. The zeta potential had a significant impact under UV exposure, which is supported by Wang et al.26 who showed UV-induced increase of the zeta potential. It is worth noticing that Wang et al.26 observed a pH reduction when UV-radiating water containing humic acid, hence such a pH change if severe would also affect an organism in our experiment. We did not observe a pH change, and we had no added organic material during the UV exposure, so this is unlikely.
For the actual nanoparticles, the normal surface force vector of Ti/Fe atoms in the shell (modelled data) correlated with the biological impact. This descriptor reflects the stability of TiO2 on NP surface, with more positive value (difference from zero) indicating higher biological response. This surface stability was especially important under UV exposure, where a negative biological response was associated with this descriptor. This relationship with the surface vectors could be explained through a link to oxidative stress, as a correlation between the surface vector and the band gap was observed, similar to the large number of oxide materials investigated in vitro and in vivo.36 Band-gap correlates with oxidative stress.20 Total particle surface area also correlated with the UV-exposure, also in agreement with the band-gap correlation under UV exposure.
There was an inverse proportionality between the descriptors related to the surface-to-volume and chemical composition of particles and the biological response, and a direct proportionality between the zeta potential and biological response (UV exposure).
UV pre-exposure alone caused a high effect on organisms’ reproduction (i.e. significant decrease in reproduction compared to non-UV controls), but without mortality (both during pre and post–exposure period). The explanation for this is probably that the organisms are thin (diameter 200–300 μm (ref. 37)) and transparent, hence the UV could have caused detrimental effects on gametes e.g. through ROS production, while the adult as a whole would not die immediately.38 A previous study using similar exposure design39 to UV-B showed also a reproduction inhibition in E. crypticus. Hence, both UV-A and UV-B radiation cause an impact to enchytraeids.
The atoms on the TiO2 terminating crystal surface experience certain forces (differences in surface energy when Ti or O are terminating element). Such difference may cause variation in the surface energies, which are significantly influenced by two forces: normal force perpendicular to shear force (acting tangentially over an area). The UV application to the TiO2 nanoparticles forces atomic displacement along a certain Müller direction [1 0 1] which may bring collective changes in the sample.40 The number of atomic displacement of Ti in Fe doped TiO2 also varies due to different surface termination (some Fe atoms might also be on the surface), which in turn reflects the biological outcome. The combination TiO2 NPs and UV seemed to have an antagonistic or protective role against the UV effects, in particular with increasing concentrations, i.e. reduction in UV effect with increasing TiO2 concentration. Since the degree of protection decreased with hydrodynamic size, one explanation could be that the higher agglomeration rate caused a deposition in the bottom of the vessel, hence less dispersed in the water column resulting in less UV absorption in the water column. The higher the TiO2 concentration the more will be absorbed in the water column, with the flattening out of the curves between 10–100 mg L−1 for some materials because 10 mg L−1 was simply a high enough concentration to induce total protection (probably close to total UV absorption). We also observed in the stereomicroscope (see Fig. S9†) that TiO2 NPs attach to the organisms’ dermis and this can reduce the direct UV exposure of the organisms. The binding at the organisms’ surface is most likely also zeta potential related, but we could not verify this since we could not quantify the attached NPs.
For non-UV treatments, TiO2 induced an effect response pattern for two exposures – 6% Fe doped and the 10 nm TiO2, for the remaining there was little change with increasing concentration. So even though agglomeration must have also occurred here, as was in the UV treatment, it did not seem to relate to possible effects. Higher effect of lower concentrations of NMs has been reported before e.g. for Ag and Ni41–43 and this highlights the importance to adapt the dose–response paradigm for NMs. Yadav et al.21 studied the antibacterial activity of Fe doped and pure TiO2 NPs under fluorescent light and showed that increase in Fe (from 1 to 3%) increased the mortality rates of the bacteria Escherichia coli and Staphylococcus aureus. The differences in the crystal structure of the TiO2 NPs tested (100% anatase in ref. 21versus a combination of anatase and rutile in our study) must account for the observed differences, this of course besides the test organisms (unicellular bacteria versus a multicellular oligochaeta) and modes of action.
4. Conclusions
Doping of TiO2 with Fe changed the biological response of organisms especially under UV exposure. Notably, the short-term water exposure induced lasting biological responses even after longer-term recovery in clean exposure. The correspondence with Fe-content correlated with the band-gap hence the reduction of UV oxidative stress. When performing a high number of extensive in vivo test across materials, the inclusion of both measured and modelled materials data benefitted the explanation of the results, when combined with machine learning. This inclusion may produce large datasets with the opportunity of embedding different features of materials but, in order to dig out a significant explanation, systematic pruning is essential for identifying automatically the most significant descriptors and consequently the key phenomena.5. Experimental
5.1. Material synthesis
The different sizes and respective iron doped TiO2 nanoparticle libraries were obtained using versatile flame spray pyrolysis adapting controlled precursor chemistry and solvent combinations (see Table 1).| Ti–isopropoxide in xylene (mL) (0.5 M by Ti) | Fe–napthenate in xylene (mL) (0.5 M by Fe) | Precursor flow rate (mL min−1) | CH4 + O2 (L min−1) | Dispersion O2 (L min−1) | Nanoparticles |
|---|---|---|---|---|---|
| 50 | 0 | 5 | 1.5 + 3.2 | 5.0 | Pure TiO2 |
| 50 | 0.43 | 5 | 1.5 + 3.2 | 5.0 | 1%Fe/TiO2 |
| 50 | 0.86 | 5 | 1.5 + 3.2 | 5.0 | 2%Fe/TiO2 |
| 50 | 1.72 | 5 | 1.5 + 3.2 | 5.0 | 4%Fe/TiO2 |
| 50 | 2.58 | 5 | 1.5 + 3.2 | 5.0 | 6%Fe/TiO2 |
| 50 | 3.44 | 5 | 1.5 + 3.2 | 5.0 | 8%Fe/TiO2 |
| 50 | 4.3 | 5 | 1.5 + 3.2 | 5.0 | 10%Fe/TiO2 |
| 50 | — | 4 | 1.5 + 3.2 | 7 | 5 nm TiO2 |
| 50 | — | 5 | 1.5 + 3.2 | 5 | 10 nm TiO2 |
| 50 | — | 7 | 1.5 + 3.2 | 3 | 27 nm TiO2 |
The TiO2 based particles were obtained by using metalorganic precursor such as titanium-(IV) isopropoxide (Strem Chemical, 99.9% pure) with (for doping) and without (for pure and differently sized TiO2) Fe–naphthenate (12% Fe by metal, Strem, 99.9% pure). For the synthesis of doped particles, titanium(IV) isopropoxide (50 mL) was separately mixed with 0.6–6.5 mL of Fe–naphthenate (0.5 M by metal) for 1–10 wt% of Fe-doped TiO2 nanoparticles. All the precursors were diluted with xylene (99.95%, Strem) to keep the metal to 0.5 M.
Combustion of the dispersed droplets is initiated by the co-delivery of CH4 and O2 (1.5 L min−1, 3.2 L min−1) to form a flame.44–46 The flame parameters shown in the Table 1 for the Fe doped particles gives rise to the primary particle size of ∼10 nm. For the synthesis of particles with different sizes, the flame and spray parameters were varied. The parameters for obtaining various TiO2 based primary particle sizes are explained as follows: (1) for the preparation of standard particles (∼10 nm), the liquid precursor was delivered at the rate of 5 mL min−1 to the flame nozzle and was atomized using 5 min−1 O2 at a constant pressure drop of 1.5 bar at the nozzle tip; (2) for synthesizing 5 nm NPs, the precursor was fed in the flame through the nozzle at the rate of 4 mL min−1 with oxygen flow rate of 7 L min−1; (3) precursor and O2 flow rates with 7 mL min−1 and 3 L min−1, respectively was used to obtain 27 nm particles. The constant premixed gas flow (CH4 = 1.5 L min−1 + O2 = 3.2 L min−1) and pressure drop of 1.5 bar at the nozzle tip was maintained for all the experiments during spray combustion. The particles were formed by reaction, nucleation, surface growth, coagulation, and coalescence in the flame environment.47,48 The particles were collected from the 257 mm glass filter placed above the flame at a distance of 60 cm.
5.2. Materials characterisation – measurements
The NPs tested were fully characterized (Table 2) as also described in George et al.20 X-ray diffraction (XRD) measurements were done using a PANalytical X'Pert MPD PRO diffracting system, and the determination of the average crystallite sizes (dXRD) was achieved by the line-broadening analysis. Specific surface areas were determined by nitrogen adsorption–desorption measurements (BET), carried out at 77 K using a NOVA system. The primary particle size was derived using the equation dBET = 6/ρSA, where dBET, ρ, and SA are defined as the average diameter of a spherical particle, theoretical density, and the measured specific surface area. High resolution transmission electron microscopy images (HRTEM) were obtained with a FEI Titan 80/300 microscope. The NPs samples were dispersed in absolute ethanol and ultrasonified for 1 h, and then applied on a TEM grid and let to evaporate before imaging. The band gap energy of the NPs was determined by UV-visible measurements using a SHIMADZU UV-vis 2101 PC spectrophotometer in reflection mode. The UV absorbance spectra were used to evaluate the band gap of TiO2 and Fe-doped TiO2 nanoparticles by plotting [F(Rα) × hν]1/2 against hν, where hν is the energy of the incident photon and F(Rα) is the reflection in Kubelka–Munk function. The linear part of the curve was extrapolated to zero reflectance and the band gap energy was derived. Particle size distribution (by dynamic light scattering – DLS) and ζ-potential of the nanoparticles in water (5 mg L−1) were assessed using a ZetaSizer Nano (Malvern Instruments, Westborough, MA) in the backscattering mode.| TiO2 materials | TEM size (nm) | Crystal structure (%) | BET (nm) | SA (m2 g−1) | Band gap Eg (eV) | UV absorbance (wavelength) |
|---|---|---|---|---|---|---|
| TiO2_12 nm | 12 | 86% anatase–14% rutile | 10.5 | 145 | 3.3 | 360 |
| 1%FeTiO2_11 nm | 11 | 81% anatase–19% rutile | 9 | 157 | 3.2 | 382 |
| 2%FeTiO2_10 nm | 10 | 69% anatase–31% rutile | 7.6 | 160 | 3.15 | 380 |
| 4%FeTiO2_8 nm | 8 | 44% anatase–56% rutile | 7.5 | 161 | 3.1 | 390 |
| 6%FeTiO2_5 nm | 5 | 31% anatase–69% rutile | 7 | 163 | 3.0 | 412 |
| 8%FeTiO2_5 nm | 5 | 19% anatase–81% rutile | 6 | 167 | 2.9 | 425 |
| 10%FeTiO2_5 nm | 5 | 14% anatase–86% rutile | 6.1 | 165 | 2.8 | 440 |
| 10%FeTiO2_10 nm | 5 | 14% anatase–86% rutile | 10 | 122 | 2.8 | 440 |
| TiO2_10 nm | 10 | 87% anatase–13% rutile | 10 | 112 | 3.3 | 375 |
| TiO2_5 nm | 5 | 86% anatase–14% rutile | 5 | 275 | 3.2 | 388 |
| TiO2_27 nm | 27 | 70% anatase–30% rutile | 27 | 54 | 3.3 | 440 |
The particles were also characterized in the media, this in all exposure concentrations and both under UV and non-UV treatment. This characterization included DLS, zeta, etc. (please see Table S1†). This characterization was performed in the aquatic exposure and not in the soil media, that was technically impossible or – for the part that was possible (i.e. following extraction) – highly uncertain.
5.3. Material characterisation – modelling
The particles were characterized by atomistic modelling, as described by Tämm et al.15 and Burk et al.,6 generating 86 NP descriptors for each material. The calculations were carried out using Lennard–Jones potential49,50 version of the conjugate gradient approach. The core and shell region is determined by Kneedle method,51 where it is assumed that shell region starts, where the change in the corresponding value is the highest. Thus, the descriptors of the core atoms are quite similar to the ones that could be obtained for perfect crystal structure. The calculated descriptors included core/shell distribution of atoms, coordination distances, lattice energies, etc. (see Table S1†).5.4. Biological test species
The test species Enchytraeus crypticus, Westheide and Graefe,37 was used. Individuals were cultured in Petri dishes containing agar medium, consisting of a sterilized mixture of four different salt solutions (2 mM CaCl2·2H2O, 1 mM MgSO4, 0.08 mM KCl, and 0.75 mM NaHCO3) and a Bacti-Agar medium (Agar No. 1, Oxoid, Lancashire, UK). The cultures were kept under controlled conditions, at 19 ± 1 °C and photoperiod 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 h light
8 h light![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dark. Organisms were fed on ground and autoclaved oats twice a week.
dark. Organisms were fed on ground and autoclaved oats twice a week.
5.5. Test media
The exposure to the test materials was performed in reconstituted ISO test water52 containing: 2 mM of CaCl2·2H2O, 0.5 mM of MgSO4·7H2O, 0.77 mM of NaHCO3 and 0.077 mM of KCl in ultra-pure water.The post-exposure (clean media) was done in the natural soil LUFA 2.2 (Speyer, Germany). The main characteristics can be described as follows: pH (0.01 M CaCl2, ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 w/v) = 5.5, organic matter = 1.77 meq per 100 g, CEC (cation exchange capacity) = 10.1%, WHC (water holding capacity) = 41.8% grain size distribution of 7.3% clay, 13.8% silt, and 78.9% sand. For the test, the soil was moistened with distilled water up to 50% of its WHC.
5 w/v) = 5.5, organic matter = 1.77 meq per 100 g, CEC (cation exchange capacity) = 10.1%, WHC (water holding capacity) = 41.8% grain size distribution of 7.3% clay, 13.8% silt, and 78.9% sand. For the test, the soil was moistened with distilled water up to 50% of its WHC.
5.6. Experimental procedures
The various treatments will be further referred to as NM_size nm_[concentration (mg L−1)] + UV, e.g. 1%FeTiO2_11 nm_[10] + UV.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 934 J m−2. The emission spectra of the UV lamp used is shown on ESI, Fig. S1.† The wavelengths emitted by this lamp cover the wavelengths absorbed by the NPs (Table 2) and respective excitation as intended.
934 J m−2. The emission spectra of the UV lamp used is shown on ESI, Fig. S1.† The wavelengths emitted by this lamp cover the wavelengths absorbed by the NPs (Table 2) and respective excitation as intended.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 hours of photoperiod, and was performed under two different scenarios: (1) standard laboratory illumination (fluorescent lamp, emission spectra on ESI, Fig. S2†) and (2) UV radiation, with ten replicates per condition.
8 hours of photoperiod, and was performed under two different scenarios: (1) standard laboratory illumination (fluorescent lamp, emission spectra on ESI, Fig. S2†) and (2) UV radiation, with ten replicates per condition.
After the 5-day pulse exposure to TiO2 (UV and no UV), the surviving adults were transferred to a clean post-exposure period in LUFA 2.2 soil. The procedure followed the ERT guideline24 (i.e. 21 days exposure) where the surviving organisms from each test condition were pooled in groups of 10 and introduced on test vessels with soil. Four replicates per pre-exposure condition were performed. The test ran under the same conditions. At the end of the test, the organisms were fixed with ethanol and stained with Bengal rose (1% in ethanol). After 24 h, the soil samples were sieved through meshes with a decreasing pore size (1.6, 0.5, and 0.3 mm) to separate the enchytraeids from most of the soil and facilitate counting. Adult and juvenile organisms were counted using a stereo microscope and survival and reproduction were assessed.
5.7. Data analysis
Simple, significant differences between the control and each treatment were investigated based on Analysis of Variance (ANOVA) with Dunnett's test for multiple comparisons (p < 0.05) (using Sigma Plot, 11.0). Effect concentrations (ECx) were calculated, for survival and reproduction (21 days’ post-exposure), modelling data to logistic or threshold sigmoid 2 parameter regression models (for details see Table S6†) (using Toxicity Relationship Analysis Program (TRAP 1.30)).Exploratory approaches previously employed in the literature include various forms of regression analysis, principal component analysis, and machine learning techniques (SAS Enterprise Guide 7.13 2016, IML studio 14.2 SAS 2013–2014). Here a novel multi-step method for identifying the descriptors for the biological response to TiO2 materials has been developed and used for both non-UV and UV exposure tests.54
Starting from the initial amount of N = 113 variables (equivalent to “descriptors”) (x1, x2, …, x113) available from both computational and experimental characterization of TiO2 materials, our data analysis protocol aims at progressively prune the redundant or less significant variables for the biological response (y) observed in the experiments, thus eventually highlighting a limited yet important set of descriptors.55 The complexity of the biological and chemical processes involved in the biological mechanism and the numerous variables initially available may lead to overfitting.56 Hence, the employed data analysis protocol was developed over four successive steps (schematically depicted in Fig. 5a) and make use of statistical and machine learning approaches: (i) pre-process data; (ii) remove correlated variables; (iii) identify the descriptors out of the variable set by means of an iterative pruning process; (iv) correlate the descriptors with biological response.
As previously described, the biological response to TiO2 particles has been assessed in vivo, with and without UV exposure, yielding 44 biological data points. Such TiO2 particles have been experimentally characterized, thus obtaining the values of several variables describing the dose (i.e., concentration), material (e.g., size, chemical composition, etc.) and surrounding environment (e.g., zeta potential) during tests. This list has then been enriched with variables computed by numerical modelling. Hence, two 44 × 114 data matrices are available at the starting point: 44 experimental results, including with and without UV exposure, each one described by 113 variables (dose, material, environment, and modelling ones) and 1 biological response. First, the initial datasets were cleaned, by removing variables with missing data and keeping only the average value of variables, not their standard deviation.
Second, redundant variables have been identified and clustered together, to achieve a shorter list of variables with low degree of correlation. To this purpose, the hierarchical clustering algorithm has been employed,57 considering the Spearman's correlation coefficient as the metric to quantify the similarity between each pair of variables. Following this criterion, pairs of similar variables have been linked hierarchically and grouped into clusters with pair-wise similarity until the stopping criteria is met (i.e., inconsistency coefficient equal to 0.8, which corresponds to roughly 1-sigma confidence level). Finally, a representative variable per each cluster is nominated, with preference to variables typically considered in the toxicity literature (although, for our purposes, any of the variable in the cluster is equivalent to the other).
Third, the uncorrelated N1 variables obtained after the clustering step were pruned iteratively to eventually sort the most significant descriptors of the biological response. As illustrated in Fig. 5b, a symbolic regression algorithm is used at each i-th pruning step to identify the most accurate and compact functions (f) relating the available variables (x1, x2, …, xNi) with the biological response (y), namely y = f(x1, x2, …, xNi). These f functions are provided by the symbolic regressor as a Pareto front, where their complexity is compared with the resulting fitting accuracy (e.g., see Fig. S3a and S3b†). Clearly, the fitting equation with the highest complexity tends to be the most accurate one, while the elbow of Pareto front can be considered as the best compromise between fitting accuracy and equation complexity. Then, the Ni variables are ranked based on their occurrence in the suitable f functions lying on the Pareto front: only the best ranked 40% of variables are kept, while the remaining ones pruned. This process is repeated until one of the chosen stopping criteria is met, either a 10% decrease in the coefficient of determination (R2) or a 20% increase in the Mean Squared Error (MSE) between the best fitted functions in two successive pruning steps. In detail, the symbolic regression algorithm implemented in the Eureqa software has been used.58 To mitigate the risk of relaxing the solution towards a local minimum, different parametrizations of the minimization algorithm have been employed and fitting results averaged. In detail, two sets of building blocks for the explored fitting equations (rational polynomial functions; rational polynomial, exponential/logarithmic and square root functions) and three target error metrics (maximize R2; minimize absolute error; maximize a hybrid correlation/error index) have been considered, thus leading to six different repetitions of the fitting procedure per each pruning step. The symbolic regression has been iterated until a stable solution is observed, typically after 2–50 million generations (e.g., see Fig. S3c and S3d†). To ease the convergence of the minimization algorithm, the processed data have been preliminary normalized via a min–max approach per each independent/dependent variable.
Only variables that survived to the pruning process are finally assumed as the relevant descriptors for the biological response to the tested TiO2 materials. The iterations of the symbolic regressor are continued up to about 100 million to refine the accuracy of the minimization process while considering only these descriptors as variables. Based on this last fitting procedure, the sensitivity between each descriptor and the biological response is assessed for both UV and non-UV exposure. For the sake of completeness, we have also performed a final fitting by means of other different supervised machine learning algorithms (based on neural networks, decision trees, elastic net regularization or ridge regression, among others). The gradient boosted greedy trees regressor with least-squares loss achieves the highest coefficient of determination R2 = 0.52 among the tested algorithms (non-UV exposure dataset), being anyway worse than the fitting by the symbolic regression algorithm proposed in our work (R2 = 0.82).
Author contributions
SILG: Formal analysis, investigation, methodology, writing – original draft; MJBA Conceptualization, funding acquisition, resources, supervision, writing – original draft. SP, LM: Investigation, methodology. MF, EC, PA: Data curation, formal analysis, writing – original draft; JJ, KT, JB: Data curation, formal analysis, writing – original draft; JJSF: Data curation, formal analysis, conceptualization, funding acquisition, resources, supervision, writing – original draft. All authors writing – review & editing.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This study was supported by funds of the European Commission NANOINFORMATIX (H2020-NMBP-14-2018, No. 814426), BIORIMA (H2020-NMBP-12-2017, GA No. 760928) and NANORIGO (H2020-NMBP-13-2018, GA No. 814530). Further support from FEDER through COMPETE Programa Operacional Factores de Competitividade (2020) and the Portuguese Science Foundation (FCT-Fundação para a Ciência e Tecnologia) within the projects BIO-chip (EXPL/AAG-MAA/0180/2013) and NM OREO (PTDC/AAG-MAA/4084/2014), and CESAM (UIDP/50017/2020 + UIDB/50017/2020) through FCT/MEC (national funds) and co-funding by FEDER within the PT2020Partnership Agreement and Compete 2020. S. I. L. Gomes is funded by national funds (OE), through FCT, I. P., in the scope of the framework contract foreseen in the numbers 4, 5 and 6 of the article 23, of the Decree-Law 57/2016, of August 29, changed by Law 57/2017, of July 19.References
- X. Hu, S. Cook, P. Wang and H. Hwang, Sci. Total Environ., 2009, 407, 3070–3072 CrossRef CAS PubMed.
- S. Pokhrel, A. E. Nel and L. Mädler, Acc. Chem. Res., 2013, 46, 632–641 CrossRef CAS PubMed.
- T. Puzyn, B. Rasulev, A. Gajewicz, X. Hu, T. P. Dasari, A. Michalkova, H.-M. Hwang, A. Toropov, D. Leszczynska and J. Leszczynski, Nat. Nanotechnol., 2011, 6, 175–178 CrossRef CAS PubMed.
- D. Fourches, D. Pu, C. Tassa, R. Weissleder, S. Y. Shaw, R. J. Mumper and A. Tropsha, ACS Nano, 2010, 4, 5703–5712 CrossRef CAS.
- T. Puzyn, D. Leszczynska and J. Leszczynski, Small, 2009, 5, 2494–2509 CrossRef CAS PubMed.
- J. Burk, L. Sikk, P. Burk, B. B. Manshian, S. J. Soenen, J. J. Scott-Fordsmand, T. Tamm and K. Tämm, Nanoscale, 2018, 10, 21985–21993 RSC.
- A. Toropov, N. Sizochenko, A. Toropova and J. Leszczynski, Nanomaterials, 2018, 8, 243 CrossRef.
- K. Van Hoecke, J. T. K. Quik, J. Mankiewicz-Boczek, K. A. C. De Schamphelaere, A. Elsaesser, P. Van der Meeren, C. Barnes, G. McKerr, C. V. Howard, D. Van De Meent, K. Rydzyński, K. A. Dawson, A. Salvati, A. Lesniak, I. Lynch, G. Silversmit, B. De Samber, L. Vincze and C. R. Janssen, Environ. Sci. Technol., 2009, 43, 4537–4546 CrossRef CAS PubMed.
- A. Ivask, I. Kurvet, K. Kasemets, I. Blinova, V. Aruoja, S. Suppi, H. Vija, A. Käkinen, T. Titma, M. Heinlaan, M. Visnapuu, D. Koller, V. Kisand and A. Kahru, PLoS One, 2014, 9, e102108 CrossRef.
- V. Aruoja, S. Pokhrel, M. Sihtmäe, M. Mortimer, L. Mädler and A. Kahru, Environ. Sci. Nano, 2015, 2, 630–644 RSC.
- S. I. L. Gomes, C. P. Roca, J. J. Scott-Fordsmand and M. J. B. Amorim, Environ. Sci. Nano, 2017, 4, 929–937 RSC.
- J. Hou, Y. Zhou, C. Wang, S. Li and X. Wang, Environ. Sci. Technol., 2017, 51, 12868–12878 CrossRef CAS PubMed.
- S. I. L. Gomes, C. P. Roca, F. von der Kammer, J. J. Scott-Fordsmand and M. J. B. Amorim, Nanoscale, 2018, 10, 21960–21970 RSC.
- S.-K. Jung, X. Qu, B. Aleman-Meza, T. Wang, C. Riepe, Z. Liu, Q. Li and W. Zhong, Environ. Sci. Technol., 2015, 49, 2477–2485 CrossRef CAS PubMed.
- K. Tämm, L. Sikk, J. Burk, R. Rallo, S. Pokhrel, L. Mädler, J. J. Scott-Fordsmand, P. Burk and T. Tamm, Nanoscale, 2016, 8, 16243–16250 RSC.
- A. Cardellini, M. Fasano, E. Chiavazzo and P. Asinari, Phys. Lett. A, 2016, 380, 1735–1740 CrossRef CAS.
- A. G. Papadiamantis, J. Jänes, E. Voyiatzis, L. Sikk, J. Burk, P. Burk, A. Tsoumanis, M. K. Ha, T. H. Yoon, E. Valsami-Jones, I. Lynch, G. Melagraki, K. Tämm and A. Afantitis, Nanomaterials, 2020, 10, 2017 CrossRef CAS PubMed.
- A. Gizzatov, J. Key, S. Aryal, J. Ananta, A. Cervadoro, A. L. Palange, M. Fasano, C. Stigliano, M. Zhong, D. Di Mascolo, A. Guven, E. Chiavazzo, P. Asinari, X. Liu, M. Ferrari, L. J. Wilson and P. Decuzzi, Adv. Funct. Mater., 2014, 24, 4584–4594 CrossRef CAS PubMed.
- E. Chiavazzo, M. Fasano and P. Asinari, Phys. A, 2013, 392, 1122–1132 CrossRef CAS.
- S. George, S. Pokhrel, Z. Ji, B. L. Henderson, T. Xia, L. Li, J. I. Zink, A. E. Nel and L. Mädler, J. Am. Chem. Soc., 2011, 133, 11270–11278 CrossRef CAS PubMed.
- H. M. Yadav, T. V. Kolekar, S. H. Pawar and J.-S. Kim, J. Mater. Sci. Mater. Med., 2016, 27, 57 CrossRef.
- K. Huang, L. Chen, M. Liao and J. Xiong, Int. J. Photoenergy, 2012, 2012, 1–8 Search PubMed.
- ISO 16387.
- OECD 220.
- C. Pelosi and J. Römbke, Appl. Soil Ecol., 2018, 123, 775–779 CrossRef.
- P. Wang, N. Qi, Y. Ao, J. Hou, C. Wang and J. Qian, Environ. Pollut., 2016, 212, 178–187 CrossRef CAS PubMed.
- F. Luan, V. V. Kleandrova, H. González-Díaz, J. M. Ruso, A. Melo, A. Speck-Planche and N. M. Cordeiro, Nanoscale, 2014, 6, 10623 RSC.
- V. V. Kleandrova, F. Luan, H. González-Díaz, J. M. Ruso, A. Speck-Planche and N. M. Cordeiro, Environ. Sci. Technol., 2014, 48, 14686–14694 CrossRef CAS PubMed.
- V. V. Kleandrova, F. Luan, H. González-Díaz, J. M. Ruso, A. Melo, A. Speck-Planche and N. M. Cordeiro, Environ. Int., 2014, 73, 288–294 CrossRef CAS PubMed.
- R. Santana, R. Zuluaga, P. Gañán, S. Arrasate, E. Onieva and H. González-Díaz, Nanoscale, 2019, 11, 21811–21823 RSC.
- R. Santana, R. Zuluaga, P. Gañán, S. Arrasate, E. Onieva and H. González-Díaz, Nanoscale, 2020, 12, 13471–13483 RSC.
- B. Ortega-Tenezaca and H. González-Díaz, Nanoscale, 2021, 13, 1318–1330 RSC.
- S. Makama, S. K. Kloet, J. Piella, H. van den Berg, N. C. A. de Ruijter, V. F. Puntes, I. M. C. M. Rietjens and N. W. van den Brink, Toxicol. Sci., 2018, 162, 79–88 CrossRef CAS PubMed.
- S. A. Ali, M. Z. Rizk, M. A. Hamed, E. I. Aboul-Ela, N. S. El-Rigal, H. F. Aly and A.-H. Z. Abdel-Hamid, Biomarkers, 2019, 24, 492–498 Search PubMed.
- F. Roohi, J. Lohrke, A. Ide, G. Schütz and K. Dassler, Int. J. Nanomed., 2012, 7, 4447 Search PubMed.
- H. Zhang, Z. Ji, T. Xia, H. Meng, C. Low-Kam, R. Liu, S. Pokhrel, S. Lin, X. Wang, Y.-P. Liao, M. Wang, L. Li, R. Rallo, R. Damoiseaux, D. Telesca, L. Mädler, Y. Cohen, J. I. Zink and A. E. Nel, ACS Nano, 2012, 6, 4349–4368 CrossRef CAS PubMed.
- W. Westheide and U. Graefe, J. Nat. Hist., 1992, 26, 479–488 CrossRef.
- T. Zan-Bar, B. Bartoov, R. Segal, R. Yehuda, R. Lavi, R. Lubart and R. R. Avtalion, Photomed. Laser Surg., 2005, 23, 549–555 CrossRef CAS PubMed.
- S. I. L. Gomes, G. Caputo, N. Pinna, J. J. Scott-Fordsmand and M. J. B. Amorim, Environ. Toxicol. Chem., 2015, 34, 2409–2416 CrossRef CAS.
- J. P. W. Treacy, H. Hussain, X. Torrelles, D. C. Grinter, G. Cabailh, O. Bikondoa, C. Nicklin, S. Selcuk, A. Selloni, R. Lindsay and G. Thornton, Phys. Rev. B, 2017, 95, 075416 CrossRef.
- R. C. Bicho, F. C. F. Santos, J. J. Scott-Fordsmand and M. J. B. Amorim, Environ. Pollut., 2017, 224, 117–124 CrossRef CAS PubMed.
- F. C. F. Santos, S. I. L. Gomes, J. J. Scott-Fordsmand and M. J. B. Amorim, Environ. Toxicol. Chem., 2017, 36, 2934–2941 CrossRef CAS PubMed.
- N. P. Rodrigues, J. J. Scott-Fordsmand and M. J. B. Amorim, Environ. Pollut., 2020, 262, 114277 CrossRef CAS PubMed.
- S. Pokhrel, C. E. Simion, V. S. Teodorescu, N. Barsan and U. Weimar, Adv. Funct. Mater., 2009, 19, 1767–1774 CrossRef CAS.
- J. A. Kemmler, S. Pokhrel, L. Mädler, U. Weimar and N. Barsan, Nanotechnology, 2013, 24, 442001 CrossRef CAS PubMed.
- H. Naatz, S. Lin, R. Li, W. Jiang, Z. Ji, C. H. Chang, J. Köser, J. Thöming, T. Xia, A. E. Nel, L. Mädler and S. Pokhrel, ACS Nano, 2017, 11, 501–515 CrossRef CAS PubMed.
- S. Pokhrel, J. Birkenstock, A. Dianat, J. Zimmermann, M. Schowalter, A. Rosenauer, L. C. Ciacchi and L. Mädler, CrystEngComm, 2015, 17, 6985–6998 RSC.
- J. A. H. Dreyer, S. Pokhrel, J. Birkenstock, M. G. Hevia, M. Schowalter, A. Rosenauer, A. Urakawa, W. Y. Teoh and L. Mädler, CrystEngComm, 2016, 18, 2046–2056 RSC.
- J. E. Jones, Proc. R. Soc. London, Ser. A, 1924, 106, 463–477 CAS.
- E. Polak and G. Ribiere, Rev. fr. Inform. Rech. Oper., Ser. rouge, 1969, 3, 35–43 Search PubMed.
- V. Satopää, J. Albrecht, D. Irwin and B. Raghavan, 31st IEEE Int. Conf. Distrib. Comput. Syst. Work. (ICDCS 2011 Work. 20-24 June 2011, Minneapolis, Minnesota, USA, 2011, pp. 166–171 Search PubMed.
- OECD 202.
- J. Rombke and T. Knacker, Hydrobiologia, 1989, 180, 235–242 CrossRef.
- V. Kovalishyn and G. Poda, Chemom. Intell. Lab. Syst., 2015, 149, 10–16 CrossRef CAS.
- L.-P. Ren, C.-X. Zhang and H.-Y. Xuan, in 2017 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), IEEE, 2017, pp. 449–454 Search PubMed.
- R. Kamala and R. J. Thangaiah, IAES Int. J. Artif. Intell., 2019, 8, 77 Search PubMed.
- L. Rokach and O. Maimon, in Data Mining and Knowledge Discovery Handbook, Springer-Verlag, New York, 2006, pp. 321–352 Search PubMed.
- M. Schmidt and H. Lipson, Science, 2009, 324, 81–85 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Tables S1–S6; Fig. S1 to S9; Movies S1 and S2. See DOI: 10.1039/d1nr03231c |
| ‡ These authors contributed equally to the paper. |
| This journal is © The Royal Society of Chemistry 2021 |