Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tailoring the mechanoresponsive release from silica nanocapsules†
Fabian
Uebel
a,
Héloïse
Thérien-Aubin
 *ab and
Katharina
Landfester
*ab and
Katharina
Landfester
 *a
*a
aMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: landfester@mpip-mainz.mpg.de
bDepartment of Chemistry, Memorial University of Newfoundland, 283 Prince Philip Dr, St. John's, NL A1B 3X7, Canada. E-mail: htherienaubin@mun.ca
First published on 6th September 2021
Abstract
Triggering the release of encapsulated cargos using mechanical stress acting on a nanocarrier is a strategy with potential applications from drug delivery to self-healing coatings. The mechanically triggered release of encapsulated molecules can be controlled by tuning the mechanical properties of the nanocapsules, which are strongly linked to the nanocapsule architecture. Here, silica nanocarriers were designed to tune precisely the release initiated by mechanical stress. We synthesized silica nanocapsules (SiNCs) with a finely tunable diameter and shell thickness and performed AFM nanoindentation experiments to determine the breaking force of single SiNCs. We demonstrated that it is possible to trigger the release of encapsulated payload by the application of an external mechanical force on the SiNCs. Furthermore, we successfully controlled the breaking force and the amount of released payload by tailoring the architecture of the nanocarriers, illustrating how such mechanoresponsive SiNCs could be used as responsive nanocarriers for the delivery of molecular cargos.
Introduction
Nanocarrier systems enable the precise delivery of a cargo, and a vast gamut of physicochemical cues are being used to initiate this delivery. Mechanical cues, like load or deformation, are becoming an essential class of triggers for new delivery applications, whether in the biomedical field or in more traditional industries. In such cases, the mechanical properties of the nanocarriers are of central importance to control the release. However, there is currently a lack of adequate design guidelines to produce nanocarriers with suitable composition and architecture to predict the release of encapsulated cargos under predetermined mechanical stresses. To address this limitation, we need to establish a relationship between the composition of the nanocarriers and the architecture of the nanocarrier, defined by their size and shell thickness, all of which can influence the mechanical properties of the nanocarriers.Independently from the encapsulated cargo or the type of nanocarrier, a successful delivery system should ensure the effective encapsulation and release of the cargo.1 The release of an encapsulated cargo from a nanocarrier can occur by two main mechanisms, either a diffusion-induced release or degradation-induced release. Both mechanisms can be triggered by different stimuli, depending on the chemical composition of the nanocarrier system. Such nanocarriers can be thermo-,2 light-,3 pH-,4 enzyme-,1 or redox-responsive.5
One trigger mechanism for the release of cargo molecules that has a broad appeal in a variety of fields is the release following the mechanical deformation or the application of controlled mechanical stress on the nanocarriers. Such mechanoresponsive systems are used to influence drug delivery inside the human body.6 More interestingly, those mechanoresponsive nanocarriers are now gaining interest in a broader range of fields, i.e., delivery,7 damage sensors,8,9 self-healing materials,8,10 stretchable electronics,11 or lubrication. For example, damage-sensing systems based on microcapsules can release dye molecules upon mechanical damages and are used to locate the affected area.12 Nanocarrier systems can combine those functionalities and simultaneously report mechanical damages to induce self-healing through the delivery of self-healing agents to the damaged area, and successful recovery of the original material properties can be achieved.8 In such systems, the application of a force results in the deformation or the breaking of the micro-/nano-carrier leading to the subsequent release of the encapsulated cargo. Therefore, controlling and understanding the physicochemical parameters that dictate the mechanical properties of the delivery system, like shell thickness or the stiffness of the shell, are critical in gaining control over the release from mechanoresponsive delivery systems.
The rational design of mechanoresponsive delivery systems relies on the study of the mechanical properties of the delivery systems at the nanoscale. One method to study the mechanical properties of micro- and nano-capsules is to use the tip of the cantilever employed in atomic force microscopy (AFM) as a nanoindenter to probe single nanocapsules by applying precise forces.13 AFM is a versatile technique that can not only be used to obtain images with subnanometer resolution but also to apply precise and localized forces as low as several piconewtons.14 By measuring the displacement of the AFM tip during the indentation process, parameters like Young's modulus, hardness, or breaking forces of nanocapsules can be determined. Previously, AFM nanoindentation has been used to analyze a variety of micro- and nano-carriers15–19 or even to initiate reactions of mechanophore molecules.20
The design of the mechanoresponsive delivery system requires a tunable platform. Silica nanocapsules (SiNCs) are model mechanoresponsive carriers. They are ideal candidate as a delivery system for various applications10,21,22 because their properties can be tuned by controlling their shape, size, shell thickness, or chemical composition.23–25 Here, we precisely manufactured SiNCs with a controlled structure (Fig. 1) to yield a class of tunable and controllable mechanoresponsive nanocarriers. In those SiNCs, a condensed silica shell of a tunable thickness encapsulated a liquid core of tunable size, acting either directly as the cargo or used to dissolve the cargo. These well-defined nanocapsules provide a blueprint to understand how to tune the structural parameters of the mechanoresponsive system to achieve the release required for specific applications and sets of mechanical stresses.
 | ||
| Fig. 1 Schematic representation of the mechanoresponsive release of encapsulated cargo after the application of a mechanical load leading to the fracture of the shell. | ||
Results and discussion
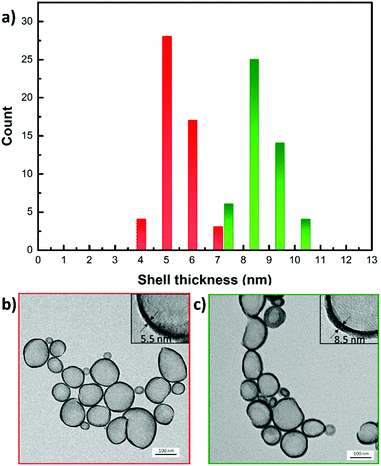
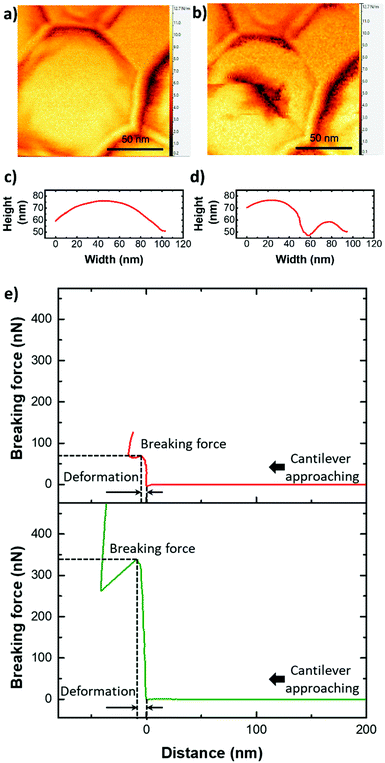
The tailored SiNCs were prepared via oil-in-water miniemulsion by dispersing a mixture of silica precursor and a specific hydrophobic cargo in an aqueous solution of surfactant. Nanodroplets formed by the microfluidization of the biphasic mixture acted as the template for the formation of the final SiNCs. By tuning the composition and size of the nanodroplets, it was possible to control the properties of the resulting SiNCs (Fig. 2). The size of the SiNCs was controlled either by the ratio of dispersed to continuous phase used during microfluidization, the concentration of surfactant used in the continuous phase, or the intensity of the high mechanical stress generated during the microfluidization process (Fig. S1†).26 After emulsification, the interfacial condensation reaction between the silica precursor tetraethylorthosilicate (TEOS) and water led to the formation of a solid silica shell around the core composed of organic solvent, and the SiNCs showed homogenous size, shell thickness, and morphology (Fig. 2). Furthermore, when the weight fraction of TEOS relative to the organic core material (e.g. hexadecane, hexane, toluene, glycerol trioleate) in the dispersed phase was increased, the shell thickness of the resulting SiNCs increased (Fig. S2†). The control of the synthetic condition allowed generating a library of SiNCs of controlled size and shelling thickness (Table S1†).The mechanical properties of the resulting SiNCs were studied by atomic force microscopy (AFM) (Fig. 3). The SiNCs were deposited on a glass substrate and imaged by AFM to identify single SiNCs.
Subsequently, the cantilever was placed at the center of the SiNCs and used to compress the SiNCs with increasing force. The resulting force–distance curves were used to characterize the mechanical properties of the SiNCs (Fig. 3e). The breaking of the silica shell resulted in an abrupt drop of the force exerted by the cantilever compressing the shell. This explicit behavior allowed for the determination of the force needed to break the SiNCs and of the maximal deformation of the SiNCs at the breaking point.
The deformation of the SiNC until breaking was defined by the distance covered by the cantilever between the jump-in contact when the AFM tip first made contact with the SiNC and the position of the tip when the shell ruptured. After the compression experiment, AFM imaging of the deformed SiNCs showed the resulting damaged silica shell (Fig. 3a and b). One could note that the SiNC in Fig. 3a appears wider than it is high, this is due to the convolution of the AFM tip and the nanocapsule.27
The compression curves (Fig. 3e) can be used to measure the mechanical properties of the SiNCs and their relation to the morphology of the nanocapsules. In the early stage of the deformation generated by the compression of the SiNC by the AFM cantilever, the theory of thin shell elasticity can be used to describe the linear elastic response for the indentation of a homogeneous spherical shell. The force (F) applied by the cantilever results in an indentation depth (Δc) and this deformation is related to the capsule shell thickness (h), the diameter of the capsule (D) and the Young's modulus (E) of the shell material:
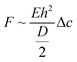 | (1) |
This relationship has been used to quantify the mechanical properties of hollow microcapsules using AFM force measurements.16 However, the thin shell elasticity theory is only valid when Δc is in the range of the shell thickness h as larger deformations can result in plastic deformation.28 In addition to the large deformation sustained by the SiNCs, the understanding of these deformations was made more complex since the shell was made of a solid material while the core contained a liquid. Assuming that the deformed capsule has an impermeable shell filled with an incompressible liquid, the displacement of the shell during deformation is constrained because the volume of the core must remain constant and results in additional restoring forces arising from the deformation and stretching of the shell needed to keep the volume constant. This force is proportional to the third power of the indentation depth:29
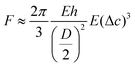 | (2) |
We studied the deformation behavior and rupture of spherical shells under point loads. The deformation experiments were used to measure the mechanical stress, which can induce the large deformation needed to break the shell of the nanocapsules. When spherical shells are deformed exceeding the range of the shell thickness, nonlinear buckling resulting from the coupling of in-plane-stretching and out-of-plane bending occurs.16,30 In the SiNCs system, the force needed to generate a plastic deformation that is large enough to induce the buckling of the shell, can be understood as the force needed to rupture the silica shell. For the compression of a spherical shell, the critical buckling pressure pc is defined by:31,32
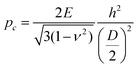 | (3) |
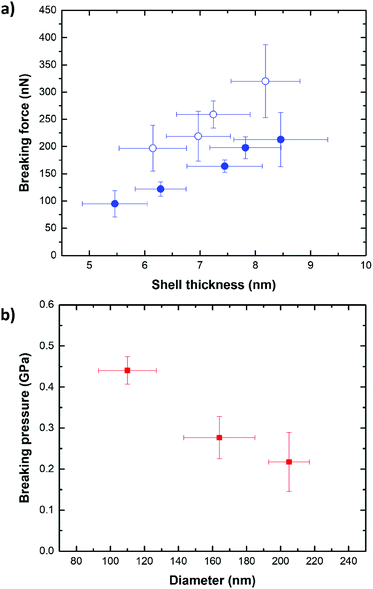
The breaking force of SiNCs of constant diameter and increasing shell thicknesses (Fig. 4a) was determined by AFM indentation. For each shell thickness and capsule diameter, a total of 10 SiNCs were compressed with the AFM cantilever tip with a force ranging from 0 to 500 nN. The AFM allowed to identify single SiNCs deposited on the substrate (Fig. S3†), and to produce reproducible and reliable analysis. The indentation experiments were performed only on SiNC deviating by no more than 5% from the average size of the batch as analyzed by electron microscopy and repeated on at least 10 individual SiNCs for each batch. The SiNCs with a thin shell (h = 5.5 nm) broke with the application of a force of ca. 95 nN and thicker SiNCs (h = 8.5 nm) broke after applying a force of ca. 213 nN. The difference observed in the breaking force between different samples of SiNCs with different shell thickness was statistically significant (t-test, p = 0.95). A general linear increase of the breaking force with increasing shell thickness was observed, in keeping with the increase in bending stiffness and extensional stiffness of the shell expected when the shell thickness increases.16,33–36
Interestingly, SiNCs filled with an incompressible liquid core systematically broke after the application of a lower force when compared to the empty SiNCs of the same size and shell thickness. The SiNCs filled with a hexadecane core represent the case of a liquid core encapsulated by an impermeable shell. In comparison, the hollow SiNCs filled with air, prepared by the evaporation of a hexane core, which has a low boiling point solvent and high vapor pressure, had a compressible inner core (Fig. S4†). Fig. 4a shows that the force needed to break hollow SiNCs was 30–40% higher than for liquid core SiNCs. This difference in the breaking force originated from the presence of the incompressible liquid. In the case of filled SiNCs, the volume of the core must remain constant during the deformation experiment, as the liquid core material cannot be compressed. As a result, additional restoring forces emerged, causing more stress on the silica shell and consequently leading to the breaking of the shell occurring at lower forces compared to hollow SiNCs.37
Additionally, the variation of the breaking force with the capsule size was studied for liquid-filled SiNCs. The results show that the highest breaking force was observed for thick and large SiNCs (h = 8.5 nm, D = 205 nm), while the lowest breaking force was observed for thin and small (h = 5.7 nm, D = 75 nm) SiNCs (Fig. S5a†). Typically, when capsules with a given shell thickness are considered, capsules with a small diameter are more robust than capsules with a larger diameter as 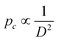 .30 The results obtained by AFM show that the force needed to break the SiNCs also induced the deformation of the capsule and we observed that larger capsules were more deformed at the breaking point than smaller SiNCs (Fig. S5b†). Consequently, the breaking force needed to be converted in a breaking pressure to analyze the results further. The critical breaking pressures were calculated using the Hertz contact mechanics to determine the contact area between the cantilever tip and the nanocapsule.38 Therefore, the deformation of the SiNCs at the breaking point was needed to calculate the contact area. The average deformation for small SiNCs of 110 nm average diameter was found to be 23.4 nm, which corresponded to a deformation of 21.3% of the capsule diameter. For medium SiNCs (164 nm) a deformation of 47.8 nm (29.1%) and for large SiNCs (194 nm) a deformation of 72.7 nm (37.5%) were observed, those deformation were used to calculate the respective breaking pressure (Fig. 4b). The results show that the critical breaking pressure increased as the size of the SiNCs decreased. The difference in the breaking pressure observed between the different SiNCs samples was statistically significant (t-test, p = 0.95). Additionally, the variation of breaking pressure with the shell thickness and the capsule diameter follow the expected behavior for the critical buckling pressure (eqn (3)) as demonstrated in Fig. S6.†
.30 The results obtained by AFM show that the force needed to break the SiNCs also induced the deformation of the capsule and we observed that larger capsules were more deformed at the breaking point than smaller SiNCs (Fig. S5b†). Consequently, the breaking force needed to be converted in a breaking pressure to analyze the results further. The critical breaking pressures were calculated using the Hertz contact mechanics to determine the contact area between the cantilever tip and the nanocapsule.38 Therefore, the deformation of the SiNCs at the breaking point was needed to calculate the contact area. The average deformation for small SiNCs of 110 nm average diameter was found to be 23.4 nm, which corresponded to a deformation of 21.3% of the capsule diameter. For medium SiNCs (164 nm) a deformation of 47.8 nm (29.1%) and for large SiNCs (194 nm) a deformation of 72.7 nm (37.5%) were observed, those deformation were used to calculate the respective breaking pressure (Fig. 4b). The results show that the critical breaking pressure increased as the size of the SiNCs decreased. The difference in the breaking pressure observed between the different SiNCs samples was statistically significant (t-test, p = 0.95). Additionally, the variation of breaking pressure with the shell thickness and the capsule diameter follow the expected behavior for the critical buckling pressure (eqn (3)) as demonstrated in Fig. S6.†
The AFM results showed the mechanical response of individual SiNCs. However, for release applications, probing a group of SiNCs simultaneously is essential. To do so, SiNCs containing a fluorescent cargo (rhodamine-labeled polyethylene glycol) were prepared. A large cargo was chosen to prevent any release from occurring by mass transport through the silica shell. The rhodamine-labeled PEG used here, like other macromolecular cargos, can only be released if the shell of the SiNCs is disrupted. After drying the suspension of SiNCs containing the rhodamine-PEG, the SiNCs were compressed with controlled load and the fraction of the cargo released was measured. The mechanical properties of individual SiNCs can be correlated with the mechanoresponsive release observed from a group of SiNCs of similar diameter and shell thickness to those used in the AFM experiments.
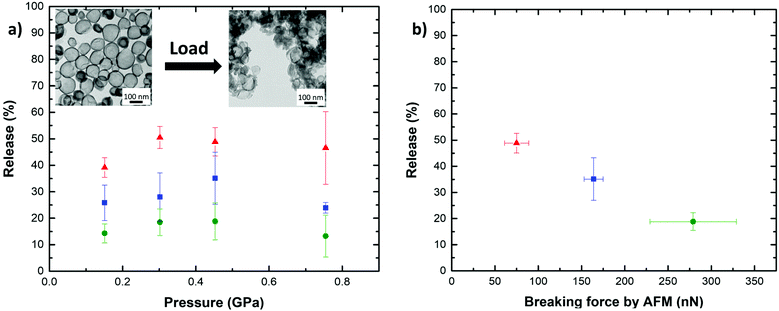
The SiNCs were compressed with a hydraulic press using a die of 13 mm diameter loaded with 15 mg of dried SiNCs. All the compressed samples contained ca. 5 × 1013 NCs. The hydraulic press allowed for the application of loads ranging from 2 to 10 t. This load equals an applied pressure of 0.15 to 0.75 GPa and is therefore of a similar magnitude as the critical breaking pressure observed in 4b. The application of such a load led to the breaking of the compressed SiNCs as visualized by TEM (Fig. 5a inset). The analysis by microscopy clearly showed the fractured shells of SiNCs after the compression of the sample with the hydraulic press.
After the compression, the SiNCs were recovered and dispersed in an EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O mixture (1
H2O mixture (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). During the redispersion, the dye contained in the broken SiNCs was extracted into the solvent mixture, and the quantification of the release was performed by measuring the fluorescence intensity of the rhodamine in solution. The mechanoresponsive release was studied for three different combinations of shell thickness and diameter either small SiNCs with a thin shell (h = 5.5 nm; D = 84 nm), medium SiNCs with an average shell thickness (h = 7.5 nm; D = 125 nm), or large SiNCs with a thick shell (h = 8.5 nm; D = 177 nm). Every SiNCs sample was compressed for 30 s with a load ranging from 2 to 10 t (Fig. 5a). For the weakest SiNCs, the release of the cargo increased with the load applied until it reached a maximal value. In the case of the most robust SiNCs sample studied, the release remained limited, and the variations observed were not statistically significant. When the load applied was increased above ca. 0.45 GPa, further compression led to an apparent decrease of the release, but this behavior was ascribed to the sintering of the SiNCs observed under compression with large loads due to sintering,39,40 reducing the redispersibility of the sample and the extraction of the cargo from the broken capsules. In the case of small SiNCs with a thin shell a release of up to ca. 50% of the encapsulated cargo was observed. While lower maximal releases of ca. 35 and 19% were observed for medium SiNCs with an average shell thickness and large SiNCs with a thick shell. The complete release of the cargo was not observed due to the combination of the sintering of the SiNCs (Fig. S7†), the uneven force distribution through the compressed sample, and the distribution in size and thickness of the SiNCs leading to only a fraction of the SiNCs experiencing a force larger than the threshold pressure needed to break and release the cargo. Higher release of the cargo can be expected in diluted samples, lower concentration of SiNCs would reduce the occurrence of SiNC/SiNC contact and interaction under the presence of a load leading to the sintering of the SiNCs. By correlating the maximum release observed for the different SiNCs with the respective breaking forces determined by AFM, the results clearly demonstrate that the tuning of the mechanoresponsive release from the SiNCs can be achieved by controlling the architecture of the SiNCs. The capsules with the lowest breaking force as measured by AFM released the largest amount of dye (Fig. 5b). In contrast, the SiNCs with the highest breaking force released the lowest amount of dye, demonstrating the controlled mechanoresponsive release for SiNCs designed with different breaking resistance.
1). During the redispersion, the dye contained in the broken SiNCs was extracted into the solvent mixture, and the quantification of the release was performed by measuring the fluorescence intensity of the rhodamine in solution. The mechanoresponsive release was studied for three different combinations of shell thickness and diameter either small SiNCs with a thin shell (h = 5.5 nm; D = 84 nm), medium SiNCs with an average shell thickness (h = 7.5 nm; D = 125 nm), or large SiNCs with a thick shell (h = 8.5 nm; D = 177 nm). Every SiNCs sample was compressed for 30 s with a load ranging from 2 to 10 t (Fig. 5a). For the weakest SiNCs, the release of the cargo increased with the load applied until it reached a maximal value. In the case of the most robust SiNCs sample studied, the release remained limited, and the variations observed were not statistically significant. When the load applied was increased above ca. 0.45 GPa, further compression led to an apparent decrease of the release, but this behavior was ascribed to the sintering of the SiNCs observed under compression with large loads due to sintering,39,40 reducing the redispersibility of the sample and the extraction of the cargo from the broken capsules. In the case of small SiNCs with a thin shell a release of up to ca. 50% of the encapsulated cargo was observed. While lower maximal releases of ca. 35 and 19% were observed for medium SiNCs with an average shell thickness and large SiNCs with a thick shell. The complete release of the cargo was not observed due to the combination of the sintering of the SiNCs (Fig. S7†), the uneven force distribution through the compressed sample, and the distribution in size and thickness of the SiNCs leading to only a fraction of the SiNCs experiencing a force larger than the threshold pressure needed to break and release the cargo. Higher release of the cargo can be expected in diluted samples, lower concentration of SiNCs would reduce the occurrence of SiNC/SiNC contact and interaction under the presence of a load leading to the sintering of the SiNCs. By correlating the maximum release observed for the different SiNCs with the respective breaking forces determined by AFM, the results clearly demonstrate that the tuning of the mechanoresponsive release from the SiNCs can be achieved by controlling the architecture of the SiNCs. The capsules with the lowest breaking force as measured by AFM released the largest amount of dye (Fig. 5b). In contrast, the SiNCs with the highest breaking force released the lowest amount of dye, demonstrating the controlled mechanoresponsive release for SiNCs designed with different breaking resistance.
A potential application for these mechanoresponsive SiNCs is in lubricant systems. Modern lubricants consist of a base oil containing various additives to improve and preserve the low friction properties the oil presents in a tribological contact. For example, solid nanoparticles have gained interest as lubricant additives,41 as they can reduce friction by rolling, sliding or exfoliation mechanisms in the contact area of two interacting surfaces in relative motion to each other.42,43 Robust SiNCs are not only able to mimic the friction-reducing properties of nanoparticles, but additionally, allow the encapsulation of friction controlling/reducing molecules. By releasing these molecules in a mechanoresponsive manner, a self-regulatory system could be developed, which would be triggered by the increasing forces in the tribological contact once a mechanical threshold is exceeded e.g. due to lubricant depletion. Typical forces present in a tribological contact are load and shear forces, both could potentially rupture the silica shell. Here, the compression experiments using a hydraulic press only focus on the effect of load, which is the predominant source of mechanical stress in typical tribological contact.44 Furthermore, the level of load applied determines the friction-reducing mechanisms of nanoparticles. Low pressure typically results in the rolling of spherical nanoparticles, while at intermediate pressures, the particles show a sliding behavior at the contacting surfaces. At high pressures, the particles can exfoliate to form a low shear strength layer on the surfaces of the interacting tribological contacts. By tailoring the architecture of the SiNCs precisely to the forces present in a given system, controlled release of the encapsulating friction modifying molecules would allow controlling friction over a long period of time.
Conclusions
We successfully prepared a model system to study the mechanoresponsive release of molecules encapsulated in silica nanocapsules (SiNC). By controlling the architecture of the SiNCs (shell thickness and diameter), the force needed to break those nanocarriers was precisely tuned as determined using AFM force spectroscopy. The breaking force of individual capsules increased with both the shell thickness and the capsule diameter. Simultaneously, the maximal deformation of the SiNCs at the breaking point increased with increasing capsule diameter, indicating the importance of monodisperse size distribution to use such systems for the controlled release of cargos.The resulting SiNCs were used to trigger the release of encapsulated cargos after the application of mechanical stress. The mechanoresponsive release during the compression of dried SiNCs in a hydraulic press showed that the critical force needed to break individual SiNCs could be used to predict the release from different carriers. The SiNCs displayed excellent properties as mechanoresponsive nanocarriers since tuning the architecture of the nanocapsule, such as shell thickness or capsule diameter, led to a precisely controlled release. This approach has a vast potential for the development of smart lubricants as the release of encapsulated cargo can be tuned to control the friction in tribological contacts.
Experimental
Chemicals
Tetraethylorthosilicate (TEOS) was purchased from TCI chemicals; toluene from Fisher chemical, cetyltrimethylammonium bromide (CTAB) from Acros organics; polyethylenglycol (35 kg mol−1) and rhodamine B isothiocyanate from Sigma-Aldrich, hexadecane, hexane and ethanol from VWR chemicals, and all chemicals were used as received.Synthesis of silica nanocapsules
Silica nanocapsules (SiNCs) were prepared via oil-in-water miniemulsion. The oil phase was composed of silica precursor TEOS (4 g; 4.255 mL; 19.2 mmol) and hexadecane (3 g; 3.896 mL; 13.3 mmol) and was mixed briefly. The aqueous phase was prepared by dissolving 78 mg CTAB (0.2 mmol) in 90 mL deionized water. The two phases were combined and stirred for 10 min at 400 rpm. Then, the mixture was pre-emulsified for 2 min with an Ultra-Turrax at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm. Finally, the pre-emulsified mixture was passed through a microfluidizer (LM10, Microfluidic corp.) equipped with an F20Y interaction chamber with channels of 75 μm at a pressure of 10
000 rpm. Finally, the pre-emulsified mixture was passed through a microfluidizer (LM10, Microfluidic corp.) equipped with an F20Y interaction chamber with channels of 75 μm at a pressure of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 PSI for two cycles. After emulsification, the miniemulsion was allowed to react for 24 h by stirring at 600 rpm to obtain final SiNCs. A library of SiNCs was prepared by following the procedure described and changing the composition of the oil phase as noted in Table S1.†
000 PSI for two cycles. After emulsification, the miniemulsion was allowed to react for 24 h by stirring at 600 rpm to obtain final SiNCs. A library of SiNCs was prepared by following the procedure described and changing the composition of the oil phase as noted in Table S1.†
AFM sample preparation
Freshly prepared SiNCs were dialyzed against water for 8 h. Afterwards, 10 μL of purified SiNCs were diluted with 10 mL deionized water and drop-casted on a clean glass slide.Release study from broken SiNCs
The SiNCs were dialyzed against ethanol for 2 d and subsequently dried with glucose (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 wt% ratio of SiNCs
1 wt% ratio of SiNCs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose). 15 mg of dried capsules were compressed in a hydraulic press from PerkinElmer for 30 s at a controlled load of 2, 4, 6, 10 t.
glucose). 15 mg of dried capsules were compressed in a hydraulic press from PerkinElmer for 30 s at a controlled load of 2, 4, 6, 10 t.
Then, 15 mg of the compressed SiNCs were redispersed in 5 mL EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (1
H2O (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and then sonicated in an ultrasound bath for 5 min. Finally, the suspension was filtered through a 100
1) and then sonicated in an ultrasound bath for 5 min. Finally, the suspension was filtered through a 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MWCO spin filter, and the fluorescence intensity of the filtrate was measured at a wavelength of 545–700 nm.
000 MWCO spin filter, and the fluorescence intensity of the filtrate was measured at a wavelength of 545–700 nm.
Characterization methods
Atomic force microscopy (AFM) was realized by using a JPK3 nanowizard with Olympus Micro Cantilevers with a resonant frequency of 70 kHz and a spring constant of 2 N m−1. For the compression experiments, the force was preset to 500 nN and the cantilever was moved towards the sample on the z-axis. Once in contact with the SiNC, the cantilever continued moving towards the substrate and thereby continuously increased the force applied to the sample. When the preset force was reached, the cantilever started to retract. Before reaching the preset force, the cantilever usually broke the silica shell. This event was observed as an abrupt step in the force/distance profile.Transmission electron microscopy (TEM) was done with a JEOL 1400 electron microscope. The shell thickness of SiNCs was determined by measuring 50 NCs in ImageJ. Dynamic light scattering (DLS) measurements were performed using a Malvern Zetasizer Nano-S90. Fluorescence spectroscopy was done by using a Tecan infinite M1000 platereader. Infrared spectroscopy was realized by using a PerkinElmer Spectrum BX FT-IR system.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support from Fuchs Petrolub and the Max Planck Society. Open Access funding provided by the Max Planck Society.References
- M. Gu, X. Wang, T. B. Toh and E. K. Chow, Drug Discovery Today, 2018, 23, 1043–1052 CrossRef CAS PubMed.
- F. U. Din, J. Y. Choi, D. W. Kim, O. Mustapha, D. S. Kim, R. K. Thapa, S. K. Ku, Y. S. Youn, K. T. Oh, C. S. Yong, J. O. Kim and H. G. Choi, Drug Delivery, 2017, 24, 502–510 CrossRef PubMed.
- V. Marturano, P. Cerruti, C. Carfagna, M. Giamberini, B. Tylkowski and V. Ambrogi, Polymer, 2015, 70, 222–230 CrossRef CAS.
- Y. Lv, L. Hao, W. Hu, Y. Ran, Y. Bai and L. Zhang, Sci. Rep., 2016, 6, 29321 CrossRef CAS PubMed.
- R. Liu, X. Zhao, T. Wu and P. Feng, J. Am. Chem. Soc., 2008, 130, 14418–14419 CrossRef CAS PubMed.
- J. Wang, J. A. Kaplan, Y. L. Colson and M. W. Grinstaff, Adv. Drug Delivery Rev., 2017, 108, 68–82 CrossRef CAS PubMed.
- R. Rajamanickam, K. Kwon and G. Tae, Mater. Sci. Eng., 2020, 111, 110789 CrossRef CAS PubMed.
- M. Hu, S. Peil, Y. Xing, D. Döhler, L. Caire da Silva, W. H. Binder, M. Kappl and M. B. Bannwarth, Mater. Horiz., 2018, 5, 51–58 RSC.
- Y. Chen, W. Li, J. Luo, R. Liu, G. Sun and X. Liu, ACS Appl. Mater. Interfaces, 2021, 13, 14518–14529 CrossRef CAS PubMed.
- J. Fickert, P. Rupper, R. Graf, K. Landfester and D. Crespy, J. Mater. Chem., 2012, 22, 2286–2291 RSC.
- C. J. Thrasher, Z. J. Farrell, N. J. Morris, C. L. Willey and C. E. Tabor, Adv. Mater., 2019, 31, e1903864 CrossRef PubMed.
- J. F. Patrick, M. J. Robb, N. R. Sottos, J. S. Moore and S. R. White, Nature, 2016, 540, 363–370 CrossRef CAS PubMed.
- H.-J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152 CrossRef CAS.
- J. D. Berry, S. Mettu and R. R. Dagastine, Soft Matter, 2017, 13, 1943–1947 RSC.
- V. C. Shunmugasamy, S. E. Zeltmann, N. Gupta and O. M. Strbik, JOM, 2014, 66, 892–897 CrossRef CAS.
- C. I. Zoldesi, I. L. Ivanovska, C. Quilliet, G. J. Wuite and A. Imhof, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 051401 CrossRef CAS PubMed.
- B. Sarrazin, N. Tsapis, L. Mousnier, N. Taulier, W. Urbach and P. Guenoun, Langmuir, 2016, 32, 4610–4618 CrossRef CAS PubMed.
- M. Ghorbanzadeh Ahangari, A. Fereidoon, M. Jahanshahi and N. Sharifi, Composites, Part B, 2014, 56, 450–455 CrossRef CAS.
- C. Preetz, A. Hauser, G. Hause, A. Kramer and K. Mader, Eur. J. Pharm. Sci., 2010, 39, 141–151 CrossRef CAS PubMed.
- A. R. Sulkanen, J. Sung, M. J. Robb, J. S. Moore, N. R. Sottos and G. Y. Liu, J. Am. Chem. Soc., 2019, 141, 4080–4085 CrossRef CAS PubMed.
- J. Fickert, D. Schaeffel, K. Koynov, K. Landfester and D. Crespy, Colloid Polym. Sci., 2013, 292, 251–255 CrossRef.
- S. M. Jo, F. R. Wurm and K. Landfester, Angew. Chem., Int. Ed., 2021, 60, 7728–7734 CrossRef CAS PubMed.
- S. Jiang, A. Kaltbeitzel, M. Hu, O. Suraeva, D. Crespy and K. Landfester, ACS Nano, 2020, 14, 498–508 CrossRef CAS PubMed.
- Q. Yin, S. Tu, M. Chen and L. Wu, Langmuir, 2019, 35, 11524–11532 CrossRef CAS PubMed.
- S. Jiang, M. Mottola, S. Han, R. Thiramanas, R. Graf, I. Lieberwirth, V. Mailänder, D. Crespy and K. Landfester, Part. Part. Syst. Charact., 2020, 37, 1900484 CrossRef CAS.
- M. S. Alkanawati, F. R. Wurm, H. Thérien-Aubin and K. Landfester, Macromol. Mater. Eng., 2018, 303, 1700505 CrossRef.
- J. Canet-Ferrer, E. Coronado, A. Forment-Aliaga and E. Pinilla-Cienfuegos, Nanotechnology, 2014, 25, 395703 CrossRef PubMed.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Elsevier, 2002 Search PubMed.
- A. Fery, F. Dubreuil and H. Möhwald, New J. Phys., 2004, 6, 18–18 CrossRef.
- A. Fery and R. Weinkamer, Polymer, 2007, 48, 7221–7235 CrossRef CAS.
- C. Gao, E. Donath, S. Moya, V. Dudnik and H. Möhwald, Eur. Phys. J. E, 2001, 5, 21–27 CrossRef CAS.
- A. V. Progorelov, Bending of Surfaces and Stability of Shells, American Mathematical Society, 1988 Search PubMed.
- C. I. Zoldesi and A. Imhof, Adv. Mater., 2005, 17, 924–928 CrossRef CAS.
- C. I. Zoldesi, C. A. van Walree and A. Imhof, Langmuir, 2006, 22, 4343–4352 CrossRef CAS PubMed.
- W. Yang, J. Yang, Y. Dong, S. Mao, Z. Gao, Z. Yue, S. J. Dillon, H. Xu and B. Xu, Carbon, 2018, 137, 411–418 CrossRef CAS.
- L. Zhang, M. Kappl, G. K. Auernhammer and D. Vollmer, Langmuir, 2009, 25, 2711–2717 CrossRef CAS PubMed.
- L. A. Taber, J. Appl. Mech., 1982, 49, 490–491 CrossRef.
- H. Hertz, J. Reine Angew. Math., 1881, 92, 156–171 Search PubMed.
- M. R. Gallas, A. R. Rosa, T. H. Costa and J. A. H. d. Jornada, J. Mater. Res., 1996, 12, 764–768 CrossRef.
- A. Jiang, D. Ke, L. Xu, Q. Xu, J. Li, J. Wei, C. Hu and S. Grasso, J. Materiomics, 2019, 5, 496–501 CrossRef.
- W. Dai, B. Kheireddin, H. Gao and H. Liang, Tribol. Int., 2016, 102, 88–98 CrossRef CAS.
- L. Rapoport, V. Leshchinsky, I. Lapsker, Y. Volovik, O. Nepomnyashchy, M. Lvovsky, R. Popovitz-Biro, Y. Feldman and R. Tenne, Wear, 2003, 255, 785–793 CrossRef CAS.
- I. Lahouij, B. Vacher, J.-M. Martin and F. Dassenoy, Wear, 2012, 296, 558–567 CrossRef CAS.
- O. Tevet, P. Von-Huth, R. Popovitz-Biro, R. Rosentsveig, H. D. Wagner and R. Tenne, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 19901 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr04697g |
| This journal is © The Royal Society of Chemistry 2021 |