A DFT study of the adsorption energy and electronic interactions of the SO₂ molecule on a CoP hydrotreating catalyst

Abstract

The adsorption energy and electronic properties of sulfur dioxide (SO₂) adsorbed on different low-Miller index cobalt phosphide (CoP) surfaces were examined using density functional theory (DFT). Different surface atomic terminations and initial molecular orientations were systematically investigated in detail to determine the most active and stable surface for use as a hydrotreating catalyst. It was found that the surface catalytic reactivity of CoP and its performance were highly sensitive to the crystal plane, where the surface orientation/termination had a remarkable impact on the interfacial chemical bonding and electronic states toward the adsorption of the SO₂ molecule. Specifically, analysis of the surface energy adsorption revealed that SO₂ on Co-terminated surfaces, especially in (010), (101) and (110) facets, is energetically more favorable compared to other low index surfaces. Charge density difference, density of states (DOS) and Gibbs free energy studies were also carried out to further understand the bonding mechanism and the electronic interactions with the adsorbate. It is anticipated that the current findings will support experimental research towards the design of catalysts for SO₂ hydrodesulfurization based on cobalt phosphide nanoparticles.

---

Introduction

Sulfur dioxide (SO₂) is a common atmospheric pollution gas¹ produced as a result of fossil fuel combustion. In fact, the serious damage caused by acid rain is a direct consequence of SO₂ oxidization in the atmosphere, which is due to its corrosive nature.^2–4 Therefore, the elimination of SO₂ has attracted attention in a variety of fields including catalysis, corrosion, and air pollution control.⁵

Today, oil-derived fuels are as much as half of the total energy produced worldwide. Sulfur molecules are abundant in all types of crude oil. These compounds not only degrade the atmosphere quality, but also degrade the feedstock quality and poison the catalysts used to purify vehicles emissions.⁶ Thus, due to their negative impact, environmental regulations require their elimination from fossil fuel feedstocks,⁷ as well as a general decrease in NO_x and SO_x emissions.^8,9

Unfortunately, due to the reduction in the availability of light petroleum, the quality of the crude feed stock has deteriorated. This makes the development of new catalysts that are both active and stable necessary for better refinery processes.⁸ One key process is hydrodesulfurization (HDS), which is one of the hydrotreating processes¹⁰ dealing with the removal of sulfur compounds for the production of cleaner fuels¹¹ and lowering the atmospheric pollution.¹² Although the hydrotreating process has been used for more than 80 years, a deep understanding of the relationship between the structure of the catalyst and its performance has only been achieved in this decade. Molybdenum sulphide nanocatalysts are currently used in industry for HDS; however, due to their lamellar structure, their active site density is very low since the active sites are mainly located on their edge planes. Thus, the current research is focused on isotropic structures, such as metal phosphides, where the active metal is exposed in all crystallographic directions.¹³

Transition metal phosphides (TMPs) are used as efficient hydrotreating catalysts for increasing the quality of oil through the HDS reaction.^14,15 TMPs show high thermal stability and high HDS conversion. Their activity is surprisingly similar to that of noble metallic catalysts.¹⁵ TMPs and noble metal phosphides exhibit better performances than metal carbides, metal nitrides, and pure metals during operation.¹⁶ The importance of phosphorous in the metal phosphide group is that it acts as a promoter for modifying the properties of the support, as well as the mechanical and thermal stability of the catalyst. Nitrogen, carbon, and boron have also been used as promoters, but phosphorous is superior in stabilizing metal phosphide catalysts under HDS conditions without significant deactivation.¹⁷ Phosphorus also offers high resistance against sulfur poisoning and high structural stability.¹⁸ Nanoparticles exhibit important crystallographic planes, which affect their physical and chemical properties. This is why it is challenging to optimize the structure of nanoparticles to meet certain criteria, both theoretically and experimentally.¹⁶ Therefore, investigating the active sites of TMPs has become significant to enhance their HDS performance.

Dibenzothiophene (DBT) and thiophene, which are common organosulfur compounds found in crude oil, have been intensively studied experimentally in the literature.^{13–15,17,19–22} In contrast, SO₂ has not been given the required attention for HDS using TMPs, although it has an undeniable influence on the environment. Specifically, it was reported by Blair and coworkers²³ that the photo-oxidation of fifty-seven volatile organic compounds (VOCs) produces organosulfates (R-OS(O)₂OH) when SO₂ molecules are present in the atmosphere. Also, hydroxyl groups (OH) can support the conversion of SO₂ to H₂SO₄.

The use of density functional theory (DFT) together with experimental data has narrowed the gap between catalysis science and technology, leading to a greater enhancement in the HDS performance of catalysts.⁸ DFT is a powerful tool to investigate the most active planes for HDS. For instance, Bai and co-workers²⁴ reported the dissociation energy for some sulfur molecules on the surface of MoP. In particular, the dissociation of H₂S was found to require 385.1 kJ mol⁻¹ to break the H–S bond, whereas around 373.4 kJ mol⁻¹ is required for C–S bond dissociation in CH₃S–C₆H₅. Conversely, the energy required for dissociating HH-DBT is lower (317 kJ mol⁻¹), which makes it comparatively easier. Tian et al.²⁵ used the generalized gradient approximation with the Perdew–Burke–Ernzerhof (GGA-PBE) functional to analyse the surface energy of the asymmetric facets of MoP. The (101) and (100) facets were found to be the most stable. However, thiophene was found to favour dissociation on the most unstable (001) surface of MoP. Moreover, using self-consistent periodic DFT calculations, the HDS of thiophene on the clean (001) plane of MoP was compared with a sulfur-modified surface.²⁵ On both surfaces, thiophene prefers the direct desulfurization pathway due to the lower activation barriers for the C–S bond. The existence of sulfur does not increase the activation barrier, but leads to a new path, for which the C–S bond can be ruptured. The adsorption energies (absolute value) of thiophene were found by Li et al.¹² to be between 2.54 to 2.6 eV on the (001) surface, with a dissociation energy of 3.93 eV. The presence of sulfur acts as a promoter since it reduces the dissociation energy by around 0.15 to 0.61 eV.¹² A similar trend was observed for the (010) surface, but the presence of sulfur on this plane reduced the barrier by only 0.28 eV due to the reduction of the C–S bond energy barrier caused by the structural deformation of the adsorbate.²⁶

Furthermore, Fuks and coworkers²⁷ found that the Ni₃P phase of the nickel phosphide family provides better adsorption for sulfur atoms. In addition, the sulfur coverage was maximum compared to Ni₂P and Ni₁₂P₅ on the (001) facet. In addition, Ren et al.²⁸ suggested that the (001) facet of MoP has better stability for the adsorption of thiophene compared to the same facet of Ni₂P.

The projector augmented wave method (PAW) was used by Li et al.²⁰ to calculate the hydrogen adsorption energies for the Ni (111), Ni₂P (001), and Ni₃PS (001) surfaces. Values of around 0.03 eV were found for all the surfaces, which indicate that the reaction is unfavourable. Recently, Scaranto et al.²⁹ used DFT to calculate the surface formation energy and the work function of the semi-metallic CoP₂. The PBE functional was compared with hybrid methods such as HSE06 and B3LYP, and it was found that the (100) and (001) planes are the most stable facets since they have the highest work functions and the lowest surface formation energies.

To develop a suitable catalyst to meet industrial requirements, it must have high selectivity, stability, and activity. Coking and catalyst poisoning are two crucial factors that affect the stability of catalysts.³⁰

Although nickel-supported catalysts have the highest activity among the metal phosphides group,²¹ they suffer from coking problems, which affect their stability, resulting in the deactivation of the catalyst.^31–33 Thus, cobalt is chosen as the active metal in metal phosphide catalysts for hydrodesulfurization since it is more resistant to coking and it has high stability and activity even at high temperatures.³⁴ One of the most promising catalysts is the CoP phase since it shows a better catalytic performance compared with other cobalt phosphide phases such as Co₂P^16,17 and CoP₂.²⁹ To the best of our knowledge, there is no report in the literature on DFT calculations of the adsorption of sulfur molecules on the CoP catalyst, which motivated us to investigate the interaction of CoP with the SO₂ molecule, which has an undeniable influence on the environment.

In this work, we present and discuss a DFT study on the adsorption of an SO₂ molecule on seven Miller index facets of the CoP orthorhombic crystal structure together with their electronic interactions by calculating important surface characteristics such as the charge density difference, density of states, Bader charge analysis,³⁵ density of states and Gibbs free energies. The chemical properties of the adsorbent/adsorbate systems are highly dependent on the chosen surface plane, surface atomic termination and molecular orientation. Therefore, to better understand the chemical reactivity and to shed light on the underlying mechanism governing the catalytic activity of SO₂/CoP, it is instructive to explore all their possible surface atomic configurations to analyse their surface interaction in more detail at the atomic level.

Computational methodology

The structural and electronic properties of the adsorption of SO₂ on low-Miller index CoP surfaces were investigated by performing spin-polarized³⁶ DFT-D3 (ref. 37 and 38) calculations as implemented in the Vienna Ab initio Simulation Package (VASP).^39–41 The dispersion term (long-range van der Waals interactions) was included since it has been reported to have a great influence in the calculations of adsorption energies, especially, when physisorption occurs.^42–46

The all-electron wave functions and the pseudopotentials for the electron–ion interaction were described within the PAW method,⁴⁷ where the exchange and correlation (XC) potential was generated within the GGA-PBE scheme.⁴⁸ The energy tolerance in the self-consistent field calculations (SCF) was set to 1 × 10⁻⁶ eV per atom⁴⁹ and a force tolerance of 1 meV Å⁻¹ (ref. 50) with 0.05 eV of Gaussian smearing was employed. The Kohn–Sham wave functions were expanded in plane waves up to an energy cut-off of 520 eV, ensuring the high accuracy of this work compared to previous theoretical studies.^29,51–54

The CoP surfaces were constructed by two-dimensional translational symmetry⁵⁵ using the repeated slab method. We considered slabs of six or more CoP layers (depending on the cleavage plane) with a lateral length size of minimum 5 Å (p(1 × 1) or replicated p(2 × 1) if needed), and a vacuum thickness corresponding to 20 Å was chosen to separate the two surface slabs to avoid artificial interactions between them.^26,42 The slab thickness was checked before, and it was validated that 6 layers are sufficient to have the ground state properties well converged, showing a difference in surface energy of less than 0.2 eV.

The upper layers (half of the layers) of the optimized structure were allowed to relax, while the half bottom layer was kept fixed.⁵⁶ The number of atoms was the same for all the surfaces (i.e., crystal formula: Co₁₆P₁₆). Moreover, after a consistency test, the Brillouin zone (BZ) was sampled using 8 × 8 × 1 Monkhorst–Pack grid.⁵⁷

Specifically, we considered seven different low-index surfaces, where the optimized bulk CoP was cleaved with different surface orientations, namely (001), (010), (011), (100), (101), (110), and (111) planes.

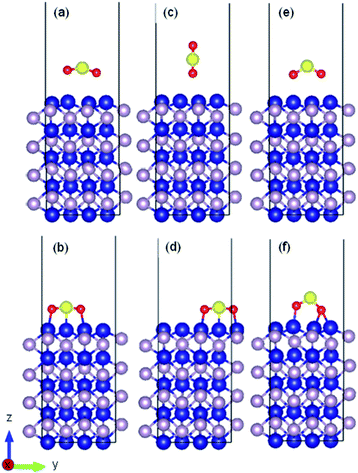
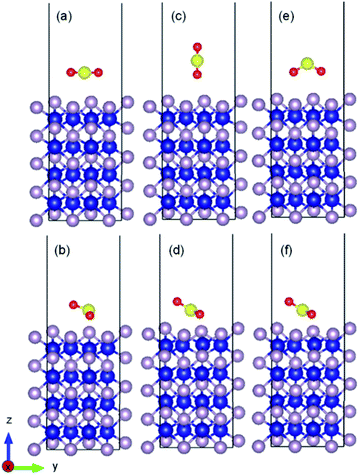
For each surface orientation, cobalt and (or) phosphorus surface terminations were examined. The SO₂ molecule was oriented for each surface configuration in parallel and perpendicular (i.e., one oxygen atom facing the surface) configurations, and with the perpendicular configuration with two oxygen atoms facing the surface to determine the most stable and favourable structure.

The adsorption energy was calculated as:

E_ads = E_system − [E_slab + E_molecule] (1)

where E_system is the total energy of the optimized system, E_slab is the total energy of the bare CoP slab and E_molecule is the total energy of an isolated SO₂ molecule. A larger negative E_ads value means a more stable configuration and exothermic adsorption.⁴³

Charge density difference plots were obtained by subtracting the total charge of the system from the individual charges of the slab and the molecule, as follows:

Δρ_system = ρ_system − [ρ_slab + ρ_molecule] (2)

where ρ_system, ρ_slab, and ρ_molecule are the electron charge distribution of the whole system, slab, and molecule, respectively.

The atoms positions and charge density illustrations were obtained using the VESTA software.⁵⁹ Further analysis was conducted using the post-processing program VASPKIT.⁶⁰ Partial atomic charges were obtained using Bader charge analysis as implemented by Henkelman and co-workers.^61–63

Additionally, the differential Gibbs free energies of adsorption (ΔG_ads) for the different surfaces were calculated using the DFT total energies, corrected by the entropic change (TΔS) and the difference in zero-point energy (ΔE_ZPE) derived from the vibrational frequencies.^64–67

ΔG_ads = ΔE_ads + ΔE_ZPE − TΔS (3)

Due to different molecular configurations and facet terminations, a nomenclature was elaborated for each corresponding case to categorize the investigated configurations. For example, for the polar surfaces, [(111)-Co-∥], [(101)-P-⊥] and [(010)-Co–O⊥] indicate a cobalt-terminated (111) facet with a parallel orientation of SO₂ molecule from the surface, a phosphorous-terminated (101) facet with an initial perpendicular orientation of the sulfur dioxide, and an SO₂ molecule initially placed perpendicular with two oxygen atoms facing the cobalt-terminated (010) surface, respectively.

Results and discussion

SO₂ adsorption

We first examined the lattice structure of cobalt phosphide. With the above computational settings, the optimized orthorhombic [Pnma [62]]-type⁵³ CoP lattice parameters were computed to be a = 3.266 Å, b = 5.064 Å, and c = 5.542 Å,⁶⁸ which are in good agreement with experimental measurements (error less than 1%)¹⁵ and other DFT calculations.⁵³

To determine the relative stability of the different facets, the surface energies were calculated considering the total energy of the bulk crystal, the number of unit cells used to replicate the slab, and the surface area,^25,29,53 and the results are summarized in Table 1.

Table 1 Surface energy of the different CoP facets studied in this work

Facet	(001)-Co	(001)-P	(010)-Co	(010)-P	(011)-Co	(011)-P
Esurf (meV Å^−2)	126.1	144.0	115.2	125.8	110.6	99.8

---

Facet	(100)	(101)-Co	(101)-P	(110)-Co	(110)-P	(111)-Co	(111)-P
Esurf (meV Å^−2)	83.8	125.4	141.3	95.7	102.3	107.8	139.1

---

The most favourable/stable surface with the lowest E_surf was found to be (100) (83.8 meV Å⁻², i.e., 1.34 J m⁻²), followed by the (111)-Co, (011)-P and (110)-Co terminated surfaces. The obtained results are comparable with other DFT calculations for different systems such as Pt (111)⁴⁵ and CoP₂.²⁹ Besides, it is worth mentioning that the bare CoP (011) slab for the hydrogen evolution reaction was also identified as the most stable facet with high stability and the lowest surface energy.⁵³

In total, thirty-nine different adsorption configurations were investigated in this work (thirteen facets, as listed in ref. 58, and three SO₂ initial configurations per surface). The adsorption energy was calculated for the different configurations, either the cobalt- or phosphorus-terminated CoP surfaces. This large range of different configurations reflects the richness of SO₂ chemistry.⁷¹

All the calculated adsorption energies are negative (Fig. 1 shows each system with the corresponding nomenclature), indicating spontaneous adsorption on the surface. The more negative the adsorption energy, the stronger the adsorption between the facet and the molecule. The analysed facet energies fall mainly into three categories, i.e., weak, medium, and strong adsorption. The weak adsorption energies range from −0.3 eV to −0.6 eV (i.e., 29 to 58 kJ mol⁻¹), which were obtained for most of the phosphorous-terminated surfaces. These structures are unlikely to provide chemisorption, and thus support the experimental findings of P as a resistant component to sulfur poisoning.¹⁸ Much stronger (medium) adsorption energies ranging from −0.8 to −1.8 eV (i.e., 77 to 173 kJ mol⁻¹) were found, for instance, for the (111)-Co–O⊥, (100)-Co–O⊥, and (001)-Co-∥ configurations, which offer relatively moderate interaction compared to the strongly bonded surfaces. Strong adsorption energies were also obtained for some of the studied facets, irrespective of the molecule orientation, which indicate exothermic binding between the SO₂ molecule and CoP surface.⁴² A preference was observed for cobalt atoms on the surface with the oxygen atoms of the SO₂. This preference can be attributed to the occurrence of lone electrons inducing a net magnetic moment, although “geometries with larger magnetic moments are usually less stable”.⁶⁴

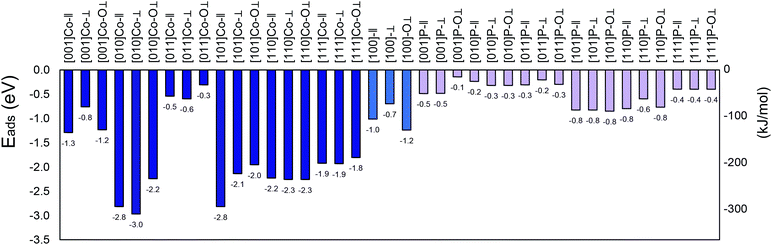Fig. 1 Adsorption energies for the (001), (010), (011), (100), (101), (110) and (111) surfaces of SO₂/CoP calculated in this work. Blue colour for cobalt termination and pink colour for phosphorous termination. See text for details.†

The large value of adsorption of SO₂ on the (010)-Co, (101)-Co and (110)-Co surfaces, in addition to the bond deformation, confirms that SO₂ is strongly chemisorbed on these surfaces.⁴²

As an example, the initial and relaxed configurations for (101)-Co and (101)-P are presented in Fig. 2 and 3, respectively, where the two atomic terminations are clearly shown. The other evaluated configurations can be found in Fig. S1–S13 in the ESI.† In most of the cases, regardless if the molecule was placed initially parallel or perpendicular, a flat-lying position was obtained after relaxation. Similar flat-lying configurations were detected in many transition metal surfaces such as Ni (111), Cu (111)¹ and Pt (111),⁶⁹ as well as in more complex structures such as Ni-doped carbon nanotubes.⁷⁰ According to the results by Lin and coworkers,⁶⁹ the adsorption energy for a configuration facing parallel to a Pt (111) surface and S and O atoms bonded on the bridge sites, was found to be −97.68 kJ mol⁻¹. This value is comparable to that obtained for the (101)-P surfaces, although the strength is half of that obtained for the other surfaces reported in this work. In addition, Pt is very sensitive toward sulfur poisoning, which leads to catalytic deactivation.⁷¹

Fig. 2 Initial and relaxed structures for SO₂ adsorbed on (010) cobalt-terminated surface with (a and b) parallel molecular configuration, (c and d) perpendicular molecular configuration, (e and f) and perpendicular molecule with two oxygen atoms facing the surface.

Fig. 3 Initial and relaxed structures for SO₂ adsorbed on (010) phosphorous terminated surface with (a and b) parallel molecular configuration, (c and d) perpendicular molecular configuration, (e and f) and perpendicular molecule with two oxygen atoms facing the surface.

Even using noble metals (e.g., Pd, Ag, Pt, and Au) as dopants of MoSe₂ for SO₂ adsorption yielded much lower adsorption affinity (E_ads ranging between −0.92 and −0.98 eV) than CoP (011), as reported by Ren et al.⁷² Doping Cu on Au (111) in a 1 : 1 ratio offered −1.0 eV for the adsorption of the SO₂ molecule, which is also weaker than that of CoP(011).² A similar range between (−0.5 to −1.08 eV) was found for the adsorption of SO₂ on Ru(001),⁷³ Pd/Pd₉, Pd/Rh₉, and Pd/W₉.⁷⁴ In addition to the weak adsorption values for noble metals, they are impractical to be used in industrial applications due to their low availability and high cost.⁷⁵

Nonetheless, we also found results in the literature with reported SO₂ adsorption energies of around −2 eV,^76–79 some of them using nickel as an adsorbing-promoter atom. However, it should be noted that nickel catalysts deactivate due to the formation of graphitic carbon, which blocks the reactor tubes and prevents the gas molecules from reaching the active material due to its strong affinity toward carbon atoms.

According to the relaxed configurations obtained, the distance between the SO₂ molecules and the surface ranged from 3.06 Å to 3.33 Å for the phosphorous-terminated facets, while for strong E_ads terminations, this distance was reduced to 1.96 Å.

In addition, the calculated bond length and angle of the free SO₂ (isolated) molecule were found to be 1.447 Å and 119.298°, respectively, which are consistent with previous reports.^80,81 After interacting with the surface, the bond angle of the adsorbed molecule was reduced from the isolated value by 9–11% on average for the cobalt/phosphorous-terminated surfaces, while the interatomic bond lengths were increased by 13–17% for the bonded oxygen atoms. In addition, the molecule was attached from the oxygen end(s) to the uppermost metal atom(s), causing a displacement of ∼0.8 Å toward the surface. The formation of strong bonding between the sulfur-oxygen-cobalt-terminated (010), (101) and (110) surfaces destabilized the ideal components of the molecule by increasing the anti-bonding orbitals occupation of the SO₂ molecule. It is worth mentioning that due to the large surface degree of freedom, the lateral distance between the Co(1) and Co(2) surface atoms also decreased by 0.07 Å on average, while the bond length between P(2) and Co(1) almost remained constant with respect to the ideal one. Table S1 (see ESI)† presents details on the bond distances and angles, work functions, adsorption energies and other calculated parameters of SO₂ adsorbed on the different surfaces.

Electronic properties

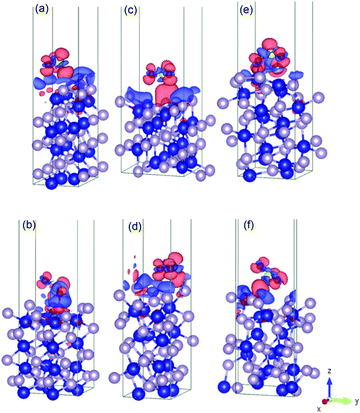
Fig. 4 shows the charge density difference for an SO₂ molecule on the cobalt-terminated surfaces. The red and blue clouds indicate the electron accumulation and depletion, respectively. Only one optimal value (strongest E_ads of each surface) is presented. It should be noted that typically the different initial configurations reached a similar relaxed arrangement, which confirms the importance of using van der Waals interactions to obtain reliable global minima during the optimization procedure.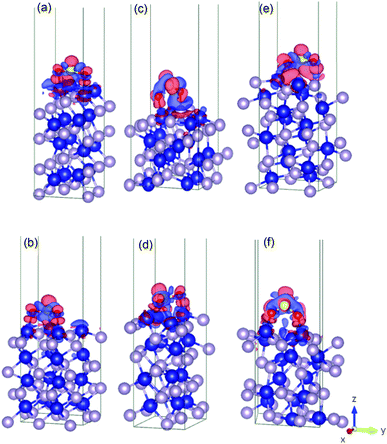

Fig. 4 Illustration of the charge density difference for the relaxed configurations of an SO₂ molecule adsorbed on the cobalt-terminated surfaces: (a) (001)-Co, (b) (101)-Co, (c) (011)-Co, (d) (101)-Co, (e) (110)-Co, (f) and (111)-Co. See text for details.†

As shown in Fig. 4, the charges are widely distributed over the molecule and there is a charge transfer from the surface to the molecule, as manifested by the charge depletion and charge accumulation regions between the surface and the molecule. The molecule is usually chemisorbed with the oxygen atoms closer to the cobalt terminations.

This large charge transfer indicates the susceptibility to sulfur poisoning, as manifested by the depletion of the charge of the active metal, which acts in this case a reducing agent.^56,71

It should be noted that the strong SO₂ adsorption induces a significant electronic redistribution at the surface, where the charges are mostly supplied from the cobalt atoms in the upper layer to the molecule to stabilize the binding between SO₂ and the CoP surface. This indicates that the cobalt atoms can easily transfer electrons, and their neighbouring phosphorous in the surface layers stabilizes the entire system.

This charge transfer also suggests that the SO₂ molecule has an acceptor character, which is supported by the Bader charge analysis. For instance, for (010)-Co, 1.46 |e⁻| is transferred from the sulfur atom, while 1.12 |e⁻| is gained by each bonded oxygen atom. This fact can be traced back to the greater electronegativity of oxygen and sulfur compared to that of the cobalt atom. Conversely, the uppermost cobalt atoms gained around 0.35 |e⁻| after transferring high charges to the molecule.

For the phosphorous-terminated surfaces, the charge density difference is shown in Fig. 5. According to the Bader charge analysis, the first layer of phosphorus gained electrons. For instance, in (011)-P, there is a charge accumulation region on the phosphorous first layer followed by a charge depletion region on the oxygen atom, where the phosphorous layer lost 0.22 |e⁻| on average.

Fig. 5 Illustration of the charge density difference for the relaxed configurations of the SO₂ molecule adsorbed on the phosphorous-terminated surfaces: (a) (001)-P, (b) (101)-P, (c) (011)-P, (d) (101)-P, (e) (110)-P, and (f) (111)-P.

Details on the atomic positions and charges for the other studied surfaces can be found in Tables S2–S8 in the ESI.†

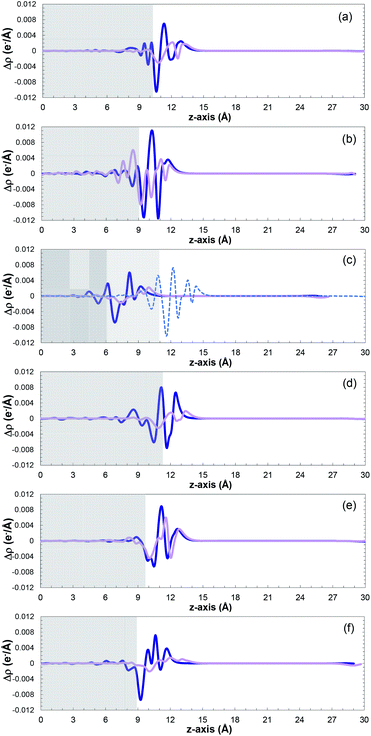
Fig. 6 shows a comparison of the planar average charge density difference, which was calculated by integrating the electron density differences along the x–y plane for all the studied facets (additional potential profiles for the studied systems can be found in Fig. S14 and S15 in the ESI†). It is clear that accumulation and depletion zones appear at the interface of the surface with the SO₂ molecule, as previously reported also for the Pt(111) surface.⁶⁹ The peak in the range of 9–14 Å on the z-axis corresponds to the adsorbed SO₂ molecule (i.e., charge accumulation between the bonded oxygen and the cobalt atoms connected to them), which is usually shown as one peak due to the typical parallel configuration found, i.e., slightly tilted, as previously mentioned.

Fig. 6 Planar average charge density as a function of position in the z-direction for the (a) (001), (b) (010), (c) (011), (100), (d) (101), (e) (110), (f) and (111) surfaces. Cobalt-terminated surfaces as blue lines, and phosphorous-terminated surfaces as pink lines ((100) surfaces in light blue). The positive and negative values indicate electron accumulation and depletion, respectively.

A normal-mode vibrational analysis^82,83 was performed to ensure that the obtained lowest energy structures were indeed local minima, which was corroborated by the absence of imaginary frequencies (see Table S9 in the ESI†). Moreover, the vibrational frequencies of SO₂ in the phosphorous-terminated structures are close to the frequencies of the free SO₂ molecule, which reaffirms the weak physisorption on these surfaces.

The small charge transfer shown in Fig. 6 between the molecule and the phosphorous-terminated surface is attributed to the weaker physical bonding, and hence lower adsorption energy. The surface induces a dipole moment in the molecule, which is manifested by higher charge accumulation at the bottom compared to the top. By comparing the adsorption energies and charge transferred between the cobalt and phosphorus-terminated surfaces, it can be concluded that the adsorption mechanism has a clear preference toward the cobalt-terminated surfaces. Specifically, the enhancement of the chemical reactivity between the SO₂ and CoP surface, and its performance, strongly depends on the formation of strong sulfur–cobalt bonds, which plays a pivotal role in stabilizing the binding of the SO₂ molecule with the CoP surface.

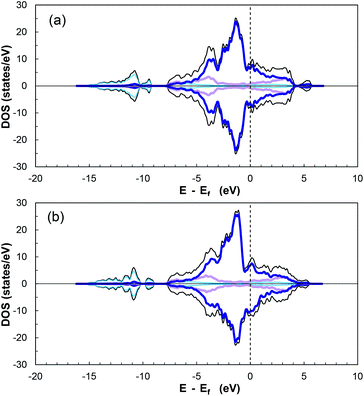
To further clarify the bond formation, the total density of states and projected density of states (TDOS and PDOS, respectively) were plotted, with the up-spin DOS above zero and down-spin DOS below zero. The PDOS parameter helps describe the transferability of electrons between the sulfur dioxide molecule and CoP. All the states above the Fermi level are considered as unoccupied states.⁸⁴

Fig. 7 displays the calculated diagrams for two of the studied structures as representatives of the obtained results from this work. The asymmetric profile of the spin-up and spin-down electrons confirms the magnetic nature of CoP.^85,86

Fig. 7 Calculated total and projected density of states for (a) (101) cobalt-terminated surface, and (b) (101) phosphorous-terminated surface. Total DOS as black lines, dark blue lines for cobalt d-orbitals, pink for phosphorous p-orbitals, and light blue for global s-orbitals. Fermi level indicated by black dashed line at 0 eV.

According to the additionally included information for the specific orbitals for each element type, it can be seen that the PDOS of P in the valence and conduction bands are mainly due to p-orbitals, while the major contributor of the interactions is the partially filled d-orbitals of cobalt. In addition, there is overlap between the cobalt 3d-orbitals and phosphorus 3p-orbitals in the range of −3.1 to −5.3 eV, indicating hybridisation²⁷ and ensuring stability and strong adsorption of a molecule on the electronically active CoP surface.

The DOS of CoP verifies its metallic nature due to the nonexistence of a band gap around the Fermi energy (E_f) (referenced at 0 eV). Moreover, the magnitude of the DOS at E_f serves as indicator for the ability to form bonds with adsorbed species.²⁷ The DOS for the other surfaces can be seen in Fig. S16–S19 in the ESI.†

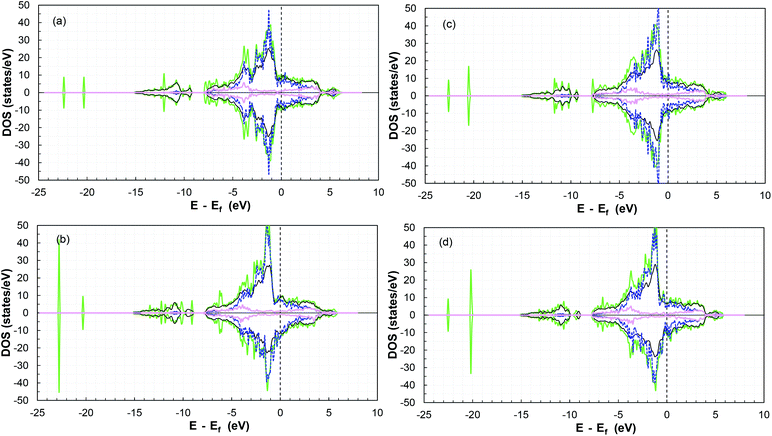
Furthermore, the TDOS and PDOS before and after SO₂ molecule adsorption are presented in Fig. 8. Analysis of the TDOS after adsorption shows a significant overlap of states, with an increase near −1.3, −2.2, −3.4, −7.7 and −10.6 eV (and −20 and −23 eV). Additional states were induced below the Fermi level in the presence of the molecule compared to the reference slab at −6, −12, −9, −20 and −23 eV, which indicate an increase in the conductivity of the surface.^87,88

Fig. 8 TDOS and PDOS for the (a) (101)-Co, (b) (101)-P, (c) (110)-Co, and (d) (110)-P surfaces before and after SO₂ adsorption. Total DOS before adsorption as black lines, green lines for TDOS after adsorption, dark blue dashed lines for cobalt d-orbitals, and pink lines for phosphorous p-orbitals (both after adsorption).

Moreover, there is a shift in the PDOS of the adsorbed molecule on the (011)-surface to lower energies compared to the isolated molecule due to the charge transfer from the slab to the molecule during the adsorption process (see the other surfaces in Fig. S20–S23 in the ESI†). This is due to the forward donation, which is driven by the fact that the SO₂ molecule is more electronegative than cobalt atoms. The electronic chemical potential difference drives the electrons to move from the partially filled d band of cobalt to the unoccupied states of the adsorbate,⁶⁹ thus causing strong adsorption.

Thermochemistry

As an additional feature to evaluate the most reactive and stable CoP surface, we used ab initio atomistic thermodynamics to determine ΔG_ads as a function of temperature (see Fig. 9). The Gibbs free energies and additional thermochemical parameters are displayed in Table S10 in the ESI,† at T = 298.15 K and a very low pressure of 0.03 atm.⁶⁵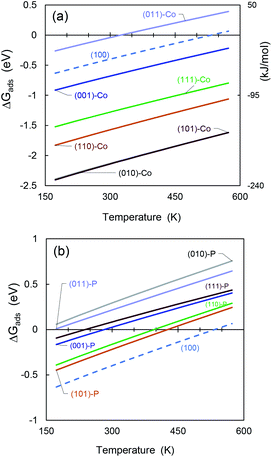

Fig. 9 Gibbs free energy differences for SO₂ molecule adsorbed on (a) cobalt-terminated CoP surfaces, and (b) phosphorous-terminated facets.

It can be seen see that mostly all the cobalt-terminated surfaces show spontaneous adsorption behaviour at ambient temperature (i.e., negative ΔG_ads values), except for (011)-Co, which also shows the lowest adsorption energy for the cobalt-terminated surfaces in the previous sections.

For favourable adsorption on the phosphorous-terminated structures, we found that ΔG_ads is below the ambient temperature. If the adsorption process occurs in a process at higher temperatures, the free energy difference becomes positive and inhibits the catalyst activity.

The obtained values are comparable to that obtained by Hu and co-workers⁵³ for hydrogen adsorption on CoP, although they are much higher due to the polarity of the SO₂ molecule.

In addition, the (100) surface appears between the cobalt- and phosphorous-terminated structures, showing an intermediate affinity for SO₂.

Furthermore, the temperature has an important effect on the catalyst stability and regeneration. We found that most of the cobalt-terminated surfaces maintained spontaneous adsorption behaviour even at temperatures as high as 600 K, which makes them promising materials for hydrodesulfuration. Using ΔG_ads as an additional criterion, we predict that the (010)-Co, (101)-Co, and (110)-Co surfaces of CoP will have good catalytic activity. However, the possibility of desorbing these sulfur-based molecules after reacting with other species must be considered because their high affinity can also act as a promoter for poisoning the catalyst material. Indeed, much more detailed studies are required in this regard.

Conclusions

We presented the DFT results of a systematic study of low-Miller-index surfaces of CoP with both cobalt and phosphorous terminations toward the adsorption of SO₂ molecules for hydrodesulfurization. SO₂ showed a high adsorption energy strength, especially for the cobalt-terminated facets. A value of −2.9 eV was obtained for the (010)-Co and (101)-Co surfaces, while typically physisorption behaviour was obtained for the phosphorous-terminated surfaces (i.e., adsorption energies ca. −0.3 eV). In addition, charge density plots were evaluated to identify the charge transfer behaviour between the CoP facet and the adsorbed SO₂ molecule. It was also found that the d-orbitals of cobalt and the p-orbitals of phosphorus hybridized, and the additional induced states in the PDOS generated by the adsorption of SO₂ indicate strong interactions between the molecule and the substrate.

Ab initio atomistic thermodynamics was used to determine the Gibbs energy of adsorption as a function of temperature, confirming a spontaneous adsorption process for most of the cobalt-terminated surfaces, even at temperatures as high as 600 K, which make them promising materials for hydrodesulfuration. However, this high affinity can also act as a promoter for poisoning the catalyst material, and hence the desorption of these sulfur-based molecules after reacting with other species must be considered in future studies.

In summary, the results confirmed that cobalt phosphide is a promising candidate as a stable and active hydrotreating catalyst, and it can provide the basis for SO₂ surface chemistry on other metal phosphide catalysts. Further studies will include the effect of multiple components and intermediate species in the adsorption behaviour of SO₂ in order to identify possible adsorption site competition and or enhancement due to pre-adsorbed molecules.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support for this work has been provided by Khalifa University of Science and Technology under project RCII-2018-024. Support from the Scientific Computing Department at Khalifa University and computational resources at the Masdar HPC cluster and the RICH Center computational lab are gratefully acknowledged.

References

1. Y. Sakai, M. Koyanagi, K. Mogi and E. Miyoshi, Surf. Sci., 2002, 513, 272–282,  DOI:10.1016/S0039-6028(02)01700-4.
2. X. Zhao, P. Liu, J. Hrbek, J. A. Rodriguez and M. Pérez, Surf. Sci., 2005, 592, 25–36,  DOI:10.1016/j.susc.2006.02.043.
3. M. J. Harrison, D. P. Woodruff and J. Robinson, Surf. Sci., 2006, 600, 1827–1836,  DOI:10.1016/j.susc.2006.02.020.
4. P. Zhang, Q. Zhao, J. Liu and B. Yang, Catal. Today, 2018, 314, 170–178,  DOI:10.1016/j.cattod.2017.12.031.
5. R. Mozo, M. K. Agusta, M. M. Rahman, W. A. Diño, E. T. Rodulfo and H. Kasai, J. Phys.: Condens. Matter, 2007, 19, 36,  DOI:10.1088/0953-8984/19/36/365244.
6. J. A. Rodriguez, J. Y. Kim, J. C. Hanson, S. J. Sawhill and M. E. Bussell, J. Phys. Chem. B, 2003, 107(26), 6276–6285,  DOI:10.1021/jp022639q.
7. A. Soriano, P. Roquero and T. Klimova, Stud. Surf. Sci. Catal., 2010, 175, 525–528,  DOI:10.1016/S0167-2991(10)75100-4.
8. C. G. Morales-Guio, L. A. Stern and X. Hu, Chem. Soc. Rev., 2014, 43, 6555–6569,  10.1039/C3CS60468C.
9. H. E. Lindstad and G. S. Eskeland, Transp. Res. D Trans. Environ., 2016, 47, 67–76,  DOI:10.1016/j.trd.2016.05.004.
10. M. A. Fahim, T. A. Alsahhaf and A. Elkilani, Fundamentals of Petroleum Refining, Elsevier, 2010, p. 516, ISBN: 978-0-444-52785-1,  DOI:10.1016/C2009-0-16348-1.
11. O. Y. Gutiérrez, F. Pérez, C. Salcedo, G. A. Fuentes, M. Aguilar, X. Bokhimi and T. Klimova, Stud. Surf. Sci. Catal., 2007, 165, 803–806,  DOI:10.1016/S0167-2991(07)80441-1.
12. G. Li, H. Zhu, L. Zhao, W. Guo, H. Ma, Y. Yu, X. Lu and Y. Liu, J. Phys. Chem. C, 2016, 120, 23009–23023,  DOI:10.1021/acs.jpcc.6b07103.
13. S. J. Danforth, D. R. Liyanage, A. Hitihami-Mudiyanselage, B. Ilic, S. L. Brock and M. E. Bussell, Surf. Sci., 2016, 648, 126–135,  DOI:10.1016/j.susc.2015.10.005.
14. A. W. Burns, A. F. Gaudette and M. E. Bussell, J. Catal., 2008, 260, 262–269,  DOI:10.1016/j.jcat.2008.10.001.
15. H. Song, Q. Yu, Y. Chen, Y. Wang and R. Niu, Chin. J. Chem. Eng., 2018, 26, 540–544,  DOI:10.1016/j.cjche.2017.09.001.
16. D. H. Ha, L. M. Moreau, C. R. Bealing, H. Zhang, R. G. Hennig and R. D. Robinson, J. Mater. Chem., 2011, 21, 11498–11510,  10.1039/C1JM10337G.
17. J. A. Cecilia, A. Infantes-Molina, E. Rodríguez-Castellón and A. Jiménez-López, Appl. Catal., B, 2009, 92, 100–113,  DOI:10.1016/j.apcatb.2009.07.017.
18. Q. Yuan, H. Ariga and K. Asakura, Top. Catal., 2015, 58, 194–200,  DOI:10.1007/s11244-015-0360-6.
19. G. H. Layan Savithra, E. Muthuswamy, R. H. Bowker, B. A. Carrillo, M. E. Bussell and S. L. Brock, Chem. Mater., 2013, 25, 825–833,  DOI:10.1021/cm302680j.
20. R. Li, Q. Guan, R. Wei, S. Yang, Z. Shu, Y. Dong, J. Chen and W. Li, J. Phys. Chem. C, 2015, 119, 2557–2565,  DOI:10.1021/jp511191e.
21. A. W. Burns, K. A. Layman, D. H. Bale and M. E. Bussell, Appl. Catal., A, 2008, 343, 68–76,  DOI:10.1016/j.apcata.2008.03.022.
22. K. S. Cho, H. R. Seo and Y. K. Lee, Catal. Commun., 2011, 12, 470–474,  DOI:10.1016/j.catcom.2010.10.016.
23. S. L. Blair, A. C. MacMillan, G. T. Drozd, A. H. Goldstein, R. K. Chu, L. Paša-Tolić, J. B. Shaw, N. Tolić, P. Lin, J. Laskin, A. Laskin and S. A. Nizkorodov, Environ. Sci. Technol., 2017, 51, 119–127,  DOI:10.1021/acs.est.6b03304.
24. J. Bai, X. Li, A. Wang, R. Prins and Y. Wang, J. Catal., 2013, 300, 197–200,  DOI:10.1016/j.jcat.2013.01.015.
25. X. Tian, T. Wang, L. Fan, Y. Wang, H. Lu and Y. Mu, Appl. Surf. Sci., 2018, 427, 357–362,  DOI:10.1016/j.apsusc.2017.08.172.
26. G. Li, L. Zhao, H. Zhu, X. Liu, H. Ma, Y. Yu and W. Guo, Phys. Chem. Chem. Phys., 2017, 19, 17449–17460,  10.1039/C7CP01859B.
27. D. Fuks, D. Vingurt, M. V. Landau and M. Herskowitz, J. Phys. Chem. C, 2010, 114, 13313–13321,  DOI:10.1021/jp1031306.
28. J. Ren, C. F. Huo, X. D. Wen, Z. Cao, J. Wang, Y. W. Li and H. Jiao, J. Phys. Chem. B, 2006, 110, 22563–22569,  DOI:10.1021/jp0640474.
29. J. Scaranto and H. Idriss, Chem. Phys. Lett.: X, 2019, 2, 100008,  DOI:10.1016/j.cpletx.2019.100008.
30. P. C. H. Mitchell and J. Hagen, Industrial catalysis: a practical approach, Wiley-VCH, 2nd edn, 2006, vol. 21, p. 525, ISBN 978-3-527-31144-6 (hardcover), 2007,  DOI:10.1002/aoc.1247.
31. Y. H. Hu, ACS Symp. Ser., 2010, 1056, 155–174,  DOI:10.1021/bk-2010-1056.ch010.
32. J. H. Kim, D. J. Suh, T. J. Park and K. L. Kim, Appl. Catal., A, 2000, 197, 191–200,  DOI:10.1016/S0926-860X(99)00487-1.
33. A. Wolfbeisser, O. Sophiphun, J. Bernardi, J. Wittayakun, K. Föttinger and G. Rupprechter, Catal. Today, 2016, 277, 234–245,  DOI:10.1016/j.cattod.2016.04.025.
34. N. Yan, J. Pandey, Y. Zeng, B. S. Amirkhiz, B. Hua, N. J. Geels, J. L. Luo and G. Rothenberg, ACS Catal., 2016, 6, 4630–4634,  DOI:10.1021/acscatal.6b01197.
35. R. F. Bader, Chem. Rev., 191, 91(5), 893–928,  DOI:10.1021/cr00005a013.
36. D. Bokhan and R. J. Bartlett, Chem. Phys. Lett., 2006, 427, 466–471,  DOI:10.1016/j.cplett.2006.07.020.
37. B. van Troeye, M. Torrent and X. Gonze, Phys. Rev. B, 2016, 93, 144304,  DOI:10.1103/PhysRevB.93.144304.
38. V. Caciuc, N. Atodiresei, M. Callsen, P. Lazic and S. Blügel, J. Phys.: Condens. Matter, 2012, 24, 424214,  DOI:10.1088/0953-8984/24/42/424214.
39. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558,  DOI:10.1103/PhysRevB.47.558.
40. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15,  DOI:10.1016/0927-0256(96)00008-0.
41. G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245,  DOI:10.1088/0953-8984/6/40/015.
42. H. Wei, Y. Gui, J. Kang, W. Wang and C. Tang, Nanomaterials, 2018, 8, 1–12,  DOI:10.3390/nano8090646.
43. S. Farmanzadeh and D. Ghazanfary, J. Serb. Chem. Soc., 2013, 78, 75–83,  DOI:10.2298/JSC120419046F.
44. S. Posada-Pérez, D. Santos-Carballal, U. Terranova, A. Roldan, F. Illas and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2018, 20, 20439–20446,  DOI:10.17035/d.2018.0046360243.
45. M. Ungerer, D. Santos-Carballal, A. Cadi-Essadek, C. G. C. E. van Sittert and N. H. de Leeuw, Catalyst, 2020, 10, 558,  DOI:10.3390/catal10050558.
46. N. Y. Dzade, A. Roldan and N. H. de Leeuw, J. Chem. Phys., 2015, 143, 094703,  DOI:10.1063/1.4929470.
47. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979,  DOI:10.1103/PhysRevB.50.17953.
48. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985,  DOI:10.1063/1.472933.
49. J. A. Owolabi, M. Y. Onimisi, S. G. Abdu and G. O. Olowomofe, Comput. Chem., 2016, 04, 73–82,  DOI:10.4236/cc.2016.43007.
50. D. H. Lim, A. S. Negreira and J. Wilcox, J. Phys. Chem. C, 2011, 115, 8961–8970,  DOI:10.1021/jp2012914.
51. L. Yan, B. Zhang, J. Zhu, S. Zhao, Y. Li, B. Zhang, J. Jiang, X. Ji, H. Zhang and P. K. Shen, J. Mater. Chem. A, 2019, 7, 14271–14279,  10.1039/C9TA03686E.
52. Z. Liang, X. Zhong, T. Li, M. Chen and G. Feng, ChemElectroChem, 2019, 6, 260–267,  DOI:10.1002/celc.201800601.
53. G. Hu, Q. Tang and D. E. Jiang, Phys. Chem. Chem. Phys., 2016, 18, 23864–23871,  10.1039/C6CP04011J.
54. M. R. Chiong and F. N. C. Paraan, RSC Adv., 2019, 9, 23254–23260,  10.1039/C9RA01990A.
55. A. A. Alkhoori, K. Polychronopolou, A. Belabbes, M. A. Jaoude, L. F. Vega, V. Sebastian, S. Hinder, M. A. Baker and A. F. Zedan, Appl. Surf. Sci., 2020, 521, 143605,  DOI:10.1016/j.apsusc.2020.146305.
56. H. N. Sharma, V. Sharma, T. Hamzehlouyan, W. Epling, A. B. Mhadeshwar and R. Ramprasad, J. Phys. Chem. C, 2014, 118, 6934–6940,  DOI:10.1021/jp501538v.
57. L. M. Liu, S. Q. Wang and H. Q. Ye, Acta Mater., 2004, 52, 3681–3688,  DOI:10.1016/j.actamat.2004.04.022.
58. R.-P. Ren, X.-W. Liu, Z.-J. Zuo and Y.-K. Lv, RSC Adv., 2015, 5, 55372–55382,  10.1039/C5RA05443E.
59. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658,  DOI:10.1107/S0021889808012016.
60. V. Wang, N. Xu, J. C. Liu, G. Tang and W. T. Geng, VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code, arXiv: 1908.08269.
61. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204,  DOI:10.1088/0953-8984/21/8/084204.
62. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908,  DOI:10.1002/jcc.20575.
63. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360,  DOI:10.1016/j.commatsci.2005.04.010.
64. Z. Zhou, F. Han, L. Guo and O. Prezhdo, Phys. Chem. Chem. Phys., 2016, 18, 16862–16869,  10.1039/C6CP02599D.
65. W. Zhang and Y. Yiao, Energy Fuels, 2020, 34, 2425–2434,  DOI:10.1021/acs.energyfuels.9b04036.
66. D.-H. Lim, J. H. Jo, D. Y. Shin, J. Wilcox, H. C. Ham and S. W. Nam, Nanoscale, 2014, 6, 5087–5092,  10.1039/C3NR06539A.
67. G. Alonso, D. Bahamon, F. Keshavarz, X. Gimenez, P. Gamallo and R. Sayos, J. Phys. Chem. C, 2018, 122(7), 3945–3957,  DOI:10.1021/acs.jpcc.8b00938.
68. K. Persson, Materials Data on CoP (SG:62) by Materials Project, https://materialsproject.org/materials/mp-22270/,  DOI:10.17188/1197496.
69. X. Lin, K. C. Hass, W. F. Schneider and B. L. Trout, J. Phys. Chem. B, 2002, 106, 12575–12583,  DOI:10.1021/jp026128f.
70. W. Li, J. J. Ma, P. Liu, Z. L. Pan and Q. Y. He, Appl. Surf. Sci., 2015, 335, 17–22,  DOI:10.1016/j.apsusc.2015.01.181.
71. M. Happel, N. Luckas, F. Viñes, M. Sobota, M. Laurin, A. Görling and J. Libuda, J. Phys. Chem. C, 2011, 115, 479–491,  DOI:10.1021/jp107171t.
72. J. Ren, Y. Xue and L. Wang, Chem. Phys. Lett., 2019, 733, 136631,  DOI:10.1016/j.cplett.2019.136631.
73. T. Jirsak, J. A. Rodriguez, S. Chaturvedi and J. Hrbek, Surf. Sci., 1998, 418, 8–21,  DOI:10.1016/S0039-6028(98)00652-9.
74. J. A. Rodriguez, T. Jirsak and S. Chaturvedi, J. Chem. Phys., 1999, 110, 3138,  DOI:10.1063/1.477910.
75. K. Takanabe, K. Nagaoka, K. Nariai and K. I. Aika, J. Catal., 2005, 232, 268–275,  DOI:10.1016/j.jcat.2005.03.011.
76. D. Chen, X. Zhang, J. Tang, J. Fang, Y. Li and H. Liu, Appl. Phys. A: Mater. Sci. Process., 2018, 124, 404,  DOI:10.1007/s00339-018-1827-7.
77. A. S. Rad and D. Zareyee, Vacuum, 2016, 130, 113–118,  DOI:10.1016/j.vacuum.2016.05.009.
78. B. Yang, Z. Li, R. Fan and J. Ma, Mol. Simul., 2020, 46, 1147–1154,  DOI:10.1080/08927022.2020.1778172.
79. H. Al-Megren and T. Xiao, Petrochemical catalyst materials, processes, and emerging technologies, 2016, p. 539, ISBN-13: 978-1466699755, ISBN-10: 146669975.
80. P. Davini, Carbon, 1990, 28, 565–571,  DOI:10.1016/0008-6223(90)90054-3.
81. V. Gaur, R. Asthana and N. Verma, Carbon, 2006, 44, 46–60,  DOI:10.1016/j.carbon.2005.07.012.
82. Q. Zhou, W. Ju, X. Su, Y. Yong and X. Li, J. Phys. Chem. Solids, 2017, 109, 40–45,  DOI:10.1016/j.jpcs.2017.05.007.
83. H. Wang, C. Zhong, Q. Ma, J. Ma and H. He, Environ. Sci.: Nano, 2020, 7, 1092–1101,  10.1039/C9EN01474H.
84. M. Vakili, R. Gholizadeh, A. Ghadi, E. Salmasi and M. Sinnokrot, J. Mol. Graphics, 2020, 101, 107752,  DOI:10.1016/j.jmgm.2020.107752.
85. I. Lucas, L. Perez, C. Aroca, P. Sánchez, E. López and M. C. Sánchez, J. Magn. Magn. Mater., 2005, 290–291, 1513–1516,  DOI:10.1016/j.jmmm.2004.11.563.
86. R. C. Da Silva, E. M. Dos Santos, M. L. Sartorelli, J. P. Sinnecker, A. Gündel, R. L. Sommer and A. A. Pasa, J. Magn. Magn. Mater., 2004, 272–276, 1460–1462,  DOI:10.1016/j.jmmm.2003.12.154.
87. X. Zhang, R. Huang, Y. Gui and H. Zeng, Sensors, 2016, 11, 1830,  DOI:10.3390/s16111830.
88. A. Infantes-Molina, J. A. Cecilia, B. Pawelec, J. L. G. Fierro, E. Rodríguez-Castellón and A. Jiménez-López, Appl. Catal., A, 2010, 390, 253–263,  DOI:10.1016/j.apcata.2010.10.019.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10634k

‡ Both authors contributed equally.

---