 Open Access Article
Open Access ArticleComment on “investigation of dielectric constants of water in a nano-confined pore” by H. Zhu, F. Yang, Y. Zhu, A. Li, W. He, J. Huang and G. Li, RSC Adv., 2020, 10, 8628
Sayantan
Mondal
 and
Biman
Bagchi
and
Biman
Bagchi
 *
*
Solid State and Structural Chemistry Unit, Indian Institute of Science, Bengaluru, Karnataka, India. E-mail: bbagchi@iisc.ac.in
First published on 28th January 2021
Abstract
Zhu et al. recently reported the spatially resolved dielectric profile and value of the average static dielectric constant of water confined inside a silica nanopore. However, the authors neglected the inherent anisotropy and non-local nature of the dielectric response under confinement. Neglect of these important issues produces erroneous results and vastly underestimates the average values. We demonstrate the correct way to incorporate the anisotropy and to obtain the average dielectric constant of cylindrically nanoconfined dipolar fluids. Use of the correct theoretical formalism expectedly shows convergence of the calculated dielectric response to the bulk value with increasing the nanopore size. On the contrary, the equation used by Zhu et al. fails to exhibit the convergence of the same. Instead, decreases as the nanopore size is gradually increased.
I. Introduction
Dielectric behaviour of nanoconfined water exhibits a strong dependence on the shape and size of the enclosure. Because of the confinement the dielectric properties become anisotropic in nature and exhibit a diverse range of anomalies. Several studies, both experimental and theoretical, that investigate the dielectric properties of nanoconfined water have emerged in recent years.1–5,15 This is because the dielectric constant carries an immense importance in the theories of solvation dynamics and charge transfer processes.6,7 At this juncture, it is important to establish a right theoretical formalism to describe the dielectric behaviour of nanoconfined dipolar liquids.In a recent study, by employing grand canonical Monte Carlo simulation, Zhu et al. have reported the spatial dielectric profile of water confined inside hydrophilic silica nanopore of diameter 1.2 nm.8 The spatially resolved dielectric profile [εp(r)] is calculated from the local polarisability [P(r)] and total dipole moment (M) obtained from simulations that are used as inputs in eqn (1) to obtain the shell-wise dielectric constants.
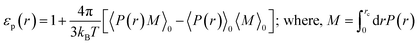 | (1) |
Here rc is the effective cut-off radius of the cylinder. From the εp(r) vs. r plot they have calculated the value of the average dielectric constant and found to be in the range of ∼23–25 which was independent on the bin width. Unfortunately, the theoretical formalism used by Zhu et al. has certain questionable ingredients, and raises both general issues and fundamental questions that we describe in Section II.
II. Issues with the theoretical formalism used by Zhu et al.
The static dielectric constant (ε) of a system is defined using eqn (2) where E is the Maxwell field and P is the macroscopic polarisation (a vector created in response to the electric filed E which is also a vector here). In general, ε is a tensor and its elements are given by eqn (2).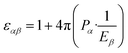 | (2) |
For isotropic bulk liquid, the right hand side produces identical elements for all α and β. One can employ Kubo's linear response theory to evaluate the ratio (P/Ec) in terms of the fluctuation in the total dipole moment [eqn (3)], where Ec denotes the cavity field. Ec is related to the Maxwell field (E) by a factor f(ε) that is a function of the dielectric constant (ε) of the medium.
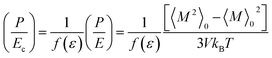 | (3) |
The situation, however, is dramatically different in a confined system. Now, we must confront three important issues. First, because of the shape of the confining geometry, there is an inherent anisotropy, leading to a dependence on the coordinate system. Second, in the presence of different dielectric boundary conditions along different directions, the three eigenvalues of the dielectric tensor are not equal. The bottomline is that one cannot define a single dielectric constant for such an anisotropic system. Third, the dielectric function is inhomogeneous, with position dependence which is non-trivial, as also discussed by others.9,10
Let us discuss these issues for the specific problems at hand. For a cylindrical specimen placed in a Cartesian coordinate system, we have two unique non-zero eigenvalues defining the dielectric tensor – (i) axial dielectric constant (εz) that arises due to an electric field that is parallel to the axis of the cylinder, and (ii) a perpendicular dielectric constant (εx = εy = εx/y) that arises due to an electric field that is perpendicular to the principle axis of the cylinder. On the other hand, if one describes the system in cylindrical coordinate system, the two non-zero eigenvalues become – (i) one axial (εz) and (ii) one radial dielectric constant (εr) that arises due to a radially emanating electric field from within the cylinder. Therefore, we have to deal with two different kinds of polarisation fluctuations leading to two different dielectric constants in a given coordinate system. The overall average static dielectric constant also gets defined in two ways, as shown in eqn (4).
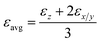 | (4) |
III. Correct linear response equations
Zhu et al. ignored the anisotropy in the dielectric constant. In the presence of dielectric anisotropy, the linear response relations modify. We first present the correct expressions to obtain εz and εx/y and then compare our results with that of Zhu et al. For the axial external field (Eextz), the cavity field (Ecz) is equal to the externally applied field, Ecz = Eextz. Hence f(εz) = 1 and eqn (2) becomes,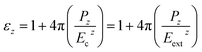 | (5) |
Now, by applying the linear response relation given in eqn (3), one can write
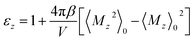 | (6) |
On the other hand, because of the presence of a cylindrical dielectric boundary, the perpendicular cavity field (Ecx/y) is not equal to the externally applied perpendicular field (Eextx/y). To obtain Ecx/y one may follow the procedure described by Zhan.11 Here we provide the final expression in eqn (7) where f(εx/y) = 2/(εx/y + 1).
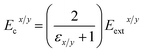 | (7) |
We can now obtain the expression for εx/y from eqn (2) as
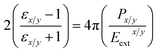 | (8) |
Again, by the application of linear response relation [eqn (3)] we arrive at the following expression [eqn (9)] where, 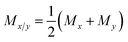 .
.
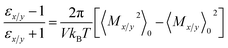 | (9) |
The detailed derivation of both the eqn (6) and (9) can be found elsewhere.12 We note that the quantities εz and εx/y are average (or effective) macroscopic quantities.
Here we compare the average macroscopic dielectric constant obtained from eqn (4) with that of Zhu et al. Although the average values conceal the inherent anisotropy, here we opt for the same in order to demonstrate the flaw in Zhu et al.'s formalism who did not consider the anisotropy. We use the expression employed by Zhu et al.8 and apply effective medium theory to express the average dielectric constant, 〈εp〉 (average over the bins/grids), in terms of the spatial dielectric profile [eqn (10)].13
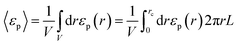 | (10) |
If one evaluates the integral in eqn (10) one obtains eqn (11) where, M is the total dipole moment of the confined dipolar fluid. We note that eqn (11) takes the same form as that of the isotropic bulk liquid.
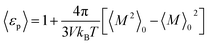 | (11) |
Additionally we discuss another different approach to obtain the spatially resolved axial and radial dielectric profiles for dipolar fluids inside nano-cylindrical confinement.10,14 It can be shown that for a cylindrical system E(r) is fixed along the Z direction and rD(r) is fixed along the radial direction; where D(r) is the radially varying electric displacement field. By employing linear response theory one can derive the following two equations [eqn (12) and (13)].
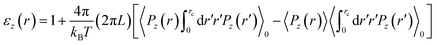 | (12) |
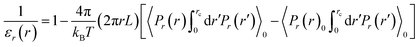 | (13) |
Here L is the length of the nanotube. Eqn (12) is the same as eqn (1) used by the authors of the paper mentioned in the title. But this is strictly valid for the axial component. The detailed derivations and results using these two equations can be found in ref. 11 and 12. One can again define two different average quantities, that is, the average axial and radial dielectric constants by employing effective medium theory.13
We note that in our calculations we do not use eqn (12) and(13); rather we avoid the calculation of the spatially resolved dielectric constant and directly obtain εz and εx/y by calculating the cavity field in the presence of external fields from outside the sample. This is a standard method also used in the derivation of the celebrated Clausius–Mossotti equation. In the next section we compare the average dielectric constants obtained from eqn (4) with that of eqn (11).
IV. Resuts and comparison
In order to show the difference between ours' and Zhu et al.’s formalism/equations, we perform several 100 ns long atomistic molecular dynamics simulations of confined SPC/E water inside carbon nanotubes of same length (L = 5.0 nm) but different diameters (d = 1.3, 1.6, 2.0, 3.0, 4.0 and 5.0 nm). We calculate the axial and perpendicular components of the dielectric constant and the average dielectric constant from the anisotropic dielectric constants. We compare them with those obtained from eqn (10) or (11) (Fig. 1a). Interestingly, εz and εx/y independently converge to the bulk value (∼68 for SPC/E water) with increasing nanotube diameter in an opposite manner (Fig. 1b). We use the effective dielectric constant (εeff) notation to denote averaged responses obtained by using external fields along different directions.12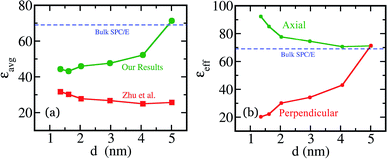 | ||
| Fig. 1 (a) The comparison of our formalism with that of Zhu et al. The total average dielectric constant converges to the bulk value when we use eqn (4). However, the average quantity described by eqn (10) fails to reproduce the bulk value with increasing nanotube diameter and rather decreases in magnitude. This apparent fallacy has not been observed as Zhu et al. did not study the size dependence. (b) The anisotropic effective dielectric constant (εeff) of water inside carbon nanotubes of different sizes. The axial (εz) and perpendicular (εx/y) components, as described in eqn (6) and (9) respectively, converge to the bulk value from the opposite direction. | ||
Hence, it is clear that the equation used by Zhu et al. cannot reproduce the bulk value of the dielectric constant of water as we increase the diameter of the nanotube (Fig. 1a). On the other hand, the method described by us in Section III beautifully converges to the bulk value with increasing size. The values of Zhu et al. decreases with increase in system size (Fig. 1a).
V. Conclusions
In this comment article we have highlighted the errors that can arise from the misconception that the dielectric constant for nanoconfined dipolar fluids can be described by a single unique value, as in the bulk. The dielectric response becomes anisotropic inside nanopores as the polarisation fluctuations are substantially different along different orthogonal directions.12 This neglect of the anisotropy and the assumption of the internal and external field to be the same in every direction, produce erroneous results. We present correct expressions and the procedure that give rise to correct results and the expected convergence, as the system size is increased.Conflicts of interest
There are no conflicts to declare.References
- L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. Novoselov and A. Geim, Science, 2018, 360, 1339–1342 CrossRef CAS PubMed.
- S. Mondal, S. Acharya and B. Bagchi, Phys. Rev. Res., 2019, 1, 033145 CrossRef CAS.
- A. Schlaich, E. W. Knapp and R. R. Netz, Phys. Rev. Lett., 2016, 117, 048001 CrossRef PubMed.
- V. Ballenegger and J. P. Hansen, J. Chem. Phys., 2005, 122, 114711 CrossRef CAS PubMed.
- S. Mondal and B. Bagchi, J. Chem. Phys., 2020, 152, 224707 CrossRef CAS PubMed.
- B. Bagchi and A. Chandra, J. Chem. Phys., 1989, 90, 7338–7345 CrossRef.
- F. Garisto, P. Kusalik and G. Patey, J. Chem. Phys., 1983, 79, 6294–6300 CrossRef CAS.
- H. Zhu, F. Yang, Y. Zhu, A. Li, W. He, J. Huang and G. Li, RSC Adv., 2020, 10, 8628–8635 RSC.
- S. Gekle and A. Arnold, Phys. Rev. Lett., 2013, 111, 089801 CrossRef PubMed.
- P. Loche, C. Ayaz, A. Schlaich, Y. Uematsu and R. R. Netz, J. Phys. Chem. B, 2019, 123, 10850–10857 CrossRef CAS PubMed.
- M. Zhan, Electromagnetic field theory: A problem solving approach, Massachusetts Institute of Technology, 1979 Search PubMed.
- S. Mondal and B. Bagchi, J. Phys. Chem. Lett., 2019, 10, 6287 CrossRef CAS PubMed.
- T. C. Choy, Effective medium theory: principles and applications, Oxford University Press, 2015 Search PubMed.
- C. Schaaf and S. Gekle, J. Chem. Phys., 2016, 145, 084901 CrossRef PubMed.
- S. Mondal and B. Bagchi, Nano Lett., 2020, 20(12), 8959–8964 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |
