Open Access Article
Open Access ArticleTailored nanotopography of photocurable composites for control of cell migration†
Sebastian Hasselmann a,
Caroline Kopittke‡
a,
Caroline Kopittke‡
 a,
Maria Götza,
Patrick Witzela,
Jacqueline Riffel§
a and
Doris Heinrich
a,
Maria Götza,
Patrick Witzela,
Jacqueline Riffel§
a and
Doris Heinrich *ab
*ab
aFraunhofer Institute for Silicate Research ISC, Neunerplatz 2, 97082 Würzburg, Germany. E-mail: doris.heinrich@isc.fraunhofer.de
bLeiden University, Huygens-Kamerlingh Onnes Laboratory, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands
First published on 21st January 2021
Abstract
External mechanical stimuli represent elementary signals for living cells to adapt to their adjacent environment. These signals range from bulk material properties down to nanoscopic surface topography and trigger cell behaviour. Here, we present a novel approach to generate tailored surface roughnesses in the nanometer range to tune surface properties by particle size and volume ratio. Time-resolved local mean-squared displacement (LMSD) analysis of amoeboid cell migration reveals that nanorough surfaces alter effectively cell migration velocities and the active cell migration phases. Since the UV curable composite material is easy to fabricate and can be structured via different light based processes, it is possible to generate hierarchical 3D cell scaffolds for tissue engineering or lab-on-a-chip applications with adjustable surface roughness in the nanometre range.
1 Introduction
The ultimate goal in the field of biofabrication and tissue engineering is to imitate the physiological environment of living cells in order to provide a controlled artificial environment as natural as possible. For the development of 3D cell scaffolds as basic modules in regenerative medicine and lab-on-chip applications, production methods including 3D printing,1 stereolithography,2 nanoimprint,3 and direct laser writing4,5 are used. These can be applied to various material classes ranging from hydrogels6 to glass7 and metals.8 Simultaneously, manifold structure designs from 2D9 to 3D10 as well as chemical11 and mechanical12 surface altering procedures are under investigation, all with the aim to mimic the native extracellular 3D matrix and to influence cell behaviour in defined ways. This is an extremely challenging task, since many factors are involved when it comes to biophysicochemical interactions at the interface of the cells' membrane and the scaffold surface.13 Besides the biochemical influence of the extracellular matrix, mechanical stimuli of the surrounding scaffold induce inter- and intracellular responses like proliferation,14 cell differentiation15 and gene expression.16Several mechanical bulk- and surface properties, e.g. the elastic modulus17 or surface topography in the micro-18 and nanometre19 range as well as different geometrical surface features,20 have been investigated over the last years. Recently the surface roughness, which is adjustable in multiple ways via additive21 or subtractive22 methods, raised special interest due to its potential to significantly influence proliferation, cell adhesion,23 and stem cell differentiation.24,25 To generate the desired surface roughness, different techniques are used like photolithography, nanoimprint, or self assembling polymer films.26 They offer a high resolution and design freedom, however, for most of them the production process is expensive, due to the costly equipment and multiple processing steps. An easier way is the utilization of particles to create an adjustable surface roughness.27 Besides the cheap and easy processing, several bulk and surface functionalities can be tuned for every specific requirement. In this way, it is easy to add and vary properties of a 3D scaffold, with custom shape and custom surface roughness. Furthermore, optimizations in terms of surface chemistry, intrinsic fluorescence for imaging purposes up to incorporated drug-delivery systems are possible. To enhance the scaffold with antibacterial or actuatoric characteristics, silver or magnetic particles can be used.28
In many physiological processes cell migration plays a crucial role, from embryogenesis to immune response and wound healing. To study amoeboid cell migration influenced by external cues, Dictyostelium discoideum (D. discoideum) is a popular cell model organism in the biophysical field,29 since many properties can be transfered to mammalian cells.30 During cell migration a distinct cell–surface interaction is necessary in order to transmit forces generated by the cytoskeleton to deform the cell body and to move it along the substrate. Simultaneously, the cell explores its surrounding via mechanosensing by its randomly arranged protrusions, where mechanical stimuli induce biochemical reactions. This can lead to cell polarization followed by directed cell migration and can be exploited for directed cell guidance.31,32 Compared to mammalian cells, D. discoideum do not carry genes for integrins or most extracellular matrix proteins and therefore do not develop focal adhesion points on the substrate.33 However, the so-called actin foci transmembrane protein SadA is found to mediate force transmission in surface adhesion and phagocytosis,34,35 among other involved proteins like phg1A, sibA and talin A. Apart from that, adhesion is based on van der Waals forces,36 which depends on the polarizability of the involved molecules and can be either attractive or repulsive and originate from permanent charges or ions inside the cell medium and are apparent at any contact site.
In this work, we present a novel approach to fabricate tailored surface roughnesses in the nanometre range by incorporating silica particles into a photo-structurable matrix, which is part of the hybrid polymer class ORMOCER®. It is widely used as smoothing37 or passivation layer38 in different applications and known for its excellent processability ranging from bulk material down to sub-micron resolution structures and from simple surface coating39 to the creation of custom freeform 3D micro structures via two-photon polymerization.40 This matrix material is processable with every light curing method and its biocompatibility has been proven with different cell types41–43 making it ideally suited for future biomedical applications. Under normal conditions, ORMOCER® I (OC-I) – like many other light curable polymers – is polymerized under exclusion of oxygen, since it acts as a radical scavenger suppressing radical curing.44 Here, we exploit this behaviour of OC-I forming a thin, oxygen-induced inhibition layer, when cured under ambient air. When dissolving this layer after curing, the surface exhibits a topography in the nanometre range corresponding to the particles protruding out of the matrix surface. The surface nanoroughness is tunable by adjusting the diameter and filling degree of incorporated particles. Here, tailored nanorough surfaces have been tested for biological application by their influence on the cell migration behaviour of D. discoideum amoebae. The living cells were seeded onto the sample surface and monitored via time-lapse fluorescent microscopy. The cell locomotion paths were analysed using a local mean-squared displacement (LMSD) algorithm in order to distinguish between directed and quasi-random migration modes depending on the surface roughness of the sample.
2 Materials and methods
2.1 Sample preparation
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.45 Adding 2 wt% of the photoinitiator Irgacure® 369 (2-benzyl-2-dimethylamino-1-(4-morpholinophenyl)-butanone-1), Ciba Geigy, Switzerland) results in a UV-curable resin.46,47
1.45 Adding 2 wt% of the photoinitiator Irgacure® 369 (2-benzyl-2-dimethylamino-1-(4-morpholinophenyl)-butanone-1), Ciba Geigy, Switzerland) results in a UV-curable resin.46,47A drop of the composite was placed onto a 1.5 H high precision cover slip (Marienfeld, Germany), doctor-bladed to a 30 μm layer and cured in an iron-light source UV-Chamber (BK 850, Beltron®, Germany) under ambient air for 5 minutes. Oxygen leads to an inhibition surface layer50 of several micrometers, which was removed during a 15 min development step in a mixture (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) of isopropanol and 4-methyl-2-pentanon (Sigma-Aldrich Chemie GmbH, Germany). The samples were UV-cured again for 5 minutes within the solvent bath to crosslink remaining carbon double bonds. This was followed by a 24 hours post heating step at 60 °C under a vaccum of 100 mbar to ensure complete evaporation of the solvent and post-curing of the anorganic network of the ORMOCER® matrix. Table 1 shows the produced surface samples with the respective particle diameter and filling ratio. Only particles with diameters smaller than 0.5 μm were utilized for the creation of nanorough surfaces to achieve surface roughness values in the nanometre range distinct from a truly three-dimensional environment.
1) of isopropanol and 4-methyl-2-pentanon (Sigma-Aldrich Chemie GmbH, Germany). The samples were UV-cured again for 5 minutes within the solvent bath to crosslink remaining carbon double bonds. This was followed by a 24 hours post heating step at 60 °C under a vaccum of 100 mbar to ensure complete evaporation of the solvent and post-curing of the anorganic network of the ORMOCER® matrix. Table 1 shows the produced surface samples with the respective particle diameter and filling ratio. Only particles with diameters smaller than 0.5 μm were utilized for the creation of nanorough surfaces to achieve surface roughness values in the nanometre range distinct from a truly three-dimensional environment.
| Sample | Particle diameter (nm) | Particle filling ratio (vol%) | Curing environment |
|---|---|---|---|
| OC-I AR | — | — | Argon |
| OC-I | — | — | Ambient air |
| 52–20 | 52 ± 8 | 20 | Ambient air |
| 165–5 | 165 ± 11 | 5 | Ambient air |
| 165–10 | 165 ± 11 | 10 | Ambient air |
| 165–20 | 165 ± 11 | 20 | Ambient air |
| 421–20 | 421 ± 22 | 20 | Ambient air |
| 421–20 AR | 421 ± 22 | 20 | Argon |
2.2 Sample characterization
To analyze the silica particle size distribution, a drop of highly diluted silica particle butanone suspension was applied onto a SEM sample holder and dried before sputter coating. A watershed separation was performed on the SEM images using ImageJ 1.51 h (National Institutes of Health, USA) in order to enhance the particle detection, before determining the particle size using the ImageJ plug-in “Analyse Particle”. The error in particle diameter is based on the standard deviation of this analysis.
For imaging of cured composite layers, the coated cover slip was cut and the layer surface and layer cross section were examined under a 60 and 90 degree angle, respectively.
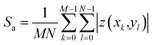 | (1) |
The peak-to-peak height Sz describes the height difference between the highest zmax and lowest zmin pixel value in the image:
| Sz = zmax − zmin | (2) |
The error bars of arithmetic mean values of the roughness parameters are based on the standard deviation of five measurements for each sample type and are below 5% and 10% for Sa and Sz, respectively.
2.3 Cell culture and microscopy imaging
For microscopy experiments, HL5 medium was exchanged by phosphate buffer (PB), adjusted to pH = 6.0. Cell suspension was kept in a polytetrafluoroethylene (PTFE) frame, placed onto the cured composite layer. Image acquisition was started after at least 45 min resting time to ensure all cells are settled down onto the sample surface.
A high number of cells is important in order to minimize biological related noise. However, even similarly treated and genetically identical cells exhibit a significant and inevitable variability in cell behaviour due to intrinsic biological noise.51,52
2.4 Cell migration analysis
The obtained cell centre-of-mass trajectories have been evaluated with the MATLAB® (The MathWorks, Inc., USA) algorithm Cell Motion Analysis, which is based on an algorithm designed for intracellular particle motion53 and was adjusted to distinguish different modes of cell migration.31,54 For amoeboid migrating cells, like D. discoideum, the migration behaviour consists of two distinct types: directed runs with higher velocities and only small changes in direction in contrast to phases of diffusion-like motion, during which the cell probes its environment. For this study a third classification was implemented additionally, which separates cells that are moving less than a given distance from their starting position over the whole time sequence. These are classified as “non-migrating” and not taken into account for the migration analysis. Here, we used 5 μm as a minimum distance for cells to move, which estimates half of an average cell diameter. The percentage of time points categorised as “non-migrating” are listed in Table S2† for every sample type.The cell motion analysis algorithm is based on the local mean-squared displacement (LMSD) 〈ΔR2(τ)〉i where the mean-squared displacement (MSD) is calculated in a rolling time window of T:
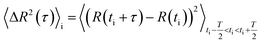 | (3) |
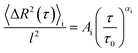 | (4) |
By choosing l = 1 μm and τ0 = 1 s, the pre-factor Ai carries no physical dimensions.55 Depending on the obtained value for α, every time point is classified as either “directed” for 1.75 ≤ α ≤ 2.00 or “quasi-random” for α < 1.75. This is based on previous work31,54 and adjusted for this experiment.
The total of the median values of the alpha and velocity distributions were subjected to a statistical analysis, in comparison to the flat reference surface without particles. Since the median values are not normally distributed, the non-parametric Mann–Whitney test was used. In order to check whether the distributions differ significantly from each other, a Kruskal–Wallis analysis was performed. All calculations were conducted using the software OriginPro 2019 9.6.0.172, (OriginLab Corporation, USA).
For each analyzed cell measurement video, the percentage of active migration phases was determined. From all videos of a sample variation a mean value with corresponding standard deviation was calculated.
3 Results and discussion
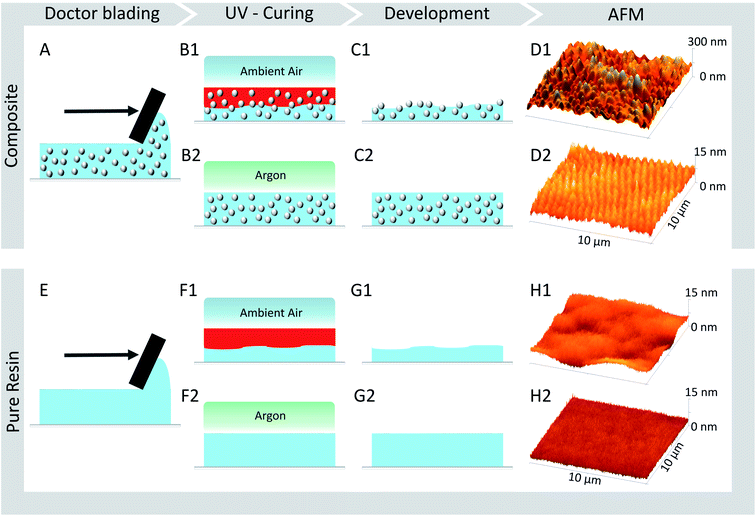
In this work, we developed a novel type of fabrication process to create tailored surface roughnesses in the nanometre range utilizing particle–polymer composites under exploitation of an oxygen inhibition layer. These nanorough surfaces are made of a biocompatible UV curable composite based on a hybrid-polymer ORMOCER® with incorporated silica particles. The polymer matrix material was successfully used as cell scaffold with different mammalian cell types, like rabbit muscle-derived myogenic stem cells41 and human microvascular endothelial cells.43 The influence of the acquired nanoroughness on the migration behaviour of D. discoideum cells has been acquired by time-lapse microscopy and analysed by the local mean-squared displacement of the cell motion.To fabricate the surfaces, the composite (Fig. 1A) or the reference material of pure resin (Fig. 1E) were applied onto a cover slip via doctor blading. According to the standard procedure, this is followed by a UV curing step under argon atmosphere (composite: Fig. 1B2, pure resin: Fig. 1F2), resulting in a smooth surface for both surface types, which is confirmed by AFM measurements of the final surfaces (composite: Fig. 1D2, pure resin: Fig. 1H2). The particles (here: 421 nm) are hidden under the polymer surface, proving the excellent surface smoothing properties of the ORMOCER® matrix. In contrast to this standard procedure, we achieve tailored nanorough surfaces by exploiting the fact, that an oxygen related inhibition layer is created at the sample surface when cured under ambient conditions (composite: Fig. 1B1. pure resin: Fig. 1F1). The monomer conversion increases with increasing distance to the air boundary due to the decreasing oxygen concentration. At a given layer depth the degree of polymerization is high enough to endure the development step while the uncured inhibition layer is dissolved (composite: Fig. 1C1, pure resin: Fig. 1G1). Since the particles are not affected by the solvent, they protrude from the polymer surface generating roughness values in the nanometre range (Fig. 1D1).
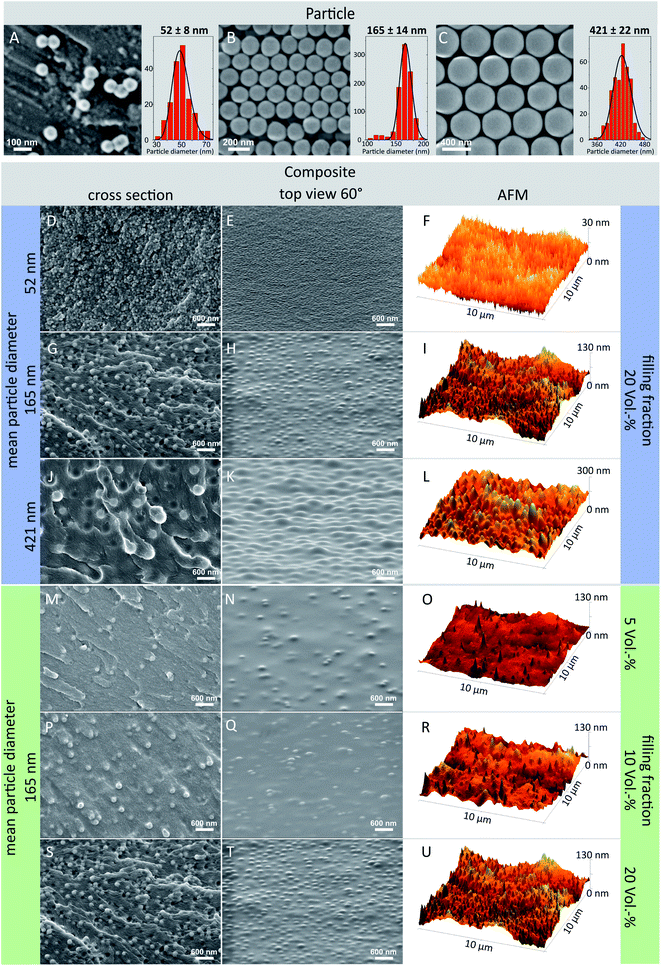
Tailored surface roughnesses has been achieved by (1) utilizing differently sized particles (marked blue in Fig. 2) and by (2) varying the volume fraction of the particles in the polymeric matrix (marked green in Fig. 2). For (1) three different surface roughnesses – each with a particle volume fraction of 20 vol% – have been manufactured with particles of diameters: 52 nm, 165 nm and 421 nm (see Table 1). To investigate the contribution of the particle volume fraction on the surface roughness, for (2) three different surfaces have been fabricated, each containing particles with a diameter of 165 nm and a varying particle volume fraction of 5 vol%, 10 vol% and, 20 vol%. Flat surfaces made of pure OC-I polymer without any particles serve as a reference. Additionally, two surface types, one of the reference material (OC-I polymer without particles) and one composite of the largest particle diameter (421 nm) have been prepared via the standard curing process under argon atmosphere, thus without oxygen inhibition layer. Table 1 lists all prepared surfaces, which are named by the used particle diameter and the particle volume fraction.
3.1 Homogeneity of prepared composites
SEM imaging and image analysis (Fig. 2A–C) were used to verify the quality and particle size distribution of the spherical silica particles. For each particle type, the arithmetic mean diameter was calculated as well as the standard deviation. Particle sizes range from (52 ± 8) nm, (165 ± 11) nm to (421 ± 22) nm. The particle size distributions were fitted with a log-normal function which reveals a FWHM of 31% in respect to the mean value of 52 nm which drops to 15% and 12% for 165 nm and 421 nm particles, respectively.The OC-I polymer has a silicate (Si–O–Si) backbone and shows a very good processability with the incorporated silica particles. Their highly matched refractive indices lead to a low opacity for a composite material and enables observation via optical methods. To obtain surfaces with isotropic roughness, the homogeneity of the particle dispersion is crucial. However, particles tend to agglomerate with decreasing particle diameter. This effect is caused by the increasing surface-to-volume ratio and thus increasing van der Waals- and surface charge forces. Moreover, the surrounding media, adsorbed molecules and other surface interactions are essential for the particle–particle interaction and hence for a stable particle dispersion.56 To circumvent particle agglomeration, which is enhanced in composites with high filling degree, several particle surface modifications, depending on the dispersion media, were reported.57,58 To minimize the amount of additional processing steps, we overcame this problem even for a particle volume density up to 20 vol% without any surface modification by choosing an appropriate ORMOCER® matrix with a high inorganic fraction of 25 wt%. Additionally, the absence of any solvents and therefore the high viscosity of the resin suppresses particle diffusion and a similar mass density of particles and matrix leads to a homogeneous particle distribution and therefore stable composite resin. The particles are inclosed by the matrix material during polymerization, resulting in a homogeneously cured particle–polymer composite.
To verify the homogeneous distribution of the particles across the surface and within the bulk material, SEM investigation of cross sections (Fig. 2D, G, J, M, P and S) and the layer surface (Fig. 2E, H, K, N, Q and T) were performed. For all prepared samples, the particle distribution was random and no agglomeration was visible neither inside nor on top of the composite layers, including for the smallest particles with 52 nm in diameter. Overall, homogeneous surface roughness was achieved for all particle sizes and filling degree variations.
3.2 Oxygen inhibition layer and resulting surface roughness
The widely used photoinitiator Irgacure® 369 is a type I initiator and exhibits a high UV absorption with a high free radical initiation rate and therefore short curing times.59 After excitation via photon absorption the initiator molecule decays and forms free radicals, which react with the carbon double bond of the 3-methacryloxypropyltrimethoxysilane (MEMO), which itself attacks another monomer forming a growing polymer radical. Depending on the photoinitiator and the monomer, several side and termination reactions are possible, finally leading to a finish of the chain reaction and a polymerized resin. However, cured under ambient conditions, oxygen molecules are solved inside the resin surface. There, they react with the initiator and growing polymer radicals, forming peroxy radicals, which leads to low monomer conversion even up to an uncured layer. This process depends on the oxygen concentration at its diffusion characteristics inside the resin, on the photoinitiator activation rate and on the chain reaction kinetics.50During the development step the inhibition layer is dissolved while the particles are not affected by the solvent. Therefore, they are washed away if their contact area to the remaining polymerized matrix is not sufficient, while embedded particles remain inside the composite and protrude from the sample surface (Fig. 1D1). During drying, the polymerized matrix material covers the enclosed particles due to the high adhesion between silica particles and siloxane based ORMOCER®. The coating of the particles can also be observed in the SEM images of the surface which exhibit a smoothed cover (Fig. 2E, H, K, N, Q and T) compared to the rough layer cross section (Fig. 2D, G, J, M, P and S). Consequently the surface chemistry is homogeneous and similar to the pure polymer reference as all particles are covered by OC-I but surface roughness is still existent. In the ESI† close-up SEM images of the top (Fig. S3A†) and cross-section (Fig. S3B†) are provided, which illustrate that the particles are completely embedded beneath an ORMOCER® layer. When using polymerization techniques at which no inhibition layer is formed a much more pronounced surface roughness can be accomplished. In this case, however the sample surface is not chemically homogeneous, since the particles are not covered by the polymer. As an example Fig. S3C† shows a 3D structure created via direct laser writing, which exhibits a distinct boundary between the particle surface and the ORMOCER® matrix.
We further measured the contact angle of water and ethylene glycol on the composite surfaces with a filling ratio of 20 vol% and calculated the surface energy. We did not find a significant difference in both values compared the flat reference surface (Fig. S4†), which is a strong indicator that the surface chemistry does not change on the different investigated surfaces. Further, the added surface roughness does not significantly change the contact angle. The fabrication process is finished with a temperature treatment inducing a condensation reaction of the unfunctionalized silica particles and the silicate fraction of the hybrid polymer matrix, ensuring a strong particle–matrix interaction.
The Young's modulus of the cell environment can trigger cell behaviour in certain ways. The bulk OC-I exhibits a value of (1.01 ± 0.03) GPa, while silica particles are in the order of 45 GPa, depending on their porosity.60 Both values are beyond those of the natural cell environment43 and the particles are covered with OC-I. Therefore we might conclude that cell behaviour is not directly affected by the silica particle's Young's modulus.
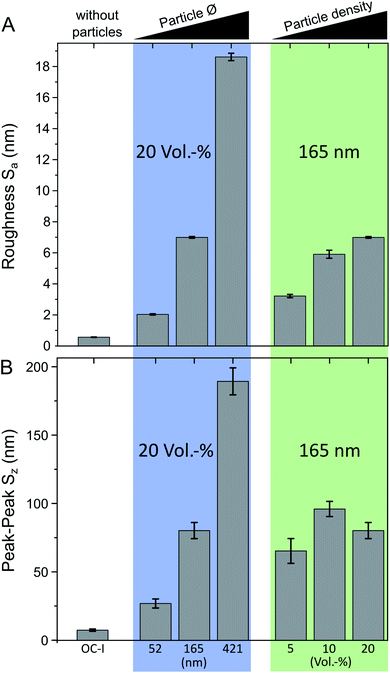
Due to the inhomogeneous diffusion of the oxygen inside the resin before and during the polymerization step, OC-I cured under ambient conditions reveals an additional waviness over a length scale of several micrometers (Fig. 1H1). In the case of the particle composite, this surface waviness is superimposed with the nanotopography, determined by the particle radius and volume fraction. In order to distinguish the surface waviness from the particle induced surface features, the AFM data was separated with a 2 μm L-filter to calculate the surface roughness parameters Sa (arithmetical mean deviation, Fig. 3A) and Sz (height difference of the highest and lowest point of the image, Fig. 3B).
For both curing cases, under argon and ambient air, the Sa values of pure OC-I (without particles) just differ slightly with Sa(OC-I AR) = 0.5 nm and Sa(OC-I) = 0.6 nm. In the case of standard curing under argon, the particle composite with the largest particle diameter exhibits a Sa value with Sa(421–20 AR) = 0.9 nm, comparable to pure OC-I, indicating that the smoothing properties of ORMOCER® hinder the formation of nanotopography. As expected, the Sa values increase with the particle size at a constant filling degree of 20 vol% (Fig. 3A, marked blue) from Sa(52–20) = 2.0 nm, Sa(165–20) = 7.0 nm to Sa(421–20) = 18.6 nm. For a constant particle diameter of 165 nm (Fig. 3A, marked green), the surface roughness can be adjusted via the volume fraction as the Sa value increases with a higher filling degree from Sa(165–5) = 3.2 nm to Sa(165–10) = 5.9 nm to Sa(165–20) = 7.0 nm.
The Sz value is an indicator for the maximum feature height cells are sensing during migration and for a particle fraction of 20 vol%, it ranges from Sz(52–20) = 27 nm to Sz(165–20) = 80 nm and to Sz(421–20) = 189 nm (Fig. 3B). As these values of the maximum height in the surface profile are in the order of half the respective particle diameter, apparently particles that protrude more than half of the particle diameter from the surface are washed away during the development step. This hypothesis is also affirmed by the Sz values of the samples with a constant particle diameter of 165 nm, which show no direct correlation of the Sz value with increasing particle volume fraction. This means that more particles protrude from the sample surface with increasing filling degree and leading to higher Sa values, but the maximum protrusion height stays constant within a certain range.
3.3 Cell migration analysis
To verify the influence of surface topographies in the nanometer range on cell behaviour, we analysed amoeboid migration behaviour of D. discoideum cells on such nanorough samples, in comparison to a chemically equivalent flat reference surface. Bright field and fluorescent images of migrating cells were obtained every 8 s for at least one hour per live-cell measurement. The centre-of-mass of every cell was determined at all time points. All cells are exploring their adjacent environment intensely by forming protrusions on all investigated surface topographies (see exemplary Videos S1–S6†). Using a local mean-squared displacement algorithm with a rolling time window,31 the trajectories of all migrating cells were separated into directed and quasi-random migration states based on the alpha value determined by the power law fit of the LMSD (eqn (4)). During directed migration (1.75 ≤ α ≤ 2.00), cells exhibit a directed and faster motion pattern as compared to the uniform search behaviour during a quasi-random phases (α < 1.75). Both cell migration modes occur alternately and can be influenced via different external cues.54 However, compared to many other cell types, for D. discoideum the directed motion pattern even occurs without any external gradient or other cues, as amoeboid migration consists of alternating directed and quasi-random phases.54 For all nanorough surfaces, approximately 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time points of cell migration were acquired in order to assure a statistically reliable data set (Table S1†). Typical migration trajectories of a single cell migrating (Fig. 4A1 and A2) on a pure polymer surface (Fig. 4B1) and on a nanorough composite surface (Fig. 4B2) illustrate that cell migration is strongly confined on the nanorough surface (note the different z-scales in Fig. 4B1 and B2).
000 time points of cell migration were acquired in order to assure a statistically reliable data set (Table S1†). Typical migration trajectories of a single cell migrating (Fig. 4A1 and A2) on a pure polymer surface (Fig. 4B1) and on a nanorough composite surface (Fig. 4B2) illustrate that cell migration is strongly confined on the nanorough surface (note the different z-scales in Fig. 4B1 and B2).
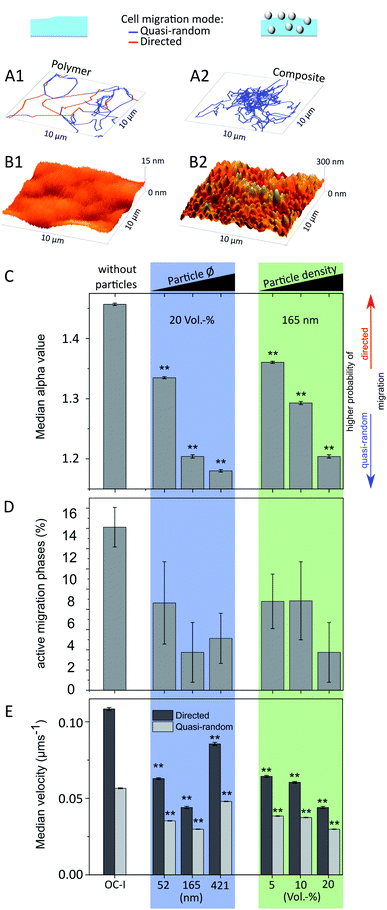 | ||
| Fig. 4 Typical migration trajectories (A1 and A2) of D. discoideum on pure polymer surfaces (B1) and on nanorough composite surfaces (B2) (note the different z-scale in the AFM images). The migration path is separated in directed (red) and quasi-random migration phases (blue) depending on the alpha value, determined via a local mean-squared displacement analysis, which was used to compare the median alpha value (C) (see eqn (4)), ratio of migration phases classified as active (D) and the cells median velocity (E) on different nanorough surfaces and on a similarly treated pure polymer surface as reference. Sample group with a constant particle volume concentration of 20 vol% and increasing particle diameter from 52 nm, 165 nm to 421 nm is highlighted in blue. Sample group with a constant particle diameter of 165 nm and increasing particle volume concentration from 5 vol%, 10 vol% to 20 vol% is highlighted in green. Significance level (**: p ≤ 0.01) is based on non-parametric Mann–Whitney test. Error bars in (C), (E) represents standard error and in (D) standard deviation. | ||
Regarding the surface roughness, there are three intertwined parameters: the particle diameter, the number of particles on the surface per area, and the resulting surface roughness. It is known that cellular behaviour can be influenced by these roughness parameters and cells are able to detect topographies down to 10 nm.61 Therefore, nanorough surfaces with a constant filling degree and varying particle diameter (marked blue) affect cell migration via the mechanical stimuli, which are generated by the density as well as the curvature of the surface features. In the case of a constant particle diameter with varying filling degree (marked green) however, only the feature density changes, which makes it ideal for direct comparison of the cell migration parameters. Estimating this particle density reveals that one particle inside the 421–20 sample, corresponds to 17 in the 165–20 sample and 531 in the 52–20 composite, respectively (see Table S3† for details).
The alpha exponent of the power law fits to the local mean-squared displacement values is a significant parameter to characterize migration behaviour, with values of 1 for a diffusion-like, quasi-random migration behaviour and values of 2 for a straight, directed cell motion. Here, we find lower median values for the alpha exponent for cell migration on all nanorough surfaces (Fig. 4C, for detailed distributions see Fig. S1†) as compared to the migration values on the polymer reference surface without particles. This means that cell migration is hindered on nanorough surfaces. For both sample groups, increasing particle diameter (blue) and increasing particle density (green), a trend towards smaller alpha values is observable with increasing surface roughness. Cell migration on both samples with the highest surface roughnesses 165–20 (Sa = 7.0 nm) and 421–20 (Sa = 18.6 nm) yields median alpha values in the diffusive range of α = 1.14 and α = 1.12, respectively, compared to a much higher median alpha value of α = 1.4 for cell migration on the smooth reference surface.
Regarding the proportion of directed migration phases, it is not possible to establish a correlation among the composite samples, due to its standard deviation (Fig. 4D). Yet, all nanorough samples provoke a significant reduction of the directed migration phases, which drops from more than (16 ± 2)% for the smooth polymer surface down to only (4 ± 2)% and (5 ± 2)% for the roughest surfaces 165–20 and 421–20, respectively. The ratio of directed and quasi-random migration phases depends upon other cues on the mechanical stimulus of the surface and can be altered for instance by aligned surface structures to induce cell guidance. In our case however, the surface features are randomly distributed and might trigger isotropical mechanical cues leading preferably to quasi-random locomotion or even non-migrating cells. A directed motion is therefore interrupted with a much higher probability compared to a surface with no or much less surface features.
Analogously to the median alpha values, the median values of the instantaneous velocities of directed and quasi-random migration states (Fig. 4E, for detailed distributions see Fig. S2†) are significantly lower compared to cell migration on the reference surface. For increasing feature density, e.g. a higher filling degree and constant particle diameter (green), a clear trend towards lower migration velocities is observable. However, for increasing particle size and a constant filling degree (blue) the sample 421–20 does not follow this trend. Its particle diameter is the highest and in the order of the diameter of bacteria (0.2–10 μm (ref. 62)), which is the standard prey of D. discoideum,30 thus other pathways regarding phagocytosis might be triggered and change the migration behaviour severely for this surface type.
Cell-surface interaction of D. discoideum is based on van der Waals forces and, among others, the transmembrane protein SadA.34–36 Both adhesion mechanisms depend strongly on the interaction area between cell body and substrate, which increases with higher surface roughness. This might explain our finding that cell migration is strongly suppressed by nanorough surfaces, since the nanotopography increases the contact area between cell membrane and the substrate, leading to higher overall adhesive forces and suppressing the ability to migrate fast and in a directed way. However, further studies regarding the adhesion mechanism are needed to elucidate these underlying phenomena by immunocytochemistry. For several cell types, an optimum in adhesive strength is observed in order to gain maximal migration rates63 providing a high adhesion to generate high cell forces as well as enabling easy detachment to move the cell body. These here presented nanorough surfaces can be used to adjust the contact area to optimize cell adhesion and migration or to manufacture heterogeneous samples combining pure resin with composite to create selective areas with fast and slow migration rates.
4 Conclusions
In this study, we developed a novel procedure to fabricate tailored surface roughnesses in the nanometre range based on a biocompatible and UV curable particle–polymer composite. This composite consists of the hybrid polymeric matrix ORMOCER® OC-I with stable incorporated silica particles. We demonstrated a tunable surface roughness via two different approaches: (1) variation of the particle diameter or (2) by changing the particle filling degree. Nanoroughness was achieved by exploiting the property of the composite matrix to create an oxygen-related polymerization inhibition layer at the surface, when cured under ambient air. After dissolving this uncured inhibition layer, the particles protrude from the surface and yield the nanorough topography. This was analyzed via AFM measurements in order to verify the homogeneous particle distribution and to determine the arithmetic mean values of the surface roughness Sa, which is adjustable from 2.0 nm to 18.6 nm compared to 0.6 nm of the flat reference.These customizable nanorough surfaces have been investigated influencing the cell migration behaviour of D. discoideum cells, which was analysed by a time-resolved local mean-squared displacement analysis. This evaluation allows for the distinction of two amoeboid migration patterns: fast, directed runs versus slow, random-like migration phases. Without exception the migration was hindered on nanorough surfaces compared to smooth reference samples lacking particles. The amount of time spent in directed migration phases, the instantaneous migration velocities, and the alpha exponent, derived from power law fits to the local mean-squared displacement values, were significantly reduced on nanorough surfaces as compared to the flat surface reference. In particular for nanorough surfaces with a constant particle diameter and varying filling degree, a direct correlation between all investigated migration parameters and the particle volume fraction exhibited that increasing surface roughness suppresses cell migration. In this case the alpha exponent can be tuned within a range of 1.4 and 1.1. As a reason for this behaviour, we assume that the randomly allocated particles perturb the cell polarization and thus hinder phases of direct migration. Additionally, the higher contact surface between cell body and substrate leads to higher adhesion forces, which slow down the overall migration velocity.
The manufactured nanorough composite material is photocurable and 3D-structurable with any light-based fabrication method, like lithography or two-photon polymerization. This material class is therefore well suited as base material for hierarchical structures in the order of centimetres and cell-relevant features in the micrometer range with an adjustable surface nanotopography. Besides that, the general incorporation of functionalized nanoparticles to the composite opens up a wide range of tuneable material characteristics in order to generate multifunctional structures and devices as cell scaffolds for lab-on-a-chip or tissue engineering applications.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge Dr Günther Gerisch (Max-Planck Institute for Biochemistry, Germany) for providing the Dictyostelium discoideum strains. We also like to thank Gerhard Domann, Carola Cronauer, and Adelheid Martin (Fraunhofer ISC, Optics & Electronics Department) for providing polymer resin OC-I and contact angle measurements as well as Sofia Dembski and Gabriele Ulm (Fraunhofer ISC, Theranostik Department) for synthesized Stoeber particles. We further acknowledge funding from the Fraunhofer Attract program for the grant “3DNanoZell” and from the Fraunhofer project center for stem cell process engineering.References
- T. Billiet, E. Gevaert, T. de Schryver, M. Cornelissen and P. Dubruel, Biomaterials, 2014, 35, 49–62 CrossRef CAS.
- R. Gauvin, Y.-C. Chen, J. W. Lee, P. Soman, P. Zorlutuna, J. W. Nichol, H. Bae, S. Chen and A. Khademhosseini, Biomaterials, 2012, 33, 3824–3834 CrossRef CAS.
- F. Viela, D. Granados, A. Ayuso-Sacido and I. Rodríguez, Adv. Funct. Mater., 2016, 26, 5599–5609 CrossRef CAS.
- S. Rekštyte, J. Laser Micro/Nanoeng., 2014, 9, 25–30 CrossRef.
- A. Accardo, M.-C. Blatché, R. Courson, I. Loubinoux, C. Vieu and L. Malaquin, Biomed. Phys. Eng. Express, 2018, 4, 027009 CrossRef.
- J. M. Seok, S. H. Oh, S. J. Lee, J. H. Lee, W. D. Kim, S.-H. Park, S. Y. Nam, H. Shin and S. A. Park, Mater. Today Commun., 2019, 19, 56–61 CrossRef CAS.
- M. N. Rahaman, D. E. Day, B. S. Bal, Q. Fu, S. B. Jung, L. F. Bonewald and A. P. Tomsia, Acta Biomater., 2011, 7, 2355–2373 CrossRef CAS.
- Z. Wang, C. Wang, C. Li, Y. Qin, L. Zhong, B. Chen, Z. Li, H. Liu, F. Chang and J. Wang, J. Alloys Compd., 2017, 717, 271–285 CrossRef CAS.
- C. Matschegewski, S. Staehlke, H. Birkholz, R. Lange, U. Beck, K. Engel and J. B. Nebe, Materials, 2012, 5, 1176–1195 CrossRef CAS.
- L. Zhao, X. Pei, L. Jiang, C. Hu, J. Sun, F. Xing, C. Zhou, Y. Fan and X. Zhang, Composites, Part B, 2019, 162, 154–161 CrossRef CAS.
- L. Treccani, T. Yvonne Klein, F. Meder, K. Pardun and K. Rezwan, Acta Biomater., 2013, 9, 7115–7150 CrossRef CAS.
- K. Czyż, J. Marczak, R. Major, A. Mzyk, A. Rycyk, A. Sarzyński and M. Strzelec, Diamond Relat. Mater., 2016, 67, 26–40 CrossRef.
- A. E. Nel, L. Mädler, D. Velegol, T. Xia, E. M. V. Hoek, P. Somasundaran, F. Klaessig, V. Castranova and M. Thompson, Nat. Mater., 2009, 8, 543–557 CrossRef CAS.
- H. Jeon, M. Lee, S. Yun, D. Kang, K.-h. Park, S. Choi, E. Choi, S. Jin, J.-H. Shim, W.-S. Yun, B.-J. Yoon and J. Park, Chem. Eng. J., 2019, 360, 519–530 CrossRef CAS.
- Y. Wang, G. Wang, X. Luo, J. Qiu and C. Tang, Burns, 2012, 38, 414–420 CrossRef.
- K. Shen, H. Kenche, H. Zhao, J. Li and J. Stone, Biochem. Biophys. Res. Commun., 2019, 508, 302–307 CrossRef CAS.
- W. J. Hadden, J. L. Young, A. W. Holle, M. L. McFetridge, Y. Du Kim, P. Wijesinghe, H. Taylor-Weiner, J. H. Wen, A. R. Lee, K. Bieback, B.-N. Vo, D. D. Sampson, B. F. Kennedy, J. P. Spatz, A. J. Engler and Y. S. Choi, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 5647–5652 CrossRef CAS.
- O. Andrukhov, R. Huber, B. Shi, S. Berner, X. Rausch-Fan, A. Moritz, N. D. Spencer and A. Schedle, Dent. Mater., 2016, 32, 1374–1384 CrossRef CAS.
- R. A. Gittens, T. McLachlan, R. Olivares-Navarrete, Y. Cai, S. Berner, R. Tannenbaum, Z. Schwartz, K. H. Sandhage and B. D. Boyan, Biomaterials, 2011, 32, 3395–3403 CrossRef CAS.
- M. J. P. Biggs, R. G. Richards, N. Gadegaard, R. J. McMurray, S. Affrossman, C. D. W. Wilkinson, R. O. C. Oreffo and M. J. Dalby, J. Biomed. Mater. Res., Part A, 2009, 91, 195–208 CrossRef.
- D. Khang, J. Lu, C. Yao, K. M. Haberstroh and T. J. Webster, Biomaterials, 2008, 29, 970–983 CrossRef CAS.
- P. Chen, T. Aso, R. Sasaki, M. Ashida, Y. Tsutsumi, H. Doi and T. Hanawa, J. Biomed. Mater. Res., Part A, 2018, 106, 2735–2743 CrossRef CAS.
- Y. Zhukova, C. Hiepen, P. Knaus, M. Osterland, S. Prohaska, J. W. C. Dunlop, P. Fratzl and E. V. Skorb, Adv. Healthcare Mater., 2017, 6, 1601244 CrossRef.
- A. B. Faia-Torres, S. Guimond-Lischer, M. Rottmar, M. Charnley, T. Goren, K. Maniura-Weber, N. D. Spencer, R. L. Reis, M. Textor and N. M. Neves, Biomaterials, 2014, 35, 9023–9032 CrossRef CAS.
- D. Khang, J. Choi, Y.-M. Im, Y.-J. Kim, J.-H. Jang, S. S. Kang, T.-H. Nam, J. Song and J.-W. Park, Biomaterials, 2012, 33, 5997–6007 CrossRef CAS.
- K. Anselme, P. Davidson, A. M. Popa, M. Giazzon, M. Liley and L. Ploux, Acta Biomater., 2010, 6, 3824–3846 CrossRef CAS.
- A. M. Lipski, C. J. Pino, F. R. Haselton, I.-W. Chen and V. P. Shastri, Biomaterials, 2008, 29, 3836–3846 CrossRef CAS.
- M. Fathi-Achachelouei, H. Knopf-Marques, C. E. Ribeiro da Silva, J. Barthès, E. Bat, A. Tezcaner and N. E. Vrana, Front. Bioeng. Biotechnol., 2019, 7, 113 CrossRef.
- E. Sackmann, F. Keber and D. Heinrich, Annu. Rev. Condens. Matter Phys., 2010, 1, 257–276 CrossRef CAS.
- S. J. Annesley and P. R. Fisher, Mol. Cell. Biochem., 2009, 329, 73–91 CrossRef CAS.
- D. Arcizet, S. Capito, M. Gorelashvili, C. Leonhardt, M. Vollmer, S. Youssef, S. Rappl and D. Heinrich, Soft Matter, 2012, 8, 1473–1481 RSC.
- M. K. Driscoll, X. Sun, C. Guven, J. T. Fourkas and W. Losert, ACS Nano, 2014, 8, 3546–3555 CrossRef CAS.
- M. Tarantola, A. Bae, D. Fuller, E. Bodenschatz, W.-J. Rappel and W. F. Loomis, PLoS One, 2014, 9, e106574 CrossRef.
- P. Fey, S. Stephens, M. A. Titus and R. L. Chisholm, J. Cell Biol., 2002, 159, 1109–1119 CrossRef CAS.
- N. Kamprad, H. Witt, M. Schröder, C. T. Kreis, O. Bäumchen, A. Janshoff and M. Tarantola, Nanoscale, 2018, 10, 22504–22519 RSC.
- W. F. Loomis, D. Fuller, E. Gutierrez, A. Groisman and W.-J. Rappel, PLoS ONE, 2012, 7(8) DOI:10.1371/journal.pone.0042033.
- B. Lamprecht, R. Thünauer, M. Ostermann, G. Jakopic and G. Leising, Phys. Status Solidi A, 2005, 202, R50–R52 CrossRef CAS.
- K.-H. Haas and K. Rose, Rev. Adv. Mater. Sci., 2003, 47–52 CAS.
- K.-H. Haas, S. Amberg-Schwab and K. Rose, Thin Solid Films, 1999, 351, 198–203 CrossRef CAS.
- S. Steenhusen, F. Burmeister, M. Groß, G. Domann, R. Houbertz and S. Nolte, Thin Solid Films, 2018, 668, 74–80 CrossRef CAS.
- P. Danilevicius, S. Rekstyte, E. Balciunas, A. Kraniauskas, R. Jarasiene, R. Sirmenis, D. Baltriukiene, V. Bukelskiene, R. Gadonas and M. Malinauskas, J. Biomed. Opt., 2012, 17, 081405 CrossRef.
- M. Malinauskas, D. Baltriukiene, A. Kraniauskas, P. Danilevicius, R. Jarasiene, R. Sirmenis, A. Zukauskas, E. Balciunas, V. Purlys, R. Gadonas, V. Bukelskiene, V. Sirvydis and A. Piskarskas, Appl. Phys. A: Mater. Sci. Process., 2012, 108, 751–759 CrossRef CAS.
- F. Burmeister, S. Steenhusen, R. Houbertz, T. S. Asche, J. Nickel, S. Nolte, N. Tucher, P. Josten, K. Obel, H. Wolter, S. Fessel, A. Schneider, K.-H. Gärtner, C. Beck, P. Behrens, A. Tünnermann and H. Walles, Optically Induced Nanostructures: Biomedical and Technical Applications: Two-photon polymerization of inorganic-organic polymers for biomedical and microoptical, 2015 Search PubMed.
- J. Bijelic-Donova, S. Garoushi, L. V. J. Lassila and P. K. Vallittu, Eur. J. Oral Sci., 2015, 123, 53–60 CrossRef CAS.
- R. Buestrich, F. Kahlenberg and M. Popall, J. Sol-Gel Sci. Technol., 2001, 181–186 CrossRef CAS.
- R. Houbertz, G. Domann, C. Cronauer, A. Schmitt, H. Martin, J.-U. Park, L. Fröhlich, R. Buestrich, M. Popall, U. Streppel, P. Dannberg, C. Wächter and A. Bräuer, Thin Solid Films, 2003, 442, 194–200 CrossRef CAS.
- S. Fessel, A. M. Schneider, S. Steenhusen, R. Houbertz and P. Behrens, J. Sol-Gel Sci. Technol., 2012, 63, 356–365 CrossRef CAS.
- S. Dembski, S. Rupp, C. Gellermann, M. Batentschuk, A. Osvet and A. Winnacker, J. Colloid Interface Sci., 2011, 358, 32–38 CrossRef CAS.
- M. Milde, S. Dembski, A. Osvet, M. Batentschuk, A. Winnacker and G. Sextl, Mater. Chem. Phys., 2014, 148, 1055–1063 CrossRef CAS.
- T. Y. Lee, C. A. Guymon, E. S. Jönsson and C. E. Hoyle, Polymer, 2004, 45, 6155–6162 CrossRef CAS.
- L. S. Tsimring, Rep. Prog. Phys., 2014, 77, 026601 CrossRef.
- A. Levchenko and I. Nemenman, Curr. Opin. Biotechnol., 2014, 28, 156–164 CrossRef CAS.
- D. Arcizet, B. Meier, E. Sackmann, J. O. Rädler and D. Heinrich, Phys. Rev. Lett., 2008, 101, 248103 CrossRef.
- M. Gorelashvili, M. Emmert, K. F. Hodeck and D. Heinrich, New J. Phys., 2014, 16, 075012 CrossRef.
- A. Nandi, D. Heinrich and B. Lindner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 021926 CrossRef.
- C. A. S. Batista, R. G. Larson and N. A. Kotov, Science, 2015, 350, 1242477 CrossRef.
- R. P. Bagwe, L. R. Hilliard and W. Tan, Langmuir, 2006, 22, 4357–4362 CrossRef CAS.
- I. A. Rahman and V. Padavettan, J. Nanomater., 2012, 2012, 1–15 CrossRef.
- C. Decker, Prog. Polym. Sci., 1996, 21, 593–650 CrossRef CAS.
- J. Douce, J.-P. Boilot, J. Biteau, L. Scodellaro and A. Jimenez, Thin Solid Films, 2004, 466, 114–122 CrossRef CAS.
- M. J. Dalby, M. O. Riehle, H. Johnstone, S. Affrossman and A. S. G. Curtis, Cell Biol. Int., 2004, 28, 229–236 CrossRef CAS.
- A. Katz, A. Alimova, M. Xu, E. Rudolph, M. K. Shah, H. E. Savage, R. B. Rosen, S. A. McCormick and R. R. Alfano, IEEE J. Sel. Top. Quantum Electron., 2003, 9, 277–287 CrossRef CAS.
- A. Huttenlocher, Curr. Opin. Cell Biol., 1995, 7, 697–706 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra06530g |
| ‡ Present address: Institute of Applied Physics, TU Wien, Getreidemarkt 9, 1060 Vienna, Austria. |
| § Present address: RWTH Aachen, Templergraben 55, 52056 Aachen, Germany. |
| This journal is © The Royal Society of Chemistry 2021 |