Open Access Article
Open Access ArticleElucidating the intercalation of methylated 1,10-phenanthroline with DNA: the important weight of the CH/H interactions and the selectivity of CH/π and CH/n interactions†
Ángel Sánchez-González*a and
Adrià Gil *ab
*ab
aBioISI – Biosystems and Integrative Sciences Institute, Faculdade de Ciências, Universidade de Lisboa, Campo Grande, 1749-016, Lisboa, Portugal. E-mail: a.gil@nanogune.eu; agmestres@fc.ul.pt; adriagilmestres@gmail.com; asgonzalez@fc.ul.pt
bCIC nanoGUNE BRTA, Tolosa Hiribidea 76, E-20018, Donostia – San Sebastian, Euskadi, Spain
First published on 5th January 2021
Abstract
Flat molecules like phenanthroline derivatives intercalate between base pairs of deoxyribonucleic acid and produce cytotoxic effects against tumoral cells. Elucidating the way of intercalation and its modulation on their efficiency by substitution still remains a challenging topic of research. In this work we analysed the intercalation via the major groove of methylated derivatives of phenanthroline, in different number and position, between guanine–cytosine base pairs. We studied our systems by using semi-empirical methods and density functional theory including dispersion corrections with the PM6-DH2 Hamiltonian and the B3LYP-D3 functional. We explored the geometry and electronic structure by means of the quantum theory of atoms in molecules and non-covalent interactions index analyses, whereas the interaction energy was estimated by means of two different approaches: one taking into account the results from the quantum theory of atoms in molecules analysis and the other based on the so-called energy decomposition analysis. The effect of solvation was also taken into consideration. Our studies show that CH/π and CH/n interactions by means of the –CH3 groups of methylated phen follow a clear pattern for any number of –CH3 groups and their position in the methylated phen ligand. That is, they try to produce the CH/π and CH/n interactions with the O and N heteroatoms of the base pairs and with the O atoms of the sugar and phosphate backbone. These findings suggest that the modulation of the intercalation of ligands that are able to form CH/π and CH/n weak interactions with the deoxyribonucleic acid is ruled not only by the number and position of the substitutions of the ligands but also by some key sites, which are the O and N atoms of the deoxyribonucleic acid in our analysed systems. It suggests some key and lock mechanism in which the interacting fragments fit like puzzle pieces in order to achieve the optimal interaction for the stabilization of the system. Interaction energies were calculated by using different approaches which converged to similar trends about the number and position of the –CH3 groups. The important weight of the CH/H interactions in the total interaction energy must be highlighted.
Introduction
Nowadays the intercalation of metal complexes in duplex DNA structures arises as an alternative and less aggressive option to the use of cisplatin in processes of chemotherapy to face cancer diseases.1,2 The intercalation between DNA base pairs (bps) of any metal complex needs a flat ligand in its structure and several studies have appeared in the literature considering this kind of structure as intercalators of DNA during the last few years.1,3,4 Some theoretical studies have been carried out considering flat ligands like 1,10-phenanthroline (phen) derivatives, 2,2′-bipyridine (bipy) and dipyridophenazine (dppz) by several authors5–9 and also in our group.10–14 On the other hand, the cytotoxic activity of metal complexes containing phen has been also proven experimentally by our collaborators.15 In addition, the interest of phen derivatives for medical applications has been increased with its potential applications as alternative treatments against antibiotic resistant bacteria.16 Because of the structural characteristics of duplex DNA, which is ruled by the hydrogen bonds of the bps and the stacking of these bps forming the double helix, the sugars of the nucleotides remain always in the same side, which produces some kind of narrow groove, which is called the minor groove. On the other hand, the opposite side of DNA without the sugars of the nucleotides is called the major groove because the width of such a groove has a higher size. Some experimental studies based on the determination of crystal structures pointed out that intercalation of metal complexes including flat ligands between bps may take place via minor groove opposite to the classic opinion, which says that intercalation through the minor groove would produce more strain to the system.17–20 Nevertheless, NMR structure analyses and several solution spectroscopic techniques seem to propose that the intercalation of these metal complexes including flat ligands may occur via major groove according to the classical point of view and it is tempting to speculate that a delicate balance between major and minor groove intercalation is found in solution.18,19 Due to the wide range of medical applications where the flat intercalators can be used21 an understanding at fundamental molecular level of the processes involved in the intercalation becomes very useful. For this reason, it is crucial to gain insight on the modulation of these processes of intercalation by means of different substituents and to stablish differences in the toxicity, which is very important in drug design to obtain efficient biological activity. Regard to the modulation by means of substituents, an inspiring experimental work was published by Brodie et al.,22 where a family of methylated phen derivatives of [Pt(en)(phen)]Cl2 was studied to observe their trends in cytotoxicity against L1210 mouse leukemia. The authors pointed out that only the derivatives 5,6-Me2phen and 5-Mephen presented remarkable cytotoxicity, which suggested that substitution at position 5 of phen could have and important role when analysing the interactions with DNA at molecular level. In order to get insight on the relation between structure and cytotoxicity we already performed a previous computational study13 in which we studied all the intercalating systems considered by Brodie et al.22 in their experiments by means of model systems. Our results based on interaction energies verified our hypothesis on the important role of the position of the methylation and the systems 5-Mephen and specially 5,6-Me2phen had the most negative interaction energy, which was in agreement with our hypothesis on the importance of the position of the substitution.In order to explore the whole scheme for the intercalation, we present in this work a complete analysis of the interactions between methylated phen derivatives and GC/CG bps. We chose GC/CG bps because of the observed better exothermicity for other intercalators when comparing to ATTA bps,23 whereas we took into account the intercalation via major groove (see Scheme 1) because this orientation could be preferred in an aqueous environment, which is the general environment in biological systems.18,19 We consider a complete geometrical study attending to the roll distortion24,25 produced in the DNA bps after the intercalation. Bond properties and non-covalent interactions like π–π, CH/π, CH/n and CH/H are also analysed with the topological tools of Quantum Theory of Atoms in Molecules (QTAIM)26 and Non-Covalent Interaction (NCI) index.27 Specially interest arise from the non-negligible role that we have found for the CH/H interactions. Actually, these CH/H interactions may have a similar weight as for the usual π–π interactions found in flat small molecules intercalating between bps. On the other hand, we found that the CH/π and CH/n interactions coming from the methyl groups, which we called Me/π and Me/n, have preferences for specific O and N atoms localized in some key sites when interacting with duplex DNA. It suggests some key and lock mechanism where the intercalator try to fit like a puzzle piece to achieve the optimal interaction with the intercalation pocket of the DNA to stabilize better the system. Interaction energies are discussed not only by means of the approach of Molins–Espinosa–Lecomte (EML)28 following the results of the electronic density coming from the QTAIM analysis but also with the so-called Energy Decomposition Analysis (EDA).29,30 We expect that this work will help to shed light on the behaviour of these important processes of intercalation, which are of biological and medical interest.
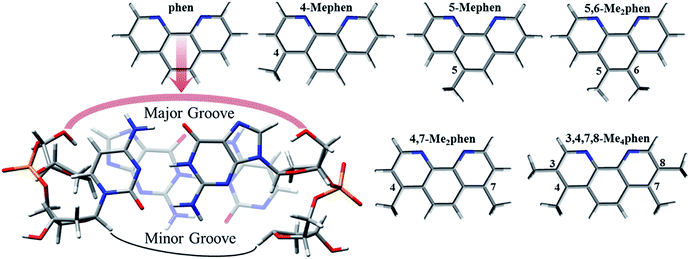 | ||
| Scheme 1 Intercalation mechanism of phen and considered methylated derivatives between GC/CG bps via major groove. | ||
Computational details
In order to study the intercalation of methylated phen derivatives the so-called ring models31 have been considered. We built these ring models from the 2ROU32 crystal structure taken from the Protein Data Bank (PDB). Starting from this structure, the (1R-trans-antibenzo[c]phenanthrene) ligand between the bps of DNA was removed and the N2 of the guanine was saturated. From the whole DNA structure, we only kept the intercalation pocket (bps, phosphates and sugars) and the rest of the sequence was removed. The remaining O atoms that limited the sugar and phosphate backbone were saturated with hydrogen atoms. The intercalator, that is, phen and methylated derivatives, was placed manually between bps considering the maximum overlap and an equidistant arrangement. Finally, in order to keep the neutral charge of the whole system a Na+ cation was put for each phosphate group present in the final ring model.The semiempirical Hamiltonian PM6-DH2,33 which includes dispersion corrections, was employed to carry out full geometry optimizations of the ring models for each studied system. Due to the nature of the studied structures, stacked aromatic moieties with noncovalent interactions, such dispersion corrections are required.33,34 This PM6-DH2 semi-empirical method was already tested with success optimizing the 1BNA structure from PDB,35 and comparing the geometrical results with the original PDB structure.13 The MOPAC2016 software36 was employed to carry out such optimizations without constrains.
In order to understand the nature of the interaction between the DNA structure and the intercalators at fundamental molecular level, from the optimized geometries, wave functions were generated at M06-2X/6-31+G(d,p)//PM6-DH2 level of theory for all the studied systems with the Gaussian software37 to carry out the analysis of the electron density (ρ) with QTAIM.26 QTAIM describes accurately the concepts of atom and chemical structure by exploring the topology of ρ. From the QTAIM point of view, two atoms are bonded when they share a common interatomic surface (zero-flux surface) through which they can interact, and where there is a point (contained in the zero-flux surface) where ρ is a minimum in an specific direction but a maximum in a plane perpendicular to it. These points are known as bond critical points (BPCs) and the pair of gradient paths that connects the BCP with each nucleus is referred as atomic interaction line or bond path. From the QTAIM studies and ρ values we also estimated the energy of interaction for the studied systems by means of the EML approach.28 Moreover, the non-covalent interactions, which play an important role in many processes related to biological systems, have been analysed with the NCI index approach developed by Johnson et al.27 This approach provides a rich and 3D representation of non-covalent interactions (π–π and different kind of hydrogen bonds), with surfaces based on the peaks that appear in the reduced density gradient at low values of ρ. These surfaces are mapped according to the second Hessian matrix eigenvalue, negative values (stabilizing interactions) are depicted in blue and pale green, while positive values (destabilizing interactions) are represented in yellow and red. This approach provides useful information in systems where π–π interactions are present between aromatic moieties (DNA bps and flat intercalators). The AIMAll software38 has been used to perform both, the QTAIM topologies and NCI index isosurfaces.
The interaction energy (ΔEint) between the intercalator and the DNA structure has been studied with the EDA that is based on the Morokuma-type decomposition method.29,30 Such methodology allows the calculation of the contributions of the different terms of the interaction energy between two fragments: (1) the intercalator and (2) the rest of DNA structure (bps, sugars and phosphates). With this analysis ΔEint is split into different contributions: orbital energy related to polarization and charge transfer terms (ΔEorb), Pauli repulsion contribution related to the destabilizing interactions between occupied orbitals (ΔEPauli), electrostatic contribution related to the classical electrostatic interaction between the unperturbed charge distributions of the rigid fragments (ΔEelstat) and dispersion energy associated to van der Waals forces (ΔEdisp). In order to perform the EDA, ADF software39–41 has been employed with single-point calculations on the PM6-DH2 optimized geometries, using the uncontracted polarized triple-ζ basis set of Slater-type orbitals (TZP) and the B3LYP-D3 functional with the Grimme's D3 correction to include dispersion forces.42–45 The solvent effects have been included with the COSMO solvent approach46 because the relevance of solvation in these biological systems has been reported previously.12 The Basis Set Superposition Error (BSSE) was not considered due to the fact that in previous works,10,11 where the intercalation of phen derivatives between DNA bps was already studied, the error was only 8–12%.
Results and discussion
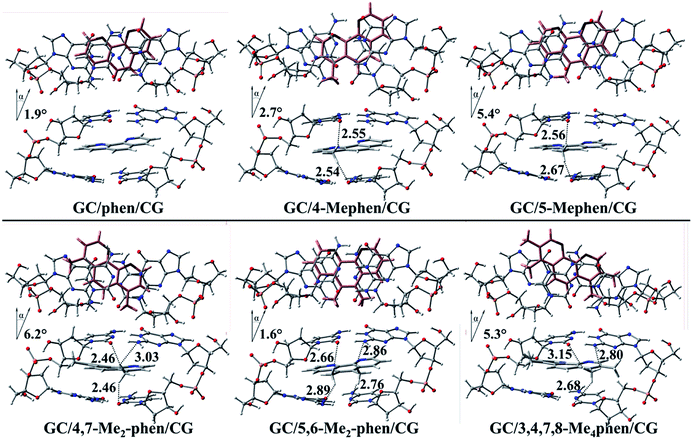
First of all the geometrical results will be presented. In Fig. 1 the coplanar arrangements for the optimized structures of the corresponding methylated derivatives of phen are shown along with the values obtained for the roll distortion24,25 (see also ESI†) produced in the process of intercalation between the bps. It is observed that the roll distortion presents relative low values for all the intercalators between 1.6 and 6.2°. Surprisingly, for the most substituted intercalator, 3,4,7,8-Me4phen, the intercalation via major groove presents a lower value in comparison to the intercalation via minor groove checked in a previous work.13 This difference can be explained because of the location of the –CH3 groups in positions 7 and 8, which remain far away from the sugar and phosphate backbone in the case of the intercalation via major groove. On the contrary, in the case of the intercalation via minor groove the –CH3 groups in positions 7 and 8 were located close to the sugar and phosphate backbone and produced destabilizing interactions with it. Another geometrical characteristic to take into account is the relative position of the aromatic moieties and how the molecular planes are facing each other. The main conclusion that arise from the geometrical arrangement is that the –CH3 groups tend to be located near and between the O and N atoms of the GC/CG bps. This behaviour allows the non-substituted phen, 5-Mephen and 5,6-Me2phen to present the best overlapped arrangement between the ligand and DNA bps planes. On the other hand, 4-Mephen, 4,7-Me2phen and 3,4,7,8-Me4phen structures present the most distorted arrangements between the aromatic moieties, leaving part of the aromatic plane of the ligand outside of the intercalation pocked and in consequence, showing less overlap. Such result will be corroborated below with the QTAIM and NCI analyses, where interactions between the –CH3 groups and O and N atoms of the bps were found.To gain insight into the role played by the electronic density in the intercalation of phen derivatives in DNA structure NCI analysis is shown, such analysis provides a 3D representation of non-covalent interactions. Due to the presence of the weak interactions between the intercalator and the DNA (π–π stacking and several kinds of hydrogen bonds), the NCI analysis will give us a complete view to describe the bonding scheme between the intercalator and DNA structure towards the non-covalent interactions. In Fig. 2 the NCI isosurfaces are plotted. Blue and pale green indicate negative values, which corresponds to stabilizing interactions, while yellow and red indicate positive values and therefore destabilizing interactions. In order to show a clearer and cleaner picture, the NCI isosurfaces have been computed only for regions surrounding the intercalator. In this way the weak interactions between phosphates and sugars in the backbone and the isosurfaces corresponding to destabilizing interactions in the inner regions of sugar rings, that will overload the picture, are not shown. Moreover, the connectivity towards the bond paths according to the QTAIM methodology is also plotted, showing a good agreement between NCI and QTAIM analyses as expected. The characteristics of the corresponding BCPs will be described below.
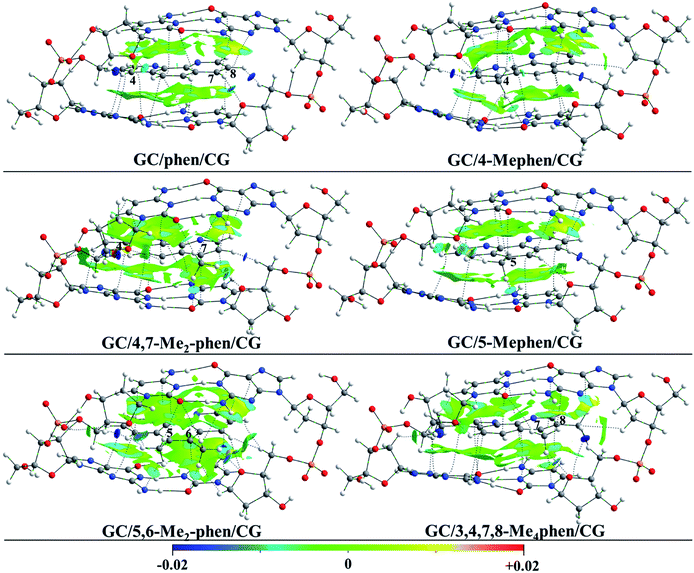 | ||
| Fig. 2 NCI index plots with gradient isosurfaces, plotted at s = 0.5 a.u. (see ref. 27 for the definition of s) for phen and all the phen methylated derivatives intercalated between GC/CG, via major groove. | ||
It is observed that for all intercalators a large green region between the aromatic moieties of DNA structure and intercalator is predominant along with a more stable negative value for the NCI index in the surrounding zones of the BCPs (depicted in cyan). This is a common result in systems where π–π stacking is produced.13,14,47,48 For the non-substituted phen it is observed that in addition to the large NCI isosurface corresponding to the interplanar region, the presence of CH/H interactions is shown with H belonging to the sugar structures for the H atoms located in positions 4 and 8 of the intercalator. Similar kind of interactions have been already depicted previously with different computational approaches.49–52 Moreover, the H atom in position 7 interacts with the O atom of sugar moiety. All these interactions present high and negative value for the NCI index, which indicates a strong and stabilizing interaction and thus, the important role of this kind of interactions in the studied systems.
When –CH3 groups are present in phen structure, as we have observed in geometrical results depicted above, –CH3 groups tend to be located in the proximity of the O and N atoms belonging to GC/CG bps. It is observed in Fig. 2 that the –CH3 groups yield interactions with a considerable negative value of the NCI index with the O atom of the cytosine and the N atom of the guanine. Moreover, another interaction with the O atom belonging to the sugar appears. This is the preferred arrangement for the –CH3 groups and it is present in all kind of substitutions at least for one –CH3 group. According to this, the most favourable scenario corresponds to the 5,6-Me2phen where both –CH3 groups present interactions with N and O atoms of the bps and at the same time with the O atoms belonging to the sugars of the sugar and phosphate backbone. All the mentioned interactions tend to present considerable negative values and they show cyan or dark cyan isosurfaces (see ESI†).
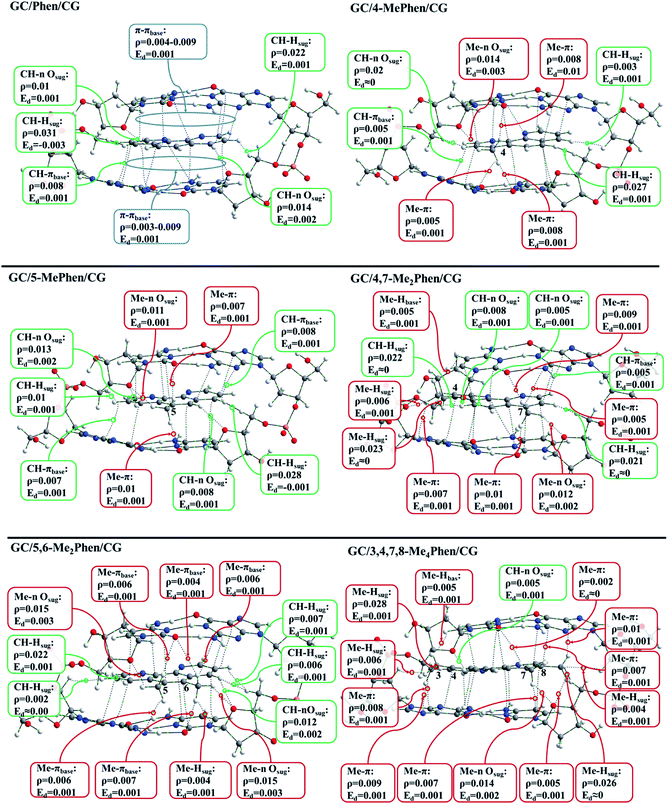
In the following lines we are going to focus on the discussion on the topological analysis of ρ provided by the QTAIM analysis. The value of ρ at the BCPs indicates the strength of the bond formed between two atoms, while the electron-energy density (Ed) describes the stability of the chemical bond. In this kind of systems where the weak interactions prevail between the intercalator and the DNA structure, the values of Ed are close to zero as characteristic of weak interactions. We observe the general agreement between the QTAIM and the NCI analyses where the regions of negative values in the NCI isosurfaces are surrounding the BCPs. In addition, the geometrical results, where the –CH3 groups tend to be located close to the heteroatoms of bps, can be explained with the interactions depicted with the analysis of the ρ. Fig. 3 shows the topological analysis of ρ for all the systems intercalating via major groove. In order to show a clearer picture, only the interactions between the intercalator and the DNA structure are presented (interactions between sugar and phosphates are omitted). For all the structures several π–π interactions were found (blue boxes), and to avoid overloaded representations these π–π interactions have been only described for the non-methylated phen (see ESI† for the whole scheme). Aside from the π–π BCPs, interactions between the DNA structure and H atoms of phen also appear: CH/nsugar, CH/πbps and CH/Hsugar, which are presented in green boxes.
After the implementation of –CH3 groups in the phen structure we can see that several interactions appear due to the presence of –CH3 groups in the surrounding environment of the pocket formed by the DNA bps. It is observed for 4-Mephen that four interactions appear because of the presence of the –CH3 group. Three of these interactions are produced with the heteroatoms belonging to the plane of bps with values of 0.005 and 0.008 a.u. for ρ, and one interaction with an O atom of the nearby sugar with a high value of ρ (0.014 a.u.). We have previously observed in the geometrical results that the preferred position of the –CH3 is located in the proximity of the O and N atoms of the interacting bps. Thus, the localization of the O and N atoms rule the global arrangement of phen derivatives intercalated between the bps. In this case where –CH3 is in position 4, the intercalator plane is slightly turned in order to satisfy such position and interactions for the –CH3. A very similar scheme is presented for 5-Mephen, showing two interactions with heteroatoms of the bps and one with the O atom of the nearby sugar, being again the interaction with the O atom of the sugar the most strong with a high value of ρ in such BCP (0.011 a.u.).
A different behaviour is presented for 4,7-Me2phen and 3,4,7,8-Me4phen. When different –CH3 groups are present in positions far away from each other. That is, one of the –CH3 groups is located close to the O and N atoms of the interacting bps, the preferred area, while the other –CH3 groups are left out, which yields most distorted arrangements between the intercalator and the DNA structure, as we have observed previously in the geometrical analysis. For these structures the –CH3 groups that are left out can also interact with the sugar and phosphate backbone and bps at the same time. Finally, it is noteworthy the bonding scheme presented by 5,6-Me2phen. In this case both –CH3 groups are located in the centre of the structure of the bps, the preferred area, close to N and O. In this position both –CH3 groups may form interactions with the heteroatoms of the bps and at the same time with the O atoms of the sugars. In this case both –CH3 groups yield eight interactions, five with the heteroatoms of the bps and three with the sugars, being the interactions formed with the O atoms of the sugar those that present higher values of ρ (0.015 a.u.). Moreover, another characteristic that should be highlighted is that when the –CH3 groups are located at positions 5 and 6, the whole aromatic plane of phen is completely overlapped with the aromatic environment of the bps. It can be appreciated in the NCI results where for this system large isosurfaces between the aromatic moieties are observed. All these contributions place the 5,6-Me2phen as the preferred phen methylated derivative for an effective intercalation between CG/GC bps via major groove.
Table 1 summarizes all the BCPs presented between the corresponding intercalator and the DNA structure. As expected, the increasing number of –CH3 groups yields more BCPs, which increase the number of weak interactions. The increasing is remarkable for 5,6-Me2phen and 3,4,7,8-Me4phen due to the interactions of the –CH3 groups with the sugars and the π environment of the bps.
| π–πbps | CH–πbps | CH–n Osugar | CH–Hsugar | Me–n Osugar | Me–Hsugar | Me–πbps | Total BCPs | |
|---|---|---|---|---|---|---|---|---|
| phen | 12 | 1 | 2 | 2 | — | — | — | 17 |
| 4-Mephen | 11 | 1 | — | 3 | 1 | — | 3 | 19 |
| 5-Mephen | 8 | 2 | 2 | 2 | 1 | — | 2 | 17 |
| 4,7-Me2phen | 10 | 1 | 2 | 2 | 1 | 3 | 4 | 23 |
| 5,6-Me2phen | 10 | — | 1 | 4 | 2 | 1 | 5 | 23 |
| 3,4,7,8-Me4phen | 11 | — | 1 | — | 1 | 4 | 8 | 25 |
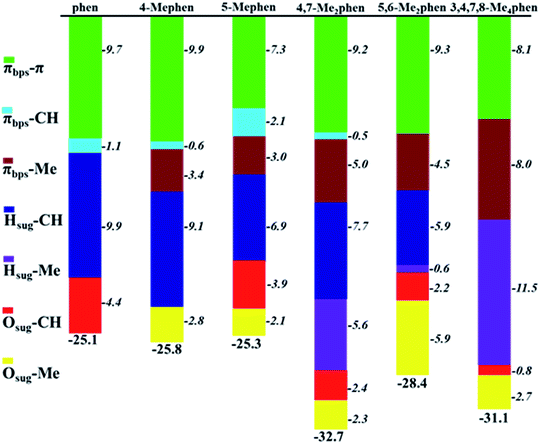
Attending to the results obtained in Table 1 and Fig. 3 the question that arises is of how much the different kind of interactions contribute to the global stability of the intercalation. Thus, based on the properties of ρ at the BCPs, the interaction energy (ΔEint) between two fragments can be calculated with the EML approach28 (eqn (1)). Such approach has been previously employed in DNA systems where the role of the backbone, in the interaction of minor groove ligand binding, has been described.53 The EML approximation was developed to consider H bonds only with O atoms, while when other kind of interactions are present, Díaz-Gómez et al.53 implemented a correction for the BCPs different from the H⋯O hydrogen bonds (eqn (2)). Attending to such approaches Fig. 4 and Table S1 of ESI† summarise all the stabilization contributions depending on the different weak interactions present between the phen derivatives and the GC/CG bps along with the total stabilization for each studied system according to the corrected EML approach.
 | (1) |
 | (2) |
It is observed in Fig. 4 that the general trend is the increasing of the strengthening of the interaction with more negative values of ΔEint when the number of methyl groups increases. For all the structures, the main stabilization in general is due to all the BCPs corresponding to π–π interactions. However, such π–π contribution is very similar for all the studied systems (from −7.3 to −9.9, which is a difference of only 2.6 kcal mol−1). Therefore, the differences in the total interaction energy, ΔEint, will be given by the other weak interactions localized in the studied systems. Moreover, the values obtained for CH/H interactions must be also highlighted since they present considerable high values (from −5.9 to −9.9 kcal mol−1). The addition of such CH/H contributions lead to estimations of the total interaction energies, ΔEint, which are very similar to the ΔEint values obtained with the EDA discussed below. It indicates not only the correct consideration of these non-conventional interactions in the extrapolation of the ΔEint with the EML approach but also the relevance of these CH/H interactions that have been reported previously in the bibliography.49–52 This behaviour can be understood with the high values for the ρ obtained from the QTAIM analysis in such interactions and in addition with the high negative values for the isosurfaces in the NCI analysis.
Another considerable contribution to the strengthening of the interaction energy and more negative values of ΔEint is obtained with the Me–π interactions, being −5.0, −4.5 and −8.0 kcal mol−1 for 4,7-Me2phen, 5,6-Me2phen and 3,4,7,8-Me4phen, respectively. Due to this contribution these three derivatives show a total ΔEint of −32.7, −28.4 and −31.1 kcal mol−1, respectively, being the most preferred intercalators for the intercalation between GC/CG bps through the major groove. Considering the different kinds of interactions with different nature it can be assumed that the values for the constants in EML approach are still too general to describe properly the interaction energies and in addition, such approach is very local and only focus on the properties of the BCPs, whereas it does not take into account the whole effect of the fragments and the feasible cooperative effects that could lead to a more strengthened interaction and therefore to more negative interaction energies.
At this point we have to say that the EDA provides an accepted and accurate way to determine the interaction energy (ΔEint) between fragments that can be decomposed into different contributions: electrostatic (ΔEelstat), charge transfer and polarization terms in the orbital contribution (ΔEorb), dispersion (ΔEdisp), and the destabilizing interaction between occupied orbitals (ΔEPauli):
| ΔEint = ΔEelstat + ΔEorb + ΔEdisp + ΔEPauli | (3) |
Fig. 5 shows the EDA results for the intercalation of phen and the studied methylated phen derivatives when intercalating between GC/CG bps via major groove. In general, the attractive terms are slightly increased with the presence of –CH3 groups. That is, the ΔEdisp is gradually increased with the presence of –CH3 groups from −50.4 to −59.4 kcal mol−1. This is also the general trend for the repulsive Pauli contribution. In the graph of Fig. 5 it is observed that such repulsion requires the small contributions of the electrostatic and orbital terms to stabilize the whole systems. Considering this fact and attending to the values of the electrostatic forces, the 5,6-Me2phen and 3,4,7,8-Me4phen are the most stabilized intercalators due to the high value of the electrostatic contribution −39.1 and −37.8 kcal mol−1, respectively.
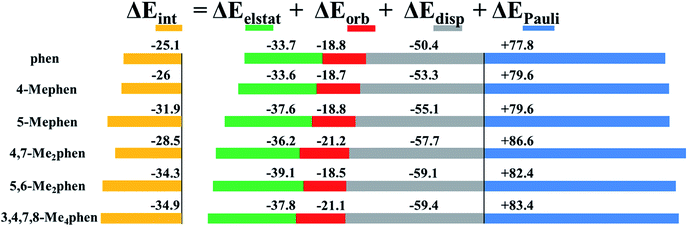 | ||
| Fig. 5 Cumulative bar diagram for the energy contributions in the EDA computed at B3LYP-D3/TZP level. Values in kcal mol−1. | ||
From the values of the EDA it is observed that the implementation of –CH3 groups stabilized the intercalation, but the most effective intercalation in terms of number of –CH3 groups vs. ΔEint corresponds to 5,6-Me2phen. With only two –CH3 groups this compound reaches a very similar value of the ΔEint when comparing to the ΔEint value of the 3,4,7,8-Me4phen that presents different kinds of weak interactions in the four –CH3 groups. Summarising, we can suggest that the most effective positions for the methylation are 5 and 6. This is in agreement with the results obtained from the topology of ρ, where we showed that in such positions –CH3 groups yield very effective weak interactions with the N and O atoms of the upper and down bps, and at the same time with O atoms of the sugars present in the sugar and phosphate backbone. In the same way the stabilization presented by 5-Mephen, −31.9 kcal mol−1, can be understood due to the position of the –CH3 that forms 3 effective weak interactions with O atoms of the bps and the sugar.
To gain more insight on the role of the solvent in the process of the intercalation, the desolvation penalty has been computed and added to the total ΔEint of the EDA and the obtained values are presented in Table 2.
| phen | 4-Mephen | 5-Mephen | 4,7-Me2phen | 5,6-Me2phen | 3,4,7,8-Me4phen | |
|---|---|---|---|---|---|---|
| a ΔESolv = ESolv(total system) − ESolv(intercalator) − ESolv(pocket).b ΔEAq = ΔEint + ΔESolv. | ||||||
| ESolv(total system) | −108.7 | −107.1 | −108.3 | −108.2 | −107.2 | −107.5 |
| ESolv(intercalator) | −15.6 | −16.7 | −15.8 | −17.3 | −16.2 | −17.2 |
| ESolv(pocket) | −104.3 | −102.6 | −103.7 | −103.1 | −105.4 | −105.0 |
| ΔEint | −25.1 | −26.0 | −31.9 | −28.5 | −34.3 | −35.9 |
| ΔESolva | 10.9 | 12.2 | 11.2 | 12.2 | 14.4 | 14.7 |
| ΔEAqb | −14.2 | −13.8 | −20.7 | −16.4 | −19.9 | −20.2 |
Looking at the ΔEAq energies, we observe that after including the solvent penalty, ΔESolv, to the interaction energy, ΔEint, 5-Mephen, 5,6-Me2phen and 3,4,7,8-Me4phen still remain as the intercalators that lead to more negative ΔEAq energies being −20.7, −19.9 and −20.2 kcal mol−1, respectively, and therefore achieving better intercalation via major groove with GC/CG bps.
Conclusions
Our present work offers important and detailed comprehension to understand the chemical reasons of the effect of methylation, in number and position, on the process of the intercalation of phen and methylated derivatives and how the strength of the interaction with DNA may be modulated. The number of –CH3 groups present in the phen aromatic rings favour the process of intercalation between GC/CG bps through the major groove, and in consequence its cytotoxicity. Nevertheless, we may affirm that the position of –CH3 groups is more important than the number. In the intercalation of methylated phen derivatives between GC/CG bps via major groove the number of –CH3 groups does not increase significantly the steric repulsion. However, from the topological analysis of the ρ it can be observed that the 5 and 6 positions yields effective weak interactions with O and N heteroatoms of the environment, O and N belonging to the bps and also O atoms belonging to sugars of the sugar and phosphate backbone. At the same time the methylation in 5 and 6 positions favours a better overlap and co-planarity between phen and bps aromatic moieties yielding a more effective π–π stacking and thus to a better inclusion and stabilization of the ligand between bps of DNA. Thus, we may affirm that the process of the intercalation of methylated phen derivatives with DNA will follow the key and lock mechanism in which each fragment, intercalator and intercalation pocket between bps, fit like puzzle pieces in order to achieve the most effective interaction. On the other hand, the importance of CH/H interactions are highlighted when calculating the interaction energy with the EML approach in which the weight of the electronic density corresponding to these CH/H interactions is very important in the total interaction energy. We compared the ΔEint obtained from the EML approximation with the ΔEint coming from the EDA, which is another different procedure to obtain the ΔEint, and the values and trends converge and are very similar, which corroborates the important role that CH/H interactions play in this kind of processes of biological and medical interest.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was financially supported by the Fundação para a Ciência e a Tecnologia (FCT) by means of the Projects PTDC/QUI-QFI/29236/2017, UIDB/04046/2020, UIDP/04046/2020 and by the Spanish Ministry of Economy, Industry and Competitiveness under the Maria Maeztu Units of Excellence Programme – MDM-2016-0618. A. Gil is grateful to Diputación Foral de Gipuzkoa for current funding in the frame of Gipuzkoa Fellows Program. A. Sánchez-González is grateful to Dr José Antonio Jiménez Madrid for all the fruitful discussions and his help.Notes and references
- H. K. Liu and P. J. Sadler, Acc. Chem. Res., 2011, 44, 349 CrossRef CAS.
- A. Kumar and U. Bora, Mini-Rev. Med. Chem., 2013, 13, 256 CAS.
- B. M. Zeglis, V. C. Pierre and J. K. Barton, Chem. Commun., 2007, 4565 RSC.
- D. R. Boer, A. Canals and M. Coll, Dalton Trans., 2009, 399 RSC.
- A. Robertazzi, A. V. Vargiu, A. Magistrato, P. Ruggerone, P. Carloni, P. de Hoog and J. Reedijk, J. Phys. Chem. B, 2009, 113, 10881 CrossRef CAS.
- A. V. Vargiu and A. Magistrato, Inorg. Chem., 2012, 51, 2046 CrossRef CAS.
- R. Galindo-Murillo, L. Ruíz-Azuara, R. Moreno-Esparza and F. Cortés-Guzmán, Phys. Chem. Chem. Phys., 2012, 14, 15539 RSC.
- P. Hazarika, B. Bezbaruah, P. Das, O. K. Medhi and C. A. Medhi, J. Biophys. Chem., 2011, 2, 152 CAS.
- D. Ambrosek, P.-F. Loos, X. Assfeld and C. A. Daniel, J. Inorg. Biochem., 2010, 104, 893 CrossRef CAS.
- A. Gil, M. Melle-Franco, V. Branchadell and M. J. Calhorda, J. Chem. Theory Comput., 2015, 6, 2714 CrossRef.
- A. Gil, V. Branchadell and M. J. Calhorda, RSC Adv., 2016, 6, 85891 RSC.
- A. Galliot, A. Gil and M. J. Calhorda, Phys. Chem. Chem. Phys., 2017, 19, 16638 RSC.
- A. Gil, A. Sanchez-Gonzalez and V. Branchadell, J. Chem. Inf. Model., 2019, 59, 3989 CrossRef CAS.
- S. Elleuchi, I. Ortiz de Luzuriaga, A. Sanchez-Gonzalez, X. Lopez, K. Jarraya, M. J. Calhorda and A. Gil, Inorg. Chem., 2020, 59, 12711 CrossRef.
- D. Bandarra, M. Lopes, T. Lopes, J. Almeida, M. S. Saraiva, M. V. Días, C. D. Nunes, V. Félix, P. Brandão, P. D. Vaz, M. Meireles and M. J. Calhorda, J. Inorg. Biochem., 2010, 104, 1171 CrossRef CAS.
- L. Viganor, O. Howe, P. McCarron, M. McCann and M. Devereux, Curr. Top. Med. Chem., 2017, 17, 1280 CrossRef CAS.
- J. P. Hall, K. O'Sullivan, A. Naseer, J. A. Smith, J. M. Kelly and C. J. Cardin, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 17610 CrossRef CAS.
- S. Neidle, Nat. Chem., 2012, 4, 594 CAS.
- H. Song, J. T. Kaiser and J. K. Barton, Nat. Chem., 2012, 4, 615 CrossRef CAS.
- H. Niyazi, J. P. Hall, K. O'Sullivan, G. Winter, T. Sorensen, J. M. Kelly and C. J. Cardin, Nat. Chem., 2012, 621 CrossRef CAS.
- C. Cordier, V. C. Pierre and J. K. Barton, J. Am. Chem. Soc., 2007, 129, 12287 CrossRef CAS.
- C. R. Brodie, J. Grant Collins and J. R. Aldrich-Wright, Dalton Trans., 2004, 1145 RSC.
- K. Kanoh, Y. Baba and A. Kagemoto, Polym. J., 1988, 20, 1135 CrossRef CAS.
- W. K. Olson, M. Bansal, S. K. Burley, R. E. Dickerson, M. Gerstein, S. C. Harvey, U. Heinemann, X.-J. Lu, S. Neidle, Z. Shakked, H. Sklenar, M. Suzuki, C.-S. Tung, E. Westhof, C. Wolberger and H. M. A. Berman, J. Mol. Biol., 2001, 313, 229 CAS.
- R. E. Dickerson, M. Bansal, C. R. Calladine, S. Diekmann, W. N. Hunter, O. Kennard, E. von Kitzing, R. Lavery, H. C. M. Nelson, W. K. Olson, W. Saenger, Z. Shakked, D. M. Soumpasis, C.-S. Tung, A. H.-J. Wang and V. B. Zhurkin, EMBO J., 1989, 8, 1 CrossRef.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon, Oxford, UK, 1990 Search PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170 CrossRef CAS.
- K. Kitaura and K. A. Morokuma, Int. J. Quantum Chem., 1976, 10, 325 CrossRef CAS.
- M. von Hopffgarten and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43 CAS.
- A. Biancardi, T. Biver, A. Marini, B. Mennucci and F. Secco, Phys. Chem. Chem. Phys., 2011, 13, 12595 RSC.
- Y. Wang, N. C. Schnetz-Boutaud, H. Kroth, H. Yagi, J. M. Sayer, S. Kumar, D. M. Jerina and M. P. Stone, Chem. Res. Toxicol., 2008, 21, 1348 Search PubMed.
- M. Korth, M. Pitonak, J. Rezac and P. A. Hobza, J. Chem. Theory Comput., 2010, 6, 344 CrossRef CAS.
- K. Strutyński, J. A. N. F. Gomes and M. Melle-Franco, J. Phys. Chem. A, 2014, 118, 9561 CrossRef.
- H. R. Drew, R. M. Wing, T. Takano, C. Broka, S. Tanaka, K. Itakura and R. E. Dickerson, Proc. Natl. Acad. Sci. U. S. A., 1981, 78, 2179 CrossRef CAS.
- MOPAC2016, J. J. P. Stewart Computational Chemistry, Colorado Springs, CO, 2016, http://OpenMOPAC.net, accessed Jul 29, 2020 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, T. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochtrerski, R. L Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresan, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- T. A. Keith, AIMAll (Version 17.11.14), TK Gristmill Software, Overland Park, KS, 2017, http://aim.tkgristmill.com Search PubMed.
- G. te Velde, F. M. Bickelhaupt, S. J. A. van Gisbergen, C. Fonseca Guerra, E. J. Baerends, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391 Search PubMed.
- ADF 2018, SCM, Theoretical Chemistry, Amsterdam, The Netherlands, http://www.scm.com, accessed Jul 29, 2020 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200 CrossRef CAS.
- C. Lee, W. Yang and G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. A. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799 RSC.
- Á. Sánchez-González, F. J. Martín-Martínez and J. A. Dobado, J. Mol. Model., 2017, 23, 80 CrossRef.
- G. R. Nagurniak, G. F. Caramori, R. L. T. Parreira, P. A. S. Bergamo, G. Frenking and A. Muñoz-Castro, J. Phys. Chem. C, 2016, 120, 15480 CrossRef CAS.
- C. F. Matta, J. Hernández-Trujillo, T.-H. Tang and R. F. W. Bader, Chem.–Eur. J., 2003, 9, 1940 CrossRef CAS.
- A. Gil, M. Sodupe and J. Bertran, Chem. Phys. Lett., 2004, 395, 27 CAS.
- I. Vidal, S. Melchor, I. Alkorta, J. Elguero, M. R. Sundberg and J. A. Dobado, Organometallics, 2006, 25, 5638 CrossRef CAS.
- K. Eskandari and C. Van Alsenoy, J. Comput. Chem., 2014, 35, 1883 CrossRef CAS.
- D. G. Díaz-Gómez, R. Galindo-Murillo and F. Cortés-Guzman, ChemPhysChem, 2017, 18, 1909 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Definition of roll distortion, roll distortions, NCI analyses and QTAIM topologies for all the studied systems phen, 4-Mephen, 4,7-Me2phen, 5-Mephen, 5,6-Me2phen and 3,4,7,8-Me4phen intercalating GC/CG bps through the major groove along with the cartesian coordinates of all the optimized studied structures. See DOI: 10.1039/d0ra07646e |
| This journal is © The Royal Society of Chemistry 2021 |