Open Access Article
Open Access ArticleCharacterizing hydrogen bonds in crystalline form of guanidinium salicylate in the terahertz range
Maojiang Song *a,
Fei Yanga,
Caixia Sub and
Bing Deng*a
*a,
Fei Yanga,
Caixia Sub and
Bing Deng*a
aGuizhou Metrology Institute, Guiyang, Guizhou 550003, China. E-mail: songmaojiang@hotmail.com
bSchool of Big Data and Computer Science, Guizhou Nornal University, Guizhou 550001, China. E-mail: 690824129@qq.com
First published on 23rd December 2020
Abstract
For pharmaceutical compounds with poor solubility, there is an effective method to address this dilemma without tampering their intrinsic chemical properties by forming weak hydrogen bonds. Guanidinium salicylate, which is a typical pharmaceutical salt with a complex crystal structure, was systematically investigated by terahertz time-domain spectroscopy combined with density functional theory in order to obtain the complete information of weak hydrogen bonds. As a result of the influence of weak hydrogen bonds, there are substantial differences between guanidinium salicylate and its parent molecule (salicylic acid) in the experimental fingerprint spectra in the range of 0.2–2.5 THz, such as the number, amplitude and frequency positions of absorption peaks. With the help of isolated molecule density functional theory calculations, the possible sites of weak hydrogen bonds were determined by natural bond orbital analysis. It can be concluded that there is an intricate hydrogen bond network due to the polar distribution of molecular electrostatic potential. Furthermore, all THz absorption peaks were assigned to their corresponding vibrational modes and the complete information of the related hydrogen bonds (including type, role, angle, and bond length) was determined by using dispersion-corrected density functional theory. The results laid a good foundation for further study on the enhancement of solubility of pharmaceutical salts by forming weak hydrogen bonds.
1. Introduction
Hydrogen bonds, with an arrangement like X–H⋯A, are a non-covalent interaction between an electronegative atom A (acceptor) and covalent bond group X–H (donor).1 It is indicated that the hydrogen bonding interaction plays a crucial role in molecular recognition for designing a new material with highly specific properties.2 This superiority is drawing increasing attention in many fields, especially in the pharmaceutical industry due to the biopharmaceutical properties of drugs. It is confirmed that the poor biopharmaceutical properties, rather than toxicity or lack of efficacy, are the main reasons why less than 1% of active pharmaceutical compounds eventually appear into the market-place.3 Among these biopharmaceutical properties, solubility remains a key issue since approximately 40% of approved drugs and nearly 90% of developmental pipeline drugs are medications with poor solubility.4 With such a predominance of poorly water-soluble compounds, the most important issue from the pharmaceutical and pharmacological point of view is to enhance the solubility of active pharmaceutical ingredients (APIs) without tampering their intrinsic chemical properties of interest based on changing intramolecular and intermolecular interactions. As a typical non-covalent interaction, hydrogen bond can address above dilemmas by forming a multi-component compound (salt or co-crystal) with superior properties,5 which may include solubility,6 bioavailability,7 chemical and physical stability8,9 and so on.Salicylic acid, which extracted from wintergreen leaves and the bark of the white willow, is a lipophilic monohydroxybenzoic acid and covers a broad spectrum of applications in medical field. In Ancient Greece and Ancient Rome, salicylate-containing plants including myrtle and willow, were used for their analgesic, keratolytic, anti-inflammatory and antiseptic properties since that salicylic acid has direct activity as an anti-inflammatory agent and acts as a topical antibacterial agent.10,11 With the rapid development of pharmaceutical technology, the salts of salicylate and their derivatives can treat diverse human maladies, such as tumor, cancer, thrombus, hyperglycemia and so on.12–14 Moreover, salicylic acid is key ingredient in many skincare products since that it can penetrate into the pores of the skin due to the special structure.15 However, there is still a limitation related to the pharmacokinetics and pharmacodynamics of salicylic acid due to the poor solubility (0.171 mg mL−1). As a poorly soluble pharmaceutical and a weak acid (pKa = 2.97), salt formation usually is the first consideration and the primary approach in the pharmaceutical industry to address the challenge of low solubility or slow dissolution rate of ionizable drug substances through hydrogen bond.16 In this respect, the most frequently used moieties with hydrogen bonding capability is carboxylic acid with N-containing compound, such as pyridine17 and benzimidazole.18 As another N-containing compound, guanidine can be used as salt bridges in supramolecular chemistry and has attracted considerable interest.19 Furthermore, guanidine can act as a perfect mediator of specific non-covalent binding in ground state recognition events and also plays a decisive role in transition state binding in various catalytic processes.20 Therefore, guanidinium salicylate (C(NH2)3C7H5O3) were obtained by controlled evaporation from an aqueous solution of the reaction product of salicylic acid and guanidinium carbonate in water and several steps of purification by fractional crystallization21 in our research. Owing to the hydrophilic guanidine and the ionic character, guanidinium salicylate would be expected to have superior dissolution and solubility properties in a polar medium. The molecular configurations of salicylic acid, guanidine and guanidinium salicylate are shown in Fig. 1.
It is exhibited evidently that there are two non-covalent hydrogen bonds existing between the salicylate anion and guanidinium cation. In fact, the network of non-covalent bonds, which is described by data on hydrogen bonds, van der Waals interactions, or other such interactions between molecules, is considered to be closely related to the solubility of pharmaceutical crystal.22 And the systematic research had confirmed that there is a positive relationship between hydrogen bonding and solubility/dissolution.23 Consequently, it is essential to characterize the hydrogen bonds in pharmaceutical crystal (especially pharmaceutical salts).
So far, the main tools to characterize and detect the hydrogen bonding interaction in pharmaceutical salts, are traditional solid material analysis tools such as X-ray powder diffraction (XRPD),24 Fourier transformation infrared spectroscopy (FT-IR)25 and Raman vibrational spectroscopy.26 However, all of these characterization methods are incompetent to obtain direct, effective and abundant information to identify the intricate hydrogen bonding interactions. Therefore, it is of great importance to find an efficient and promising alternative method as a supplement for direct monitoring of hydrogen bonds in pharmaceutical salts. In principle, H⋯A stretching vibration is the most direct spectroscopic indicator of hydrogen bonding. For the weak hydrogen bond, there are some vibrational characteristics in the frequency range of 30–200 cm−1 (ref. 27) because that the radio waves in this range have about the same energy level as the hydrogen bonds between molecules. Terahertz time-domain spectroscopy (THz-TDS), as a typical spectroscopic technique of terahertz radio waves (3–300 cm−1), can probe the active vibrational modes in the far-infrared and sub-millimeter region of the electromagnetic spectrum. Furthermore, as an attractive analytical tool, THz-TDS has some superior advantages such as nondestructive nature, nonionizing radiation, short acquisition time, and simplicity of sample preparation. As a result, THz-TDS can characterize the solid-state materials through the excitations of intramolecular vibrational and intermolecular modes as well as hydrogen-bonding networks inherent to the molecular assembly in the solid state.28 For example, A series of biomolecules, such as nucleic acid bases and amino acids, have been investigated by Terahertz time-domain spectroscopy (THz-TDS) with the unique characteristic features because of the intricate hydrogen bonding networks.29,30 It is demonstrated that THz spectroscopy can provide distinct fingerprints to different DNA sequences and hybridization states with high sensitivity.31–33 Recently, the function of the hydrogen bonding interaction in cocrystal had been investigated by using THz spectroscopy.34 On the other hand, density functional theory (DFT) calculation is an effective tool to predict molecular structure, charge transfer interaction, IR and Raman bands, inter- and intramolecular hydrogen bonds due to the rapid development of hardware and the continuous improvement in computer coding.35 This is especially attractive when experimental data are not available or incomplete. Therefore, it is feasible to characterize the hydrogen bonds in the crystalline form of guanidinium salicylate by employing terahertz time-domain spectroscopy (THz-TDS) combining with DFT calculations.
In this paper, the terahertz fingerprint spectra of guanidinium salicylate were investigated by THz-TDS at room temperature. In order to assign the absorption peaks and obtain the complete information, the isolate-molecule and dispersion-corrected density functional theory calculations were employed to simulate the gaseous and the solid-state guanidinium salicylate respectively. At first, the absorption spectrum and the refractive indices of guanidinium salicylate were investigated by utilizing THz-TDS at room temperature. It is demonstrated that there are obvious absorption peaks for guanidinium salicylate, which have substantial differences with that of salicylic acid. These results are reconfirmed by theoretical results of natural bond orbital analysis, frontier molecular orbitals analysis, as well as solid state calculations employing DMol3 (GGA + PBE). The remainder of the paper is organized as follows: in Section 2, the experimental samples and method are introduced. In Section 3, theoretical method is introduced for confirming the validity. In Section 4, the experimental and theoretical results are displayed and discussed systematically. At last, we summarized the main conclusions in Section 5.
2. Experimental section
2.1 Sample preparation
Salicylic acid is crystalline organic carboxylic acid possessing an aromatic ring with a hydroxyl group. The appearance of salicylic acid is colorless crystalline powder and would become white immediately when exposed to light. Due to the lipophilicity and the configuration of planar dimer, salicylic acid should be amenable to formation of cocrystals or salts with ideal physicochemical properties (including absorption, distribution, metabolism, excretion, and toxicity).36,37 Guanidine, as a small molecule, is a strong organic base (pKa = 13.6) and can dissolve in polar solvents. It is the compound with the formula HNC(NH2)2 and exists as guanidinium ions at physiological pH. Owing to the planar and symmetric configuration,38 the configuration of guanidinium ion is very stable and the properties of guanidinium cations are independent from environment constituted from different chemical anions.39 As a result, guanidine can form a broad family of hydrogen-bonded crystals and act as a perfect mediator of specific non-covalent binding in ground state recognition events. In this work, salicylic acid (CAS-number: 69-72-7) and guanidinium carbonate (CAS-number: 593-85-1) were purchased from Sigma-Aldrich Chemicals Corporation and were used immediately without further purification because they were analytical grade (purity: 99% for salicylic acid and 98% for guanidinium carbonate). In order to obtain samples of guanidinium salicylate, analytical grade salicylic acid and guanidinium carbonate were taken in 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio and placed in the ball mill respectively. The mixture was ground at the speed of 120 rpm at temperatures ranging from 60 °C to 70 °C by adding the cooling medicinal ethanol until the end of reaction. At last, the crystals of guanidinium salicylate were obtained by controlled evaporation from an aqueous solution of reaction product and purified by several steps of recrystallization. The above process can be simplified as the reaction scheme shown in Fig. 2.
1 molar ratio and placed in the ball mill respectively. The mixture was ground at the speed of 120 rpm at temperatures ranging from 60 °C to 70 °C by adding the cooling medicinal ethanol until the end of reaction. At last, the crystals of guanidinium salicylate were obtained by controlled evaporation from an aqueous solution of reaction product and purified by several steps of recrystallization. The above process can be simplified as the reaction scheme shown in Fig. 2.
In order to ensure the purity, the reaction product was detected by NMR instrument and its 1H NMR is shown in Fig. 3. The last purity of guanidinium salicylate is 98%.
All the samples were pressed as pellets in a 13 mm diameter vacuum die at the lowest possible pressures to minimize decomposition from transient heating or high pressure. The samples were not diluted with polyethylene powder or other diluents and three replicates of each sample were prepared. All pellets have thickness among 0.8 and 1.2 mm to provide a sufficient path length to eliminate the effect of the multiple reflection that occurs between the two surfaces of the pellet sample in the spectra.40 Each of the pellets was measured three times in order to give up the random noise produced in the measurement process.
2.2 Terahertz time-domain spectroscopy (THz-TDS)
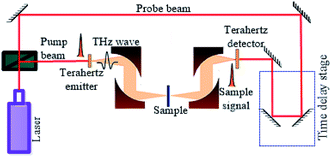
It is demonstrated that terahertz time-domain spectroscopy is highly sensitive to the subtle changes in intermolecular interactions.41 The THz spectra were measured by a setup similar to that described in reference previously.42 The system is mainly composed of an ultrafast pulsed laser, a terahertz emitter, a terahertz detector, and a time delay stage, as shown in Fig. 4. The femtosecond pulse was produced by a Ti-sapphire laser with a repetition rate of 100 MHz, a central wavelength of 1560 nm, and a duration of <100 fs. The femtosecond laser pulse is split into a pump beam and a probe beam. The pump beam is incident on the terahertz emitter to generate terahertz pulses, and then the terahertz pulses are collimated and focused on the sample by a pair of off-axis parabolic mirrors. After passing through the sample, the terahertz pulses are collimated by another pair of off-axis parabolic mirrors and refocused on the terahertz detector. Owing to the dispersion and absorption of the sample material, electric field intensity of the terahertz pulse is modified when it pass through the sample. Neglecting dispersion, the electric field intensity of the terahertz pulse is attenuated by the sample via absorption. In order to eliminate the influence of ambient water vapor, the THz propagation path is purged with dry air until the relative humidity to about 3.0%. The samples were measured at a temperature of 293.15 ± 0.5 K with signal-to-noise ratio (SNR) higher than 60 dB in all experiments.2.3 Data processing
In order to clearly characterize the sample, it is necessary to obtain its real refractive index n(ω) and absorption coefficient α(ω). According to ref. 43, a complex refractive index describing the optical properties of the samples could be defined as:| N(ω) = n(ω) − jk(ω) | (1) |
 | (2) |
In this equation, Esample(ω) and Eref(ω) are electric fields of terahertz wave passing through sample and reference respectively. d is the thickness of the pellet. c is the speed of light in the vacuum. ρ(ω) is the amplitude ratio of the sample to the reference signals. And φ(ω) is the phase difference between the sample and reference signals. Then, refractive index n(ω) and absorption coefficient α(ω) can be calculated as follows:
 | (3) |
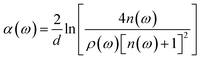 | (4) |
3. Theoretical method
In order to characterize the weak hydrogen bonds and get their original information, the fast density functional theory (DFT) calculations were performed by using the Gaussian03 electronic structure program44 for the dimer molecule of guanidinium salicylate in gaseous state. Initial starting atomic geometry of guanidinium salicylate was obtained from the NIST chemical structure database45 and the structure was optimized as a free space molecule. The geometry optimization and normal mode analysis of the dimer molecule were implemented by using Becke-3-Lee-Yang-Parr (B3LYP) in combination with the standard 6-311G (d,p)46 Gaussian-type basis set. In order to understand the original reasons of the possible hydrogen bonds, the molecular electrostatic potential was then calculated for the dimer molecule of guanidinium salicylate. Furthermore, natural bond orbital (NBO) analysis was also performed by NBO 3.1 program47 in Gaussian03 at the same level in order to determine the possible sites of the intra- and intermolecular hydrogen bonds based on the geometry optimization and the normal mode analysis.48Moreover, DFT calculations for the solid-state guanidinium salicylate were performed by using the DMol3 software package based on Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA)49 in order to obtain the more detailed description of the hydrogen bonds in the crystal. The calculations were performed with all electrons and used a double numerical plus polarization (DNP) atomic orbital basis set (equivalent to a double-ζ),50 and continued with program option “fine” grid sizes (corresponding to a k-point separation of 0.04 Å−1) until reaching a geometry optimization convergence criteria (corresponding to an energy convergence ΔEopt b < 5 × 10−7 hartree) or a density convergence being 10−6 during the SCF minimization. By solving the self-consistent field equation iteratively, the optimized geometry corresponding to the minimum value on the potential energy surface was obtained, which is confirmed by the fact that no virtual frequency was found in the analysis of vibration spectrum. Based on the theory of similar energy levels, the harmonic vibration frequency of the optimized geometry is calculated analytically by taking the second-order derivative of energy. However, DMol3 can neither calculate solid-state IR intensities, nor can the static electric fields be applied in solid-state calculations for calculating the IR intensity by atomic polar tensor methods.51 In this paper, the method for calculating IR intensities in the solid-state spectrum was obtained through calculating the square of the change in dipole moments for the unit cell that results from atomic displacements along each normal-mode coordinate (∂![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) /∂Qk)2 using Hirshfeld charge analysis52 as follow:
/∂Qk)2 using Hirshfeld charge analysis52 as follow:
 | (5) |
It is well known that pure DFT does not describe a noncovalent interaction such as hydrogen bonding and van der Waals interaction, although it is a widely used method for electronic structure calculation in condensed matter physics and quantum chemistry as well as could predict many properties of various materials successfully.53 Therefore, London-type dispersion interactions must be incorporated into the DFT functional as these forces are largely responsible for the packing configurations for predicting the hydrogen bonds accurately.54 In this work, an empirical dispersion correction proposed by Grimme55 was applied with the pair-wise interaction terms as follow:
 | (6) |
 | (7) |
At last, the lineshapes were convolved with a Lorentzian line in the theoretical spectra with 0.03 THz full width at half-maximum (FWHM). It is possible that there are some differences between experimental results and theoretical results about frequency positions of signal peaks, which the reason is that theoretical calculations were implemented at absolute zero while the experimental spectra of the crystal samples were obtained at 293.15 ± 0.5 K.56 The crystal system of guanidinium salicylate is Triclinic and its space group is P1. The other crystal data for the compound are as follows: a = 9.221 Å, b = 9.221 Å, c = 9.877 Å, and α = β = γ = 90°. It is worth to mention that all of these crystal parameters used in DFT calculations were download from CCDC.57
4. Results and discussion
4.1 Experimental results
In this paper, the signals of reference and samples were measured alternately for three times, and their mean values are used in order to eliminate the random noise. The time windows for all measurements are about 30 ps, corresponding to the resolution 0.006 THz. The time and frequency domain spectra of guanidinium salicylate, salicylic acid and reference are shown in Fig. 5 in order to obtain the characteristics of the weak hydrogen bonds. It is displayed that there are distinctive attenuations in amplitudes of the transmitted electrical fields relative to that of reference electrical field after the THz wave propagation through the samples because of the absorption and dispersion. In addition, there is little difference in time delay between the signal peaks of the guanidinium salicylate and salicylic acid when THz wave transmit through the samples. By comparing the obtained time domain spectra, it can be seen obviously that the attenuation of the signal intensity of guanidinium salicylate is larger than that of salicylic acid. The corresponding frequency domain spectra, as are also shown in Fig. 5, exhibit clearly that the amplitude spectra drop down dramatically and have several evident absorption bands for guanidinium salicylate and salicylic acid relative to that of the references. These results reveal the reality that there are different spectral signatures in THz range for guanidinium salicylate and salicylic acid.The spectra of absorption and refractive index for guanidinium salicylate and salicylic acid are shown in Fig. 6, where the spectral data among 0 to 0.2 THz were cut off to eliminate zigzag reflections and only the spectral data among 0.2 to 2.5 THz were regarded as fingerprint spectrum. It is easy to find that every dip in frequency domain spectra shown in Fig. 5 corresponds to an absorption peak both for guanidinium salicylate and salicylic acid. It is evident that the two kinds of samples possess distinctive fingerprint spectra owing to diverse vibrational modes, including frequency positions of absorption peaks, absorption amplitudes, and spectral lines. There are four absorption peaks between 0.2-2.5 THz for salicylic acid, perfectly agreeing with the result reported in ref. 58. For guanidinium salicylate, there are five distinct absorption peaks locating at the frequencies of 0.749 THz, 1.332 THz, 1.664 THz, 1.970 THz, 2.358 THz respectively. Moreover, there are obvious baselines increasing with frequencies both in the absorption spectra of guanidinium salicylate and salicylic acid, which may result from terahertz scattering related to the particle features as size, shape, distribution, and so on.58
In addition, the refractive indexes have conspicuous decreasing features at frequency positions corresponding to the absorption peaks both for guanidinium salicylate and salicylic acid owing to their abnormal chromatic dispersion although indistinguishable in amplitude, as shown in Fig. 6. All of these results demonstrate that there are distinctive fingerprint characteristics between guanidinium salicylate and its parent molecule in terahertz region. These differences may originate from the weak hydrogen bonds in crystalline form of guanidinium salicylate due to the similar planar dimer configuration to salicylic acid and the stable symmetric configuration of guanidinium cation.38
4.2 Molecular electrostatic potential (MEP)
The formation of weak hydrogen bonds is a significant phenomenon that determines the indispensable properties of many chemical and biological systems. A large number of experimental and theoretical studies have shown that molecular electrostatic potential (MEP) is a very useful descriptor in understanding weak hydrogen bonding interaction.59,60 For example, the position of minimum MEP related to electron donating center in the isolated molecules have been successfully used to predict the locations and directions of weak hydrogen bonds in a variety of molecular systems.61 In crystal engineering, the electrostatic potential V(r) is also highly suitable for analyzing processes based on the “recognition” of one molecule by another, such as in drug-receptor, enzyme–substrate interactions, because it is through their potentials that the two species first “see” each other. In order to obtain the possible electron donor and acceptor sites (corresponding to reactive sites of electrophilic and nucleophilic attacks) for guanidinium salicylate, the MEP of the dimer molecule at the B3LYP/6-311G(d,p) optimized geometry was calculated using the Gaussian03 software in gaseous state.46 The MEP distribution with transparent form is shown in Fig. 7.In Fig. 7, the different values of the electrostatic potential on the surface are represented by different kinds of colors. The potential increases in the order as red < orange < yellow < green < blue. It can be clearly seen that there is positive potential (blue) on the side of guanidinium cation. This result describes that guanidinium cation can act as hydrogen donor and interact with other molecules via weak hydrogen bonds. On the other hand, it is displayed that there is negative potential (red) around the oxygen atoms. Then the hydrogen acceptor site can be determined and the possible hydrogen bonds can be formed at the corresponding points. It is concluded that the intricate hydrogen bond network can be formed due to the obvious polar distribution of molecular electrostatic potential for the dimer molecule of guanidinium salicylate.
4.3 Natural bond orbital (NBO) analysis
The natural bond orbital (NBO) analysis provides a description of the conformer structure by a set of localized bonds, anti-bonds and Rydberg extra-valence orbitals. It has been shown that a useful aspect of the NBO method is that provides information on the interaction of between the filled orbital space and the virtual orbital space, which can enhance the analysis of intramolecular and intermolecular interactions.62 On the basis of NBO, the second-order Fock-matrix was used to evaluate the donor–acceptor interaction that leads to a loss of occupancy from the localized NBO of the idealized Lewis structure into an empty non-Lewis orbital. For each donor (i) and acceptor (j) the stabilization energy E(2) associated with the delocalization i → j is determined as:
 | (8) |
| Donor NBO (i) | Occupancy | Hybrid | AO (%) | Acceptor NBO (j) | NBOs | E(2) (kcal mol−1) | E(j) −E(i) (a. u.) | F(i,j) (a. u.) |
|---|---|---|---|---|---|---|---|---|
| Within unit 1 | ||||||||
| σ(C5–C6) | 1.61253 | sp(C5) | s(0.00)p(99.98) | σ*(C11–C13) | 0.313 | 23.93 | 0.29 | 0.075 |
| sp(C6) | s(0.00)p(99.96) | |||||||
| σ(C7–C9) | 1.71172 | sp(C7) | s(0.00)p(99.95) | σ*(C5–C6) | 0.421 | 22.6 | 0.28 | 0.074 |
| sp(C9) | s(0.00)p(99.95) | |||||||
| σ(C11–C13) | 1.69301 | sp(C11) | s(0.00)p(99.96) | σ*(C7–C9) | 0.32 | 23.15 | 0.28 | 0.072 |
| sp(C13) | s(0.00)p(99.95) | |||||||
| LP(3)O1 | 1.6834 | sp | s(0.00)p(99.94) | LP*(1)C15 | 0.753 | 135.8 | 0.16 | 0.151 |
| LP(3)O2 | 1.6328 | sp | s(0.00)p(99.92) | LP*(1)C15 | 0.753 | 172.52 | 0.15 | 0.16 |
| LP(2)O3 | 1.83139 | sp | s(0.00)p(99.94) | σ*(C5–C6) | 0.421 | 35.34 | 0.33 | 0.103 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| From unit 1 to unit 2 | ||||||||
| LP(2)O1 | 1.85087 | sp53.18 | s(1.85)p(98.13) | σ*(N19–H24) | 0.088 | 27 | 0.66 | 0.121 |
| LP(2)O2 | 1.82971 | sp7.75 | s(11.42)p(88.55) | σ*(N17–H21) | 0.113 | 46.48 | 0.7 | 0.163 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Within unit 2 | ||||||||
| LP(1)N17 | 1.66094 | sp99.99 | s(0.04)p(99.92) | LP*(1)C16 | 0.832 | 193.3 | 0.1 | 0.146 |
| LP(1)N18 | 1.80639 | sp18.03 | s(5.25)p(94.72) | LP*(1)C16 | 0.832 | 81.69 | 0.16 | 0.125 |
| LP(1)N19 | 1.68613 | sp69.03 | s(1.43)p(69.03) | LP*(1)C16 | 0.832 | 166.68 | 0.11 | 0.142 |
Within unit of salicylate anion, there are very strong intramolecular hyperconjugative interactions between the lone pairs of electrons of oxygen atoms and the lone pairs of electrons of carbon atom on the carboxyl group, which are [n3(O1) → n*1(C15)] and [n3(O2) → n*1(C15)] with charge transfer energy values of 135.8 kJ mol−1 and 172.52 kJ mol−1 respectively as shown in Table 1. It is indicated there is strong intramolecular charge transfer from LP(O1) and LP(O2) to LP*(C15) due to the strong electronegativity and a deprotonation process on the carboxyl group of salicylate anion. In addition, it is also exhibited that there is important intramolecular charge transfer from LP(O3) to σ*(C5–C6) with energy values of 35.34 kJ mol−1. The intramolecular charge transfer with the unit of salicylate anion demonstrated that O1, O2 and O3 can act as hydrogen acceptors due to their active lone pairs of electrons. Within the unit of guanidinium cation, there are also strong intramolecular hyperconjugative interactions between the lone pairs of electrons of nitrogen atoms and the lone pairs of electrons of carbon atom on the carboxyl group, which are [n1(N17) → n*1(C16)], [n1(N18) →n*1(C16)] and [n1(N19) →n*1(C16)] respectively. Furthermore, there are important interactions [n2(O1) →σ*(N19–H24)] and [n2(O2) →σ*(N17–H21)] with charge transfer energy values of 27 kJ mol−1 and 46.48 kJ mol−1 from the unit of salicylate anion to the unit of guanidinium cation. These two hyperconjugative interactions correspond to the weak hydrogen bonds N119–H24⋯O1 and N17–H21+⋯O2− in the dimer molecule of guanidinium salicylate. All above results obtained by NBO analysis reveal the possible formation sites of weak hydrogen bonds for the dimer molecule of guanidinium salicylate.
4.4 The pattern of hydrogen bonds
In this paper, all experimental data about configuration parameters are excerpted from ref. 64 and are download from CCDC.57 However, the reliable information about the strength of intermolecular contacts can't be obtained through simple measurement of the molecular packing arrangement based only on geometrical criteria, since the short contact between atoms does not necessarily imply intermolecular (noncovalent) interaction being existence.65 In addition, the geometric criteria, even for strong hydrogen bonds, can only provide a variation range of Eint rather than its accurate value. Therefore, the geometry optimizations of isolated-molecule and solid-state DFT for guanidinium salicylate were performed by employing Gaussian03 and DMol3 respectively. In order to confirm the correctness of the calculations, the important bond lengths calculated by isolated-molecule and solid-state optimizations are compared with that of X-ray diffraction experiments as show in Table 2, in which their root mean square deviations (RMSDs) from experimental values are calculated.| Experiment | Isolated-molecule | Solid-state | |
|---|---|---|---|
| O1–C15 | 1.274 | 1.294 | 1.284 |
| O2–C15 | 1.244 | 1.269 | 1.258 |
| O3–C6 | 1.363 | 1.363 | 1.347 |
| C5–C15 | 1.493 | 1.496 | 1.494 |
| C5–C6 | 1.395 | 1.423 | 1.415 |
| C6–C7 | 1.384 | 1.402 | 1.402 |
| C7–C9 | 1.362 | 1.391 | 1.386 |
| C9–C11 | 1.367 | 1.403 | 1.4 |
| C11–C13 | 1.377 | 1.395 | 1.387 |
| C13–C5 | 1.394 | 1.405 | 1.402 |
| C16–N17 | 1.321 | 1.343 | 1.322 |
| C16–N18 | 1.326 | 1.345 | 1.367 |
| C16–N19 | 1.315 | 1.335 | 1.328 |
| RMSE | 0.0214 | 0.0195 |
It is demonstrated that the calculated bond lengths for isolated-molecule and solid-state optimizations are consistent with that of experimental geometry obtained from X-ray diffraction with sufficient small RMSDs. Wherein, the solid-state optimized geometry is more approximated to the experimental geometry since it involves crystal packing interactions and weak intermolecular hydrogen-bonding interactions.
In the crystal packing of guanidinium salicylate, the 3-dimension network is constituted by the Hierarchical structure composed of guanidinium cations and salicylate anions, as shown in Fig. 8. At first, it must be underlined that the protonated N17 and the amino group (N19) are hydrogen bonded to carboxylate oxygen atoms (O2 and O1) through Brønsted interaction (N17–H21+⋯O2−) and a weak hydrogen bonding interaction (N19–H24⋯O1). In this paper, the weak hydrogen bonds N19–H24⋯O1 and N17–H21+⋯O2− are named inter-monomer hydrogen bonds since that they are located between guanidinium cation and salicylate anion. Then a cyclic hydrogen-bonded motif, which designated by the graph-set notation R22(8),66 are formed and resulted a planar dimer molecule with guanidinium cation and salicylate anion, as shown in Fig. 8c.
The adjacent molecules in x–y plane have an isometric parallel arrangement along z axis with head to tail due to their polar distribution of molecular electrostatic potential (shown in Fig. 7). Meanwhile, there is same arrangement for the molecules in x–z plane along x-axis. As a universal example of the planar dimer molecule in x–z plane (Fig. 8c), the deprotonated O2 of salicylate anion is bonded to two amino groups (N17 and N18) of a planar molecule in x-y plane by bifurcated N17–H20⋯O2−/N18–H23⋯O2− and the protonated N17 and N18 of guanidinium cations are bonded to the deprotonated O2 of another alternate planar molecule in x–y plane by another bifurcated N17–H20⋯O2−/N18–H23⋯O2− on the right. On the left, O3 of salicylate anion is bonded N19 on the amino group of a planar molecule in x–y plane by N19–H25⋯O3 and N19 of guanidinium anion is bonded to O3 on the hydroxyl group of alternate planar molecule in x–y plane by another N19–H25⋯O3. The weak hydrogen bonds N17–H20⋯O2−, N18–H23⋯O2− and N19–H25⋯O3 are named inter-dimer hydrogen bond since they are located between two dimer molecules in different planes. The 3-dimensional network structures are formed since that every dimer molecule is bonded to four different dimer molecules on the both sides by 6 inter-dimer hydrogen bonds mentioned above. In addition, there is an intra-monomer hydrogen bond (O3–H4⋯O1) in the salicylate anion.
4.5 Vibrational modes assignment
In order to assign the vibrational modes to THz fingerprint, the vibrational modes of guanidinium salicylate are calculated by dispersion-corrected DFT with full geometry optimization. The theoretical spectra, as shown in Fig. 9, are plotted as both stick plots and convolved plots with empirical Lorentzian line shape (0.03 THz FWHM) to reproduce the room-temperature experimental spectrum more realistically. In order to compare the experimental results with theoretical results, the experimental results are also shown in Fig. 9. It can be seen clearly that there are eight vibrational modes (shown in stick plots) locating at 0.732 THz, 1.319 THz, 1.547 THz, 1.589 THz, 1.856 THz, 1.960 THz, 2.350 THz, 2.382 THz, with intensity 17.27, 15.59, 4.18, 61.55, 28.64, 43.84, 72.99 and 7.01 correspondingly for the calculated results, although there are only five absorption peaks in convolved plots. By contrast, the calculated vibrational modes locating at 0.732 THz, 1.319 THz, 1.589 THz, 1.960 THz and 2.350 THz correspond to the experimental ones locating at 0.749 THz, 1.331 THz, 1.664 THz, 1.970 THz and 2.358 THz respectively. In addition, there are two vibrational modes with relative weak intensity located at 1.547 THz and 2.382 THz corresponding to the weak absorption peak at 1.470 THz and a shoulder at 2.413 THz in the experimental spectrum respectively. Due to increasing heterogeneity of broadening effect with temperature, some absorption peaks become shoulders or overlay with their neighboring absorption peaks at room temperature. Therefore, the vibrational mode located at the frequency positions of 1.856 THz in stick plots of theoretical spectrum has no corresponding absorption peak in the experimental spectrum. Overall, there is a good agreement between the calculated and the experimental absorption spectra except with slight shift in the frequency positions of absorption peaks due to the electron correlation approximate treatment, anharmonicity effects and basis set deficiencies, etc.67Furthermore, the experimental spectral features are assigned to theoretical modes and their origins are explored for the purpose of explaining the mechanism of the vibrational modes. It was verified that a pure vibrational mode would lead to a molecule's atom motion with the same amplitude and identical or at least highly aligned direction. All vibrational modes of guanidinium salicylate and the corresponding hydrogen bonds in the unit cell are exhibited in Fig. 10.
Each theoretical vibrational mode is described by the main molecular motion although some of them are not a pure intermolecular mode or a pure intramolecular mode. For example, the vibrational mode at frequency position of 0.732 THz, which has 80% translation and 20% bend of whole molecule, is assigned to translation of the whole molecule approximately. It is worth noting that there are obvious motions in every vibrational mode for carboxyl group due to the influence of hydrogen bonds. For example, the bend of salicylate located at 2.35 THz is the result of the synchronous motions of carboxyl group combined with that of hydroxyl group by intramolecular hydrogen binding interaction (O3–H4⋯O1), even though it is an intra-monomer vibrational mode. As shown in Fig. 10, it is demonstrated clearly that there are more than half of vibrational modes caused by hydrogen bonds due to its complex hydrogen bonding network in 0.2–2.5 THz range. Perhaps, a part of vibrational modes are neglected because their amplitudes are inhibited by hydrogen bonding network.
In order to describe molecular motions more clearly, all of vibrational modes about guanidinium salicylate are analyzed explicitly in Table 3. It is indicated that the intensities of all vibrational modes are less than 100 Debye^2. The vibrational mode located at 1.856 THz, which overlay with its neighboring one in the experimental results at room temperature, has distinct displacement patterns about all atoms comparing to the adjacent vibrational modes.
| Mode | Exp. | Simu. | Description | |
|---|---|---|---|---|
| Fre. (THz) | Fre. (THz) | Int. (Debye^2) | ||
| a | 0.749 | 0.732 | 17.27 | Translation of all atoms caused by interdimer hydrogen bond |
| b | 1.331 | 1.319 | 15.59 | Butterfly of molecule caused by intermonomer hydrogen bond |
| c | 1.47 | 1.547 | 4.18 | Intramonomer torsion of salicylate |
| d | 1.664 | 1.589 | 61.55 | Torsion of carboxyl group caused by interdimer hydrogen bonds |
| e | 1.856 | 28.64 | Intramonomer torsion of carboxyl group | |
| f | 1.97 | 1.96 | 43.84 | Bend of molecule caused by intermonomer hydrogen bond |
| g | 2.358 | 2.35 | 72.99 | Intramonomer bend of salicylate |
| h | 2.413 | 2.382 | 7.01 | Rock of molecule caused by interdimer hydrogen bond |
Overall, there is intricate 3-Dimension hydrogen bond network which is composed of intra-monomer, inter-monomer and inter-dimer hydrogen bonds for guanidinium salicylate. It is concluded that the intricate hydrogen bond network plays an important role in the enhancement of solubility and the concomitant of good biopharmaceutical properties for guanidinium salicylate.23 It is confirmed that all of them can be determined by THz-TDS clearly but without any characteristic information, such as angle, type, bond length, and so on. Using dispersion-corrected density functional theory calculations on a periodic system, every absorption peak can be assigned accurately and all of vibrational modes can be described in detail. The complete characteristics of all hydrogen bonds, including type, role, bond length, angle and the THz fingerprint, are obtained by THz-TDS combining with DFT calculation for guanidinium salicylate, as shown in Table 4.
| D–H⋯A | Type | Role | Length/Å | Angle/o | Fingerprint (THz) | |
|---|---|---|---|---|---|---|
| D–H | H⋯A | D–H⋯A | ||||
| O3–H4⋯O1 | Intra-monomer | Bonding interaction between hydroxyl group and carboxyl group in salicylate | 1.022 | 1.514 | 155.32 | 2.35 |
| N17–H21+⋯O2− | Inter-monomer | Brønsted interaction between amino group of guanidinium and amino group of guanidinium in the same plane | 0.959 | 1.833 | 175.48 | 1.319 |
| N19–H24⋯O1 | Inter-monomer | Bonding interaction between carboxyl group of salicylate and amino group of guanidinium in the same plane | 0.945 | 2.052 | 178.97 | 1.96 |
| N19–H25⋯O3 | Inter-dimer | Bonding interaction between amino group of a dimer and hydroxyl group of another dimer in different plane | 0.906 | 2.077 | 162.29 | 0.732 |
| N18–H23⋯O2− | Inter-dimer | Bonding interaction between amino group of a dimer and carboxyl group of another dimer in different plane | 0.904 | 2.104 | 159.08 | 2.358 |
| N17–H20⋯O2− | Inter-dimer | Bonding interaction between amino group of a dimer and carboxyl group of another dimer in different plane | 0.871 | 2.313 | 150.30 | 1.589 |
5. Conclusion
The weak hydrogen bonds are significant intermolecular interactions for the enhancement of the poorly water-soluble pharmaceutical compounds and can be characterized accurately by powerful technique of terahertz time-domain spectroscopy. The distinctive differences in THz spectra between guanidinium salicylate and its parent molecule (salicylic acid), including the amount, amplitude, and frequency position of absorption peaks, were determined by THz-TDS in the range of 0.2–2.5 THz. With help of isolate-molecule density functional theory calculations, it can be concluded that there is an intricate hydrogen bond network due to the polar distribution of molecular electrostatic potential and the possible sites of weak hydrogen bonds were determined by natural bond orbital analysis. Then the full geometry optimizations were performed and all THz absorption peaks were assigned to their corresponding vibrational modes by using dispersion-corrected density functional theory. Furthermore, it was confirmed that there are three kind of weak hydrogen bonds (intra-monomer, inter-monomer and inter-dimer hydrogen bonds) for guanidinium salicylate and the complete information of the related hydrogen bonds (including type, role, angle, bond length) were determined by using dispersion-corrected density functional theory. All of above results laid a good foundation for further study on the enhancement solubility about of pharmaceutical salts by forming weak hydrogen bonds.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was accomplished by the team of metrology academician workstation of Guizhou. The authors would like to acknowledge Funds for Local Science and Technology Development Guided by the Central Committee Grant No. 20204001 and National Natural Science Foundation of China under Grant No. 220640006. Furthermore, the authors are grateful to professor Gaojie for his valuable help.References
- L. Pauling, J. Am. Chem. Soc., 1935, 57, 2680–2684 CrossRef CAS.
- Y. Q. Li, Y. F. Yang and Y. Ding, Sci. Rep., 2017, 7, 1574 CrossRef.
- C. B. Aakeröy, S. Forbes and J. Desper, Using cocrystals to systematically modulate aqueous solubility and melting behavior of an anticancer drug, J. Am. Chem. Soc., 2009, 131, 17048–17049 CrossRef.
- T. Loftsson and M. E. Brewster, Pharmaceutical applications of cyclodextrins: basic science and product development, J. Pharm. Pharmacol., 2010,(62), 1607–1621 CrossRef CAS.
- E. Grothe, H. Meekes, E. Vlieg, J. H. ter Horst and R. de Gelder, Cryst. Growth Des., 2016, 16, 3237–3243 CrossRef CAS.
- Z. J. Li, Y. Abramov, J. Bordner, J. Leonard, A. Medek and A. V. Trask, J. Am. Chem. Soc., 2006, 128, 8199–8210 CrossRef CAS.
- D. P. McNamara, S. L. Childs, J. Giordano, A. Iarriccio, J. Cassidy, M. S. Shet, R. Mannion, E. O'Donnell and A. Park, Pharm. Res., 2006, 23, 1888–1897 CrossRef CAS.
- A. V. Trask, W. D. S. Motherwell and W. Jones, Int. J. Pharm., 2006, 320, 114–123 CrossRef CAS.
- C. C. Sun and H. Hou, Cryst. Growth Des., 2008, 8, 1575–1579 CrossRef CAS.
- P. Dioscorides, De Materia Medica: aromatics, translation ed T.A. Osbaldeston and R.P.A. Wood. Ibidis Press, Johannesburg, 2000 Search PubMed.
- K. D. Rainsford. History and development of the salicylates: Aspirin and related drugs, Taylor and Francis, Boca Raton; 2004, pp. 28–51 Search PubMed.
- J. R. Paterson and J. R. Lawrence, Q. J. Med., 2001, 94, 445–448 CrossRef CAS.
- K. K. Wu, Anti-Inflammatory Anti-Allergy Agents Med. Chem., 2007, 6, 278–292 CrossRef CAS.
- G. Rena and K. Sakamoto, Diabetol. Int., 2014, 5, 212–218 CrossRef.
- R. K. Madan and J. Levitt, A review of toxicity from topical salicylic acid preparations, J. Am. Acad. Dermatol., 2014, 70, 788–792 CrossRef CAS.
- Y. He, C. Ho, D. L. Yang, J. Chen and E. Orton, J. Pharm. Sci., 2017, 106, 1190–1196 CrossRef CAS.
- G. S. Nichol and W. Clegg, Cryst. Growth Des., 2009, 9, 1844 CrossRef CAS.
- M. Amudhu, P. P. Kumar and G. Chakkaravarthi, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2015, 71, o794–o795 CrossRef.
- T. Suhs and B. Konig, Mini-Rev. Org. Chem., 2006, 3, 315–331 CrossRef CAS.
- T. Ishikawa, Angew. Chem., 2009, 121, 9385 CrossRef.
- M. Fleck, E. Tillmanns and S. Haussühl, Z. Kristallogr. NCS, 2000, 215, 105–106 CAS.
- K. Ajito, J. Y. Kim, Y. Ueno and H. J. Song, NTT Tech. Rev., 2014, 12, 1–6 Search PubMed.
- R. Thakuria and A. Nangia, Cryst. Growth Des., 2013, 13, 3672–3680 CrossRef CAS.
- S. Eliška, B. Daniel and H. Michal, et al., Cryst. Growth Des., 2017, 17, 5283–5294 CrossRef.
- M. Joshi and A. R. Choudhury, ACS Omega, 2018, 3, 2406–2416 CrossRef CAS.
- H. G. Brittain, Cryst. Growth Des., 2010, 10, 1990–2003 CrossRef CAS.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- M. Walther, B. Fischer, M. Schall, H. Helm and P. U. Jepsen, Chem. Phys. Lett., 2000, 32, 389–395 CrossRef.
- P. H. Bolivar, M. Brucherseifer, M. Nagel, H. Kurz, A. Bosserhoff and R. Buttner, Phys. Med. Biol., 2002, 47, 3815–3821 CrossRef CAS.
- B. M. Fischer, M. Walther and P. Uhd Jepsen, Phys. Med. Biol., 2002, 47, 3807–3814 CrossRef CAS.
- X. Li, T. Globus, B. Gelmont, L. C. Salay and A. Bykhovski, J. Phys. Chem. A, 2008, 112, 12090–12096 CrossRef CAS.
- X. J. Wu, E. Yi wen, X. L. Xu and L. Wang, Appl. Phys. Lett., 2012, 101, 033704 CrossRef.
- A. Arora, T. Q. Luong, M. Kruger, Y. J. Kim, C. H. Nam, A. Manz and M. Havenith, Analyst, 2012, 137, 575–579 RSC.
- L. Shi, X. H. Duan, L. G. Zhu, X. Liu and C. H. Pei, J. Phys. Chem. A, 2016, 120, 1160 CrossRef CAS.
- T. M. Korter, R. Balu, M. B. Campbell, M. C. Beard, S. K. Gregurick and E. Heilweil, J. Chem. Phys., 2006, 418, 65–70 CAS.
- S. Skovsgaard and A. D. Bond, CrystEngComm, 2009, 11, 444–453 RSC.
- S. F. Marina, V. G. Eduard, S. B. Stepan, A. L. Konstantin, J. Z. Michael and C. K. Victor, Cryst. Growth Des., 2010, 10, 5210–5220 CrossRef.
- Y. Marcus, J. Chem. Thermodyn., 2012, 48, 70–74 CrossRef CAS.
- M. Drozd, Mater. Sci. Eng., B, 2007, 136, 20–28 CrossRef CAS.
- Y. Ueno, R. Rungsawang, I. Tomita and K. Ajito, Anal. Chem., 2006, 78, 5424–5428 CrossRef CAS.
- E. P. J. Parrott, J. A. Zeitler and M. Pepper, et al., Cryst. Growth Des., 2009, 9, 1452–1460 CrossRef CAS.
- M. J. Song, F. Yang, L. P. Liu, L. Shen, P. F. Hu and C. X. Su, Spectrochim. Acta, Part A, 2018, 202, 18–19 CrossRef CAS.
- I. Taniuchi and H. Nakanishi, Electron. Lett., 2004, 40, 327–328 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian03, Revision B.05; Gaussian Inc.: 340 Quinnipiac St. Bldg40, Wallingford, CT 06492, USA. http://www.gaussian.com accessed Mar 11, 2009 Search PubMed.
- See: http://webbook.nist.gov/chemistry.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, TCI, University of Wisconsin, Madison, 1998 Search PubMed.
- C. Jana, V. Spirko and P. Hobza, Phys. Chem. Chem. Phys., 2004, 6, 37–41 RSC.
- B. Delley, J. Chem. Phys., 2000, 113, 7756 CrossRef CAS.
- B. Delley, J. Chem. Phys, 1990, 113, 508–517 CrossRef.
- D. G. Allis, D. A. Prokhorova and T. M. Korter, J. Phys. Chem. A, 2006, 110, 1951–1959 CrossRef CAS.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- W. Koch and M. C. Holthausen, A Chemist's Guide to Density Functional Theory, Wiley-VCH, Weinheim, 2001 Search PubMed.
- M. D. King and T. M. Korter, J. Phys. Chem. A, 2012, 116, 6927–6934 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- D. G. Allis, J. A. Zeitler, P. F. Taday and T. M. Korter, Chem. Phys. Lett., 2008, 463, 84–89 CrossRef CAS.
- F. H. Allen and O. Kennard, J. Mol. Graphics, 1993, 8, 31–37 Search PubMed.
- F. Garet, M. Hofman, J. Meilhan, F. Simoens and J. L. Coutaz, Appl. Phys. Lett., 2014, 105, 031106 CrossRef.
- U. Singh and P. Kollman, J. Chem. Phys., 1984, 80, 353–355 CrossRef CAS.
- F. J. Luque, J. M. Lopez and M. Orozco, Theor. Chem. Acc., 2000, 103, 343–345 Search PubMed.
- P. Kollman, J. McKelvey, A. Johansson and S. Rothenberg, J. Am. Chem. Soc., 1975, 97, 955–965 CrossRef CAS.
- N. T. Abdel-Ghani and A. M. Mansour, Spectrochim. Acta, Part A, 2012, 91, 272–284 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- M. Fleck, E. Tillmanns and S. Haussühl, NCS, 2000, 215, 105–106 CAS.
- M. V. Vener, A. N. Egorova, D. P. Fomin and V. G. Tsirelson, J. Phys. Org. Chem., 2009, 22, 177–185 CrossRef CAS.
- J. Bernstein, R. E. Davis, L. Shimoni and N. L. Chang, Angew. Chem., Int. Ed., 1995, 34, 1555–1573 CrossRef CAS.
- G. Rauhut and P. Pulay, J. Phys. Chem., 1995, 99, 3093–3100 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |