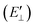Open Access Article
Open Access ArticleNegative ion formation by neutral hydrogen atom grazing scattering from a LiF(100) surface
Bo Jin a,
Hu Zhou*ab,
Zewen Zonga,
Xin Zhang
a,
Hu Zhou*ab,
Zewen Zonga,
Xin Zhang a,
Guangyi Wangc,
Lihua Zhoua and
Ximeng Chena
a,
Guangyi Wangc,
Lihua Zhoua and
Ximeng Chena
aSchool of Nuclear Science and Technology, Lanzhou University, Lanzhou 730000, China
bCollege of Chemistry and Chemical Engineering, Lanzhou University, Lanzhou 730000, China
cSchool of Electronic and Information Engineering, Lanzhou City University, Lanzhou 730000, China
First published on 22nd January 2021
Abstract
We present a theoretical description of negative ion conversion of the grazing scattering of neutral hydrogen atoms on LiF(100) surface. Here, in addition to the capture of a valence band electron near a surface F− site by an incident H atom, the Coulomb repulsive barrier tunneling behavior is also considered to treat the detachment of the affinity electron from the formed H− ion to vacuum through its interaction with the surface F− site. With incorporation of the image-attraction-induced increase on the vertical component of the projectile energy and the collective dielectric screening effect of surrounding anions and cations on the charge of surface F− site which participates in the electron detachment, the image attractive interaction was revealed to obviously increase the electron detachment probability, in turn obviously decreasing the final negative ion yield. Moreover, the sub-eV order of the energy defect between the H− affinity level and the unoccupied image state induced by the potential field of the H− image charge in LiF leads to an additional H− destruction channel in which H− affinity electron transfers to the unoccupied image state without electron emission by a nearly resonant charge transfer manner. A clear picture of this electron loss process is also presented. Our present results well reproduce the experimental observation in the whole velocity range and the high fraction of H− ion yield as an alternative solution can be used on the implantation of ITER device.
1. Introduction
Charged particle-surface interactions as an important field have been intensively researched over several decades. Most studies have focused on, for instance, ion- or electron-induced sputtering and desorption,1 ion stimulated surface electron emission,2–4 energy loss,5 and ion induced surface nanostructures.6–9 The charge state in scattered beams after projectile scattering from an insulator ionic-crystal surface has received much attention.10 Specifically, the interesting phenomenon of an unexpectedly large fraction of negative ions yield by positive or neutral projectile grazing scattering from insulator alkali halide or oxide surfaces have been experimentally observed.11 This large negative ion conversion yield and the related charge-transfer mechanism have received much attention because of the wide applications of negative ions in various fields, such as laser cooling,12–14 using C− ions to facilitate nerve tissue growth,15 using O2− ions for indoor environment purification,16 using H− ions as a probe for the subband electronic structures of nanosurfaces,17 applying H−/D− ion beam implantation to ITER devices,18 using negative ions in astrophysics evolution studies,19 designing negative ion sources20 and constructing neutral particle detectors in space research.21The negative ion conversion mechanism of atomic particle scattering at grazing angles on metal surfaces has already been comprehensively studied.22–25 In this case, charge-exchange is dominated by electronic resonant transitions between states of metal surface and the affinity level of a projectile. When the projectile approaches the surface, its energy level is drastically shifted downward by the image potential, which increases with decreasing distance between the projectile and the surface. By this shift, the affinity level of the projectile was shifted below the Fermi level and an electron was captured from the metal states to the projectile during the approaching to the surface. In contrast, when the negative ion leaves away from the surface, its affinity level shifted above the Fermi level and couples with the unoccupied states of the metal, which makes the electron can be lost back to the surface of the metal. Different from metals, insulating ionic crystals have a wide band gap (typically within 6–14 eV (ref. 20)), and the image potential shifts on such surfaces are approximately 1–2 eV (ref. 26). Clearly, this relatively small shift of the projectile affinity level cannot move it to near the valence band level and leads to the valence band electron capture being impossible. However, most experimental results27 have shown that the measured negative ion yield from neutral atom grazing scattering from the surface of a wide band gap material is unexpected large, which needs to be explained. In the study of negative ion conversion arising from neutral atoms grazing scattering from the surface of an AB-type ionic crystal, Borisov et al.28 proposed that the Madelung potential produced by the constituent anions and cations of the insulating ionic crystal leads to an prominent downward shift of neutral projectiles' affinity level during their approach to the surface. In addition, the Coulomb interaction between the negative ion and the positively charged hole on the surface after an electron capture in the final state of the charge transfer reaction also affords a large reduction of the energy defect. Both the effects above can reduce the electron capture energy defect to several eV and result in a low velocity threshold for negative ion formation. While on the other hand, the neglect of the possible electron loss channels in theoretical model leads to the calculated negative ion yield tending to saturate with velocity, obviously contrary to the decrease observed in experiments at large velocity.
Recently, a simple model29–31 that incorporates the electron detachment from a negative ion to vacuum by regarding it as a Coulomb barrier tunneling behavior caused by the Coulomb interaction between the formed negative ion and surface anions well reproduced the F0 and O0 experimental results in the whole velocity range. For the H0 case, an electron loss based on 3D wave-packet propagation was proposed.32 This model includes three electron destruction channels: (1) the kinematically assisted electron loss to the conduction band, (2) the resonant coherent electron detachment induced by the periodic potential in front of the surface and (3) the electron loss in a binary-type collision with the surface anions. In these three channels, electrons will be mainly lost to vacuum. The energy spectrum of H0 atoms grazing scattering from a LiF(100) surface measured by Roncin et al.33 shows a fraction of scattered H atoms without electron emission which reveals the existence of a H− loss channel without electron emission to vacuum. Consequently, Winter et al.34 considered the affinity electron loss from a H− ion to the surface exciton state by the Landau–Zener model to explain this electron loss channel. In which they combined a constant detachment probability of 0.5 and several adjustable parameters, the calculation of their model matched the experimental result in the low velocity range (v < 0.2 a.u.), but a large divergence between the results of experiment and their simulation appeared at high velocity. Therefore, a clear physical picture of electron loss needs to be revealed to reproduce the experimental negative ion yield in the whole velocity range.
In this work, a simple theoretical description of negative ion conversion from grazing scattering of neutral hydrogen atoms from a LiF(100) surface in the whole velocity range was presented. Here, in addition to the capture of a valence band electron near a surface F− site by a neutral H projectile, the Coulomb barrier tunneling behavior of the detachment of the affinity electron from the formed H− ion to vacuum during its interaction with the surface F− site was considered. By including in the image attraction-induced increase in the vertical component of the projectile energy and the collective dielectric screening effect of surrounding anions and cations on the charge of surface F− site that participates in the electron detachment, the image attractive interaction was revealed to increase the electron detachment probability, in turn drastically decreasing the final H− ion yield. Additionally, the calculated sub-eV order of energy defect between the H− affinity level and the unoccupied image state induced by the potential field of the H− image charge in LiF surface implies that the H− destruction without electron emission was due to its affinity electron loss to the unoccupied image state by a nearly resonant charge transfer manner. A clear picture of this H− destruction channel is also presented here.
The paper is arranged as follows. Section 2 is devoted to the presentation of a simple model description. Where the basic valence band electron capture energy defect, electron capture probability, and the electron loss channel of the Coulomb barrier tunneling detachment to vacuum during the formed negative ion interaction with a surface anion site are presented. For the negative ions detachment, corrections of the image potential attraction and the effective charge resulting from the collective dielectric screening effect of LiF crystal on the surface F− site to the Coulomb barrier tunneling detachment to vacuum behavior are discussed in detail. In addition, a clear picture of unoccupied surface image state loss in a nearly resonant charge transfer (RCT) used to explain the H− ions destruction without accompany electron emission is also presented. In Section 3, the simulation results are compared with available experimental results, and finally, the major conclusions are drawn in Section 4. Atomic units are used unless otherwise stated.
2. Methods
2.1 The basic model and energy defect of electron capture
As shown in Fig. 1, the surface of an alkali-metal halide consists of alternating anions (Hal−) and cations (Alk+) located at lattice sites with charges of qi = ±1. The valence band of alkali-metal halides originates from the Hal−(npx,y,z) orbitals.35,36 The charge transfer between an incident projectile and the surface mainly occurs at the surface Hal− site; that is, when a neutral projectile A0gas scatters from an alkali-metal halide surface, electron capture occurs at the Hal− site. This guarantees the validity of the binary interaction picture. Thus, the interaction between an incident projectile and an alkali-metal halide surface in grazing scattering can be simply regarded as a series of binary collision events between the projectile and surface halogen sites along its trajectory. The small incident angle makes the projectile trajectory near the surface parallel to the surface plane. Hence, the actual trajectory of a projectile is approximated as piece wise parallel to the surface plane.20 | ||
| Fig. 1 Sketch of a projectile scattering from a LiF(100) surface, which consists of one active site and 899 surrounding ions of crystal organized in four parallel layers.30 The direction of the incident beam is parallel to the 〈100〉 channel of the surface plane. α = 10 is the incident angle and D is the diameter of the incident beam. | ||
In a single binary collision of the studied H0gas–LiF(100) scattering, the electron capture process can be expressed by
| H0gas + F−as → H−gas + F0as | (1) |
The subscript ‘as’ in eqn (1) denotes the specific F− that actually participates in the binary collision charge-transfer with H atom and was taken as the origin of the coordinates. All crystal sites except for the F−as are regarded as point charges in the energy defect calculation. The energy defect between the initial and final states plays a crucial role in the electron capture process and can be expressed as30,31
| ΔE(R,v) = ΔEPC(R) + Uimage(Z,v) + PML(R) | (2) |
In eqn (2), 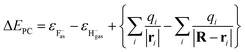 is the energy defect caused by non-polarized point charges (PC energy defect),28 where
is the energy defect caused by non-polarized point charges (PC energy defect),28 where 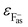 and
and 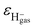 are the binding energies and electron affinities of free F−as and H−gas ions,
are the binding energies and electron affinities of free F−as and H−gas ions, 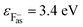 (ref. 27) and
(ref. 27) and 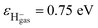 (ref. 27) The parameters R = {X,Y,Z} and ri are the position vectors of the projectile and all lattice sites except the active site. The two terms in the brackets are the Madelung potential induced by PCs at F−as(|R| = 0) and H−gas. The system of {899 point charges + F−as} organized in four parallel layers was used here to guarantee that the accuracy of the calculated Madelung potential on the active surface F−as was better than 5 × 10−4 eV (ref. 20, 28 and 30) PML(R)is the Mott–Littleton (ML) polarization interaction,20,28,37 which is created by the dipolar potential field produced by the formed negative ion and the hole on the surface in the final state of the electron capture reaction. Uimage(Z,v) is the image interaction between the formed H− and the image charge which produced by the field polarization of the H−gas to the LiF crystal in the final state of the electron capture reaction.38,39
(ref. 27) The parameters R = {X,Y,Z} and ri are the position vectors of the projectile and all lattice sites except the active site. The two terms in the brackets are the Madelung potential induced by PCs at F−as(|R| = 0) and H−gas. The system of {899 point charges + F−as} organized in four parallel layers was used here to guarantee that the accuracy of the calculated Madelung potential on the active surface F−as was better than 5 × 10−4 eV (ref. 20, 28 and 30) PML(R)is the Mott–Littleton (ML) polarization interaction,20,28,37 which is created by the dipolar potential field produced by the formed negative ion and the hole on the surface in the final state of the electron capture reaction. Uimage(Z,v) is the image interaction between the formed H− and the image charge which produced by the field polarization of the H−gas to the LiF crystal in the final state of the electron capture reaction.38,39
For a projectile with charge Q and parallel velocity v‖ = v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α flying above a dielectric surface, the related image potential is calculated in a surface response formalism as follows,40
α flying above a dielectric surface, the related image potential is calculated in a surface response formalism as follows,40
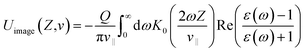 | (3) |
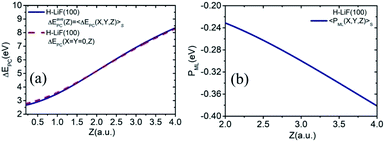
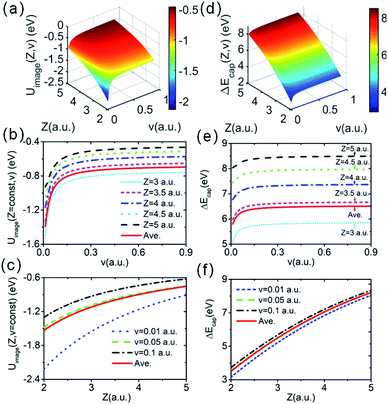
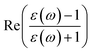 is the real part of the surface response function with dielectric constant ε(ω) induced by a two-oscillator model.41 Fig. 3(a) shows the calculated 3D image potential as a function of the incident velocity v and the surface altitude Z of a H− ion in front of a LiF(100) surface. Fig. 3(b) presents its projection on velocity v for fixed surface altitude respectively at Z = 3, 3.5, 4, 4.5, 5 a.u. and the Z averaged result, 〈Uimage(Z,ν)〉Z ∈ [2,5] a.u. Fig. 3(c) displays its projection on surface altitude Z for fixed velocities respectively at v = 0.01, 0.05, 0.1 a.u. and the v averaged result, 〈Uimage(Z,ν)〉ν ∈ [0.01,0.9] a.u. It's observed |Uimage(Z,ν)| decrease with both surface altitude Z and velocity v.
is the real part of the surface response function with dielectric constant ε(ω) induced by a two-oscillator model.41 Fig. 3(a) shows the calculated 3D image potential as a function of the incident velocity v and the surface altitude Z of a H− ion in front of a LiF(100) surface. Fig. 3(b) presents its projection on velocity v for fixed surface altitude respectively at Z = 3, 3.5, 4, 4.5, 5 a.u. and the Z averaged result, 〈Uimage(Z,ν)〉Z ∈ [2,5] a.u. Fig. 3(c) displays its projection on surface altitude Z for fixed velocities respectively at v = 0.01, 0.05, 0.1 a.u. and the v averaged result, 〈Uimage(Z,ν)〉ν ∈ [0.01,0.9] a.u. It's observed |Uimage(Z,ν)| decrease with both surface altitude Z and velocity v.
To simplify the actually energy defect calculation of the valence band electron capture reaction, here according to ref. 30, the effective scale of a surface F−as is S = {−a/4 ≤ X ≤ a/4, −a/4 ≤ Y ≤ a/4} (a = 7.592 a.u., the lattice constant of the LiF crystal27). In addition, considering the scale of the H0 projectile, the actual effective area of a single binary collision electron capture event should be 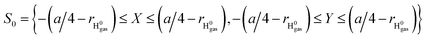 . Therefore, the real PC energy defect for a F−as of scale S is calculated in S0. Because of the averaging of the PC energy defect on the (X, Y) plane,
. Therefore, the real PC energy defect for a F−as of scale S is calculated in S0. Because of the averaging of the PC energy defect on the (X, Y) plane,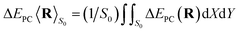 is well approximated by the PC energy defect at X = Y = 0 as shown in Fig. 2(a) (also see ref. 30 and 31 for other collision systems), one can use the ΔEPC(X = Y = 0, Z) to approximate the average PC energy defect in S here to calculate the localized valence band electron capture energy defect of ΔEave(Z,v) near a surface F−as. Moreover, we have calculated the average ML polarization interaction
is well approximated by the PC energy defect at X = Y = 0 as shown in Fig. 2(a) (also see ref. 30 and 31 for other collision systems), one can use the ΔEPC(X = Y = 0, Z) to approximate the average PC energy defect in S here to calculate the localized valence band electron capture energy defect of ΔEave(Z,v) near a surface F−as. Moreover, we have calculated the average ML polarization interaction 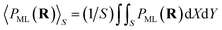 , as shown in Fig. 2(b). It's observed that 〈PML(R)〉S slightly decreases with surface altitude Z and within a range of 〈PML(R)〉S ∈ [−0.38,−0.23] eV.
, as shown in Fig. 2(b). It's observed that 〈PML(R)〉S slightly decreases with surface altitude Z and within a range of 〈PML(R)〉S ∈ [−0.38,−0.23] eV.
Now, considering the actually averaged electron capture energy defect, ΔEave(Z,v) = 〈ΔE(R,v)〉S, eqn (2) changes to30,31
| ΔEave(Z,v) ≈ ΔEPC(X = Y = 0,Z) + 〈PML(R)〉S + Uimage(Z,v) | (4) |
Fig. 3(d) displays a 3D plot of the energy defect as a function of both Z and v. Fig. 3(e) and (f) display the two-dimensional projections of the energy defect ΔEave(Z,v) respectively on Z or v by fixing the other variable. Considering the PC energy defect ΔEPC(R) in eqn (2), the first term in the brackets is approximately 12.05 eV for the LiF crystal,42 which is the main source of the large energy difference between the initial and final states. Additionally, for the case of single electron capture by a neutral atom, the second term in the brackets is approximately  , which drastically reduces the energy defect is the so-called “energy level confluence”.28 Moreover, in addition to the PC energy defect, the image potential and ML polarization could also reduce the energy defect. Due to the Uimage(Z,v), the energy defect was reduced by approximately 0.7 to 1.4 eV in the velocity range of 0 ≤ v ≤ 0.9 a.u. (see the red solid line in Fig. 3(b)). As shown in ref. 20, 28, and 30, the detailed expression of the ML polarization interaction is completely controlled by the charge state of the formed negative ions and the polarizations of the constituent cations and anions of the ionic crystal. This leads to the 〈PML(R)〉S of the H− + (LiF)+ system being the same as that in the F− + (LiF)+case, roughly 〈PML(R)〉S ∈ [−0.38,−0.23] eV (ref. 30) as shown in Fig. 2(b) (also can be obtained from ref. 30). Thus, for the surface altitude range of Z ∈ [2.0,5.0] a.u., which is regarded as the effective Z range of charge-transfer,30,31 the Uimage(Z,v)-induced reduction in the total energy defect is obviously larger than that induced by the ML polarization interaction. Noted here even though the reduction effect of |Uimage(Z,v)| ∈ [0.7,1.4] eV on ΔEave(Z,v) (ΔEave(Z,v) > 5 eV within Z ∈ [2,5] a.u. range, see Fig. 3(d) and (e)) is small, the sensitive dependence of the electron capture probability Pcap(Z,v) on ΔEave(Z,v) leads to a considerable of Uimage(Z,v) correction to Pcap(Z,v).
, which drastically reduces the energy defect is the so-called “energy level confluence”.28 Moreover, in addition to the PC energy defect, the image potential and ML polarization could also reduce the energy defect. Due to the Uimage(Z,v), the energy defect was reduced by approximately 0.7 to 1.4 eV in the velocity range of 0 ≤ v ≤ 0.9 a.u. (see the red solid line in Fig. 3(b)). As shown in ref. 20, 28, and 30, the detailed expression of the ML polarization interaction is completely controlled by the charge state of the formed negative ions and the polarizations of the constituent cations and anions of the ionic crystal. This leads to the 〈PML(R)〉S of the H− + (LiF)+ system being the same as that in the F− + (LiF)+case, roughly 〈PML(R)〉S ∈ [−0.38,−0.23] eV (ref. 30) as shown in Fig. 2(b) (also can be obtained from ref. 30). Thus, for the surface altitude range of Z ∈ [2.0,5.0] a.u., which is regarded as the effective Z range of charge-transfer,30,31 the Uimage(Z,v)-induced reduction in the total energy defect is obviously larger than that induced by the ML polarization interaction. Noted here even though the reduction effect of |Uimage(Z,v)| ∈ [0.7,1.4] eV on ΔEave(Z,v) (ΔEave(Z,v) > 5 eV within Z ∈ [2,5] a.u. range, see Fig. 3(d) and (e)) is small, the sensitive dependence of the electron capture probability Pcap(Z,v) on ΔEave(Z,v) leads to a considerable of Uimage(Z,v) correction to Pcap(Z,v).
2.2 Electron capture probability
For a neutral H0 projectile capturing a valence band electron from a F−as of a LiF(100) surface to its affinity level, the capture probability Pcap can be calculated by the Demkov model as follows,28,43
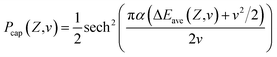 | (5) |
The prefactor 1/2 results from the averaging over the trajectories with different impact parameters. 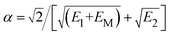 characterizes the exponential decay of the electron transfer interaction between the two collision participants, where E1 and E2 are the ionization potentials of the free F− ion and H− projectile, respectively. EM = 12.05 eV (ref. 27 and 42) represents the Madelung potential at the surface active F−as of the LiF crystal. The electron capture energy defect ΔEave(Z,v), as discussed in part 2.1 of Section 2, has been corrected by a translational factor v2/2, which arises from the projectile motion with respect to F−as.
characterizes the exponential decay of the electron transfer interaction between the two collision participants, where E1 and E2 are the ionization potentials of the free F− ion and H− projectile, respectively. EM = 12.05 eV (ref. 27 and 42) represents the Madelung potential at the surface active F−as of the LiF crystal. The electron capture energy defect ΔEave(Z,v), as discussed in part 2.1 of Section 2, has been corrected by a translational factor v2/2, which arises from the projectile motion with respect to F−as.
Fig. 4(a) presents a 3D plot of the valence band electron capture probability Pcap(Z,v) as a function of surface altitude Z and projectile velocity v. Fig. 4(b) displays the electron capture probability Pcap as a function of projectile velocity v for fixed surface altitudes of Z = 3,3.5,4 a.u. Considering the generally effective electron capture surface altitude range of Z ∈ [2,5] a.u.30,44 for a neutral atom under grazing scattering from an insulator surface with keV projectile energy, the Z averaged probability of 〈Pcap(Z,v)〉Z ∈ [2,5] a.u. as a function of velocity v is also shown. The electron capture probability increases with projectile velocity v and decreases with surface altitude Z. The averaged probability 〈Pcap(Z,v)〉Z ∈ [2,5] a.u. is located between the electron capture probabilities of theZ = 3.0 a.u. and Z = 3.5 a.u. cases, which is in reasonable agreement with the conclusion that electron transfer mainly occurs near the trajectory turning point (within the Z ∈ [2,5] a.u. range) of the projectile trajectory.27 The large velocity threshold (vTh = 0.15 a.u.) compared with the F–LiF(100) (vTh = 0.05 a.u.30 and vTh = 0.06 a.u.40) and O–LiF(100) (vTh = 0.1 a.u.) cases27,29 is due to the relatively large valence band electron capture energy defect for our present H–LiF(100) collision system (see Fig. 3(d)–(f)).
2.3 Electron loss models
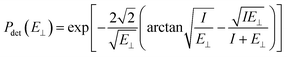 | (6) |
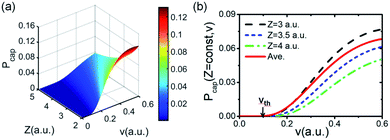
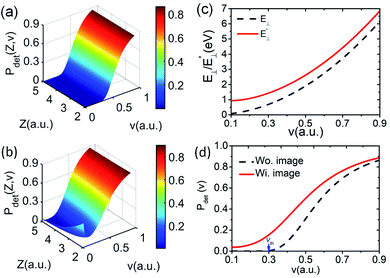
The image attractive potential of a H− ion Uimage(Z,v) increases the projectile vertical energy, i.e., the actually vertical energy can be corrected by 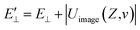 . This correction to the vertical energy changes the detachment probability Pdet. Fig. 5 displays this change using the image potential, where Fig. 5(a) and (b) show 3D plots of Pdet as a function of Z and v without and with include the Uimage(Z,v) correction. Fig. 5(c) shows the difference between E⊥ (black dashed line) and
. This correction to the vertical energy changes the detachment probability Pdet. Fig. 5 displays this change using the image potential, where Fig. 5(a) and (b) show 3D plots of Pdet as a function of Z and v without and with include the Uimage(Z,v) correction. Fig. 5(c) shows the difference between E⊥ (black dashed line) and 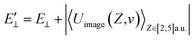 (red solid line). Fig. 5(d) shows the difference in the detachment probability with (Wi. image) (red solid line) and without (Wo. image) (black dashed line) include the 〈Uimage(Z,v)〉Z ∈ [2,5] a.u. correction to E⊥. For the calculated probability neglecting 〈Uimage(Z,v)〉Z ∈ [2,5] a.u., E⊥ quadratically increases with velocity from zero, and the threshold at which the probability rapidly increases is approximately vth = 0.3 a.u. (see the blue arrow in Fig. 5(d)). For the case of considering the 〈Uimage(Z,v)〉Z ∈ [2,5] a.u. correction, the vertical energy at v = 0.1 a.u. is even larger than that at v = 0.3 a.u. without considering it (see Fig. 5(c)). This result consequently leads to a considerable detachment probability, especially for v < 0.3 a.u. range. Considers the low velocity threshold of the electron capture probability, the modified detachment probability may obviously affect the negative ion fraction at low velocity compared without considering the Uimage(Z,v) correction (detail discussion see part 3).
(red solid line). Fig. 5(d) shows the difference in the detachment probability with (Wi. image) (red solid line) and without (Wo. image) (black dashed line) include the 〈Uimage(Z,v)〉Z ∈ [2,5] a.u. correction to E⊥. For the calculated probability neglecting 〈Uimage(Z,v)〉Z ∈ [2,5] a.u., E⊥ quadratically increases with velocity from zero, and the threshold at which the probability rapidly increases is approximately vth = 0.3 a.u. (see the blue arrow in Fig. 5(d)). For the case of considering the 〈Uimage(Z,v)〉Z ∈ [2,5] a.u. correction, the vertical energy at v = 0.1 a.u. is even larger than that at v = 0.3 a.u. without considering it (see Fig. 5(c)). This result consequently leads to a considerable detachment probability, especially for v < 0.3 a.u. range. Considers the low velocity threshold of the electron capture probability, the modified detachment probability may obviously affect the negative ion fraction at low velocity compared without considering the Uimage(Z,v) correction (detail discussion see part 3).
The probability of Coulomb repulsive barrier tunneling detachment relates to the Coulomb interaction between the negative projectile and the active site F−as. Due to the screening of the field of surrounding crystal sites, the effective charge of the F−as is reduced to qeff = −0.86 in the LiF crystal.46 This reduction leads to the Coulomb repulsive barrier 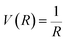 decreasing to
decreasing to 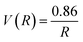 and increases the detachment probability Pdet (that is, multiply the exponent of eqn (6) by |qeff| = 0.86), as observed by comparing Pdet with (Wi. effective charge) (red solid line) and without (Wo. effective charge) (black dashed line) considering the effective charge in Fig. 6.
and increases the detachment probability Pdet (that is, multiply the exponent of eqn (6) by |qeff| = 0.86), as observed by comparing Pdet with (Wi. effective charge) (red solid line) and without (Wo. effective charge) (black dashed line) considering the effective charge in Fig. 6.
Here, a detailed calculation of the energy defect from the H− + F0 to H0 + F−* system is presented. The energy of the initial state can be expressed by
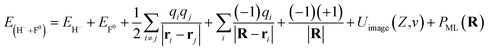 | (7) |
The field of the crystal with one neutralized site can be represented as the field of a perfect crystal plus one additional positive charge localized at position r0 = 0 (ref. 40) R is the position vector of the projectile. The first and second terms are the total energies of free H− and F0, respectively. The third term represents the interaction energy between PCs (qi = ±1) of all the crystal sites. The fourth term is the electrostatic interaction of a H− projectile with an undisturbed neutral LiF crystal. Due to the neutrality of the LiF crystal, this term is small and amounts to only approximately 1 eV.33 The fifth term is the Coulomb attractive interaction between a H− ion and a hole located at the r0 = 0 position. Uimage(Z,v) is the image interaction between a H− projectile and its own polarization image charge in the LiF crystal. PML(R) is the ML polarization interaction produced by the potential of the dipole formed by the H− ion and the hole created by electron capture.
Similarly, the expression of the final state is
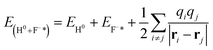 | (8) |
The first term corresponds to the total energy of a free H0 atom. The second term represents the total energy of a neutralized F0 that produced by one valence band electron capture plus the total energy of a surface exciton state F−* of LiF crystal. The energy defect can be written as
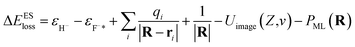 | (9) |
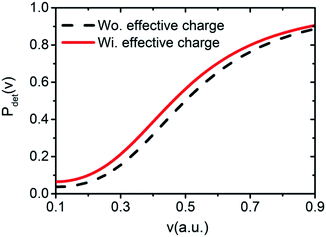
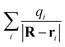 resulting from the electrostatic interaction is on the order of 1 eV.40 Thus, the large energy defect (ΔEESloss ≥ 6 eV) shown in Fig. 7(a) and (c) mainly results from the Coulomb attractive interaction between the H− ion and the hole located at the active site in the initial state, i.e., the fifth term −1/|R| in eqn (7). That is this term results in a +1/|R| term in ΔEESloss of eqn (9) which drastically increase with the decreasing of surface altitude Z, in turn leads to an unexpectedly large energy defect between the initial and final states within the effective charge-transfer surface altitude range of Z ∈ [2,5] a.u. and finally inhibits the electron loss to the surface exciton state of F−*.
resulting from the electrostatic interaction is on the order of 1 eV.40 Thus, the large energy defect (ΔEESloss ≥ 6 eV) shown in Fig. 7(a) and (c) mainly results from the Coulomb attractive interaction between the H− ion and the hole located at the active site in the initial state, i.e., the fifth term −1/|R| in eqn (7). That is this term results in a +1/|R| term in ΔEESloss of eqn (9) which drastically increase with the decreasing of surface altitude Z, in turn leads to an unexpectedly large energy defect between the initial and final states within the effective charge-transfer surface altitude range of Z ∈ [2,5] a.u. and finally inhibits the electron loss to the surface exciton state of F−*.
Additionally, one can simply estimate the strength of electron-transfer interaction Vtransfer(R) of the exciton state F−* loss process of H− → F−* by 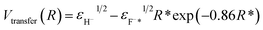 47 where
47 where 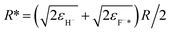 , εH− = 0.75 eV and εF−* = (1.1 ± 0.5) eV are the binding energy of H− and F−*, respectively. Compare with the typical electron-transfer interaction strength Vtransfer(R) > 1 eV (ref. 20, 27, 28, and 36) the excessively small calculated electron-transfer interaction of Vtransfer(Rc) < 0.4 eV of H− → F−* process at a large value of the energy levels crossing point Rc ≈ 8.6 a.u.48 also makes the electron loss to the surface exciton state F−* impossible.
, εH− = 0.75 eV and εF−* = (1.1 ± 0.5) eV are the binding energy of H− and F−*, respectively. Compare with the typical electron-transfer interaction strength Vtransfer(R) > 1 eV (ref. 20, 27, 28, and 36) the excessively small calculated electron-transfer interaction of Vtransfer(Rc) < 0.4 eV of H− → F−* process at a large value of the energy levels crossing point Rc ≈ 8.6 a.u.48 also makes the electron loss to the surface exciton state F−* impossible.
It should be kept in mind that an effective electron loss channel of H− ions have to satisfy two essential conditions of within the projectile approaching surface altitude range of Z ∈ [2,5] a.u., the energy defect of electron-transfer between the initial and final states is small enough and the interaction strength of the electron-transfer is large enough. Clearly, as detailed discussed above, the large energy defect (ΔEESloss ≥ 6 eV) and small electron-transfer interaction (Vtransfer < 0.4 eV) both make the surface excition state F−* loss of H− → F−* unable to occur.
An unoccupied image state (IS) was theoretically confirmed to exist near a LiF crystal surface.49,50 The image attractive potential created by an electron in front of a dielectric surface may cause an unoccupied image state that can trap an electron close to the vacuum level. Since the image potential is approximately the same at a fixed surface altitude over the whole surface, the wave function of the electron in this state can be seen as nonlocal. Here, for a H− ion in front of a LiF crystal surface, the field of H− polarization of the LiF crystal produces a polarization image charge in the LiF crystal; in turn, an unoccupied image state is induced by this polarization image charge near the vacuum level. If one considers the loosely bound affinity electron of a H− ion transitioning to this unoccupied image state, then the energy of the initial state is
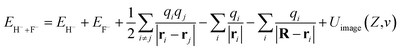 | (10) |
The first two terms denote the total energies of free H− and F− ions, respectively. The final state is
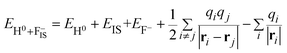 | (11) |
EIS = 0.3 eV (ref. 49) is the binding energy of the unoccupied image potential state induced by a H− ion in front of a LiF surface. The corresponding energy defect is expressed by
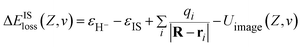 | (12) |
The 3D plot of ΔEISloss(Z,v) as a function of Z and v is shown in Fig. 7(b). Fig. 7(c) displays the v averaged energy defect, ΔEISloss(Z) = 〈ΔEISloss(Z,v)〉v ∈ [0.01,0.9] a.u. (blue solid line) as a function of surface altitude Z. Even though ΔEISloss(Z) exhibits a small increase with Z, compare with the region of ΔEISloss(Z) = ±1 eV defined by the black dotted-dashed lines, the average energy defect is approximate remains near sub-eV order within Z ∈ [2,5] a.u. range. Additionally, considering (1) the turning point of the projectile trajectory of H0 → LiF(100)is in the range of Z ∈ [2,5] a.u. and negative ions are mainly formed near the trajectory turning point. Therefore, Z ∈ [2,5] a.u. is the effective surface altitude range of H− formation, that is within which, the requirement of electron-transfer interaction of the IS loss H− → IS is strong enough is naturally satisfied. (2) The wave function of the H− ion can obvious overlap with the widely distributed unoccupied IS wave function, which also implies the electron-transfer interaction is sufficiently strong. Therefore, the H− ion can lose its affinity electron to the IS by a nearly RCT manner.
As shown in Fig. 8(a), after an electron capture, the affinity level of a H− ion overlaps with the nonlocal image state induced by a H− ion. This state has a loose wave function in the Z direction49 (see Fig. 8(a)). Consequently, the electron can transfer to this unoccupied image state.
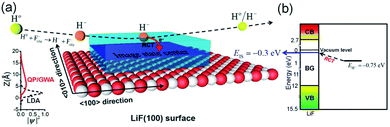 | ||
| Fig. 8 (a) Sketch of the electron transfer from H− to the surface image state via a nearly RCT process. The translucent blue space with a central plane represents the distribution of the nonlocal unoccupied image state on the surface. The diagram on the left shows the broadening of the unoccupied image state in Z direction.49 (b) Diagram of the energy levels of a H− ion in front of a LiF(100) surface and also the H− → IS state electron-transfer by a nearly RCT process (see the black dashed arrow). | ||
Fig. 8(a) shows the electron transfer from a H− ion to the unoccupied image state. Fig. 8(b) presents a diagram of the relative energy levels of the H− ion, surface unoccupied image state and energy band structure of the LiF crystal. Additionally, the loss of the affinity electron of a H− ion to the unoccupied image state IS via a nearly RCT process is schematically displayed by the black dashed arrow.
In contrast to the unexpectedly large energy defect (ΔEESloss ≥ 6 eV, see Fig. 7(a) and (c)) and excessively small electron-transfer interaction (Vtransfer < 0.4 eV) of F−* state electron loss inhibits the electron loss to the surface F−* state, the sub-eV order of the energy defect (ΔEISloss < 1 eV, see Fig. 7(b) and (c)) and sufficiently strong electron-transfer interaction lead to the electron loss to the unoccupied IS state by a nearly RCT manner possible.
The probability PRCT of electron loss to the unoccupied image state IS can be simply expressed as51
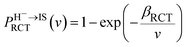 | (13) |
Here, v ≈ v‖ = v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α (α = 10). βRCT is proportional to the coupling strength between the H− ion and the unoccupied IS. Because the coupling strength between the initial and final states decreases with surface altitude Z,
α (α = 10). βRCT is proportional to the coupling strength between the H− ion and the unoccupied IS. Because the coupling strength between the initial and final states decreases with surface altitude Z, 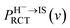 decreases with Z. It should be noted here that although the formal H− has been transferred to a H0 atom in the final state, the active electron is still in the image potential state induced by the electron itself, that is the electron in the final state was trapped in the bounded image potential state induced by itself.
decreases with Z. It should be noted here that although the formal H− has been transferred to a H0 atom in the final state, the active electron is still in the image potential state induced by the electron itself, that is the electron in the final state was trapped in the bounded image potential state induced by itself.
3. Results and discussion
Incorporating the probabilities of electron capture and loss to both vacuum and the IS state, the negative ion fraction P(N) can be calculated. Here, the iteration is similar to the method used in ref. 34, P(N) is calculated by iteration of the effective collision number Neff with initial (Neff = 0) neutral H0 fraction of n0 = 1 and the H− fraction of nmin = 0,
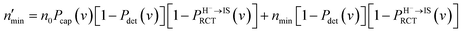 | (14) |
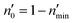 | (15) |
Where 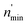 and
and 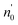 are respectively the negative ions and neutral atoms fraction after a binary collision. Pcap(v) and Pdet(v) in eqn (14) are averaged for the typical effective surface altitude range of, Z ∈ [2,5] a.u. (ref. 30 and 31) and
are respectively the negative ions and neutral atoms fraction after a binary collision. Pcap(v) and Pdet(v) in eqn (14) are averaged for the typical effective surface altitude range of, Z ∈ [2,5] a.u. (ref. 30 and 31) and 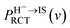 is the probability of electron loss from a H− ion to the unoccupied image state IS. The trajectory of a projectile is determined by the effective surface scattering potential between projectile and surface and the vertical component of projectile energy. But for a dielectric surface, the trajectories and turning points calculated by classical binary interaction potential, such as ZBL, OCB, TFMF and TFML models and ab initio calculation are quite different since the large discrepancy of the potential curves via the altitude from surface calculated by these methods.20 Thus an accurate trajectory is hard to obtain. While considering (1) the turn point Zmin of projectile trajectory is approximate in the surface altitude range of Z ∈ [2,5] a.u. at incident angle α = 10 for H0 projectiles with energy of Ep ∈ [0.25, 25] keV (ref. 28) studied here (the plausible of the choosing of this surface altitude range can be seen by: (i) the Z ∈ [2,3] a.u. range, measured from the last atomic plane, is representative of the turning point of the trajectory in grazing-angle experiments with a perpendicular energy in the eV range;26,32,33 (ii) the range of projectile trajectory turning point of F–MgO(100)20 and F–LiF(100)/KI(100)28 collision systems are respectively Z ∈ [1.8, 3] a.u. and Z ∈ [2, 4] a.u., and (iii) the final charge fraction is determined at surface altitude of Z ≈ 5 a.u. for H–LiF collision system32). (2) The negative ions are mainly formed near the turn point Zmin of a projectile trajectory.27 (3) For grazing scattering geometry, at small projectile-surface altitude where most of the charge-transfer takes place, the projectile H0 moves almost parallel to the surface.28 One can expect that the projectile moves along a trajectory parallel to the surface during its binary encounter with a surface active site F−as. (4) The energy defect of an valence band electron capture of an incident H0 atom near a surface F−site are a series of Zi dependent ΔEcap(Zi,v). An effective electron-capture energy defect exists and can be obtained by
is the probability of electron loss from a H− ion to the unoccupied image state IS. The trajectory of a projectile is determined by the effective surface scattering potential between projectile and surface and the vertical component of projectile energy. But for a dielectric surface, the trajectories and turning points calculated by classical binary interaction potential, such as ZBL, OCB, TFMF and TFML models and ab initio calculation are quite different since the large discrepancy of the potential curves via the altitude from surface calculated by these methods.20 Thus an accurate trajectory is hard to obtain. While considering (1) the turn point Zmin of projectile trajectory is approximate in the surface altitude range of Z ∈ [2,5] a.u. at incident angle α = 10 for H0 projectiles with energy of Ep ∈ [0.25, 25] keV (ref. 28) studied here (the plausible of the choosing of this surface altitude range can be seen by: (i) the Z ∈ [2,3] a.u. range, measured from the last atomic plane, is representative of the turning point of the trajectory in grazing-angle experiments with a perpendicular energy in the eV range;26,32,33 (ii) the range of projectile trajectory turning point of F–MgO(100)20 and F–LiF(100)/KI(100)28 collision systems are respectively Z ∈ [1.8, 3] a.u. and Z ∈ [2, 4] a.u., and (iii) the final charge fraction is determined at surface altitude of Z ≈ 5 a.u. for H–LiF collision system32). (2) The negative ions are mainly formed near the turn point Zmin of a projectile trajectory.27 (3) For grazing scattering geometry, at small projectile-surface altitude where most of the charge-transfer takes place, the projectile H0 moves almost parallel to the surface.28 One can expect that the projectile moves along a trajectory parallel to the surface during its binary encounter with a surface active site F−as. (4) The energy defect of an valence band electron capture of an incident H0 atom near a surface F−site are a series of Zi dependent ΔEcap(Zi,v). An effective electron-capture energy defect exists and can be obtained by 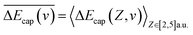 , this specific
, this specific 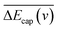 and the corresponding electron-capture probability of
and the corresponding electron-capture probability of 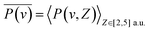 actually represent the effective electron-capture energy defect and electron-capture probability in the negative-ion formation surface altitude range of Z ∈ [2,5] a.u. Therefore, similar to our previous treatment,30,31 both the electron capture energy defect and electron capture probability were averaged over this surface altitude range here.
actually represent the effective electron-capture energy defect and electron-capture probability in the negative-ion formation surface altitude range of Z ∈ [2,5] a.u. Therefore, similar to our previous treatment,30,31 both the electron capture energy defect and electron capture probability were averaged over this surface altitude range here.
Considering the obtained effective collision number range of Neff = 5.3 → 7.8 for the H–LiF collision system48 and Neff = 10 used to fit the energy spectrum for grazing scattering of H atoms of 600 eV on a LiF(100) surface,33 the results of the negative ion fraction calculated by iteration of eqn (14) with Neff = 6, 8, and 10 and the available experimental data34 are displayed in Fig. 9(a). In addition, considering that (i) the simple cubic structure of the LiF crystal makes the LiF(100) surface the same as the LiF(001) surface, the experimentally measured H− ion yield of the H0 → LiF(100) collision system under a grazing incidence (α ≈ 10) is the same as that of the H0 → LiF(001) case. (ii) For the H+ → LiF(100) and H0 → LiF(100) collision systems, the energy level of H+ (1s) is EH+(1s) = −13.6 eV,52 clearly lower than the energy level of the valence band top (ETopVB ≈ −12.05 eV (ref. 27 and 42) of the LiF crystal. Therefore, the conversion probability of one valence band electron capture by resonant charge transfer for H+ → H0 neutralization is nearly 100%. This leads to the H+ incidence is completely equivalent to that of H0 incidence under the same incident geometry (α ≈ 10) for the LiF (100) surface, and the experimental H− ion yields of the two cases are almost the same. Here, both the experimental negative ion yields of H+ → LiF(100) (dark solid yellow triangles)44 and H0 → LiF(001) (black solid spheres)34 collision systems were also presented in Fig. 9(a) for comparison. For the results with different Neff, the discrepancy mainly lies in the velocity range of v ∈ [0.2,0.4] a.u. When the velocity increases to above v = 0.4 a.u., the discrepancy nearly disappear. Our present model calculation results well reproduced the experimental data in the whole velocity range, as displayed by the red solid line in Fig. 9(a). For comparison, the previous theoretical result34 which considered the electron loss to the surface exciton state by the Landau–Zener model with an adjustable parameter of β = 0.21 (β = 0.22 (ref. 48)) and a constant detachment probability of Pdet = 0.5 was presented by the black dashed line in Fig. 9(a). The calculated negative ion fraction monotonically increases with velocity and finally tends to saturate at large velocities. In contrast, the actual experimental negative ion yield decreases. This large difference mainly results from the assumption of a constant detachment probability of Pdet = 0.5 for the whole velocity range. The comparison between the present results and previous results clearly implies that the loss of H− affinity electrons through Coulomb barrier tunneling to vacuum plays a key role in the destruction of high velocity negative ions. Moreover, due to the rapid decrease in the RCT loss probability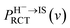 with v for the H− affinity electrons loss to the unoccupied surface image state IS (with βRCT = 0.02), as shown in Fig. 9(b), the unoccupied image state loss without accompanying electron emission is only efficient in the low velocity range of v ≤ 0.45 a.u., which can be seen by comparing the results with (red solid line) and without (violet short-dashed line) include the electron loss to the unoccupied image state in Fig. 9(a). The value of parameter βRCT here relies on an accurate electron-transfer coupling strength, which requires a complicated quantum chemical calculation that is beyond the main scope of our present work and temporarily treated as an adjustable parameter in our present simulation.
with v for the H− affinity electrons loss to the unoccupied surface image state IS (with βRCT = 0.02), as shown in Fig. 9(b), the unoccupied image state loss without accompanying electron emission is only efficient in the low velocity range of v ≤ 0.45 a.u., which can be seen by comparing the results with (red solid line) and without (violet short-dashed line) include the electron loss to the unoccupied image state in Fig. 9(a). The value of parameter βRCT here relies on an accurate electron-transfer coupling strength, which requires a complicated quantum chemical calculation that is beyond the main scope of our present work and temporarily treated as an adjustable parameter in our present simulation.
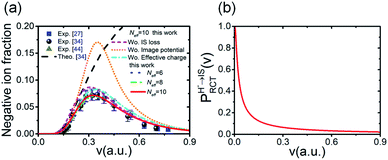 | ||
| Fig. 9 (a) Comparison of the negative ion fraction versus velocity calculated by the present approach (blue dotted, green dash-dot-dotted and red solid lines for Neff = 6, 8 and 10, respectively) and the experimentally measured negative ion yields of the H0–LiF(100) surface (blue solid squares),27 H0–LiF(001) surface (black solid spheres),34 and H+–LiF(100) surface (dark-yellow solid triangles)44 for scattering with a grazing incidence angle of α ≈ 1°. A previous theoretical calculation is shown as a black dashed line.34 The results that respectively without include (Wo.) the change in Pdet(v) due to the image potential correction to E⊥ (Wo. Image potential) (orange short-dotted line), the change in Pdet(v) due to the effective charge (Wo. effective charge) (cyan dash-dotted line) and the electron loss to the unoccupied image state IS (Wo IS loss) (violet short-dashed line) are also shown. (b) Probability of electron loss to the unoccupied image state IS PHRCT−→IS(v) versus velocity v for parameter βRCT = 0.02. | ||
To demonstrate the influence ofUimage(Z,v) and q = qeff on the final negative ion yield, the results with or without include one of these two effects were obtained for a typical effective collision number of Neff = 10, as displayed by the various lines in Fig. 9(a). The following is observed: (1) by comparing the results with (qeff = −0.86) (red solid line) and without (q = −1) (cyan dashed-dotted line) considered the effective charge, the smaller charge of the active site (F−site) caused by the dielectric screening of the crystal environment is shown to lead to a reduction in the Coulomb tunneling barrier, in turn increasing Pdet relative to the q = −1 case (see Fig. 6). This causes a reduction to the final negative ion yield. (2) A comparison between the results with (red solid line) and without (orange short-dotted line) include the increase in the projectile's vertical energy E⊥ due to the image potential attractive clearly shows that Uimage(Z,v) can drastically reduce the final negative ion yield. This phenomenon obviously results from the largeUimage(Z,v)-induced an increasing in E⊥ (see Fig. 5(c)) and, consequently, the large increase in Pdet (see the comparison of Fig. 5(a), (b) and (d)). Here, the maximum difference of the final negative yields between with and without include Uimage at v ≈ 0.4 a.u. shown in Fig. 9(a) results from the maximum Pdet(v) difference between with and without considering Uimage at the same v (see Fig. 5(d)). Above v = 0.4 a.u., this negative ion yields' difference rapidly decrease with v which can be understood by the decrease of |Uimage| with v leads to an obvious decreasing of the difference of Pdet(v) with v between with and without include Uimage (see Fig. 5(d)). Moreover, the calculated results at Neff = 6, 8, 10 imply that the negative ion yield is not sensitive to a change in the effective collision number of ΔNeff = 2.
4. Conclusions
A simple model of the negative ion conversion produced by neutral H0 atom grazing scattering from a LiF(100) surface in the whole velocity range was presented. The mechanisms that dominate this process are as follows: (1) electron capture from the valence band near a surface F−site to the affinity level of the neutral H0 projectile. This is attributed to the Coulomb attraction between the H− ion and the hole created by electron capture together with the ML-polarization and the image interactions in the final state which significantly reduce the energy defect of valence band electron capture reaction and make the electron capture possible; (2) Coulomb repulsive barrier tunneling detachment of the H− ion's affinity electron to vacuum during the interaction with the surface F−site along its trajectory. Here, by comparing the collective dielectric screening effect of surrounding anions and cations on the charge of the surface F−as that participates in the electron detachment process and the correction of the image attraction-induced increase to E⊥, the image attractive interaction was revealed to obviously increase the electron detachment probability, in turn drastically reducing the final negative ion yield. This implies the possibility of achieving higher negative ion yield from neutral H atoms in grazing scattering by choosing an ionic-crystal target which has lower image interaction. According to our recent study,53 this can be achieved by using an ionic crystal with a small value of optical limit dielectric constant. Compare with the magnitude of H− formation on metal surfaces,54,55 the large order of magnitude of H− ions yield here provides a potential utility in the ion implantation of fusion ITER devices18,56 and the use of H− ion to probe the subband electronic structures of nanosurfaces.17Moreover, detailed calculations revealed that the unexpectedly large energy defect and excessively small electron-transfer interaction inhibiting electron loss to the generally accepted surface exciton state, in contrast the sub-eV order of the energy defect and sufficiently strong electron-transfer interaction leads to the electron loss to the unoccupied image state by a nearly RCT process possible, which is efficient at low velocity and corresponds to a fraction of H− destruction without electron emission. Noted that only the physical picture of this H− destruction channel was presented here. An accurate coupling strength dependence of the parameter βRCT for this H− loss channel requires resorting to a full quantum chemical calculation, which is beyond the main scope of our present work but provides a clear direction for its improvement in future. Moreover, in the follow-up work the effect of surface reconstruction and electron-phonon coupling on the negative ion conversion will be quantitatively investigated. The present study is much more limited, we hope this work will stimulate further theoretical and experimental studies on this topic.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financially supported by National Natural Science Foundation of China (Grant No. 11775103).References
- P. Phadke, J. M. Sturm, R. W. E. van der Kruijs and F. Bijkerk, Appl. Surf. Sci., 2020, 505, 144529 CrossRef CAS.
- M. Bercx, B. Partoens and D. Lamoen, Phys. Rev. B, 2019, 99, 085413 CrossRef CAS.
- C.-H. Li, C. Tusche, F. O. Schumann and J. Kirschner, Phys. Rev. Lett., 2007, 118, 136402 CrossRef.
- J. He, J. Yang, W. Zhao, J. Long, C. Lan and E. Liu, Appl. Surf. Sci., 2020, 15, 145990 CrossRef.
- A. Martín-Jiménez, J. M. Gallego, R. Miranda and R. Otero, Phys. Rev. Lett., 2019, 122, 176801 CrossRef.
- A. S. El-Said, R. A. Wilhelm, R. Heller, M. Sorokin, S. Facsko and F. Aumayr, Phys. Rev. Lett., 2016, 117, 126101 CrossRef.
- X. Mei, J. Fu, X. Li, W. Sun, C. Dong and Y. Wang, Appl. Surf. Sci., 2012, 258, 8061 CrossRef CAS.
- R. M. Papaléo, M. R. Silva, R. Leal, P. L. Grande, M. Roth, B. Schattat and G. Schiwietz, Phys. Rev. Lett., 2008, 101, 167601 CrossRef.
- F. Krok, J. Kolodziej, B. Such, P. Piatkowski and M. Szymonski, Appl. Surf. Sci., 2003, 210, 112 CrossRef CAS.
- H. Winter, Phys. Rep., 2002, 367, 387 CrossRef CAS.
- A. G. Borisov and V. A. Esaulov, J. Phys.: Condens. Matter, 2000, 12, R177 CrossRef CAS.
- C. W. Walter, N. D. Gibson, D. J. Matyas, C. Crocker, K. A. Dungan, B. R. Matola and J. Rohlén, Phys. Rev. Lett., 2014, 113, 063001 CrossRef CAS.
- R. Tang, R. Si, Z. Fei, X. Fu, Y. Lu, T. Brage, H. Liu, C. Chen and C. Ning, Phys. Rev. Lett., 2019, 123, 203002 CrossRef CAS.
- G. Cerchiari, P. Yzombard and A. Kellerbauer, Phys. Rev. Lett., 2019, 123, 103201 CrossRef CAS.
- H. Tsuji, P. Somman, T. Kitamura, M. Hattori, H. Sato, Y. Gotoh and J. Ishikawa, Surf. Coat. Technol., 2007, 201, 8123–8126 CrossRef CAS.
- L. Gao, W. Gan, G. Cao, X. Zhang, T. Qiang and J. Li, Appl. Surf. Sci., 2017, 425, 889 CrossRef CAS.
- J. Shaw, D. Monismith, Y. Zhang, D. Doerr and H. S. Chakraborty, Phys. Rev. A, 2018, 98, 052705 CrossRef CAS.
- G. Cartry, D. Kogut, K. Achkasov, J. Layet, T. Farley, A. Gicquel, J. Achard, O. Brinza, T. Bieber, H. Khemliche, P. Roncin and A. Simonin, New J. Phys., 2017, 19, 025010 CrossRef.
- T. J. Millar, C. Walsh and T. A. Field, Chem. Rev., 2017, 117, 1765 CrossRef CAS.
- S. A. Deutsche, A. G. Borisov and V. Sidis, Phys. Rev. A, 1999, 59, 4446 CrossRef.
- F. W. Meyer, E. Galutschek and M. Hotchkis, AIP Conf. Proc., 2009, 1099, 308 CrossRef CAS.
- J. J. C. Geerlings and J. Los, Phys. Rep., 1990, 190, 133 CrossRef.
- A. G. Borisov, D. Teillet-Billy, J. P. Gauyacq, H. Winter and G. Dierkes, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17166 CrossRef CAS.
- D. Goebl, D. Valdés, E. Abad, R. C. Monreal, D. Primetzhofer and P. Bauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165428 CrossRef.
- L. Gao, Y. Zhu, Y. Shi, P. Liu, Y. Xiao, G. Li, Y. Liu, V. A. Esaulov, X. Chen, L. Chen and Y. Guo, Phys. Rev. A, 2017, 96, 052705 CrossRef.
- C. Auth, A. G. Borisov and H. Winter, Phys. Rev. Lett., 1995, 75, 2292 CrossRef CAS.
- C. Auth, A. Mertens, H. Winter, A. G. Borisov and V. Sidis, Phys. Rev. A, 1998, 57, 351 CrossRef CAS.
- A. G. Borisov and V. Sidis, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 10628 CrossRef CAS.
- H. Zhou, L. Chen, D. Feng, Y. Guo, M. Ji, G. Wang, W. Zhou, Y. Li, L. Zhao and X. Chen, Phys. Rev. A, 2012, 85, 014901 CrossRef.
- H. Zhou, W. Zhou, M. Zhang, L. Zhou, Y. Ma, G. Wang, Y. Wu, B. Li and X. Chen, Phys. Rev. A, 2016, 93, 062708 CrossRef.
- W. Zhou, H. Zhou, M. Zhang, L. Zhou, Y. Li, B. Li and X. Chen, Phys. Rev. A, 2016, 94, 052708 CrossRef.
- A. G. Borisov and J. P. Gauyacq, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 4265 CrossRef CAS.
- P. Roncin, J. Villette, J. P. Atanas and H. Khemliche, Phys. Rev. Lett., 1999, 83, 864 CrossRef CAS.
- H. Winter, A. Mertens, S. Lederer, C. Auth, F. Aumayr and H. P. Winter, Nucl. Instrum. Methods Phys. Res., Sect. B, 2003, 212, 45 CrossRef CAS.
- G. K. Wertheim, J. E. Rowe, D. N. E. Buchanan and P. H. Citrin, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 13675 CrossRef CAS.
- A. G. Borisov, J. P. Gauyacq, V. Sidis and A. K. Kazansky, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 045407 CrossRef.
- N. F. Mott and M. J. Littleton, Trans. Faraday Soc., 1938, 34, 485 RSC.
- P. M. Echenique and A. Howie, Ultramicroscopy, 1985, 16, 269 CrossRef CAS.
- N. R. Arista, Phys. Rev. A, 1994, 49, 1885 CrossRef CAS.
- A. G. Borisov, V. Sidis, P. Roncin, A. Momeni, H. Khemliche, A. Mertens and H. Winter, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 115403 CrossRef.
- E. D. Palik and W. R. Hunter, Handbook of Optical Constants of Solids, Academic press, New York, 1985 Search PubMed.
- P. Roncin, A. G. Borisov, H. Khemliche, A. Momeni, A. Mertens and H. Winter, Phys. Rev. Lett., 2002, 89, 043201 CrossRef CAS.
- H. Winter, A. Mertens, C. Auth and A. Borisov, Phys. Rev. A, 1996, 54, 2486 CrossRef CAS.
- H. Winter, C. Auth and A. G. Borisov, Nucl. Instrum. Methods Phys. Res., Sect. B, 1996, 115, 133 CrossRef CAS.
- J. M. Rost, Phys. Rev. Lett., 1999, 82, 1652 CrossRef CAS.
- Y. Wang, P. Nordlander and N. H. Tolk, J. Chem. Phys., 1988, 89, 4163 CrossRef CAS.
- R. E. Olson, F. T. Smith and E. Bauer, Appl. Opt., 1971, 10, 1848 CrossRef CAS.
- A. Mertens, S. Lederer, K. Maass, H. Winter, J. Stöckl, H. P. Winter and F. Aumayr, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 132410 CrossRef.
- M. Rohlfing, N. Wang, P. Krüger and J. Pollmann, Phys. Rev. Lett., 2003, 91, 256802 CrossRef.
- F. J. Bonetto, E. A. García, C. Gonzalez and E. C. Goldberg, J. Phys. Chem. C, 2014, 118, 8359 CrossRef CAS.
- A. G. Borisov, D. Teillet-Billy, J. P. Gauyacq, J. A. M. C. Sliva, A. Mertens, C. Auth and H. Winter, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8218 CrossRef CAS.
- W. N. Shelton, E. S. Leherissey and D. H. Madison, Phys. Rev. A, 1971, 3, 242 CrossRef.
- Z. Zong, H. Zhou, B. Jin, X. Zhang, G. Wang, L. Zhou and X. Chen, J. Phys. Chem. C, 2020, 124, 18054 CrossRef CAS.
- A. G. Borisov, D. Teillet-Billy and J. P. Gauyacq, Phys. Rev. Lett., 1992, 68, 2842 CrossRef CAS.
- T. Hecht, H. Winter, A. G. Borisov, J. P. Gauyacq and A. K. Kazansky, Phys. Rev. Lett., 2000, 84, 2517 CrossRef CAS.
- G. Cartry, L. Schiesko, C. Hopf, A. Ahmad, M. Carrère, J. M. Layet, P. Kumar and R. Engeln, Phys. Plasmas, 2012, 19, 063503 CrossRef.
| This journal is © The Royal Society of Chemistry 2021 |