Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Endohedral metallofullerene electrides of Ca12O12 with remarkable nonlinear optical response
Annum Ahsana,
Saima Khana,
Mazhar Amjad Gilani*b and
Khurshid Ayub *a
*a
aDepartment of Chemistry, COMSATS University Islamabad, Abbottabad Campus, Abbottabad, KPK 22060, Pakistan. E-mail: khurshid@cuiatd.edu.pk; Tel: +92-992-383591
bDepartment of Chemistry, COMSATS University Islamabad, Lahore Campus, Defence Road, Off-Raiwind Road, Lahore 54000, Pakistan. E-mail: mazhargilani@cuilahore.edu.pk
First published on 5th January 2021
Abstract
Herein, the structural, electronic, thermodynamic, linear and nonlinear optical properties of inorganic electrides, generated by alkali metal doping in group II–VI Ca12O12 fullerene, are studied. Endohedral doping of alkali metal leads to the formation of electrides whereas no such phenomenon is seen for exohedral doping. The electride nature of the endohedral fullerenes is confirmed through the analysis of frontier molecular orbitals. The results show that doping of alkali metal atoms leads to a reduction of the HOMO–LUMO gap and increase of the dipole moment, polarizability and hyperpolarizability of nanocages. Doping causes shifting of electrons from alkali metal atoms towards the Ca12O12 nanocage, which serve as excess electrons. Furthermore, the participation of excess electrons for enhancing the NLO response of these nanocages has been confirmed through the calculation of hyperpolarizability (βo). For exploring the controlling factors of hyperpolarizability, a two level model has been employed and the direct relation of hyperpolarizability with Δμ & fo, while an inverse relation of hyperpolarizability with ΔE has been studied. The electrides possess remarkable nonlinear response where the highest hyperpolarizability can reach up to 1.0 × 106 a.u. for endo-K@Ca12O12. This electride has the lowest ΔE of 0.63 eV among all compounds studied here. These intriguing results will be expedient for promoting the potential applications of the Ca12O12-based nano systems in high-performance nonlinear optical (NLO) materials.
1. Introduction
Since the discovery of (C60) fullerene in 1985 by Kroto et al.1 extensive research on fullerenes revealed that the spherical allotropes of carbon possess very interesting properties. Because of the revelation of their exclusive properties and diverse applications, research has been extensively dedicated to explore new nanoscale materials.2–5 Recently, a variety of different inorganic-based fullerene like nanomaterials have been reported.6,7 Among these inorganic nanocages, very appealing nanocages are the ones with general formula (XY)n, where n is the number of atoms. Among these nanocages, the most stable nanocages are the ones with n = 12.8–11 However, adequate explanation about this magic number i.e. 12 is not reported but one fact that favors the fascinating nature of these (XY)12 nanocages is that these cages satisfy the tetragonal rule.12 These (XY)12 nanoclusters are condensed octahedrons comprising of six squares and eight hexagons. Among these cages, B12N12 and Al12N12 are very well-known nanostructures.13,14 These nanocages besides various other applications are potential candidates for smart materials with large nonlinear optical response.Nonlinear optical materials have received great attention due to wide range of applications15 such as optical communication,16 optical computing,17,18 dynamic image processing and other laser devices.19 In this regard, different strategies for designing NLO materials have also been introduced. One of the strategies i.e. introduction of excess electron20–29 into different structures is employed recently, where a metal atom (preferably alkali metal atom) is doped into different structures (mostly the cages). The presence of excess electron enhances the nonlinear optical properties of the structures, especially their hyperpolarizability (βo). Excess electrons can be introduced in a system by doping with alkali metals,27,30 superalkalis,31,32 transition metals33,34 and alkaline earth metals.35,36 The literature reveals extensive examples where transition metals or alkali metal atoms are introduced in the system by exohedral,33,37–39 endohedral40,41 and substitutional doping.29,42–44 Two main classes of compounds which contain free excess electrons are electrides and alkalides. They possess significantly higher nonlinear optical responses.23,25,26,45 Remarkable NLO response of electrides and alkalides has led the researchers to design new electrides and alkalides with even better properties. For this purpose, alkali metal/superalkali doped complexes of 26 Adz, 36 Adz,46 calix4 pyrrole,24 cyclic polyamine,47 cyclacene,48 organic amines,49,50 fluorocarbon51 etc. are reported. Electrides are formed when ns1 electron of the alkali metal atom is pushed out by the complexant which then becomes an excess electron in the system. These well-known (X12Y12) nanocages are studied for their nonlinear optical response through doping of metals. For example, Huang et al. have shown through density functional calculations that alkali metal atoms doped Al12N12 nanocages show remarkable nonlinear optical response (because of introduction of excess electron) with the highest hyperpolarizability of 8.89 × 105 a.u. for Li@r6–Al12N12.13 Exohedral as well as endohedral doping of alkali metals on different organic52/inorganic fullerenes such as B12P12, Al12P12,38 B12N12 (ref. 53) and other related structures consistently reveal that alkali metals doping is an effective strategy for enhancing the nonlinear optical response through the introduction of excess electrons.
Density functional calculations for nonlinear optical properties of alkali metal substituted boron nitride (MB12N11/MB11N12) nanocages reveal that the substitutional doping is also an effective strategy where the first hyperpolarizability (βo) of B12N12 is increased up to 1.3 × 104 a.u. for KB12N11 nanocage (the βo was 0 a.u. for pure B12N12).29 Quite similar to alkali metal doping, superalkali doping also causes significant enhancement in the first hyperpolarizability.54,55 Computational results reveal that Li3O@Al12N12 contains diffuse excess electrons with considerable first hyperpolarizability (βo) up to 1.86 × 107 a.u.11
Other than these clusters, metal oxide clusters of X12Y12 type i.e. Be12O12, Mg12O12, Ca12O12, Zn12O12 etc. are studied frequently as they show remarkable properties because of the larger ionic character of bonds in these metal-oxides. These metal oxide clusters can be used for catalysis,56 adsorption processes,57,58 gas sensors59 and nonlinear optical applications as well (where NLO properties are induced through doping). The studies involving nonlinear optical properties of such metal oxide clusters include doping of alkali metals, superalkali clusters and transition metals in Be12O12 and Mg12O12 nanoclusters. The interaction of alkali metals (Li, Na and K) with Be12O12 and Mg12O12 nanocages introduces the excess electron into them which results in the reduction of their HOMO–LUMO gaps and enhancement of their first hyperpolarizabilities from 0.091 and 0.081 a.u. to 9.4 × 103 and 2.3 × 104 a.u. for Be12O12 and Mg12O12 nanocages, respectively.60 Similarly, the adsorption of alkali metal oxides MnO (M = Li, Na and K; n = 2, 3 and 4) on Mg12O12 nanocages also shows reduction in HOMO–LUMO gap along with a significant increase in hyperpolarizability. In this case, the highest increase is seen in the case of superalkalis (M3O, where M = Li, Na and K) on Mg12O12 with the highest hyperpolarizability of 6.0 × 106 a.u. for K3O@Mg12O12.61 Moreover, substitutional doping of transition metals on Mg12O12 nanocages was studied where doping of transition metals significantly increases the hyperpolarizability of these nanocages and the highest hyperpolarizability of 4.7 × 104 a.u. is observed for Sc@Mg12O12.62 In a similar way, NLO properties of superalkalis (Li3O, Na3O and K3O) doped Zn12O12 clusters are studied.63 These superalkalis doped nanocages also possess remarkably high first hyperpolarizability (βo) values up to 3.9 × 105 a.u. for K3O@Zn12O12.
Among Be12O12, Mg12O12 and Ca12O12 nanoclusters, Mg12O12 has been studied extensively for its physical and chemical properties as compared to Be12O12 and Ca12O12. The interest in such a nanocage was developed due to ionic character of Mg–O bond in Mg12O12 nanocluster. The ionic character provides this cluster remarkable properties and invokes the need for its further investigation. Other than Mg12O12, Ca12O12 nanocage with the larger cavity size and larger ionic radius12 (possessing the appealing properties) is more interesting candidate for further studies especially for its nonlinear optical properties. Ca12O12 is also expected to show NLO response when doped with metals. In this report, we are dedicated to study the doping of Ca12O12 with alkali metals both exohedrally and endohedrally. The effect of doping on different sites of this nanocage on NLO properties is investigated in detail.
2. Computational methodology
Geometry optimization of M@Ca12O12 (M = Li, Na and K) nanoclusters is performed at ωB97X-D/6-31G(d,p) level of theory. ωB97X-D is a reliable method for the geometry optimization of systems containing alkali metals and systems with non-covalent interactions.64–67 Because of the presence of both these features in our system, this functional is selected in combination with 6-31G(d,p) basis set. ωB97X-D is a long range and dispersion corrected method64,66 which is well known for the prediction of non-covalent interactions. For optimization, a number of possible orientations for alkali metals on calcium oxide nanocages are considered. Then, frequency analysis is performed for all these structures at the same level of theory to confirm that the optimized structures correspond to real local minima (absence of imaginary frequencies). The stabilities of these alkali metals doped calcium oxide nanocages are evaluated by the calculation of interaction energies at the same level of theory through the formula i.e.| Eint = [E(M@Ca12O12)] − [E(M) + E(Ca12O12)] (where, M = Li, Na and K) | (1) |
For the calculation of first hyperpolarizability (βo), the crucial selection of a functional is required. Range separation is very important for accurate calculations of hyperpolarizabilities. Earlier studies69,70 have reported that for better estimates of nonlinear optical properties, a full range-separated functional is preferable. ωB97X-D is reliable in this regard as well.
The mean polarizability (αo) and hyperpolarizability (βo) are defined as follows:
| αo = 1/3(αxx + αyy + αzz) | (2) |
| βo = [βx2 + βy2 + βz2]1/2 | (3) |
The time-dependent density functional theory (TD-DFT) calculations are performed at the TD-ωB97X-D/6-31G(d,p) level to get the crucial excitation energies (ΔE) and oscillator strength (fo). All calculations are carried out by using the Gaussian 09 program package.71 Molecular structures and orbitals are generated with the Gauss View program.
3. Results and discussions
3.1. Geometrical characteristics
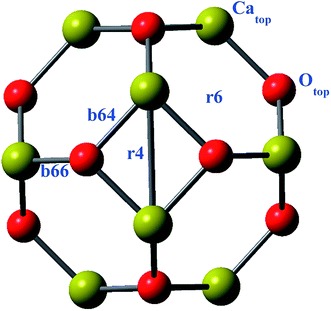
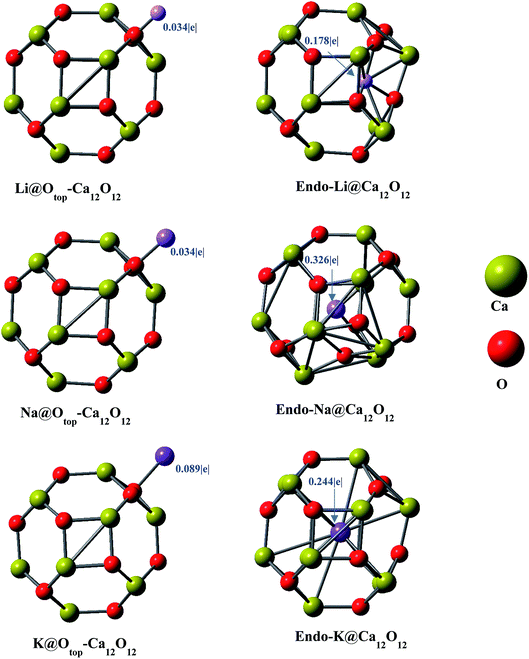
Geometries of the alkali metals (Li, Na and K) doped (exohedrally and endohedrally) Ca12O12 nanocages are studied at ωB97X-D/6-31G(d,p) level of theory. The nanocage consists of six hexagonal rings and four tetrahedral rings. For doping alkali metals exohedrally, six different sites are selected namely, b64, b66, r6, r4, Catop and Otop (Fig. 1). The site “b” represents the cases where alkali metal resides on a bond whereas “r” represents the cases where alkali metal is located on a ring. Specifically, b66 represents the case where alkali metal is doped on Ca–O bond shared between two six membered rings of the cage while b64 represents the case where alkali metal is present on Ca–O bond shared between a six membered ring and a four membered ring of the cage. Similarly, r4 and r6 represent the cases where alkali metal is placed at the center of four and six membered ring of the cage, respectively. However, Catop and Otop represent the cases where alkali metal resides on the top of Ca and O atom of the cage, respectively. For endohedral doping, alkali metals are placed inside the cage.The Li doped (at different positions) nanocages are optimized in C1 symmetry. For different input geometries of lithium atom on cage (b66, b64, r4, r6, Catop and Otop), the optimized geometries are Otop except for r6 input where the optimized geometry matches with the input geometry (Fig. 2). This is because of oxygen's electronegative nature for which the electropositive metal is driven to lie on top of it. However, when doped at the center of six membered ring exohedrally (r6 position), Li moves inward towards inside of the cage because of the size of hexagon larger enough to allow the smaller sized metal (Li) to move in, and hence optimized geometry contains Li inside the cage (not at the center of cage but at one side inside the cage) (Fig. 2). Moreover, upon endohedral doping Li moves to one side inside the cage because of its smaller size not fitting center of the cavity. This geometry is similar to the optimized geometry obtained as a result of doping Li at r6 position.
Similarly, the same positions for optimization are selected for Na with respect of the Ca12O12 nanocage. Na optimizes at Otop (because of its higher electronegativity) for all inputs including r6 site (unlike Li) which may be attributed to its larger size. The larger size of sodium does not allow it to cross the six membered ring. Moreover, endohedrally doped Na optimizes exactly at the center of the cage (with some distortion of the cage because of its larger size) because of its size fitting the cavity (Fig. 2). In the similar way, the same positions are selected for K and the optimized geometries show that the results are similar to that of the sodium doping. Exohedrally doped K optimizes at oxygen top finally and endohedrally doped K optimizes exactly at the center of the cage because of its size fitting the cavity (with some distortion of the cage as well) (Fig. 2). For all alkali metal atoms, only two structures could be identified; endohedral doped alkali metal in Ca12O12 and Otop Ca12O12.
Concerning the thermodynamic stability of alkali metals doped Ca12O12 complexes, interaction energies are calculated by using formula given as eqn (1). All the optimized geometries (both with exohedrally doped and endohedrally doped alkali metals) show negative values of interaction energies which reveal the stability of these complexes. The interaction energy of Li@Otop–Ca12O12 is −68.88 kcal mol−1 while for endo-Li@Ca12O12 (optimized geometry with Li lying endohedrally), the interaction energy is −77.47 kcal mol−1. The interaction energy for endohedrally doped Li complex is higher than that of Li@Otop–Ca12O12. For Na doped complexes, the interaction energies for Na@Otop–Ca12O12 and endo-Na@Ca12O12 are −52.78 kcal mol−1 and −59.81 kcal mol−1, respectively. In this case, the higher value of interaction energy is also for endohedral doping which reflects its higher stability compared to the exohedral doping. Moreover, the interaction energies are higher for lithium complexes than those of sodium complexes which may be attributed to higher charge density in the former than the latter. For K doped complexes, the interaction energies are −45.31 kcal mol−1 and −47.87 kcal mol−1 for K@Otop–Ca12O12 and endo-K@C12O12, respectively. Quite similar to the lithium and sodium complexes, the higher value of interaction energy is seen for endohedral doping of K. Overall, the interaction energies for Li@Ca12O12 are higher as compared to the interaction energies calculated for Na@Ca12O12. While the interaction energies for Na@Ca12O12 are higher than interaction energies calculated for K@Ca12O12 complexes. This shows the better interaction of smaller sized metal with the cage as compared to the larger sized metal atoms. The interaction becomes weaker with the increase in size of metal atom. This is consistent with various reports in the literature where higher interaction energies are observed with smaller alkali metals.60
For Na doped at different positions, dipole moments for Na@Otop–Ca12O12 and endo-Na@Ca12O12 are 4.77 D and 8.17 D, respectively. The larger charge transfer from internally lying Na to the cage might be the reason for this larger dipole moment for endohedrally lying Na. For K doped at different positions, the dipole moments for K@Otop–Ca12O12 and endo-K@Ca12O12 are 3.45 D and 10.94 D, respectively. The higher value (10.94 D) is because of the larger interaction distance between the charges in this case, as compared to doping at other sites. In this case, the reason might be the greater charge transfer from K to the cage as compared to K doped at other sites. For all these geometries, the direction of dipole moment is away from the alkali metal atoms (towards the cage) indicating that the charge is transferred from the electropositive metal to the electronegative oxygen atoms of the nanocage.
Overall, the dipole moments calculated for exohedrally doped metal complexes show that the values of μo are higher for Li@Ca12O12 complexes as compared to the Na@Ca12O12 which in turn are higher than the K@Ca12O12 complexes. For endohedral doping, the larger metals show larger values i.e. 8.17 D and 10.94 D for dipole moment (for Na and K, respectively) which is due to the greater transfer of charge as compared to the charge transfer in case of Li doped endohedrally. This is because of the large volume size of the Ca12O12 encapsulating the larger ions in a better way resulting into more charge transfer as compared to the cases where there are the smaller ions.
3.2. Electronic properties
The electronic properties i.e. NBO charges and HOMO–LUMO gaps are studied. The results of the NBO analyses (Table 1) show positive charges on alkali metals with negative charges on oxygen atoms. An increase in magnitude of negative charge on O in doped nanocages as compared to the bare nanocage is observed, which indicates that the charge has been transferred from alkali metal toward the cage. The cases, where Li lies outside the nanocage (Otop position, Li@Otop–Ca12O12), the NBO charge of 0.034|e| on Li is observed. However, the NBO charge on Li is 0.178|e| in endo-Li@Ca12O12. The higher value of positive charge on Li in endo-Li@Ca12O12 is because of its interaction with larger number of oxygen atoms. In endo-Li@Ca12O12, Li is surrounded by three oxygen atoms (Fig. 2), whereas Li interacts with single oxygen in Li@Otop–Ca12O12. The increase in number of interacting oxygen atoms increases the charge transfer from metal toward atoms of the cage.| M@Ca12O12 | Sym. | QM+ | Eint | μo | VIP | EHOMO | ELUMO | H–L gap |
|---|---|---|---|---|---|---|---|---|
| endo-Li@Ca12O12 | C1 | 0.178 | −77.47 | 4.47 | 3.09 | −3.09 | 0.08 | 3.01 |
| Li@Otop–Ca12O12 | C1 | 0.034 | −68.88 | 5.43 | 3.94 | −3.94 | 0.17 | 3.77 |
| endo-Na@Ca12O12 | C1 | 0.326 | −59.81 | 8.17 | 3.24 | −3.24 | 0.03 | 3.21 |
| Na@Otop–Ca12O12 | C1 | 0.034 | −52.77 | 4.77 | 3.92 | −3.92 | 0.18 | 3.74 |
| endo-K@Ca12O12 | C1 | 0.244 | −47.87 | 10.94 | 2.63 | −2.63 | 0.05 | 2.58 |
| K@Otop–Ca12O12 | C1 | 0.089 | −45.31 | 3.45 | 3.57 | −3.57 | 0.16 | 3.41 |
In case of Na doped Ca12O12 nanocages, the NBO charge of 0.034|e| is observed for Na@Otop–Ca12O12. However, the NBO charge is 0.326|e| in endo-Na@Ca12O12. The reasons for higher charge on Na in endo-Na@Ca12O12 are very similar to those for endo-Li@Ca12O12. However, the charge on Na in endo-Na@Ca12O12 is higher (than that of lithium in endo-Li@Ca12O12) because it is surrounded by larger number of atoms, as compared to Li which is surrounded by three atoms in endo-Li@Ca12O12. The NBO analysis of the K doped Ca12O12 nanocages shows the NBO charge of 0.089|e| on K in K@Otop–Ca12O12. The NBO charge of K in endo-K@Ca12O12 is 0.244|e|. This is because of the fact that K is surrounded by large number of electronegative oxygen atoms which enhances the transfer of charge. Comparing endo-M@Ca12O12 nanocages, the charge on Na (0.326|e|) is larger compared to Li (0.178|e|) and K (0.244|e|). This may be due to slight distortion of cage in the presence of Na. Distortion occurs in such a way that it causes some of the atoms of the cage to come closer to Na, thereby enhancing the charge transfer. Such a distortion is not observed in case of K because of its large size which hardly fits in the cavity. The potassium atom lies at the center of the cage (almost equidistant from all the surrounding atoms). On the other hand, Li in endo-Li@Ca12O12 does not stay at the center of the cage rather it is shifted to one side (inside the cage) without causing any distortion of the cage.
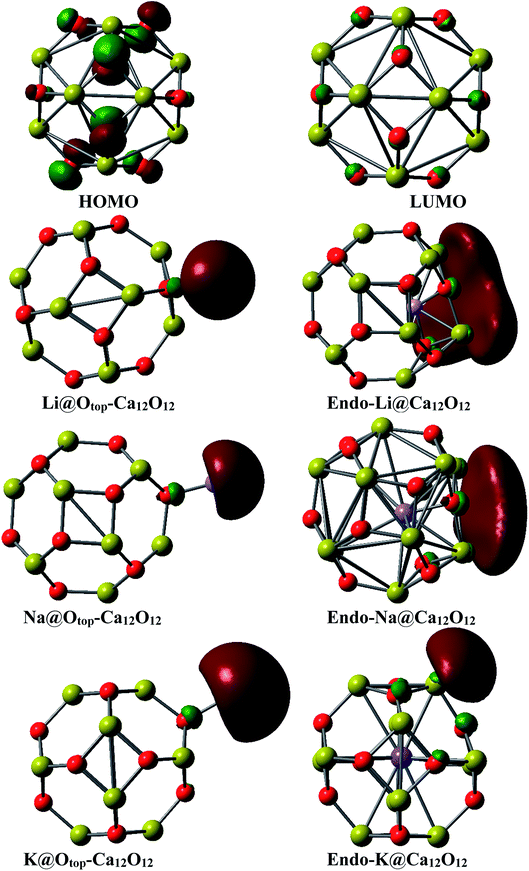
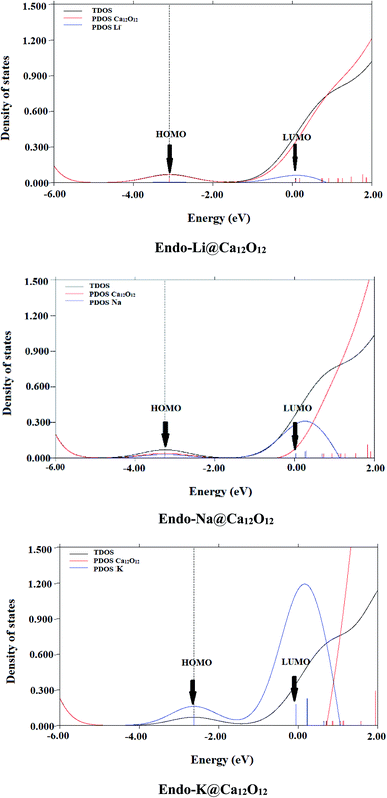
The pictorial representation of HOMO and LUMO orbitals is given in Fig. 3. The frontier molecular orbital analysis for the pure cage depicts that the HOMO is concentrated on O atoms of the cage. For the doped nanocages, the HOMO–LUMO diagrams depict the distribution of the densities is changed. In case of exohedral doping, HOMO lies on the dopant i.e. alkali metal atom. The position of HOMO reveals these materials are excess electron compounds. In case of endohedral doping, HOMO lies outside the cage. Careful analysis of the distribution of densities in the endohedral complexes reveals that these are electrides where densities of HOMO are present in empty spaces. These excess electrons don't belong to any atom rather they are present in empty spaces. The behavior of these endohedral complexes is quite contrary to the endohedral complexes based on group III–V fullerenes which we had reported previously. In endohedral complexes of alkali metals in B12N12, B12P12, Al12N12 and Al12P12, no such electride behavior was seen.
There is a slight decrease in the HOMO–LUMO gap as well (Table 1). The reason for the decrease in the EH–L gap is the increase in the energies of HOMOs and decrease in the energies of LUMOs after doping. The energies of HOMOs are increased due to the presence of excess electrons. The bare nanocage shows the H–L gap of 3.85 eV with EHOMO = −6.77 eV and ELUMO = 2.93 eV. HOMO–LUMO gap analysis reveals that the cases where metal lies endohedrally (endo-Li@Ca12O12, endo-Na@Ca12O12 and endo-K@Ca12O12), the gaps are lower than their respective M@exo-Ca12O12 cases. For example, the H–L gap of endo-Li@Ca12O12 (3.01 eV) is lower than Li@exo-Ca12O12 (3.77 eV), the H–L gap of endo-Na@Ca12O12 (3.21 eV) is lower than Na@exo-Ca12O12 (3.74 eV) and the H–L gap of endo-K@Ca12O12 (2.58 eV) is lower than K@exo-@Ca12O12 (3.41 eV). The lower HOMO–LUMO gaps for endohedral complexes are due to the electride characteristic of endohedral complexes. Such electrides are well known for low HOMO–LUMO gaps. Although the HOMO–LUMO gaps for all these geometries are lower but yet, these gaps are moderately high to impart enough electronic stability.
Vertical ionization potential (VIP) of these excess electron compounds is comparatively higher than the other excess electron compounds in literature which shows the electronic stability in these NLO compounds. However, VIP in all these compounds also depends upon the position of doping. For endohedrally doped metal complexes, VIP is lower as compared to the exohedrally doped metal complexes.
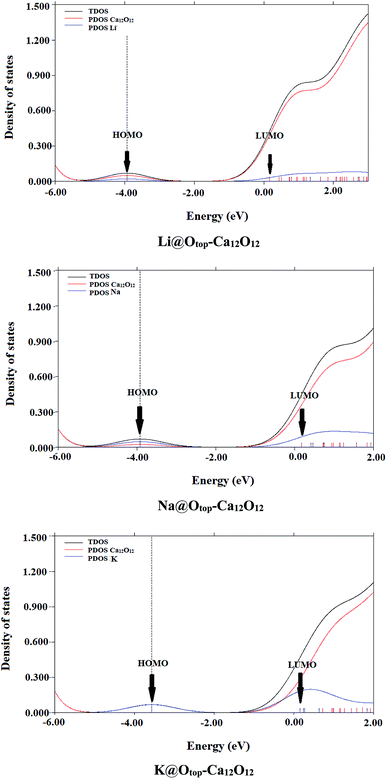
The comparison of spectrum of bare nanocage and spectra of doped nanocages clearly show the reduction in EH–L gap of doped cages compared to the bare nanocage which is attributed to excess electrons generated by the alkali metals. Doping alkali metals on Ca12O12 nanocage creates new energy levels, as a result of the transfer of excess electrons from alkali metals to the nanocage. The newly generated HOMOs have higher energy compared to the energies of HOMOs of pure nanocage.
| M@Ca12O12 | αo | βo | λmax | fo | ΔE | Δμ | Dominated transitions |
|---|---|---|---|---|---|---|---|
| endo-Li@Ca12O12 | 1373.72 | 1.5 × 105 | 2037 | 0.2290 | 0.6086 | 0.02 | H → L |
| Li@Otop–Ca12O12 | 582.46 | 2.4 × 104 | 689 | 0.2243 | 1.7987 | 1.46 | H → L |
| endo-Na@Ca12O12 | 622.85 | 3.5 × 104 | 1048 | 0.2203 | 1.1827 | 0.02 | H → L+1 |
| Na@Otop–Ca12O12 | 662.02 | 1.6 × 104 | 755 | 0.3407 | 1.6402 | 3.34 | H → L |
| endo-K@Ca12O12 | 1427.86 | 1.0 × 106 | 1752 | 0.2566 | 0.7074 | 0.97 | H → L+2 |
| K@Otop–Ca12O12 | 1061.59 | 1.2 × 104 | 1064 | 0.3526 | 1.1643 | 1.39 | H → L |
3.3. Nonlinear optical properties
It is reported previously in the literature that NLO response of a system can be enhanced by introducing the excess electrons into it. The excess electrons in the system result in increasing the energy of HOMO which in turn reduce the EH–L and increase the first hyperpolarizability (βo) value of the system. In these metal doped Ca12O12 nanocages, the presence of excess electron (which has been confirmed through the charge analysis and HOMO analysis) awards large NLO response to the system. First hyperpolarizability (βo) is a decisive factor for NLO response of any system. In this regard, polarizability (αo) and hyperpolarizability (βo) are calculated by using eqn (2) and (3) and are given in Table 2.Isolated Ca12O12 nanocage is centrosymmetric, therefore first hyperpolarizability (βo) and dipole moment (μo) of pure nanocage are zero. The doping of alkali metals brings significant enhancement of the dipole moment (μo) and first hyperpolarizability (βo) for the Ca12O12 nanocage. This is due to the distortion of symmetry of the nanocage. The calculated values of polarizability show an increase with the increase in size of doped alkali metal atom. The polarizability of Li@Otop–Ca12O12 complex is 582 a.u. The polarizability of Na@Otop–Ca12O12 is 662 a.u. which is higher than that of Li@Otop–Ca12O12. While the polarizability of K@Otop–Ca12O12 complex (1062 a.u.) is higher than that of Na@Otop–Ca12O12. The results of polarizability show clear dependence on size of alkali metal atom. By the increase in size of alkali metal atom, its ionization energy decreases. Hence, the donation of electron becomes easier.13 The monotonic increase in polarizability seen for exo-complexes is not observed for endohedral complexes. For endohedral complexes, the polarizability of endo-Na@Ca12O12 is lower than those of endo-K@Ca12O12 and endo-Li@Ca12O12.
This exception is also observed for hyperpolarizability where the hyperpolarizability of endo-Na@Ca12O12 (3.5 × 104 a.u.) is lower than that of endo-Li@Ca12O12 (1.5 × 105 a.u.) and endo-K@Ca12O12 (1.0 × 106 a.u.). Overall, for these M@Ca12O12 complexes, the hyperpolarizability of most of the geometries ranges up to four powers of magnitude (104). For exohedral doped systems, the hyperpolarizability shows a monotonic decrease where the hyperpolarizability of Li@Otop–Ca12O12 is the highest in the series (2.4 × 104 a.u.) whereas K@Otop–Ca12O12 has the lowest hyperpolarizability (1.2 × 104 a.u.). Such a decreasing trend for βo can be attributed to the geometric distance between M and oxygen atom of the ring, rather than the ionization potential of alkali atom M. The vertical distance (between metal and atoms of ring) can dominate the trend of the βo values, which is responsible for the decrease of βo value in M@OtopCa12O12 (M = Li, Na, and K) series with increasing the alkali atomic number.13
Observing the hyperpolarizability for each of these series i.e. Li@Ca12O12, Na@Ca12O12 and K@Ca12O12 nanocages, it is evaluated that for Li@Ca12O12 series, the highest value of hyperpolarizability is calculated to be for the geometry with Li lying endohedrally i.e. 1.5 × 105 a.u. while the other geometries with Li lying exohedrally show the hyperpolarizability of 2.4 × 104 a.u. The same trend is seen for Na and K doped systems (endohedral complexes show higher hyperpolarizability than the exohedral complexes).
These results can be justified based on the results of VIP. The geometries with lower VIP have higher hyperpolarizability and vice versa. For example, the VIP of endo-Li@Ca12O12 (3.09 eV) is lower than Li@exo-@Ca12O12 (3.94 eV) while the hyperpolarizability of endo-Li@Ca12O12 (1.5 × 105 a.u.) is higher than Li@exo-@Ca12O12 (2.4 × 104 a.u.). Similarly, the VIP of endo-Na@Ca12O12 (3.24 eV) is lower than Na@exo-@Ca12O12 (3.92 eV) and that of endo-K@Ca12O12 (2.63 eV) is lower than K@exo-@Ca12O12 (3.57 eV). Both of these Na and K doped Ca12O12 complexes show the same trend for hyperpolarizability as that shown by Li@Ca12O12 i.e. hyperpolarizability of endo-Na@Ca12O12 (3.5 × 104 a.u.) is higher than Na@exo-@Ca12O12 (1.6 × 104 a.u.) and that of endo-K@Ca12O12 (1.0 × 106 a.u.) is higher than K@exo-@Ca12O12 (1.6 × 104 a.u.). Moreover, the HOMO–LUMO gaps also justify the trend. The endo geometries with lower H–L gaps also show the higher hyperpolarizabilities when compared to their respective exo-geometries. The hyperpolarizability values of these clusters are also compared with the hyperpolarizability response of some well known NLO standards such as urea, p-nitroaniline and KDP. The hyperpolarizability values of urea, p-nitroaniline and KDP are 31.18, 76.76 and 376.75 a.u., respectively which are much lower than the hyperpolarizability values calculated for our systems where the values reach up to 1 × 106 a.u.
3.4. Controlling factors of hyperpolarizability
Two level model is employed to understand the controlling factors of hyperpolarizability. According to two level model| βo ≈ Δμ × fo/ΔE3 |
The transition energies of the studied compounds are very small ranging from 0.63–1.29 eV. The hyperpolarizability values calculated for these compounds show an inverse relation with these ΔE values. endo-Li@Ca12O12 and endo-K@Ca12O12, show the hyperpolarizabilities of 1.5 × 105 a.u. and 1.0 × 106 a.u., respectively. These values are the largest of all the values (compared to the values calculated for all the other geometries of Li, Na and K@Ca12O12 nanocages). The transition energies for these two cases are the lowest of all i.e. 0.65 and 0.63 eV for endo-Li@Ca12O12 and endo-K@Ca12O12, respectively. This clearly reveals the inverse relation between βo and ΔE. Moreover, for each of these series i.e. Li@Ca12O12, Na@Ca12O12 and K@Ca12O12, it is observed that the highest hyperpolarizability is calculated for the geometry which contains metal endohedrally. While it is also observed that for each metal, the exohedral complex has high transition energy than the corresponding endohedral complex (Table 2).
The oscillator strength (fo) which possesses the direct relation with hyperpolarizability (βo) is consistent with βo for all complexes i.e. Li@Ca12O12, Na@Ca12O12 and K@Ca12O12. endo-Li@Ca12O12 shows the highest hyperpolarizability of 1.5 × 105 a.u. and this geometry has the highest value of fo i.e. 0.21 as compared to the corresponding exohedral Li@Otop–Ca12O12. The same is the case with Na and K doped Ca12O12 systems, both these systems possess highest hyperpolarizabilities of 3.5 × 104 and 1.0 × 106 a.u. for endohedrally lying Na and K geometries with the oscillator strengths of 0.18 and 0.22, respectively, higher than the fo of corresponding exohedral geometries. Overall, out of all the three types of systems, the highest oscillator strength is 0.22 for endo-K@Ca12O12 which also has the hyperpolarizability of 1.0 × 106 a.u. (highest of all the other configurations).
For Δμ (difference of dipole moment between the crucial excited state and the ground state), which possesses direct relation with βo, it is observed that out of all endo-M@Ca12O12 (where M = Li, Na and K), the highest value for change in dipole moment is shown by endo-K@Ca12O12. Along with highest Δμ, highest βo is also shown by the same complex (Table 2). In a similar way, for exo-M@Ca12O12 (where M = Li, Na and K), the highest Δμ is observed for exo-Na@Ca12O12 which also possesses the highest hyperpolarizability among these three, showing direct relation of Δμ with βo.
4. Conclusions
Because of the diverse applications of NLO compounds in different fields, excess electrons containing NLO compounds using Ca12O12 nanocages have been designed. These alkali metals doped nanocages are thermodynamically stable with interaction energies up to −77.47 kcal mol−1. Along with thermal stability, these doped systems show excellent nonlinear optical responses when doped with alkali metals because alkali metals donate their electrons to the nanocages and thus introduce excess electron into them. The presence of excess electron has been confirmed through the NBO analysis, HOMO analysis and partial density of states (PDOS) spectra. Furthermore, the participation of excess electron for enhancing the NLO response of these nanocages has been confirmed through the hyperpolarizability of these doped nanocages, which is a decisive factor for the NLO response of compounds. The electrides possess remarkable nonlinear response where the highest hyperpolarizability can reach up to 1.0 × 106 a.u. for endo-K@Ca12O12. This electride has the lowest ΔE of 0.63 eV among all compounds studied here. Moreover, the controlling factors of hyperpolarizability have been explored through TD-DFT calculations and two level model. The detailed study of these excess electron compounds marks them as capable of being used in NLO materials.Conflicts of interest
Authors declare no conflict of interest.References
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, C60: Buckminsterfullerene, Nature, 1985, 318, 162–163, DOI:10.1038/318162a0.
- N. V. Sibirev, V. G. Dubrovskii, A. V. Matetskiy, L. V. Bondarenko, D. V. Gruznev, A. V. Zotov and A. A. Saranin, Size distributions of fullerene surface clusters, Appl. Surf. Sci., 2014, 307, 46–51, DOI:10.1016/j.apsusc.2014.03.132.
- J. Beheshtian, A. A. Peyghan and Z. Bagheri, Functionalization of [60] fullerene with butadienes: A DFT study, Appl. Surf. Sci., 2012, 258, 8980–8984, DOI:10.1016/j.apsusc.2012.05.134.
- A. F. Jalbout, Endohedral metallo [80] fullerene interactions with small polar molecules, Comput. Mater. Sci., 2009, 44, 1065–1070, DOI:10.1016/j.commatsci.2008.07.038.
- J. H. Lee, B. S. Lee, F. T. K. Au, J. Zhang and Y. Zeng, Vibrational and dynamic analysis of C60 and C30 fullerenes using FEM, Comput. Mater. Sci., 2012, 56, 131–140, DOI:10.1016/j.commatsci.2012.01.019.
- Y. Li, G. Zhou, J. Li, B.-L. Gu and W. Duan, Alkali-Metal-Doped B80 as High-Capacity Hydrogen Storage Media, J. Phys. Chem. C, 2008, 112, 19268–19271, DOI:10.1021/jp807156g.
- M. Moradi, A. A. Peyghan and Z. Bagheri, Tuning the electronic properties of C30B15N15 fullerene via encapsulation of alkali and alkali earth metals, Synth. Met., 2013, 177, 94–99, DOI:10.1016/j.synthmet.2013.06.018.
- M. Kazemi and A. S. Rad, Sulfur mustard gas adsorption on ZnO fullerene-like nanocage: Quantum chemical calculations, Superlattices Microstruct., 2017, 106, 122–128, DOI:10.1016/j.spmi.2017.03.046.
- J. Beheshtian, Z. Bagheri, M. Kamfiroozi and A. Ahmadi, A comparative study on the B12N12, Al12N12, B12P12 and Al12P12 fullerene-like cages, J. Mol. Model., 2012, 18, 2653–2658, DOI:10.1007/s00894-011-1286-y.
- J. Kakemam and A. A. Peyghan, Electronic, energetic, and structural properties of C- and Si-doped Mg12O12 nano-cages, Comput. Mater. Sci., 2013, 79, 352–355, DOI:10.1016/j.commatsci.2013.06.036.
- W.-M. Sun, X.-H. Li, D. Wu, Y. Li, H.-M. He, Z.-R. Li, J.-H. Chen and C.-Y. Li, A theoretical study on superalkali-doped nanocages: unique inorganic electrides with high stability, deep-ultraviolet transparency, and a considerable nonlinear optical response, Dalton Trans., 2016, 45, 7500–7509, 10.1039/C6DT00342G.
- O. V. de Oliveira, J. M. Pires, A. C. Neto and J. Divino dos Santos, Computational studies of the Ca12O12, Ti12O12, Fe12O12 and Zn12O12 nanocage clusters, Chem. Phys. Lett., 2015, 634, 25–28, DOI:10.1016/j.cplett.2015.05.069.
- M. Niu, G. Yu, G. Yang, W. Chen, X. Zhao and X. Huang, Doping the Alkali Atom: An Effective Strategy to Improve the Electronic and Nonlinear Optical Properties of the Inorganic Al12N12 Nanocage, Inorg. Chem., 2014, 53, 349–358, DOI:10.1021/ic4022917.
- Maria, J. Iqbal and K. Ayub, Enhanced electronic and non-linear optical properties of alkali metal (Li, Na, K) doped boron nitride nano-cages, J. Alloys Compd., 2016, 687, 976–983, DOI:10.1016/j.jallcom.2016.06.121.
- D. F. Eaton, Nonlinear Optical Materials, Science, 1991, 253, 281–287, DOI:10.1126/science.253.5017.281.
- P. W. Smith, On the role of photonic switching in future communications systems, IEEE Circ. Dev. Mag., 1987, 3, 9–14, DOI:10.1109/MCD.1987.6323271.
- S. Muhammad and M. Nakano, Computational Strategies For Nonlinear Optical Properties Of Carbon Nano-Systems, in Nanosci. Comput. Chem., Apple Academic Press, 2013: pp. 309–332. DOI:10.1201/b16368-10.
- B. G. Kushner and J. A. Neff, Nonlinear Optical Materials & DoD Device Requirements, MRS Online Proc. Libr., 1987, 109, 3, DOI:10.1557/PROC-109-3.
- L. L. Beecroft and C. K. Ober, Nanocomposite Materials for Optical Applications, Chem. Mater., 1997, 9, 1302–1317, DOI:10.1021/cm960441a.
- G. Yu, X. Huang, S. Li and W. Chen, Theoretical insights and design of intriguing nonlinear optical species involving the excess electron, Int. J. Quantum Chem., 2015, 115, 671–679, DOI:10.1002/qua.24878.
- J.-J. Wang, Z.-J. Zhou, Y. Bai, H.-M. He, D. Wu, Y. Li, Z.-R. Li and H.-X. Zhang, A new strategy for simultaneously enhancing nonlinear optical response and electron stability in novel cup–saucer+–cage−shaped sandwich electride molecules with an excess electron protected inside the cage, Dalton Trans., 2015, 44, 4207–4214, 10.1039/C4DT03282A.
- M. Miyakawa, S. W. Kim, M. Hirano, Y. Kohama, H. Kawaji, T. Atake, H. Ikegami, K. Kono and H. Hosono, Superconductivity in an Inorganic Electride 12CaO·7Al2O3:e-, J. Am. Chem. Soc., 2007, 129, 7270–7271, DOI:10.1021/ja0724644.
- A. S. Ichimura, J. L. Dye, M. A. Camblor and L. A. Villaescusa, Toward Inorganic Electrides, J. Am. Chem. Soc., 2002, 124, 1170–1171, DOI:10.1021/ja016554z.
- W. Chen, Z.-R. Li, D. Wu, Y. Li, C.-C. Sun and F. L. Gu, The Structure and the Large Nonlinear Optical Properties of Li@Calix[4]pyrrole, J. Am. Chem. Soc., 2005, 127, 10977–10981, DOI:10.1021/ja050601w.
- W.-M. Sun, D. Wu, Y. Li and Z.-R. Li, Substituent Effects on the Structural Features and Nonlinear Optical Properties of the Organic Alkalide Li+(calix[4]pyrrole)Li−, ChemPhysChem, 2013, 14, 408–416, DOI:10.1002/cphc.201200805.
- B. Li, C. Xu, X. Xu, C. Zhu and F. L. Gu, Remarkable nonlinear optical response of excess electron compounds: theoretically designed alkali-doped aziridine M–(C2NH5)n, Phys. Chem. Chem. Phys., 2017, 19, 23951–23959, 10.1039/C7CP04764A.
- Maria, J. Iqbal, R. Ludwig and K. Ayub, Phosphides or nitrides for better NLO properties? A detailed comparative study of alkali metal doped nano-cages, Mater. Res. Bull., 2017, 92, 113–122, DOI:10.1016/j.materresbull.2017.03.065.
- K. Ayub, Are phosphide nano-cages better than nitride nano-cages? A kinetic, thermodynamic and non-linear optical properties study of alkali metal encapsulated X12Y 12 nano-cages, J. Mater. Chem. C, 2016, 4, 10919–10934, 10.1039/C6TC04456E.
- Maria, J. Iqbal and K. Ayub, Enhanced electronic and non-linear optical properties of alkali metal (Li, Na, K) doped boron nitride nano-cages, J. Alloys Compd., 2016, 687, 976–983, DOI:10.1016/j.jallcom.2016.06.121.
- X. Li and S. Li, Investigations of electronic and nonlinear optical properties of single alkali metal adsorbed graphene, graphyne and graphdiyne systems by first-principles calculations, J. Mater. Chem. C, 2019, 7, 1630–1640, 10.1039/C8TC05392H.
- F. Ullah, N. Kosar, K. Ayub, M. A. Gilani and T. Mahmood, Theoretical study on a boron phosphide nanocage doped with superalkalis: novel electrides having significant nonlinear optical response, New J. Chem., 2019, 43, 5727–5736, 10.1039/C9NJ00225A.
- H. Sajid, K. Ayub and T. Mahmood, Exceptionally high NLO response and deep ultraviolet transparency of superalkali doped macrocyclic oligofuran rings, New J. Chem., 2020, 44, 2609–2618, 10.1039/C9NJ05065E.
- Y. Arshad, S. Khan, M. A. Hashmi and K. Ayub, Transition metal doping: A new and effective approach for remarkably high nonlinear optical response in aluminum nitride nanocages, New J. Chem., 2018, 42, 6976–6989, 10.1039/c7nj04971d.
- M. A. Gilani, S. Tabassum, U. Gul, T. Mahmood, A. I. Alharthi, M. A. Alotaibi, M. Geesi, R. Sheikh and K. Ayub, Copper-doped Al12N12 nano-cages: potential candidates for nonlinear optical materials, Appl. Phys. A: Mater. Sci. Process., 2018, 124, 14, DOI:10.1007/s00339-017-1425-0.
- F. Ullah, N. Kosar, A. Ali, Maria, T. Mahmood and K. Ayub, Alkaline earth metal decorated phosphide nanoclusters for potential applications as high performance NLO materials; A first principle study, Phys. E, 2020, 118, 113906, DOI:10.1016/j.physe.2019.113906.
- N. Kosar, S. Gul, K. Ayub, A. Bahader, M. A. Gilani, M. Arshad and T. Mahmood, Significant nonlinear optical response of alkaline earth metals doped beryllium and magnesium oxide nanocages, Mater. Chem. Phys., 2020, 242, 122507, DOI:10.1016/j.matchemphys.2019.122507.
- E. Shakerzadeh, E. Tahmasebi and Z. Biglari, A quantum chemical study on the remarkable nonlinear optical and electronic characteristics of boron nitride nanoclusters by complexation via lithium atom, J. Mol. Liq., 2016, 221, 443–451, DOI:10.1016/j.molliq.2016.05.090.
- S. Munsif, Maria, S. Khan, A. Ali, M. A. Gilani, J. Iqbal, R. Ludwig and K. Ayub, Remarkable nonlinear optical response of alkali metal doped aluminum phosphide and boron phosphide nanoclusters, J. Mol. Liq., 2018, 271, 51–64, DOI:10.1016/j.molliq.2018.08.121.
- E. Shakerzadeh, M. Yousefizadeh and M. Bamdad, Electronic and nonlinear optical features of first row transition metals-decorated all-boron B40 fullerene: A promising route to remarkable electro-optical response, Inorg. Chem. Commun., 2020, 112, 107692, DOI:10.1016/j.inoche.2019.107692.
- E. Tahmasebi, E. Shakerzadeh and Z. Biglari, Theoretical assessment of the electro-optical features of the group III nitrides (B12N12, Al12N12 and Ga12N12) and group IV carbides (C24, Si12C12 and Ge12C12) nanoclusters encapsulated with alkali metals (Li, Na and K), Appl. Surf. Sci., 2016, 363, 197–208, DOI:10.1016/j.apsusc.2015.12.001.
- K. Ayub, Are phosphide nano-cages better than nitride nano-cages? A kinetic, thermodynamic and non-linear optical properties study of alkali metal encapsulated X12Y12 nano-cages, J. Mater. Chem. C, 2016, 4, 10919–10934, 10.1039/c6tc04456e.
- A. Shokuhi Rad and K. Ayub, Substitutional doping of zirconium-, molybdenum-, ruthenium-, and palladium: An effective method to improve nonlinear optical and electronic property of C20 fullerene, Comput. Theor. Chem., 2017, 1121, 68–75, DOI:10.1016/j.comptc.2017.10.015.
- A. S. Rad and K. Ayub, Nonlinear optical and electronic properties of Cr-, Ni-, and Ti- substituted C20 fullerenes: A quantum-chemical study, Mater. Res. Bull., 2018, 97, 399–404, DOI:10.1016/j.materresbull.2017.09.036.
- A. S. Rad and K. Ayub, Nonlinear optical, IR and orbital properties of Ni doped MgO nanoclusters: A DFT investigation, Comput. Theor. Chem., 2018, 1138, 39–47, DOI:10.1016/j.comptc.2018.06.003.
- W. Chen, Z. R. Li, D. Wu, R. Y. Li and C. C. Sun, Theoretical Investigation of the Large Nonlinear Optical Properties of (HCNS)n Clusters with Li Atom, J. Phys. Chem. B, 2005, 109, 601–608, DOI:10.1021/jp0480394.
- F. F. Wang, Z. R. Li, D. Wu, B. Q. Wang, Y. Li, Z. J. Li, W. Chen, G. T. Yu, F. L. Gu and Y. Aoki, Structures and Considerable Static First Hyperpolarizabilities: New Organic Alkalides (M+@n6adz)M‘ - (M, M‘ = Li, Na, K; n = 2, 3) with Cation Inside and Anion Outside of the Cage Complexants, J. Phys. Chem. B, 2008, 112, 1090–1094, DOI:10.1021/jp076790h.
- Z. J. Li, Z. R. Li, F. F. Wang, C. Luo, F. Ma, D. Wu, Q. Wang and X.-R. Huang, A Dependence on the Petal Number of the Static and Dynamic First hyperpolarizibility for Electride Molecules: Many-Petal-Shaped Li-Doped Cyclic Polyamines, J. Phys. Chem. A, 2009, 113, 2961–2966, DOI:10.1021/jp8109012.
- H. L. Xu, Z. R. Li, D. Wu, F. Ma, Z. J. Li and F. L. Gu, Lithiation and Li-Doped Effects of [5]Cyclacene on the Static First hyperpolarizibility, J. Phys. Chem. C, 2009, 113, 4984–4986, DOI:10.1021/jp806864w.
- Z. J. Zhou, H. Li, X. R. Huang, Z. J. Wu, F. Ma and Z. R. Li, The structure and large nonlinear optical properties of a novel octupolar electride Li@36Adz, Comput. Theor. Chem., 2013, 1023, 99–103, DOI:10.1016/j.comptc.2013.09.015.
- H. L. Xu, S. L. Sun, S. Muhammad and Z. M. Su, Three-propeller-blade-shaped electride: remarkable alkali-metal-doped effect on the first hyperpolarizibility, Theor. Chem. Acc., 2011, 128, 241–248, DOI:10.1007/s00214-010-0837-0.
- H. L. Xu, Z. R. Li, D. Wu, B. Q. Wang, Y. Li, F. L. Gu and Y. Aoki, Structures and Large NLO Responses of New Electrides: Li-Doped Fluorocarbon Chain, J. Am. Chem. Soc., 2007, 129, 2967–2970, DOI:10.1021/ja068038k.
- A. Shokuhi Rad and K. Ayub, Substitutional doping of zirconium, molybdenum, ruthenium, and palladium: An effective method to improve nonlinear optical and electronic property of C20 fullerene, Comput. Theor. Chem., 2017, 1121, 68–75, DOI:10.1016/j.comptc.2017.10.015.
- N. Hou, Y. Y. Wu and J. Y. Liu, Theoretical studies on structures and nonlinear optical properties of alkali doped electrides B12N12-M (M = Li, Na, K), Int. J. Quantum Chem., 2016, 116, 1296–1302, DOI:10.1002/qua.25177.
- W. M. Sun, L. T. Fan, Y. Li, J. Y. Liu, D. Wu and Z. R. Li, On the Potential Application of Superalkali Clusters in Designing Novel Alkalides with Large Nonlinear Optical Properties, Inorg. Chem., 2014, 53, 6170–6178, DOI:10.1021/ic500655s.
- J.-J. Wang, Z.-J. Zhou, Y. Bai, Z.-B. Liu, Y. Li, D. Wu, W. Chen, Z.-R. Li and C.-C. Sun, The interaction between superalkalis (M3O, M = Na, K) and a C20F20 cage forming superalkali electride salt molecules with excess electrons inside the C20F20 cage: dramatic superalkali effect on the nonlinear optical property, J. Mater. Chem., 2012, 22, 9652, 10.1039/c2jm15405f.
- B. Yoon, Charging Effects on Bonding and Catalyzed Oxidation of CO on Au8 Clusters on MgO, Science, 2005, 307, 403–407, DOI:10.1126/science.1104168.
- A. A. Peyghan and M. Noei, Electronic Response of Nano-sized Cages of ZnO and MgO to Presence of Nitric Oxide, Chin. J. Chem. Phys., 2013, 26, 231–236, DOI:10.1063/1674-0068/26/02/231-236.
- Y. Zhang, X. Zheng, S. Zhang, S. Huang, P. Wang and H. Tian, Bare and Ni decorated Al12N12 cage for hydrogen storage: A first-principles study, Int. J. Hydrogen Energy, 2012, 37, 12411–12419, DOI:10.1016/j.ijhydene.2012.06.056.
- M. Solimannejad, H. Jouypazadeh, S. Kamalinahad and M. Noormohammadbeigi, Adsorption of F-, Cl-, Li+ and Na+ on the exterior surface of Mg12O12 nanocage in the gas phase and water media: a DFT study, Phys. Chem. Res., 2016, 4, 591–596, DOI:10.22036/PCR.2016.16051.
- E. Shakerzdeh, E. Tahmasebi and H. R. Shamlouei, The influence of alkali metals (Li, Na and K) interaction with Be12O12 and Mg12O12 nanoclusters on their structural, electronic and nonlinear optical properties: A theoretical study, Synth. Met., 2015, 204, 17–24, DOI:10.1016/j.synthmet.2015.03.008.
- A. Mohammadi Hesari, H. R. Shamlouei and A. Raoof Toosi, Effects of the adsorption of alkali metal oxides on the electronic, optical, and thermodynamic properties of the Mg12O12 nanocage: a density functional theory study, J. Mol. Model., 2016, 22, 189, DOI:10.1007/s00894-016-3044-7.
- H. R. Shamlouei, A. Nouri, A. Mohammadi and A. D. Tehrani, Influence of transition metal atoms doping on structural, electronic and nonlinear optical properties of Mg12O12 nanoclusters: A DFT study, Phys. E, 2016, 77, 48–53, DOI:10.1016/j.physe.2015.10.035.
- N. Kosar, T. Mahmood, K. Ayub, S. Tabassum, M. Arshad and M. A. Gilani, Doping superalkali on Zn12O12 nanocage constitutes a superior approach to fabricate stable and high-performance nonlinear optical materials, Opt. Laser Technol., 2019, 120, 105753, DOI:10.1016/j.optlastec.2019.105753.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799, DOI:10.1002/jcc.20495.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104, DOI:10.1063/1.3382344.
- S. Grimme, Accurate description of van der Waals complexes by density functional theory including empirical corrections, J. Comput. Chem., 2004, 25, 1463–1473, DOI:10.1002/jcc.20078.
- J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615, 10.1039/b810189b.
- T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592, DOI:10.1002/jcc.22885.
- M. Maria, J. Iqbal and K. Ayub, Theoretical study of the non linear optical properties of alkali metal (Li, Na, K) doped aluminum nitride nanocages, RSC Adv., 2016, 6, 94228–94235, 10.1039/C6RA21797D.
- M. B. Oviedo, N. V. Ilawe and B. M. Wong, Polarizabilities of π-Conjugated Chains Revisited: Improved Results from Broken-Symmetry Range-Separated DFT and New CCSD(T) Benchmarks, J. Chem. Theory Comput., 2016, 12, 3593–3602, DOI:10.1021/acs.jctc.6b00360.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Blonio, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, J. B. Foresman, and D. J. Fox, Gaussian, Inc.Wallingford CT, 2016.
| This journal is © The Royal Society of Chemistry 2021 |