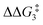Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
DFT calculations bring insight to internal alkyne-to-vinylidene transformations at rhodium PNP- and PONOP-pincer complexes†
Nasir A. Rajabi * and
Claire L. McMullin
* and
Claire L. McMullin
Department of Chemistry, University of Bath, Claverton Down, Bath, BA2 7AY, UK. E-mail: N.A.Rajabi@gmail.com
First published on 23rd March 2021
Abstract
Density Functional Theory (DFT) has been used to investigate the alkyne-to-vinylidene isomerisation reaction mediated by [Rh(PXNXP)]+ complexes (X = CH2: 2,6-bis(di-tert-butylphosphinomethyl)pyridine (PNP) and X = O: 2,6-bis(di-tert-butylphosphinito)pyridine (PONOP)) for terminal alkynes HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR, where R = tBu and Ar′ (3,5-tBu2C6H3). Calculations suggest the reaction mechanism proceeds via the slippage of π-bound alkyne at the Rh centre into a Rh–alkyne σC–H complex followed by an indirect 1,2-H shift to give the Rh–vinylidene species. NBO (Natural Bond Orbital) analysis of the transition states corresponding to the latter indirect 1,2-H shift step indicates that the migrating hydrogen atom exhibits protic character and hence, the basicity of the H-accepting centre (Cβ) is controlled by the substituents at that same atom and can tune the 1,2-H shift transition state. QTAIM (Quantum Theory of Atoms in Molecule) and NBO analyses of the Rh–vinylidene complexes indicate that these species exhibit a Rh ← C dative bond as well as π-back bonding from the Rh centre into the empty pz orbital of the carbene centre (Cα), showing the Rh–vinylidene complexes are Fischer type carbenes. Analysis of the alkyne and vinylidene complex HOMOs show that the equilibrium between the isomers can be tuned by the P–Rh–P bite angle of the [Rh(pincer)]+ fragment. Dictated by the nature of the pincer backbone, wider bite angles shift the equilibrium toward the formation of the Rh–vinylidene isomer (e.g., X = CH2 and R = Ar′), while tighter bite angles shift the equilibrium more to the formation of the Rh–alkyne isomer (e.g., X = O and R = Ar′).
CR, where R = tBu and Ar′ (3,5-tBu2C6H3). Calculations suggest the reaction mechanism proceeds via the slippage of π-bound alkyne at the Rh centre into a Rh–alkyne σC–H complex followed by an indirect 1,2-H shift to give the Rh–vinylidene species. NBO (Natural Bond Orbital) analysis of the transition states corresponding to the latter indirect 1,2-H shift step indicates that the migrating hydrogen atom exhibits protic character and hence, the basicity of the H-accepting centre (Cβ) is controlled by the substituents at that same atom and can tune the 1,2-H shift transition state. QTAIM (Quantum Theory of Atoms in Molecule) and NBO analyses of the Rh–vinylidene complexes indicate that these species exhibit a Rh ← C dative bond as well as π-back bonding from the Rh centre into the empty pz orbital of the carbene centre (Cα), showing the Rh–vinylidene complexes are Fischer type carbenes. Analysis of the alkyne and vinylidene complex HOMOs show that the equilibrium between the isomers can be tuned by the P–Rh–P bite angle of the [Rh(pincer)]+ fragment. Dictated by the nature of the pincer backbone, wider bite angles shift the equilibrium toward the formation of the Rh–vinylidene isomer (e.g., X = CH2 and R = Ar′), while tighter bite angles shift the equilibrium more to the formation of the Rh–alkyne isomer (e.g., X = O and R = Ar′).
Introduction
Transition metal (TM) vinylidene complexes are key species in organometallic chemistry.1–9 These compounds can be subjected to a variety of reactions such as hydrogenation, dehydrogenation and C–C bond formation processes.10 The most general strategy to form TM–vinylidene complexes under facile and simple conditions is the reaction of TM complexes with alkynes. This process can lead to the coordination of alkynes to a metal centre to give η2-alkyne complexes, which are stable enough to be characterised experimentally11–17 or can act as transient intermediates that undergo C–R (R = C6H5, Ar′ and H) bond cleavage and migration of the R group to yield TM–vinylidene complexes.18–31 Such reactivity can be feasibly modulated by factors such as changing the nature of alkynes or the transition metal.Mutoh, Ishii and co-workers described the reaction of [CpRu(dppe)]+ (1) (dppe = 1,2-diphenylphosphinoethane) with internal alkynes (PhC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CAr′) and showed that both aryl substituents undergo the 1,2-migration process to generate the disubstituted Ru–vinylidene species 2 (Fig. 1).16,32 They demonstrated that groups featuring electron-donating substituents decrease the relative migratory aptitude of the Ar′ group over Ph. However, the migratory aptitude becomes opposite when Ar′ groups have electron-withdrawing substituents. Based on these results, the authors suggested that this is due to the stabilisation of the negative charge on the Ar′ group in the 1,2-Ar′ shift transition state, suggesting the 1,2-Ar′ migration proceeds via an electrophilic mechanism (Fig. 1).16 DFT (Density Functional Theory) studies by Tsuchida, Takano and co-workers on internal alkyne transformations at [CpRu((C6H5)C
CAr′) and showed that both aryl substituents undergo the 1,2-migration process to generate the disubstituted Ru–vinylidene species 2 (Fig. 1).16,32 They demonstrated that groups featuring electron-donating substituents decrease the relative migratory aptitude of the Ar′ group over Ph. However, the migratory aptitude becomes opposite when Ar′ groups have electron-withdrawing substituents. Based on these results, the authors suggested that this is due to the stabilisation of the negative charge on the Ar′ group in the 1,2-Ar′ shift transition state, suggesting the 1,2-Ar′ migration proceeds via an electrophilic mechanism (Fig. 1).16 DFT (Density Functional Theory) studies by Tsuchida, Takano and co-workers on internal alkyne transformations at [CpRu((C6H5)C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CC6H4R-p)(dppe)]+ (R = OMe, CO2Et) into the corresponding vinylidene complexes shows that this reaction proceeds with a direct 1,2-migration mechanism.33 In accordance with the experimental findings of Ishii et al., Tsuchida, Takano and co-workers showed that alkyne substrates with an electron-donating substituent (R = OMe) favours the Ph-migration over the Ar′-migration reaction. However, using NBO (Natural Bond Orbital) donor–acceptor interaction analysis, they stated that this reaction proceeds via a nucleophilic mechanism; as in the 1,2-Ar′/Ph migration process, the electron-donating substituted Ar′ group stabilises the positive charge of the accepting carbon centre (Cβ), which facilitates the 1,2-Ph migration process.
CC6H4R-p)(dppe)]+ (R = OMe, CO2Et) into the corresponding vinylidene complexes shows that this reaction proceeds with a direct 1,2-migration mechanism.33 In accordance with the experimental findings of Ishii et al., Tsuchida, Takano and co-workers showed that alkyne substrates with an electron-donating substituent (R = OMe) favours the Ph-migration over the Ar′-migration reaction. However, using NBO (Natural Bond Orbital) donor–acceptor interaction analysis, they stated that this reaction proceeds via a nucleophilic mechanism; as in the 1,2-Ar′/Ph migration process, the electron-donating substituted Ar′ group stabilises the positive charge of the accepting carbon centre (Cβ), which facilitates the 1,2-Ph migration process.
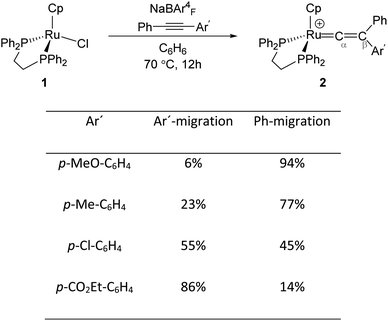 | ||
Fig. 1 Reaction of the Ru-precursor 1 with internal alkyne substrates PhC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CAr′ to give the Ru–vinylidene species 2.16 CAr′ to give the Ru–vinylidene species 2.16 | ||
Werner and co-workers proposed the reaction of [(η3-C3H5)Rh(PiPr3)2] (3) with terminal alkynes HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR (R = H, Me, tBu and Ph) eliminates C3H6 and yields the Rh–alkyne species 4, which undergoes a C–H bond oxidative cleavage at the Rh centre to form the Rh–H species 5 (Scheme 1).34 Complex 5 then undergoes a further transformation and gives the Rh–vinylidene species, 6. A DFT study by Hall and co-workers featured these reaction systems and shows that oxidative cleavage of the first HC
CR (R = H, Me, tBu and Ph) eliminates C3H6 and yields the Rh–alkyne species 4, which undergoes a C–H bond oxidative cleavage at the Rh centre to form the Rh–H species 5 (Scheme 1).34 Complex 5 then undergoes a further transformation and gives the Rh–vinylidene species, 6. A DFT study by Hall and co-workers featured these reaction systems and shows that oxidative cleavage of the first HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR substrate (R = Ph) followed by a C–H reductive elimination at the Rh centre releases propene and forms a Rh-alkenyl intermediate.35 Addition of a second HC
CR substrate (R = Ph) followed by a C–H reductive elimination at the Rh centre releases propene and forms a Rh-alkenyl intermediate.35 Addition of a second HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR substrate to the Rh-alkenyl intermediate forms the bridging hydrogen intermediate 7 (Scheme 1), through which the H-migration proceeds with a 1,2-H shift mechanism to give [(PhC
CR substrate to the Rh-alkenyl intermediate forms the bridging hydrogen intermediate 7 (Scheme 1), through which the H-migration proceeds with a 1,2-H shift mechanism to give [(PhC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)Rh(PiPr3)2(C
C)Rh(PiPr3)2(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(Ph)(H)] (6).
C(Ph)(H)] (6).
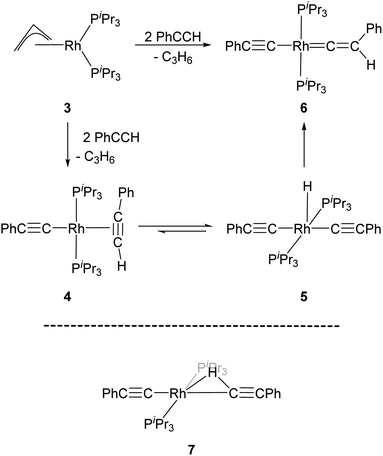 | ||
| Scheme 1 Reaction scheme for the formation of the Rh–vinylidene species 6,34 and the DFT computed Rh–H alkenyl intermediate 7 featuring a bridging hydrogen between the Rh and C centres.35 | ||
A DFT study by Angelis and co-workers on the isomerisation of [(Cp)(PMe3)2Ru(HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)]+ to the vinylidene isomer shows that this reaction proceeds via an indirect 1,2-H shift reaction.36 The second possible pathway to from the vinylidene isomer is the C–H oxidative cleavage of the alkyne at the Ru centre followed by a 1,3-H migration reaction to give the Ru–vinylidene complex. However, this was reported to be kinetically inaccessible, as the energy barrier of the 1,3-H shift reaction is significantly higher than the 1,2-H shift pathway. Later on, the same authors demonstrated that upon increasing the electron-richness of the Ru centre, the oxidative cleavage product can be both kinetically and thermodynamically accessible.37 Particularly notable is the joint experimental and computational study by Lynam, Fey and co-workers on factors such as the nature of substituents, the metal and the ligands, which can control the thermodynamic preference of metal–vinylidene isomers over the corresponding metal–alkyne isomers.38 The authors proposed a protocol to design ideal conditions to stabilise metal–vinylidene isomers. For instance in [RuCl2(PR′3)(
CR)]+ to the vinylidene isomer shows that this reaction proceeds via an indirect 1,2-H shift reaction.36 The second possible pathway to from the vinylidene isomer is the C–H oxidative cleavage of the alkyne at the Ru centre followed by a 1,3-H migration reaction to give the Ru–vinylidene complex. However, this was reported to be kinetically inaccessible, as the energy barrier of the 1,3-H shift reaction is significantly higher than the 1,2-H shift pathway. Later on, the same authors demonstrated that upon increasing the electron-richness of the Ru centre, the oxidative cleavage product can be both kinetically and thermodynamically accessible.37 Particularly notable is the joint experimental and computational study by Lynam, Fey and co-workers on factors such as the nature of substituents, the metal and the ligands, which can control the thermodynamic preference of metal–vinylidene isomers over the corresponding metal–alkyne isomers.38 The authors proposed a protocol to design ideal conditions to stabilise metal–vinylidene isomers. For instance in [RuCl2(PR′3)(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHR)], with electron-withdrawing substituents (R) and phosphine ligands with electron-rich groups (R′), formation of the Ru–vinylidene isomer is thermodynamically favoured over the Ru–alkyne isomer.
CHR)], with electron-withdrawing substituents (R) and phosphine ligands with electron-rich groups (R′), formation of the Ru–vinylidene isomer is thermodynamically favoured over the Ru–alkyne isomer.
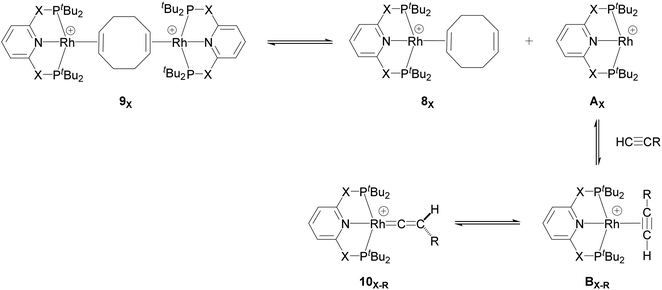
Recently, Chaplin and co-workers described the substitution reaction in [Rh(COD)2][BArF4] with the pincer ligands PXNXP (COD = 1,5-cyclooctadiene, ArF = 3,5-(CF3)2C6H3)) (X = CH2: 2,6-bis(di-tert-butylphosphinomethyl)pyridine (PNP) and X = O: 2,6-bis(di-tert-butylphosphinito)pyridine (PONOP)) which leads to the formation of the corresponding PNP and PONOP-pincer complexes 8X and 9X.39 As shown in Scheme 2, this reaction gives the monomeric complex 8X ([Rh(PXNXP)(η2-COD)][BArF4]) as the major product and the dimeric complex 9X ([{Rh(PXNXP)}2(μ-η2:η2-COD)][BArF4]2) as the minor product.
 | ||
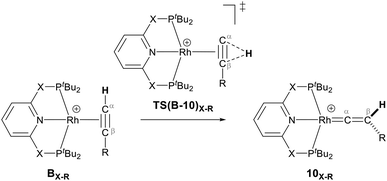
| Scheme 2 Reaction of the pincer ligand with the dimeric Rh precursor, [Rh(COD)2]2+, to form 8X and 9X. The counter ions (BArF4) are omitted for clarity.39 | ||
They demonstrated that reaction of the dimeric and monomeric Rh complexes 8X and 9X with L-type ligands such as CO results in the formation of the Rh–CO adduct, inferring the COD ligand dissociation from the Rh species forms the cationic 14e− {Rh(pincer)}+ species, which can be trapped out by CO to form the adduct. The authors also explored the reactivity of the active species, {Rh(pincer)}+, by the reaction of the dimeric complex 9X with HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR (R = tBu and Ar′ (3,5-tBu2C6H3)) in 1,2-difluorobenzene (DFB) solvent at room temperature which gives the Rh–vinylidene complex 10X–R (Scheme 3).39 With the dimeric {Rh(PNP)}2+, this process was found to be very fast (ca. five minutes) whereas, with the dimeric {Rh(PONOP)}+, it took significantly longer (ca. 18 h). It should be noted that with the dimeric {Rh(PONOP)}2+ and R = Ar′, this process forms the Rh–alkyne as the major product and the Rh–vinylidene complex as the minor product (70% vs. 30%). This suggests that the alkyne-to-vinylidene transformation process is reversible, a process that is also seen at [RuCl(η5-C9H7)(PPh3)2]17 and [CpRu(dppe)]+ complexes.32
CR (R = tBu and Ar′ (3,5-tBu2C6H3)) in 1,2-difluorobenzene (DFB) solvent at room temperature which gives the Rh–vinylidene complex 10X–R (Scheme 3).39 With the dimeric {Rh(PNP)}2+, this process was found to be very fast (ca. five minutes) whereas, with the dimeric {Rh(PONOP)}+, it took significantly longer (ca. 18 h). It should be noted that with the dimeric {Rh(PONOP)}2+ and R = Ar′, this process forms the Rh–alkyne as the major product and the Rh–vinylidene complex as the minor product (70% vs. 30%). This suggests that the alkyne-to-vinylidene transformation process is reversible, a process that is also seen at [RuCl(η5-C9H7)(PPh3)2]17 and [CpRu(dppe)]+ complexes.32
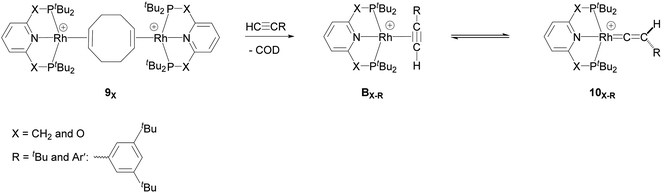 | ||
Scheme 3 Reaction of the dimeric {Rh(PNP)}2+ complex 9X with terminal alkynes HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR (R = tBu and Ar′ (3,5-tBu2C6H3)) to form the Rh–alkyne (BX–R) and the Rh–vinylidene complex (10X–R). The counter ions (BArF4) are omitted for clarity.39 CR (R = tBu and Ar′ (3,5-tBu2C6H3)) to form the Rh–alkyne (BX–R) and the Rh–vinylidene complex (10X–R). The counter ions (BArF4) are omitted for clarity.39 | ||
Herein, DFT calculations were carried out to rationalise the mechanism of the formation of these Rh–vinylidene complexes, to characterise the nature of the Rh–carbene bond in the Rh–vinylidene complexes and to understand factors that can affect the equilibrium between the Rh–alkyne and Rh–vinylidene isomers.
Computational methodology
Gas phase DFT calculations were run with Gaussian 09 (Revision D.01).40 The Rh and P centres were described with the Stuttgart RECPs and associated basis sets,41 and the 6-31G** basis set was used for all other atoms (BS1).42 A polarization function was also added to P (ζd = 0.387) and S (ζd = 0.503) atoms. Initial BP86 (ref. 43 and 44) optimizations were performed using the ‘grid = ultrafine’ option, with all stationary points being fully characterized via analytical frequency calculations as either minima (all positive eigenvalues) or transition states (one negative eigenvalue). IRC (Intrinsic Reaction Coordinate) calculations and subsequent geometry optimizations were used to confirm the minima are linked by the isolated transition state. All energies were recomputed with a larger basis set featuring cc-pVTZ-PP for Rh, cc-pVTZ-dk for S and the 6-311++G** basis set for all other atoms (BS2). 1,2-Difluorobenzene is not a parameter defined solvent in the Gaussian program. To overcome this its dielectric constant (ε = 13.4) was specified when applying a polarizable continuum model solvent correction with BS1.45 It should be noted that similar trends to the 1,2-difluorobenzene results were obtained when using fluorobenzene (ε = 5.42, see ESI† for more details) as the solvation medium. Additional single-point dispersion corrections to the BP86 results employed Grimme's D3 parameter set with Becke–Johnson damping as implemented in Gaussian 09.46 QTAIM (Quantum Theory of Atoms in Molecules)47 and NBO (Natural Bonding Orbital)48 were performed on the BP86-optimised geometries of the Rh–vinylidene complexes 10X–R to characterise the nature of the Rh–carbene bond. The complete computational approach is described in shorthand as BP86-D3BJ (BS2,1,2-difluorobenzene)//BP86(BS1). All free energies are reported in kcal mol−1 and are given relative to 9X.Results and discussion
Our computed mechanism starts with the splitting of 9X (as reported by Chaplin and co-workers39) to give the 14e− Rh species AX (Scheme 4, X = CH2 and O, R = tBu and Ar′). This process is endergonic by ΔG = +20.0 kcal mol−1 for X = CH2 and ΔG = +23.0 kcal mol−1 for X = O. The cationic Rh moiety can be stabilised by the coordination of HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR to AX in a π-binding mode to the Rh centre to give the Rh–alkyne species BX–R. For X = CH2 and O and R = tBu, BX–tBu lies at a free energy of −0.2 and −3.7 kcal mol−1 respectively, showing formation of the PONOP complex (BO–tBu) is energetically favoured by 3.5 kcal mol−1. Coordination of HC
CR to AX in a π-binding mode to the Rh centre to give the Rh–alkyne species BX–R. For X = CH2 and O and R = tBu, BX–tBu lies at a free energy of −0.2 and −3.7 kcal mol−1 respectively, showing formation of the PONOP complex (BO–tBu) is energetically favoured by 3.5 kcal mol−1. Coordination of HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CAr′ to the Rh centre significantly stabilises the cationic Rh species to form BX–Ar at ΔG = −12.6 kcal mol−1 for X = CH2 and ΔG = −11.0 kcal mol−1 for X = O.
CAr′ to the Rh centre significantly stabilises the cationic Rh species to form BX–Ar at ΔG = −12.6 kcal mol−1 for X = CH2 and ΔG = −11.0 kcal mol−1 for X = O.
 | ||
| Scheme 4 Formation of the 14e− Rh species AX and its onward reaction with the alkyne substrates to form the Rh–alkyne (BX–R) and Rh–vinylidene species (10X–R). | ||
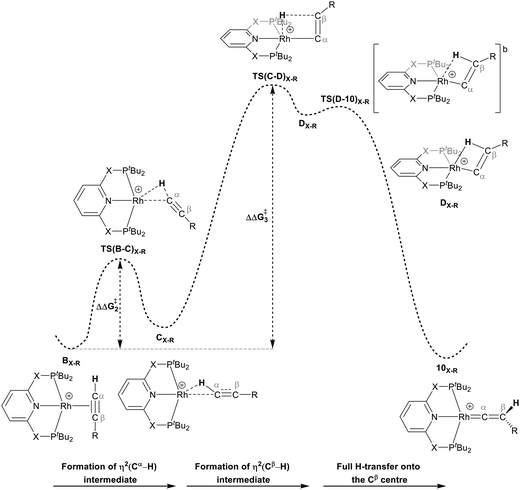
As shown in Scheme 5, once the Rh–alkyne π-complex BX–R has formed, it can undergo an intra-molecular transformation via three possible pathways (I, II and III) to afford the Rh–vinylidene complex 10X–R. In Pathway I, the Rh–alkyne species BX–R undergoes a direct 1,2-R/H migration to form 10X–R. In Pathway II, transfer of the R/H groups onto the Rh centre occurs via a four-member transition structure to yield 10X–R. Pathway III proceeds with the initial formation of the Rh–C bond that induces the 1,2-H/R shift reaction simultaneously to give 10X–R.
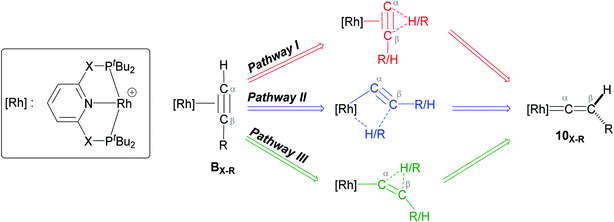 | ||
| Scheme 5 Transition states for three potential mechanisms (Pathways I, II and III) to form the Rh–vinylidene complex 10X–R. | ||
Both the tBu and Ar′ alkyne substituents could migrate from the Cβ centre to the Cα centre from BX–R to form 10X–R. However, the energy barriers for migration of Ar′ or tBu groups via the pathways shown in Scheme 3 are computed to be too high (between 37 to 58 kcal mol−1)49 and hence, unsurmountable under the experimental reaction conditions of 9X and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR39 (see ESI, Tables S2 and S3†).
CR39 (see ESI, Tables S2 and S3†).
The most obvious route to form the Rh–vinylidene species involves H migration. In Pathway I (Table 1) for the PNP-pincer ligand and R = tBu, the direct 1,2-H shift reaction in BC–tBu proceeds via TS(B-10)C–tBu at ΔG‡ = +40.1 kcal mol−1 to afford the Rh–vinylidene species 10C–tBu at ΔG = −12.1 kcal mol−1. The free energy barrier for this process (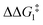 ) is computed to be 40.3 kcal mol−1 (relative to BC–tBu), which is too high to be accessible under the reaction conditions. Changing the pincer ligand from PNP to PONOP slightly lowers the free energy (by 0.7 kcal mol−1) of the transition state corresponding to the 1,2-H shift process (TS(B-10)O–tBu) to +39.4 kcal mol−1 to give the Rh–vinylidene species 10O–tBu at −8.9 kcal mol−1. The free energy barrier for this process is still too high (
) is computed to be 40.3 kcal mol−1 (relative to BC–tBu), which is too high to be accessible under the reaction conditions. Changing the pincer ligand from PNP to PONOP slightly lowers the free energy (by 0.7 kcal mol−1) of the transition state corresponding to the 1,2-H shift process (TS(B-10)O–tBu) to +39.4 kcal mol−1 to give the Rh–vinylidene species 10O–tBu at −8.9 kcal mol−1. The free energy barrier for this process is still too high (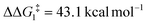 ), going from R = tBu to R = Ar′, with the PNP-pincer ligand the transition state TS(B-10)C–Ar lies at
), going from R = tBu to R = Ar′, with the PNP-pincer ligand the transition state TS(B-10)C–Ar lies at 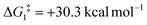 ; significantly lower than when R = tBu. With respect to BO–Ar, the free energy barrier for this process is computed to be 42.9 kcal mol−1 – again too high and not accessible at room temperature. A similar trend can be seen for the PONOP-pincer ligand when R = Ar′ (
; significantly lower than when R = tBu. With respect to BO–Ar, the free energy barrier for this process is computed to be 42.9 kcal mol−1 – again too high and not accessible at room temperature. A similar trend can be seen for the PONOP-pincer ligand when R = Ar′ (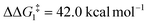 ). Therefore, the high energy barriers associated with the direct 1,2-H shift reaction in Pathway I are not in agreement with experiment.
). Therefore, the high energy barriers associated with the direct 1,2-H shift reaction in Pathway I are not in agreement with experiment.
| X | R | BX–R | TS(B-10)X–R | 10X–R | |
|---|---|---|---|---|---|
a DFT method = BP86-D3(BJ)-1,2-difluorobenzene/BS2//BP86/BS1. Computed energy barrier (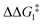 ) is relative to BX–R. All free energies are quoted relative to 9X (X = CH2 and O, R = tBu and Ar′). ) is relative to BX–R. All free energies are quoted relative to 9X (X = CH2 and O, R = tBu and Ar′). |
|||||
| CH2 | tBu | −0.2 | +40.1 | 40.3 | −12.1 |
| O | tBu | −3.7 | +39.4 | 43.1 | −8.9 |
| CH2 | Ar′ | −12.6 | +30.3 | 42.9 | −15.7 |
| O | Ar′ | −11.0 | +31.0 | 42.0 | −10.9 |
For Pathway II (Table 2), BC–tBu undergoes slippage of the π-coordination mode to a σC–H coordination mode via TS(B-C)C–tBu at 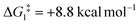 to give CC–tBu, featuring an elongated Cα–H bond (1.22 Å) to give a short Rh⋯H of 1.73 Å. NBO analysis of CC–tBu indicates a donor–acceptor interaction between the Cα–H bonding orbital and a vacant Rh orbital with stabilisation energy (ΔE(2)) of 82.9 kcal mol−1, showing a Cα–H agostic interaction with the Rh centre (see ESI, Fig. S3† for details). With respect to BC–tBu, formation of CC–tBu proceeds with a free energy barrier (
to give CC–tBu, featuring an elongated Cα–H bond (1.22 Å) to give a short Rh⋯H of 1.73 Å. NBO analysis of CC–tBu indicates a donor–acceptor interaction between the Cα–H bonding orbital and a vacant Rh orbital with stabilisation energy (ΔE(2)) of 82.9 kcal mol−1, showing a Cα–H agostic interaction with the Rh centre (see ESI, Fig. S3† for details). With respect to BC–tBu, formation of CC–tBu proceeds with a free energy barrier (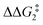 ) of 9.0 kcal mol−1 and is energetically downhill by 2.8 kcal mol−1. CC–tBu can undergo the H-transfer into the bridging position between the Cβ and Rh centre via TS(C-D)C–tBu at +37.7 kcal mol−1 to give the four-membered intermediate DC–tBu at ΔG = +36.4 kcal mol−1.
) of 9.0 kcal mol−1 and is energetically downhill by 2.8 kcal mol−1. CC–tBu can undergo the H-transfer into the bridging position between the Cβ and Rh centre via TS(C-D)C–tBu at +37.7 kcal mol−1 to give the four-membered intermediate DC–tBu at ΔG = +36.4 kcal mol−1.
| X | R | TS(B-C)X–R | CX–R | TS(C-D)X–R | DX–R | 10X–R | ||
|---|---|---|---|---|---|---|---|---|
a Estimated free energies by freezing the key distances in TS(C-D)X–Ar.b Transition state is not calculated.c DFT method = BP86-D3(BJ)-1,2-difluorobenzene/BS2//BP86/BS1. Computed energy barriers (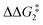 and and 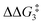 ) are relative to BX–R. All free energies are quoted relative to 8X (X = CH2 and O, R = tBu and Ar′). ) are relative to BX–R. All free energies are quoted relative to 8X (X = CH2 and O, R = tBu and Ar′). |
||||||||
| CH2 | tBu | +8.8 | 9.0 | −3.0 | +37.7 | 37.9 | +36.4 | −12.1 |
| O | tBu | +6.5 | 10.2 | +1.3 | +38.5 | 42.2 | +37.0 | −8.9 |
| CH2 | Ar′ | +0.2 | 12.8 | −4.5 | +29.8a | 42.4a | —b | −15.7 |
| O | Ar′ | +2.8 | 13.8 | −1.0 | +31.6a | 42.6a | —b | −10.9 |
The H atom then fully transfers onto the Cβ centre to give 10C–tBu. Attempts to locate the transition state (TS(D-10)X–R) corresponding to this process were inconclusive as it was a very flat potential free energy surface. A systematic increase of the Rh–H distance revealed that the energy barrier for this process is approximately 1.0 kcal mol−1 (relative to DC–tBu). Thus, formation of 10C–tBu via Pathway II is a high energy-process that requires a free energy barrier (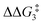 ) of 37.9 kcal mol−1 (relative to BC–tBu). Likewise, for the PONOP ligand and R = tBu formation of the σC–H intermediate CO–tBu (Cα–H: 1.21 Å and Rh⋯H: 1.75 Å, ΔE(2) = 72.2 kcal mol−1) proceeds with a low free energy barrier (
) of 37.9 kcal mol−1 (relative to BC–tBu). Likewise, for the PONOP ligand and R = tBu formation of the σC–H intermediate CO–tBu (Cα–H: 1.21 Å and Rh⋯H: 1.75 Å, ΔE(2) = 72.2 kcal mol−1) proceeds with a low free energy barrier (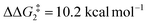 ). However, this process is energetically uphill by 5.0 kcal mol−1, suggesting it can be reversed to reform the Rh–alkyne species BO–tBu. The H transfer into the bridging position between the Rh and Cβ centres occurs via TS(C-D)O–tBu at ΔG‡ = +38.5 kcal mol−1 to give DO–tBu at ΔG = +37.0 kcal mol−1. A very flat free energy surface sees the full H-transfer onto the Cβ centre to give 10O–tBu at ΔG = −8.9 kcal mol−1. Thus, for Pathway II, formation of the Rh–vinylidene species 10O–tBu requires a high free energy barrier of 42.2 kcal mol−1. For R = Ar′ and the PNP-pincer ligand, the transition state (TS(C-D)C–Ar) corresponding to the formation of the intermediate CC–Ar (Cα–H: 1.19 Å and Rh⋯H: 1.78 Å, ΔE(2) = 73.9 kcal mol−1) has a free energy of 12.8 kcal mol−1 – higher than when R = tBu and computed to be energetically uphill by 8.1 kcal mol−1. Unfortunately, all attempts to locate the four-member transition state (TS(C-D)X–Ar) corresponding to the H transfer onto the Cβ centre and the subsequent intermediate DX–Ar remained allusive. Thus, the transition state free energy value was estimated by freezing the corresponding bond distances and TS(C-D)C–Ar was calculated to be approximately ΔG‡ = +29.8 kcal mol−1,50 with a free energy barrier of 42.4 kcal mol−1 that again is too high to be accessible under the reaction conditions. In comparison to the PNP ligand, the PONOP intermediate CO–Ar (Cα–H: 1.18 Å and Rh⋯H: 1.82 Å, ΔE(2) = 67.1 kcal mol−1) formed via a slightly higher energy barrier (
). However, this process is energetically uphill by 5.0 kcal mol−1, suggesting it can be reversed to reform the Rh–alkyne species BO–tBu. The H transfer into the bridging position between the Rh and Cβ centres occurs via TS(C-D)O–tBu at ΔG‡ = +38.5 kcal mol−1 to give DO–tBu at ΔG = +37.0 kcal mol−1. A very flat free energy surface sees the full H-transfer onto the Cβ centre to give 10O–tBu at ΔG = −8.9 kcal mol−1. Thus, for Pathway II, formation of the Rh–vinylidene species 10O–tBu requires a high free energy barrier of 42.2 kcal mol−1. For R = Ar′ and the PNP-pincer ligand, the transition state (TS(C-D)C–Ar) corresponding to the formation of the intermediate CC–Ar (Cα–H: 1.19 Å and Rh⋯H: 1.78 Å, ΔE(2) = 73.9 kcal mol−1) has a free energy of 12.8 kcal mol−1 – higher than when R = tBu and computed to be energetically uphill by 8.1 kcal mol−1. Unfortunately, all attempts to locate the four-member transition state (TS(C-D)X–Ar) corresponding to the H transfer onto the Cβ centre and the subsequent intermediate DX–Ar remained allusive. Thus, the transition state free energy value was estimated by freezing the corresponding bond distances and TS(C-D)C–Ar was calculated to be approximately ΔG‡ = +29.8 kcal mol−1,50 with a free energy barrier of 42.4 kcal mol−1 that again is too high to be accessible under the reaction conditions. In comparison to the PNP ligand, the PONOP intermediate CO–Ar (Cα–H: 1.18 Å and Rh⋯H: 1.82 Å, ΔE(2) = 67.1 kcal mol−1) formed via a slightly higher energy barrier (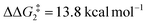 ). This process is computed to be more energetically uphill (by 1.9 kcal mol−1). The H transfer process onto the Cβ occurs with a high free energy barrier of +42.6 kcal mol−1 to form the Rh–vinylidene species. Thus, as outlined above, although formation of the σC–H intermediate CX–R occur with low free energy barriers, the hydrogen transfer onto the Cβ involves a large free energy barrier, which is not accessible under reaction conditions.
). This process is computed to be more energetically uphill (by 1.9 kcal mol−1). The H transfer process onto the Cβ occurs with a high free energy barrier of +42.6 kcal mol−1 to form the Rh–vinylidene species. Thus, as outlined above, although formation of the σC–H intermediate CX–R occur with low free energy barriers, the hydrogen transfer onto the Cβ involves a large free energy barrier, which is not accessible under reaction conditions.
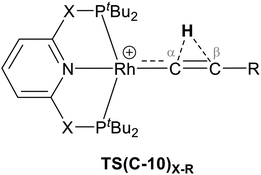
The indirect 1,2-H shift reaction via Pathway III involves the Rh sigma C–H complex CX–R. As shown in Table 3, in CX–R, the H centre can either transfer to the Rh centre to give EX–R or it can transfer onto the Cβ centre to form 10X–R. The H-transfer onto the Rh centre occurs with a C–H oxidative cleavage at the Rh centre via TS(C-E)X–R to form the terminal Rh(III)–H species EX–R. As listed in Table 3, in all cases, the H-transfer process to the Rh centre proceeds with a very flat free energy surface, an essentially barrierless process to give EX–R, suggesting a facile reaction and importantly consistent with the findings reported by Hall and co-workers.35 With respect to CX–R, formation of the terminal Rh–H species EX–R is slightly exergonic. However, EX–R is considerably less thermodynamically favoured than the experimentally observed Rh–vinylidene species 10X–R (by x kcal mol−1).
| X | R | TS(C-10)X–R | CX–R | 10X–R | TS(C-E)X–R | EX–R | |
|---|---|---|---|---|---|---|---|
a DFT method = BP86-D3(BJ)-1,2-difluorobenzene/BS2//BP86/BS1. Computed energy barrier (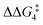 ) is relative to BX–R. All free energies are quoted relative to 9X (X = CH2 and O, R = tBu and Ar′). ) is relative to BX–R. All free energies are quoted relative to 9X (X = CH2 and O, R = tBu and Ar′). |
|||||||
| CH2 | tBu | +8.7 | −3.0 | 8.9 | −12.1 | −2.8 | −8.1 |
| O | tBu | +10.2 | +1.3 | 13.9 | −8.9 | +0.8 | −0.6 |
| CH2 | Ar′ | +7.6 | −4.5 | 20.2 | −15.7 | −5.5 | −11.4 |
| O | Ar′ | +9.1 | −1.0 | 20.1 | −10.9 | −1.2 | −4.4 |
For the H transfer process onto the Cβ centre via CX–R, with R = tBu and the PNP-pincer ligand, the bridging hydrogen indirectly can transfer onto the Cβ centre via TS(C-10)C–tBu, which lies at ΔG‡ = +8.7 kcal mol−1 to generate 10C–tBu. Interestingly, with respect to BC–tBu, the free energy barrier for this process (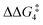 ) is computed to be only 8.9 kcal mol−1, significantly lower than those in Pathways I and II. With the PONOP-pincer ligand, the indirect 1,2-H shift process proceeds with a free energy barrier of 13.9 kcal mol−1, which is 4.0 kcal mol−1 higher than with the PNP-pincer ligand. The free energy barriers of the indirect 1,2-H migration process for the aryl-substituted alkyne with the PNP or the PONOP-pincer ligands increase to 20.2 kcal mol−1 and 20.1 kcal mol−1 respectively. However, they are significantly lower than those in Pathways I and II and values would be accessible at room temperature. Thus, Pathway III exhibits the energetically viable mechanism, consistent with the facile formation of Rh vinylidene species 10X–R seen experimentally.
) is computed to be only 8.9 kcal mol−1, significantly lower than those in Pathways I and II. With the PONOP-pincer ligand, the indirect 1,2-H shift process proceeds with a free energy barrier of 13.9 kcal mol−1, which is 4.0 kcal mol−1 higher than with the PNP-pincer ligand. The free energy barriers of the indirect 1,2-H migration process for the aryl-substituted alkyne with the PNP or the PONOP-pincer ligands increase to 20.2 kcal mol−1 and 20.1 kcal mol−1 respectively. However, they are significantly lower than those in Pathways I and II and values would be accessible at room temperature. Thus, Pathway III exhibits the energetically viable mechanism, consistent with the facile formation of Rh vinylidene species 10X–R seen experimentally.
It should be noted that the Rh–H species EX–R may undergo a reverse process via low free energy barriers (1.4–5.9 kcal mol−1) to reform CX–R and then follow the H-transfer reaction onto the Cβ centre to generate 10X–R which is more stable than the Rh–H species EX–R. For R = tBu and X = CH2, the rate-determining step (RDS) is the indirect 1,2-H shift (TS(C-10)X–R) while for other systems, RDS is the formation of the 14e− Rh intermediate AX–tBu.
Hydrogen character in the indirect 1,2-H shift reaction: protic or hydridic?
We have shown that formation of the Rh–vinylidene species proceeds via Pathway III, in which 1,2-H migration is a key step. However, it is not clear whether in the H-migration process, the H centre migrates as a proton or hydride (i.e., via an electrophilic or a nucleophilic mechanism respectively). In this regard, as listed in Table 4, both TS(C-10)C–tBu and TS(C-10)O–tBu exhibit a shorter Cα⋯H distance than Cβ⋯H by 0.36 Å and 0.35 Å respectively. This shows that the H centre exhibits a greater tendency to interact with the Cα centre than with the Cβ centre. A similar trend can also be seen in TS(C-10)C–Ar and TS(C-10)O–Ar (0.19 Å and 0.12 Å respectively). However, for R = Ar′ the H centre has a considerably shorter distance to Cβ, showing a stronger interaction between the H and Cβ centres when R = Ar′. NBO charge analysis of the transition state TS(C-10)X–R shows that for R = tBu, the Rh centre exhibits a very similar negative charge value (qRh = −0.54 to −0.55), implying the nature of the X moiety in the pincer ligands has a negligible effect on the charge of the Rh centre. For R = Ar′, the Rh centre features a slightly more negative charge (qRh = −0.64 to −0.66) than when R = tBu, which can be attributed to the π-electrons of the aryl group of the alkyne. In all cases, the H centre features similar positive charges (qH = +0.39 to +0.40), implying the H centre exhibits protic character, showing it can transfer via an electrophilic mechanism. For R = tBu, the Cβ centre displays small positive charges, while for R = Ar′, the Cβ centre possesses negative charges, indicating the electronic character of the Cβ centre is sensitive to the nature of the R substituent. Interestingly, as the charge of the Cβ centre becomes slightly negative (e.g., R = Ar′), the transition state TS(C-10)X–R lies at a lower free energy (by 1.1 kcal mol−1 for both PNP and PONOP relative to R = tBu), whereas, when the Cβ has a positive charge (e.g., R = tBu), the transition state TS(C-10)X–R lies at a higher free energy. This suggests that π-donor R substituents donate electron density to the empty Cβ pz orbital and hence increases its basicity, consistent with the electrophilic mechanism in the 1,2-H migration process. In order to examine this, the indirect 1,2-H shift process was computed for X = CH2 and R = NMe2. Our calculations show that the transition state TS(C-10)C–NMe2 exhibits a short Cβ–H distance of 1.26 Å, showing a stronger interaction between the H and the Cβ centres. This is due to NMe2 being a strong π-donor substituent that significantly populates the Cβ pz orbital to give a more stable transition state (at ΔG‡ = +4.7 kcal mol−1), supporting the electrophilic character of the H centre in the indirect 1,2-H shift process.Characterisation of the Rh–vinylidene complexes 10X–R: Fischer or Schrock-type complex?
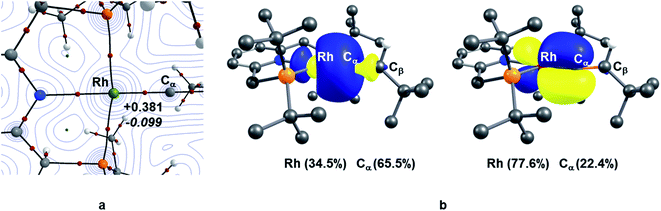
TM–carbene complexes can be described as a Fischer or Schrock carbene complex, depending on the nature of the metal–carbene bond. In Fischer type carbene complexes, the carbene centre donates two electrons to the metal centre via a dative interaction whereas the metal centre donates electron density to the pz orbital of the carbene centre through π-back bonding (i.e., singlet carbene). In Schrock type carbene complexes, the carbene centre shares two single electron with the metal centre to form a σ and π metal–carbene bonds (i.e., triplet carbene). Thus, the nature of the metal–carbene interactions in 10X–R can provide useful information whether these species are Fischer or Schrock-type carbene complexes. In this context, in order to elucidate the nature of the metal–carbene bond in the Rh–vinylidene species 10X–R, QTAIM and NBO analyses were performed on the BP86-optimised geometries of 10X–R. As shown in Fig. 2, the QTAIM plot of 10C–tBu exhibits a BCP (Bond Critical Point) along the Rh⋯Cα bond path, which is characterised by a positive Laplacian of electron density and small negative total energy density. This is indicative of a dative interaction between the Rh and carbene centres.51 A similar trend can also be observed for the other Rh–vinylidene species (see ESI, Fig. S4†). NBO analysis of 10C–tBu identifies a Rh σ-bonding orbital that is dominated by carbene character (Rh (34.5%) and Cα (66.5%)), showing a Rh ← Cα dative interaction. Additionally, the NBO analysis reveals the presence of π-back donation from the Rh centre into the empty pz orbital of the carbene, which is dominated by the Rh character (Rh (77.6%) and Cα (22.4%), see ESI, Fig. S4† for more details). Thus, the QTAIM and NBO data are fully consistent with a Rh(I) centre ligated by vinylidene (Cα![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CβHR) ligand and hence the Rh–vinylidene complexes 10X–R can be described as a Fischer TM–carbene complex, seen previously in d8 TM–carbene complexes.52 It should be noted that in all the Rh–vinylidene complexes, the Rh–Cα σ-bond is polarised toward the Cα centre, while the Rh–Cα π-interaction is polarised toward the Rh centre (see ESI, Fig. S4†).
CβHR) ligand and hence the Rh–vinylidene complexes 10X–R can be described as a Fischer TM–carbene complex, seen previously in d8 TM–carbene complexes.52 It should be noted that in all the Rh–vinylidene complexes, the Rh–Cα σ-bond is polarised toward the Cα centre, while the Rh–Cα π-interaction is polarised toward the Rh centre (see ESI, Fig. S4†).
Stability of Rh–alkyne vs. Rh–vinylidene complexes
As shown above, for R = Ar′ and the PNP pincer ligand, the Rh–vinylidene isomer is more stable than the Rh–alkyne isomer, while with the PONOP pincer ligand, the Rh–alkyne isomer is more stable. In order to explore the equilibrium between the Rh–alkyne and Rh–vinylidene isomers, the difference between the free energies of BX–R and 10X–R species were calculated and is represented by ΔGr ((ΔGr = ΔG(10X–R) − ΔG(BX–R), Table 5). A negative ΔGr value indicates that the equilibrium is toward the Rh–vinylidene isomer while a positive value indicates the equilibrium is toward the Rh–alkyne isomer. As listed in Table 5, our computational findings show that for R = tBu and both PNP or PONOP-pincer ligands, ΔGr is negative, with the PNP-pincer complex being significantly more negative than the PONOP-pincer complex (−11.9 and −5.2 kcal mol−1, respectively). For R = Ar′ and the PNP-pincer ligand, ΔGr is also negative (−3.1 kcal mol−1) yet for the PONOP-pincer ligand ΔGr becomes slightly positive (+0.1 kcal mol−1). This trend implies that with the aryl substituent, the Rh–vinylidene complex is less stable than the alkyl substituent. This becomes critically important when switching from the PNP pincer ligand to the PONOP pincer ligand, as in this case, the Rh–alkyne isomer becomes more stable than the Rh–vinylidene isomer. This highlights the influence of the nature of both substituent and pincer ligand on the stability of the Rh–vinylidene species.| X | R | ΔGr | HOMO (BX–R) | HOMO (10X–R) | ΔHOMO |
|---|---|---|---|---|---|
| CH2 | tBu | −11.9 | −7.05 | −7.31 | +0.26 |
| O | tBu | −5.2 | −7.54 | −7.65 | +0.11 |
| S | Ar′ | −3.2 | −7.25 | −7.31 | −0.06 |
| CH2 | Ar′ | −3.1 | −6.87 | −6.96 | −0.09 |
| NH | Ar′ | −2.1 | −7.01 | −7.04 | −0.03 |
| O | Ar′ | +0.1 | −7.29 | −7.23 | +0.06 |
A detailed analysis of the electronic structure of the Rh–alkyne and Rh–vinylidene complexes can help to understand the origin of the equilibrium between the two isomers. As shown in Fig. 3, the molecular orbital analysis of the Rh–vinylidene species 10X–R shows that when R = tBu, the HOMO of 10X–R predominantly consists of the Rh dz2 character, whereas for R = Ar′, the HOMO consists of the Rh dxy orbital and the π-system of the aryl moiety. With the PNP-pincer ligand, when R = Ar′, the Rh–vinylidene complex exhibits a higher HOMO than when R = tBu (−7.31 eV and −6.96 eV, respectively). This can be attributed to the presence of the π-system of the aryl moiety, which in conjugation with the Cα–Cβ π-bond and the {Rh(pincer)}+ moiety can destabilise the HOMO of the system and hence affects the stability of the Rh–vinylidene complex. Thus, it suggests that the HOMO energy is a reasonable descriptor that can capture the stability of the Rh–vinylidene isomer versus the Rh–alkyne isomer.
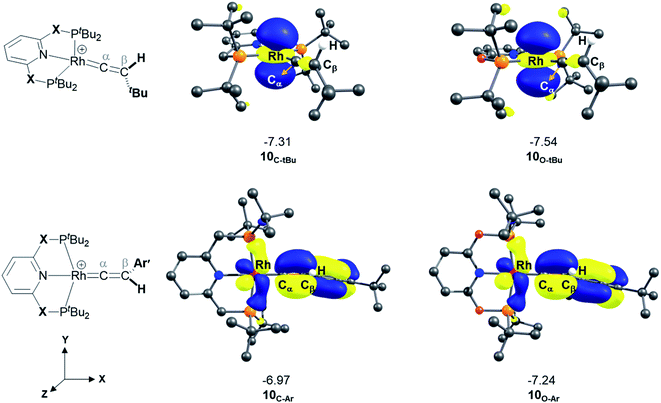 | ||
| Fig. 3 HOMOs (in eV) of Rh–vinylidene species 10X–R (X = CH2 and O; R = tBu and Ar′). Substituent hydrogen atoms removed for clarity. | ||
Table 5 lists the energy difference between the HOMOs of BX–R and 10X–R species, represented by ΔHOMO (ΔHOMO = ΔHOMO(10X–R) − ΔHOMO(BX–R)). For R = tBu and the PNP pincer ligand, ΔHOMO is +0.26 eV, showing the Rh–vinylidene isomer possess a more stable HOMO than the Rh–alkyne isomer. Similarly, for R = tBu and the PONOP pincer ligand, ΔHOMO is also a positive value (+0.11 eV). However, the PONOP analogue has a smaller ΔHOMO than the PNP complex. A similar trend can also be seen for R = Ar′ (+0.09 eV). Interestingly, for R = Ar′, when the pincer ligand is PONOP, the Rh–alkyne complex features a more stable HOMO than the Rh–vinylidene isomer (ΔHOMO = −0.06 eV). This suggests that for R = Ar′, the nature of the pincer ligand plays an important role on the stability of the HOMO of the Rh–vinylidene isomer versus the Rh–alkyne isomer. In order to investigate this further, the relative free energies of the vinylidene complex against the alkyne isomer was also computed for X = NH and S, and R = Ar′. Both X = NH and S showed a similar trend to X = CH2, with the Rh–vinylidene complex being more stable than the Rh–alkyne complex (ΔGr = −2.1 and −3.2 kcal mol−1 respectively) in which the Rh–vinylidene isomer features a more stable HOMO than the Rh–alkyne isomer (ΔHOMO = −0.03 and −0.06 eV respectively). Interestingly, a reasonable correlation (R2 = 0.95, Fig. S1†) was found between ΔGr and ΔHOMO values, showing when ΔHOMO is negative, the Rh–vinylidene species is more stable than the Rh–alkyne species and when ΔHOMO is positive, the Rh–alkyne species is more stable than the Rh–vinylidene species. This therefore indicates that for R = Ar′, ΔHOMO can capture the stability of the Rh–vinylidene versus the Rh–alkyne species, however, raises the question; why is ΔHOMO negative for X = CH2, NH or S, while for X = O, ΔHOMO is positive?
As shown in Fig. 3, the HOMO of the Rh–vinylidene complex 10X–Ar consists of the Rh dxy orbital that is affected by the P–Rh–P bite angle (θ) of the supporting pincer ligand. For X = O, the θ value of 10O–Ar is 163.0° and its HOMO energy is −7.23 eV (Fig. 4). In comparison to X = O, for X = S, the θ value of 10S–Ar is considerably larger (176.4°) and its HOMO is more stable than 10O–Ar (−7.31 eV). Interestingly, an excellent correlation (R2 = 0.9999, Fig. S2†) was found between the free energy of the Rh–vinylidene species 10X–R and its θ value, showing tighter P–Rh–P bite angles result in more reactive Rh–vinylidene species (i.e., higher HOMOs), while wider bite angles give more stable Rh–vinylidene species 10X–R (i.e., lower HOMO), consistent with recent work from Mansell.53 Thus, the bite angle is dictated by the nature of the X moiety and can therefore tune the reactivity of the Rh–vinylidene species versus the Rh–alkyne species BX–R.
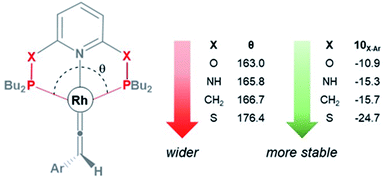 | ||
| Fig. 4 The P–Rh–P bite angle (θ, in degree) and the free energy (kcal mol−1) of the Rh–vinylidene species 10X–Ar. | ||
Conclusions
DFT calculations on the transformation of Rh–alkyne BX–R into the Rh–vinylidene complex 10X–R reveal that this process involves the slippage of the Rh–alkyne π-complex into the Rh–alkyne σC–H complex – followed by an indirect 1,2-H shift reaction. The H atom in the indirect 1,2-H shift transition state has protic character. The presence of π-donor groups at the accepting carbon centre (Cβ) can populate the Cβ empty pz orbital and hence increase its basicity to give stronger Cβ⋯H interactions, which consequently lower the free energy of the 1,2-H shift transition state. The equilibrium between the alkyne and vinylidene species can be tuned by the P–Rh–P bite angle, which is dictated by the nature of the X moiety in the PXNXP pincer ligand coordinated to the Rh-centre.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge EPSRC (UK) for financial support under award EP/R020752/1 (CLM and NAR). This research made use of the Balena High Performance Computing (HPC) Service at the University of Bath. The authors would like to thank Adrian Chaplin (University of Warwick) for discussions on his group's experimental research that initiated this study.Notes and references
- F. Ye, J. Chen and T. Ritter, J. Am. Chem. Soc., 2017, 139, 7184–7187 CrossRef CAS PubMed.
- Y. Yamamoto, K. Matsui and M. Shibuya, Chem.–Eur. J., 2015, 21, 7245–7255 CrossRef CAS PubMed.
- S. Takano, T. Kochi and F. Kakiuchi, Organometallics, 2016, 35, 4112–4125 CrossRef CAS.
- S. W. Roh, K. Choi and C. Lee, Chem. Rev., 2019, 119, 4293–4356 CrossRef CAS PubMed.
- L. Nunes dos Santos Comprido, J. E. M. N. Klein, G. Knizia, J. Kästner and A. S. K. Hashmi, Chem.–Eur. J., 2016, 22, 2892–2895 CrossRef CAS PubMed.
- F. Kakiuchi, S. Takano and T. Kochi, ACS Catal., 2018, 8, 6127–6137 CrossRef CAS.
- R.-S. Liu, Synlett, 2008, 2008, 801–812 CrossRef.
- B. M. Trost and J. T. Masters, Chem. Soc. Rev., 2016, 45, 2212–2238 RSC.
- M. Otsuka, N. Tsuchida, Y. Ikeda, N. Lambert, R. Nakamura, Y. Mutoh, Y. Ishii and K. Takano, Organometallics, 2015, 34, 3934–3943 CrossRef CAS.
- A. B. Antonova, Coord. Chem. Rev., 2007, 251, 1521–1560 CrossRef CAS.
- P. Barrio, M. A. Esteruelas and E. Oñate, Organometallics, 2003, 22, 2472–2485 CrossRef CAS.
- M. J. Cowley, J. M. Lynam and J. M. Slattery, Dalton Trans., 2008, 4552–4554, 10.1039/B806358C.
- V. K. Singh, E. Bustelo, I. de los Ríos, I. Macías-Arce, M. C. Puerta, P. Valerga, M. Á. Ortuño, G. Ujaque and A. Lledós, Organometallics, 2011, 30, 4014–4031 CrossRef CAS.
- M. Jiménez-Tenorio, M. C. Puerta, P. Valerga, M. A. Ortuño, G. Ujaque and A. Lledós, Inorg. Chem., 2013, 52, 8919–8932 CrossRef PubMed.
- Y. Ikeda, Y. Mutoh, K. Imai, N. Tsuchida, K. Takano and Y. Ishii, Organometallics, 2013, 32, 4353–4358 CrossRef CAS.
- Y. Mutoh, Y. Ikeda, Y. Kimura and Y. Ishii, Chem. Lett., 2009, 38, 534–535 CrossRef CAS.
- M. Bassetti, V. Cadierno, J. Gimeno and C. Pasquini, Organometallics, 2008, 27, 5009–5016 CrossRef CAS.
- D. B. Grotjahn, X. Zeng and A. L. Cooksy, J. Am. Chem. Soc., 2006, 128, 2798–2799 CrossRef CAS PubMed.
- W. Debrouwer and A. Fürstner, Chem.–Eur. J., 2017, 23, 4271–4275 CrossRef CAS PubMed.
- I. de los Ríos, E. Bustelo, M. C. Puerta and P. Valerga, Organometallics, 2010, 29, 1740–1749 CrossRef.
- P.-Y. Chia, C.-C. Kuo, S.-L. Huang, Y.-H. Liu, L.-K. Liu and Y.-C. Lin, Chem.–Asian J., 2018, 13, 3885–3894 CrossRef CAS PubMed.
- J. M. Lynam, C. E. Welby and A. C. Whitwood, Organometallics, 2009, 28, 1320–1328 CrossRef CAS.
- R. H. Lam, D. B. Walker, M. H. Tucker, M. R. D. Gatus, M. Bhadbhade and B. A. Messerle, Organometallics, 2015, 34, 4312–4317 CrossRef CAS.
- F. Mo, H. N. Lim and G. Dong, J. Am. Chem. Soc., 2015, 137, 15518–15527 CrossRef CAS PubMed.
- V. Cadierno, M. P. Gamasa, J. Gimeno, C. González-Bernardo, E. Pérez-Carreño and S. García-Granda, Organometallics, 2001, 20, 5177–5188 CrossRef CAS.
- M. Bassetti, P. Alvarez, J. Gimeno and E. Lastra, Organometallics, 2004, 23, 5127–5134 CrossRef CAS.
- I. Jourdain, L. Vieille-Petit, S. Clément, M. Knorr, F. Villafañe and C. Strohmann, Inorg. Chem. Commun., 2006, 9, 127–131 CrossRef CAS.
- M. J. Cowley, J. M. Lynam and A. C. Whitwood, J. Organomet. Chem., 2010, 695, 18–25 CrossRef CAS.
- J. M. Lynam, Chem.–Eur. J., 2010, 16, 8238–8247 CrossRef CAS PubMed.
- D. G. Johnson, J. M. Lynam, J. M. Slattery and C. E. Welby, Dalton Trans., 2010, 39, 10432–10441 RSC.
- F. De Angelis, A. Sgamellotti and N. Re, Organometallics, 2007, 26, 5285–5288 CrossRef CAS.
- Y. Mutoh, K. Imai, Y. Kimura, Y. Ikeda and Y. Ishii, Organometallics, 2011, 30, 204–207 CrossRef CAS.
- M. Otsuka, N. Tsuchida, Y. Ikeda, Y. Kimura, Y. Mutoh, Y. Ishii and K. Takano, J. Am. Chem. Soc., 2012, 134, 17746–17756 CrossRef CAS PubMed.
- M. Schäfer, J. Wolf and H. Werner, Organometallics, 2004, 23, 5713–5728 CrossRef.
- B. A. Vastine and M. B. Hall, Organometallics, 2008, 27, 4325–4333 CrossRef CAS.
- F. De Angelis, A. Sgamellotti and N. Re, Organometallics, 2002, 21, 5944–5950 CrossRef CAS.
- F. De Angelis, A. Sgamellotti and N. Re, Dalton Trans., 2004, 3225, 10.1039/b408452g.
- O. J. S. Pickup, I. Khazal, E. J. Smith, A. C. Whitwood, J. M. Lynam, K. Bolaky, T. C. King, B. W. Rawe and N. Fey, Organometallics, 2014, 33, 1751–1761 CrossRef CAS.
- M. R. Gyton, T. M. Hood and A. B. Chaplin, Dalton Trans., 2019, 48, 2877–2880 RSC.
- M. J. Frisch, et al., Gaussian 09, Gaussian Inc., Wallingford, CT, 2009 (see the full reference in ESI†)..
- D. Andrae, U. Häussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- AIMAll (Version 13.02.26), TK Gristmill Software, Overland Park KS, USA, 2015 Search PubMed.
- A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1 Search PubMed.
- For Pathway III, no intermediate with bridging tBu or Ar′ between the Rh and Cβ centres was characterised. For R = tBu, the indirect transfer of tBu led to the formation of the Rh–tBu complex and for R = Ar′, the indirect transfer of Ar′ group results in the formation of the Rh–vinylidene complex (see ESI for more details).†.
- The computed geometry features only one imaginary frequency..
- N. A. Rajabi, PhD thesis, Heriot-Watt University, 2018.
- N. M. Kostic and R. F. Fenske, Organometallics, 1982, 1, 974–982 CrossRef CAS.
- S. M. Mansell, Dalton Trans., 2017, 46, 15157–15174 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra08764e |
| This journal is © The Royal Society of Chemistry 2021 |