Open Access Article
Open Access ArticleProduction of modified sunflowers seed shells for the removal of bisphenol A†
Bahdja Hayoun*ac,
Saliha Bourouina-Bachab,
Marta Pazos c,
Ma Angeles Sanrománc,
Hayette Benkhennouche-Boucheneb,
Ourida Deflaouib,
Nassima Hamaidi-Maoucheb and
Mustapha Bourouinaa
c,
Ma Angeles Sanrománc,
Hayette Benkhennouche-Boucheneb,
Ourida Deflaouib,
Nassima Hamaidi-Maoucheb and
Mustapha Bourouinaa
aDepartment of Chemistry, Faculty of Exact Sciences, University of Bejaia, Bejaia 06000, Algeria. E-mail: hayba.bahdja@gmail.com; bouryas@yahoo.fr
bDepartment of Process Engineering, Faculty of Technology, University of Bejaia, Bejaia 06000, Algeria. E-mail: lgebej@yahoo.fr; hayette.bouchene@gmail.com; deflaoui1993@gmail.com; nmaouchehamaidi@yahoo.fr
cCINTECX-Universidade de Vigo, Department of Chemical Engineering Campus As Lagoas-Marcosende, University of Vigo, 36310 Vigo, Spain. E-mail: mcurras@uvigo.es; sanroman@uvigo.es
First published on 18th January 2021
Abstract
In this present study, an abundant, available lignocellulosic biomass, sunflower seed shells, SSS, was used as a precursor to prepare an effective eco-adsorbent by treatment with H2SO4. A study of the surface characteristics of raw and acid-treated SSS (ACS) has shown that the addition of H2SO4 greatly affected the physicochemical properties of the obtained eco-adsorbent, improving the BET surface area from 6.106 to 27.145 m2 g−1 and surface oxygen-rich functional groups. Batch experiments were performed to assess the removal efficiency of a phenolic compound, bisphenol A (BPA), on the adsorbents. Several parameters were evaluated and are discussed (contact time, pollutant concentration, adsorbent dosage, and pH), determining that the adsorption efficiency of BPA onto SSS was notably improved, from 20.56% to 87.81% when a sulfuric acid solution was used. Different canonical and stochastic isotherm models were evaluated to predict the experimental behaviour. A dynamic study was performed based on the models of reaction kinetics and those of mass transfer. The results showed that the adsorption kinetics of BPA obey the fractal like-kinetic model of Hill for all experimental conditions. The equilibrium data are well suited to the Hill–Sips isotherm model with a determination coefficient >0.999. The kinetic modelling also indicates that the adsorption processes of BPA onto ACS are exothermic and proceed through a physical mechanism. A mass transfer study, using simplified models, proved that the process is controlled by intraparticle and film resistances to mass transfer of the BPA.
1. Introduction
Over recent years, the rapid increase in industrialisation and development has seriously increased the environmental impact in receiving water bodies, which is caused by the discharge of huge quantities of industrial water containing highly toxic organic and inorganic pollutants.1–3 This has a considerable negative influence on the health of the environment and humans.2,4 Consequently, various industries such as primary plastic, polymer, paper, mining, leather, paint, and pharmaceutical industries generate phenolic pollutants that are extra toxic and need to be eliminated.3 Among the latter, bisphenol A (BPA), is a stabiliser monomer classified as an endocrine disrupting compound (EDC).1,5–7 Because of its extensive applications, there is global contamination in general, particularly in aqueous environments, including various waters, such as freshwater, seawater, and groundwater.4 BPA is a highly toxic substance: it possesses carcinogenic and mutagenic activity and it can accumulate in the human body through the food chain causing dysfunction of the reproductive organs and, hence, poses a major security threat to the safety and health of all living organisms.4,8–10 That is why there is an urgent need to develop simple, easy, and efficient methods to remove BPA from the environment.5,7For this purpose, several water-treatment methods have been developed for the elimination of BPA.7,8 Nevertheless, the adsorption technique represents the most common approach due to its high efficiency, easy operation, and the fact it does not lead to the formation of toxic intermediate products.10–12 Although adsorption onto activated carbon is considered a promising technique for the removal of a wide variety of contaminants in wastewater, the high cost of activated carbon production has limited its application at an industrial scale.4,12,13 This limitation prompted researchers to scout for alternative adsorbents from a wide variety of materials, like waste and agricultural by-products, which are considered low-cost, efficient, available, and highly abundant.3,14–16
In this context, a wide variety of adsorbents have been developed to remove BPA from the aqueous phase, such as pomelo peel, corncobs, Eucalyptus globulus and silkworm excrement,16 miscanthus straw, wheat straw, softwood, seed rape straw, sewage sludge, and rice husk,17 barley husk,18 argan nutshells,19 and potato peel.20 Many of them have limitations that make it necessary to explore other materials and to develop techniques that increase their adsorption capacity. SSS, an abundant, available, and non-toxic lignocellulosic biomass, falls into this category. To the best of our knowledge, there have been no studies for the removal of BPA using adsorbents developed from SSS.
However, SSS as raw material or derived activated carbon has been used for the removal of dyes in water,21–23 metal ions,24 or pesticides.25 Therefore, this study aims to develop a new eco-adsorbent with better properties that can simplify the purification processes and make them less expensive. SSS has several physicochemical properties that can result in significant adsorbent activity.22,23 However, it is known that the treatment of lignocellulosic biomass with acid can lead to an increase and/or improvement in the surface characteristics which is caused either by a reduction in the cellulose, hemicellulose and lignin content in the precursor, by an increase in the porosity of the matrix or the surface area of the adsorbent or by the activation of the functional adsorption sites which leads to an increase in the binding capacity of the adsorbent to remove adsorbates.16,22,26,27
For more than two decades now, the Brouers–Sotolongo fractal kinetics model (BSf (n,a)) and General Brouers–Sotolongo fractal isotherm models (GBS (a,b,c)) have been invoked and used in some problems and especially in the modelling of the adsorption solid–liquid process.28–34 The two most commonly applied BSf models are Weibull (n = 1) and Hill (n = 2) kinetics, which are the corresponding fractal-like models of the canonical Pseudo First Order (PFO) and Pseudo Second Order (PSO) models. In comparison to canonical models, widely used in adsorption, for kinetic or equilibrium studies, stochastic/fractal-like models offer greater flexibility and are based on phenomenological laws, taking into account the heterogeneity of the adsorbent surface.35
Consequently, this work aims to enhance the adsorption ability of BPA onto SSS by treatment with sulfuric acid, named ACS. Therefore, the morphologies of SSS and ACS75 were characterised, and the effects of sulfuric acid treatment and other parameters such as adsorption time, BPA concentration, adsorbent dosage or pH, on the elimination efficiency of BPA were determined. The equilibrium and kinetic data were modelled using equation fitting of several classical and Brouers–Sotolongo models to better understand the adsorption mechanism of BPA onto the SSS adsorbent. Therefore, to our knowledge, this is the first comprehensive study that has evaluated the modelling of data using the Brouers–Sotolongo family of models from the study of BPA adsorption onto SSS.
Besides, for all parameter determinations of kinetic and isotherm models, the use of the nonlinear regression performed under Minitab 17 allows an easy and precise fitting of the data.
2. Materials and methods
2.1. Materials
SSS, purchased from a local store, was selected in this study because of its high adsorption capacity and large surface area, even in its natural state compared to other biomass.22,23 Bisphenol A (BPA) was chosen as a relatively hydrophobic organic contaminant, and its chemical properties were purity > 98%, pKa 9.8–10.3, molecular weight 228.3 g mol−1, solubility in water 300.0 mg L−1, Log Kow 3.2. Concentrated sulfuric acid 98% purity, density 1.84 g cm−1³, molecular weight 98.1 g mol−1 (supplied by Biochem Chemopharma) was used for the treatment of SSS, and diluted solutions (0.1 M) of hydrochloric acid, purity 37%, density 1.18 g cm−1³, molecular weight 36.5 g mol−1 (Sigma-Aldrich) and sodium hydroxide, purity 97%, molecular weight 40 g mol−1 (Biochem Chemopharma) were used for pH adjustment. All solutions were prepared with distilled water of a conductivity of 1–1.6 μS.2.2. Procedure for the preparation of adsorbents
SSS was repeatedly washed with distilled water (hot then cold washing) to remove inorganic impurities, then filtered and dried in an oven overnight at 333 K to reduce the moisture content. Thereafter, the dried SSS was crushed and then sieved to obtain a particle size ≤ 0.3 mm. Chemical treatment of the dry SSS was performed using sulfuric acid (H2SO4) (named ACS). So, 2.5 g of the dried material was immersed in 50 ml of different H2SO4 solutions: 25, 50, 75, 98% (v/v), at room temperature and maintained under stirring for 1 d. The different ACS were dried in the oven for approximately 24 h at 383 K. The black solid adsorbent was then washed using distilled water (hot then cold washing) and the pH of the washing water was measured until a pH of distilled water was obtained to eliminate all acid and it was kept in an oven at 353 K until it reached constant weight. Finally, the ACS adsorbents named ACS25, ACS50, ACS75, and ACS98 were stored in a desiccator for characterisation and later use in adsorption experiments.2.3. Characterisation methods
Different techniques were used to characterise the SSS and ACS75. Fourier Transform Infrared Spectroscopy (FTIR) was carried out using a 630 Cary infrared spectrometer (400 to 4000 cm−1) to characterise the surface functional groups of the adsorbents.The textural properties and BET surface area were established by adsorption–desorption isotherms of N2 at 77.3 K, using a surface area analyser Quanta Chrome Nova 2000e.
A liquid displacement method was used in order to measure the real and apparent density, porosity, and porous volume of these adsorbents.36
The pH of the zero point charge (pHZPC) of the adsorbents was determined using the salt addition method.37
2.4. Adsorption experiment
To assess the effect of SSS treatment on the BPA removal efficiency, SSS and ACS (ACS25, ACS50, ACS75, ACS98) adsorption experiments were performed. Based on previously published work,38–41 we carried out preliminary tests and then set the operating conditions: namely, concentration of BPA (50 mg L−1), adsorbent dosage (1.5 g L−1), and pH (2) at room temperature (298 ± 2 K).Once the most effective adsorbent for the elimination of BPA was determined, the experiments were carried out at different values of concentration (25–125 mg L−1) of BPA, adsorbent dosage (0.5–2 g L−1), and pH (2–7) at room temperature (298 ± 2 K) and stirring speed (300 rpm). Therefore, all experiments were performed by introducing a precisely weighed quantity of the most effective adsorbent for BPA removal into a 250 ml Erlenmeyer flask containing 150 ml of BPA solution at the required concentration C0 (mg L−1). Samples were taken at different time intervals ranging from 0 to 360 min, then the solution was separated from the adsorbent using a Hettich brand centrifuge at 6000 rpm for 3 minutes. The absorbance of the supernatant solution was measured with a UV/visible spectrophotometer (UV min-1240 Shimadzu) at the wavelength corresponding to the maximum absorbance of the sample (λmax = 276 nm). In addition, all experiments were performed in duplicate; thus, all data was calculated and the average values were taken to show the results. The pH of the solutions was adjusted by adding a small quantity of dilute solutions of HCl (0.1 M) or NaOH (0.1 M).
The uptakes of BPA at different times (t) and at equilibrium were calculated using the following equations:
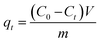 | (1) |
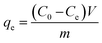 | (2) |
The removal efficiency (R%) of BPA from the aqueous solution was calculated from the following equation:
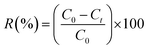 | (3) |
The average relative error (ARE) and the root mean square error (RMSE) were calculated from the following equations:42
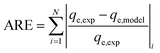 | (4) |
 | (5) |
2.5. Data analysis
| Models | Equation in batch system | Half time of adsorption | Eq. number |
|---|---|---|---|
| a Where qe and qt represent the uptake at equilibrium and at time t (mg g−1), t is the contact time in the batch system. k1 (min−1), k1f (min−(1−h)) and k2 (g mg−1 min−1), k2f (g mg−1 min−(1−h)) are the rate sorption constants of the PFO and PSO canonical and fractal models, respectively. τn,α, τ1,α, and τ2,α (min) are the characteristic times of the process for the BSf, Weibull and Hill models, respectively, α is the fractional time index, h is the fractal exponent, and n is the rate order. | |||
| PFO | 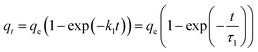 |
t0.5 = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/k1 2/k1 |
(6) |
| PSO | 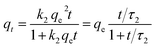 |
t0.5 = 1/k2qe | (7) |
| BSf (n,a) | 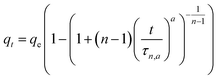 |
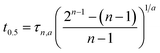 |
(8) |
| Weibull n = 1 | 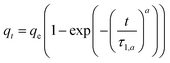 |
t0.5 = τ1,a(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)1/a 2)1/a |
(9) |
| Hill n = 2 | 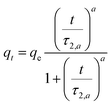 |
t0.5 = τ2,a | (10) |
| PFOf | 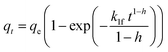 |
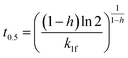 |
(11) |
| PSOf |  |
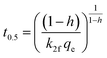 |
(12) |
The half-time of adsorption (t0.5 (min)) is the time required to reach 50% of the adsorption at equilibrium, and it is used to describe the time scale of adsorption kinetics. Its value is calculated from the experimental curve qt vs. t and is also often used as a measure of the adsorption rate. Another criterion for choosing the best kinetic model is the half-adsorption time calculated by comparison with the experimental value.
To clarify the adsorption mechanism, intraparticle48 and film diffusion49 models were applied to infer the limiting step in this solid/liquid mass transport process (Table 2).
| Kinetic model | Equation | Eq. number |
|---|---|---|
| a Where C is the concentration of the sorbate in the bulk of the solution; C0 is the initial concentration; F = q/qe the fraction of attainment of equilibrium at time t; Rp is the particle radius where the particle is assumed to be spherical, 0.015 cm; ms is the adsorbent mass per unit of the volume of solution (g L−1); εp is particle porosity; ρp is the particle density (g L−1); SA is the external particle area per unit of the volume of solution cm−1; kWM (mg g−1 min−0.5) is the internal diffusion constant and c (mg g−1) is the constant related to the external mass transfer resistance in the boundary layer. kMW and kFS are the external mass transfer coefficient (m s−1) of the Mathews and Weber, and Furusawa and Smith models, respectively. K is a constant (L g−1). Dst, Dapp, DV, and DVf (m2 s−1) are the effective diffusion coefficient of the solute in the solid phase given by the short time approach, homogeneous intraparticular, Vermeulen and fractal-like Vermeulen models, respectively. | ||
| Mathews and Weber | 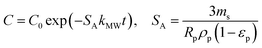 |
(13) |
| Furusawa and Smith | 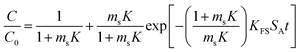 |
(14) |
| Weber and Morris | qt = kWM(t)1/2 + c | (15) |
| Short time approach | 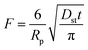 |
(16) |
| Vermeulen | 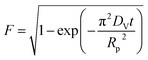 |
(17a) |
| Fractal-like Vermeulen | 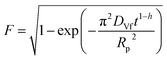 |
(17b) |
| Homogeneous internal diffusion model | 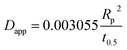 |
(18) |
On this basis, various classical and stochastic adsorption isotherm models were selected among many others to represent the schemas of the evolution of the experimental data (Table 3). The isotherm equations allow deductions, in addition to the maximum quantities adsorbed by the surface of the adsorbents and the equilibrium parameters, of the residual concentration corresponding to half the initial value Ce.
| Models | qe | Ce,0.5 | Eq. number |
|---|---|---|---|
| a Where Ce is the equilibrium concentration of the sorbate in the bulk of the solution, Ce,0.5 is the half-equilibrium concentration in the bulk solution, qe is the uptake at equilibrium. qmJ, qmL, qmDR, qmGBS, qmBG, qmHS, and qmBS (mg g−1) are the maximum uptake of the adsorbent of the Jovanovich, Langmuir, D–R, GBS, BG, HS and BS canonical and fractal isotherm models, respectively. KL (L mg−1) is the Langmuir constant. KF (mg g−1) (L g−1)n and nF are the Freundlich constants, which are indicators of adsorption capacity and adsorption intensity, respectively. BT (J mol−1) and KT (L g−1) are the Temkin constants. BD–R is the D–R constant. a and c of the GBS isotherm are the coefficients related to the form, while b is a scale parameter. The coefficient a describes the shape and width of the adsorption energy distribution which is related to the heterogeneity of the material.33,35 When the parameters a, b and c of the GBS model developed on a statistical basis have well-defined values, it is easy to deduce the equations of the canonical isotherms (Langmuir, Freundlich, Jovanovich) and those bases on the fractal model (BS, HS and BG). This unified general formulation makes it possible to pass easily from one to another of the models by using the same equation.35,45 | |||
| Canonical isotherms | |||
| Jovanovich | 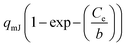 |
b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
(19) |
| Langmuir | 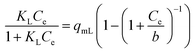 |
b(=1/KL) | (20) |
| Freundlich | KFCe1/nF | — | (21) |
| Temkin | BT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(KTCe) ln(KTCe) |
— | (22) |
| D–R | qmDR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−BD–Rε²) exp(−BD–Rε²) |
— | (23) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Fractal-like isotherms | |||
| General Brouers–Sotolongo (GBS) (a,b,c) | 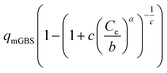 |
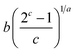 |
(24) |
| Brouers Gaspard (BG) | 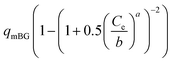 |
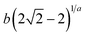 |
(25) |
| Hill–Sips (HS) | 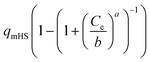 |
b | (26) |
| Brouers–Sotolongo (BS) | 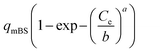 |
b(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)1/a 2)1/a |
(27) |
3. Results and discussions
3.1. Effect of acid treatment on the adsorption efficiency of BPA
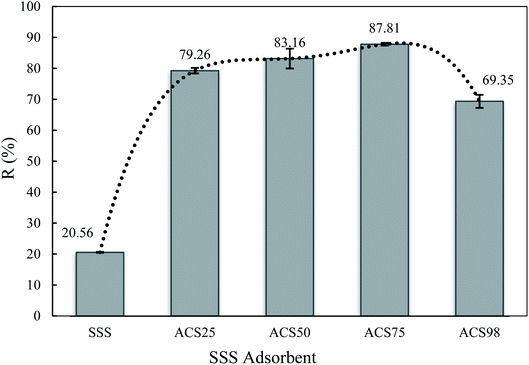
The effect of the quantity of sulfuric acid added as a chemical activator on adsorbent efficiency is shown in Fig. 1. As one can see, the SSS without treatment was able to remove just 20% of BPA during 5 h, whereas the ACS removed more than 60% of the BPA from the solution. In addition, the removal efficiency of the ACS for BPA was strongly dependent on the amount of sulfuric acid added, showing a significant increase in BPA removal efficiency with increasing H2SO4 dosage. Thus, when SSS is treated with H2SO4 at 75%, the adsorbent could remove nearly 90% of BPA from the solution. The significantly improved adsorption efficiency was mainly due to the addition of H2SO4 increasing the surface porosity and providing more sorption sites.27 However, the use of an excess of H2SO4 (98%, pure acid) caused a decrease in the removal efficiency to 68%. This fact could be explained due to the excess of acid causing a disorder in its porosity. Similar profiles were observed by Guo et al.50 and Girgis et al.,51 when they performed a study on adsorbents prepared from palm shells impregnated with sulfuric acid and sugar cane bagasse impregnated with several inorganic acids at different concentrations, respectively. Considering these results, the next experiments of this study were followed with the best adsorbent ACS75.3.2. Adsorbent characterisation
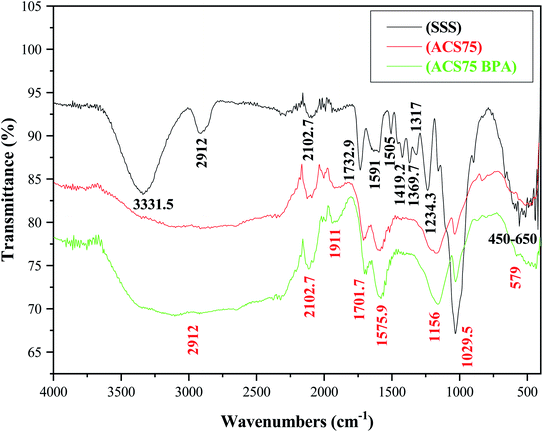
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (stretching vibrations in the ketone, aldehyde, lactone, and carbonyl groups and the aromatic ring) and to the –NH of the amide groups. We can also observe that the peak around 1575 cm−1 of the ACS75 spectrum after adsorption of BPA appears more intense than in the ACS75 spectrum before adsorption of BPA. This is related to the appearance of the aromatic ring of the BPA molecule.13,52 The weak peaks that appeared around 1420–1300 cm−1 were probably due to the vibration of the –CN bond.52
O (stretching vibrations in the ketone, aldehyde, lactone, and carbonyl groups and the aromatic ring) and to the –NH of the amide groups. We can also observe that the peak around 1575 cm−1 of the ACS75 spectrum after adsorption of BPA appears more intense than in the ACS75 spectrum before adsorption of BPA. This is related to the appearance of the aromatic ring of the BPA molecule.13,52 The weak peaks that appeared around 1420–1300 cm−1 were probably due to the vibration of the –CN bond.52
The peak detected around 1234 cm−1 for natural SSS was assigned to the bending vibration of carboxylic groups, whereas the peak at nearly 1156 cm−1 for ACS75 is strongly linked to the SO3– stretching following the sulfuric acid treatment. This peak is more intense in the spectrum of ACS75 after adsorption of BPA, which is probably related to the hydroxyl group of BPA.52,53 In both adsorbents, the peak at 1029 cm−1 can be assigned to the valence vibrational binding of Si (Si–O).52,53 The weak peaks that occurred between 450 cm−1 and 650 cm−1 could be due to the deformation of the aromatic C–H bond.19
| Parameters | Values | ||
|---|---|---|---|
| SSS | ACS75 | ||
| Specific surface (m2 g−1) | 6.106 | 27.145 | |
| Average pore radius (Å) | 3.17330 | 4.22635 | |
| Total pore volume (cm3 g−1) | 9.689 | 10.736 | |
| Porosity (%) | 82.92 | 87.8 | |
| Porous volume (cm3 g−1) | 2.217 | 20.902 | |
| Apparent density (g cm−3) | 0.374 | 0.042 | |
| Real density (g cm−3) | 2.189 | 0.344 | |
| pHZPC | 7.14 | 4.6 | |
| SA (cm−1) | ms = 0.5 g L−1 | — | 2.383 |
| ms = 1 g L−1 | — | 4.766 | |
| ms = 1.5 g L−1 | 0.802 | 7.148 | |
| ms = 2 g L−1 | — | 9.531 | |
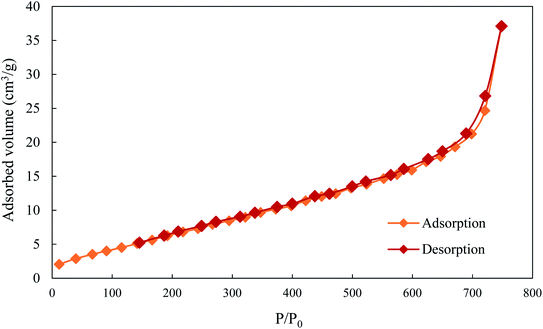
Fig. 3 represents the isotherm of the adsorption–desorption of nitrogen on the adsorbent ACS75 at 77 K. It can be seen that the isotherm is type II according to the IUPAC classification.56 This corresponds to a dominant macroporous structure of the adsorbent and the adsorption takes place in multiple layers.
3.3. Effect of contact time
In order to determine the equilibrium time required for maximum BPA adsorption and time of half-adsorption, adsorption experiments in discontinuous mode with ACS75 were performed according to various parameters: initial concentrations of BPA, adsorbent dosage and solution pH, operating in the range shown in Fig. 4.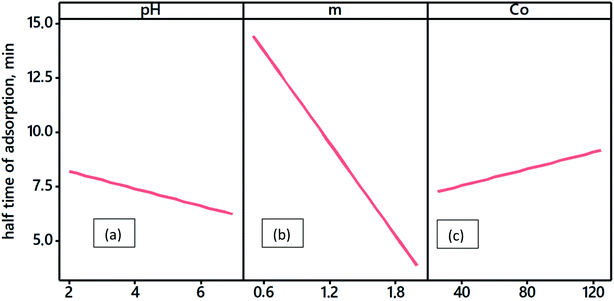 | ||
| Fig. 4 Variation of the half-time of adsorption with experimental conditions: (a): solution pH, (b): adsorbent dosage (g L−1), (c) BPA initial concentration (mg L−1). | ||
BPA removal efficiency increased quickly in the initial stages (from 0 to 100 min); while, beyond 100 min, BPA removal progressively increases until equilibrium is reached at 300 min with 87.8% maximum removal for a concentration of 50 mg L−1. This variation may be because, initially, a significant number of vacant active sites are available on the ACS75 surface, but after some time, the active sites will be occupied so that the surface fills up.18 However, after equilibrium (300 min) no important change was observed in the removal efficiency of BPA, because of the slow pore diffusion or saturation of the adsorbent.57
The half-adsorption time t0.5 changes very little with pH or modification of the initial concentration of BPA (Fig. 4). However, it decreases very quickly with an increase in biomass dosage. This result is probably related to the fact that the availability of a large mass of particles in the volume of the solution containing the BPA molecules offers the possibility of faster fixation on the surface. Thus, the increase in adsorbent from 0.5 to 2 g L−1 shortens the half-adsorption time from 17 to 5 min.
3.4. Effect of initial BPA concentration
These adsorption experiments were realised with different initial BPA concentrations from 25 to 125 mg L−1, keeping other experimental conditions constant, such as the contact time (360 min), adsorbent dosage (1.5 g L−1), solution pH (2), stirring speed (300 rpm), and temperature (298 ± 2 K). According to Fig. 5, the results show that the increase in initial concentration reduces BPA removal efficiency from 86.9% to 75.99%. The evolution of the adsorption efficiency, R% = 100 (1 − [BPA]/[BPA]0) depending on the initial BPA content, passes through a maximum of 87.81% around a concentration of 50 mg L−1, beyond which a gradual decrease to 76%, is recorded at 125 mg L−1. In fact, the decrease in the adsorbed fraction R% in highly concentrated adsorbate solutions is probably due either to the saturation of ACS75 sites relating to BPA or a phenomenon of aggregation of BPA molecules in solution, which could thus form molecular clusters unsuitable for their attachment to the adsorption sites.18 Nevertheless, the uptake of BPA increased from 14.86 mg g−1 to 63.16 mg g−1 when the initial concentration of BPA increased from 25 to 125 mg L−1. Let us note in passing that as the quantity q is directly proportional to ([BPA]0 − [BPA]), it also increases proportionally with the zero-time contents of BPA. Even if the residual content of [BPA] increases with the initial concentration, this does not affect the value of q because it is related to the absolute and not the relative difference in the concentrations. These results can be attributed to several effects, such as the increase in the driving force of the process, the massive use of the active sites of the adsorbent and/or the competing effect of a greater number of adsorbate molecules for the adsorbent binding sites.12,18,22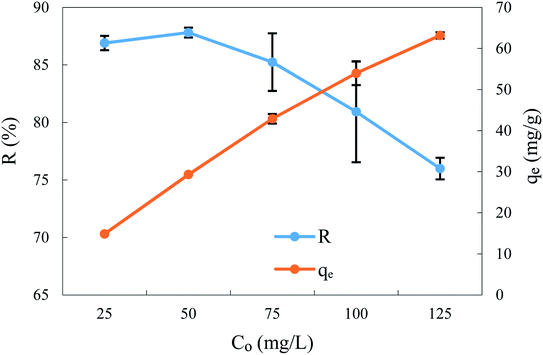 | ||
| Fig. 5 Effect of initial BPA concentration on the removal efficiency and uptake at equilibrium time. Adsorbent: 1.5 g L−1, pH: 2.0 and stirring speed: 300 rpm at T: 298 ± 2 K. | ||
3.5. Effect of adsorbent dosage
The adsorbent dose is considered a major parameter from an economic point of view, being ranked among the parameters with the greatest effect on the adsorption process. Thus, several runs were performed with four different dosages of ACS75 (0.5–2 g L−1) with a solution of BPA (50 mg L−1), contact time 360 min, initial pH of BPA solution, and 300 rpm agitation speed at room temperature (298 ± 2 K). The experimental results, given in Fig. 6, show that the removal efficiency of BPA increased from 56.71 to 90.06% when the dose of adsorbent increased from 0.5 to 1.5 g L−1. This behaviour is very common and has been reported in the literature. It is due to the increase in the surface area of the adsorbent, so the number of adsorption active sites increases, which facilitates the adsorption of BPA molecules on the adsorbent.57 However, the uptake decreased from 57.07 to 22.54 mg g−1 when the adsorbent dose was increased from 0.5 to 2 g L−1, which is also very common in the literature. Similar profiles have been observed for the adsorption of BPA onto goethite/activated carbon composite57 and onto activated carbons impregnated with iron oxide nanoparticles.58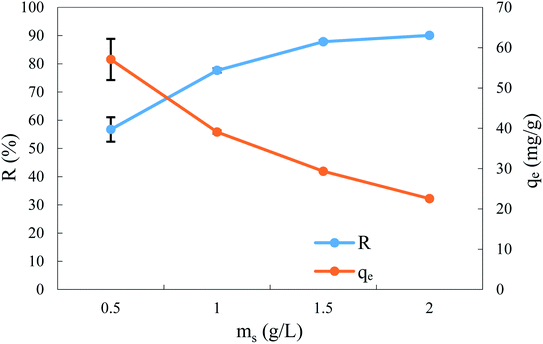 | ||
| Fig. 6 Effect of adsorbent dosage on the removal efficiency and uptake at equilibrium time: BPA concentration: 50 mg L−1, pH: 2.0 and stirring speed: 300 rpm at T: 298 ± 2 K. | ||
Finally the removal efficiency beyond 1.5 g L−1 of adsorbent dosage is almost stable. For this reason, this dose has been selected as the optimal adsorbent dosage for BPA removal.
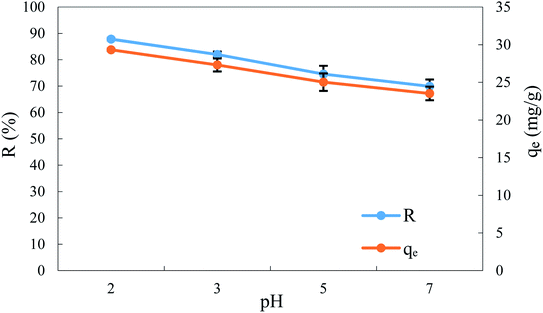
3.6. Effect of pH and adsorption mechanism
Thus, the adsorption efficiency was evaluated in the pH range 2.0 to 7.0, keeping the other operating parameters the same. The results are shown in Fig. 7. This shows that the removal efficiency and the uptake of BPA were a maximum in an acidic medium (pH 2) with values of 87.81% and 29.32 mg g−1, respectively. While the increase in pH decreases the removal efficiency and the uptake of BPA.Regarding the effect of pH on BPA adsorption, uneven results have already been reported in the literature.8,9,59 In this study, it can be seen that electrostatic interactions do not affect the adsorption of BPA on this adsorbent since the pHZPC of ACS75 was 4.6, as listed in Table 3. Although BPA carries two hydroxyl groups, at neutral pH it takes on a molecular form but it undergoes protonation in an acidic medium and deprotonation in a basic medium (pH > 7).60 Therefore, the electrostatic interactions play no role in the adsorption of BPA on ACS75. However, these results can be elucidated by the existence of interactions between the bonds. In this case, two other adsorption mechanisms may exist: π–π interaction and/or H bonding, where the electrostatic repulsion is dominant. These facts could probably be liable for the adsorption of BPA onto ACS75.10,60
Therefore, the adsorption of the BPA molecule onto ACS75 can be produced on the one hand, between the aromatic rings of the BPA molecules and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds of ACS75 through π–π electron coupling interaction. On the other hand, it is known that the ACS75 surface is rich in oxygen groups: in particular, the sulfonate groups (which are indicated by the FTIR spectrum), which can form hydrogen bonds with the hydroxyl group of BPA. Consequently, it can be assumed that adsorption of BPA onto ACS75 could be produced because of two types of adsorbent–adsorbate interactions, such as the π–π interaction and hydrogen bonding.3,60 As a result, the maximum adsorption of BPA onto ACS75 occurs at acidic pH (around 2).
C double bonds of ACS75 through π–π electron coupling interaction. On the other hand, it is known that the ACS75 surface is rich in oxygen groups: in particular, the sulfonate groups (which are indicated by the FTIR spectrum), which can form hydrogen bonds with the hydroxyl group of BPA. Consequently, it can be assumed that adsorption of BPA onto ACS75 could be produced because of two types of adsorbent–adsorbate interactions, such as the π–π interaction and hydrogen bonding.3,60 As a result, the maximum adsorption of BPA onto ACS75 occurs at acidic pH (around 2).
3.7. BPA adsorption kinetics
Study of the adsorption kinetics is considered to be crucial for describing the adsorption process. This latter in its turn allows control of the equilibrium time and the mass transfer of the adsorbate molecules. In comparison with model linearization techniques, nonlinear fitting using the Levenberg–Marquardt algorithm executed under Minitab allows us to obtain much better precision in the estimation of the kinetic parameters of the models.Therefore, the BPA adsorption onto ACS75 adsorbent was processed with the aim of canonical kinetic models (PFO and PSO), the Vermeulen model and also with fractal-like kinetic models (Weibull, Hill, PFOf and PSOf) and the fractal Vermeulen model.
Besides, a model with higher R2 value and lower ARE and RMSE values is considered a more appropriate model (see Tables S1–S4 in ESI Results†).
A comparison of the kinetic model results shows that for the fractal models, the determination coefficient R2 values are the highest and the ARE and RMSE values are the lowest for all operating conditions which suggests that the adsorption system follows fractal-like kinetic models.
However, an examination of the half-adsorption times t0.5 and the uptake at equilibrium qe estimated by these models shows the estimation for these two parameters compared to conventional models. In particular, concerning the experimental data obtained in a solution with a low concentration of BPA (25 mg L−1), the estimated half-adsorption time tends to infinity and the value of qe greatly exceeds the experimental value. However, the simulation of these data is perfectly relayed by the Vermeulen model (fractal version) which allows deduction of an effective diffusivity three times higher compared to that estimated for a solution of 50 mg L−1. This result suggests that the adsorption of BPA from dilute solutions is limited by mass transfer resistance and not by the surface process. Consequently, models based on mass transfer are better suited than those based on kinetics for the simulation of adsorption in the case of diffusion limitation.
To clarify the adsorption mechanism, the mass transfer resistance, in the liquid film surrounding adsorbent particles and in the internal porous structure of the solid, was evaluated by the intraparticle diffusion and film diffusion coefficients using standard simplified models.
The model of Weber and Morris for intraparticle diffusion is the third most common model applied to the kinetics of adsorption. The parameters of this model calculated from the multilinear curve q vs. √t are reported in Table S5 (ESI Results†). Fig. 8 exhibits two linear portions and as the 1st line does not go through the origin; this indicates that the intraparticle resistance is not the only one to control the adsorption process. Similar results have been determined by Şenol et al.39 in a study of BPA adsorption onto lichen biomass and by Supong et al.40 in a study of adsorption of BPA by Tithonia diversifolia biomass activated carbon.
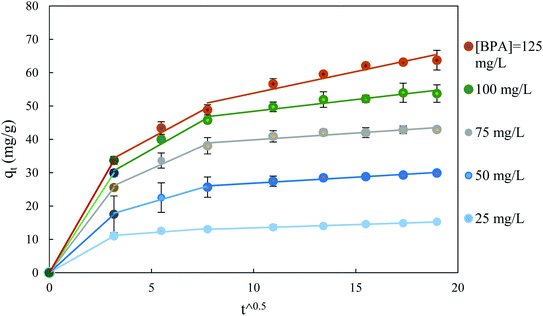 | ||
| Fig. 8 Application of the Weber and Morris model to the adsorption data of BPA on ACS75 obtained under various initial concentrations of BPA: ms: 1.5 g L−1, pH: 2 at T: 298 ± 2 K. | ||
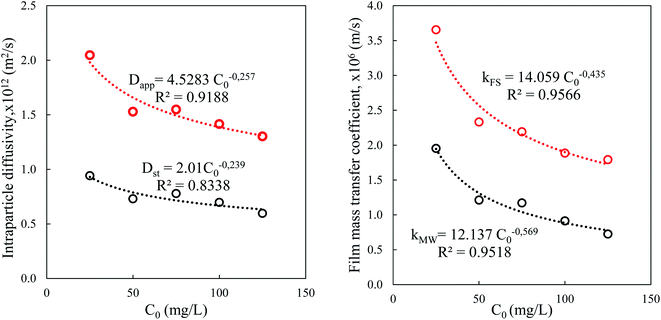
The variation of the diffusivity of BPA in the porous particles of the adsorbent follows the decreasing power law as a function of the content of BPA in solution (Fig. 9). The apparent diffusivity calculated from the half-adsorption time is approximately twice as great as that calculated from the short adsorption time Dst. This fact can be explained by the apparent diffusivity and its contribution from diffusion in the pores and on the internal surface, while Dst can be linked only to diffusion in macropores. Thus, the external mass transfer in the film is likely to rule the adsorption process over a short time <15 min, while intraparticle diffusion influences the long-term process.
The model of the film of Furusawa and Smith supposes the existence of a solid–liquid equilibrium in the case where the internal resistance is not the limiting stage. In the same way, the Mathews and Weber kMW coefficient is based on an assumption of rapid adsorption on the external surface so that the content of the adsorbate is zero. The driving force of this speed of transfer in the film is the difference in concentration between the surface and the front of the liquid phase which is supposed to be perfectly agitated. The decrease in these transfer coefficients as a function of the concentration is linked to the decrease in the concentration gradient.
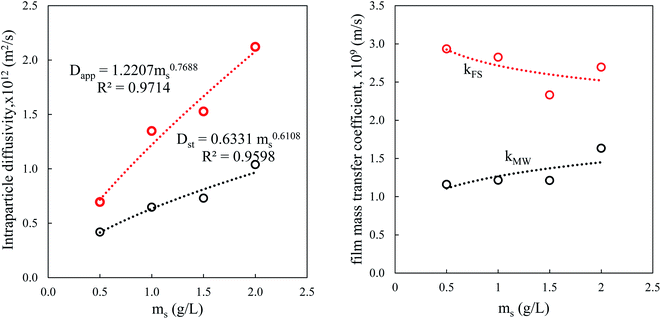
In the presence of a large quantity of adsorbent in solution, the surface available for solid/liquid contact is large, which facilitates the mass transfer between the bulk of the solution and the surface. Dapp and Dst are higher in a solution containing a large concentration of the suspension of particles because mass transport is easier. However, the decrease in the external coefficient kFS is because it is inversely proportional to the external surface A, which is itself proportional to the concentration of the suspension ms (Fig. 10).
The values of the apparent diffusivity Dapp in the adsorbent treated particles vary from 0.69 to 2.1 × 10−12 m2 s−1, whereas the short time diffusivity increases from 0.4 to 0.8 × 10−12 m2 s−1 for all operating conditions (Table S5†). Dapp is the apparent diffusion coefficient that is related to the internal volume and surface diffusion in the pores of the adsorbent particles, and its values are calculated from the experimental time of half-adsorption via the simple relation reported among others by eqn (18) in Table 2.61,62
The Vermeulen equation applied to the data for the amount of the fractions adsorbed vs. contact time for the whole experimental conditions allows a determination of the intraparticle diffusivity of BPA in the adsorbent. The results of the nonlinear fitting and the corresponding errors are gathered in Table S5.† The values of Dv vary from 0.46 to 2.61 10−12 m2 s−1, which are close to the values of Dapp. The large adjustment errors of this one parameter model prompted us to apply its fractal version (2 parameter model).
The molecular diffusivity of BPA in water is approximately 300 times greater than the apparent diffusivity, which indicates the great resistance to the mass transport of BPA in the internal porosity of the solid compared to its molecular diffusion in a quiet liquid medium. The values of the Biot numbers lie between 1 and 100, which also indicates that the global adsorption process is governed by the two resistances. These results agree with those in the literature.
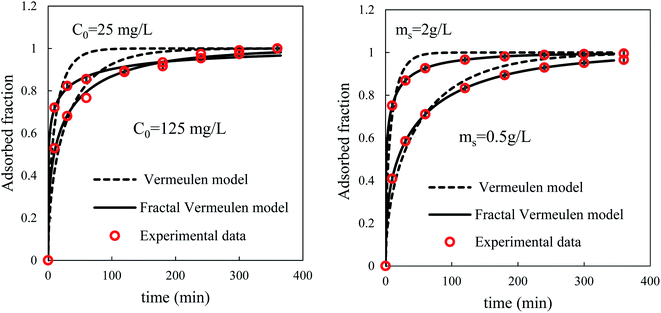
The simulation results depicted in Fig. 11 show that the fractal Vermeulen model is highly adapted to the whole time dependence process.
The fractal Vermeulen diffusivity (Fig. 12) decreased quickly with time. When the contact time varies from 1 to 10 min, the value of this diffusivity drops by 4 times.
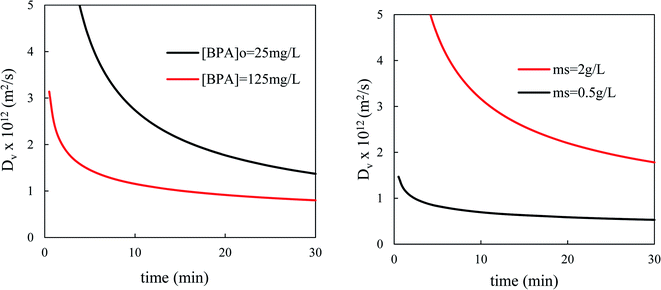 | ||
| Fig. 12 Variation of fractal Vermeulen diffusivity versus contact time for different initial concentrations of BPA (left) and for different adsorbent dosages (right). | ||
This slowing down of the internal diffusion flux as the contact time increases is certainly linked, still according to the concept of fractal kinetics, to the fact that the solute molecules rearrange themselves over time, which reduces the probability of shocks between them or with the walls of the pores and therefore their diffusion. On the other hand, the estimated value of the coefficient Dvf is higher than the quantity of adsorbent in suspension and the weakly concentrated BPA solutions.
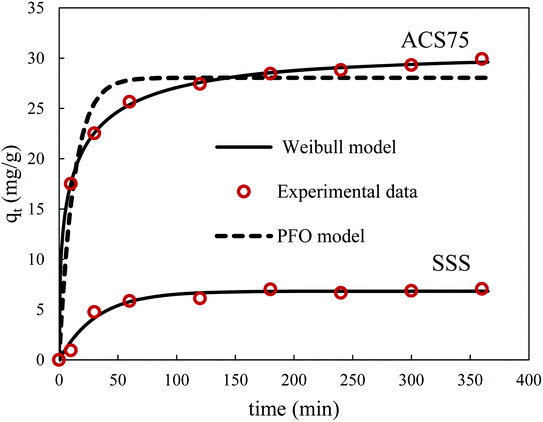
Fig. 13 shows the experimental and theoretical time evolution of the BPA uptake on natural SSS and ACS75. The maximum uptake of BPA on the treated material is 4.2 times greater than on the natural material, and the corresponding half-adsorption time is 3/10 times shorter. This performance of the treated adsorbent is linked to the increase in the pore volume (9.2 times higher) and the specific surface (4.4 times greater). The diffusion barrier to the passage of BPA molecules is easily overcome. The simplified models of intraparticle diffusion have also shown that the values of the characteristic diffusivities of BPA in the material treated are approximately 3 times higher than those in the natural adsorbent. Likewise, the application of models based on the kinetics of chemical reactions, PFO and PSO, for adsorption on the two materials, made it possible to deduce rate constants 2.6 times greater in the case of the adsorbent treated with acid.
Note that the application of the fractal models to the experimental data obtained for the adsorption on the natural SSS made it possible to deduce an alpha value of 0; the fractal models of Weibull and Hill therefore merge with those of PSO and of PFO, respectively. Indeed, before the acid treatment, it can be assumed that the surface of this adsorbent is homogeneous and in this case, the classical models are perfectly suited for simulating kinetic data.
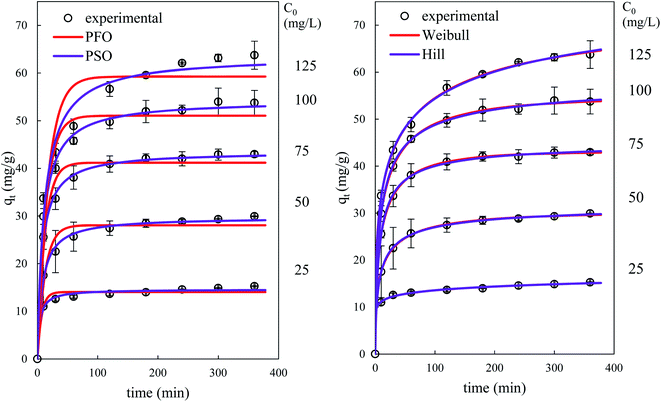
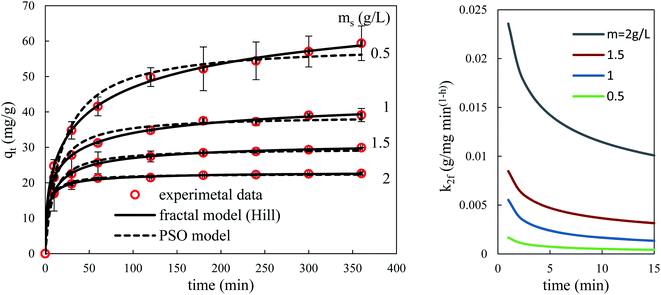
Fig. 14 and 15 show the evolution over time of the quantity adsorbed for different initial concentrations of BPA and different adsorbent dosages. The rate constants are functions of the process conditions. Increasing the initial bulk concentration shows a decrease in these constants (see Tables S1 and S2, ESI Results†). The parameters 1/k1 and 1/k2qe of both PFO and PSO models, respectively, present the time scale for the adsorption process to reach equilibrium; a longer time is required if the initial concentration is higher (smaller k1 or k2). In contrast, the PSO model is considered to be superior to the other models, because most kinetic solid–liquid adsorption can be well modelled by this model.
Observation of Fig. 14 and 15 clearly shows that fractal models are better suited than canonical models for the dynamic simulation of the adsorption process over the entire time range. This is linked to the fact that these models with three parameters are more suitable than models with one or two parameters. Furthermore, the factor a (or h) which takes account of the fractal aspect of adsorption varies according to the operating conditions. The fractal-like kinetic coefficients follow a law of decrease as a function of time, which gives an account of the local reality of the process. The rate of the process is always higher at the beginning than at the end.
According to the literature, there are several studies on the adsorption of BPA by biomass-based adsorbents whose kinetic studies have been carried out with the most widely used classical kinetic models, such as the PFO, PSO, and intraparticle diffusion models, the majority of whose BPA adsorption kinetics follow the PSO model and sometimes the PFO model.39–41,63,64 However, to our knowledge, no studies of fractal kinetics have ever been performed on BPA adsorption by biomasses.
3.8. BPA adsorption isotherms
In order to understand how the adsorbate interacts with the eco-adsorbent, the experimental data of BPA adsorption onto ACS75 were adjusted to the canonical isotherm models (Langmuir, Freundlich, Temkin, D–R and Jovanovich) and the fractal like-type isotherm models (GBS, BS, BG, and HS). The results for the nonlinear fitting are presented in Tables S6 and S7 (ESI Results†).The Langmuir model assumes monolayer adsorption on the adsorbent surface that contains a finite number of identical active sites. The separation factor of this model (RL) defines the state of the adsorption process: if it is irreversible, favourable, linear or unfavourable for (RL > 1) (RL = 0), (0 < RL > 1), (RL = 1), respectively. According to the results obtained, the RL values range from 0.299 to 0.827; which confirms the favourability of BPA adsorption onto ACS75.2,18
The Freundlich model assumes multilayer adsorption by the interaction between molecules adsorbed onto a non-uniform surface adsorbent. The nF parameter of this model allows determination of the adsorption efficiency. According to the results, the value of nF is greater than 1, indicating that the BPA is favourably adsorbed onto ACS75 over the entire concentration range studied.2,18
The Temkin model is related to the heat of adsorption; it assumes that the heat of adsorption of all molecules in the layer would decrease in a linear way with an increase in the adsorbent coverage. The constant BT of this model indicates the nature of the adsorption reaction. The results show a BT value of 20.237 J mol−1 (BT > 1 J mol−1), indicating that the BPA adsorption process on ACS75 is exothermic in nature.2,18
However, the value of the adsorption energy E (kJ mol−1) of the D–R model indicates the nature of the adsorption mechanism. In the present study, E = 0.36 kJ mol−1 (E < 8 kJ mol−1), which indicates that the adsorption of BPA onto ACS75 unfolds through a physical mechanism.2
The stochastic isotherm models are adapted to describe highly heterogeneous and complex systems. They are based on a sorption energy distribution model. It is possible to represent an adsorption process involving materials with interesting surface characteristics while assuming that the surface of the adsorbent is constituted of a finite plot number of sites with different energies of adsorption. In addition, it has been demonstrated that the heterogeneity of the material was derived from its chemical composition but also from its geometrical structure, which is linked to different morphologies, such as the size and shape of the pores.32,35,65 The parameter a describes the fractal properties of a non-uniform system and its adsorption mechanisms.35,65,66 While the parameter c is related to the agglomeration on the adsorbent surface, it gives an idea of the degree of heterogeneity of the adsorbent surface. Furthermore, it has been shown that an increase in the c value indicates a decrease in surface heterogeneity or the opposite.33
Fig. 16 illustrates the fit of BPA adsorption data onto ACS75 at pH = 2 by the models enumerated in the materials and methods section (canonical: Langmuir, Freundlich, D–R, Jovanovich, Temkin and fractal models: BS, GBS, BG, HS).
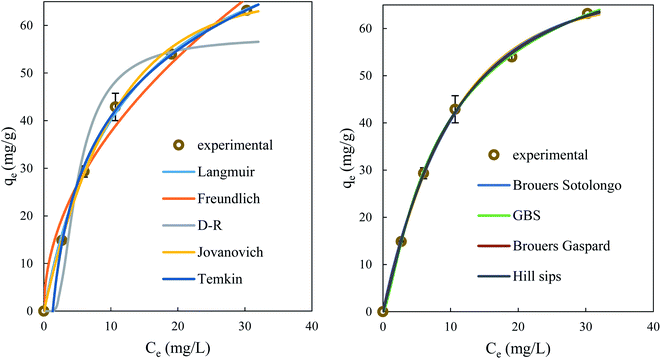 | ||
| Fig. 16 Adsorption isotherms of BPA on adsorbent fitted by canonical models (left) and by fractal models (right) operating at pH: 2, ms: 1.5 g L−1, T: 298 ± 2 K. | ||
Based on the R2, RMSE and ARE values, the adsorption isotherm studies showed that the HS model is appropriate for the experimental results obtained (R2 > 0.999, RMSE < 0.8, ARE < 0.05). Indeed, this model is a combined form of Langmuir and Freundlich expressions inferred to predict the heterogeneous adsorption systems and circumvent the limitation of the increase in adsorbate concentration associated with the Freundlich isotherm model. At high adsorbate concentrations, it predicts the Langmuir monolayer adsorption characteristics, while, at low adsorbate concentrations, it reduces to the Freundlich isotherm.67
The parameter a gives the measure of the scale properties of the adsorbent surface, its fitting value a = 1.2 > 1 is related to rapid initial adsorption as it may also indicate that adsorption to active sites is not monomolecular. The parameter c = 1 is related to the grouping of SSS particles to form agglomerates and also to the fractal distribution of the pores.
As a comparison, Şenol et al.39 have found that the adsorption isotherm was more consistent with the Langmuir and Redlich–Peterson models with two and three parameters, respectively, and in a study of BPA adsorption onto lichen biomass, Supong et al.40 have determined that the adsorption of BPA by Tithonia diversifolia biomass-based activated carbon is more correlated with the Langmuir isotherm model. In contrast, Juhola et al.41 have determined that the Sips isotherm is the most appropriate model for all adsorbents in a study of BPA adsorption onto biomass-based carbons, and Hernández-Abreu et al.63 have determined that the adsorption of BPA by Kraft lignin-based activated carbon is more correlated with the Sips model.
4. Conclusion
In this work, a novel eco-adsorbent modified with sulfuric acid (ACS75) was successfully prepared for BPA removal. First, the effect of acid treatment was evaluated; the best percentage by volume of H2SO4 was determined to be 75% (v/v). This caused a noteworthy improvement in the physicochemical properties of the SSS. A significant increase of 6.106 to 27.145 m2 g−1 was noted in the specific surface area. However, the adsorption efficiency of BPA has been remarkably increased, from 20.56% for raw SSS to 87.81% for ACS75 under conditions of 50 mg L−1 BPA concentration, 1.5 g L−1 adsorbent dosage and pH = 2 at room temperature (298 ± 2 K).The isotherm and kinetic model analysis revealed that the classical models, which assume time-invariant kinetic constants and diffusivities, are not adapted for the simulation of BPA adsorption onto SSS. In this framework, only the stochastic models (the kinetic model of Hill and isotherm model of HS) are applicable for these heterogeneous diffusion-limited processes. Also, it was found that the adsorption process was controlled by external mass transfer in the earlier stages (mean value of mass transfer coefficient of about 10−5 cm s−1) and by intraparticle diffusion in the later stages (mean value of Dapp of about 10−8 m2 s−1).
Consequently, the used treated SSS showed excellent adsorptive characteristics for the removal of BPA from an aqueous solution.
Conflicts of interest
The authors state that they have no personal relationships and no known competing financial interests that can influence the work presented in this paper.Acknowledgements
This study was funded by the Algerian Ministry of Higher Education and Scientific Research, research project code No. A16N01UN060120190001 and the Spanish Ministry of Science, Innovation and Universities and ERDF (Grant No. CTM2017-87326-R).References
- H. Zhu, Z. Li and J. Yang, A novel composite hydrogel for adsorption and photocatalytic degradation of bisphenol A by visible light irradiation, Chem. Eng. J., 2018, 334, 1679–1690 CrossRef CAS.
- K. Y. Foo and B. H. Hameed, Insights into the modelling of adsorption isotherm systems, Chem. Eng. J., 2010, 156, 2–10 CrossRef CAS.
- J. Fan, W. Yang and A. Li, Adsorption of phenol, bisphenol A and nonylphenol ethoxylates onto hypercrosslinked and aminated adsorbents, React. Funct. Polym., 2011, 71, 994–1000 CrossRef CAS.
- H. Javed, D. X. Luong, C. G. Lee, D. Zhang, J. M. Tour and P. J. J. Alvarez, Efficient removal of bisphenol-A by ultra-high surface area porous activated carbon derived from asphalt, Carbon, 2018, 140, 441–448 CrossRef CAS.
- T. Geens, D. Aerts, C. Berthot, J. P. bourguignon, L. Goeyens, P. Lecomte, G. Maghuin-Rogister, A. M. Pironnet, L. Pussemier, M. L. Scippo, J. V. Loco and A. Covaci, A review of dietary and non-dietary exposure to bisphenol-A, Food Chem. Toxicol., 2012, 50, 3725–3740 CrossRef CAS.
- I. Escalona, J. Grooth, J. Font and K. Nijmeijer, Removal of BPA by enzyme polymerisation using NF membranes, J. Membr. Sci., 2014, 468, 192–201 CrossRef CAS.
- A. B. Hernández-Abreu, S. Álvarez-Torrellas, V. I. Águeda, M. Larriba, J. A. Delgado, P. A. Calvo and J. García, New insights from modelling and estimation of mass transfer parameters in fixed-bed adsorption of Bisphenol A onto carbon materials, J. Contam. Hydrol., 2020, 228, 103566 CrossRef.
- V. K. Gupta, S. Agarwal, H. Sadegh, G. A. M. Ali, A. K. Bharti and A. S. H. Makhlouf, Facile route synthesis of novel graphene oxide-β-cyclodextrin nanocomposite and its application as adsorbent for removal of toxic bisphenol A from the aqueous phase, J. Mol. Liq., 2017, 237, 466–472 CrossRef CAS.
- W. Han, L. Luo and S. Zhang, Adsorption of bisphenol A on lignin: effects of solution chemistry, Int. J. Environ. Sci. Technol., 2012, 9, 543–548 CrossRef CAS.
- G. Bayramoglu, M. Y. Arica, G. Liman, O. Celikbicak and B. Salih, Removal of bisphenol A from aqueous medium using molecularly surface imprinted microbeads, Chemosphere, 2016, 10, 275–284 CrossRef.
- A. Bhatnagar and I. Anastopoulos, Adsorptive removal of bisphenol A (BPA) from aqueous solution: A review, Chemosphere, 2017, 168, 885–902 CrossRef CAS.
- B. Heibati, S. Rodriguez-Couto, A. Amrane, M. Rafatullah, A. Hawari and M. A. Al-Ghouti, Uptake of Reactive Black 5 by pumice and walnut activated carbon: Chemistry and adsorption mechanisms, J. Ind. Eng. Chem., 2014, 20, 2939–2947 CrossRef CAS.
- D. C. W. Tsang, J. Hu, M. Y. Liu, W. Zhang, K. C. K. Lai and I. M. C. Lo, Activated Carbon Produced from Waste Wood Pallets: Adsorption of Three Classes of Dyes, Water, Air, Soil Pollut., 2007, 184, 141–155 CrossRef CAS.
- S. Rangabhashiyam and P. Balasubramanian, The potential of lignocellulosic biomass precursors for biochar production: Performance, mechanism and wastewater application–A review, Ind. Crops Prod., 2019, 128, 405–423 CrossRef.
- N. Tapia-Orozco, R. Ibarra-Cabrera, A. Tecante, M. Gimeno, R. Parra and R. Garcia-Arrazola, Removal strategies for endocrine disrupting chemicals using cellulose-based materials as adsorbents: A review, J. Environ. Chem. Eng., 2016, 4, 3122–3142 CrossRef CAS.
- J. Li, N. Liang, X. Jin, D. Zhou, H. Li, M. Wu and B. Pan, The role of ash content on bisphenol A sorption to biochars derived from different agricultural wastes, Chemosphere, 2017, 171, 66–73 CrossRef CAS.
- L. Zhou, C. Richard, C. Ferronato, J. M. Chovelon and M. Sleiman, Investigating the performance of biomass-derived biochars for the removal of gaseous ozone, adsorbed nitrate and aqueous bisphenol A, Chem. Eng. J., 2018, 334, 2098–2104 CrossRef CAS.
- D. Balarak, Kinetics, Isotherm and Thermodynamics Studies on Bisphenol A Adsorption using Barley husk, Int. J. ChemTech Res., 2016, 9, 681–690 CAS.
- M. Zbair, K. Ainassaari, Z. El Assal, S. Ojala, N. El Ouahedy, R. L. Keiski, M. Bensitel and R. Brahmi, Steam activation of waste biomass: highly microporous carbon, optimisation of bisphenol A, and diuron adsorption by response surface methodology, Environ. Sci. Pollut. Res., 2018, 25, 35657–35671 CrossRef CAS.
- A. C. Arampatzidou and E. A. Deliyanni, Comparison of activation media and pyrolysis temperature for activated carbons development by pyrolysis of potato peels for effective adsorption of endocrine disruptor bisphenol-A, J. Colloid Interface Sci., 2016, 466, 101–112 CrossRef CAS.
- J. M. Salman and F. D. Almutairi, Bath Adsorption Study of Methylene Blue Dye Onto Sunflower Seeds Husks Activated Carbon, Adv. Nat. Sci., 2013, 6, 44–47 CAS.
- E. Tomczak and P. Tosik, waste plant material as a potential adsorbent of a selected azo dye, Chem. Eng. Process., 2017, 38(2), 283–294 CAS.
- D. Suteu, C. Zaharia and T. Malutan, Removal of Orange 16 reactive dye from aqueous solutions by waste sunflower seed shells, J. Serb. Chem. Soc., 2011, 76(4), 607–624 CrossRef CAS.
- A. Witek-Krowiak, Analysis of temperature-dependent biosorption of Cu2+ ions on sunflower hulls: Kinetics, equilibrium and mechanism of the process, Chem. Eng. J., 2012, 192, 13–20 CrossRef CAS.
- R. Rojas, J. Usero, E. Vanderlinden and H. El Bakouri, Adsorption study of low-cost and locally available organic substances and a soil to remove pesticides from aqueous solutions, J. Hydrol., 2015, 520, 461–472 CrossRef CAS.
- K. Mahmoudi, N. Hamdi and E. Srasra, Preparation and characterisation of activated carbon from date pits chemical activation with zinc chloride for methyl orange adsorption, J. Mater. Environ. Sci., 2014, 5, 1758–1769 Search PubMed.
- X. P. Luo, S. Y. Fu, Y. M. Du, J. Z. Guo and B. Li, Adsorption of methylene blue and malachite green from aqueous solution by sulfonic acid group modified MIL-101, Microporous Mesoporous Mater., 2017, 237, 268–274 CrossRef CAS.
- S. Guiza, F. Brouers and M. Bagane, Fluoride removal from aqueous solution by montmorillonite clay: Kinetics and equilibrium modeling using new generalized fractal equation, Environ. Technol. Innov., 2020, 101187 CrossRef.
- M. Wakkel, B. Khiari and F. Zagrouba, Textile wastewater treatment by agro-industrial waste: Equilibrium modelling, thermodynamics and mass transfer mechanisms of cationic dyes adsorption onto low-cost lignocellulosic adsorbent, J. Taiwan Inst. Chem. Eng., 2019, 96, 439–452 CrossRef CAS.
- K. L. Tan and B. H. Hameed, Insight into the adsorption kinetics models for the removal of contaminants from aqueous solutions, J. Taiwan Inst. Chem. Eng., 2017, 1–24 Search PubMed.
- M. C. Ncibi, B. Mahjoub, M. Seffen, F. Brouers and S. Gaspard, Sorption dynamic investigation of chromium (VI) onto Posidonia oceanica fibres: Kinetic modelling using new generalised fractal equation, Biochem. Eng. J., 2009, 46, 141–146 CrossRef CAS.
- T. Selmi, M. Seffen, H. Sammouda, S. Mathieu, J. Jagiello, A. Celzard and V. Fierro, Physical meaning of the parameters used in fractal kinetic and generalised adsorption models of Brouers–Sotolongo, Adsorption, 2018, 24, 11–27 CrossRef CAS.
- S. Karoui, R. Ben Arfi, K. Mougin, A. Ghorbal, A. Assadi and A. Amrane, Synthesis of novel biocomposite powder for simultaneous removal of hazardous ciprofloxacin and methylene blue: Central composite design, kinetic and isotherm studies using Brouers Sotolongo family models, J. Hazard. Mater., 2020, 37, 121675 CrossRef.
- A. M. Ben Hamissa, F. Brouers, M. C. Ncibi and M. Seffen, Kinetic Modeling Study on Methylene Blue Sorption onto Agave americana fibers: Fractal Kinetics and Regeneration Studies, Sep. Sci. Technol., 2013, 48(18), 2834–2842 CrossRef.
- F. Brouers, The Fractal (BSf) Kinetics Equation and Its Approximations, J. Mod. Phys., 2014, 5, 1594–1601 CrossRef.
- M. K. Narbat, F. Orang, M. S. Hashtjin and A. Goudarzi, Fabrication of porous hydroxyapatite-gelatin composite scaffolds for bone tissue engineering, Iran. Biomed. J., 2006, 10, 215–223 CAS.
- S. Muhammad, S. T. Hussain, M. Waseem, A. Naeem, J. Hussain and M. T. Jan, Surface charge properties of zirconium dioxide, Iran. J. Sci. Technol., 2012, 4, 481–486 Search PubMed.
- A. Bhatnagar and I. Anastopoulos, Adsorptive removal of bisphenol A (BPA) from aqueous solution: A review, Chemosphere, 2017, 168, 885–902 CrossRef CAS.
- Z. M. Şenol, Ü. D. Gül and R. Gürkan, Bio-sorption of bisphenol a by the dried- and inactivated-lichen (Pseudoevernia furfuracea) biomass from aqueous solutions, J. Environ. Health Sci. Eng., 2020, 18, 853–864 CrossRef.
- A. Supong, P. C. Bhomick, M. Baruah, C. Pongener, U. B. Sinha and D. Sinha, Adsorptive removal of Bisphenol A by biomass activated carbon and insights into the adsorption mechanism through density functional theory calculations, Sustainable Chem. Pharm., 2019, 13, 100159 CrossRef.
- R. Juhola, H. Runtti, T. Kangas, T. Hu, H. Romar and S. Tuomikoski, Bisphenol A removal from water by biomass-based carbon: Isotherms, kinetics and thermodynamics studies, Environ. Technol., 2018, 41, 1–27 Search PubMed.
- S. M. Miraboutalebi, S. K. Nikouzad, M. Peydayesh, N. Allahgholi, L. Vafajoo and G. McKay, Methylene blue adsorption via maise silk powder: Kinetic, equilibrium, thermodynamic studies and residual error analysis, Process Saf. Environ. Prot., 2017, 6, 191–202 CrossRef.
- S. Langergen and B. K. Svenska, Zur theorie der sogenannten adsoption geloester stoffe, Vetensk. Handl., 1898, 24, 1–39 Search PubMed.
- Y. S. Ho and G. Mckay, Pseudo-second order model for sorption processes, Process Biochem., 1999, 34, 451–465 CrossRef CAS.
- G. Crini and E. Lichtfouse, Green adsorbents for pollutant removal fundamentals and design, Springer, France, 2018, DOI:10.1007/978-3-319-92111-2.
- N. El Bardiji, K. Ziat, A. Naji and M. Saidi, Fractal-Like Kinetics of Adsorption Applied to the Solid/Solution Interface, J. Am. Chem. Soc., 2020, 5(10), 5105–5115 CAS.
- R. Kopelman, Fractal Reaction Kinetics, J. Plankton Res., 1988, 241, 1620–1626 CAS.
- W. J. Weber and J. C. Morris, Kinetics of adsorption on carbon from solution, J. Sanit. Eng. Div., 1963, 89, 31–60 Search PubMed.
- G. E. Boyd, A. W. Adamson and L. S. Myers, The exchange adsorption of ions from aqueous solutions by organic zeolites. II. Kinetics1, J. Am. Chem. Soc., 1947, 69, 2836–2848 CrossRef CAS.
- J. Guo, W. S. Xu, Y. L. Chen and A. C. Lua, Adsorption of NH3 onto activated carbon prepared from palm shells impregnated with H2SO4, J. Colloid Interface Sci., 2005, 281, 285–291 CrossRef CAS.
- B. S. Girgis, L. B. Khalil and T. A. M. Tawfik, Activated carbon from sugar cane bagasse by carbonisation in the presence of inorganic acids, J. Chem. Technol. Biotechnol., 1994, 61, 87–92 CrossRef CAS.
- R. R. Krishni, K. Y. Foo and B. H. Hameed, Food cannery effluent, pineapple peel as an effective low-cost biosorbent for removing cationic dye from aqueous solutions, Desalin. Water Treat., 2014, 52, 6096–6103 CrossRef CAS.
- J. Wang, W. Xu, J. Ren, X. Liu, G. Lu and Y. Wang, Efficient catalytic conversion of fructose into hydroxymethylfurfural by a novel carbon-based solid acid, Green Chem., 2011, 13, 2678–2681 RSC.
- X. Hu, Y. Xue, L. Long and K. Zhang, Characteristics and batch experiments of acid- and alkali-modified corncob biomass for nitrate removal from aqueous solution, Environ. Sci. Pollut. Res., 2018, 25, 19932–19940 CrossRef CAS.
- M. D. T. Islam, R. Saenz-Arana, C. Hernandez, T. Guinto, M. D. A. Ahsan, H. Kim, Y. Lin, B. Alvarado-Tenorio and J. C. Noveron, Adsorption of methylene blue and tetracycline onto biomass-based material prepared by sulfuric acid reflux, RSC Adv., 2018, 8, 32545 RSC.
- K. S. W. Sing, Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity, Pure Appl. Chem., 1982, 64, 2201–2218 Search PubMed.
- J. R. Koduru, L. P. Lingamdinne, J. Singh and K. H. Choo, Effective removal of bisphenol A (BPA) from water using a goethite/activated carbon composite, Process Saf. Environ., 2016, 103, 87–96 CrossRef CAS.
- H. S. Park, J. R. Koduru, K. H. Choo and B. W. Lee, Activated carbons impregnated with iron oxide nanoparticles for enhanced removal of bisphenol A and natural organic matter, J. Hazard. Mater., 2015, 286, 315–324 CrossRef CAS.
- A. Stavrinou, C. A. Aggelopoulos and C. D. Tsakiroglou, Exploring the adsorption mechanisms of cationic and anionic dyes onto agricultural waste peels of banana, cucumber and potato: Adsorption kinetics and equilibrium isotherms as a tool, J. Environ. Chem. Eng., 2018, 6, 6958–6970 CrossRef CAS.
- I. Bautista-Toledo, M. A. Ferro-Garcia, J. Rivera-Utrilla, C. Moreno-Castilla and F. J. Vegas Fernandez, Bisphenol A removal from water by activated carbon. Effects of carbon characteristics and solution chemistry, Environ. Sci. Technol., 2005, 39, 6246–6250 CrossRef CAS.
- F. G. Helfferich, Principles of adsorption & adsorption processes, by D. M. Ruthven, John Wiley & Sons, AIChE J., 1985, 31, 523–524 CrossRef.
- C. R. Girish and V.R. Murty, Mass Transfer Studies on Adsorption of Phenol from Wastewater Using Lantana camara, Forest Waste. Int. J. Chem. Eng., 2016, 1–11 Search PubMed.
- A. B. Hernández-Abreu, S. Álvarez-Torrellas, V. I. Águeda, M. Larriba, J. A. Delgado, P. A. Calvo and J. García, Enhanced removal of the endocrine disruptor compound Bisphenol A by adsorption onto green-carbon materials. Effect of real effluents on the adsorption process, J. Environ. Manage., 2020, 266, 110604 CrossRef.
- M. H. Dehghani, R. R. Karri, Z. T. Yeganeh, A. H. Mahvi, H. Nourmoradid, M. Salari and A. Zarei, Mika Sillanpää, Statistical modelling of endocrine disrupting compounds adsorption onto activated carbon prepared from wood using CCD-RSM and DE hybrid evolutionary optimization framework: Comparison of linear vs. non-linear isotherm and kinetic parameters, J. Mol. Liq., 2020, 302, 112526 CrossRef CAS.
- F. Brouersa and T. J. Al-Musawi, On the Optimal Use of Isotherm Models for the Characterisation of Biosorption of Lead Onto Algae, J. Mol. Liq., 2015, 212, 46–51 CrossRef.
- A. Kesraoui, T. Selmi, M. Seffen and F. Brouers, Influence of alternating current on the adsorption of indigo carmine, Environ. Sci. Pollut. Res., 2017, 24, 9940–9950 CrossRef CAS.
- R. Sips, Combined form of Langmuir and Freundlich equations, J. Chem. Phys., 1948, 16, 490–495 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra09137e |
| This journal is © The Royal Society of Chemistry 2021 |