Open Access Article
Open Access ArticleAdsorption of CO2 on the ω-Fe (0001) surface: insights from density functional theory
S. Assa Aravindh *a,
Wei Cao
*a,
Wei Cao a,
Matti Alataloa,
Marko Huttulaa and
Jukka Kömib
a,
Matti Alataloa,
Marko Huttulaa and
Jukka Kömib
aNano and Molecular Systems Research Unit, University of Oulu, FIN-90014, Finland
bMaterials and Mechanical Engineering Research Unit, University of Oulu, FIN-90014, Finland. E-mail: Assa.Sasikaladevi@oulu.fi
First published on 10th February 2021
Abstract
The stabilization of a hexagonal phase known as the ω-phase in steel has recently been identified. The presence of C in steel samples is found to be helping the formation of this otherwise meta stable phase. This indicates that the probability of degradation of the surface is high in steel samples containing the ω-phase, through surface adsorption. Here we calculate the adsorption process of CO2 on the ω-Fe(0001) surface, for different sites and find that it strongly adsorbs horizontally with a bent configuration. The adsorption is characterized by significant charge transfer from the surface Fe atoms to the CO2 molecule, and structural modification of the molecule is occurring. The density of states calculations indicate that hybridization and subsequent charge transfer is probable between the d orbitals of Fe and p orbitals of CO2, resulting in strong chemisorption, that further leads to spontaneous dissociation of the molecule.
1 Introduction
A hexagonal phase, known as omega (ω) has been identified in transmission electron microscopy (TEM) measurements in steel samples.1–12 The ω phase is supposed to be metastable, yet getting trapped in crystal defects and it has been shown that the stabilization of ω occurs as an intermediate phase between the bcc–fcc transition in steel7 and the presence of C is known to influence its formation. Ping et al.1 have shown that the ω phase possesses 3.6% lower volume and 0.18 eV per cell higher energy than bcc-Fe, with atoms in alternate layers coupling anti-ferromagnetically. The increase in C concentration is found to assist in the stabilization of the ω phase and at higher concentrations, it will be stabilized as ω-Fe3C. This hexagonal phase often acts as a sink for vacancies and impurities such as H or He atoms. In this scenario, the probability of CO2 corrosion in steel, aided by the presence of the ω phase and dissolved CO2 is highly probable, and that will be detrimental to many industries.13 The mechanisms underlying CO2 corrosion consist of many mechanical and environmental factors.14 Temperature is one of the prominent factors in CO2 corrosion, as it affects the formation of a protective layer. Hence, the possibility of formation of a protective layer is lower in omega-Fe surfaces as this meta stable structure is often formed due to mechanical constraints at grain/twin boundaries.6 The ω-phase forms mostly at interfaces or twin boundaries in steel in the presence of atomic constraints,6 which was earlier attributed to extra electron diffraction spots arising from internal twins or carbides. Another important factor influencing the formation of ω is the presence of C in steel.1,7,8 Since the ω-phase is found to be formed at the interfaces and boundaries, exposure to gases and contaminants is higher than that of the bulk part of the material. Hence the possibility of CO2 induced corrosion is highly probable in this meta stable phase and present investigation focus on the energetic of CO2 adsorption on ω-Fe surfaces. It has been reported that the presence of CO2 combined with moisture exposure can lead to formation of carbonic acid and cause corrosion in steel pipe lines.15 Hence it is important to investigate the stability and structural changes caused by the adsorption of CO2 as well as the possibility of activation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds, that leads to dissociation. In this scenario, we employ density functional theory (DFT) to investigate the adsorption energy, electronic structure and quantify the charge transfer properties of CO2 on ω surface. Our results provide useful insights into the CO2 dissociation mechanism at the ω-Fe surface, since we have seen that the activation of the molecule occurs at the surface followed by dissociation, due to the strong charge transfer between surface and adsorbates. This indicates that compared to the more inert CO2 molecule, the CO moiety can interact with atmospheric moisture and enhance the degradation of the surface.
O bonds, that leads to dissociation. In this scenario, we employ density functional theory (DFT) to investigate the adsorption energy, electronic structure and quantify the charge transfer properties of CO2 on ω surface. Our results provide useful insights into the CO2 dissociation mechanism at the ω-Fe surface, since we have seen that the activation of the molecule occurs at the surface followed by dissociation, due to the strong charge transfer between surface and adsorbates. This indicates that compared to the more inert CO2 molecule, the CO moiety can interact with atmospheric moisture and enhance the degradation of the surface.
2 Computational methodology
The DFT calculations are carried out using plane wave-based pseudopotential code Vienna Ab initio Simulation Package (VASP).16–18 A kinetic energy cut-off of 520 eV is used to expand the plane waves included in the basis set. Spin polarization is included in the calculations with Gaussian smearing and a smearing width of 0.01 eV is used.19 The ω-Fe(0001) surface is modeled using the optimized atomic coordinates of a unit cell of (1 × 1 × 1) ω-Fe. The optimized lattice parameters for the ω-Fe unit cell are a = 3.85 Å and c = 2.42 Å, and are in agreement with previously reported values.1 To construct a surface slab, vacuum layers are added along the z-direction to make the interaction between the periodically repeated images negligible. The supercell dimensions are a = 7.94 Å, b = 7.94 Å and c = 17.18 Å respectively such that 36 Fe atoms are present. For the integration of the Brillouin zone, a Gamma centered k grid of (5 × 5 × 2) dimensions is used. The ω-Fe(0001) surface is relaxed without symmetry constraints such that corresponding energy and force tolerances of 10−6 eV and 0.001 eV Å−1, respectively, are achieved. The exchange and correlation is described using generalized gradient approximation (GGA). We employ the projected augmented wave method (PAW) in the parameter-free Perdew–Burke–Ernzerhof (PBE) formalism.19,20 The above choices are based on previous studies that have shown that the PBE approximation accurately reproduces the energetic and magnetic properties of Fe based systems and specifically those of ω-Fe in the presence of alloying elements.1,5,21 Initially we optimized the slab supercell relaxing all layers and upon addition of CO2 molecule, bottom layers are fixed to bulk positions and top layers are relaxed.The adsorption energy of CO2 on the ω-Fe (0001)surfaces is calculated using the relation,22
| Eads = Esurf+CO2 − Esurf + ECO2 | (1) |
3 Results and discussion
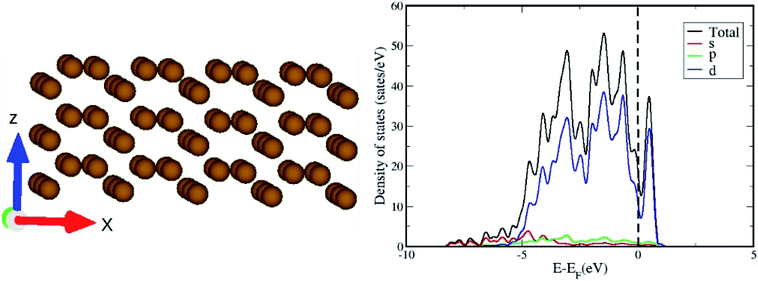
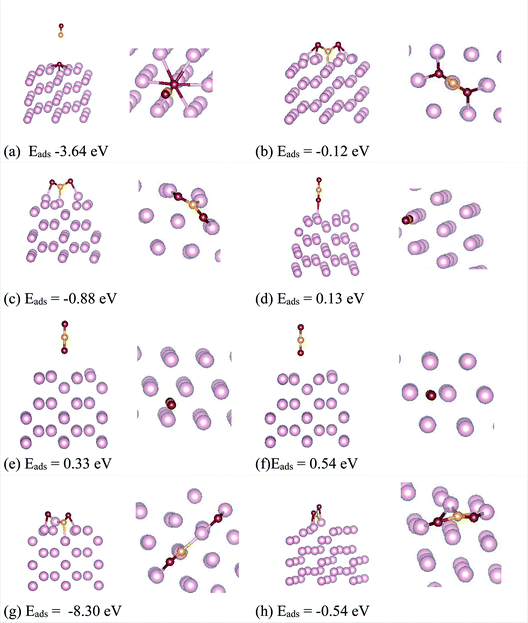
The optimized geometry and orbital resolved density of states of ω-Fe (0001) are shown in Fig. 1(a) and (b) respectively. The density of states is metallic and dominated by the contribution from Fe-d orbitals surrounding the Fermi level. This indicates that the chances of hybridization of Fe-d orbitals and p-orbitals of the CO2 molecule are highly probable. After the pristine surface is optimized, CO2 molecule is placed on the surface and the adsorption energies are calculated after optimization. It is worthwhile to mention that to model the adsorption of CO2 with the Fe surface, both the atoms of CO2 and three topmost layers of the slab are subjected to unconstrained relaxation, such that the residual forces on all atoms reached 0.001 eV Å−1. Furthermore, no symmetry constraints are imposed during the structural optimization; and the CO2 molecule was free to move laterally and vertically from the initial site as well as to reorient itself to the minimum energy geometry. Total 8 configurations were considered including both vertical and horizontal orientations of CO2. The configurations are chosen in such a way that, the vertical CO2 perpendicularly aligned above the top of an Fe atom, attached over an Fe–Fe bond, attached in the hollow space formed by three Fe atoms situated at the three corners of a triangle and also on top of an Fe atom in the middle of the hexagonal ring. Same configurations were considered for the horizontal alignment of CO2. The stable adsorption geometries after relaxation are presented in Fig. 2. The perpendicularly oriented linear CO2 configurations (d), (e) and (f) present very weak adsorption with the omega surface, indicating a physisorption, evident from the longer Fe–O distances. The adsorption energies are positive in these three cases, indicating that the reaction is endothermic.The linear configuration (a) on the other hand, spontaneously dissociates into O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species with adsorption energy of −3.64 eV. For the configurations (a) and (g) a spontaneous CO
O species with adsorption energy of −3.64 eV. For the configurations (a) and (g) a spontaneous CO![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond cleavage is occurring, indicating that the dissociation process occurs without an energy barrier. The configurations (c) and (h) showed the lowest adsorption energies for CO2 adsorption. Both (c) and (h) are almost equivalent positions geometrically, where CO2 adsorbs in a bent configuration whereby the C and O atoms are adsorbed on top of nearby Fe atoms constituting the hexagonal ring on the surface. The calculated bond lengths are presented in Table 1. Though the bond lengths are almost similar between the two configurations, the O–C–O bond angles are 124.22 degree for (c) and 129.32 degree for (h) respectively. The lower bond angle for the configuration (c) indicates that the molecule is activated more in this case. The chemisorption of CO2 on the ω-Fe(0001) surface in turn affects the C–O bond strength, and consequently, the possibility of decomposition of CO2 moiety into surface bound oxygen and CO is possible. It can be seen that the C–O bonds for the configurations with least adsorption energy are elongated to 1.29–1.34 Å, compared to the gas phase C–O bond length which is 1.17 Å signifying that the C–O bonds are activated. For the most stable configurations adsorbed through chemisorption, it can be seen that the CO2 adsorb in a bent configuration such that CO2 molecule interacts with two surface Fe atoms through both oxygen atoms. The extended C–O bond lengths signify that these bonds are weakened due to the π-antibonding occupation, which may further lead to activation of the molecule, and help in the reduction of the CO2 molecule on the surface. It can be seen that in the chemisorbed configurations, all the atoms share bonds with the substrate Fe atoms. Further, since the CO2 molecule can receive electrons into the lowest unoccupied molecular orbital to become negatively charged bent species, the charge transfer between atoms are calculated.
O bond cleavage is occurring, indicating that the dissociation process occurs without an energy barrier. The configurations (c) and (h) showed the lowest adsorption energies for CO2 adsorption. Both (c) and (h) are almost equivalent positions geometrically, where CO2 adsorbs in a bent configuration whereby the C and O atoms are adsorbed on top of nearby Fe atoms constituting the hexagonal ring on the surface. The calculated bond lengths are presented in Table 1. Though the bond lengths are almost similar between the two configurations, the O–C–O bond angles are 124.22 degree for (c) and 129.32 degree for (h) respectively. The lower bond angle for the configuration (c) indicates that the molecule is activated more in this case. The chemisorption of CO2 on the ω-Fe(0001) surface in turn affects the C–O bond strength, and consequently, the possibility of decomposition of CO2 moiety into surface bound oxygen and CO is possible. It can be seen that the C–O bonds for the configurations with least adsorption energy are elongated to 1.29–1.34 Å, compared to the gas phase C–O bond length which is 1.17 Å signifying that the C–O bonds are activated. For the most stable configurations adsorbed through chemisorption, it can be seen that the CO2 adsorb in a bent configuration such that CO2 molecule interacts with two surface Fe atoms through both oxygen atoms. The extended C–O bond lengths signify that these bonds are weakened due to the π-antibonding occupation, which may further lead to activation of the molecule, and help in the reduction of the CO2 molecule on the surface. It can be seen that in the chemisorbed configurations, all the atoms share bonds with the substrate Fe atoms. Further, since the CO2 molecule can receive electrons into the lowest unoccupied molecular orbital to become negatively charged bent species, the charge transfer between atoms are calculated.
| Configuration | Relaxed bond lengths (Å) | Bader charges | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| d(C–O1) | d(C–O2) | d(Fe–O1) | d(Fe–O2) | d(Fe–C) | O1 | O2 | C | Fe(C) | Fe(O1) | Fe(O2) | |
| (a) | 3.63 | 1.14 | 1.87 | −1.04 | −1.83 | 1.83 | 0.34 | ||||
| (b) | 1.34 | 1.34 | 2.07 | 2.07 | 1.93 | −1.71 | −1.71 | 1.94 | |||
| (c) | 1.29 | 1.29 | 1.97 | 1.93 | 1.97 | −1.74 | −1.72 | 2.38 | 0.10 | 0.14 | −0.01 |
| (d) | 1.18 | 1.17 | 2.37 | −2.07 | −1.98 | 4 | 0.14 | ||||
| (e) | 1.18 | 1.18 | 2.72 | −2.02 | −2.04 | 4 | |||||
| (f) | 1.18 | 1.17 | 2.76 | −2.03 | −2.01 | 4 | |||||
| (g) | 5.24 | 1.30 | 2.96 | 1.79 | 1.97 | −1.84 | −1.01 | 0.61 | 0.37 | 0.28 | 0.24 |
| (h) | 1.29 | 1.27 | 1.99 | 2.05 | 1.97 | −1.81 | −1.72 | 2.44 | 0.09 | −0.05 | −0.17 |
Bader charge analysis was carried out23,24 to quantify the charge transfer mechanism between the surfaces and CO2. The calculated values are shown in Table 1. It can be seen that there exist significant charge transfer between the Fe surface and the C, O atoms for the chemisorbed configurations. The negative charge on the O atoms indicate that electrons are gained, results in a net charge gain as CO2 molecule. For the most stable CO2 adsorbed configuration (c), while the C atom and Fe atoms bonded to C and first O atom lose charge, the Fe atom bonded to the second O atom, slightly gains charge. For the three physisorbed configurations (d), (e) and (f), there is no change in charge of the C atom. While the C atom is attached to the Fe atom at the center of the hexagonal ring, the detached O atom moves to a nearest neighbor Fe atom, such that the O atoms acquire charges, and C and Fe atoms loose charge. For the configuration (g) where, the CO2 dissociates to O and CO moieties, there is significant charge transfer between the C and O atoms. This combined with the elongated bonds establish the fact that the CO2 molecule dissociates without energy barriers in this configuration.
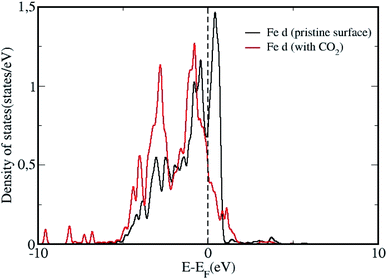
We analyze the partial density of states (PDOS) projected onto molecular orbitals of the most stable configuration with CO2 adsorption and presented in Fig. 3. As the DOS for all chemisorbed CO2 configurations are not so different from each other, we have only shown the DOS for the most stable surface + CO2 geometry. The PDOS calculated for the isolated CO2 molecule, projected on to the p orbitals are also shown in Fig. 3. Owing to the chemisorption, the p orbitals of CO2 shift downwards from the Fermi level, presenting strong overlap with the d orbitals of Fe, indicating strong interaction and chemisorption on the surface. We plot the density of states (DOS) projected on to the d orbital for a surface Fe atom for the pristine surface and for the most stable CO2 adsorbed configuration in Fig. 4. The Fe site is the one where the C atom is attached to form a Fe–C bond, such that the changes in d band can be analyzed before and after adsorption. It can be seen that the density of states of the Fe atom shift towards the Fermi level after adsorption of the CO2 molecule, indicating the strong adsorption. The p orbitals of CO2 can effectively hybridize with the d orbitals of the Fe surface, creating strong Fe–C and Fe–O bonds with the bent CO2 molecule making significant charge transfer from the Fe d orbitals in to the p orbitals of CO2 molecule results in the formation of a negatively charged CO2 species as evidenced by the Bader charge analysis. This strong charge transfer is related to the elongation of the C–O bond, resulting in its activation.
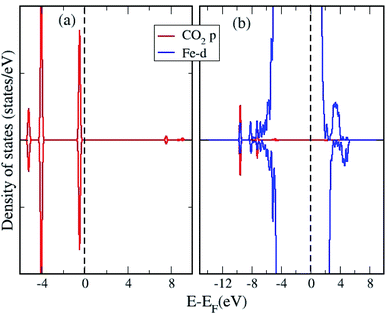 | ||
| Fig. 3 The orbital projected density of states of (a) isolated CO2 molecule and (b) ω-Fe(0001) surface with chemisorbed CO2 molecule. | ||
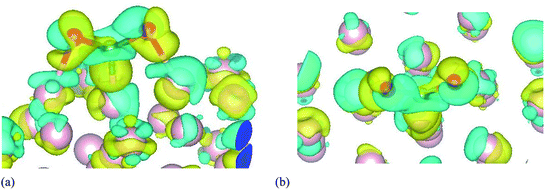
To get deeper understanding of the charge redistribution at the ω-Fe(0001) surface caused by the CO2 adsorption, we have calculated the charge density difference. It is calculated by subtracting the sum of the charge densities of the CO2 molecule and the pristine ω-Fe(0001) surface, from the charge density of the adsorbate–substrate system. The charge density difference is calculated for the most stable CO2 adsorption configuration and shown in Fig. 5. It can be seen that all the three Fe atoms directly bonded to the CO2 molecule presents charge depletion, which is extended towards the Fe–O and Fe–C bonds. The O atoms are surrounded by fractions of negative charge. The positive and negative charges are plotted with the same isosurface level. It can be seen from the figure that significant charge rearrangement happens only at the surface Fe layers. There is significant charge depletion from the Fe atoms and charge gain by the O atoms, and the positive charge is accumulated towards the Fe–C and Fe–O bonds. The significant charge transfer is evidenced by the Bader charge, that helps in strong chemisorption and further dissociation of the molecule. This indicates that compared to the inert CO2, CO can stay at the surface, interacting with other species and enhance the degradation of the Fe surface.
4 Conclusions
We have carried out a study of the adsorption of CO2 on ω-Fe(0001) surface. Among the 8 configurations considered, a horizontal bent configuration attaches with the least adsorption energy. It is observed that the CO2 molecule is getting activated when attached in the horizontal bent configuration and dissociates spontaneously without an energy barrier. Strong charge transfer is noticed between the adsorbed CO2 atom and the surface Fe atoms, which is further quantified from Bader charge analysis and charge density difference plots. The possibility of charge transfer from Fe d orbitals to p orbitals of CO2 molecule is confirmed from the density of states, which aids in its stabilization at the surface. Our study provides important insights into the possibility of stabilization and dissociation of CO2 on ω-Fe surface, which is important in the context of degradation aspects of Fe surfaces.Funding information
The funding of this research activity is under the auspices of the Genome of Steel (Profile3) by the Academy of Finland through project #311934.Research resources
The CSC – IT Center for Science, Finland.Conflicts of interest
The authors declare no conflict of interest.References
- D. H. Ping and W. T. Geng, Mater. Chem. Phys., 2013, 139, 830–835 CrossRef CAS.
- T. Liu, D. Zhang, Q. Liu, Y. Zheng, Y. Su, X. Zhao, J. Yin, M. Song and D. Ping, Sci. Rep., 2015, 5, 15331 CrossRef CAS.
- P. D. Frost, W. M. Parris, L. L. Hirsch, J. R. Doig and C. M. Schwartz, Trans. ASME, 1954, 46, 231–256 CAS.
- B. S. Hickman, J. Mater. Sci., 1969, 4, 554–563 CrossRef CAS.
- Y. Ikeda and I. Tanaka, Phys. Rev. B, 2016, 93, 094108 CrossRef.
- Y. Ikeda and I. Tanaka, J. Alloys Compd., 2016, 684, 624–627 CrossRef CAS.
- A. Togo and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184104 CrossRef.
- S. Q. Wu, D. H. Ping, Y. Yamabe-Mitarai, W. L. Xiao, Y. Yang, Q. M Hu, G. P. Li and R. Yang, Acta Mater., 2014, 62, 122–128 CrossRef CAS.
- D. H. Ping and M. J. Ohnuma, J. Mater. Sci., 2018, 53, 5339–5355 CrossRef CAS.
- Y. K. Vohra, S. K. Sikka and R. Chidambaram, J. Phys. F: Met. Phys., 1979, 9, 1771 CrossRef CAS.
- D. H. Ping, H. P. Xiang, H. Chen, L. L. Guo, K. Gao and X. Lu, Sci. Rep., 2020, 10, 6081 CrossRef CAS.
- A. A. S. Devi, S. Pallaspuro, W. Cao, M. Somani, M. Alatalo, M. Huttula and J. Kömi, Int. J. Quantum Chem., 2020, 120, e26223 Search PubMed.
- J. B. Sun, G. A. Zhang, W. Liu and M. X. Lu, Corros. Sci., 2012, 57, 131–138 CrossRef CAS.
- S. D. Zhu, A. Q. Fu, J. Miao, Z. F. Yin, G. S. Zhou and J. F. Wei, Corros. Sci., 2011, 53, 3156–3165 CrossRef CAS.
- A. Pfennig and A. Kranzmann, Corros. Sci., 2012, 65, 441–452 CrossRef CAS.
- G. Kresse, J. Non-Cryst. Solids, 1995, 192, 222–229 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Daniel, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- A. De Vita, PhD thesis, Keele University, 1992, A. De Vita and M. J. Gillan, preprint, 1992.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- S. Assa Aravindh, W. Cao, M. Alatalo and M. Huttula, Appl. Surf. Sci., 2020, 512, 146019 CrossRef.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, London, 1994 Search PubMed.
| This journal is © The Royal Society of Chemistry 2021 |