Open Access Article
Open Access ArticleBiobased foams for thermal insulation: material selection, processing, modelling, and performance
Rebecca Mort
ac,
Keith Vorst
*bc,
Greg Curtzwiler
 *bc and
Shan Jiang
*bc and
Shan Jiang
 *ac
*ac
aMaterials Science and Engineering, Iowa State University, Ames, Iowa 50011, USA. E-mail: sjiang1@iastate.edu
bFood Science and Human Nutrition, Iowa State University, Ames, Iowa 50011, USA
cPolymer and Food Protection Consortium, Iowa State University, Ames, Iowa 50011, USA
First published on 22nd January 2021
Abstract
With the urgent need for the development of sustainable materials and a circular economy, a surge of research regarding biobased materials and associated processing methods has resulted in many experimental biobased foams. Although several biobased foams are already shown to have thermal and mechanical properties competitive with expanded polystyrene, there remains a fundamental knowledge gap leading to limited understanding of the principles that determine performance. This review outlines the progress in this burgeoning field, introducing materials selection and processing, comparing performance, examining efforts in modelling physical properties, and discusses challenges in applying models to real biobased systems. The focus is on low thermal conductivity, which is a critical property for temperature-controlled applications such as packaging for refrigerated/frozen foods, medications, and vaccines as well as building materials. Currently, the trend in the field is moving towards fully biobased and compostable foams, though partially biobased polyurethane foams remain the most consistent performers. To illustrate the foam structure–property relationship, thermal conductivity, cell size, and density data were compiled. Given the complexity of biobased foams, heat transfer models aid in identifying crucial variables. However, data relevant to the insulation capability of biobased foams is not fully reported in many references. To address this issue, we employed a dimensional analysis to fill the gaps, revealing a power law correlation between thermal conductivity and relative density. Our approach is not intended as a robust prediction technique, but rather a simple demonstration of how biobased foams data could be utilized to predict the most promising materials and methods.
1. Introduction
The growing push towards a more sustainable, circular economy has increased attention on biobased materials that are useful in many applications including coatings, adhesives, medical equipment and single use packaging.1–4 Besides being more sustainable, multiple studies show that replacing petroleum-based materials with biobased alternatives significantly reduces environmentally harmful emissions.5–10 Additionally, biobased materials are often biodegradable, thus reducing landfill waste accumulation.11,12 Development of biobased foams has realized significant advancements in recent years utilizing a multitude of materials and foaming methods. Low thermal conductivity is highly desirable for thermal insulation foams that could be used for packaging and building materials. Several studies have demonstrated biobased or partially biobased foams with thermal conductivity comparable (within 10%) to commercial petroleum-based foams, which are widely used in industry due to their low cost and excellent thermal insulation properties.13–27 Expanded polystyrene (EPS), commonly referred to by the brand name Styrofoam™, and extruded polystyrene (XPS) are the current standards of foam.Though petroleum-based foams possess high performance for lightweight, insulating packaging, the materials are highly problematic with regard to sustainability. For example, the production of polystyrene is associated with consumption of non-renewable resources as well as environmentally harmful emissions.28,29 The foaming process, particularly for extruded foams, has historically contributed to ozone depletion. For example, the use of hydrochlorofluorocarbon (HCFC) blowing agents caused increases in ozone degradation prior to being phased out as mandated by the Clean Air Act and Montreal Protocol.30,31 Additionally, EPS and XPS products are often disposed in landfills after one-time use rather than recycling. This is in part due to limitations in recycling infrastructure as well as difficulty in shipping and low economic benefit from recovering and recycling polystyrene foams.32 It is important to note that there has been progress in making recycling EPS more practical. Businesses and governments across the globe are currently increasing their recycling efforts.33 Along with recycling, finding a more sustainable alternative to EPS/XPS that is comparable in performance is extremely desirable. Given the progress made in recent years, biobased foams have the potential to provide desired properties and eventually replace EPS/XPS.15,22,23
Since foaming methods are usually selected based on the raw material, it is critical to understand different processing methods in order to choose the appropriate processing approach and conditions for biobased materials. Foaming methods can be categorized by the blowing agent mechanism: physical or chemical. The blowing agent is a material that rapidly expands inside a polymer melt upon a reduction in pressure.31,34 Both physical blowing agents (PBAs) and chemical blowing agents (CBAs) are commonly applied to make foams with different mechanical properties. PBAs currently in use are either supercritical fluids (e.g. supercritical carbon dioxide) or low boiling point liquids (e.g. pentane) introduced and blended directly into a polymer melt.31,34 CBAs, on the other hand, are solid materials that are added to the polymer melt and decompose to generate dissolved gases during processing. These reactions can be endothermic (e.g. citric acid/sodium bicarbonate) or exothermic (e.g. azodicarbonamide).31 PBAs and CBAs both typically require a heated and pressurized vessel such as an extruder, injection mold, or autoclave. Despite similar processing equipment, PBAs and CBAs will typically produce drastically different structures. CBAs often create denser foams and PBAs sometimes result in cell collapse due to oversaturation and fast diffusion.31,34 In cases for which forming a melt at high pressure is not feasible, a foam structure can be formed through other methods including mixing, phase separation, or a chemical reaction between primary components.35–37 In some cases, the term “chemical blowing agent” may refer to a reactive component that is not necessarily an independent solid additive. The most typical example of this is using water as a CBA with polyurethane foams, which undergo a chemical reaction induced free rise foaming process. It should be noted this review paper only focuses on foaming methods which produce structurally stable foams. Methods such as Pickering emulsions38,39 that produce insulating foams with short lifetimes on the order of days or hours are not discussed here.
Biobased foams have been demonstrated with diverse sets of materials, additives, and processing methods, producing structures different from the traditional foam EPS/XPS. Wicklein et al.15 developed anisotropic foams which incorporated graphene nanoparticles to dramatically reduce thermal conductivity in the radial direction. Mihai et al.40 explored the impact of polymer structure on foam crystallinity and resulting density. Qu et al.41 selected a blowing agent specifically to create a disparity between foaming kinetics in the two components of a blend causing a bimodal cell distribution to form. These methods greatly expand the selection of biobased foams. However, the downside of having such wide variety of options is that comparing foam performance and predicting which methods are most promising becomes increasingly complex.
Heat transfer models offer a means to compare and predict foam thermal conductivity. When utilized with knowledge of processing, models can provide insight to how these materials can be manipulated to achieve improved performance. In the majority of cases, convection cannot occur due to gas flow restrictions within closed cells. Therefore, conduction and radiation are generally the main heat transfer mechanisms, but the degree to which they act varies.42–44 In XPS, conduction accounts for roughly 60–80% of heat transfer while radiation accounts for 20–40%.43 Thermal conductivity models are able to calculate the contributions of these mechanisms by making assumptions about foam structure and the molecular structure of materials with equations derived from physics of heat transfer.45,46 Historically, many models have taken a simplified approach to defining structure in order to make separation and analysis of physical variables easier. Wang et al. created a model which reduced the structure down to two dimensions and was able to thoroughly examine a large range of average cell sizes and foam void fractions on each heat transfer component.47 More recent models have increased applicability to less simplified structures. Bernardo et al. used parallel and series setups to account for a complete cell size distribution rather than just an average cell size.48 Though no single model captures the full array of structures displayed by various experimental biobased foams, each model can provide crucial insight into different factors which generally impact thermal performance.
By tuning the assumptions in a model to more accurately reflect materials and processing conditions, models are becoming increasingly effective in fitting and predicting the experimental data. However, even with well-constructed models, there remain gaps in current literature on reported data of thermal conductivity and structure characterization for biobased foams. For example, relative density has been shown to be a reasonably good predictor of thermal conductivity in EPS and polypropylene foams,26 but is not always reported for biobased foams. Some studies may report apparent density but, as discussed later in this review, these data are insufficient for providing a holistic understanding of foam structure and thermal conductivity. Underreporting thermal conductivity data and critical structural characteristics have created a challenge in validating model performance in predicting properties for biobased systems. Therefore, at the end of this review, we present a new dimensional analysis to fill the data gaps by optimizing fitting parameters. Our mathematical fit is preliminary and not intended to be viewed as a robust model. It does, however, offer a simple means to compare multiple biobased foams datasets to quickly determine which experimental foams are likely to be competitive with EPS. The potential value in applying fitting parameters could be to make heat transfer models more adaptive and representative of real-world scenarios.
This review will first discuss different types of biobased materials used for fabricating foams along with the foaming methods typically employed for each of those materials. The next section will discuss heat transfer modelling in depth by providing background on heat transfer mechanisms and common assumptions and conclusions of various models. The applicability of heat transfer models to biobased foam systems is discussed by comparing the validity of different assumptions and how more recent models derived conclusions which contradict the assumptions of past models. In the last section, thermal conductivity data and structural characteristics of these biobased foams are compiled to identify potential trends present. Finally, a dimensional analysis method is applied to the biobased foam data available in the literature, allowing us to gain a clearer view of trends and to fill in data gaps.
2. Biobased foams
Biobased foams exist in a broad spectrum. As shown in Fig. 1, materials selection is the first step towards making a biobased foam. Examples of common biobased materials are listed in Fig. 1 along with the key product properties that are typical of those materials. Materials selection then determines possible processing methods. Some processing methods, such as extrusion with a PBA, are relatively universal and can be applied to many different materials. Other methods may be completely exclusive to specific materials, such as the free-rise foaming of partially biobased polyurethanes. In general, each foaming method follows a few fundamental steps: (1) mixing of bulk materials and additives, (2) dispersion of a blowing agent within the bulk mixture, (3) phase separation of blowing agent from bulk to form voids. Beyond these fundamental steps however, the exact mechanisms of each foaming method vary. For example, in the extrusion method, the phase separation of the blowing agent from the bulk occurs via a drop in pressure, allowing the blowing agent to expand into a gas phase. Contrastingly, in the freeze-drying method, phase separation occurs when ice crystals are formed and the bulk material is no longer in solution.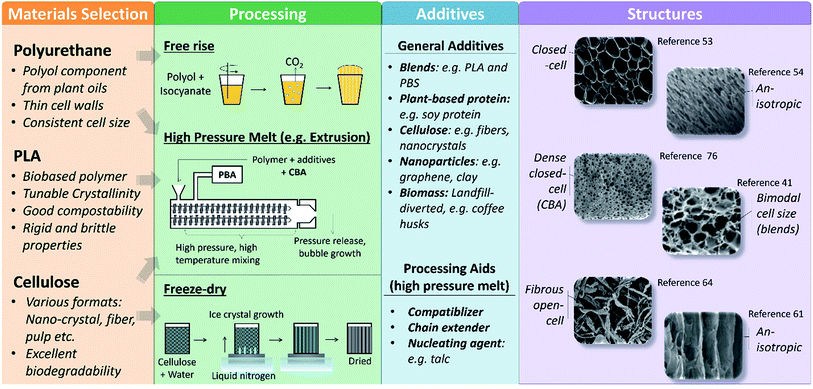 | ||
| Fig. 1 Schematic plot summarizing biobased materials, their corresponding foaming methods, common additives, and possible foam structures. For simplicity, this review focuses on cellulose, polyurethane, and poly(lactic acid) (PLA) though other materials have also been explored. Portions of this figure have been adapted with permission from ref. 41, 53, 53, 61, 64 and 76. | ||
The materials, processing, and additives collectively determine the foam structure and properties. Though some of the resulting foam structures are similar to foams made with traditional materials and foaming methods (e.g. XPS), there is a much wider variety in possible structures of biobased foams. As seen in Fig. 1, processing methods determined by the materials selection have influence on structure density, anisotropy, and closed-cell fraction. Typically, the factors which can alter foam structure include temperature, mixing parameters, pressure, time, blowing agents selection and additives. For example, extrusion can provide extensive control over the final structure through adjustments in temperature profile, screw rotation speed, screw element selection, etc.31 The temperature of the polymer melt as it leaves the die is a determining factor in how much the foam is able to expand and how stable the foam structure is upon cooling. A very low temperature at the die could cause the outer skin of the foam to rapidly become rigid, preventing expansion. Contrastingly, a very hot temperature prevents the foam from becoming rigid quickly enough, resulting in collapse as it cools. Every processing method can produce multiple foam structure characteristics by adjusting method parameters.15,23,36,41 In addition, additives influence the structure of foams in a variety of ways highly dependent on how the additive interacts with the bulk material and blowing agent. For instance, an additive which acts as a nucleating agent will typically reduce average cell size of the foam.27 Alternatively, if an additive acts as a filler material (e.g. biomass) it may increase the foam density or disrupt the formation of cell walls, thus reducing the closed-cell fraction.21
The next sections will explore specific materials in depth and provide examples of biobased foam structures. Processing methods and additives will be discussed within the context of corresponding biobased materials rather than separately. This review will focus on some of the most popular biobased materials for producing foams, biobased polyurethanes, cellulose, and poly(lactic acid) (PLA).
2.1 Polyurethanes synthesized with biobased polyols
Traditional polyurethanes are made with petroleum-based components: polyols and isocyanates. Biobased polyurethanes are mostly synthesized using biobased polyols. Polyurethane foams are most commonly made using an exothermic “self-rising” method in which an isocyanate reacts with a water molecule and generates carbon dioxide gas.49 Thus, water is referred to as a chemical blowing agent in this context. The nature of this foaming method tends to yield very low thermal conductivity foams with closed-cell structures and low density. Additionally, polyurethane (PU) foams have strong hydrogen bonding which results in superior mechanical properties relative to other traditional and biobased foams. Because these properties are so desirable, a vast amount of research has been dedicated to finding biobased replacements for the traditionally petroleum-based polyols.16–22,50–56 The alternative polyols are commonly developed from different plant oils, of which the typical structure does not contain the functional groups (epoxy, amine, thiol, hydroxyl) necessary to react with the isocyanate. Most plant oils consist of a glycerol backbone and an oleic, a linoleic, and a linolenic acid chain.50,51 In order to generate hydroxyl groups, these oils must first undergo an epoxidation reaction followed by opening up the epoxide ring. While shown to be successful in many cases, this modification will not always have the same results for every type of plant oil.50,51 Castor oil is an exception to this rule as it already contains the necessary functional groups to be reacted with isocyanates without modification. Compounded with the fact that each plant oil has different chemical structures to begin with, the type of oil used has a significant impact on the reaction with the isocyanate and the overall foam structure.Most of these partially biobased PU foams share similar structure properties of closed cells and very high void fractions (i.e. percentage of void space within the foam). An example of this kind of structure can be seen in Fig. 2(a). The question of compostability must be addressed for these foams. Fig. 2(b) shows the results of a three-month composting experiment.53 Some degradation clearly occurred. Although, given that the standard timescale for complete degradation of a compostable material is six months maximum,57 it is not entirely plausible that these foams could be diverted from a landfill. Partially biobased PU foams already tend to display excellent low thermal conductivity properties. The next step in improving the sustainability of PU foams is by increasing biodegradability.
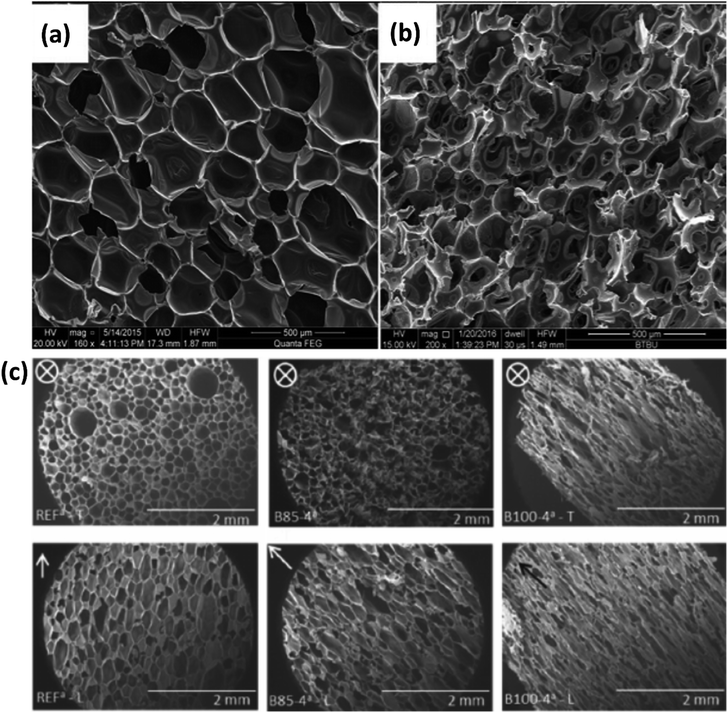 | ||
| Fig. 2 Examples of partially biobased PU foam structures. (a and b) SEM micrographs of PU and soy protein composite foams (a) before and (b) after composting for 3 months reproduced from ref. 53 with permission from the authors, copyright 2018. (c) SEM micrographs of PU foam samples reproduced from ref. 54 with permission from Wiley, copyright 2018. Transverse (top) and longitudinal (bottom); biobased polyol percent from left to right: 0, 85, 100.53,54 | ||
Partially biobased PU foams tend to be consistent with regard to having homogeneous, closed-cell structures. Some studies have shown, however, that adjusting foaming parameters can result in an increase or decrease of cell anisotropy. Fig. 2(c) shows an example of an array of anisotropic foams with cells elongated in the longitudinal (axial) direction. Under one condition, the cells actually became open pores. These foams were generated by adjusting the biobased polyol content along with the ratio of PBA (CO2) to CBA (water) used.54 The fact that an anisotropic foam structure can be formed both with this method for PU and with freeze dried cellulose (see Section 2.2) exemplifies how much of an impact processing conditions have on the outcome of producing foams.
Though partially biobased PUs synthesized with plant oil polyols are the most common and most thoroughly developed form of biobased PUs, other chemistry approaches have been researched. In recent years, a significant amount of research has gone into developing PUs that do not require the use of isocyanates, which are petroleum-based and associated with toxic gases from synthesis.58 One of the most common methods for generating non-isocyanate PU (NIPU) is through reacting cyclic carbonates and polyamines.58 Both of these components can be synthesized from biobased sources through a variety of mechanisms. NIPUs, however, still require further research to make them competitive with traditional PUs from a processing standpoint as they typically suffer from low polymerization rate and unwanted side products.58 Researchers have explored simpler methods to synthesize NIPUs, such as reacting sugars or lignin with a dimethyl carbonate component, forgoing the complex step of cyclization.59,60 This secondary approach also has drawbacks such as the high temperatures required for foaming. More research is needed before NIPUs can become as scalable as biobased polyol PUs.
2.2 Cellulose
Cellulose is one of the most important biobased materials as it has abundant and diverse renewable sources. In addition, nano-cellulose fiber (NCF) and crystalline nano-cellulose (CNC) are of high interest as a sustainable material for use in composites for various applications. These composites can be categorized either as neat cellulose with added plasticizers or other processing aids, or cellulose as an additive in a polymer blend matrix.35 The same categories are true for cellulose-based foams and both present their own opportunities and challenges for foaming. On its own, a cellulose-based material typically is not foamed using the traditional methods used to make EPS and XPS. For these cases, the most common method employed is freeze drying.13–15,61–63 Mixing neat cellulose with water and other additives (e.g. surfactant, nanoparticles) and then freezing causes ice crystals to nucleate and grow surrounded by the cellulose matrix. After drying is complete, only the cellulose matrix remains with void space where ice had formed. A consequence of this method is that the direction of ice formation has a substantial impact on the foam structure. As shown in Fig. 3(a), the foam cell structure is essentially homogenous when an even temperature gradient is used (e.g. placing inside a freezer). However, there are downsides to this method of freezing as it can lead to cell collapse61 and is generally not scalable or easily reproducible. It is also possible in homogeneous freezing conditions to form an open-cell, more disordered structure as opposed to a closed-cell structure as would typically be observed in EPS. If the temperature gradient is unidirectional as in Fig. 3(b), the cells become elongated in the axial direction. This kind of anisotropic structure will cause the thermal conductivity to differ depending on direction of measurement, with one study even reporting an order of magnitude difference between the radial and axial directions, radial having the lower value.15 Other methods, less commonly used than freeze drying, for making neat cellulose foams have also been proposed. One alternative was presented by He et al. and involved vigorously mixing a solution containing cellulose pulp and a surfactant and then drying the solution without freezing or heating.64 Similar to the structure shown in Fig. 3(e and f), the resulting foam had an open and fibrous structure.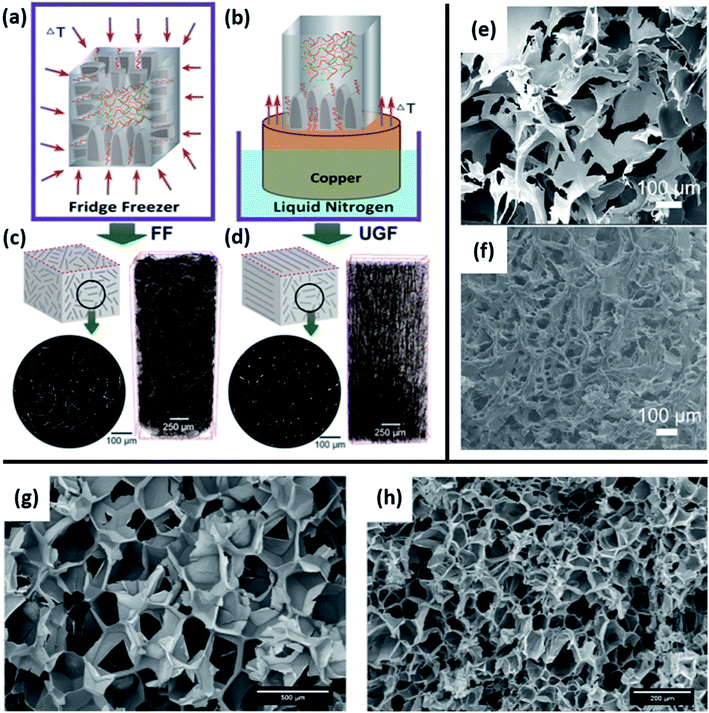 | ||
| Fig. 3 Examples of cellulose foaming methods and structures. (a–d) Freeze drying conditions and structures for cellulose foam reproduced from ref. 61 with permission from American Chemical Society, copyright 2019. (a and b) Schematics of homogeneous freezer freezing (FF), unidirectional gradient freezing (UGF); (c and d) micro-CT scans of the foam structure for each freezing condition. (e and f) SEM micrographs of open-cell, non-ordered foams generated with homogeneous freeze drying conditions reproduced from ref. 14 with permission from Elsevier, copyright 2019. (e) Pure CNC foam; (f) CNC blend with 10% PVA and 25 wt% BTCA. (g and h) SEM images of extruded with isobutene used as PBA reproduced from ref. 65 with permission from Wiley, copyright 2019. (g) No cellulose added; (h) 20% cellulose fiber blend.14,61,65 | ||
When used as an additive or a component of a blend, cellulose often influences the structure of the resulting foam by altering melt flow. For example, one study which blended cellulose pulp with poly(lactic acid) (PLA) with a PBA extrusion foaming method reported that increasing the cellulose content in the blend resulted in reduced melt viscosity and smaller cell size displayed in Fig. 3(g and h).65 The theory behind this phenomenon was that the cellulose acted as a nucleating agent by introducing interfaces where it is more energetically favorable for a bubble to form.66,67 Additionally, the cellulose provided a kinetic barrier to PLA strand reconfiguration during bubble growth, thus restricting the expansion of each individual cell. The crystallinity of nano-cellulose additives can also have an impact on the outcome. According to Stanzione et al., amorphous and crystalline cellulose nanoparticles blended in a polyurethane foam both caused a reduction in cell size and a reduction in thermal conductivity.68 The blends with amorphous particles, however, contained more fully closed cells (i.e. cell walls in tact) and had improved mechanical ductility compared to the blends with crystalline particles. This difference was attributed to the fact that the amorphous cellulose was more evenly dispersed and was more reactive with the isocyanate.
In summary, cellulose-based foams are made with a variety of methods. Freeze drying is most commonly used when cellulose is the primary component as opposed to a blend or an additive. Freeze drying has the potential to create interesting anisotropic structures which have been shown to very effectively reduce thermal conductivity in the radial direction. This method comes at the cost of scalability and reproducibility. As a result, cellulose is ultimately more often used as an additive in other foaming methods.
2.3 Poly(lactic acid)
PLA is a thermoplastic polyester derived from a variety of plant sources including corn, cassava, beets, and sugarcane. Various grades of PLA targeted at specific applications have been developed and are commercially available. Lactic acid monomers have two molecular configurations, L and D, in which the orientation of the methyl group is opposite (i.e. stereoisomers). The stereochemistry of PLA allows control over the polymer crystallinity. In a majority L-LA strand, increasing the D-LA content will result in the polymer becoming more amorphous.69,70 As a result of its properties, which are often compared to polystyrene, and commercial availability, PLA has been a major material of interest for a multitude of applications including foams.70 However, unlike polystyrene, PLA faces some major obstacles with regard to processing, namely degradation from water exposure and a lower glass transition temperature (approximately 60 °C). These issues can be avoided by ensuring material is properly dried and tuning the polymer architecture to optimize the crystallinity for stabilizing the foam structure.69,70 Additionally, foam grade PLA is typically modified with a chain extender to improve its processing range and properties.71,72Given the processing capability of PLA as a thermoplastic polymer, more traditional foaming methods, such as extrusion, injection molding, and autoclaving (i.e. enclosed in a high pressure, temperature controlled vessel) are employed.23,25,73,74 PLA foams have been made with a variety of blowing agents. For PBAs, supercritical CO2 (scCO2) is usually preferred to N2 due to the higher solubility of CO2 as well as its known plasticizing effect on PLA.40,69 Fig. 4(a) depicts the results of a study which explored the impact of D-LA content and amount of scCO2 PBA.73 The PLA with 2% D-LA content had the highest crystallinity that increased with the scCO2 content, PLA with 4% D-LA had lower crystallinity, and PLA with 10% D-LA was completely amorphous regardless of scCO2 content. Taking note of the density values measured for each sample along with physical structure, it is clear that designing the polymer to be partially crystalline allows for more expansion even at low PBA doses. More recent research has further explored the role of crystalline spherulites in bubble nucleation.75
 | ||
| Fig. 4 Examples of PLA foam structures. (a) Impact of D-LA and PBA content on PLA foam structure and crystallinity: SEM micrographs corresponding to PLA1 (2% D-LA), PLA2 (4% D-LA), and PLA3 (10% D-LA) reproduced from ref. 40 with permission from Wiley, copyright 2009. (b and c) PLA foamed with endothermic CBA in extruder set at different screw speeds: (b) 20 rpm; (c) 120 rpm reproduced from ref. 76 with permission from Elsevier, copyright 2009.40,76 | ||
CBAs have also been explored for use with PLA.76,77 As is typical for CBAs in traditional foam practices, the resulting foams are denser than those made with PBAs. The structure of these dense foams can still be altered through other processing parameters, as shown in Fig. 4(b) and (c), although foam expansion is limited by the nature of CBAs.76 However, CBAs can offer advantages as nucleating agents, to increase cell density and impede excessive bubble growth, maintaining a narrower distribution of cell size.66,67 Other additives have been explored with the same goal of promoting nucleation and controlling cell structure. Some nanoparticle additives (e.g. nanoclay) have been found to contribute to other foam properties as well, such as mechanical strength.52 Carbon nanotubes (CNTs) have also been used to generate an electrically conducting network within a PLA foam.24,78 Wang et al. wrapped expanded PLA beads in a carbon nanotube network and then displayed how their own thermal conductivity model would need to be adapted to account for the network component shown in Fig. 5(a–c). Their model will be discussed later in this review (see Fig. 7).
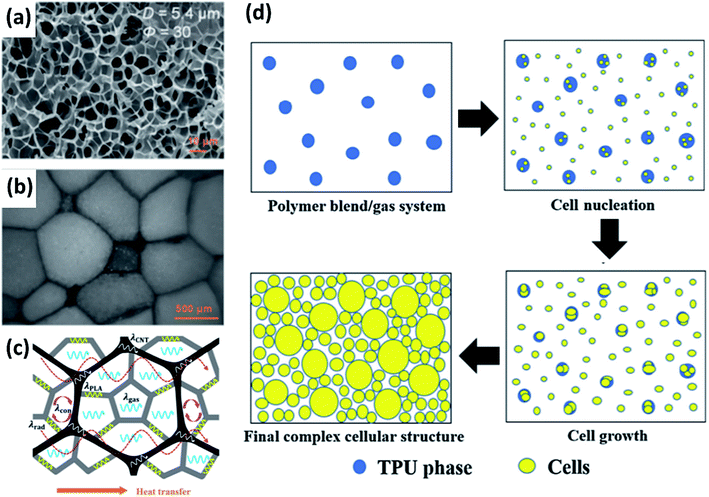 | ||
| Fig. 5 Examples of PLA foam structures. (a–c) Foamed PLA beads wrapped in a carbon nanotube network reproduced from ref. 24 with permission from American Chemical Society, copyright 2017. (a) SEM micrograph of expanded PLA; (b) sintered expanded PLA beads with CNT network; (c) heat transfer diagram. (d) Schematic of proposed formation process of bimodal cell structure dependent on difference in nitrogen diffusion through the two polymer phases reproduced from ref. 41 with permission from Elsevier, copyright 2019. White areas denote PLA, blue areas denote thermoplastic PU, and yellow denotes a cell.24,41 | ||
PLA has also been the primary material of choice to explore unique biobased and partially biobased polymer blends. Blending polymers during foaming can lead to unique structures and properties. As was alluded to previously in this review, cellulose and PLA were extrusion foamed together while comparing isobutene and scCO2 as PBAs.65 The resulting foams (refer back to Fig. 3(h)) showed a clear trend of reducing cell size with increasing cellulose content regardless of the blowing agent. Cellulose, in this case, restricts the motion of the PLA chains during bubble growth. Another interesting blend, involving PLA and (non-biobased) thermoplastic PU, was studied by Qu et al. to determine the impact of using nitrogen as a PBA with two polymers with different N2 solubility and diffusion coefficients.41 The result was a bimodal distribution of cell sizes. The proposed mechanism behind this foam structure is summarized in Fig. 5(d). Thermal conductivity measurements revealed that this bimodal cell structure performed better as a thermal insulator than the even cell distribution foam used as a ref. 41 In summary, PLA foams, more so than other biobased foams, have a wide array of potential foaming methods and variables in processing that can be adjusted to create different structures.
2.4 Others
Other biobased materials have been explored for creating foams, including starch, plant-derived proteins and polybutylene succinate (PBS). Starch offers a great deal of flexibility in terms of possible foaming methods.36 Extruded starch foams produce structures which are likely to have the greatest potential for thermal insulation applications.36,79,80 Other methods, such as baking, freeze drying, and microwave heating have been demonstrated as well.36,81 Most of the research regarding starch foams have focused on other applications than insulation such as foam trays to replace single-use disposable food packaging and foams with antimicrobial properties.81,82 Much of the research has also focused on starch composite foams, incorporating other additives or blends. Engel et al. used grape stalks, generally considered a waste product, in their foams as a filler.83 Similarly, Rojas et al. developed insulating foam using fibrous starch material from agriculture waste as the primary component.84Plant-based protein plastics have limited processing capability, so require the use of plasticizers or blending with other polymers such as PU and PLA.37,85–88 A great deal of work has gone into identifying effective biobased plasticizers. Foaming of these materials can be accomplished through methods such as injection molding.37 It is important to note that plant-based proteins, while not as frequently used as the primary material in foams, are very often employed as additives to cross-link or otherwise adjust material properties.53,89
PBS foams are often made using similar methods to PLA foams. Injection molding and autoclave methods with scCO2 as the blowing agent have produced a number of PBS foams with closed-cell structures.90–92 Chemical blowing agents are also popular.93–95 The focus of PBS foams research so far has been mainly on mechanical properties and the impact of processing aids such as plasticizers and cross-linking agents.95–97 Beyond mechanical properties, one study incorporated carbon black nanoparticles into a PBS foam to increase electrical conductivity90 and another reported achieving thermal conductivity as low as 0.022 W m−1 K−1 in a PBS foam by tuning endothermic and exothermic CBA components.94
There are more biobased materials and blends beyond what is discussed here.98–101 It is important to emphasize that the research done with these materials shows as great deal of progress in the field. For the sake of simplicity, the remainder of the discussion on biobased foams in this review will focus on cellulose, PU, and PLA as the primary materials.
3. Heat transfer modelling
Thermal conductivity (i.e., low thermal conductivity) is the most important parameter for temperature stabilizing packaging. The theoretical calculation of thermal conductivity is given in eqn (1), where thermal conductivity (k) has SI units of W m−1 K−1, q is the heat flux, t is time, L is distance of heat transfer (i.e. material thickness), A is the area over which heat is transferred, and ΔT is the temperature difference.102 Note that many publications use the symbol, λ, to denote thermal conductivity rather than k. It is important to understand the possible mechanisms for heat transfer and how to account for the foam structure when defining those mechanisms mathematically.
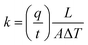 | (1) |
In general, there are three possible modes of heat transfer: conduction, convection, and radiation. For foam structures, convection is not typically a possible heat transfer mode, particularly for closed cell structures since air flow is restricted. While definite limits for which convection is negligible are debated, conservative estimates suggest that cells less than 3 mm in diameter or a Rayleigh number (relating to fluid flow turbulence) below 50 will meet the requirement.103 Conduction in foams can occur through the solid material (foam structure) or gas conduction within the pores. Crucially, it must be recognized that for standard gas conduction conditions, the cell size must be greater than the mean free path distance of gas molecules (approximately 70 nm for air at room temperature).104 When cell sizes fall below this distance and gas molecules are more likely to collide with cell walls than with other gas molecules, gas conductivity is reduced. This mechanism is known as the Knudsen effect.104,105 Heat transfer via radiation is also possible in foams and, while conduction is usually the dominant mode, radiation can be a significant component as well.43,44
| kt = ks + kg + kr | (2) |
Each heat transfer mode will contribute towards the overall thermal conductivity of a foam as shown by eqn (2) where kt is the total thermal conductivity, ks is thermal conductivity from solid conduction, kg is gas conduction, and kr is thermal conductivity from radiation. Each of these individual terms can be defined using concepts from physics and mathematics, although not every model will define them in the same way. Thus, the differences between foam heat transfer models lie both in the assumptions made about foam structure as well as the theory behind heat transfer modes.
3.1 Model evolution: assumptions and validations
Thermal conductivity models have evolved significantly over time to incorporate both improved understanding of heat transfer mechanisms and more sophisticated modelling of foam structures. Early models took a one-dimensional approach to simplify the system while recent models have made use of stochastic generation algorithms to create virtual 3D structures. Each of these models, regardless of complexity, employ a base set of assumptions about heat transfer mechanisms and structure which range in validity. To understand how each model works and the context in which it could be reasonably used, these assumptions must be outlined.One of the earliest models, commonly cited for its definition of radiative thermal conductivity, described microcellular polystyrene foams.106 This model uses a simplistic design for foam structure: n layers of parallel polymer membranes of thickness Ls each separated by a gas layer of thickness Lg. This one-dimensional heat flow approach is not representative of real foam structures, but significantly simplifies calculations. The conduction contributions, solid and gas, are defined using Fourier's laws of heat conduction. This definition is now understood to be invalid for heat transfer through nanocellular structures,107,108 but given the scope of this model only includes conventional foams with micro-scale cells, it is reasonable. The radiation contribution is calculated using refractive index and Bouguer's law to define the net fraction of radiant energy which passes through one solid membrane. The structure factor generated by the simple model geometry then is used to find the apparent radiative thermal conductivity for the full structure.
Some recent models have used similar approaches to define the structure of a foam.42 Fig. 6(a) shows a one-dimensional heat flow structure. A major difference between this structure and the one-dimensional structure previously described is that the cell wall thickness and cell size are not fixed. Adjusting these parameters allows this model to describe the impact of porosity on thermal conductivity. This model improves its accuracy through a coupled approach to defining heat conduction and radiation which uses the steady state condition that the sum of the derivatives of each heat flux component must be zero. The radiative flux in this case was determined using a P1-approximation.46 The scope of this model encompasses both microcellular and nanocellular foams.42 The findings of this model, shown in Fig. 6(b) and (c), suggest that generally, increasing porosity will decrease thermal conductivity. However, if wall size is held constant, the radiative contribution significantly increases at high porosity, as does total thermal conductivity.
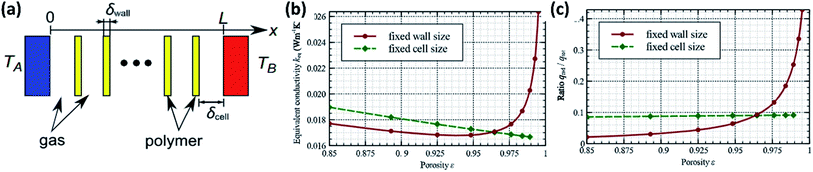 | ||
| Fig. 6 One-dimensional heat transfer model diagram and trends. (a) Diagram of simplified foam structure. Trends in heat transfer relative to foam porosity while keeping either wall size or cell size fixed: (b) equivalent thermal conductivity; (c) ratio of radiative heat flux to total heat flux. Reproduced from ref. 42 with permission from Elsevier, copyright 2013.42 | ||
The one-dimensional approach can provide valuable predictions for trends in thermal conductivity without the need to account for multiple paths of heat transfer. However, this approach drastically simplifies the geometry. Several models have taken a more complex approach in the pursuit of more accurately describing real foam structures. Wang et al. proposed a 3-dimensional wall and strut model simplified to 2D to account for multiple possible paths for heat transfer in one direction.47 A schematic of how this model was applied to determine the radiation component is shown in Fig. 7(a–e). This model applies the Knudsen equation for determining gas thermal conductivity over a range of possible cell sizes.109 The model defines the Knudsen number, a dimensionless factor quantified as the ratio of the cell size to the mean free path of a gas molecule. Additionally, this model employed a characteristic size of the solid skeleton when calculating solid conductivity given that for nanocellular foams, boundary scattering of phonons at the cell walls becomes a significant factor.110–112 Fig. 7(f) and (g) show the predictions for total thermal conductivity relative to void fraction and cell size. These results suggest that increasing void fraction will reduce thermal conductivity up to the point where the radiation component becomes more significant.47 Additionally, very small (nanoscale) cell size has a dramatic effect, causing a thermal conductivity increase despite the Knudsen effect reducing the contribution from gas conduction.
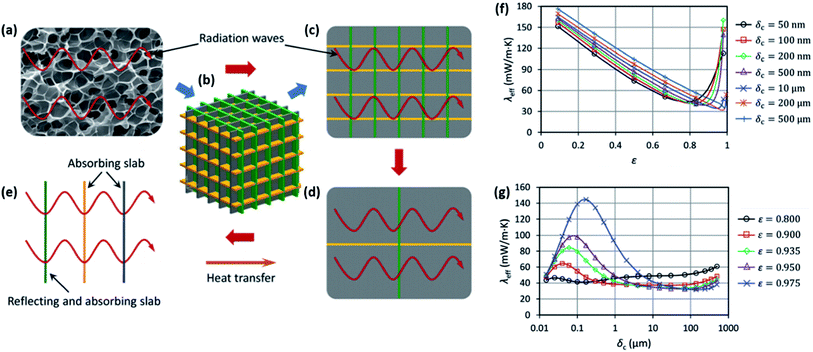 | ||
| Fig. 7 Wall and strut heat transfer model. (a–e) Model schematic for radiative heat transfer. (a) Example of a real foam structure; (b) 3D model will cubic cells; (c) 2D representation; (d) 2D cubic unit cell containing three planes; (e) analysis model for a unit cell considering one reflecting slab and two absorbing slabs. Trends in total thermal conductivity relative to: (f) void fraction, ε, where each curve accounts for different cell size; (g) cell size where each curve accounts for different void fraction. Reproduced from ref. 47 from Royal Society of Chemistry, copyright 2017.47 | ||
The “wall and strut” method to constructing a foam skeleton harkens back to previous work by Smits, who developed a wall and strut model for polyurethane foams and explored polymer distribution in the foam structure.113 Specifically of interest was what percentage of the material lies within the struts versus the walls at different cell sizes. The model predicted that the percentage of material in the walls increases for smaller cell sizes, leading to a trend in radiation opposite that of solid conduction. At small cell sizes, the cell walls are thicker films which can more readily block radiative heat transfer but allow more paths for phonon transport. Additionally, it is noted that if the foam density is reduced past a certain threshold point while maintaining cell size, the cell walls will no longer be stable resulting in an open cell structure.113 This suggests that some characteristic cell wall thickness is likely specific to the foaming material. Since the cell walls act as a barrier to diffusion, the loss of cell wall stability thereby resulting in an open cell structure has major implications for foam thermal conductivity. Smits suggests that an open structure will have higher thermal conductivity than a closed structure with the same cell size and slightly higher density.
More recently, Bernardo et al. created a more structurally complex model to explore the impact of a bimodal cell size distribution.48 Fig. 8(a) and (b) shows schematics of the model structure. Mathematically, this structure is described in two ways: series and parallel as shown in eqn (3) and (4) respectively. In the equations, λi and Vi are the thermal conductivity and volume fraction of the i-th phase. The reasoning to test both series and parallel approaches is to change the level of interaction between the two phases present (i.e. large cell phase and small cell phase).114,115 It should be noted these models presented by Bernardo et al. only account for conduction, choosing to ignore radiation.48 The results of the two models applied to a theoretical PMMA foam are displayed in Fig. 8(c). Increasing the fraction of nanocells decreases the thermal conductivity according to both series and parallel models. The impact of the width of the cell size distribution was also determined to be an important factor, with broader distributions resulting in higher thermal conductivity than narrower distributions even given the same average cell size.48
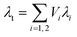 | (3) |
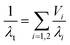 | (4) |
 | ||
| Fig. 8 Schematic of bimodal cell structure (a) accounting only for the two average cell sizes; (b) accounting for a full cell size distribution. (c) Series and parallel models for thermal conductivity of a bimodal structured PMMA foam with thermal conductivity determined relative to the volume fraction of the nanocell phase. Reproduced from ref. 48 with permission from Elsevier, copyright 2019.48 | ||
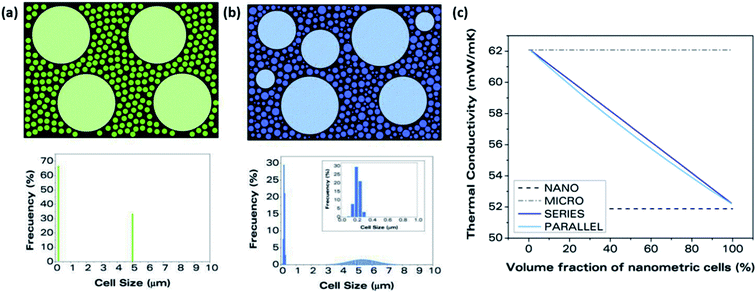
All of the models discussed to this point have created simplified (to varying degrees) geometric approximations of real foam structures. In contrast, van de Walle et al. developed a model which employs micro-CT scanning and/or stochastic generation algorithms to get a more accurate representation of a true foam structure.116,117 An overview of the simulation process is given in Fig. 9. The virtually produced structures were generated using stochastic algorithms exemplified in the previous literature.118–121 The structures which this model is capable of analyzing are undoubtedly more accurate than those presented by the models previously discussed in this review. Of particular note, the usefulness of this model was demonstrated for granular foam structures (e.g. EPS). However, the more complex structures lead to more variables that must be accounted for within the thermal conductivity calculation. For this model, the thermal conductivity was calculated using the relatively simple approach of applying Fourier's heat conduction law, which has previously been shown to be invalid for nanocellular structures.116
 | ||
| Fig. 9 Schematic of simulation process: (a) micro-CT image of real foam sample; (b) virtually generated image of foam structure; (c) finite element mesh applied to input; (d) simulation temperature profile. Reproduced from ref. 116 with permission from Elsevier, copyright 2018.116 | ||
3.2 Limitations of models
Due to the unusual physical structures of biobased foams, they are often not well represented in the previous models discussed. On the other hand, in recent years models have been considerably improved as the understanding of heat transfer mechanisms and structural factors has enhanced. Adapting current models to biobased foams will be an important future task in this field of study. The trends predicted by models can inform engineers and scientists developing new foam materials on the optimum structure to obtain the desired thermal conductivity.It is still crucial to point out that all models have limitations. These limitations are perhaps best analyzed by compiling the assumptions upon which they are based. Table 1 gives a list of some major assumptions made in various models. The references used to make this assessment were chosen as they represent a variety of modelling approaches. Table 1 also provides a list of conclusions drawn from these models. By comparing the columns of Table 1, it is clear a few assumptions cannot accurately capture the key features of the foams. For example, the assumption that only average cell size needs to be considered as opposed to the full distribution is used in many models. However, Bernardo et al. concluded that the distribution has a major impact on thermal conductivity.48 Other problematic assumptions include neglecting the radiation component and taking the reflectance and refraction coefficients to be constant for all cell sizes and void fractions.
| Assumptions | References | Conclusions | References |
|---|---|---|---|
| Cells have a uniform size distribution | 42, 43, 47, 106, 113 and 122 | Conduction is the most significant mode of heat transfer | 42, 43, 47, 48, 106 and 122 |
| Considering only the average cell size is representative of the whole | 42, 43, 47, 106, 113 and 122 | Generally, reducing cell size reduces thermal conductivity | 43, 47, 106, 113 and 122 |
| Cells are generally spherical (isotropic) | 42, 43, 47, 48, 106 and 122 | Generally, increasing void fraction reduces thermal conductivity | 42, 43, 47 and 116 |
| Cells are closed | 42, 43, 47, 48, 106, 113 and 122 | Nanocellular foams display different trends than microcellular foams | 47, 48 and 113 |
| Convection is negligible | 42, 43, 47, 48, 106, 113, 116 and 122 | Impact radiation increases for high void fraction (low relative density) foams | 42, 47 and 122 |
| Radiation is ignored | 48 | Refractive index and absorption index have a significant impact on thermal conductivity | 47 and 106 |
| Reflectance and refraction index is constant for all cell sizes and void fractions | 42, 43, 48, 106, 113, 116 and 122 | Reflectance depends on cell size, void fraction, etc. | 47 |
| Consider only foam structure and primary material. No consideration for blends or additives | 42, 43, 47, 48, 106, 113, 116 and 122 | Width of cell size distribution is significant | 48 |
| Cell wall thickness remains essentially constant as cell size is changed | 113 | Changes in cell wall thickness and ratio of polymer present in cell walls to struts significantly impact thermal conductivity | 113 |
Furthermore, it is important to assess how well model assumptions apply to experimental systems. Table 2 compares model assumptions to observations in experimental biobased foams. It is clear that some foam structures, particularly open-cell and anisotropic structures, are not uncommon in biobased foams. Given that most current models do not account for these non-traditional structures, this presents a research gap. Micro-CT scanning of experimental foams to create structural information inputs for a model is a potential means fill this gap.116 Additionally, all models assessed here have neglected to account for the possibility of polymer blends or solid additives. Granted, it is not reasonable to consider every possible additive, but certainly it would be desirable to have a better understanding of how different polymer domains in a blend impact thermal conductivity depending on how those domains are arranged. An excellent example to demonstrate the importance of blends on the structure an experimental foam is given by Qu et al.41
| Assumption | References | Experiment observation | References |
|---|---|---|---|
| Cells have a uniform size distribution | 42, 43, 47, 106, 113 and 122 | Cells have a uniform size distribution | 13, 14, 16, 17, 18, 20, 22, 23, 24, 62 and 123 |
| Cells have a bimodal size distribution | 41 and 73 | ||
| Cells are generally spherical (isotropic) | 42, 43, 47, 48, 106 and 122 | Cells are spherical (isotropic) | 16, 17, 18, 23, 41 and 73 |
| Cells are oblong or cylindrical (anisotropic) | 15, 20, 22, 54, and73 | ||
| Cells are closed | 42, 43, 47, 48, 106, 113 and 122 | Cells are fully closed | 17, 18, 22, 24, 41, 73 and 123 |
| Closed cell structure with significant portion of cells having ruptured walls | 13, 16, 20, 21 and 54 | ||
| Cells are open | 27, 62 and 64 | ||
| Radiation is ignored | 48 | Radiation is a significant component | 23 and 24 |
| Consider only foam structure and primary material | 42, 43, 47, 48, 106, 113, 116 and 122 | Thermal conductivity changes with presence of additives or blends | 13, 14, 17, 18, 20, 21, 24, 27, 41, 54, 64 and 123 |
| Foam structure changes with presence of additives or blends | 15, 17, 18, 20, 21, 24, 27, 41, 54, 64 and 123 |
4. Comparison of biobased foam properties
4.1 Raw data analysis
Due to the fact that so many variables impact the properties of biobased foams, it can be difficult to distinguish if any given material holds more promise for thermal insulation applications. Ideally, drawing a thorough and direct comparison between these experimental biobased foams would require datasets of thermal conductivity, apparent and relative density, average cell size, cell size distribution, closed cell fraction, and anisotropy ratio. These data would first help form an understanding of how these foams stack up purely on insulation performance (thermal conductivity) and then fully describe the foam structures to understand how any particular trends in structure are impacting performance.In compiling performance data on cellulose, PU and PLA foams, it has become evident that reporting of the datum categories mentioned above in the literature is somewhat insubstantial. For example, many papers which list thermal insulation as a potential application for the experimental foam have not quantitatively described the foam structure or even measured thermal conductivity. This is in large part due to the fact that, in many cases, the focus of the research may not be thermal insulation properties. The result, however, is a gap between the amount of research assessing biobased foams and the amount of directly comparable data. Fig. 10 shows the references found by the authors to contain complete datasets for thermal conductivity arranged by primary foam material. Not only is the compiled dataset relatively small, it also contains huge fluctuations within materials and between materials. All three materials have at least one experimental foam that is on par or better than EPS/XPS. Additionally, PU foams seem to have more consistent thermal conductivity performance than cellulose and PLA. Besides these points, it is difficult to discern a clear trend from this figure alone. A few references display particularly large thermal conductivity ranges. Some of these can be explained by anisotropic foam structure, and others (shown shaded) are the result of adjusting blend components or additives.
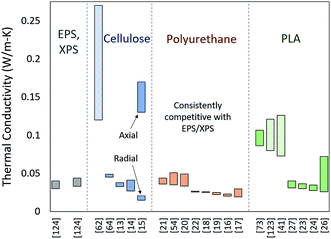 | ||
| Fig. 10 Reported thermal conductivity ranges for experimental biobased foams arranged by material with EPS and XPS124 and a general comparison. Bars that are shaded rather than solid indicate a large thermal conductivity range arising from additives or blends15 has two ranges shown since the anisotropic foam samples were characterized in both the radial and axial directions. | ||
Not all the papers reported thermal conductivity values together with quantitative structure data, which makes it difficult to compare the performance precisely. There are multiple potentially informative structural characteristics which are underreported. Of the biobased foams which report thermal conductivity, the most commonly reported structure characterizations are apparent density and average cell size shown in Fig. 11(a) and (b). It is immediately evident that apparent density is not very informative and does not follow any clear trend even among similar materials. The lack of trends is initially confusing given that several models previously discussed in this review specifically show the impact of void fraction (or equivalent terms), which is a term derived from apparent density. Similar to apparent density, the average cell size data does not reveal any useful information. Complete cell size distribution parameters are very rarely reported and having only average cell size makes it far more difficult to compare foams with non-traditional structures. Some have specified directionality of the cell size measurement if the foam was anisotropic, but fewer have provided an anisotropy ratio or measurements in other directions. The thermal conductivity value of anisotropic foams is also typically only measured in one direction, and at times, directionality is not specified. Notably, both the compiled density and cell size data do not follow clear trends. Very little insight could be gained from either of these plots.
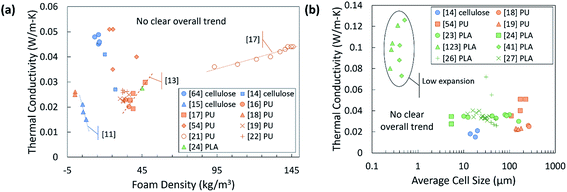 | ||
| Fig. 11 Reported thermal conductivity data relative to (a) apparent density and (b) average cell size. Blue points are cellulose, orange points are PU, and green points are PLA. The points plotted from ref. 15 are specifically thermal conductivity measurements in the radial direction.41 Foam samples were bimodal; the average size of the smaller cells is plotted here. A few trend lines are added for samples from the same reference. | ||
The lack of comprehensive datasets posts a barrier in understanding the true performance of these experimental biobased foams. At this point, one option is to look for models that may allow us to better understand the relationship between foam structure and properties. Refining models will lead to better predictions for foams with non-traditional structure characteristics, and ultimately, fill in these data gaps. An alternative approach is to display the data that are already available and fit the gap through a simple mathematical dimensional analysis.
4.2 Dimensional analysis approach
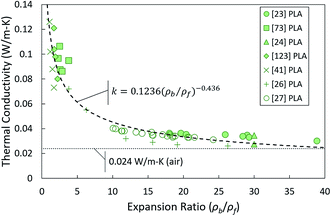
To make better use of the data available, the most commonly reported structural characteristics, apparent density and average cell size, must be compiled and translated into a form which is possible to directly compare across studies. Apparent density is problematic since it is not directly comparable across studies; different materials and blends cause differences in density not related to foam structure. One way to make apparent density data more useful is by translating it into relative density, i.e. the density of the foam divided by the density of the bulk material prior to foaming. Relative density is valuable since it removes the specific material properties from the picture, making it easy to compare across datasets. Reporting of either expansion ratio (the inverse of relative density) or void fraction (one minus the relative density) is equivalent.The only group of biobased foams for which all these data are available is closed-cell PLA foams, shown in Fig. 12. These data follow a clear trend, similar to other plots of compiled data in previous literature which include more traditional insulation materials such as EPS or polypropylene foams. It would indicate that thermal conductivity is low for high expansion ratio (i.e. low relative density) foams and increases rapidly in low expansion ratio ranges. The fact that these particular PLA foams follow this trend is unsurprising since the structures involved are on the whole quite similar to traditional foams. From a theoretical standpoint, the power law behavior is supported by the fact that solid conduction will be very high when foams are very dense. The introduction of any barriers (cells) to phonon transport should cause the solid conduction to rapidly decrease. Then, as the foam becomes mostly void space, the foam should asymptotically approach the thermal conductivity of air.
Given the strong trend revealed here with relative density, it stands to reason that displaying foam structural and thermal data in relative, dimensionless terms is needed to obtain useful insight. In particular, a dimensionless approach to data analysis could be valuable for foams with complex, non-traditional structures for which it is difficult to accurately apply current models. Here, we propose a rudimentary dimensional analysis approach to help fill in the data gaps. The mathematical fit was constructed using the datasets previously analyzed in Section 4.1. It is important to note that this method does not rely on true physical understanding of the material structures. It is only based on mathematical correlation.
To make the available data on biobased foams easier to compare, all variables involved were first made to be dimensionless. Table 3 shows a summary of how all variables for this analysis were defined. Relative thermal conductivity, krel, was calculated by dividing measured foam thermal conductivity values by the assumed thermal conductivity of the bulk material. Values of bulk material thermal conductivity are given in Table 3. It should be noted that it is not necessarily accurate to assume that all the solid materials used to make these experimental foams had these thermal conductivities, but there are not substantial data provided to improve this assumption. Similarly, the relative density, ρrel, was calculated by dividing the reported apparent foam densities by the assumed density of the solid material (see Table 3). The calculation of relative density was not necessary in all cases since some studies reported expansion ratio, which is the inverse of relative density. Thus, the assumed solid material density values were only employed when expansion ratio data was not available. To transform reported average cell sizes into a dimensionless parameter, drel, the measured average cell size was divided by a theoretical maximum cell size, dmax. The calculation of dmax is done by assuming a one meter cube of material containing a single cell, large enough to achieve the void fraction of the foam. Consequently, drel essentially reflects the number of barriers to heat transfer in 1 meter of material. A smaller drel implies a larger number of barriers that must be passed to get from one end to the other.
| Property | Measured variables | Dimensionless variables |
|---|---|---|
| Thermal Conductivity (k) | kf ≡ foam k | 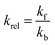 |
| kb ≡ bulk material k | ||
| kcellulose = 0.23 W m−1 K−1 (ref. 125) | ||
| kPU = 0.19 W m−1 K−1 (ref. 126) | ||
| kPLA = 0.18 W m−1 K−1 (ref. 127) | ||
| Density (ρ) | ρf ≡ foam apparent ρ | 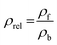 |
| ρb ≡ bulk material ρ | ||
| ρcellulose = 1500 kg m−3 (ref. 128) | Expansion ratio ≡ θ = 1/ρrel | |
| ρPU = 1225 kg m−3 (ref. 126) | Void fraction ≡ γ = 1 − ρrel | |
| ρPLA = 1240 kg m−3 (ref. 129) | ||
| Average cell size (d) | d ≡ measured average cell size | 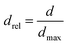 |
| dmax ≡ max cell size in 1 m3 at given γ | ||
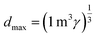 |
All references from which data was pulled to calculate our mathematical fit have reported thermal conductivity, average cell size, and either apparent foam density or expansion ratio. After converting all variables into dimensionless forms, a predicted krel was calculated from drel and ρrel using eqn (5) where x and y are the respective fit parameters. The solver function in Microsoft® Excel® was used to minimize the mean square error between predicted krel and the measured krel by adjusting x and y. Errors were given different weighting depending on the density data available. If expansion ratio was measured and reported directly, the point was given weighting of 1. If only apparent density was reported and relative density had to be calculated using material constants in Table 3, the point was given a weighting of 0.5. Fig. 13 displays the master curve of the measured versus predicted relative thermal conductivity and the final fit equation with optimized x and y. If the correlation were perfect, all points in the master curve would lie along the diagonal. There are some clusters of data which deviate from the trend, but in general, the equation fits reasonably well. Unsurprisingly, the optimized value for y is remarkably close to the exponent for the trend line observed in the reported expansion ratio data shown in Fig. 12. The same optimization process was done considering only drel or ρrel and with/without weighting errors. The results of each scenario are given in Table 4. Regardless of weighting, including both drel and ρrel minimizes the error of the prediction. It is notable, however, that ρrel on its own is a far better predictor of thermal conductivity than drel despite the fact that drel is affected by both cell size and density.
| krel = drelxρrely | (5) |
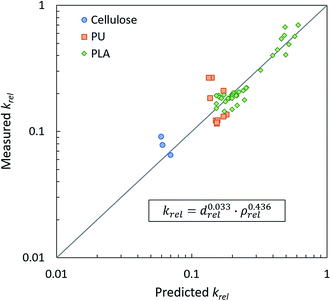 | ||
| Fig. 13 Master curve of measured relative thermal conductivity vs. predicted relative thermal conductivity. | ||
| Prediction equation | X | Y | Mean squared error | |
|---|---|---|---|---|
| Weighted errors | krel = drelxρrely | 0.03288 | 0.43578 | 0.03179 |
| krel = drelx | 0.12835 | — | 0.43044 | |
| krel = ρrely | — | 0.54263 | 0.06549 | |
| Unweighted errors | krel = drelxρrely | 0.03472 | 0.42473 | 0.04787 |
| krel = drelx | 0.13658 | — | 0.52388 | |
| krel = ρrely | — | 0.52914 | 0.08776 | |
To assess the trends presented by our mathematical fit and begin to fill data gaps, cell size and relative density data for biobased foams that do not have reported thermal conductivity values have been compiled in Fig. 14(a). These data were selected as they encompass a wide range of relative density and cell size. The predicted krel values were then plotted with the reported cell size in Fig. 14(b). This data was overlaid with four theoretical curves produced from the optimized eqn (5). Each curve corresponds to a fixed ρrel value. The curves display how krel changes with cell size given that fixed value for ρrel. These curves suggest that at very low relative densities, changes in cell size have virtually no impact on foam thermal conductivity. However, at higher relative densities, a change cell size can be quite significant, particularly if transitioning from a nanocellular foam to a microcellular foam or vice versa. It should also be noted that some regions of the theoretical curves are not necessarily possible in real foams; it is unlikely to achieve a foam with both very low density and very small cell size. Therefore, the most important observation from this analysis is that for thermally insulating foams, low relative density is the most influential factor with cell size being somewhat inconsequential. The predicted effective thermal conductivity of the compiled data was obtained by multiplying the predicted krel values by the appropriate material thermal conductivity constants in Table 3. As seen in Fig. 14(c), only two of the studies have predicted values which compare with the thermal conductivity of EPS: Li et al. created low density PLA foams using a high pressure vessel with CO2 as a PBA130 and Zhang et al. created a castor oil-based PU foam with soy protein as a crosslinking agent using the free-rise foaming method.53
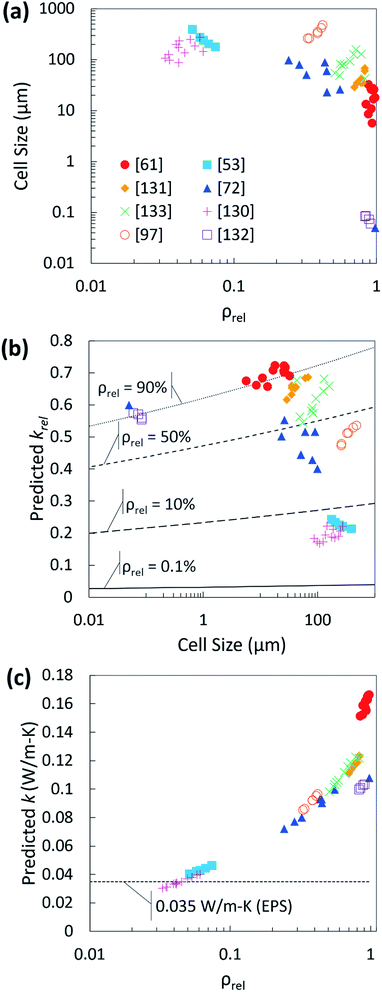 | ||
| Fig. 14 (a) Compiled biobased foam relative density and cell size data;53,61,72,97,130–133 (b) predicted krel plot for compiled data in terms of cell size overlaid with theoretical curves produced by the dimensional analysis fit equation showing impact of cell size for four different values of ρrel; (c) predicted krel converted to predicted effective thermal conductivity and plotted relative to ρrel. | ||
The dimensional analysis shown here is by no means comprehensive and it has not been validated experimentally. It should also be noted that, given the limitations of the available data, our mathematical fit provides no insight to how specific heat transfer mechanisms impact the thermal conductivity nor does it identify how foams with specific, non-traditional structures behave. The purpose of generating this correlation was twofold. First, the dimensional analysis explores a different approach to predicting thermal conductivity. Second, it provides a preliminary method for filtering through data in biobased foams literature to predict which experimental foams are most promising for thermal insulation. The analysis is not without merit, as it identified a trend in cell size which is not initially apparent from the raw data. Specifically, it suggests that the impact of cell size cannot be viewed independently of relative density. It also demonstrates the potential value in creating a model which is adaptive. The exponential fit parameters in our analysis can be adjusted as more data are added in the future. This will enable us to predict the thermal conductivity, cell size, or relative density for foams where the structure has not been thoroughly characterized. Furthermore, when more data for other structural characteristics becomes available, it is straightforward to add new fitting parameters or combine with current ones in the analysis.
5. Concluding remarks
Great strides have been made in recent years in the development of biobased foams for many applications including thermal insulation. The wide variety of materials and processing methods result in a diverse range of foam structures. Several experimental foams have already demonstrated thermal conductivity that is competitive with the industry standard. It would be ideal to benchmark the performance of these foams quantitatively and determine if there is any preferable structure, material and/or additive for producing biobased insulating foams. However, the lack of comparable data makes such an assessment challenging.The field of heat transfer modelling has also made impressive improvements, both in terms of more accurately reflecting true foam structures and calculating the contributions of individual heat transfer modes. As a result, these models have enabled researchers to identify the structural features which are desirable for thermally insulating foams and adjust processing conditions to achieve those structures. Notable structure features including, closed versus open cells, cell anisotropy, cell wall thickness and cell size distribution, are all shown to relate directly to thermal conductivity and other foam properties. The importance of heat transfer models in helping to inform new research endeavors cannot be understated. There remains a gap however, between what information current models can provide and the foam structures which are possible experimentally, particularly for biobased foams. Therefore, it is important to engage an adaptive approach. This may not only help fill the data gap in characterization of biobased foams, but also deepen our understanding of foam structure–property relationships.
There remain ways in which the properties of biobased foams could be improved and there is a need to more thoroughly compare those properties. Some foams have achieved highly desirable properties but are only partially biobased. Some materials have extremely wide ranges of thermal conductivity depending on additives and processing conditions. Additionally, the foaming methods which can be employed are limited by the material being used. Finding ways to manipulate biobased materials to improve the ease of processing is crucial from a practicality standpoint and would broaden potential capabilities. The complexity in foaming process and unknown variables post challenges in biobased foam research. On the other hand, these challenges also represent opportunities. Current and future heat transfer models may serve as a means to help address the challenges specific to processing conditions and material properties. The results will enable further progress by providing insight to structure property relationships for biobased foam systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the Polymer and Food Protection Consortium at Iowa State University for funding this work.References
- E. Olson, F. Liu, T. Bahns, S. Jiang, K. Vorst and G. Curtzwiler, Sustainable Mater. Technol., 2020, 25, e00193 CrossRef CAS.
- E. Olson, Y. Li, F.-Y. Lin, A. Miller, F. Liu, A. Tsyrenova, D. Palm, G. W. Curtzwiler, K. L. Vorst, E. Cochran and S. Jiang, ACS Appl. Mater. Interfaces, 2019, 11, 24552–24559 CrossRef CAS.
- S. Chen, E. Olson, S. Jiang and X. Yong, Nanoscale, 2020, 12, 14560–14572 RSC.
- S. Jiang, A. Van Dyk, A. Maurice, J. Bohling, D. Fasano and S. Brownell, Chem. Soc. Rev., 2017, 46, 3792–3807 RSC.
- D. Maga, M. Heibel and V. Aryan, Sustainability, 2019, 11, 5324 CrossRef CAS.
- C.-A. Gabriel, N. A. Bortsie-Aryee, N. Apparicio-Farrell and E. Farrell, J. Cleaner Prod., 2018, 182, 1095–1106 CrossRef.
- F. Razza, F. Degli Innocenti, A. Dobon, C. Aliaga, C. Sanchez and M. Hortal, J. Cleaner Prod., 2015, 102, 493–500 CrossRef CAS.
- C. Inagrao, A. Lo Guidice, J. Bacenetti, A. Mousavi Khaneghah, A. S. Sant'Ana, R. Rana and V. Siracusa, Food Res. Int., 2015, 76, 418–426 CrossRef.
- A. Zabaniotou and E. Kassidi, J. Cleaner Prod., 2003, 11, 549–559 CrossRef.
- C. Inagrao, A. Lo Guidice, J. Bacenetti, A. Mousavi Khaneghah, A. S. Sant'Ana, R. Rana and V. Siracusa, Food Res. Int., 2015, 76, 418–426 CrossRef.
- G. Kale, T. Kijchavengkul, R. Auras, M. Rubino, S. E. Selke and S. P. Singh, Macromol. Biosci., 2007, 7, 255–277 CrossRef CAS.
- E. Chiellini and R. Solaro, Adv. Mater., 1996, 8, 305–313 CrossRef CAS.
- S. Ahmadzadeh, A. Nasirpour, J. Keramat, N. Hamdami and T. Behzad, Colloids Surf., A, 2015, 468, 201–210 CrossRef CAS.
- P. Wang, N. Aliheidari, X. Zhang and A. Ameli, Carbohydr. Polym., 2019, 218, 103–111 CrossRef CAS.
- B. Wicklein, A. Kocjan, G. Salazar-Alvarez, F. Carosio, G. Camino, M. Antonietti and L. Bergström, Nat. Nanotechnol., 2015, 10, 277–283 CrossRef CAS.
- D. Ji, Z. Fang, W. He, K. Zhang, Z. Luo, T. Wang and K. Guo, ACS Sustainable Chem. Eng., 2015, 3, 1197–1204 CrossRef CAS.
- R. Yang, B. Wang, M. Li, X. Zhang and J. Li, Ind. Crops Prod., 2019, 136, 121–128 CrossRef CAS.
- J. Paciorek-Sadowska, M. Borowicz, B. Czuprynski and M. Isbrandt, Polymers, 2018, 10, 1334 CrossRef.
- P. Furtwengler, R. M. Boumbimba, A. Sarbu and L. Averous, ACS Sustain. Chem. Eng., 2018, 6, 6577–6589 CrossRef CAS.
- B. Li, M. Zhou, W. Huo, D. Cai, P. Qin, H. Cao and T. Tan, Ind. Crops Prod., 2020, 143, 111887 CrossRef CAS.
- N. Gama, L. C. Costa, V. Amaral, A. Ferreira and A. Barros-Timmons, Compos. Sci. Technol., 2017, 138, 24–31 CrossRef CAS.
- A. Arbenz, A. Franche, F. Cuttica and L. Averous, Polym. Degrad. Stab., 2016, 132, 62–68 CrossRef CAS.
- P. Gong, S. Zhai, R. Lee, C. Zhao, P. Buahom, G. Li and C. B. Park, Ind. Eng. Chem. Res., 2018, 57, 5464–5471 CrossRef CAS.
- G. Wang, L. Wang, L. H. Mark, V. Shaayegan, G. Wang, H. Li, G. Zhao and C. B. Park, ACS Appl. Mater. Interfaces, 2018, 10, 1195–1203 CrossRef CAS.
- K. Parker, J.-P. Garancher, S. Shah and A. Fernyhough, J. Cell. Plast., 2011, 47, 233–243 CrossRef CAS.
- G. Wang, J. Zhao, G. Wang, H. Zhao, J. Lin, G. Zhao and C. B. Park, Chem. Eng. J., 2020, 390, 124520 CrossRef.
- J. Wang, J. Chai, G. Wang, J. Zhao, D. Zhang, B. Li, H. Zhao and G. Zhao, Int. J. Biol. Macromol., 2019, 138, 144–155 CrossRef CAS.
- C. J. Cleveland, Energy, 2005, 30, 769–782 CrossRef.
- R. Kunic, Energy Effic., 2017, 10, 1511–1528 CrossRef.
- S. Lee, R. Smith, S. Costeux, J. Alcott, M. Barger, D. Beaudoin, H. Clayton, S. Donati, J. Duffy, R. Fox, D. Frankowski, K. Giza, L. Hood, T. Hu, C. Kruse, T. Morgan, C. Shmidt, W. Stobby and C. Vo, presented in part at the, SPE FOAMS, Iselin, NJ, 2009 Search PubMed.
- T. Pontiff, in Foam extrusion: principles and practice, ed. S. T. Lee, Technomic Publishing Company, Lancaster, PA, 2000 Search PubMed.
- M. Chandra, C. Kohn, J. Pawlitz and G. Powell, Real cost of styrofoam, Saint Louis University, 2016 Search PubMed.
- EUMEPS, EPS recycling international, https://epsrecycling.org/global-recycling-access, 2020 Search PubMed.
- G. Wypych, Handbook of foaming and blowing agents, ChemTec Publishing, Toronto, CA, 1st edn, 2017 Search PubMed.
- R. J. Moon, A. Martini, J. Nairn, J. Simonsen and J. Youngblood, Chem. Soc. Rev., 2011, 40, 3941–3994 RSC.
- N. Soykeabkaew, C. Thanomsilp and O. Suwantong, Composites, Part A, 2015, 78, 246–263 CrossRef CAS.
- H. Tian, G. Guo, X. Fu, Y. Yao, L. Yuan and A. Xiang, Int. J. Biol. Macromol., 2018, 120, 475–490 CrossRef CAS.
- P. Lu, M. Guo, Y. Yang and M. Wu, Polymers, 2018, 10, 1111 CrossRef.
- N. T. Cervin, L. Andersson, J. B. S. Ng, P. Olin, L. Bergstrom and L. Wagberg, Biomacromolecules, 2013, 14, 503–511 CrossRef CAS.
- M. Mihai, M. A. Huneault and B. D. Favis, J. Appl. Polym. Sci., 2009, 113, 2920–2932 CrossRef CAS.
- Z. Qu, D. Yin, H. Zhou, X. Wang and S. Zhao, Eur. Polym. J., 2019, 116, 291–301 CrossRef CAS.
- P. Ferkl, R. Pokorny, M. Bobak and J. Kosek, Chem. Eng. Sci., 2013, 97, 50–58 CrossRef CAS.
- A. Kaemmerlen, C. Vo, F. Asllanaj, G. Jeandel and D. Baillis, J. Quant. Spectrosc. Radiat. Transfer, 2010, 111, 865–877 CrossRef CAS.
- A. Rizvi, R. K. M. Chu and C. B. Park, ACS Appl. Mater. Interfaces, 2018, 10, 38410–38417 CrossRef CAS.
- F. Kreith, R. M. Manglik and M. S. Bohn, Principles of heat transfer, Cengage Learning, Stamford, CT, 7th edn, 2011 Search PubMed.
- M. Modest, Radiative heat transfer, Academic Press, Cambridge, MA, 2nd edn, 2003 Search PubMed.
- G. Wang, C. Wang, J. Zhao, G. Wang, C. B. Park and G. Zhao, Nanoscale, 2017, 9, 5996–6009 RSC.
- V. Bernardo, J. Martin-de-Leon, J. Pinto, R. Verdejo and M. A. Radriguez-Perez, Polymer, 2019, 160, 126–137 CrossRef CAS.
- J. O. Akindoyo, M. D. H. Beg, S. Ghazali, M. R. Islam, N. Jeyaratnam and A. R. Yuvaraj, R. Soc. Chem. Adv., 2016, 6, 114453–114482 CAS.
- M. Kirpluks, D. Kalnbunde, H. Benes and U. Cabulis, Ind. Crops Prod., 2018, 122, 627–636 CrossRef CAS.
- M. Desroches, M. Escouvois, R. Auvergne, S. Caillol and B. Boutevin, Polym. Rev., 2012, 52, 38–79 CrossRef CAS.
- N. N. Pauzi, R. Majid, M. H. Dzulkifli and M. Y. Yahya, Composites, Part B, 2014, 67, 521–526 CrossRef.
- S. Zhang, A. Xiang, H. Tian and A. V. Rajulu, J. Polym. Environ., 2018, 26, 15–22 CrossRef CAS.
- P. Furtwengler, R. M. Boumbimba and L. Averous, Macromol. Mater. Eng., 2018, 303, 1700501 CrossRef.
- N. Ozveren and M. O. Seydibeyoglu, Int. J. Polym. Sci., 2017, 2017, 6310198 Search PubMed.
- H. Fan, A. Tekeei, G. J. Suppes and F.-H. Hsieh, Int. J. Polym. Sci., 2012, 2012, 474803 Search PubMed.
- ASTM D6400-19, Standard Specification for Labeling of Plastics Designed to be Aerobically Composted in Municipal or Industrial Facilities, ASTM International, West Conshohocken, PA, 2019 Search PubMed.
- M. Ghasemlou, F. Daver, E. P. Ivanova and B. Adhikari, Eur. Polym. J., 2019, 118, 668–684 CrossRef CAS.
- X. Xi, A. Pizzi, C. Geradin, H. Lei, X. Chen and S. Amirou, Polymers, 2019, 11, 1802 CrossRef CAS.
- X. Xi, A. Pizzi, C. Geradin and G. Du, J. Renewable Mater., 2019, 7, 301–312 CAS.
- Y. Chen, S. Yang, D. Fan, G. Li and S. Wang, ACS Sustainable Chem. Eng., 2019, 7, 12878–12886 CrossRef CAS.
- H. G. Kim, Y.-S. Kim, L. K. Kwac, H. J. Shin, S. O. Lee, U. S. Lee and H. K. Shin, Nanomaterials, 2019, 9, 158 CrossRef CAS.
- R. Li, H. Lin, P. Lan, J. Gao, Y. Huang, Y. Wen and W. Yang, Polymers, 2018, 10, 1319 CrossRef.
- S. He, C. Liu, X. Chi, Y. Zhang, G. Yu, H. Wang, B. Li and H. Peng, Chem. Eng. J., 2019, 371, 34–42 CrossRef CAS.
- T. Rokkonen, H. Peltola and D. Sandquist, J. Appl. Polym. Sci., 2019, 136, 48202 CrossRef.
- J. S. Colton and N. P. Suh, Polym. Eng. Sci., 1987, 27, 500–503 CrossRef CAS.
- J. S. Colton and N. P. Suh, Polym. Eng. Sci., 1987, 27, 485–492 CrossRef CAS.
- M. Stanzione, M. Oliviero, M. Cocca, M. E. Errico, G. Gentile, M. Avella, M. Lavorgna, G. G. Buonocore and L. Verdolotti, Carbohydr. Polym., 2020, 231, 115772 CrossRef CAS.
- M. Nofar and C. B. Park, Prog. Polym. Sci., 2014, 39, 1721–1741 CrossRef CAS.
- M. Nofar, D. Scligil, P. J. Carreau, M. R. Kamal and M.-C. Heuzey, Int. J. Biol. Macromol., 2019, 125, 307–360 CrossRef CAS.
- J. Ludwiczak and M. Kozlowski, J. Polym. Environ., 2015, 23, 137–142 CrossRef CAS.
- S. Li, G. He, X. Liao, C. B. Park, Q. Yang and G. Li, RSC Adv., 2017, 7, 6266–6277 RSC.
- A. Ameli, D. Jahani, M. Nofar, P. U. Jung and C. B. Park, Compos. Sci. Technol., 2014, 90, 88–95 CrossRef CAS.
- T. Standau, C. Zhao, S. M. Castellon, C. Bonten and V. Altstadt, Polymers, 2019, 11, 306 CrossRef.
- J. Li, X. Liao, Q. Yang and G. Li, Ind. Eng. Chem. Res., 2017, 56, 11111–11124 CrossRef CAS.
- L. M. Matuana, O. Faruk and C. A. Diaz, Bioresour. Technol., 2009, 100, 5947–5954 CrossRef CAS.
- A. Kmetty, K. Litauszki and D. Reti, Appl. Sci., 2018, 8, 1960 CrossRef.
- T. He, X. Liao, Y. He and G. Li, Prog. Nat. Sci.: Mater. Int., 2013, 23, 395–401 CrossRef.
- S. Mali, F. Debiagi, M. V. E. Grossmann and F. Yamashita, Ind. Crops Prod., 2010, 32, 353–359 CrossRef CAS.
- I. Mariam, K. Y. Cho and S. S. H. Rizvi, Int. J. Food Prop., 2008, 11, 415–426 CrossRef CAS.
- A. E. S. Vercelheze, F. M. Fakhouri, L. H. Dall'Antonia, A. Urbano, E. Y. Youssef, F. Yamashita and S. Mali, Carbohydr. Polym., 2012, 87, 1302–1319 CrossRef CAS.
- S. Ketkaew, P. Kasemsiri, S. Hiziroglu, W. Mongkolthanaruk and R. Wannasutta, J. Polym. Environ., 2018, 26, 311–318 CrossRef CAS.
- J. B. Engel, A. Ambrosi and I. C. Tessaro, Carbohydr. Polym., 2019, 225, 115234 CrossRef CAS.
- C. Rojas, M. Cea, A. Iriarte, G. Valdes, R. Navia and J. P. Cardenas-R, Sustainable Mater. Technol., 2019, 20, e00102 CrossRef CAS.
- D. Liu, H. Tian and L. Zhang, J. Appl. Polym. Sci., 2007, 106, 130–137 CrossRef CAS.
- H. Tian, D. Liu and L. Zhang, J. Appl. Polym. Sci., 2009, 111, 1549–1556 CrossRef CAS.
- P. Chen, H. Tian, L. Zhang and P. R. Chang, Ind. Eng. Chem. Res., 2008, 47, 9389–9395 CrossRef CAS.
- G. Guo, C. Zhang, Z. Du, W. Zou and H. Li, J. Polym. Environ., 2015, 23, 183–189 CrossRef CAS.
- B. Liu, L. Jiang and J. Zhang, Macromol. Mater. Eng., 2011, 296, 835–842 CrossRef CAS.
- Z. Chen, J. Hu, J. Ju and T. Kuang, Polymers, 2019, 11, 1852 CrossRef CAS.
- S. C. Frerich, J. Supercrit. Fluids, 2015, 96, 349–358 CrossRef CAS.
- K. Ru, S. Zhang, X. Peng, J. Wang and H. Peng, Polymer, 2019, 185, 121967 CrossRef CAS.
- Y. Zhang, B. Lu, F. Lv, W. Guo, J. Ji, P. K. Chu and C. Zhang, J. Appl. Polym. Sci., 2012, 126, 756–761 CrossRef CAS.
- J.-F. Yue, L. Gan, C.-H. Liu, X.-Z. Ma, D. Wang and J. Huang, Polymer, 2018, 155, 50–57 CrossRef CAS.
- A.-K. Lim, S.-G. Jang, S.-I. Lee, K.-H. Lee and I.-J. Chin, Macromol. Res., 2008, 16, 218–223 CrossRef.
- S. Bonham and M. Misra, Macromol. Mater. Eng., 2011, 296, 788–801 CrossRef CAS.
- J. Zhou, Z. Yao, C. Zhou, D. Wei and S. Li, J. Appl. Polym. Sci., 2014, 131(18), 40773 Search PubMed.
- H. Ventrua, L. Sorrentino, E. Languna-Gutierrez, M. A. Rodriguez-Perez and M. Ardanuy, Polymers, 2018, 10, 249 CrossRef.
- D. M. Panaitescu, R. Trusca, A. R. Gabor, C. A. Nicolae and A. Casarica, Int. J. Biol. Macromol., 2020, 164, 1867–1878 CrossRef CAS.
- R. E. Lee, T. Azdast, G. Wang, X. Wang, P. C. Lee and C. B. Park, Int. J. Biol. Macromol., 2020, 155, 286–292 CrossRef CAS.
- D.-D. Ye, T. Wang, W. Liao, H. Wang, H.-B. Zhao, Y.-T. Wang, S. Xu and Y.-Z. Wang, ACS Sustainable Chem. Eng., 2019, 7, 11582–11592 CrossRef CAS.
- A. Fraleoni-Morgera and M. Chhikara, Adv. Eng. Mater., 2019, 21(7), 1801162 CrossRef.
- F. A. Govan, D. M. Greason and J. D. McAllister, Thermal insulation, materials, and systems for energy conservation in the 80's, ASTM International, West Conshohocken, PA, 1983 Search PubMed.
- B. Notario, J. Pinto, E. Solorzano, J. A. de Saja, M. Dumon and M. A. Rodriguez-Perez, Polymer, 2015, 56, 57–67 CrossRef CAS.
- X. Lu, R. Caps, J. Fricke, C. T. Alviso and R. W. Pekala, J. Non-Cryst. Solids, 1995, 188, 226–234 CrossRef CAS.
- R. J. J. Williams and C. M. Aldao, Polym. Eng. Sci., 1983, 23, 293–298 CrossRef CAS.
- Z. M. Zhang, Nano/Microscale Heat Transfer, McGraw-Hill Education, NY, 1st edn, 2007 Search PubMed.
- J. Lee, J. Lim and P. Yang, Nano Lett., 2015, 15, 3273–3279 CrossRef CAS.
- X. Lu, M. C. Arduini-Schuster, J. Kuhn, O. Nilsson, J. Fricke and R. W. Pekala, Science, 1992, 255, 971–972 CrossRef CAS.
- M. G. Ghossoub, K. V. Valavala, M. Seong, B. Azerdo, K. Hsu, J. S. Sadhu, P. K. Singh and S. Sinha, Nano Lett., 2013, 13, 1564–1571 CrossRef CAS.
- H. Malekpour, P. Ramnani, S. Srinivasan, G. Balasubramanian, D. L. Nika, A. Mulchandani, R. K. Lake and A. A. Balandin, Nanoscale, 2016, 8, 14608–14616 RSC.
- H. Ma and Z. Tian, Appl. Phys. Lett., 2015, 107, 073111 CrossRef.
- G. F. Smits, J. Therm. Insul. Build. Envelopes, 1994, 17, 309–329 CrossRef CAS.
- D. M. Bigg, in Thermal and Electrical Conductivity of Polymer Materials, Springer, Berlin, Heidelberg, 1995, vol. 119, pp pp. 1–30 Search PubMed.
- Z. Han and A. Fina, Prog. Polym. Sci., 2011, 36, 914–944 CrossRef CAS.
- W. Van De Walle, S. Claes and H. Janssen, Constr. Build. Mater., 2018, 182, 427–440 CrossRef.
- W. Van De Walle and H. Janssen, J. Build. Phys., 2019, 43, 277–300 CrossRef.
- M. Wang, J. Wang, N. Pan and S. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 036702 CrossRef.
- W. She, Y. Zhang and M. R. Jones, Constr. Build. Mater., 2014, 50, 421–431 CrossRef.
- J. Randrianalisoa, D. Baillis, C. L. Martin and R. Dendievel, Int. J. Therm. Sci., 2015, 98, 277–286 CrossRef.
- G. Gaiselmann, M. Neumann, V. Schmidt, O. Pecho, T. Hocker and L. Holzer, AIChE J., 2014, 60, 1983–1999 CrossRef CAS.
- R. Hasanzadeh, T. Azdast, A. Doniavi and M. Rostami, Heat and Mass Transfer, 2019, 55, 2845–2855 CrossRef CAS.
- Y. Li, J. Mi, H. Fu, H. Zhou and X. Wang, ACS Omega, 2019, 4, 12512–12523 CrossRef CAS.
- E. Cuce, P. M. Cuce, C. J. Wood and S. B. Riffat, Renewable Sustainable Energy Rev., 2014, 34, 273–299 CrossRef CAS.
- Engineering ToolBox, Thermal Conductivity of selected Materials and Gases, https://www.engineeringtoolbox.com/thermal-conductivity-d_429.html, accessed, 25 June, 2020 Search PubMed.
- L. V. Nielsen, H.-P. Ebert, F. Hemberger, J. Fricke, A. Biedermann, M. Reichelt and U. Rotermund, High Temp. – High Pressures, 2000, 32, 701–707 CrossRef CAS.
- R. Guo, Z. Ren, H. Bi, M. Xu and L. Cai, Polymers, 2019, 11, 549 CrossRef.
- National Center for Biotechnology Information, Cellulose, https://pubchem.ncbi.nlm.nih.gov/compound/CELLULOSE#section=Density, https://pubs.acs.org/doi/10.1021/acsami.8b22134, accessed, June 25, 2020 Search PubMed.
- Ingeo™ Biopolymer 8052D Technical Data Sheet, https://www.natureworksllc.com/~/media/Files/NatureWorks/Technical-Documents/Technical-Data-Sheets/TechnicalDataSheet_8052D_foam_pdf.pdf?la=en, accessed Dec 22, 2020 Search PubMed.
- D.-c. Li, T. Liu, L. Zhao, X.-s. Lian and W.-k. Yuan, Ind. Eng. Chem. Res., 2011, 50, 1997–2007 CrossRef CAS.
- N. Najafi, M.-C. Heuzey, P. J. Carreau, D. Therriault and C. B. Park, Eur. Polym. J., 2015, 73, 455–465 CrossRef CAS.
- J. Li, G. He, X. Liao, Q. Yang and G. Li, RSC Adv., 2015, 5, 36320–36324 RSC.
- P. Bhati and N. Bhatnagar, Mater. Lett., 2017, 209, 602–605 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |