Open Access Article
Open Access ArticleSoft-chemistry synthesis, solubility and interlayer spacing of carbon nano-onions
Aoping Guo
ab,
Kuo Baoab,
Song Sanga,
Xiaobao Zhangab,
Baiyi Shaoab,
Ce Zhangb,
Yangyang Wang b,
Fangming Cui
b,
Fangming Cui *b and
Xiaojing Yang
*b and
Xiaojing Yang
 *a
*a
aBeijing Key Laboratory of Energy Conversion and Storage Materials, College of Chemistry, Beijing Normal University, No. 19, Xinjiekouwai Street, Haidian District, Beijing 100875, China. E-mail: yang.xiaojing@bnu.edu.cn
bQian Xuesen Laboratory of Space Technology, China Academy of Space Technology, No. 104, Youyi Road, Haidian District, Beijing 100094, China. E-mail: cuifangming@qxslab.cn
First published on 10th February 2021
Abstract
Carbon nano-onions (CNOs), as one of the allotropes of carbon, have attracted great attention because of their excellent performance in many fields, especially in capacitors. Developing soft-chemistry synthesis methods is critically of importance, while the forming mechanism in this area is not clear. In this paper, we present a critical review of CNOs regarding the structure, especially interlayer spacing, and synthesis processes, elaborating the recent progress on soft-chemistry methods. Hansen solubility parameter theory is applied to predict and regulate the solubility of CNOs. This article would be inspirational and give new insights into understanding the formation and properties of CNOs.
1. Introduction
Shortly after the discovery of C60 and other hollow spherical carbon molecules, it was predicted that a hyperfullerene structure that would be composed of carbon multi-shells like a Russian doll would exist.1 Initially Iijima observed CNOs in an amorphous carbon film by vacuum evaporation using TEM in 1980 (Fig. 1a).2 During the process of preparing C60 by the electric arc method in 1991, Iijima found a concentric multi-shell fullerene structure, which was known as multi-walled carbon nanotubes (WMCNTs) afterwards.3 In 1992, Ugarte reported the in situ formation process of this multi-shell fullerene defined as CNOs by virtue of an onion-like structure consisting of multilayered concentric shells by transformation of carbon soot under electro-beam irradiation.4 Various synthesis methods for CNOs have been developed, including pyrolysis,5 chemical vapour deposition,6,7 nanodiamond-derived CNOs,8 arc discharge,9 electron beam irradiation,4 detonation,10–12 laser irradiation,13,14 ball-milling15 and ion-implantation.16,17 Most of these traditional methods require rigorous conditions, like high temperatures or high vacuum degrees, costly in terms of process. Most recently, soft-chemistry methods including solvothermal reduction and hydrothermal treatment are reported. They are meaningful and environment-friendly alternatives for synthesizing CNOs. Hence, we would focus on these progressive methods after shortly reviewing the common synthesis methods from the viewpoints of carbon precursors and synthesis conditions.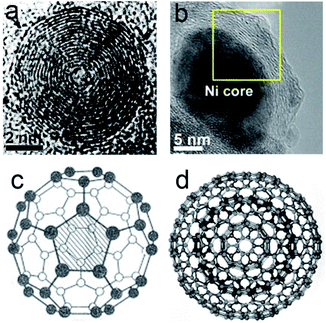 | ||
| Fig. 1 (a) TEM images of hollow CNOs by Iijima, Copyright 1980, Elsevier2 and (b) metal-filled CNOs, Copyright 2014, Elsevier;33 illustrations of (c) fundamental C60 buckyball, Copyright 2005, Elsevier34 and (d) ideal spherical CNOs, Copyright 2008, Elsevier.35 | ||
Owing to their outstanding properties, such as high specific surface area, broad absorption spectra, high thermal stability and electrical conductivity,18–20 CNOs have been considered as the desirable candidates for multiple applications ranging from biological imaging,21,22 capacitors,23–26 to catalysis27,28 and friction.29 For example, CNOs could be used as active materials, conductive additives and substrates for capacitors. To improve the performance of specific capacitance, chemical activation and hybrid with metal oxide or conducting polymer are generally adopted on CNOs.30 For such applications, an inferior solubility of CNOs in organic and inorganic solvents motives some researchers to investigate surface modification. We consider that the formation of CNOs may be related with the solubility of precursors. Therefore, we also review the utility of Hansen solubility parameter (HSP) to predict and select solvents for CNOs.
Depending on the synthesis methods and conditions, the CNOs differ in radius, specific surface area and chemical composition. The sizes of CNOs are generally at a range of 5–100 nm and exhibit a relatively high specific surface area up to 600 m2 g−1,31,32 while their morphologies reported are hollow or solid sphere, quasi-sphere or polyhedron. However, there is hardly a consensus about the interlayer spacings. We would summarize the interlayer spacings reported and furthermore report a preliminary theoretical calculation.
2. Structure
CNOs can be categorized as hollow and solid structures with concentric carbon multi-shells (Fig. 1b).33 The core of the CNOs could be transition metal particles or transition metal oxide.36–39 In some cases, the outer graphitic layers would linked together to form CNOs with multi-core structure.40 The number of carbon atoms C(n) of each layer was given as follows:25| C(n) = 60n2 | (1) |
It can be speculated that the innermost layer of CNOs, that n = 1, is well known as C60 cage or fullerene with a diameter of 0.71 nm, which is a representative zero-dimensional (0D) carbon allotrope (Fig. 1c).34 The ideal shape of CNOs is spherical (Fig. 1d), while in some cases the shape vary from sphere to polyhedron.35 According to Euler's phase rule in topology, the geometry relationship of a polyhedron m can be described as
| n − s + f = 2 | (2) |
| 3n = 2s | (3) |
| ∑mf(m) = 2s | (4) |
| f(5) = 12 | (5) |
| 5 × 12 + 6 × f(6) = 2s | (6) |
In other words, a fullerene can be expressed as C20+2p, p is the number of hexagons. Each type of fullerene contains exactly 12 pentagons and arbitrary number of hexagonal faces. For example, C60, the smallest fullerene that exists stably, consisted of 12 pentagons and 20 hexagonal rings.41 Generally, carbon atoms are in the forms of heptagonal, hexagonal and pentagonal rings. The most common carbon nanomaterial is graphene consisted of two-dimensional (2D) hexagonal networks. However, the non-hexagonal carbon rings are quite crucial for curling the structure and hence, closing the cage. Without the occurrence of non-hexagonal rings, it is impossible to form the curved cap of carbons, such as carbon nanotubes with closed ends. Moreover, pentagonal carbon rings avoid pairing with heptagons as they are likely to recombine leading to two hexagons.42 Apart from that, for fullerene, they also follow Isolated Pentagon Rule (IPR), that a stable fullerene structure would not contains adjacent five-number rings.43
According to Fowler' report,56 for a closed carbon cage formed by pentagons, hexagons and heptagons, the relation between the number of pentagons and heptagons, that f(5) and f(7), satisfy the following relationship:
| f(5) − f(7) = 12 | (7) |
Based on theory and practice, the general structural characteristics of closed cages should meet the constraining principles as follows:
(1) π-electron stabilization. Hexagonal rings have the mostly stable π-electron followed by pentagons and heptagons. Rings of 3, 4 and 8 are quite unstable because of σ-strain.
(2) Higher symmetry. The tension related to spherical curvature caused by pentagons should distribute uniformly.
(3) Euler law.
3. Synthesis of CNOs
In this section, the traditional synthesis methods from the viewpoints of carbon precursors and synthetic condition are summarized and at the same time, the soft-chemistry methods with mild conditions are highlighted.3.1 Overview of the common synthesis
Zeiger and Plonska–Brzezinskain made a detailed review about the traditional synthesis methods.32,57In 1994, Kuznetsov first reported nanodiamond-derived CNOs by heating treatment of ultradisperse diamond (2–6 nm) in high-vacuum chamber.44 While until today, annealing nanodiamond under a high vacuum and temperature have been the most common and industrial synthesis method so far because of a high atom utilization. Zeiger et al. reported that this transformation starts from outside to the inside.32 Solid state carbonization of phenolic–formaldehyde resin with ferric nitrate as the catalyst at 1000 °C was reported to synthetize CNOs in a great quantity, which showed quasi-spherical structure of well-aligned graphene layers.45,47 The process of flame assisted pyrolysis of ghee oil to synthesize CNOs was believed to follow bottom-up mechanism that ghee oil decomposed and generated chemically reactive radicals (like –C2H3), hydrogen atoms or sp2 carbon creating aromatic rings and curved polycyclic aromatic hydrocarbons.46 Arc discharge technology is a traditional route to synthesize fullerene-like materials and could be achieved in liquid nitrogen or organic solvent without offering vacuum system additionally according to Sano group.47,58 The sample produced by submerged arc in liquid nitrogen with Ni-contained graphite anode would resulted in carbon nano-capsule with the core of Ni particle.48 Arc in liquid C6H6 was verified to do not produce CNT which may give it a possibility to large-scale production for CNOs.47 Lithium ionic salts system had been proved to realize graphitization at a much low temperature (550–600 °C).49 In 2002, Sano made improvements to optimize this device by applying a direct current arc discharge between two graphite electrodes submerged in water.50 In most cases, catalysts are introduced in chemical vapor deposition (CVD) approach to decompose carbonaceous material dispersed on the substrates or floating in the chamber. Small molecules, like CH4,6,59,60 and C2H2 (ref. 51, 61 and 62) are the most common carbon sources to produce CNOs in CVD.
While with the presence of catalysts, the precursor would deposit on the surface of it and achievegraphitization at much a lower temperature (600–900 °C) since catalysts reduce the activation energy.52
Induced by high-energy e-beam, sp2-hybrid C of graphene had proven to be converted into fullerene.53 This course experienced “graphene route” that the carbon atoms at the edge of graphene are more labile compared with those in the middle since the energy needed almost one third less than the other, the loss of carbon atoms at margin can increase the dangling bonds and the defect graphene would lead in the formation of pentagons, which could caused the curve of the plane, this course is thermodynamically preferably. The structure continues curving until forming closed fullerene owing to the energy minimization theory. Treating single-walled carbon nanotubes (SWCNTs) in 30% HNO3 solution at 100 °C could lead to various phase, such as short bamboo-like multi-walled carbon nanotubes (MWCNTs) and CNOs, while in the medium of HCl solution would not cause any structural change.63
Sumio Iijima revealed the conversion from MWCNTs to CNOs by in situ TEM.54 The corresponding formation mechanism would be that the whole process involved two steps of growth and shrinkage. Sequential HRTEM images manifested that closed fullerene cages functioned as the nucleus and CNOs were produced and enlarged from the center to the outside converted by the MWCNTs layers (Fig. 2a–h). They raised that the polygonal carbon onion was formed from inward to outward in the first step and experienced a shrinkage course at high temperature. Under further irradiation, the arches got to be smoothed and annealed into spherical-shaped CNOs (Fig. 2i–l). In addition, irradiating of supercritical benzene with UV laser could formed aromatic hydrocarbons, such as naphthalene, biphenyl and realized graphitization.55,64 Generally, ball-milling uses stainless steel balls colliding with the material with a high milling speed. Chen declared of curved or closed-shell carbon nanostructures by ball-milling of graphite. The pristine graphite was composed of parallel layers while after the treatment of ball milling for 150 h the polyhedral structure appeared.15 Table 1 compared the details of these different synthesis methods.
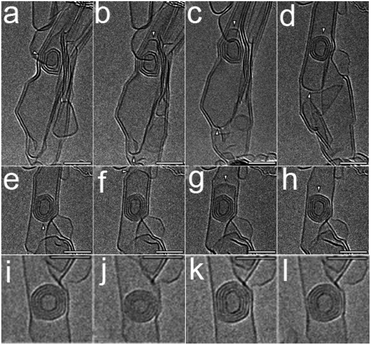 | ||
| Fig. 2 (a–h) Sequential HRTEM images showing a dynamic process for the shell-by-shell formation of a carbon polygon starting with a defective MWCNT; (i–l) sequential HRTEM images with further irradiation.54 Copyright 2009, ACS. | ||
| Synthesis method | Carbon precursor | Condition | Sample | Reference |
|---|---|---|---|---|
| Pyrolysis | Nano-diamond (2–6 nm) | Vacuum, 1000–1500 °C | Onion-like carbon | 44 |
| Phenolic–formaldehyde resin, ferric nitrate | 1000 °C, nitrogen gas | Quasi-spherical structure, 30–50 nm | 45 | |
| Ghee oil | Flame assisted pyrolysis | ≤60 nm | 46 | |
| Arc discharge | Graphite | Liquid C6H6 | CNOs, 10–30 nm | 47 |
| Ni-contained graphite anode | Liquid nitrogen | Carbon capsule with the core of Ni particle, CNT | 48 | |
| Graphite | Lithium ionic salts, 550–600 °C | CNT, CNOs | 49 | |
| Graphite | Water | CNT, spherical CNOs | 50 | |
| Chemical vapor deposition | Acetylene | Fe/Al2O3, 1100 °C | 15–40 nm | 51 |
| Polyvinyl alcohol | Nitrogen flow, 600 °C | Multi-walled graphite shells and nanotubes, graphite filaments | 52 | |
| Electron beam irradiation | Graphene | 80 kV | Fullerene cage | 53 |
| MWCNTs | Joule heating, 1.7 V | CNOs | 54 | |
| Laser irradiation | Supercritical benzene | UV laser | Aromatic hydrocarbons naphthalene, biphenyl and anthracene | 55 |
| Ball-milling | Graphite | High milling speed | Curved or closed-shell carbon nanostructures | 15 |
3.2 Soft-chemistry synthesis
Obviously, these ways mentioned above in this section require rigorous conditions, like high temperatures or high vacuum degrees, which are costly in terms of process. Therefore, developing soft-chemistry method in mild conditions to realize graphitization is incredibly significant. Recently, using a one-step of CHCl3 and potassium metal as low temperature as 100 °C have been put forward to synthesize hydrogenated CNOs successfully, which opens the way of graphitization.65 Time-dependent growth mechanism in this approach determined by the inspections of TEM, Raman and IR revealing that graphitic carbon were created within the first 2 h of the course and the degrees of hydrogenation increased with the reaction time. Convinced by XRD pattern of the existing KCl, it was likely that the thermal reduction of CHCl3 with potassium would lead to cleavages of C–Cl and C–H bonds, generating C-radicals followed by assembling into curved graphitic fragments and CNOs driven by the energy minimization theory. The whole process involved the transformation from sp3-hybridized carbon (CHCl3) to CNOs. Other organic solvent, including C2H3Cl3 and C2H4Cl2 have been reported to be the promising precursors.66 Instead of using active metal, sodium azide (NaN3) could be applied to produce sodium followed by reducing hexachlorobenzene (C6Cl6), which had been proven to be a feasible approach as well.67 Phenyl radicals produced during the dechlorination process as the sharp raise in temperature and pressure which was reported as the intermediates to create CNOs.Zhu group devised a reaction using calcium carbide (CaC2) reacting with chloride aluminum hexahydrate (AlCl3·6H2O) and obtained CNOs at a low temperature of 250 °C.68 By a sequence of experiments regarding to various precursors and reaction conditions, the authors supposed that the AlCl3·6H2O was of significance as it can not only be reduced to generate catalyst of Al, but also provide water to react with CaC2 producing C2H2 gases functioned as carbon source. Inspired by this, NiCl2·6H2O and CuCl2·2H2O were verified as well and hollow carbon polyhedrons were existed in the sample.69,70 They raised that the graphitization of carbon would cause the self-compression accompanying with high pressure, which may give a rise to apexes. Defects were likely to emerge when the pressure was out of boundaries and the polyhedral-shaped Ni particles were squeezed out to yield hollow carbon polyhedrons.
Our group71 found a novel way of hydrothermal carbon of citric acid at 180 °C with the existence of KNO3 to synthesize CNOs. By formation process determined by TEM, we proposed that the whole process involved three stages, including the dehydration of citric acids into the graphene quantum dots (GQD) and then grew and stacked into graphitic nanosheets (GS), which curved into graphitic hollow polyhedrons (GHP) due to the interface energy followed by spherical CNOs with the lowest interface energy in the hydrothermal solution by disordering and rearrangement of the carbon shell (Fig. 3). It should be noted that in this work we explained the transformation process as well as the function of KNO3 using interface energy and cohesion, which, we considered, are the reason of instable dispersion of carbon materials in the aqueous system. To describe the cohesion, Hanson solubility parameter (to be discussed below) can be used.
 | ||
| Fig. 3 Formation process of the hydrothermal synthesized CNOs.71 Copyright 2020, WILEY. | ||
4. Solubility
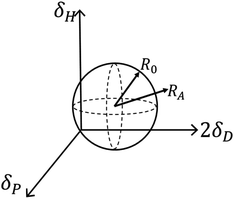
Actually pristine CNOs, similar to the case of carbon nanotubes, are insoluble in both polar and nonpolar solvent. The strong intermolecular interactions of CNOs, for example van der Waals and π-stacking forces, make their weak solubility in solvents.72 This inferior solubility largely limits their application. Therefore, predicting the solubility and developing strategies to improve their solubility is definitely a meaningful topic. Hansen solubility parameter (HSP) could be employed to evaluate a solubility.73 As mentioned above, HSP may have an important role in the formation of CNOs too.The solubility of CNOs (∼5 nm) synthesized from nano-diamond in 20 various types of solvents were investigated from the mixture of CNOs powder and solvent with a concentration of 1 mg mL−1 for 1 h.72 Fig. 4 showed that CNOs displayed enhanced “solubility affinity” in 8 kinds of solvents while precipitated in other 12 substances. Intermolecular forces are composed of dispersion force, polar force and hydrogen bonding. Hildebrand measured solubility parameters (δt) of a series of solvents and Hansen developed it by partitioning δt into three parts respectively and can be expressed in eqn (8)74
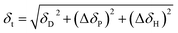 | (8) |
| RED = Ra/R0 | (9) |
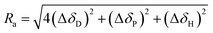 | (10) |
 | ||
| Fig. 4 Photographs of CNOs dispersed in (a) good and (b) bad solvents.72 Copyright 2019, Elsevier. | ||
If the value of RED less than 1, it implies a strong interaction between the two particles. Inferior insolvent has a RED value more than 1. In other words, the good solvents would exist within the sphere while all bad solvents stay outside. The computer optimization program located the centre (2δD, δP and δH) for CNOs as (31.8, 10, 8) MPa1/2 in this experiment and the value of R0 was 3.9 MPa1/2. By looking up to the HSP of the solvents and calculating the RED values, HSP theory can give a detailed explanation on this phenomenon. On the flip side, HSP theory is the most effective tool in selecting good solvents that predicted to be compatible with CNOs in terms of the solubility.
The poor solubility of CNOs in certain solvents limit and hinder their application. In order to improve the solubility, researchers have tried a great number of strategies to synthesize covalent and non-covalent functionalization of CNOs, such as cycloaddition,77 amidation of oxidized CNOs,78 cyclopropanation,64 radical addition79 to acquire CNOs with a variety of functional groups by regulating and controlling the three components of HSP for further applications. For example, using candle soot and oxidizing acid with the treatment of sonication can gain carbon onion clusters functionalized with –OH and –COOH groups that can maintain stability of dynamics in water within a year.80
5. Interlayer spacing
Interlayer spacing refers to the distance of the two adjacent carbon shells. Because the existence of pentagonal rings in the fullerene-like shells may lead to the interactions between the shells different from the those between the layers of graphite, the interlayer spacing of CNOs are different from the basal spacing (0.335 nm) of graphite.96 Herein, we summarize the interlayer spacings in the literatures, and then present a preliminary theoretical calculation result.5.1 Experimental measurement
The morphology and interlayer spacing of CNOs synthesized by different methods are exhibited in Table 2. Generally, the interlayer spacings of CNOs by various methods are slightly larger than 0.335 nm since CNOs with smaller curvature are likely lead to larger interlayer spacings.| Synthesis method | Carbon precursor | Morphology | Interlayer spacing (nm) | Reference |
|---|---|---|---|---|
| Electro-beam irradiation | Amorphous carbon film | Solid spherical structure | 0.36 | 81 |
| Amorphous carbon | Hollow spherical structure | 0.38, 0.39, 0.44 | 82 | |
| Amorphous carbon | Tetrahedral structure | 0.35 | 83 | |
| Ultrathin evaporated carbon | Nested polyhedron and rounded structure | 0.35 | 84 | |
| Heating/pyrolysis | Ultra-disperse diamond | Quai-spherical or polyhedron, with closed concentric graphite shells | 0.35 | 44 |
| Silicon carbide | Hollow or filled, enclosing graphitic onion-type structure | 0.344, 0.36 | 85 | |
| 120 KeV C+ | Solid, with circular crystallized carbon layers | 0.343 | 86 | |
| Plastic wastes | Solid, spherical, with concentric graphitic shells | 0.354 | 5 | |
| Naphthalene and graphite powder | Crystalline, solid and spherical with graphitic sheets | 0.36 ± 0.02 | 87 | |
| Combustion/flame | Clarified butter | Quasi-spherical, concentric, with randomly arranged graphite layers | 0.34–0.36 | 88 |
| Propane | Solid or hollow, spherical or polyhedral, with concentric multi-shells | 0.34 | 51 | |
| Chemical vapour deposition or plasma | Acetylene (C2H2) | Concentric graphitic layers with high graphitization degree | 0.346 | 89 |
| Methane (CH4) | Concentric carbon layers, hollow or encapsulated nickel particles | 0.35 | 90 | |
| Radio frequency plasma | Coal and graphite | Polyhedral or quasi-spherical with hollow center, high graphitization degree | 0.35 | 13 |
| Laser irradiation | Amorphous SiC layers | Small or large, quasi-spherical concentric structures with defective | 0.37 ± 0.02 | 91 |
| Ball milling | SiC powder | Hollow, polyhedral structures with graphite layers | 0.342–0.372 | 92 |
| Chemical treatment | Low-quality coals | Polyhedral or quasi-spherical onion-like fullerenes with hollow center | ∼0.38 | 93 |
| Ultrasonic irradiation | MWCNTs | Hollow, polyhedral structures with graphite layers | 0.35–0.36 | 94 |
| HF-etched silicon nanowires | Solid, quasi-spherical, with rough, wavy layers | 0.42 | 95 |
5.2 Theoretical calculation
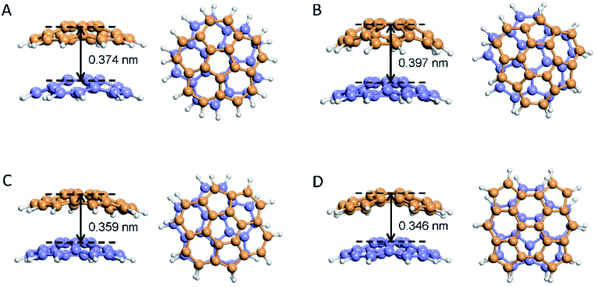
In fullerene chemistry, it is known that the introduction of a pentagon into the hexagonal structure of graphene will lead to the appearance of curvature according to Euler's Theorem. The curvature involves the p-orbitals of hybridized carbon atoms, which results in a highly pyramidic shape and the electronegative properties of fullerene.97 Notably, bowl-shaped polycyclic aromatic hydrocarbons (PAHs), also called buckybowls, can be regarded as a basic constituent fragment of a fullerene.Our group investigate four stable states of the pentagon contained carbon debris/fragments and the corresponding spacings of 0.346–0.397 nm obtained by Ab initio calculation method. We simulated the interlayer spacing of corannulene (C20H10), the smallest constituent fragment of a fullerene, when assembled with another bowl-shaped PAH (Fig. 6). The results showed that the interlayer spacing ranged from 0.346 nm to 0.397 nm, and the specific value was related to the molecular mass and relative position of the buckybowls. A repulsion effect from the electronegative induced curvature may also have contributed to the layer spacing. This explains why the interlayer spacing in CNOs, a structure nested by multiple fullerene-like spherical shells, was larger than the spacing found in graphite. Since the curvature was related to the shell diameter, there was a slight difference among the interlayer spacing of CNOs from the centre to the outside.
6. Summary
We summarized the reported synthesis methods of CNOs and gave a relatively detailed review on the soft-chemistry progress. A wide range of raw materials have been reported to be transformed into CNOs through certain synthesis methods. Large-scale synthesis is still one of the challenges, and developing novel, economical, environmentally-friendly and efficient soft-chemistry methods with high yield and purity is attractive.The solubility of CNOs in solvent could be explained and predicted utilizing HSP theory, moreover one can tune this property by regulating and controlling the three components of HSP for further applications.
The interlayer spacing of CNOs is slightly larger than 0.335 nm, which is the basal spacing of graphite, since the shells of CNOs with a small curvature leads to a large interlayer spacing. The spacing value can be a criterion to differentiate CNOs and graphite.
Author contributions
Aoping Guo: resources, formal analysis, investigation, writing-original draft. Kuo Bao: investigation, resources, formal analysis, validation. Song Sang: resources, formal analysis, validation. Xiaobao Zhang: formal analysis, validation. Baiyi Shao: editing, validation. Ce Zhang: formal analysis, validation, resources. Yangyang Wang: software, theoretical calculation. Fangming Cui: writing – review & editing, supervision. Xiaojing Yang: conceptualization, writing – review & editing, supervision.Conflicts of interest
There are no conflicts of interest in this manuscript.Acknowledgements
The financial support of the National Science Foundation of China (project No. 51572031) is gratefully acknowledged by the authors.Notes and references
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- S. Iijima, J. Cryst. Growth, 1980, 50, 675–683 CrossRef CAS.
- S. Iijima, Nature, 1991, 354, 56–58 CrossRef CAS.
- D. Ugarte, Nature, 1992, 359, 707–709 CrossRef CAS.
- S. Y. Sawant, R. S. Somani, A. B. Panda and H. C. Bajaj, Mater. Lett., 2013, 94, 132–135 CrossRef CAS.
- C. Zhang, J. Li, E. Liu, C. He, C. Shi, X. Du, R. H. Hauge and N. Zhao, Carbon, 2012, 50, 3513–3521 CrossRef CAS.
- C. N. He, N. Q. Zhao, C. S. Shi, X. W. Du, H. J. Li, L. Cui and F. He, Scr. Mater., 2006, 54, 1739–1743 CrossRef CAS.
- Y. V. Butenko, S. Krishnamurthy, A. K. Chakraborty, V. L. Klznetsov, V. R. Dhanak, M. R. C. Hunt and L. Siller, Phys. Rev. B, 2005, 71, 075420 CrossRef.
- S. M. Liu, M. Kobayashi, S. Sato and K. Kimura, Chem. Commun., 2005, 37, 4690–4692 RSC.
- N. Luo, H. Shen, H. Jing, Z. Ma and W. Yang, Particuology, 2017, 35, 78–83 CrossRef CAS.
- N. Luo, J.-X. Xiang, T. Shen, H.-L. Liang and S. Xin, Diamond Relat. Mater., 2019, 97, 107448 CrossRef CAS.
- B. Liu, D. Jia, Q. Meng and J. Rao, Carbon, 2007, 45, 668–670 CrossRef CAS.
- T. Gorelik, S. Urban, F. Falk, U. Kaiser and U. Glatzel, Chem. Phys. Lett., 2003, 373, 642–645 CrossRef CAS.
- S. Hu, P. Bai, F. Tian, S. Cao and J. Sun, Carbon, 2009, 47, 876–883 CrossRef CAS.
- X. H. Chen, H. S. Yang, G. T. Wu, M. Wang, F. M. Deng, X. B. Zhang, J. C. Peng and W. Z. Li, J. Cryst. Growth, 2000, 218, 57–61 CrossRef CAS.
- T. Cabioc'h, E. Thune and M. Jaouen, Chem. Phys. Lett., 2000, 320, 202–205 CrossRef.
- T. Cabioch, J. P. Riviere and J. Delafond, J. Mater. Sci., 1995, 30, 4787–4792 CrossRef CAS.
- D. M. Guldi and M. Prato, Acc. Chem. Res., 2000, 33, 695–703 CrossRef CAS.
- W. Krätschmer, L. D. Lamb, K. Fostiropoulos and D. R. Huffman, Nature, 1990, 347, 354–358 CrossRef.
- B. Xie, Z. Xu, W. Guo and Q. Li, Environ. Sci. Technol., 2008, 42, 2853–2859 CrossRef CAS.
- S. Giordani, J. Bartelmess, M. Frasconi, I. Biondi, S. Cheung, M. Grossi, D. Wu, L. Echegoyen and D. F. O'Shea, J. Mater. Chem. B, 2014, 2, 7459–7463 RSC.
- J. Bartelmess, E. De Luca, A. Signorelli, M. Baldrighi, M. Becce, R. Brescia, V. Nardone, E. Parisini, L. Echegoyen, P. P. Pompa and S. Giordani, Nanoscale, 2014, 6, 13761–13769 RSC.
- E. G. Bushueva, P. S. Galkin, A. V. Okotrub, L. G. Bulusheva, N. N. Gavrilov, V. L. Kuznetsov and S. I. Moiseekov, Phys. Status Solidi B, 2008, 245, 2296–2299 CrossRef CAS.
- J. K. McDonough, A. I. Frolov, V. Presser, J. Niu, C. H. Miller, T. Ubieto, M. V. Fedorov and Y. Gogotsi, Carbon, 2012, 50, 3298–3309 CrossRef CAS.
- D. Pech, M. Brunet, H. Durou, P. Huang, V. Mochalin, Y. Gogotsi, P.-L. Taberna and P. Simon, Nat. Nanotechnol., 2010, 5, 651–654 CrossRef CAS.
- C. Portet, G. Yushin and Y. Gogotsi, Carbon, 2007, 45, 2511–2518 CrossRef CAS.
- N. Keller, N. I. Maksimova, V. V. Roddatis, M. Schur, G. Mestl, Y. V. Butenko, V. L. Kuznetsov and R. Schlögl, Angew. Chem., Int. Ed., 2002, 41, 1885–1888 CrossRef CAS.
- D. Su, N. I. Maksimova, G. Mestl, V. L. Kuznetsov, V. Keller, R. Schlögla and N. Keller, Carbon, 2007, 45, 2145–2151 CrossRef CAS.
- N. Matsumoto, L. Joly-Pottuz, H. Kinoshita and N. Ohmae, Diamond Relat. Mater., 2007, 16, 1227–1230 CrossRef CAS.
- Y. Gao, Y. S. Zhou, M. Qian, X. N. He, J. Redepenning, P. Goodman, H. M. Li, L. Jiang and Y. F. Lu, Carbon, 2013, 51, 52–58 CrossRef CAS.
- Y. Zheng and P. Zhu, RSC Adv., 2016, 6, 92285–92298 RSC.
- M. Zeiger, N. Jäckel, V. N. Mochalin and V. Presser, J. Mater. Chem. A, 2016, 4, 3172–3196 RSC.
- J. Xiao, G. Ouyang, P. Liu, C. X. Wang and G. W. Yang, Nano Lett., 2014, 14, 3645–3652 CrossRef CAS.
- L. E. Murr and K. F. Soto, Mater. Charact., 2005, 55, 50–65 CrossRef CAS.
- B.-s. Xu, New Carbon Mater., 2008, 23, 289–301 CrossRef CAS.
- Z. Abdullaeua, E. Omurzak, C. Iwamoto, H. S. Ganapathy, S. Sulaimankulova, L. Chen and T. Mashimo, Carbon, 2012, 50, 1776–1785 CrossRef.
- X. Liu, S. W. Or, C. Jin, Y. Lv, C. Feng and Y. Sun, Carbon, 2013, 60, 215–220 CrossRef CAS.
- X. Liu, N. Bi, C. Feng, S. W. Or, Y. Sun, C. Jin, W. Li and F. Xiao, J. Alloys Compd., 2014, 587, 1–5 CrossRef CAS.
- X. Liu, S. W. Or, C. Jin, Y. Lv, W. Li, C. Feng, F. Xiao and Y. Sun, Electrochim. Acta, 2013, 100, 140–146 CrossRef CAS.
- B. S. Xu and S. I. Tanaka, Multiple-nuclei onion-like fullerenes cultivated by electron beam irradiation, 1998, pp. 619–624 Search PubMed.
- R. E. Smalley, Acc. Chem. Res., 1992, 25, 98–105 CrossRef CAS.
- X. H. Chen, F. M. Deng, J. X. Wang, H. S. Yang, G. T. Wu, X. B. Zhang, J. C. Peng and W. Z. Li, Chem. Phys. Lett., 2001, 336, 201–204 CrossRef CAS.
- Y. Morinaka, S. Sato, A. Wakamiya, H. Nikawa, N. Mizorogi, F. Tanabe, M. Murata, K. Komatsu, K. Furukawa, T. Kato, S. Nagase, T. Akasaka and Y. Murata, Nat. Commun., 2013, 4, 1554 CrossRef.
- V. L. Kuznetsov, A. L. Chuvilin, Y. V. Butenko, I. Y. Mal'kov and V. M. Titov, Chem. Phys. Lett., 1994, 222, 343–348 CrossRef CAS.
- M. Zhao, H. Song, X. Chen and W. Lian, Acta Mater., 2007, 55, 6144–6150 CrossRef CAS.
- T. H. Mongwe, B. J. Matsoso, B. K. Mutuma, N. J. Coville and M. S. Maubane, Diamond Relat. Mater., 2018, 90, 135–143 CrossRef CAS.
- N. Sano, Mater. Chem. Phys., 2004, 88, 235–238 CrossRef CAS.
- F. Cataldo, Polyhedron, 2004, 23, 1889–1896 CrossRef CAS.
- W. K. Hsu, M. Terrones, J. P. Hare, H. Terrones, H. W. Kroto and D. R. M. Walton, Chem. Phys. Lett., 1996, 262, 161–166 CrossRef CAS.
- N. Sano, H. Wang, I. Alexandrou, M. Chhowalla, K. B. K. Teo, G. A. J. Amaratunga and K. Iimura, J. Appl. Phys., 2002, 92, 2783–2788 CrossRef CAS.
- X. Liu, C. Wang, Y. Yang, X. Guo, H. Wen and B. Xu, Chin. Sci. Bull., 2009, 54, 137–141 CrossRef CAS.
- O. P. Krivoruchko, N. I. Maksimova, V. I. Zaikovskii and A. N. Salanov, Carbon, 2000, 38, 1075–1082 CrossRef CAS.
- A. Chuvilin, U. Kaiser, E. Bichoutskaia, N. A. Besley and A. N. Khlobystov, Nat. Chem., 2010, 2, 450–453 CrossRef CAS.
- C. Jin, K. Suenaga and S. Iijima, J. Phys. Chem. C, 2009, 113, 5043–5046 CrossRef CAS.
- T. Fukuda, N. Watabe, R. L. D. Whitby and T. Maekawa, Nanotechnology, 2007, 18, 415604 CrossRef.
- P. W. Fowler, T. Heine, D. Mitchell, G. Orlandi, R. Schmidt, G. Seifert and F. Zerbetto, J. Chem. Soc., Faraday Trans., 1996, 92, 2203–2210 RSC.
- M. E. Plonska-Brzezinska, Chemnanomat, 2019, 5, 568–580 CrossRef CAS.
- N. Sano, T. Kikuchi, H. L. Wang, M. Chhowalla and G. A. J. Amaratunga, Carbon, 2004, 42, 95–99 CrossRef CAS.
- M. Ghosh, S. K. Sonkar, M. Saxena and S. Sarkar, Small, 2011, 7, 3170–3177 CrossRef CAS.
- F. Tian and C. N. He, Mater. Chem. Phys., 2010, 123, 351–355 CrossRef CAS.
- V. Serin, R. Brydson, A. Scott, Y. Kihn, O. Abidate, B. Maquin and A. Derréc, Carbon, 2000, 38, 547–554 CrossRef CAS.
- X. M. Wang, B. S. Xu, H. S. Jia, X. G. Liu and I. Hideki, J. Phys. Chem. Solids, 2006, 67, 871–874 CrossRef CAS.
- K. H. An, K. K. Jeon, J. M. Moon, S. J. Eum, C. W. Yang, G. S. Park, C. Y. Park and Y. H. Lee, Synth. Met., 2004, 140, 1–8 CrossRef CAS.
- A. Palkar, F. Melin, C. M. Cardona, B. Elliott, A. K. Naskar, D. D. Edie, A. Kumbhar and L. Echegoyen, Chem. - Asian J., 2007, 2, 625–633 CrossRef CAS.
- C. Zhai, X. Kong, K. Hu, L. Wang and X. Fan, Chem. Phys. Lett., 2020, 738 Search PubMed.
- S. Zhao, Y. Fan, K. Zhu, D. Zhang, W. Zhang, S. Chen, R. Liu, M. Yao and B. Liu, Nanoscale, 2015, 7, 1984–1993 RSC.
- M. Bystrzejewski, M. H. Rummeli, T. Gemming, H. Lange and A. Huczko, New Carbon Mater., 2010, 25, 1–8 CrossRef CAS.
- H.-L. Zhu, Y.-J. Bai, Y.-X. Qi, N. Lun and Y. Zhu, Carbon, 2012, 50, 1871–1878 CrossRef CAS.
- Y. Zhu, Y.-J. Bai, N. Lun, Y.-X. Qi, R. Liu and H.-L. Zhu, Mater. Chem. Phys., 2012, 134, 639–645 CrossRef CAS.
- F.-D. Han, B. Yao and Y.-J. Bai, J. Phys. Chem. C, 2011, 115, 8923–8927 CrossRef CAS.
- S. Sang, S. Yang, A. Guo, X. Gao, Y. Wang, C. Zhang, F. Cui and X. Yang, Chem. - Asian J., 2020, 15, 3428–3431 CrossRef CAS.
- J. C. Zuaznabar-Gardona and A. Fragoso, J. Mol. Liq., 2019, 294, 111646 CrossRef CAS.
- C. M. Hansen, Ind. Eng. Chem. Prod. Res. Dev., 1969, 8, 2–8 CrossRef CAS.
- C. M. Hansen, Hansen Solubility Parameters: A user's Handbook, CRC Press, Florida, 2nd edn, 2007 Search PubMed.
- S. Yong, On Solubility Parameter, 2007, pp. 9–12 Search PubMed.
- J. Howell, M. Roesing and D. Boucher, J. Phys. Chem. B, 2017, 121, 4191–4201 CrossRef CAS.
- V. Georgakilas, D. M. Guldi, R. Signorini, R. Bozio and M. Prato, J. Am. Chem. Soc., 2003, 125, 14268–14269 CrossRef CAS.
- J. Luszczyn, M. E. Plonska-Brzezinska, A. Palkar, A. T. Dubis, A. Simionescu, D. T. Simionescu, B. Kalska-Szostko, K. Winkler and L. Echegoyen, Chem. - Eur. J., 2010, 16, 4870–4880 CrossRef CAS.
- A. S. Rettenbacher, M. W. Perpall, L. Echegoyen, J. Hudson and D. W. Smith, Jr., Chem. Mater., 2007, 19, 1411–1417 CrossRef CAS.
- W. Sun, X. Zhang, H.-R. Jia, Y.-X. Zhu, Y. Guo, G. Gao, Y.-H. Li and F.-G. Wu, Small, 2019, 15, 1804575 CrossRef.
- B. S. Xu and S. I. Tanaka, Acta Mater., 1998, 46, 5249–5257 CrossRef CAS.
- T. Oku, G. Schmid and K. Suganuma, J. Mater. Chem., 1998, 8, 2113–2117 RSC.
- I. Narita, T. Oku, K. Suganuma, K. Hiraga and E. Aoyagi, J. Mater. Chem., 2001, 11, 1761–1762 RSC.
- H. E. Troiani, A. Camacho-Bragado, V. Armendariz, J. L. G. Torresday and M. J. Yacaman, Chem. Mater., 2003, 15, 1029–1031 CrossRef CAS.
- S. Welz, Y. Gogotsi and M. J. McNallan, J. Appl. Phys., 2003, 93, 4207–4214 CrossRef CAS.
- T. Cabioc'h, J. P. Rivière, M. Jaouen, J. Delafond and M. F. Denanot, Synth. Met., 1996, 77, 253–256 CrossRef.
- D. Mohapatra, S. Badrayyana and S. Parida, Mater. Chem. Phys., 2016, 174, 112–119 CrossRef CAS.
- T. Garcia-Martin, P. Rincon-Arevalo and G. Campos-Martin, Cent. Eur. J. Phys., 2013, 11, 1548–1558 CAS.
- C. N. He, N. Q. Zhao, C. S. Shi, X. W. Du and H. J. Li, Mater. Chem. Phys., 2006, 97, 109–115 CrossRef CAS.
- A. B. Du, X. G. Liu, D. J. Fu, P. D. Han and B. S. Xu, Fuel, 2007, 86, 294–298 CrossRef CAS.
- J. Xu, R. Zhang, J. Wang, S. Ge and F. Wen, Mater. Lett., 2012, 88, 168–170 CrossRef CAS.
- R. Bajpai, L. Rapoport, K. Amsalem and H. D. Wagner, Crystengcomm, 2016, 18, 230–239 RSC.
- T. Das, P. K. Boruah, M. R. Das and B. K. Saikia, RSC Adv., 2016, 6, 35177–35190 RSC.
- O. V. Kharissova, H. V. R. Dias, B. I. Kharisov and J. Jiang, RSC Adv., 2015, 5, 57764–57770 RSC.
- X. H. Sun, C. P. Li, N. B. Wong, C. S. Lee, S. T. Lee and B. K. Teo, J. Am. Chem. Soc., 2002, 124, 14856–14857 CrossRef CAS.
- Z. Xu, L. Liu, Y. Huang, Y. Sun, X. Wu and J. Li, Mater. Lett., 2009, 63, 1814–1816 CrossRef CAS.
- A. Hirsch, Synthesis, 1995, 895–913 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |