Open Access Article
Open Access ArticleSubstitutional 4d transition metal doping in atomically thin lead
Daniel Hashemi * and
Hideo Iizuka
* and
Hideo Iizuka
Toyota Research Institute of North America, Toyota Motor North America, Ann Arbor, MI 48105, USA. E-mail: daniel.hashemi@toyota.com
First published on 3rd February 2021
Abstract
To study the potential of plumbene as a dilute magnetic semiconductor, we computationally investigate the structural, electronic, and magnetic properties of 4d transition metal (TM) doped plumbene using density functional theory (DFT). These calculations show that Zr, Nb, Mo, Tc-doped plumbene systems are magnetic while no magnetic solution was found for Y, Ru, Rh, and Pd-doped cases. We also calculate the magnetic couplings between two TM impurities in the system with an impurity concentration of less than 2%. Strong exchange couplings and large magnetic anisotropic energies, indicate the potential for spintronics applications.
I. Introduction
Two-dimensional (2D) materials offer unusual physical properties compared to their bulk counterparts. Graphene, the world's first 2D material, exhibits exceptional physical properties in terms of its thickness, stability, conductivity, and flexibility. Drawing inspiration from graphene, there has been intensive research into other single-layer thick materials, mostly composed of group 14 atoms arranged in a honeycomb lattice.From this group of materials, plumbene has attracted attention since it has the strongest spin–orbit interaction among all the group 14 members.1 Moreover, compared with graphene and phosphorene, plumbene can take advantage of rich physical characteristics due to strong spin–orbit coupling (SOC). Regarding mechanical properties, a recent molecular dynamics simulation has demonstrated that plumbene is several times stronger than bulk lead.2 In respect to topological insulating properties, ab initio calculations3 confirmed that plumbene becomes a topological insulator with a large bandgap of ≈200 meV through electron doping. Theoretical calculations also showed that plumbene is the right candidate for realizing the quantum spin Hall effect at room temperature (RT).4 Unexpected quantum spin Hall insulating properties were also reported for bilayer and decorated plumbene.5,6
Over the past decades, many types of research have been conducted on the fundamental science of dilute magnetic semiconductors (DMSs).7–11 The combination of 2D semiconductors and magnetic data storage devices could result in 2D spintronics devices with a wide range of applications such as non-volatile magnetoresistive memories, spin valves, spin-based transistors, and magnetically enhanced optoelectronic devices.12
DMSs in the 2D case can be obtained by the engineering of the electronic and magnetic properties of 2D materials through substitutional doping or adsorption of 3d-TM elements.13–17 Magnetic substitutional doping can induce spin and valley polarization due to the spin–orbit and exchange interaction in transition-metal dichalcogenides (TMDs).18
None of these species is magnetic in the bulk. However, a spontaneous magnetization should appear for certain elements if their dimensionality is reduced. For example, large magnetic moments were calculated for monoatomic Ru, Rh, and Ir overlayers on Ag 001 ref. 22 and for Mo and Tc wires on Ag(117) vicinal surfaces.
In this work, ab initio DFT calculations, that include SOC are performed to systematically investigate the structural, electronic, and magnetic properties of 4d TM-doped plumbene systems. First, the stability, electronic, and magnetic properties of TM defects in plumbene are studied. After that, the magnetic orders are obtained through the long-range interaction between the diluted TM-doped systems, followed by the magnetic anisotropy energy calculations.
II. Computational details
The vienna ab initio simulation package (VASP)19,20 was used to perform the calculations within the framework of spin-polarized DFT including SOC. The electronic properties of plumbene can be highly influenced by SOC. The frozen-core full-potential projector augmented-wave method (PAW) was used21 with the Perdew, Burke, and Ernzernhof (PBE)22 generalized gradient approximation (GGA). These functionals have been shown to provide accurate description of the electronic and magnetic properties of TM nanostructures such as adatoms23,24 and nanowires.25–27The convergence with respect to the size of k-sampling, cutoff radius, and vacuum thickness was checked. These resulted in a k-point mesh of 2 × 2 × 1 for Density of States (DOS) of the TM-doped system, a plane-wave cutoff radius of 600 eV, and a vacuum distance between the periodic images of 15 Å. The conjugate-gradient algorithm for structural relaxation with a force convergence criterion of 0.01 eV Å−1 was used.
To obtain the fundamental bandgap, the electronic band structures were calculated using the PBE functional, hybrid Heyd–Scuseria–Ernzerhof functionals (HSE03)28–30 and (HSE06).31 We used the standard values for the mixing parameter (0.25) and the range-separation parameters of 0.3 Å−1 and 0.2 Å−1 for the HSE03 and HSE06 functionals, respectively. Bader formalism32–34 was used to carry out charge transfer analysis between TM and plumbene. A 6 × 6 × 1 k-points mesh in the Brillouin zone of the primitive unit cell was used to sample the reciprocal space. To study the electronic and magnetic properties of TM-doped systems, the PBE-optimized structures were used. To determine the easy magnetization axis and to calculate the magnetic interaction between two TM impurities, the noncollinear spin polarization in a fully relativistic framework for the TM-doped plumbene systems was used. The structures and charge densities were visualized using VESTA code.35
III. Results and discussions
A. Structure and energetics
The calculated band gap energy, lattice constant, and buckling height of freestanding plumbene are 0.43 eV, 4.93 Å, and 1.01 Å, respectively.36To model the single impurity TM-doped systems, we chose a 4 × 2 supercell along the zigzag and armchair directions with lattice constants of a = 19.74 Å and b = 17.09 Å, as shown in Fig. 1. This corresponds to 31 Pb atoms in a TM atom in the supercell. For structural relaxations of the TM-doped system in this supercell, we used only the Γ point sampling of the Brillouin zone. We first test the equilibrium configuration of a pristine plumbene sheet. As obtained by PBE calculations, the equilibrium lattice constant, Pb–Pb bond length, and buckling height were estimated to be 4.93 Å, 3.02 Å, and 1.01 Å, respectively, which are consistent with previous studies.3,36–38
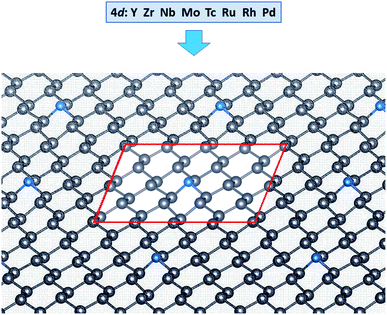 | ||
| Fig. 1 Schematic representation of the system under study. The unit cell is highlighted by the red rectangle. | ||
Table 1 lists the geometric, electronic, and magnetic characters of TM-substituted plumbene. The binding energy in our calculations is defined as follows:
| Eb = EPb–Vac + ETM − EPb–TM, | (1) |
| Dopant | Y | Zr | Nb | Mo | Tc | Ru | Rh | Pd | Pristine |
|---|---|---|---|---|---|---|---|---|---|
| Eb (eV) | 3.47 | 3.77 | 3.45 | 4.82 | 3.28 | 4.01 | 4.57 | 3.08 | 1.97 |
| TM-Pb (Å) | 3.06 | 2.89 | 2.83 | 2.80 | 2.68 | 2.63 | 2.61 | 2.64 | 3.02 |
| Ex − Ez (meV) | 13.98 | 16.25 | −19.96 | ||||||
| |ms| (μB) | 0.46 | 1.59 | 2.69 | 1.77 | 0.04 | ||||
| |mo| (μB) | 0.21 | 0.20 | 0.11 | 0.12 | 0.04 | ||||
| TM charge transfer (e) | −1.16 | −0.84 | −0.42 | −0.08 | +0.14 | +0.42 | +0.51 | +0.49 | |
| Pb charge transfer (e) | +0.37 | +0.31 | +0.17 | +0.04 | −0.04 | −0.13 | −0.17 | −0.14 | |
| ΔE(short) (meV) | −19 | 33 | 29 | ||||||
| ΔE(far) (meV) | −3 | −24 | 13 |
Generally, the Eb values are significantly higher than those form 3d TM-doped in plumbene36 and phosphorene,13 but still lower than those from 4d TM-doped doped in graphene.39 The binding energy values suggest that the bonding strength of the 4d TM impurities to plumbene is rather strong (see Fig. 3).
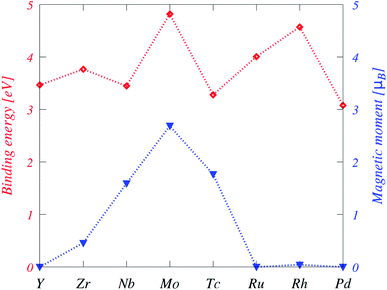 | ||
| Fig. 2 Binding energies (red) and magnetic moments (blue) of the TM-doped plumbene system. The dotted lines between symbols are a guide to the eye. | ||
Moreover, the Eb trend is not monotonic as the atomic number increases and it decreases when 4d shells are fully filled or almost empty. For instance, Eb is minimized for Y and Pd. Additionally, Eb is maximized twice at Mo and Rh, while Mo forms the strongest interaction among this series. This trend is shown in Fig. 2. The Eb shows a different trend in the case of 3d TM-doped plumbene so that it has a minimum value at the middle of the 3d series indicating that the binding is weakest when the d shell is half-filled.
TM–Pb bond length decreases from Y to Pd as the atomic radius decreases, except for Pd, for which the binding energy is the weakest among this series. The TM–Pb bond length is smaller than Pb–Pb bond length in plumbene because the atomic radii of 4d series TM are smaller than that of Pb, except for Y, for which the atomic radius is the same as Pb.40 The presence of Jahn–Teller distortion was explored for the 4d series by placing them at asymmetric sites, but all the 4d TM atoms relaxed back to the symmetric sites in order to maintain C3v symmetry.
Charge transfer is an important feature for the substitutional systems. The charge transfer is mainly from TM to the neighboring Pb atoms for the early 4d TM elements up to Mo, then from Pb atoms to the TM. TM atoms bond with three Pb atoms, retaining some unpaired electrons, which eventually leads to magnetic quality, however, for the electrons of 4d orbitals more than five, it is more complicated.
Since Pd-doped plumbene exhibited the Eb, we explored its thermal stability via ab initio molecular dynamics (MD) simulations at room temperature. These simulations showed that the Pd-doped system is structurally stable throughout the entire MD simulation. Since Pd-doped plumbene was structural stable, TM-doped systems with higher binding energies are expected to be even more stable.
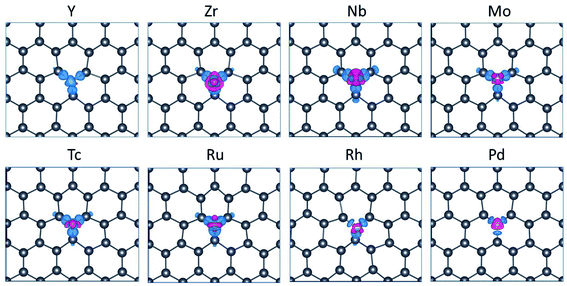
The DOS and projected DOS (PDOS) of TM-doped systems (Fig. 4) show that the energy splitting between the TM-4d peaks is large, signifying that magnetism mainly originates from TM impurities. Several resonance peaks can be found in the DOS, which is caused by the strong hybridization between the 4d orbitals of TM and 3p orbitals of Pb.
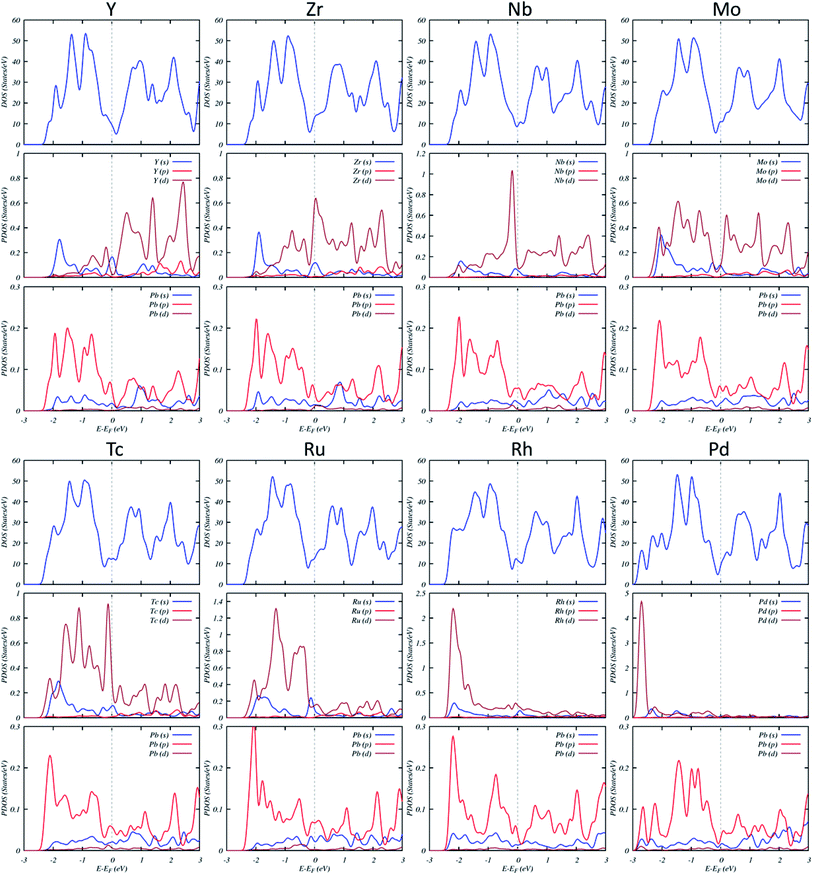 | ||
| Fig. 4 DOS and projected DOS of the TM-substituted systems. The Fermi level has been set to zero and indicated by a vertical gray dashed line. | ||
B. Magnetic properties
DFT calculations suggest doping with Y, Ru, Rh, and Pd results in nonmagnetic states, while magnetism is observed for Zr, Nb, Mo, and Tc-doped plumbene systems. Particularly, the impurities from Mo to Tc have magnetic states due to more valence electrons than Pb and an open shell structure. Isolated TM atoms have large spin and orbital magnetic moments according to Hund's rules. However, electron delocalization and crystal field effects compete with intra-atomic Coulomb interactions leading to an overall reduction of spin moments as well as a quenching of orbital moments in TM impurities dissolved in nonmagnetic hosts. As shown in Table 1,the absolute values of spin magnetic moments are 0.46μB, 1.59μB, 2.69μB, 1.77μB for Zr, Nb, Mo, and Tc, respectively. Plumbene doped with TM impurities has a fractional magnetic moment due to a partially occupied 4s orbital, which is unoccupied for TM-substituted graphene. The orbital magnetic moments of the TM-doped systems are 0.21μB for Zr, 0.20μB for Nb, 0.11μB for Mo, 0.12μB for Tc, and 0.04μB for Rh.In order to determine the magnetic exchange coupling between two impurities in magnetic systems, two TM (Nb, Mo, and Tc) atoms are doped in a 7 × 4 supercell with a TM concentration of 1.79%. The lattice constants of this supercell are a = 34.54 Å and b = 34.18 Å, respectively, which correspond to 110 Pb atoms and two TM atoms in the supercell. Zr-doped system was not considered in this study due to the small exchange coupling constants, even though it is slightly magnetic.
Energy difference between ferromagnetic (FM) and antiparallel spins (AF) is exchange coupling. The spins are oriented along the corresponding preferential orientation (easy axis) in each case. The FM and AF spin configurations are considered to check the magnetic ground state. We consider two different distances between the two impurities; short (4.89 Å) and far (10.30 Å).
According to the exchange coupling constants between FM and AF states in Table 1, the AF ground state is energetically favorable in the Nb doped cases with either short or far distance. On the contrary, the Tc-doped case is FM ordered and independent of the distance between two Tc impurities. Interestingly, the Mo-doped case shows FM ordering for the short distance and AF ordering for the far distance. It is worth noting that these exchange couplings decay as the inter-impurity separation increases.
C. Magnetic anisotropy energy
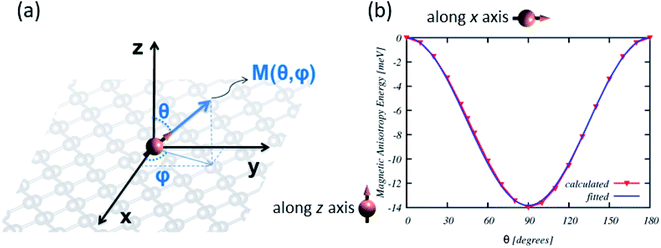
The total energy of the orientation dependent magnetization M(ϕ,θ) of TM impurity (see Fig. 5) in the lowest non-vanishing terms can be written as41
Et = E0 + sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(E1 − E2 θ(E1 − E2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ), ϕ),
| (2) |
As shown in Table 1, Nb, Mo, and Tc-doped systems have large magnetic anisotropy energies (MAE) of 13.98 meV, 16.25 meV, and −19.96 meV, respectively. We have attempted to relate these MAEs to the electronic structure, using the PDOS (Fig. 4). We noticed that MAE is related to a hybridization of the s and d states of TM and Pb atoms. The dominant contributions to the MAE arise from a change in the occupation of states below the Fermi level. The contributions from these states are overally increased from Nb to Tc.
IV. Conclusions
Our DFT calculations suggest that the proper choice of 4d TM doped in the ultrathin lead can control its electronic and magnetic properties. The spin polarization is found in Zr, Nb, Mo, Tc, and Rh-doped systems. The long-range and anisotropic interactions between two TM impurities in plumbene with an impurity concentration of 1.79% were calculated. Nb has an AF ordering, but Tc has an FM ordering for both short and long distances. However, Mo has an FM ordering for the short length and changes to an AF order as the interatomic distance increases. Non-collinear spin-polarized DFT is employed to calculate the MAEs. Nb, Mo, and Tc-doped plumbene exhibit large MAE, which is a strong indication of spintronics applications' potential.Conflicts of interest
There are no conflicts to declare.References
- F. Herman, C. D. Kuglin, K. F. Cuff and R. L. Kortum, Relativistic corrections to the band structure of tetrahedrally bonded semiconductors, Phys. Rev. Lett., 1963, 11, 541–545 CrossRef.
- D. K. Das, J. Sarkar and S. Singh, Effect of sample size, temperature and strain velocity on mechanical properties of plumbene by tensile loading along longitudinal direction: a molecular dynamics study, Comput. Mater. Sci., 2018, 151, 196–203 CrossRef CAS.
- X.-L. Yu, L. Huang and J. Wu, From a normal insulator to a topological insulator in plumbene, Phys. Rev. B, 2017, 95, 125113 CrossRef.
- X.-L. Yu and J. Wu, Evolution of the topological properties of two-dimensional group iva materials and device design, Phys. Chem. Chem. Phys., 2018, 20, 2296–2307 RSC.
- H. Zhao, C.-w. Zhang, W.-x. Ji, R.-w. Zhang, S.-s. Li, S.-s. Yan, B.-m. Zhang, P. Li and P.-j. Wang, Unexpected giant-gap quantum spin hall insulator in chemically decorated plumbene monolayer, Sci. Rep., 2016, 6, 20152 CrossRef CAS.
- L. Zhang, H. Zhao, W. x. Ji, C. w. Zhang, P. Li and P. j. Wang, Discovery of a new quantum spin hall phase in bilayer plumbene, Chem. Phys. Lett., 2018, 712, 78–82 CrossRef CAS.
- T. Dietl, H. Ohno, F. Matsukura, J. Cibert and D. Ferrand, Zener model description of ferromagnetism in zinc-blende magnetic semiconductors, Science, 2000, 287, 1019–1022 CrossRef CAS.
- H. Ohno, D. Chiba, F. Matsukura, T. Omiya, E. Abe, T. Dietl, Y. Ohno and K. Ohtani, Electric-field control of ferromagnetism, Nature, 2000, 408, 944–946 CrossRef CAS.
- K. Sato, L. Bergqvist, J. Kudrnovský, P. H. Dederichs, O. Eriksson, I. Turek, B. Sanyal, G. Bouzerar, H. Katayama-Yoshida, V. A. Dinh, T. Fukushima, H. Kizaki and R. Zeller, First-principles theory of dilute magnetic semiconductors, Rev. Mod. Phys., 2010, 82, 1633–1690 CrossRef CAS.
- T. Dietl, A ten-year perspective on dilute magnetic semiconductors and oxides, Nat. Mater., 2010, 9, 965 CrossRef CAS , review article.
- J. M. D. Coey, M. Venkatesan and C. B. Fitzgerald, Donor impurity band exchange in dilute ferromagnetic oxides, Nat. Mater., 2005, 4, 173–179 CrossRef CAS.
- I. Žutić, J. Fabian and S. Das Sarma, Spintronics: fundamentals and applications, Rev. Mod. Phys., 2004, 76, 323–410 CrossRef.
- A. Hashmi and J. Hong, Transition metal doped phosphorene: first-principles study, J. Phys. Chem. C, 2015, 119, 9198–9204 CrossRef CAS.
- T. Hu and J. Hong, First-principles study of metal adatom adsorption on black phosphorene, J. Phys. Chem. C, 2015, 119, 8199–8207 CrossRef CAS.
- Y. C. Cheng, Z. Y. Zhu, W. B. Mi, Z. B. Guo and U. Schwingenschlögl, Prediction of two-dimensional diluted magnetic semiconductors: doped monolayer MoS2 systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 100401 CrossRef.
- L. Seixas, A. Carvalho and A. H. Castro Neto, Atomically thin dilute magnetism in co-doped phosphorene, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155138 CrossRef.
- J. He, K. Wu, R. Sa, Q. Li and Y. Wei, Magnetic properties of nonmetal atoms absorbed MoS2 monolayers, Appl. Phys. Lett., 2010, 96, 082504 CrossRef.
- Y. C. Cheng, Q. Y. Zhang and U. Schwingenschlögl, Valley polarization in magnetically doped single-layer transition-metal dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 155429 CrossRef.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for open-shell transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- I. G. Rau, S. Baumann, S. Rusponi, F. Donati, S. Stepanow, L. Gragnaniello, J. Dreiser, C. Piamonteze, F. Nolting, S. Gangopadhyay, O. R. Albertini, R. M. Macfarlane, C. P. Lutz, B. A. Jones, P. Gambardella, A. J. Heinrich and H. Brune, Reaching the magnetic anisotropy limit of a 3d metal atom, Science, 2014, 344, 988–992 CrossRef CAS.
- C. F. Hirjibehedin, C.-Y. Lin, A. F. Otte, M. Ternes, C. P. Lutz, B. A. Jones and A. J. Heinrich, Large magnetic anisotropy of a single atomic spin embedded in a surface molecular network, Science, 2007, 317, 1199–1203 CrossRef CAS.
- H. Hashemi, G. Fischer, W. Hergert and V. S. Stepanyuk, Magnetic properties of 3d transition metal wires on vicinal Cu(111) surfaces at finite temperature, J. Appl. Phys., 2010, 107, 09E311 CrossRef.
- H. Hashemi, W. Hergert and V. Stepanyuk, Magnetic properties of 3d transition metal chains on vicinal Cu(111) surface, J. Magn. Magn. Mater., 2010, 322, 1296–1299 CrossRef CAS , proceedings of the Joint European Magnetic Symposia.
- D. Hashemi, M. J. Waters, W. Hergert, J. Kieffer and V. S. Stepanyuk, Substrate-controlled magnetism: Fe nanowires on vicinal cu surfaces, Nanomaterials, 2020, 10, 159 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Erratum: “hybrid functionals based on a screened coulomb potential” [j. chem. phys. 118, 8207 (2003)], J. Chem. Phys., 2006, 124, 219906 CrossRef.
- J. Heyd and G. E. Scuseria, “Efficient hybrid density functional calculations in solids: assessment of the heyd–scuseria–ernzerhof screened coulomb hybrid functional, J. Chem. Phys., 2004, 121, 1187–1192 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125, 224106 CrossRef.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- W. Tang, E. Sanville and G. Henkelman, A grid-based bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, Improved grid-based algorithm for bader charge allocation, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS.
- K. Momma and F. Izumi, VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- D. Hashemi and H. Iizuka, “Magnetic properties of 3d transition metal (Sc–Ni) doped plumbene, RSC Adv., 2020, 10, 6884–6892 RSC.
- D. K. Das and S. K. Singh, Plumbene: a new 2d-material resembling graphene, in Advances in Industrial and Production Engineering, Springer Singapore, 2019, pp. 193–197 Search PubMed.
- Y. Li, J. Zhang, B. Zhao, Y. Xue and Z. Yang, Constructive coupling effect of topological states and topological phase transitions in plumbene, Phys. Rev. B, 2019, 99, 195402 CrossRef CAS.
- M. Sun, Q. Ren, Y. Zhao, J.-P. Chou, J. Yu and W. Tang, Electronic and magnetic properties of 4d series transition metal substituted graphene: a first-principles study, Carbon, 2017, 120, 265–273 CrossRef CAS.
- J. C. Slater, Atomic radii in crystals, J. Chem. Phys., 1964, 41, 3199–3204, DOI:10.1063/1.1725697.
- A. Aharoni, Introduction to the theory of Ferromagnetism, Oxford Science Publications, 2nd edn, 2000 Search PubMed.
| This journal is © The Royal Society of Chemistry 2021 |