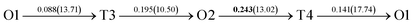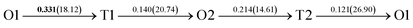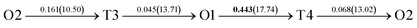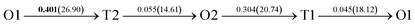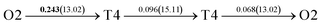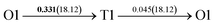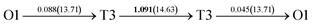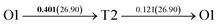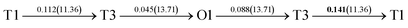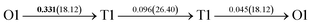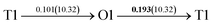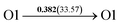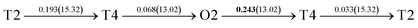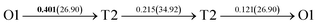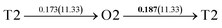Open Access Article
Open Access ArticleHydrogen solubility and diffusivity at Σ3 grain boundary of PdCu†
L. C. Liuab and
H. R. Gong *a
*a
aState Key Laboratory of Powder Metallurgy, Central South University, Changsha, Hunan 410083, China. E-mail: gonghr@csu.edu.cn
bCollege of Physics and Electronics, Gannan Normal University, Ganzhou, Jiangxi 341000, China
First published on 13th April 2021
Abstract
First principles calculations have been performed to comparatively reveal hydrogen solubility and diffusivity at grain boundaries of BCC and FCC PdCu phases. It is found that the temperature-dependent hydrogen solubility at BCC Σ3 (112) GB of PdCu seems much higher than that in BCC PdCu bulk, while hydrogen solubility in FCC Σ3 (111) GB of PdCu is much lower than that in its corresponding FCC bulk. Calculations also reveal that grain boundary has an important effect on hydrogen diffusion of BCC and FCC PdCu, i.e., hydrogen diffusivities of BCC Σ3 (112) and FCC Σ3 (111) grain boundaries of PdCu seem much smaller and bigger than those of its corresponding bulks, respectively. The predicted results could deepen the comprehension of hydrogen solubility and diffusion of PdCu phases.
1. Introduction
Hydrogen solution and diffusion at grain boundaries of various metals have raised great research interest in the past decades due to the hydrogen embrittlement, intergranular cracking, increased creep rates, and decreased fatigue lift etc., while the main conclusions available in the literature are not consistent with each other.1–13 For instance, hydrogen diffusion in grain boundaries of nickel was reported to be much faster than that in the bulk, which would be fundamentally due to a lower activation energy of diffusion in the area of the grain.3,6 On the other hand, the effects of grain boundary on hydrogen solution and diffusion are related to the grain size and the type of grain boundary, e.g., hydrogen diffusivity in the grain boundary of aluminum and nickel with fine grains is smaller than that in the bulks.7,10,11,13 Nevertheless, some researchers also reported that grain boundary has no effect on the solution or diffusion of hydrogen.7,9As to the hydrogen permeated Pd membranes, Mütschele and Kirchheim found that hydrogen solubility in nanocrystalline Pd is much bigger than that in its single crystalline counterpart.14 With the decrease of the grain size, hydrogen solution in the α phase of PdH becomes bigger, whereas smaller in the β phase of PdH.14,15 Interestingly, Stuhr et al. made a quite different conclusion that compared with coarse-grained Pd, no change of hydrogen solubility was discovered for nanocrystalline Pd.16 In addition, hydrogen diffusion in grain boundaries of Pd seems much faster than that within the grains,8 and is also found to be concentration dependent, i.e., hydrogen diffusion coefficients are lower than single crystalline value at low hydrogen contents, and vice versa for higher contents.14
It is well known that the PdCu membrane is a kind of excellent candidates for hydrogen separation and purification, and compared with pure Pd and other Pd alloys, PdCu possesses excellent hydrogen selectivity, high thermal stability, superior resistance against poisoning, moderate mechanical properties, relatively low price, and wide operating temperature range.17–20 Regarding hydrogen solubility and hydrogen diffusivity of various PdCu phases, there are already a lot of experimental and theoretical investigations in the literature.17,19–43 These experimental studies are mainly concentrated on polycrystalline phases of PdCu,19–22,24–35,37,39 while the reported theoretical calculations are all related to single crystals of PdCu.17,23,36,38,40–42 In other words, the effects of grain boundary on hydrogen behaviors of PdCu membranes need further research investigations.
By means of highly accurate first principles calculations based on density functional theory,43–47 the present study is aimed to have a comparative investigation of hydrogen solubility and diffusivity at grain boundaries of BCC and FCC PdCu. Both BCC and FCC structures of PdCu are intentionally selected as they are two main phases in the Pd–Cu phase diagram.43 Specifically, the PdCu phases with the stoichiometric ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are intentionally selected due to their superior performance of H permeability.18,35,37,38 In addition, a lot of investigations have found that the Σ3 (112) grain boundary of BCC metals has the lowest grain boundary energy,48–52 and the Σ3 (111) grain boundaries of FCC metals are energetically stable structure with the lowest grain boundary energy in the literature.13,51,53 Accordingly, the Σ3 (112) grain boundaries of BCC PdCu and Σ3 (111) of FCC PdCu are therefore chosen in the present study. And the hydrogen solubility and hydrogen diffusivity of PdCu bulks38 are used for the sake of comparison. The derived results will be compared with available experimental and theoretical evidence in the literature, and could provide a deep understanding of the effects of grain boundary on hydrogen solubility and diffusivity of BCC and FCC PdCu.
1 are intentionally selected due to their superior performance of H permeability.18,35,37,38 In addition, a lot of investigations have found that the Σ3 (112) grain boundary of BCC metals has the lowest grain boundary energy,48–52 and the Σ3 (111) grain boundaries of FCC metals are energetically stable structure with the lowest grain boundary energy in the literature.13,51,53 Accordingly, the Σ3 (112) grain boundaries of BCC PdCu and Σ3 (111) of FCC PdCu are therefore chosen in the present study. And the hydrogen solubility and hydrogen diffusivity of PdCu bulks38 are used for the sake of comparison. The derived results will be compared with available experimental and theoretical evidence in the literature, and could provide a deep understanding of the effects of grain boundary on hydrogen solubility and diffusivity of BCC and FCC PdCu.
2. Method of calculation
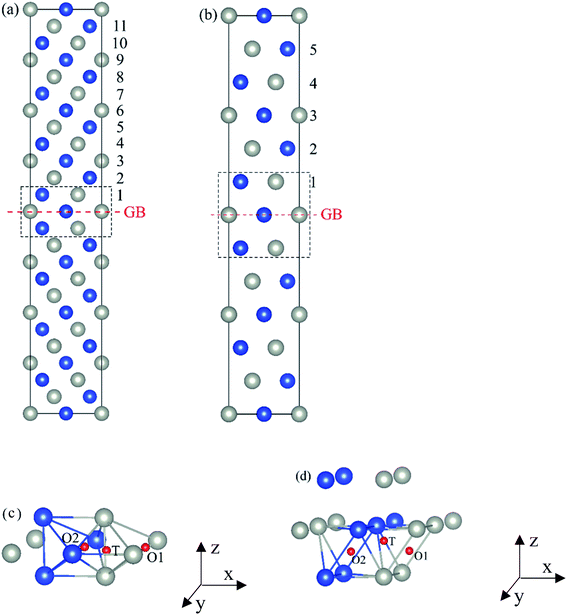
The present first principles calculations are implemented based on density functional theory with the projector-augmented wave (PAW) method using Vienna Ab initio Simulation Package (VASP).44,45,48,49 The generalized gradient approximation (GGA) of Perdew–Burke–Enzerof (PBE) is selected to describe exchange-correlation function,50 and the cutoff energy of plane wave basis is 400 eV. The temperature-smearing method of Methfessel–Paxton51 and the tetrahedron method with the Blöchl corrections52 are adopted for structure relaxation and static calculations, respectively. The convergence criteria of relaxation and static calculations are 10−5 and 10−6 eV, respectively. The conjugate gradient method is used to minimize the Hellmann–Feynman forces in the ionic relaxations with the force stopping criterion of 0.02 eV Å−1.Accordingly, the atomic composition of Pd50Cu50 is purposely chosen as a result of its superior hydrogen permeability.18,35,37,38 The grain boundaries of BCC Σ3 (112) (48 atoms) and FCC Σ3 (111) (48 atoms) of PdCu are constructed based on coincidence site lattice theory (CSL),53 and are shown vividly in Fig. 1. It should be noted that the CSL and structural-unit (SU) models yield the same structure and energy for the Σ3 (112) or Σ3 (111) grain boundary.53 The lattice constants of BCC PdCu (3.026 Å) and FCC PdCu (3.817 Å) obtained recently38 are used in the present study. After the test calculations, the dimensions of BCC Σ3 (112) and FCC Σ3 (111) of PdCu are 5.241 × 4.279 × 29.769 Å3 and 5.398 × 4.675 × 26.445 Å3, respectively. To simulate hydrogen solubility and hydrogen diffusivity, one hydrogen atom is added at the octahedral (O) and tetrahedral (T) sites of each supercell. It should be pointed out that the O1 site is surrounded by four Pd atoms and two Cu atoms, and the O2 site by two Pd and four Cu atoms. During each calculation, periodic boundary conditions are added to the model in three directions. To determine the GB structure with the lowest energy, multiple initial configurations are sampled with a series of rigid body translations (RBTs) in the direction perpendicular to the GB. After the test calculations, the k-meshes of 7 × 7 × 1 and 9 × 9 × 1 are chosen for relaxation and static calculations, respectively.
For the calculation of H diffusion in BCC Σ3 (112) and FCC Σ3 (111) of PdCu, the climbing image nudged elastic band (CI-NEB) method54 is used to search the minimum energy paths. The spring constant and force convergence criterion are 5.0 and 0.05 eV Å−1, respectively. The frequency calculations are performed for the diffusion paths to verify the saddle points with only one imaginary frequency, and the energy barrier is derived as the difference between the total energy of saddle point and initial configuration.
3. Results and discussion
3.1. Hydrogen solubility at Σ3 grain boundary of PdCu
A lot of researches have shown that the hydrogen solubility of FCC PdCu phase is much higher than that of BCC counterpart, which is due to the stronger binding of hydrogen at FCC PdCu phase.20,34,38,55 As to the effect of grain boundary (GB) on hydrogen solubility at PdCu phases, however, there is not any report so far in the literature. The present first principles calculation is therefore executed to have a comparative study of fundamental influence of GB on hydrogen solubility of PdCu phases.Accordingly, the binding energy (Eb) and zero point energy (ZPE) of hydrogen at Σ3 GB of PdCu could be calculated as follows:38,40,42
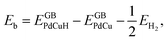 | (1) |
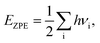 | (2) |
The segregation energy (Eseg) of hydrogen at GB of PdCu is then calculated according to the following formula:
| Eseg = EGBb − Ebulkb, | (3) |
The hydrogen solubility (C) in GB of PdCu could be then derived by the Sieverts' law:
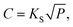 | (4) |
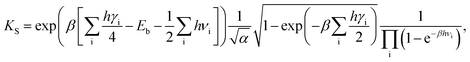 | (5) |
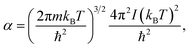 | (6) |
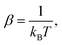 | (7) |
Consequently, the Eb, ZPE, and Eseg values of hydrogen in BCC Σ3 (112) and FCC Σ3 (111) GB of PdCu are obtained and summarized in Table 1. In addition, the temperature-dependent hydrogen solubility of BCC Σ3 (112) and FCC Σ3 (111) GB of PdCu is also derived and shown in Fig. 2. The corresponding bind energies and ZPE of H in PdCu bulks38 are also listed in Table 1, and hydrogen solubility of PdCu bulks38 is included in Fig. 2 for the sake of comparison. Several characteristics could be discerned from Table 1 and Fig. 2.
| Site | H in BCC PdCu | H in FCC PdCu | ||||
|---|---|---|---|---|---|---|
| Eb (eV) | Eseg (eV) | Eb (eV) | Eseg (eV) | |||
| Σ3 (112) | Bulk38 | Σ3 (111) | Bulk38 | |||
| O1 | −0.172 (0.133) | −0.029 (0.138) | −0.136 | −0.042 (0.154) | −0.069 (0.089) | 0.036 |
| O2 | −0.039 (0.127) | 0.060 (0.120) | −0.085 | 0.149 (0.149) | 0.136 (0.070) | 0.013 |
| T | −0.157 (0.211) | −0.059 (0.192) | −0.119 | 0.193 (0.205) | 0.160 (0.155) | 0.04 |
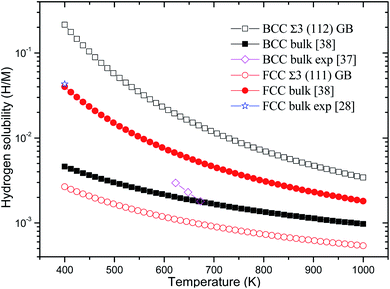 | ||
| Fig. 2 Temperature-dependent hydrogen solubility at BCC Σ3 (112) and FCC Σ3 (111) GB of PdCu. The corresponding values in BCC and FCC PdCu bulks38 are also listed for comparison. H and M represent hydrogen and metal atoms, respectively. | ||
Firstly, the bind energy (Eb) of H in each interstitial site (O1, O2, and T) of BCC Σ3 (112) GB of PdCu is lower than the corresponding value in BCC PdCu bulk,38 suggesting that H should be energetically more favorable in BCC Σ3 (112) GB of PdCu. Consequently, the hydrogen solubility at BCC Σ3 (112) GB of PdCu seems much higher than that in BCC PdCu bulk.38 That is to say, hydrogen energetically prefers to stay at the GB area of BCC PdCu, rather than within the grain. The calculated hydrogen solubility of BCC PdCu bulk38 is slightly lower than the corresponding experimental measurement,37 probably due to the higher hydrogen solubility at the BCC PdCu Σ3 (112) GB. Such a theoretical prediction about hydrogen solubility at BCC Σ3 (112) GB of PdCu from the present study is similar to the experimental observations regarding hydrogen solubility in nanocrystalline Pd and the α phase of Pd.14,15
Secondly, for each interstitial site of O1, O2, and T, FCC Σ3 (111) GB of PdCu possesses higher binding energy of hydrogen than its bulk. This comparison signifies that hydrogen would be thermodynamically unfavorable in FCC Σ3 (111) GB of PdCu. As shown in Fig. 2, the curve of temperature-dependent hydrogen solubility in FCC Σ3 (111) GB of PdCu is therefore much lower than that in its corresponding FCC bulk. In other words, GB has an important effect to reduce hydrogen solubility of FCC PdCu, which is consistent with similar experimental discovery of the β phase of Pd15 as well as the theoretical prediction of Ni GB.13 It should be noted that the ZPE values of H at BCC Σ3 (112) GB are close to that in bulk, while the ZEP values at FCC Σ3 (111) GB are higher than that in the bulk.
Thirdly, the Eseg values of H at the O1, O2, and T sites of BCC Σ3 (112) GB of PdCu are big and negative values of −0.136, −0.085, and −0.119 eV, respectively, indicating that hydrogen has a strong tendency to segregate in the GB area of BCC PdCu. Such a theoretical prediction from the present study is compatible with similar experimental observations of Pd.16 On the contrary, hydrogen seems difficult to segregate to the GB area of FCC PdCu due to its slightly positive Eseg values. Interestingly, the above drastic comparison regarding hydrogen segregation in GB of BCC and FCC PdCu is very similar to that reported about Σ3 grain boundary of Fe in the literature.56 It should be pointed out that thermal expansion of the lattice and vacancy would have some effects on H binding energy and hydrogen solubility of PdCu, and further studies are welcome to find out these effects.
To have a deep understanding of the effects of grain boundary on hydrogen solubility of PdCu, the electronic structures of H at various interstitial sites of PdCu are calculated and compared with each other. As a typical example, Fig. 3 displays the total density of states of H atom at the T site of BCC and FCC Σ3 GBs and bulk of PdCu. It can be seen from Fig. 3 that the DOSs of H atom BCC Σ3 (112) GB below the Fermi level (Ef) are more centralized than those in BCC PdCu bulk. In addition, the DOS peak value of H atom at BCC Σ3 (112) GB of PdCu is 0.716 states per eV per atom, which is higher than the corresponding value of 0.535 states per eV per atom in BCC PdCu bulk. Similarly, the H atom at the T site of FCC Σ3 (111) GB has a DOS peak of 1.49 states per eV per atom below Ef, and this DOS peak is smaller than the corresponding value (1.85 states per eV per atom) of H atom in FCC PdCu bulk. By means of the Bader analysis, the charge of H atom at the T site of BCC Σ3 (112) GB of PdCu is derived to be 1.15, which is bigger than the value of 1.108 for the corresponding PdCu bulk. The above characteristics of electronic structures indicate that H atom should have formed a stronger bonding at BCC Σ3 (112) GB than that at BCC PdCu bulk, which would therefore bring about higher hydrogen solubility at BCC Σ3 (112) GB of PdCu shown in Fig. 2.
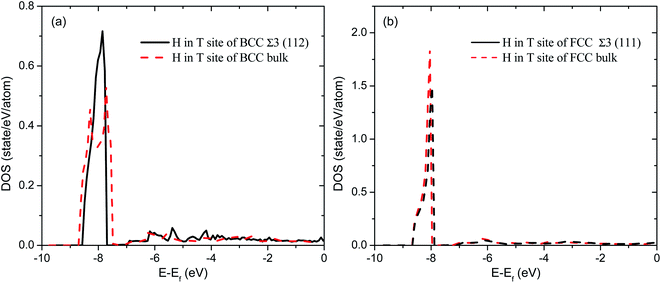 | ||
| Fig. 3 Comparison of total densities of states (DOS) of H atom at the T site of (a) Σ3 (112) GB and bulk of BCC PdCu (b) Σ3 (111) GB and bulk of FCC PdCu. | ||
3.2. Hydrogen diffusivity at Σ3 grain boundary of PdCu
It is well known that hydrogen diffusion in GB of various metal materials is quite different from that in single crystals or within the grain. Interestingly, some experimental studies reveal that hydrogen diffusion in GB of nickel is much faster than that in bulks due to a lower activation energy,3,6 whereas the hydrogen diffusivity in GB of aluminum and nickel with fine grains is smaller than that in the bulks.7,10,11,13 As to hydrogen diffusion in PdCu membranes, the reported experimental results are mainly concentrated on the polycrystalline phases,19–22,24–35,37,39 while the theoretical investigations are all related to single crystals.17,23,36,38,40–42 It is therefore of importance to find out the effect of GB on hydrogen diffusion of PdCu by means of first principles calculation.According to lattice symmetry, the BCC Σ3 (112) and FCC Σ3 (111) GBs of PdCu have eight and seven hydrogen diffusion paths, respectively, which are shown clearly in Fig. 4. For BCC Σ3 (112) GB, the four hydrogen diffusion paths along GB are O1 → T3 → O2 → T4 → O1, O2 → T3 → O1 → T4 → O2, O2 → T4 → T4 → O2, and O1 → T3 → T3 → O1, while the four diffusion paths across GB are T1 → T3 → O1 → T3 → T1, T1 → O1 → T1, T2 → T4 → O2 → T4 → T2, and T2 → O2 → T2. Similarly, the hydrogen diffusion paths along GB of FCC Σ3 (111) are O1 → T1 → O2 → T2 → O1, O1 → T2 → O2 → T1 → O1, O1 → T1 → O1, and O1 → T2 → O1, and the diffusion paths across GB are O1 → T1 → T1 → O1, O1 → O1, and O1 → T2 → T2 → O1.
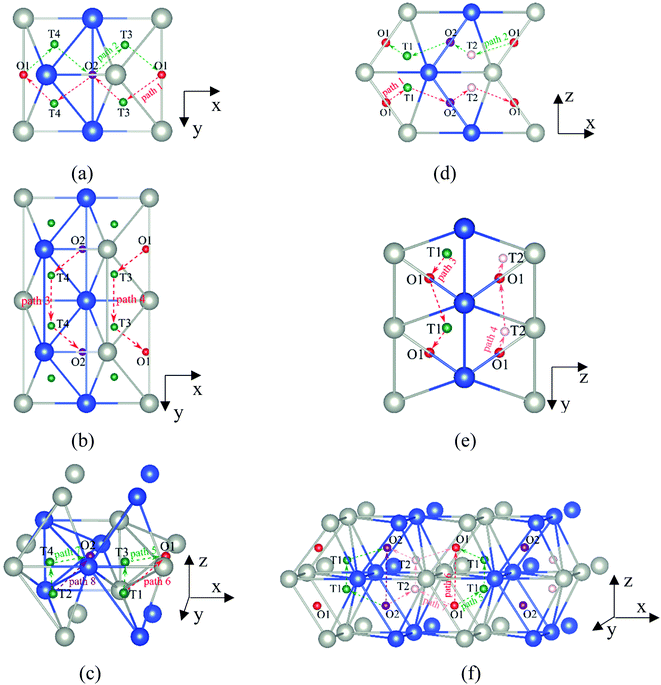 | ||
Fig. 4 The three layers atomic structure of the black dotted area in Fig. 1. And hydrogen diffusion through BCC PdCu Σ3 (112) GB along (a) x direction (along GB) (path 1: O1 → T3 → O2 → T4 → O1, path 2: O2 → T3 → O1 → T4 → O2), (b) y direction (along GB) (path 3: O2 → T4 → T4 → O2, path 4: O1 → T3 → T3 → O1), and (c) z direction (across GB) (path 5–8: T1 → T3 → O1 → T3 → T1, T1 → O1 → T1, T2 → T4 → O2 → T4 → T2, and T2 → O2 → T2), respectively; hydrogen diffusion through FCC PdCu Σ3 (111) GB along (d) x direction (along GB) (path 1: O1 → T1 → O2 → T2 → O1, path 2: O1 → T2 → O2 → T1 → O1), (e) y direction (along GB) (path 3: O1 → T1 → O1, path 4: O1 → T2 → O1), and (f) z direction (across GB) (path 5–7: O1 → T1 → T1 → O1, O1 → O1, and O1 → T2 → T2 → O1). The x-axis is [11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ]BCC and [01 ]BCC and [01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ]FCC, the y-axis is [1 ]FCC, the y-axis is [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]BCC and [1 0]BCC and [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]FCCu, the z-axis is [112]BCC and [111]FCC. The gray and blue spheres represent Pd and Cu atoms, respectively. The small balls stand for the interstitial sites. 0]FCCu, the z-axis is [112]BCC and [111]FCC. The gray and blue spheres represent Pd and Cu atoms, respectively. The small balls stand for the interstitial sites. | ||
After a series of calculations, the derived energy barrier (Ed,i) of various diffusion paths are summarized in Table 2. It should be pointed out that the highest diffusion barrier has been regarded as the activation energy (Ea,i) for each diffusion path. Several features could be observed from Table 2. Firstly, for BCC Σ3 (112) GB of PdCu, diffusion path 5 possesses the lowest activation energies of 0.141 eV among the four paths across GB, which is much smaller than the corresponding lowest Ea,i of 0.243 eV of paths 1 and 3 along GB. This comparison suggests that hydrogen is energetically more favorable to diffuse across the BCC Σ3 (112) GB of PdCu, rather than diffusion along GB. On the other hand, the lowest Ea,i along and across FCC Σ3 (111) GB of PdCu are the same value of 0.331 eV, indicating that hydrogen has an equal probability to diffuse along and across FCC Σ3 (111) GB of PdCu.
Secondly, the lowest activation energy (0.141 eV) of hydrogen diffusion in BCC Σ3 (112) GB of PdCu seems much bigger than the corresponding value of 0.057 eV of BCC PdCu bulk.38 This characteristic implies that hydrogen diffusion in BCC Σ3 (112) GB should be energetically more difficult than that in BCC PdCu bulk. On the contrary, the lowest activation energy (0.331 eV) of hydrogen diffusion in FCC Σ3 (111) GB is slightly lower than the derived value of 0.347 eV of FCC PdCu bulk,38 suggesting that it should be easier for hydrogen to diffuse in FCC Σ3 (111) GB than in FCC PdCu bulk.
Thirdly, the lowest activation energies (0.243 and 0.141 eV) of hydrogen diffusion along and across BCC Σ3 (112) GB of PdCu are much smaller than the corresponding value of 0.331 eV of FCC Σ3 (111) GB of PdCu. A similar feature has been discovered about the relative magnitude of the lowest activation energies (0.057 and 0.347 eV) of BCC and FCC bulks of PdCu.38 In other words, hydrogen has energetically easier diffusion in BCC Σ3 (112) GB and bulks of PdCu than its FCC counterpart. Interestingly, the difference of lowest activation energies of hydrogen diffusion between BCC and FCC GB of PdCu becomes smaller that the corresponding value between BCC and FCC PdCu bulks. It should be pointed out that the ballistic diffusion may probably occur at the GBs and further studies are welcome to find out this effect on H diffusion at PdCu GB in the future.
We now turn to calculate the diffusivity of hydrogen (D) through the GB of PdCu by means of the following formula:57
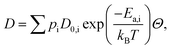 | (8) |
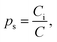 | (9) |
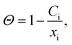 | (10) |
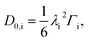 | (11) |
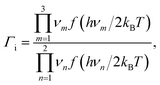 | (12) |
| f(x) = sinh(x)/x, | (13) |
The temperature-dependent diffusivity of hydrogen through BCC Σ3 (112) and FCC Σ3 (111) GB of PdCu is thus obtained and shown in Fig. 5. One can discern from this figure that GB has a quite effect on hydrogen diffusivity of BCC and FCC PdCu. For BCC PdCu, the curve of hydrogen diffusivity of GB is well below that of bulk,38 signifying that GB should decrease hydrogen diffusivity of BCC PdCu. Such a feature is consistent with similar experimental observations regarding hydrogen diffusion in GB of nickel and aluminum.7,9,10,58
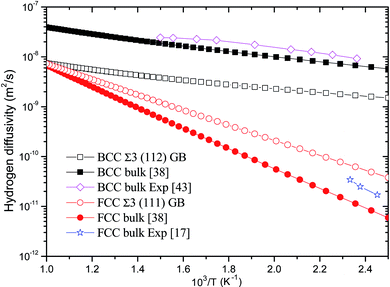 | ||
| Fig. 5 Temperature-dependent hydrogen diffusivity through BCC Σ3 (112) and FCC Σ3 (111) GB of PdCu. The corresponding values of BCC and FCC PdCu bulks38 are also listed for comparison. | ||
On the contrary, hydrogen diffusivity of FCC Σ3 (111) GB of PdCu at each temperature is bigger than that of FCC PdCu bulk.38 It therefore follows that GB has an important effect to increase hydrogen diffusivity of FCC PdCu, which is just opposite to the decrease of hydrogen diffusivity of BCC PdCu as a result of GB. This increase (decrease) of hydrogen diffusivity due to GB is mainly attributed to the lower (higher) activation energies shown in Table 2. The higher hydrogen diffusivity of FCC Σ3 (111) GB of PdCu from the present study is also compatible with similar experimental evidence of nickel in the literature.3,6,57,59 It should be noted that the calculated hydrogen diffusivities of BCC PdCu bulk38 and FCC PdCu Σ3 (111) GB agree well with the corresponding calculation values in the literature.20
In addition, hydrogen diffusivity through BCC Σ3 (112) GB of PdCu is significantly higher than that of FCC Σ3 (111) GB, and the same statement could be made for hydrogen diffusivity at BCC and FCC bulks of PdCu.38 It can be seen clearly from Fig. 5 that at each temperature, the descending sequence of hydrogen diffusivity of PdCu is as follows: BCC bulk → BCC Σ3 (112) GB → FCC Σ3 (111) GB → FCC bulk. Such a comparison confirms that the BCC PdCu Σ3 (112) GB and bulk have much higher hydrogen diffusivity than its FCC counterpart. It should be pointed out that the hydrogen defect complexes would possibly arise in the GB of PdCu and have some effects on H diffusivities and solubilities.60
4. Conclusions
First principles calculations have been performed to comparatively study the effects of grain boundary on hydrogen solubility and hydrogen diffusivity at PdCu phases with BCC and FCC structures. It is found that the hydrogen solubility at BCC PdCu Σ3 (112) GB is higher than that at BCC PdCu bulk. On the contrary, the hydrogen solubility at FCC PdCu Σ3 (111) GB is lower than that at its bulk. Calculations also reveal that hydrogen diffusion across BCC PdCu Σ3 (112) GB is easier than along the corresponding GB, while hydrogen diffusion along and across FCC PdCu Σ3 (111) GB should have an equal probability. Moreover, BCC Σ3 (112) GB could impede hydrogen diffusion and FCC PdCu Σ3 (111) GB would accelerate hydrogen diffusion. The calculated results could provide a deep understanding of the effects of GB on hydrogen solubility and diffusivity of BCC and FCC PdCu.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Natural Science Foundation of Hunan Province (No. 2018JJ25081), Project supported by the Fundamental Research Funds for the Central Universities of Central South University (No. 2018zzts126), and Project supported by State Key Laboratory of Powder Metallurgy, Central South University, Changsha, China.References
- B. Ladna and H. K. Birnbaum, SIMS study of hydrogen at the surface and grain boundaries of nickel bicrystals, Acta Metall., 1987, 35, 2537–2542 CrossRef CAS.
- A. Kimura and H. K. Birnbaum, Hydrogen induced grain boundary fracture in high purity nickel and its alloys—enhanced hydrogen diffusion along grain boundaries, Acta Metall., 1988, 36, 757–766 CrossRef CAS.
- T. M. Harris and M. Latanision, Grain boundary diffusion of hydrogen in nickel, Metall. Trans. A, 1991, 22, 351–355 CrossRef.
- G. Palumbo, D. M. Doyle, A. M. Elsherik, U. Erb and K. T. Aust, Intercrystalline hydrogen transport in nanocrystalline nickel, Scr. Metall. Mater., 1991, 25, 679–684 CrossRef CAS.
- T. Tsuru and R. M. Latanision, Grain boundary transport of hydrogen in nickel, Scr. Metall., 1982, 16, 575–578 CrossRef CAS.
- J. Y. Lee and S. M. Lee, Hydrogen trapping phenomena in metals with B. C. C. and F. C. C. crystals structures by the desorption thermal analysis technique, Surf. Coat. Technol., 1986, 28, 301–314 CrossRef CAS.
- M. Ichimura, Y. Sasajima and M. Imabayashi, Grain Boundary Effect on Diffusion of Hydrogen in Pure Aluminum, Mater. Trans., JIM, 1991, 32, 1109–1114 CrossRef CAS.
- U. Stuhr, T. Striffler, H. Wipf, H. Natter, B. Wettmann and S. Janssen, et al., An investigation of hydrogen diffusion in nanocrystalline Pd by neutron spectroscopy, J. Alloys Compd., 1997, 253, 393–396 CrossRef.
- R. M. Latanision and M. Kurkela, Hydrogen Permeability and Diffusivity in Nickel and Ni-Base Alloys, Corrosion, 1983, 39, 174–181 CrossRef CAS.
- J. Yao and J. R. Cahoon, Experimental studies of grain boundary diffusion of hydrogen in metals, Acta Metall. Mater., 1991, 39, 119–126 CrossRef CAS.
- J. Yao and J. R. Cahoon, Theoretical modeling of gain boundary diffusion of hydrogen and its effect on permeation curves, Acta Metall. Mater., 1991, 39, 111–118 CrossRef CAS.
- A. Pedersen and H. Jonsson, Simulations of hydrogen diffusion at grain boundaries in aluminum, Acta Mater., 2009, 57, 4036–4045 CrossRef CAS.
- D. D. Stefano, M. Mrovec and C. Elsasser, First-principles investigation of hydrogen trapping and diffusion at grain boundaries in nickel, Acta Mater., 2015, 98, 306–312 CrossRef.
- T. Mutschele and R. Kirchheim, Segregation and diffusion of hydrogen in grain boundaries of palladium, Scr. Metall., 1987, 21, 135–140 CrossRef.
- J. A. Eastman, L. J. Thompson and B. J. Kestel, Narrowing of the palladium–hydrogen miscibility gap in nanocrystalline palladium, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 84–92 CrossRef CAS PubMed.
- U. Stuhr, H. Wipf, T. J. Udovic, J. Weismuller and H. Gleiter, Inelastic neutron scattering study of hydrogen in nanocrystalline Pd, Nanostruct. Mater., 1995, 6, 555–558 CrossRef.
- S. M. Opalka, W. Huang, D. Wang, T. B. Flanagan, O. M. Lovvik and S. C. Emerson, et al., Hydrogen interactions with the PdCu ordered B2 alloy, J. Alloys Compd., 2007, 446, 583–587 CrossRef.
- L. Yuan, A. Goldbach and H. Xu, Permeation hysteresis in PdCu membranes, J. Phys. Chem. B, 2008, 112, 12692–12695 CrossRef CAS PubMed.
- Y. Matsumura, A basic study of high-temperature hydrogen permeation through bcc Pd–Cu alloy foil, Sep. Purif. Technol., 2014, 138, 130–137 CrossRef CAS.
- N. A. Al-Mufachi, S. Nayebossadri, J. D. Speight, W. Bujalski, R. Steinberger-Wilckens and D. Book, Effects of thin film Pd deposition on the hydrogen permeability of Pd60Cu40 wt% alloy membranes, J. Membr. Sci., 2015, 493, 580–588 CrossRef CAS.
- E. Acha, J. Requies, V. L. Barrio, J. F. Cambra, M. B. Guemez and P. L. Arias, et al., PdCu membrane applied to hydrogen production from methane, J. Membr. Sci., 2012, 415, 66–74 CrossRef.
- N. Almufachi and R. Steinbergerwilckens, X-ray diffraction study on the effects of hydrogen on Pd60Cu40 wt% foil membranes, J. Membr. Sci., 2018, 545, 266–274 CrossRef CAS.
- M. C. Gao, L. Ouyang and O. N. Dogan, First principles screening of B2 stabilizers in CuPd-based hydrogen separation membranes: (1) substitution for Pd, J. Alloys Compd., 2013, 574, 368–376 CrossRef CAS.
- N. Endo, Y. Furukawa, K. Goshome, S. Yaegashi, K. Mashiko and M. Tetsuhiko, Characterization of mechanical strength and hydrogen permeability of a PdCu alloy film prepared by one-step electroplating for hydrogen separation and membrane reactors, Int. J. Hydrogen Energy, 2019, 44, 8290–8297 CrossRef CAS.
- H. T. Hoang, H. D. Tong, F. C. Gielens, H. Jansen and M. C. Elwenspoek, Fabrication and characterization of dual sputtered Pd–Cu alloy films for hydrogen separation membranes, Mater. Lett., 2004, 58, 525–528 CrossRef CAS.
- V. M. Ievlev, A. S. Prizhimov and A. I. Dontsov, Structure of the α–β interface in a PdCu solid solution, Phys. Solid State, 2020, 62, 59–64 CrossRef CAS.
- S. Nayebossadri, J. Speight and D. Book, Pd–Cu–M (M = Y, Ti, Zr, V, Nb, and Ni) Alloys for the Hydrogen Separation Membrane, ACS Appl. Mater. Interfaces, 2017, 9, 2650–2661 CrossRef CAS PubMed.
- M. H. Martin, J. Galipaud, A. Tranchot, L. Roue and D. Guay, Measurements of hydrogen solubility in CuxPd100−x thin films, Electrochim. Acta, 2013, 90, 615–622 CrossRef CAS.
- A. Kulprathipanja, G. O. Alptekin, J. L. Falconer and J. D. Way, Pd and Pd–Cu membranes: inhibition of H2 permeation by H2S, J. Membr. Sci., 2005, 254, 49–62 CrossRef CAS.
- J. Tang, S. Yamamoto, T. Koitaya, A. Yoshigoe, T. Tokunaga and K. Mukai, et al., Mass transport in the PdCu phase structures during hydrogen adsorption and absorption studied by XPS under hydrogen atmosphere, Appl. Surf. Sci., 2019, 480, 419–426 CrossRef CAS.
- H. Jia, P. Wu, G. Zeng, E. Salascolera, A. Serrano and G. R. Castro, et al., High-temperature stability of Pd alloy membranes containing Cu and Au, J. Membr. Sci., 2017, 544, 151–160 CrossRef CAS.
- R. J. Westerwaal, E. A. Bouman, W. G. Haije, H. Schreuders, S. Dutta and M. Y. Wu, et al., The hydrogen permeability of Pd–Cu based thin film membranes in relation to their structure: a combinatorial approach, Int. J. Hydrogen Energy, 2015, 40, 3932–3943 CrossRef CAS.
- L. Yuan, A. Goldbach and H. Xu, Real-time monitoring of metal deposition and segregation phenomena during preparation of PdCu membranes, J. Membr. Sci., 2008, 322, 39–45 CrossRef CAS.
- A. Goldbach, L. Yuan and H. Xu, Impact of the fcc/bcc phase transition on the homogeneity and behavior of PdCu membranes, Sep. Purif. Technol., 2010, 73, 65–70 CrossRef CAS.
- L. Yuan, A. Goldbach and H. Xu, Segregation and H2 transport rate control in body-centered cubic PdCu membranes, J. Phys. Chem. B, 2007, 111, 10952–10958 CrossRef CAS PubMed.
- P. Kamakoti and D. S. Sholl, A comparison of hydrogen diffusivities in Pd and CuPd alloys using density functional theory, J. Membr. Sci., 2003, 225, 145–154 CrossRef CAS.
- S. Nayebossadri, J. Speight and D. Book, Effects of low Ag additions on the hydrogen permeability of Pd–Cu–Ag hydrogen separation membranes, J. Membr. Sci., 2014, 451, 216–225 CrossRef CAS.
- L. C. Liu, J. W. Wang, Y. H. He and H. R. Gong, Solubility, diffusivity, and permeability of hydrogen at PdCu phases, J. Membr. Sci., 2017, 542, 24–30 CrossRef CAS.
- C. Zhao, A. Goldbach and H. Xu, Low-temperature stability of body-centered cubic PdCu membranes, J. Membr. Sci., 2017, 542, 60–67 CrossRef CAS.
- L. C. Liu, H. R. Gong and S. F. Zhou, Hydrogen flux of BCC and FCC PdCuAg membranes, Int. J. Hydrogen Energy, 2019, 44, 31160–31171 CrossRef CAS.
- C. Ling and D. S. Sholl, Using first-principles calculations to predict surface resistances to H2 transport through metal alloy membranes, J. Membr. Sci., 2007, 303, 162–172 CrossRef CAS.
- L. C. Liu, H. R. Gong, S. F. Zhou and X. Gong, Adsorption, diffusion, and permeation of hydrogen at PdCu surfaces, J. Membr. Sci., 2019, 588, 117206 CrossRef CAS.
- C. Decaux, R. Ngameni, D. Solas, S. Grigoriev and P. Millet, Time and frequency domain analysis of hydrogen permeation across PdCu metallic membranes for hydrogen purification, Int. J. Hydrogen Energy, 2010, 35, 4883–4892 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- L. Sun, H. R. Gong and X. Gong, Magnetic ground state of face-centered-cubic structure of iron, J. Phys.: Condens. Matter, 2020, 32, 165806 CrossRef CAS PubMed.
- C. Y. Wu, L. Sun, C. Liang, H. R. Gong, M. L. Chang and D. C. Chen, Electronic structures and thermoelectric properties of polytype phases of bismuth, J. Phys. Chem. Solids, 2019, 134, 52–57 CrossRef CAS.
- P. E. Blochl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. P. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. Methfessel and A. Paxton, High-precision sampling for Brillouin-zone integration in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef PubMed.
- J. Xu, Y. Jiang, L. Yang and J. Li, Assessment of the CSL and SU models for bcc-Fe grain boundaries from first principles, Comput. Mater. Sci., 2016, 122, 22–29 CrossRef CAS.
- G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- L. Qin and C. Jiang, First-principles based modeling of hydrogen permeation through Pd–Cu alloys, Int. J. Hydrogen Energy, 2012, 37, 12760–12764 CrossRef CAS.
- Y. Du, L. Ismer, J. Rogal, T. Hickel, J. Neugebauer and R. Drautz, First-principles study on the interaction of H interstitials with grain boundaries in α- and γ-Fe, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 144121 CrossRef.
- X. Zhou, N. Mousseau and J. Song, Is Hydrogen Diffusion along Grain Boundaries Fast or Slow? Atomistic Origin and Mechanistic Modeling, Phys. Rev. Lett., 2019, 122, 215501 CrossRef CAS.
- J. Wang, N. Li and A. Misra, Structure and stability of Σ3 grain boundaries in face centered cubic metals, Philos. Mag., 2013, 93, 315–327 CrossRef CAS.
- J. Yang, J. Huang, Z. Ye, D. Fan, S. Chen and Y. Zhao, First-principles investigation on the interaction of Boron atom with nickel part II: absorption and diffusion at grain boundary, J. Alloys Compd., 2017, 708, 1089–1095 CrossRef CAS.
- J. Polfus, O. Løvvik, R. Bredesen and T. A. Peters, Hydrogen Induced Vacancy Clustering and Void Formation Mechanisms at Grain Boundaries in Palladium, Acta Mater., 2020, 195, 708–719 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra10133h |
| This journal is © The Royal Society of Chemistry 2021 |