Open Access Article
Open Access ArticleBonding and stability of donor ligand-supported heavier analogues of cyanogen halides (L′)PSi(X)(L)†
Sai Manoj N. V. T. Gorantlaa,
Maria Francis b,
Sudipta Roy
b,
Sudipta Roy *b and
Kartik Chandra Mondal
*b and
Kartik Chandra Mondal *a
*a
aDepartment of Chemistry, Indian Institute of Technology Madras, Chennai 600036, India. E-mail: csdkartik@iitm.ac.in
bDepartment of Chemistry, Indian Institute of Science Education and Research (IISER), Tirupati 517507, India. E-mail: roy.sudipta@iisertiruapti.ac.in
First published on 10th February 2021
Abstract
Fluoro- and chloro-phosphasilynes [X–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P (X = F, Cl)] belong to a class of illusive chemical species which are expected to have Si
P (X = F, Cl)] belong to a class of illusive chemical species which are expected to have Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P multiple bonds. Theoretical investigations of the bonding and stability of the corresponding Lewis base-stabilized species (L′)PSi(X)(L) [L′ = cAACMe (cyclic alkyl(amino) carbene); L = cAACMe, NHCMe (N-heterocyclic carbene), PMe3, aAAC (acyclic alkyl(amino) carbene); X = Cl, F] have been studied using the energy decomposition analysis-natural orbitals for chemical valence (EDA-NOCV) method. The variation of the ligands (L) on the Si-atom leads to different bonding scenarios depending on their σ-donation and π-back acceptance properties. The ligands with higher lying HOMOs prefer profoundly different bonding scenarios than the ligands with lower lying HOMOs. The type of halogen (Cl or F) on the Si-atom was also found to have a significant influence on the overall bonding scenario. The reasonably higher value and endergonic nature of the dissociation energies along with the appreciable HOMO–LUMO energy gap may corroborate to the synthetic viability of the homo and heteroleptic ligand-stabilized elusive PSi(Cl/F) species in the laboratory.
P multiple bonds. Theoretical investigations of the bonding and stability of the corresponding Lewis base-stabilized species (L′)PSi(X)(L) [L′ = cAACMe (cyclic alkyl(amino) carbene); L = cAACMe, NHCMe (N-heterocyclic carbene), PMe3, aAAC (acyclic alkyl(amino) carbene); X = Cl, F] have been studied using the energy decomposition analysis-natural orbitals for chemical valence (EDA-NOCV) method. The variation of the ligands (L) on the Si-atom leads to different bonding scenarios depending on their σ-donation and π-back acceptance properties. The ligands with higher lying HOMOs prefer profoundly different bonding scenarios than the ligands with lower lying HOMOs. The type of halogen (Cl or F) on the Si-atom was also found to have a significant influence on the overall bonding scenario. The reasonably higher value and endergonic nature of the dissociation energies along with the appreciable HOMO–LUMO energy gap may corroborate to the synthetic viability of the homo and heteroleptic ligand-stabilized elusive PSi(Cl/F) species in the laboratory.
Introduction
Cyanogen halides [N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–X; X = halogen = F, Cl] are stable volatile compounds, often utilized in the laboratory for organic synthesis.1 The N
C–X; X = halogen = F, Cl] are stable volatile compounds, often utilized in the laboratory for organic synthesis.1 The N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond in cyanogen halides is highly stable due to the efficient overlap of the 2s and 2p orbitals of the N and C atoms. In contrast, the P
C bond in cyanogen halides is highly stable due to the efficient overlap of the 2s and 2p orbitals of the N and C atoms. In contrast, the P![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si bond in the heavier analogues of cyanogen halide [P
Si bond in the heavier analogues of cyanogen halide [P![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–X; X = F, Cl] would involve the participation of significantly more diffused 3s and 3p orbitals with internal nodes within each type of orbital, leading to a huge deviation from the compact overlap of these orbitals.2 The P
Si–X; X = F, Cl] would involve the participation of significantly more diffused 3s and 3p orbitals with internal nodes within each type of orbital, leading to a huge deviation from the compact overlap of these orbitals.2 The P![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si bond is thus expected to be significantly weaker when compared with the N
Si bond is thus expected to be significantly weaker when compared with the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond. Although, the chemistry of low coordinate silicon and phosphorus compounds is still in its infancy when compared to that of the lighter analogues containing carbon and nitrogen; molecules containing the exotic Si
C bond. Although, the chemistry of low coordinate silicon and phosphorus compounds is still in its infancy when compared to that of the lighter analogues containing carbon and nitrogen; molecules containing the exotic Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P moiety3 have received significant attention over the years. As an example, tBu–C
P moiety3 have received significant attention over the years. As an example, tBu–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P is kinetically stable and was isolated about four decades ago,4 but the analogous phosphasilynes (R–Si
P is kinetically stable and was isolated about four decades ago,4 but the analogous phosphasilynes (R–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P) are still not known. On the other hand, half a decade ago phosphasilenylidenes, Si
P) are still not known. On the other hand, half a decade ago phosphasilenylidenes, Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P–R, had been stabilized by strong σ-donation from NHC [NHC→Si
P–R, had been stabilized by strong σ-donation from NHC [NHC→Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P–R; NHC = N-heterocyclic carbene].5 Switching the ligand field from NHC to cAAC resulted in the isolation of the cAAC-stabilized dimer in the solid state (cAAC→Si–P–R)2 [cAAC = cyclic alkyl(amino) carbene]. However, NMR studies showed that the monomeric species cAAC→Si
P–R; NHC = N-heterocyclic carbene].5 Switching the ligand field from NHC to cAAC resulted in the isolation of the cAAC-stabilized dimer in the solid state (cAAC→Si–P–R)2 [cAAC = cyclic alkyl(amino) carbene]. However, NMR studies showed that the monomeric species cAAC→Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P–R is stable in THF solution nearly for a day.6 The phosphasilenylidenes (Si
P–R is stable in THF solution nearly for a day.6 The phosphasilenylidenes (Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P–R) and phosphasilynes (R–Si
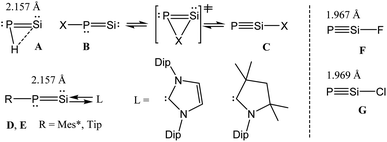
P–R) and phosphasilynes (R–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P, R = X) are isomers of each other.7,8 Early theoretical works showed that the phosphasilynes (C) are more stable than the phosphasilenylidenes (B), when R = electron withdrawing group, e.g., R = F. The presence of electropositive R groups/atoms stabilize B (Scheme 1).7,8 Phosphasilenylidenes (D) were stabilized by NHC carbene, when R = 2,4,6-triisopropylphenyl.5 The cAAC analogue (E) was only characterized in solution (Scheme 1).6 Though it has been predicted that X–Si
P, R = X) are isomers of each other.7,8 Early theoretical works showed that the phosphasilynes (C) are more stable than the phosphasilenylidenes (B), when R = electron withdrawing group, e.g., R = F. The presence of electropositive R groups/atoms stabilize B (Scheme 1).7,8 Phosphasilenylidenes (D) were stabilized by NHC carbene, when R = 2,4,6-triisopropylphenyl.5 The cAAC analogue (E) was only characterized in solution (Scheme 1).6 Though it has been predicted that X–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P compounds with electronegative substituents will be more stable than Si
P compounds with electronegative substituents will be more stable than Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P–X, till now there is no synthetic report on stable and isolable X–Si
P–X, till now there is no synthetic report on stable and isolable X–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P (phosphasilyne) (F, G) (Scheme 1). Such species are not even characterized by matrix isolation method. However, there is a report on theoretical investigation of very bulky ligand (Tbt = 2,4,6-tris[bis(trimethylsiyl)methyl]phenyl) shielded R–Si
P (phosphasilyne) (F, G) (Scheme 1). Such species are not even characterized by matrix isolation method. However, there is a report on theoretical investigation of very bulky ligand (Tbt = 2,4,6-tris[bis(trimethylsiyl)methyl]phenyl) shielded R–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P–R cation.8a
P–R cation.8a
Ph3P, NHC, cAAC and aAAC [acyclic alkyl(amino) carbene] are often utilized as donor ligands for the stabilization of exotic species, transient species, small clusters, and bare atoms through coordination.9–11 Triphenylphosphine (Ph3P) stabilized divalent carbon compound, C(PPh3)2 has been synthesized in 1961 by Ramirez et al.12 The bonding analysis of this compound by Frenking et al.13 in 2006 showed the formation two Ph3P→C dative σ-bonds and Ph3P←C π-bonds, leading to the accumulations of two lone pairs of electrons on the central C-atom. The notation of arrow for a dative bond was first used by Sidgwick in the 1920s14a and it was implemented for divalent carbon(0) compounds, L→C←L as suggested by Varshavskii in 1980.14b,c
Herein, we report the theoretical investigation on bonding and stability of donor ligand-stabilized phosphasilyne (F, G) with the general formula (L′)PSi(X)(L) [L′ = cAACMe; L = cAACMe, NHCMe, PMe3, aAAC; X = Cl, F] (n-Cl, n-F; n = 1 (cAACMe), 2 (NHCMe), 3 (aAAC), 4 (aAAC)). Additionally, the central PSi–X molecular unit containing one L ligand on either of P or Si atoms have been theoretically studied and the computed results have been compared and discussed.
Computational methods
Geometry optimizations and vibrational frequencies calculations of cAAC–PSi(Cl)–L (1-Cl to 4-Cl) and cAAC–PSi(F)–L (1-F to 4-F) with L = cAACMe (1-Cl, 1-F), NHCMe (2-Cl, 2-F), PMe3 (3-Cl, 3-F) and L = aAAC (4-Cl, 4-F) in singlet and triplet electronic states have been carried out at the BP86-D3(BJ)/Def2-TZVPP level15 in gas phase. The absence of imaginary frequencies assures the minima on potential energy surface. All the calculations have been performed using gaussian 16 program package.16 Natural bond orbital (NBO)17 analysis have been performed using NBO 6.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 program to evaluate the partial charges, Wiberg bond indices (WBI)19 and natural bond orbitals. The nature of bonds in cAAC–PSi(X)–L (X = Cl, F) were analyzed by energy decomposition analysis (EDA),20 coupled with natural orbital for chemical valence (NOCV)21 using ADF 2018.105 program package.22 EDA-NOCV calculations were carried out at the BP86-D3(BJ)/TZ2P23 level using the geometries optimized at BP86-D3(BJ)/def2-TZVPP level. EDA-NOCV method involves the decomposition of the intrinsic interaction energy (ΔEint) between the two fragments into four energy components as follows:
18 program to evaluate the partial charges, Wiberg bond indices (WBI)19 and natural bond orbitals. The nature of bonds in cAAC–PSi(X)–L (X = Cl, F) were analyzed by energy decomposition analysis (EDA),20 coupled with natural orbital for chemical valence (NOCV)21 using ADF 2018.105 program package.22 EDA-NOCV calculations were carried out at the BP86-D3(BJ)/TZ2P23 level using the geometries optimized at BP86-D3(BJ)/def2-TZVPP level. EDA-NOCV method involves the decomposition of the intrinsic interaction energy (ΔEint) between the two fragments into four energy components as follows:| ΔEint = ΔEelstat + ΔEPauli + ΔEorb + ΔEdisp | (1) |
 | (2) |
The combined EDA-NOCV method is able to partition the total orbital interactions into pairwise contributions of the orbital interactions, which is important in providing a complete picture of the bonding. The charge deformation, Δρk(r) which comes from the mixing of the orbital pairs, ψk(r) and ψ−k(r) of the interacting fragments, gives the magnitude and the shape of the charge flow due to the orbital interactions (eqn (3)), and the associated orbital energy, ΔEorb presents the amount of orbital energy coming from such interaction (eqn (4)).
 | (3) |
 | (4) |
Readers are further referred to the recent review articles to know more about the EDA-NOCV method and its applications.24
Results and discussion
We initiated our studies with the geometry optimization of F and G and all the ligands (aAAC, cAACMe, NHCMe, PMe3). The energy gap between HOMO and LUMO increases in the order of aAAC > cAACMe > NHCMe > PMe3 (Fig. S14†). The energy of HOMO also follows the same order with highest lying for aAAC and lowest lying for PMe3. F and G are singlet species and have a linear geometry with a Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P bond.
P bond.
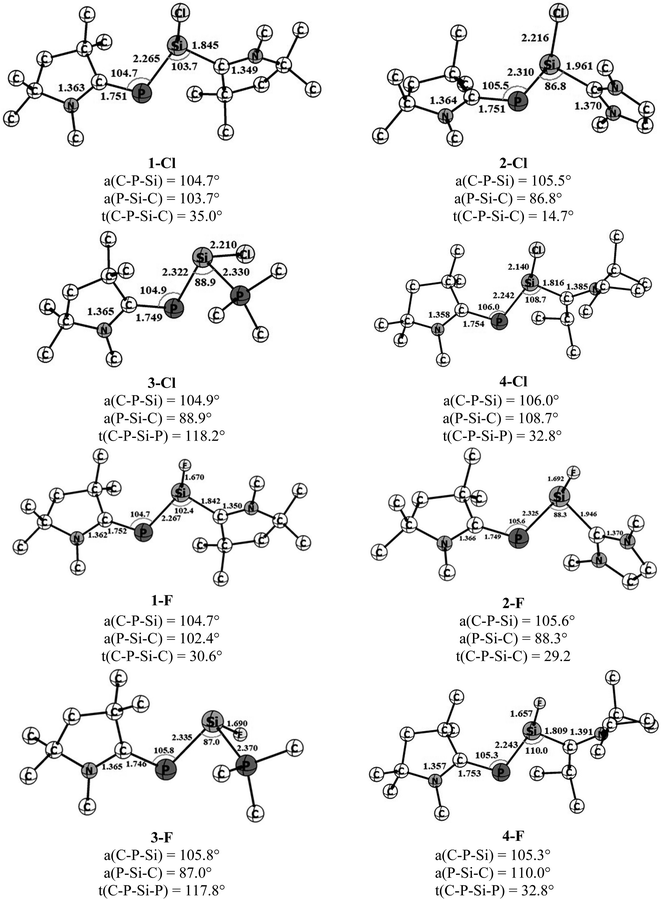
The optimized geometries of four cAAC–PSi(Cl)–L (1-Cl to 4-Cl) and four cAAC–PSi(F)–L compounds (1-F to 4-F) with L = cAACMe (1-Cl, 1-F), NHCMe (2-Cl, 2-F), PMe3 (3-Cl, 3-F) and L = aAAC (4-Cl, 4-F) in their electronic singlet states are shown in Fig. 1. The choice of ligands is based on their σ-donating and π-accepting ability and their effect in stabilizing the group 14 and 15 elements. The π-accepting ability of ligands increases in the order of PMe3 < NHC < aAAC < cAAC with cAAC being a very good σ donor as well as better π-acceptor compared to NHC which is a good σ-donor, but a poor π-acceptor followed by PMe3 which is only a σ-donor. Since (cAAC)P− anion is now readily accessible in the laboratory, cAACMe (L′) has been kept fixed at P-atom.25 The singlet states of all the complexes are found to be lower in energy than the corresponding triplet states by 21.2 to 40.7 kcal mol−1 (Fig. S1†). Theoretical calculations at BP86/Def2-TZVPP level of theory suggests that the both Si bonded ligands and P bonded cAACMe ligand in compounds 1-Cl, 2-Cl, 4-Cl and 1-F, 2-F, 4-F are slightly perpendicular to each other with respect to C–P–Si and P–Si–C planes which has reflected through C–P–Si–C torsion angles of 14.7–35° (Fig. 1). It is noteworthy to mention that the C–P–Si–C torsion angle significantly increases from 14.7° in 2-Cl to 29° in 2-F. This suggests different orbital interactions between terminal cAACMe/NHCMe ligands and central P–Si moieties of these two compounds (2-Cl, 2-F). The C–P–Si–P torsion angles of 117.8–118.2° in 3-Cl and 3-F (L = PMe3) indicate deviation from planarity. The CcAAC–P bond lengths of 1.746–1.754 Å in the present compounds are very close to those of the reported values, 1.740(2) and 1.739(2) for (cAAC)P–Si(cAAC)–P(cAAC).26 The Si–CL bond length varies with varying the ligand (L = cAACMe, NHCMe, PMe3, aAAC) and also with substitution (Cl or F) on Si-atom. In Cl substituted compounds, the Si–C bond length varies from 1.816 Å in 4-Cl (L = aAAC), 1.842 Å in 1-Cl (L = cAACMe),27 1.961 Å in 2-Cl (L = NHCMe),28 suggesting significant π-backdonation (Si→CcAAC) as expected and observed in (cAAC)2Si2Cl2 (1.823(3)/1.826(3) Å) containing a partial Si–CcAAC double bond (Si←CcAAC and, Si→CcAAC).27 The Si–P bond distance is 2.330 Å in 3-Cl (L = PMe3), which is slightly shorter than that of H2Si←PH3 (2.39 Å) and longer than that of electron sharing covalent Si–P single bond distance in H3Si–PH2 (2.258 Å).8c On replacement of Cl with F on Si, the Si–CL bond length almost remains same in 1-F (1.842 Å),27 while, it slightly decreases in 2-F (1.946 Å), 4-F (1.809 Å) and the Si–PPMe3 bond length slightly increases in 3-F (Si–P 2.370 Å). The Si–CL bond lengths are comparable to the reported Si–Ccarbene bond lengths of 1.985 Å and 1.939 Å in (NHC)SiCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 and (NHC)2Si2Cl2,29 respectively. The π-back acceptance property of NHC is negligible in these compounds.28,29 The calculated (cAAC)P–Si bond distance ranges from 2.265 to 2.335 Å, depending on the ligand coordinated to Si with 2.265–2.267 Å (P–Si–cAAC), 2.310–2.325 Å (P–Si–NHC), 2.322–2.335 Å (P–Si–PMe3) and 2.243 Å (P–Si-aAAC), which are lower than P
28 and (NHC)2Si2Cl2,29 respectively. The π-back acceptance property of NHC is negligible in these compounds.28,29 The calculated (cAAC)P–Si bond distance ranges from 2.265 to 2.335 Å, depending on the ligand coordinated to Si with 2.265–2.267 Å (P–Si–cAAC), 2.310–2.325 Å (P–Si–NHC), 2.322–2.335 Å (P–Si–PMe3) and 2.243 Å (P–Si-aAAC), which are lower than P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si bond lengths (2.125 Å)30 and comparable to P–Si single bond distance (2.29 Å)31 though differ by substituents. All the compounds possess rather acute ∟Caac–P–Si (∼105–106°) and ∟P–Si–CL (86.8–110.0°) bond angles. The ∟P–Si–CL bond angles varies in the order of L = NHCMe < PMe3 < cAACMe < aAAC for chloro-substituted Si (Si–Cl) and the order changes for fluoro-substituted Si (Si–F) as L = PMe3 < NHCMe < cAACMe < aAAC. The steric crowding of ligand L bonded to Si influences the ∟P–Si–CL bond angles. The larger ∟P–Si–CL bond angles 108.7–110° in 4-Cl and 4-F is due to higher steric crowding in aAAC ligands followed by cAAC ligands in 1-Cl and 1-F (102.4–103.7°). While, the lower steric crowding in NHC and PMe3 ligands resulted in acute bond angles (86.8–88.9°). The ∟C–C–N bond angle is slightly higher in aAAC (114.1–114.5°) (4-Cl, 4-F) than that in cAAC (107.0–107.4°) ligand in 1-Cl and 1-F. This increase in ∟C–C–N bond angle might influence the bonding in the corresponding compounds.
Si bond lengths (2.125 Å)30 and comparable to P–Si single bond distance (2.29 Å)31 though differ by substituents. All the compounds possess rather acute ∟Caac–P–Si (∼105–106°) and ∟P–Si–CL (86.8–110.0°) bond angles. The ∟P–Si–CL bond angles varies in the order of L = NHCMe < PMe3 < cAACMe < aAAC for chloro-substituted Si (Si–Cl) and the order changes for fluoro-substituted Si (Si–F) as L = PMe3 < NHCMe < cAACMe < aAAC. The steric crowding of ligand L bonded to Si influences the ∟P–Si–CL bond angles. The larger ∟P–Si–CL bond angles 108.7–110° in 4-Cl and 4-F is due to higher steric crowding in aAAC ligands followed by cAAC ligands in 1-Cl and 1-F (102.4–103.7°). While, the lower steric crowding in NHC and PMe3 ligands resulted in acute bond angles (86.8–88.9°). The ∟C–C–N bond angle is slightly higher in aAAC (114.1–114.5°) (4-Cl, 4-F) than that in cAAC (107.0–107.4°) ligand in 1-Cl and 1-F. This increase in ∟C–C–N bond angle might influence the bonding in the corresponding compounds.
We have also evaluated the thermochemical stability with respect to dissociation, (cAAC)P–Si(X)(L) → (cAAC) + P–Si(X) + L (X = Cl, F; L = cAACMe, NHCMe, PMe3 and aAAC). The bond dissociation energy (BDE) values were calculated at 0 K and change in Gibbs free energy at 298 K (ΔG298). The dissociation energy (De) values of all eight complexes varies with L in the order of PMe3 < NHCMe < aAAC < cAACMe. The dissociation is found to be the highest (127.4–129.0 kcal mol−1) in case of cAAC–PSi(Cl/F)–cAAC, 1-Cl, 1-F, followed by cAAC–PSi(Cl/F)–aAAC, 4-Cl, 4-F (120.5–122.6 kcal mol−1), cAAC–PSi(Cl/F)–NHC, 2-Cl, 2-F (114–115.35 kcal mol−1) and the lowest in case of cAAC–PSi(Cl/F)–PMe3, 3-Cl, 3-F (100–102.2 kcal mol−1). The De of fluoro-substituted compounds are found to be higher compared to their chloro-substituted counterparts with the exception of cAAC–PSi(Cl/F)–PMe3, where cAAC–PSi(Cl)–PMe3 have slightly higher De compared to cAAC–PSi(F)–PMe3. The dissociation is endergonic in nature at room temperature and the endergonicity follows the same trend of De in the order of L with L = PMe3 (ΔG298 = 86.3–87 kcal mol−1) < NHCMe (ΔG298 = 100.7–101.7 kcal mol−1) < aAAC (ΔG298 = 104.4–106.4 kcal mol−1) < cAACMe (ΔG298 = 111.5–113.7 kcal mol−1). The reasonably high De and endergonic nature of dissociation indicates the stability of the compounds. The HOMO–LUMO energy gap (ΔH–L) determines the electronic stability and reactivity of a molecule in its ground state. High ΔH–L denotes higher electronic stability and less reactivity. The present compounds under study showed good HOMO–LUMO energy gap in the range of 46–60 kcal mol−1. We have found that the HOMO–LUMO energy gap varies with L in the order of cAACMe < aAAC < NHCMe < PMe3 (Table S1†).
We have utilized NBO method to understand the electronic structure, charge distribution and the nature of bonding. The results in Table 1 identifies the CcAAC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P bonds (σ and π). While, the σ bonds are polarized towards the C-atom of cAACMe ligand (C→P), the π bonds (C←P) are polarized towards P atom. The cAAC
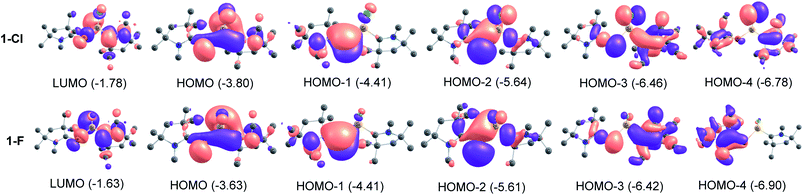
P bonds (σ and π). While, the σ bonds are polarized towards the C-atom of cAACMe ligand (C→P), the π bonds (C←P) are polarized towards P atom. The cAAC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P bond order of 1.23–1.50 supports the above description of donor–acceptor type. The Si–C/PL bond order of 0.76–0.77 in 2-Cl and 3-Cl suggests that Si–C/PL bond is a single bond which is polarized toward the ligand (L). The bond order of 1.14–1.23 and σ and π bond occupancies in 1-Cl and 4-Cl suggests a Si–CcAAC weak π contribution (Si←CcAAC). NBO analysis shows that the P–Si bond is predominantly single bond in all compounds. The bond order of 0.93–0.97 testifies a P–Si single bond. MO analysis shows that HOMO is essentially MO containing lone pairs of P and Si atoms (Fig. 2). The HOMO−1 is clearly the cAACMe
P bond order of 1.23–1.50 supports the above description of donor–acceptor type. The Si–C/PL bond order of 0.76–0.77 in 2-Cl and 3-Cl suggests that Si–C/PL bond is a single bond which is polarized toward the ligand (L). The bond order of 1.14–1.23 and σ and π bond occupancies in 1-Cl and 4-Cl suggests a Si–CcAAC weak π contribution (Si←CcAAC). NBO analysis shows that the P–Si bond is predominantly single bond in all compounds. The bond order of 0.93–0.97 testifies a P–Si single bond. MO analysis shows that HOMO is essentially MO containing lone pairs of P and Si atoms (Fig. 2). The HOMO−1 is clearly the cAACMe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P π-bonding MO with little contribution towards cAAC. HOMO−2 represents the lone pair on P and some overlap of lobes on Si with adjacent atoms. HOMO−3 is a σ type orbital on cAACMe, extending towards P-atom of cAAC
P π-bonding MO with little contribution towards cAAC. HOMO−2 represents the lone pair on P and some overlap of lobes on Si with adjacent atoms. HOMO−3 is a σ type orbital on cAACMe, extending towards P-atom of cAAC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P unit and ligand specific interactions like C–N interaction, when L = cAACMe and delocalization of electrons, when L = NHCMe. HOMO−4 represents Si–Cl orbital with π type interaction. The MOs of fluoro-substituted compounds (1-F to 4-F) (Table S2†) are similar to that of the chloro-substituted ones (1-Cl to 4-Cl), but it is to be noted that the orbitals on F are too small to extend interaction towards the lobes of Si which is present in HOMO−4 of chloro-substituted compounds (Fig. 2, S2 and S3†).
P unit and ligand specific interactions like C–N interaction, when L = cAACMe and delocalization of electrons, when L = NHCMe. HOMO−4 represents Si–Cl orbital with π type interaction. The MOs of fluoro-substituted compounds (1-F to 4-F) (Table S2†) are similar to that of the chloro-substituted ones (1-Cl to 4-Cl), but it is to be noted that the orbitals on F are too small to extend interaction towards the lobes of Si which is present in HOMO−4 of chloro-substituted compounds (Fig. 2, S2 and S3†).
| Complex | Bond | ON | Polarization and hybridization (%) | WBI | q | ||
|---|---|---|---|---|---|---|---|
| P | Si | ||||||
| 1-Cl | CcAAC–P | 1.91 | C: 39.8 s(0.0), p(99.8) | P: 60.2 s(0.0), p(99.5) | 1.49 | −0.08 | 0.65 |
| 1.97 | C: 65.2 s(38.6), p(61.1) | P: 34.8 s(18.8), p(80.3) | |||||
| P–Si | 1.91 | P: 57.7 s(14.4), p(84.7) | Si: 42.3 s(33.5), p(65.9) | 0.94 | |||
| Si–CL | 1.64 | Si: 42.1 s(43.9), p(55.5) | C: 57.9 s(24.6), p(68.8) | 1.14 | |||
| 1.53 | Si: 61.0 s(3.10), p(96.6) | C: 39.0 s(16.2), p(73.5) | |||||
| 2-Cl | CcAAC–P | 1.90 | C: 40.1 s(0.0), p(99.8) | P: 59.9 s(0.0), p(99.6) | 1.49 | −0.14 | 0.39 |
| 1.97 | C: 65.1 s(38.8), p(60.9) | P: 34.9 s(20.1), p(79.1) | |||||
| P–Si | 1.88 | P: 62.5% s(15.1), p(84.3) | Si: 37.5% s(11.7), p(87.3) | 0.93 | |||
| Si–CL | 1.94 | Si: 22.9 s(10.6), p(88.2) | C: 77.1 s(43.1), p(56.8) | 0.76 | |||
| 3-Cl | CcAAC–P | 1.97 | C: 65.2% S(38.8), p(60.8) | P: 34.8 S(20.1), p(79.1) | 1.50 | −0.14 | 0.27 |
| 1.91 | C: 40.9 s(0.1), p(99.8) | P: 59.1 S(0.0), p(99.5) | |||||
| P–Si | 1.91 | P: 61.9 s(14.4), p(85.0) | Si: 38.1 s(10.9), p(88.0) | 0.94 | |||
| Si–PL | 1.94 | Si: 26.6 s(7.5), p(91.5) | P: 73.4 s(30.1), p(69.6) | 0.77 | |||
| 4-Cl | CcAAC–P | 1.96 | C: 65.1% s(38.3), p(61.7) | P: 34.9 s(19.5), p(80.5) | 1.46 | −0.08 | 0.79 |
| P–Si | 1.90 | P: 57.9 s(14.7), p(84.3), d(1) | Si: 42.1 s(34.3), p(65.7) | 0.97 | |||
| Si–CL | 1.90 | Si: 34.3 s(44.9), p(55.1) | C: 65.7 s(28.1), p(71.9) | 1.23 | |||
| 1.84 | Si: 41.5 s(2.5), p(97.5) | C: 58.5 s(10.7), p(89.3) | |||||
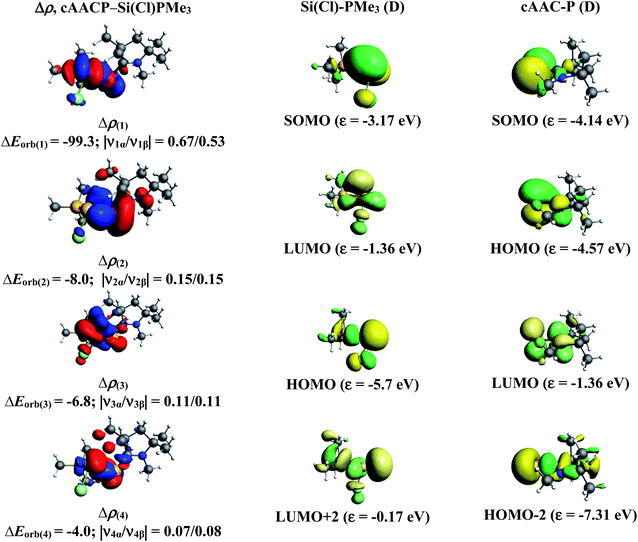
The NBO results, however cannot distinguish the dative or electron sharing interactions and thus not the true nature of the bond. NBO also cannot produce the clear picture of electronic structure of each fragment and the corresponding bonding between them. In this respect, energy decomposition analysis-natural orbital with chemical valence (EDA-NOCV) approach is useful to give a detailed insight into the nature of the chemical bonds of cAAC–PSi(Cl/F)–L (L = cAACMe, NHCMe, PMe3, aAAC) (1-Cl to 4-Cl and 1-F to 4-F) by its ability to provide the best bonding model to represent the overall bonding situation in the molecule. The bonding possibility with lowest ΔEorb is considered as the best bonding representation, since it needs the least change in the electronic charge of the fragments to make the electronic structure of the molecule.32
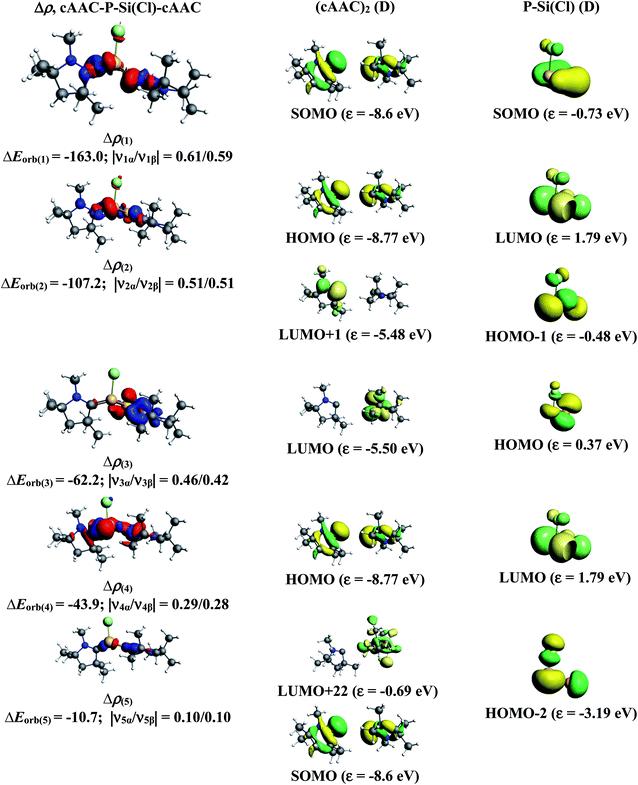
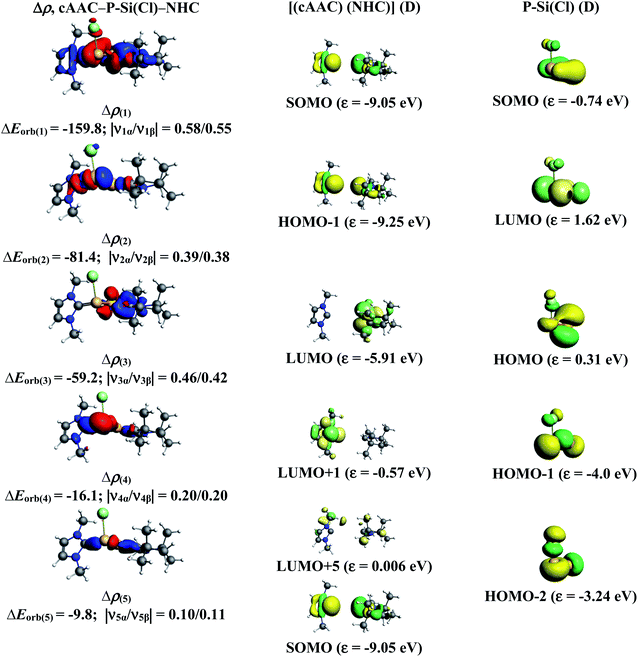
In the present study, the best bonding description of cAAC–PSi(X)–L molecules (X = Cl for 1-Cl to 4-Cl and X = F for 1-F to 4-F) is portrayed by considering five different bonding possibilities (Scheme 2) by varying the charge and electronic states of the interacting fragments [(cAAC)(L)] and P–Si(X), viz., (1) neutral [(cAAC)L] and P–Si(X) fragments in their electronic singlet state forming dative bonds, (2) neutral [(cAAC)L] and P–Si(X) fragments in their electronic triplet state leading to the formation of σ and π electron sharing bonds and other σ and π dative bonds, (3) neutral [(cAAC)(L)] and P–Si(X) fragments in their electronic triplet state leading to the formation σ electron sharing bonds and π dative bonds, (4) singly charged [(cAAC)L]+ and [P–Si(X)]− fragments in electronic doublet state, which would interact to form both electron sharing and dative bonds and (5) neutral [(cAAC)(L)] and P–Si(X) fragments in their electronic quintet state leading to the formation four electron sharing bonds. Energy decomposition analysis (EDA) coupled with natural orbital for chemical valence (NOCV) results from Table 2 shows that for carbene containing compounds 1-Cl, 2-Cl and 4-Cl, the fragmentation scheme involving singly charged [(cAAC)L]+ and [P–Si(X)]− fragments in electronic doublet state (Scheme 2; (4)) forming both electron sharing and dative bonds gives the smallest ΔEorb and hence fits the best bonding scenario. In fact, for 2-Cl (L = NHC) bonding possibility (2) forming σ and π electron sharing bonds also have comparable ΔEorb value with the best bonding possibility (4), indicating that the σ and π electron sharing bonding model might also be valid in describing the bonding. Similarly, for 4-Cl (L = aAAC) the bonding model can also be expressed in terms of all electron sharing bonds with neutral interacting fragments in quintet states (5). On the other hand, for complex 3-Cl (L = PMe3) the best bonding description of cAAC–PSi(Cl)–L bonds comes from the interaction of neutral [(cAAC)L] and P–Si(Cl/F) fragments in triplet electronic states (Scheme 2; (2)) with cAAC forming both electron sharing σ and π bonds with P-atom of P–Si(Cl) unit and PMe3 forming dative bonds with Si-atom.
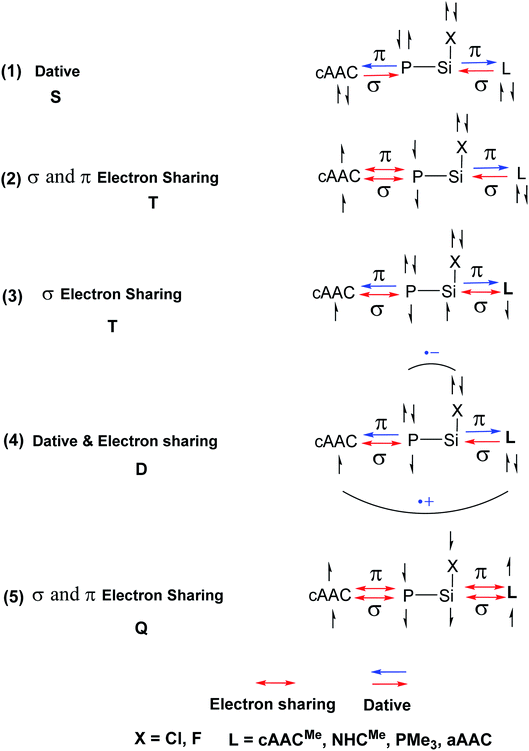 | ||
| Scheme 2 Bonding possibilities of cAAC–P–Si(X)–L bonds of cAAC–P–Si(X)–L (L = cAACMe, NHCMe, PMe3, aAAC; X = Cl, F) 1-Cl to 4-Cl and 1-F to 4-F. | ||
| Molecule | Bond typea | Fragments | ΔEint | ΔEPauli | ΔEelstat | ΔEdisp | ΔEorb |
|---|---|---|---|---|---|---|---|
| a D = dative bond; E = electron sharing bond. | |||||||
| cAAC–P–Si(Cl)–cAAC | D | (cAACMe)2 (S) + P–Si(Cl) (S) | −205.8 | 651.3 | −408.9 | −23.6 | −424.7 |
| E (σ, π) | (cAACMe)2 (T) + P–Si(Cl) (T) | −339.9 | 556.0 | −344.8 | −23.6 | −527.6 | |
| E (σ, σ) | (cAACMe)2 (T) + P–Si(Cl) (T) | −218.3 | 609.5 | −371.8 | −23.6 | −432.4 | |
| D + E | [(cAACMe)2]+ (D) + [P–Si(Cl)]− (D) | −252.5 | 622.1 | 440.2 | −23.6 | −410.8 | |
| E | (cAACMe)2 (Q) + P–Si(Cl) (Q) | −304.7 | 499.9 | −341.0 | −23.6 | −440.0 | |
| cAAC–P–Si(Cl)–NHC | D | [(cAACMe)(NHCMe)] (S) + P–Si(Cl) (S) | −192.1 | 548.3 | −356.6 | −21.9 | −362.0 |
| E (σ, π) | [(cAACMe)(NHCMe)] (T) + P–Si(Cl) (T) | −203.2 | 487.7 | −312.9 | −21.9 | −356.1 | |
| E (σ, σ) | [(cAACMe)(NHCMe)] (T) + P–Si(Cl) (T) | −369.4 | 507.0 | −332.6 | −21.9 | −521.8 | |
| D + E | [(cAACMe)(NHCMe)]+ (D) + [P–Si(Cl)]− (D) | −246.3 | 514.6 | −390.6 | −21.9 | −348.5 | |
| E | [(cAACMe)(NHCMe)] (Q) + P–Si(Cl) (Q) | −334.7 | 436.8 | −299.5 | −21.9 | −450.2 | |
| cAAC–P–Si(Cl)–PMe3 | D | [(cAACMe)(PMe3)] (S) + P–Si(Cl) (S) | −177.1 | 743.7 | −391.3 | −21.5 | −507.9 |
| E (σ, π) | [(cAACMe)(PMe3)] (T) + P–Si(Cl) (T) | −189.4 | 465.9 | −289.2 | −21.5 | −344.6 | |
| E (σ, σ) | [(cAACMe)(PMe3)] (T) + P–Si(Cl) (T) | −359.2 | 517.7 | −297.7 | −21.5 | −557.7 | |
| D + E | [(cAACMe)(PMe3)]+ (D) + [P–Si(Cl)]− (D) | −236.9 | 651.7 | −427.8 | −21.5 | −439.3 | |
| E | [(cAACMe)(PMe3)] (Q) + P–Si(Cl) (Q) | −339.1 | 429.1 | −282.7 | −21.5 | −464.0 | |
| cAAC–P–Si(Cl)–aAAC | D | [(cAACMe)(aAAC)] (S) + P–Si(Cl) (S) | −222.6 | 684.8 | −428.6 | −26.6 | −452.2 |
| E (σ, π) | [(cAACMe)(aAAC)] + P–Si(Cl) (T) | −198.9 | 717.4 | −415.7 | −26.6 | −473.8 | |
| E (σ, σ) | [(cAACMe)(aAAC)] (T) + P–Si(Cl) (T) | −321.4 | 605.8 | −370.5 | −26.6 | −530.0 | |
| D + E | [(cAACMe)(aAAC)]+ (D) + [P–Si(Cl)]− (D) | −259.4 | 675.8 | −469.4 | −26.6 | −439.1 | |
| E | [(cAACMe)(aAAC)] (Q) + P–Si(Cl) (Q) | −2889 | 5562 | −369.9 | −26.6 | −448.5 | |
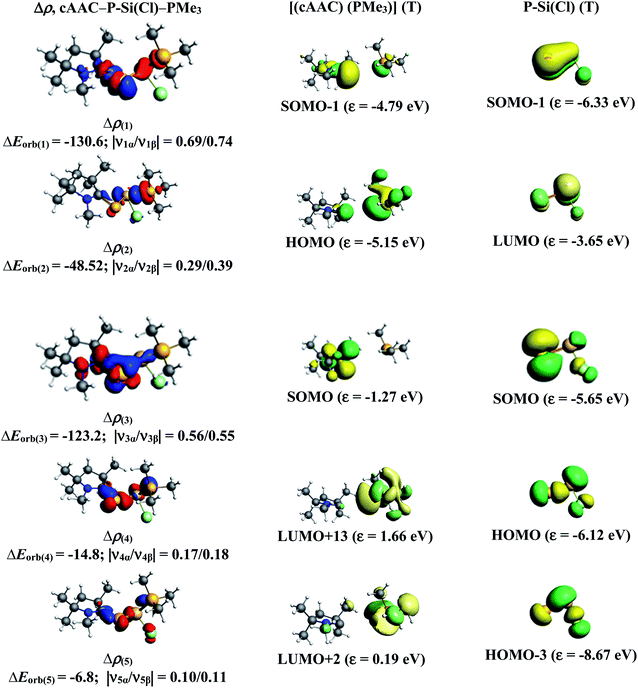
The results of EDA-NOCV for the most favorable bonding model are given in Table 3. In compounds 1-Cl, 2-Cl and 4-Cl (L = carbene), the cAAC–PSi(Cl)–L (L = cAACMe and NHCMe) bonds are 50.3 to 51.3% electrostatic in nature and the remaining 45.8 to 46.9% comes from covalent interactions and 2.6–2.9% from dispersion contribution. Further breakdown of ΔEorb into pairwise contributions gives more detailed information about the nature of bonding. There are five relevant orbital contributions, ΔEorb(1)–ΔEorb(5) and the nature of orbital terms and corresponding fragment molecular orbitals can be understood with the help of associated deformation densities, Δρn (Fig. 3–5 and S4†). Notable to mention that the symmetry assignments, σ and π in Table 3 have been made with respect to the CcAAC–P–Si–CL plane. The strongest interaction, ΔEorb(1) (36.6–45.8%) comes from electron sharing σ interaction in out-of-phase (+−) combination of the unpaired electrons in the SOMO of the fragments. The dative in-phase (++) σ donation from HOMO of the ligands [(cAAC)(L)]+ into LUMO of the [P–Si(Cl)]− forms the slightly weaker ΔEorb(2) (23.3–26.1%) in 1-Cl, 2-Cl and much weaker (12.1%) in 4-Cl. In 1-Cl along with in-phase (++) σ donation, the backdonation form HOMO−1 of [P–Si(Cl)]− to LUMO+1 of ligands [(cAAC)(L)]+ contributes to ΔEorb(2). The ΔEorb(3) is due to π backdonation from HOMO of [P–Si(Cl)]− to LUMO of ligands [(cAAC)(L)]+ and contributes 15.1–17% in 1-Cl, 2-Cl and 30% in 4-Cl. The strength of π contribution is significantly high in 4-Cl compared to 1-Cl and 2-Cl. While, the other weak interaction, ΔEorb(4) (4.6–13.4%) in 1-Cl is due to σ donation from HOMO of the ligands [(cAAC)(L)]+ into LUMO of the [P–Si(Cl)]−, in 2-Cl it is due to σ backdonation from HOMO−1 of [P–Si(Cl)]− to LUMO+1 of ligands [(cAAC)(L)]+ and 4-Cl it is due to π back-donation. The last and very weak contribution, ΔEorb(5) (2.6–2.8%) is a backdonation from [P–Si(Cl)]−, majorly into the SOMO and to a little extent into the higher lying vacant orbitals of the ligands [(cAAC)(L)]+. In case of 3-Cl, the cAAC–PSi(Cl)–L (L = PMe3) bonds are 52.6% covalent in nature and the remaining part is shared by coulombic or electrostatic interaction (44.1%) and dispersion interaction (3.3%). Thus the cAAC–PSi(Cl)–L bonds in 3-Cl are more covalent in nature compared to those of 1-Cl and 2-Cl. Similar to the other two compounds, there are five significant orbital terms, ΔEorb(1)–ΔEorb(5) in 3-Cl. The strongest interaction, ΔEorb(1) (37.9%) comes from the electron sharing σ interaction in out-of-phase (+−) combination of the unpaired electrons in the SOMO−1 of the fragments. The third orbital term, ΔEorb(3) (35.7%) is as strong as ΔEorb(1) and is due to electron sharing π interaction of the unpaired electrons in the SOMO of the fragments. ΔEorb(2) term is a dative in-phase (++) σ donation from HOMO of the ligands [(cAAC)(L)] into LUMO of the P–Si(Cl). It is rather weak (14.1%) compared to σ and π electron sharing contributions. The other two orbital terms, ΔEorb(4) and ΔEorb(5) are due to σ back donations from HOMO and HOMO−3 of P–Si(Cl) into higher lying LUMO+13 and LUMO+2 vacant orbitals of [(cAAC)(L)] ligands, respectively.
| Energy | Interaction | [(cAAC)2]+ (D) + [P–Si(Cl)]− (D) | [(cAAC)(NHC)]+ (D) + [P–Si(Cl)]− (D) | [(cAAC)(PMe3)] (T) + P–Si(Cl) (T) | [(cAAC)(aAAC)]+ (D) + [P–Si(Cl)]− (D) |
|---|---|---|---|---|---|
| a The values in the parentheses show the contribution to the total attractive interaction ΔEelstat + ΔEorb + ΔEdisp.b The values in parentheses show the contribution to the total orbital interaction ΔEorb. | |||||
| ΔEint | −252.5 | −246.3 | −189.4 | −259.4 | |
| ΔEPauli | 622.1 | 514.6 | 465.9 | 675.8 | |
| ΔEdispa | −23.6 (2.6%) | −21.9 (2.9%) | −21.5 (3.3%) | −26.6 (2.8%) | |
| ΔEelstata | −440.2 (50.3%) | −390.6 (51.3%) | −289.2 (44.1%) | −469.4 (50.2%) | |
| ΔEorba | −410.8 (46.9%) | −348.5 (45.8%) | −344.6 (52.6%) | −439.1 (47%) | |
| ΔEorb(1)b | cAAC–P–Si(Cl)–L σ e− sharing (+,−) | −163.0 (39.6%) | −159.8 (45.8%) | −130.6 (37.9%) | −157.9 (36%) |
| ΔEorb(2)b | cAAC→P–Si(Cl)←L σ donation (+,+) | −107.2 (26.1%) | −81.4 (23.3%) | −48.5 (14.1%) | −53.0 (12.1%) |
| ΔEorb(3)b | cAAC–P–Si(Cl)–L π e− sharing | −123.2 (35.7%) | |||
| cAAC←P–Si(Cl)→L π back donation | −62.2 (15.1%) | −59.2 (17.0%) | −131.2 (30%) | ||
| ΔEorb(4)b | cAAC→P–Si(Cl)←L σ donation | −43.9 (10.7%) | |||
| cAAC←P–Si(Cl)→L back donation | −16.1 (4.6%) | −14.8 (4.3%) | −59.1 (13.4%) | ||
| ΔEorb(5)b | cAAC←P–Si(Cl)→L back donation | −10.7 (2.6%) | −9.8 (2.8%) | −6.8 (1.9%) | −11.1 (2.5%) |
| ΔEorb(rest)b | −23.8 (5.8%) | −22.2 (6.3%) | −20.7 (6.0%) | −26.8 (6.1%) | |
Similarly, we have analyzed cAAC–PSi(F)–L bonds of the fluoro-substituted cAAC–P–Si(F)–L (L = cAACMe, NHCMe, PMe3) compounds 1-F to 4-F, using EDA-NOCV by considering five different bonding possibilities on the similar lines of chloro-substituted complexes 1-Cl to 3-Cl. EDA-NOCV results from Table 4 suggests that for 1-F, the fragmentation scheme involving singly charged [(cAAC)(L)]+ and [P–Si(F)]− fragments in electronic doublet state forming both electron sharing and dative bonds gives the best bonding description. It is to be observed that for 1-F bonding possibility (1) forming dative bonds also have comparable ΔEorb value with the best bonding possibility (4), indicating that the dative bonding model might also be valid in describing the bonding. Whereas, for 2-F and 3-F, the best bonding description of cAAC–PSi(F)–L bonds comes from the interaction of neutral [(cAAC)(L)] and P–Si(Cl/F) fragments in triplet electronic state forming σ and π electron sharing bonds and other σ and π dative bonds. Interestingly, for complex 4-F, the best bonding description comes almost equally from two bonding possibilities, (4) and (5), where the bonding can be explained in terms of mixture of electron sharing and dative bonds (4), as well as all electron sharing bonds (5), since, ΔEorb value differ by less than 1 kcal mol−1. It is to be noted that the fluoro-substituted compound cAAC–PSi(F)–NHC (2-F), in contrast to its chloro substituted counterpart (2-Cl), prefers to form σ and π electron sharing cAAC–PSi(F)–L bonds with interacting fragments in triplet state. This change in bonding preference is in agreement with the significant increase in C–P–Si–C torsion angle for fluoro-substituted complex (Fig. 1), which might have altered the PSi(F)–L orbital interactions.
| Molecule | Bond typea | Fragments | ΔEint | ΔEPauli | ΔEelstat | ΔEdisp | ΔEorb |
|---|---|---|---|---|---|---|---|
| a D = dative bond; E = electron sharing bond. | |||||||
| cAAC–P–Si(F)–cAAC | D | (cAACMe)2 (S) + P–Si(F) (S) | −203.9 | 638.2 | −406.3 | −21.3 | −414.6 |
| E (σ, π) | (cAACMe)2 (T) + P–Si(F) (T) | −216.5 | 601.6 | −370.2 | −21.3 | −426.6 | |
| E (σ, σ) | (cAACMe)2 (T) + P–Si(F) (T) | −344.3 | 553.5 | −347.6 | −21.3 | −528.7 | |
| D + E | [(cAACMe)2]+ (D) + [P–Si(F)]− (D) | −252.7 | 619.9 | −443.5 | −21.3 | −407.8 | |
| E | (cAACMe)2 (Q) + P–Si(F) (Q) | −305.8 | 498.2 | −345.8 | −21.3 | −436.8 | |
| cAAC–P–Si(F)–NHC | D | [(cAACMe)(NHCMe)] (S) + P–Si(F) (S) | −188.0 | 575.8 | −367.3 | 19.4 | −377.1 |
| E (σ, π) | [(cAACMe)(NHCMe)] (T) + P–Si(F) (T) | −199.9 | 495.8 | −319.1 | −19.4 | −357.3 | |
| E (σ, σ) | [(cAACMe)(NHCMe)] (T) + P–Si(F) (T) | −373.1 | 526.7 | −339.8 | −19.4 | −540.6 | |
| D + E | [(cAACMe)(NHCMe)]+ (D) + [P–Si(F)]− (D) | −346.2 | 497.5 | −338.5 | −19.4 | −485.7 | |
| E | [(cAACMe)(NHCMe)] (Q) + P–Si(F) (Q) | −248.0 | 543.8 | −405.1 | −19.4 | −367.4 | |
| cAAC–P–Si(F)–PMe3 | D | [(cAACMe)(PMe3)] (S) + P–Si(F) (S) | −169.7 | 711.8 | −377.3 | −19.3 | −484.8 |
| E (σ, π) | [(cAACMe)(PMe3)] (T) + P–Si(F) (T) | −184.0 | 447.1 | −279.2 | −19.3 | −332.6 | |
| E (σ, σ) | [(cAACMe)(PMe3)] (T) + P–Si(F) (T) | −373.5 | 564.8 | −313.2 | −19.3 | −605.8 | |
| D + E | [(cAACMe)(PMe3)]+ (D) + [P–Si(F)]− (D) | −234.2 | 631.5 | −421.1 | −19.3 | −425.2 | |
| E | [(cAACMe)(PMe3)] (Q) + P–Si(F) (Q) | −336.8 | 402.3 | −268.9 | −19.3 | −450.9 | |
| cAAC–P–Si(F)–aAAC | D | [(cAACMe)(aAAC)] (S) + P–Si(F) (S) | −219.4 | 691.0 | −433.0 | −23.6 | −453.8 |
| E (σ, π) | [(cAACMe)(aAAC)] + P–Si(F) (T) | −197.1 | 719.0 | −416.6 | −23.6 | −475.9 | |
| E (σ, σ) | [(cAACMe)(aAAC)] (T) + P–Si(F) (T) | −327.4 | 602.9 | −373.4 | −23.6 | −533.4 | |
| D + E | [(cAACMe)(aAAC)]+ (D) + [P–Si(F)]− (D) | −260.1 | 691.4 | −480.9 | −23.6 | −447.0 | |
| E | [(cAACMe)(aAAC)] (Q) + P–Si(F) (Q) | −290.7 | 552.5 | −373.3 | −23.6 | −446.3 | |
The numerical results from Table 5 gives the detailed information on the pairwise interactions of cAAC–PSi(F)–L bonds. cAAC–PSi(F)–L bonds in 2-F (51.4%), 3-F (52.7%) and 4-F (53%) are more covalent in nature compared to 1-F (46.7%). There are five orbital terms, ΔEorb(1)–ΔEorb(5) and associated deformation densities, Δρn (Fig. S6–S9†) for all three compounds 1-F to 4-F. For 1-F, the strongest interaction, ΔEorb(1) (40.3%) comes from electron sharing σ interaction in out-of-phase (+−) combination of the unpaired electrons in the SOMO of the fragments. The dative in-phase (++) σ donation from HOMO of the ligands [(cAAC)(L)]˙+ into LUMO of the [P–Si(F)]− forms the slightly weaker ΔEorb(2) (25.3%). Along with in-phase (++) σ donation, the back donation form HOMO−1 of [P–Si(F)]− to LUMO+1 of ligands [(cAAC)(L)]+ contributes to ΔEorb(2). The ΔEorb(3) (15.0%) is due to π backdonation from HOMO of [P–Si(F)]− to LUMO of ligands [(cAAC)(L)]+. The σ contribution is higher compared to π contribution. While, the other weak interaction ΔEorb(4) (11.5%) is due to σ donation from HOMO of the ligands [(cAAC)(L)]+ into LUMO of the [P–Si(F)]−. The last and very weak contribution, ΔEorb(5) (2.6%) is a backdonation from HOMO−2 of [P–Si(F)]− into the SOMO of ligands [(cAAC)(L)]+. Whereas, in case of complexes 2-F and 3-F, the strongest interaction, ΔEorb(1) (45.2–46.5%) comes from the electron-sharing σ interaction in out-of-phase (+−) combination of the unpaired electrons in the SOMO−1 of the fragments. Third orbital term ΔEorb(3) (20.5–28.5%) is slightly weaker than ΔEorb(1) and is due to electron sharing π interaction of the unpaired electrons in the SOMO of the fragments. ΔEorb(2) term is a dative in-phase (++) σ donation from HOMO of the ligands [(cAAC)(L)] in to LUMO of the P–Si(F). It is equivalent to π interaction in complex 2-F (20.1%) and rather weak (13.2%) in complex 3-F. The other two orbital terms ΔEorb(4) and ΔEorb(5) are due to σ back donations from HOMO and HOMO−1 of P–Si(F) in to LUMO+1 and SOMO−1 orbitals of [(cAAC)L)] ligands, respectively in compound 2-F. The orbital terms ΔEorb(4) and ΔEorb(5) in 3-F are σ backdonations from HOMO and HOMO−3 of P–Si(F) in to LUMO+3 and LUMO+2 orbitals of [(cAAC)(L)] ligands. In 4-F, the four significant orbital terms, ΔEorb(1)–ΔEorb(4) between the neutral fragments in the quintet states are identified as strong in-phase (+,+) and out-of-phase (+,−) electron sharing σ interactions, ΔEorb(1) and ΔEorb(2) and the weaker but still rather strong π interactions, ΔEorb(3) and ΔEorb(4). The weaker ΔEorb(5) is a σ interaction between HOMO−2 of P–Si(F) and SOMO− of [(cAAC)(L)] ligands.
| Energy | Interaction | [(cAAC)2]+ (D) + [P–Si(F)]− (D) | [(cAAC)(NHC)] (T) + P–Si(F) (T) | [(cAAC)(PMe3)] (T) + P–Si(F) (T) | [(cAAC)(aAAC)] (Q) + P–Si(F) (Q) |
|---|---|---|---|---|---|
| a The values in the parentheses show the contribution to the total attractive interaction, ΔEelstat + ΔEorb + ΔEdisp.b The values in parentheses show the contribution to the total orbital interaction, ΔEorb. | |||||
| ΔEint | −252.7 | −199.9 | −184.0 | −290.7 | |
| ΔEPauli | 619.9 | 495.8 | 447.1 | 552.5 | |
| ΔEdispa | −21.3 (2.4%) | −19.4 (2.8%) | −19.3 (3.0%) | −23.6 (2.8%) | |
| ΔEelstata | −443.5 (50.8%) | −319.1 (45.8%) | −279.2 (44.3%) | −373.3 (44.2%) | |
| ΔEorba | −407.8 (46.7%) | −357.3 (51.4%) | −332.6 (52.7%) | −446.3 (53%) | |
| ΔEorb(1)b | cAAC–P–Si(F)–L σ e− sharing (+,−) | −164.6 (40.3%) | −161.7 (45.2%) | −154.6 (46.5%) | −136.1 (30.5%) |
| ΔEorb(2)b | cAAC→P–Si(F)←L σ donation (+,+) | −102.3 (25.3%) | −72.0 (20.1%) | 44.0 (13.2%) | |
| cAAC→P–Si(F)←L σ e− sharing (+,+) | −146.5 (32.8%) | ||||
| ΔEorb(3)b | cAAC–P–Si(F)–L π e− sharing | −73.4 (20.5%) | −95.0 (28.5%) | −65.8 (14.7%) | |
| cAAC←P–Si(F)→L π back donation | −61.3 (15.0%) | ||||
| ΔEorb(4)b | cAAC→P–Si(F)←L σ donation | −47.0 (11.5%) | |||
| cAAC←P–Si(F)→L σ back donation | −19.5 (5.4%) | −15.6 (4.7%) | |||
| cAAC–P–Si(F)–L π e− sharing | −59.3 (13.3%) | ||||
| ΔEorb(5)b | cAAC←P–Si(F)→L σ back donation | −10.8 (2.6%) | −10.5 (2.9%) | −7.4 (2.2%) | −12.6 (2.8%) |
| ΔEorb(rest)b | −21.8 (5.3%) | −20.2 (5.6%) | −16.0 (4.8%) | −26 (5.8%) | |
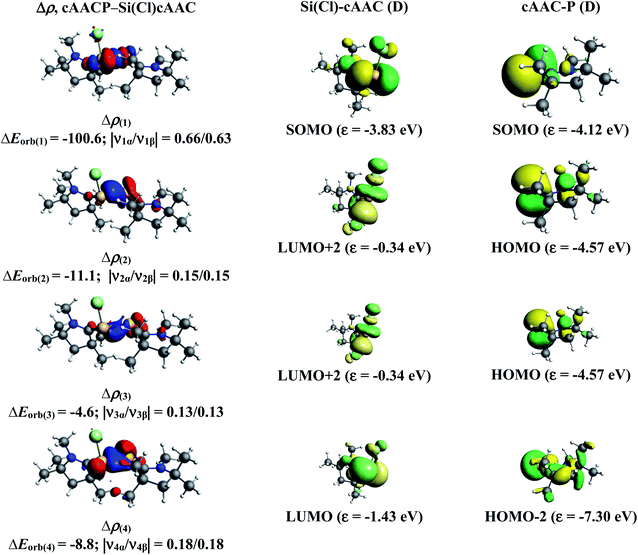
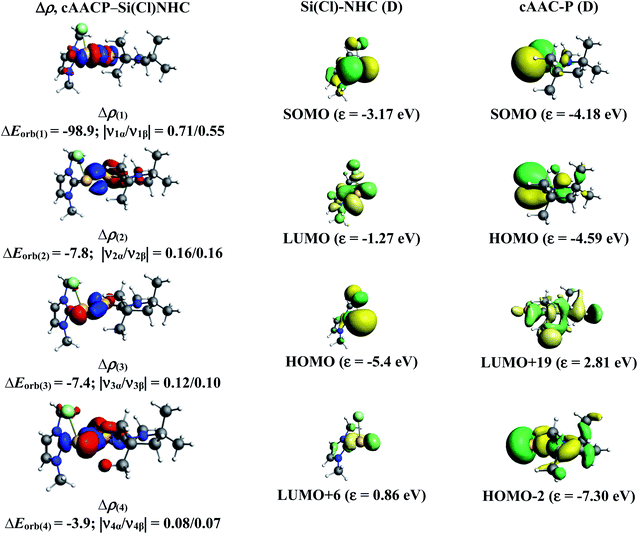
We have further focussed our study on understanding the nature of P–Si bonds of all cAAC–PSi(Cl/F)–L (L = cAACMe, NHCMe, PMe3, aAAC) molecules (1-Cl to 4-Cl and 1-F to 4-F). We have considered three different bonding possibilities (Scheme 3) by varying the charge and electronic states of the interacting fragments, cAAC–P and Si(Cl/F)–L, viz., (1) neutral cAAC–P and Si(Cl/F)–L fragments in their electronic doublet states leading to the formation of electron sharing and dative bonds, (2) singly charged [cAAC–P]− and [Si(Cl/F)–L]+ fragments in electronic singlet state forming dative bonds and (3) singly charged [cAAC–P]+ and [Si(Cl/F)–L]− fragments in electronic singlet state forming dative bonds. EDA-NOCV results from Tables 6 and S3† show that the best bonding description of central P–Si bond in all eight compounds (1-Cl to 4-Cl and 1-F to 4-F) comes from the interaction of neutral fragments in doublet state forming electron sharing and dative bonds. Whereas, the best bonding description of P–Si bond in unsubstituted P–Si(Cl) comes from the interaction of neutral P and Si(Cl) fragments in quartet state forming three electron sharing bonds (Table S17†). This change in nature of bonding is owed to the presence of donor ligands which weakens the P–Si bond.
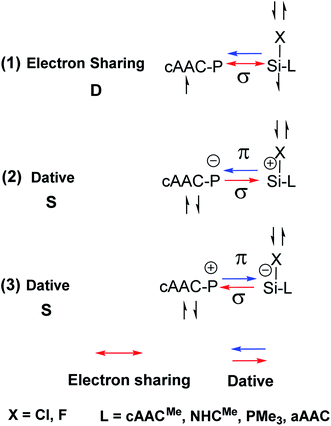 | ||
| Scheme 3 Bonding possibilities of cAAC–P–Si(X)–L bond of cAAC–P–Si(X)–L (L = cAACMe, NHCMe, PMe3, aAAC; X = Cl, F) 1-Cl to 4-Cl and 1-F to 4-F. | ||
| Molecule | Bond typea | Fragments | ΔEint | ΔEPauli | ΔEelstat | ΔEdisp | ΔEorb |
|---|---|---|---|---|---|---|---|
| a D = dative bond; E = electron sharing bond. | |||||||
| cAAC–P–Si(Cl)–cAAC | E | cAACMe–P (D) + Si(Cl)–cAACMe (D) | −62.8 | 200.6 | −119.9 | −13.7 | −129.8 |
| D | [cAACMe–P]− (S) + [Si(Cl)–cAACMe]+ (S) | −194.9 | 265.5 | −239.6 | −13.7 | −207.1 | |
| D | [cAACMe–P]+ (S) + [Si(Cl)–cAACMe]− (S) | −211.7 | 222.7 | −202.7 | −13.7 | −218.0 | |
| cAAC–P–Si(Cl)–NHC | E | cAACMe–P (D) + Si(Cl)–NHCMe (D) | −60.5 | 188.1 | −113.6 | −12.1 | −123.0 |
| D | [cAACMe–P]− (S) + [Si(Cl)–NHCMe]+ (S) | −178.3 | 230.7 | −224.2 | −12.1 | −172.7 | |
| D | [cAACMe–P]+ (S) + [Si(Cl)–NHCMe]− (S) | −223.8 | 230.2 | −209.7 | −12.1 | 232.2 | |
| cAAC–P–Si(Cl)–PMe3 | E | cAACMe–P (D) + Si(Cl)–PMe3 (D) | −64.2 | 192.0 | −119.8 | −13.2 | −123.1 |
| D | [cAACMe–P]− (S) + [Si(Cl)–PMe3]+ (S) | −192.7 | 226.5 | −231.0 | −13.2 | −174.9 | |
| D | [cAACMe–P]+ (S) + [Si(Cl)–PMe3]− (S) | −229.8 | 253.3 | −231.1 | −13.2 | −238.7 | |
| cAAC–P–Si(Cl)–aAAC | E | cAACMe–P (D) + Si(Cl)–aAAC (D) | −65.5 | 200.5 | −120.0 | −14.0 | −131.8 |
| D | [cAACMe–P]− (S) + [Si(Cl)–aAAC]+ (S) | −205.4 | 264.7 | −241.6 | −14.0 | −214.8 | |
| D | [cAACMe–P]+ (S) + [Si(Cl)–aAAC]− (S) | −203.8 | 219.4 | −196.4 | −14.0 | −212.6 | |
Further analysis of the best bonding description indicates four pairwise interactions ΔEorb(1)–ΔEorb(4) in all the compounds (Tables 7 and S4†) (Fig. 6–8, S5 and S10–S13†). The strongest interaction ΔEorb(1) (77.5–81.4%) is due to the electron sharing σ interaction of the unpaired electrons in the SOMO of the fragments. The second orbital term, ΔEorb(2) is a π donation from HOMO of cAAC–P into LUMO of Si(Cl/F)–L and contributes 6.3–9.2% to the total orbital interaction. The π contributions are very weak compared to the σ contributions. The remaining two orbital terms, ΔEorb(3) and ΔEorb(4) are from weak σ/π donation and back donations and are slightly different due to the improper molecular planes of the two fragments. In all compounds, the P–Si bond is slightly more covalent in nature rather with significant coulombic or electrostatic interaction. The pairwise interactions of P–Si bond in donor ligand free P–Si(Cl) molecule indicates strong electron sharing σ interaction and two equally contributing, rather strong electron sharing π interactions (Table S18 and Fig. S25†).
| Energy | Interaction | cAAC–P (D) + Si(Cl)–cAAC (D) | cAAC–P (D) + Si(Cl)–NHC (D) | cAAC–P (D) + Si(Cl)–PMe3 (D) | cAAC–P (D) + Si(Cl)–aAAC (D) |
|---|---|---|---|---|---|
| a The values in the parentheses show the contribution to the total attractive interaction ΔEelstat + ΔEorb + ΔEdisp.b The values in parentheses show the contribution to the total orbital interaction ΔEorb. | |||||
| ΔEint | −62.8 | −60.5 | −64.2 | −65.5 | |
| ΔEPauli | 200.6 | 188.1 | 192.0 | 200.5 | |
| ΔEdispa | −13.7 (5.2%) | −12.1 (4.8%) | −13.2 (5.2%) | −14.0 (5.2%) | |
| ΔEelstata | −119.9 (45.5%) | −113.6 (45.7%) | −119.8 (46.7%) | −120.0 (45.2%) | |
| ΔEorba | −129.8 (49.3%) | −122.9 (49.5%) | −123.1 (48.1%) | −131.9 (49.6%) | |
| ΔEorb(1)b | cAACP–Si(Cl)L σ e− sharing | −100.6 (77.5%) | −98.9 (80.4%) | −99.3 (80.6%) | −100.6 (76.2%) |
| ΔEorb(2)b | cAACP→Si(Cl)L π donation | −11.1 (8.5%) | −7.8 (6.3%) | −7.8 (6.3%) | −10.3 (7.8%) |
| ΔEorb(3)b | cAACP→Si(Cl)L π donation | −4.6 (3.5%) | −10.8 (8.2%) | ||
| cAACP←Si(Cl)L σ back donation | −7.4 (6.0%) | −6.8 (5.5%) | |||
| ΔEorb(4)b | cAACP→Si(Cl)L σ donation | −8.8 (6.7%) | −3.9 (3.8%) | −4.0 (3.2%) | −5.0 (3.8%) |
| ΔEorb(rest)b | −4.7 (3.6%) | −4.9 (4.0%) | −5.2 (4.2%) | −5.2 (3.9%) | |
We have modelled and optimized the geometries of compounds, L–PSi(X) and L–Si(X)P (L = cAACMe, NHCMe, PMe3, aAAC) (X = Cl, F) to shade light on the effect of single donor ligand on P and Si atoms in bonding and stabilization of such species. The singlet states of all the compounds are found to be lower in energy than the corresponding triplet states by 30.16 to 36.53 kcal mol−1 in case of L–PSi(X) and 8.16 to 21.0 kcal mol−1 in case of L–Si(X)P [L = cAACMe, NHCMe, PMe3, aAAC; X = Cl, F]. The higher singlet–triplet energy gap (ΔES–T) indicates higher stability of L–PSi(X) compared to L–Si(X)P. The optimized geometries of P-bonded L–PSi(X) compounds (Fig. S15†) show that the chlorine atom is oriented cis to the cAAC ligand in cAAC–PSi(Cl), whereas the fluorine atom is trans to the cAAC ligand in cAAC–PSi(F). The shift in halogen orientation is supported by the change in C–P–Si–X (X = Cl/F) torsion angle from 2.2° (cAAC–PSi(Cl)) to 3.4° (cAAC–PSi(F)) and can lead to a difference in L–P bonding in these compounds. Similar situation is observed in compounds with L = aAAC. The replacement of chlorine with fluorine caused in large shift in C–P–Si–X (X = Cl/F) torsion angle from 177.1° in aAAC–PSi(Cl) to 5.2° in aAAC–PSi(F). The C–P–Si–X (X = Cl/F) torsion angle of 0.0° in L–PSi(X) with L = NHCMe, PMe3 shows that the halogen atom is in the same plane of the ligand. The optimised structures of the Si bonded compounds L–Si(X)P are shown in Fig. S16.† The optimized geometries indicate that the Si(X)P unit is almost perpendicular to the ligand in all compounds with L = cAACMe, NHCMe, PMe3, aAAC (X = Cl, F). The acute C–Si–P bond angle of 66.8° indicates a C–Si–P semi-bridging possibility. The L–Si bond lengths in compounds L–Si(X)P are slightly longer compared to the L–Si bond lengths in cAAC–PSi(X)–L with L = cAACMe, aAAC and are slightly shorter in case of L–Si(X) with L = NHCMe, PMe3.
The dissociation energies, De of L–P/Si bonds in L–PSi(X) and L–Si(X)P compounds were calculated at BP86-D3(BJ)/Def2-TZVPP level to understand the thermodynamic stability of these species. The comparison of results in Tables S5 and S6† show higher dissociation energy for L–P bonds (52–78 kcal mol−1) than L–Si bonds (35–69 kcal mol−1). The endergonicity of dissociation in L–PSi(X) (ΔG298 = 42–68 kcal mol−1) is also higher than that of L–Si(X)P (ΔG298 = 27–59 kcal mol−1). The results indicate a higher thermodynamic stability of the P-bonded species L–PSi(X) compared to the Si-bonded species L–Si(X)P. The low HOMO–LUMO energy gap (ΔH–L) of L–Si(X)P compounds (Tables S5 and S6†) can be correlated with their low singlet–triplet energy gaps (ΔES–T) indicating that such speces are electronically less stable and more reactive compared to L–PSi(X) and cAAC–PSi(X)–L compounds (L = cAACMe, NHCMe, PMe3, aAAC) (X = Cl, F).
The NBO analysis of L–PSi(X) and L–Si(X)P molecules (L = cAACMe, NHCMe, PMe3, aAAC) (X = Cl, F) shows the Wiberg bond indices (WBI) in the range of 1.1–1.34 for L–P bond and 1.22–1.42 for P–Si bond in L–PSi(X), indicating the double bond character for L–P and P–Si bonds, respectively (Tables S7–S10†). Whereas, in L–Si(X)P compounds the WBI values for L–Si and P–Si bonds are found in the range of 0.72 to 0.89 and 1.69–2.42, respectively indicating a single bond character for the L–Si bond and a weak triple bond character for the P–Si bond. The WBI values indicate higher bond order for the P–Si bond in L–Si(X)P when compared to that in L–PSi(X) and cAAC–PSi(X)–L molecules.
To understand the effect of ligand on the L–P and L–Si bonding, we have performed EDA-NOCV calculations on L–PSi(X) and P(X)Si–L (L = cAACMe, NHCMe, PMe3, aAAC; X = Cl, F). The calculations revealed (Tables S11–S14†) that except for cAAC–PSi(Cl) and aAAC–PSi(Cl), the nature of L–P bond is predominantly dative in nature. While, the L–P bond in cAAC–PSi(Cl) and aAAC–PSi(Cl) is a mixture of both dative and electron sharing in nature with electron sharing σ bond and dative π backdonation from cAAC←P. The L–P bond in fluorine substituted counterparts of L–PSi(X) molecules is found to be dative in nature, irrespective of the ligand field. Whereas, the L–Si bond in all P(X)Si–L compounds, except P(Cl)Si–aAAC is found to be dative in nature. The L–Si bond in P(Cl)Si–aAAC is found to be electron sharing covalent in nature. The instantaneous interaction energy (ΔEint) of L–P bonds are higher compared to L–Si bond, but lower than that of the hetero ligand-stabilized cAAC–PSi(X)–L molecules. This indicates that the L–P bonds are stronger compared to the L–Si bonds of P(X)Si–L but weaker than that in cAAC–PSi(X)–L. The pairwise interactions (Fig. S17–S24†) of L–PSi(X) and P(X)Si–L (Tables S15 and S16†) show higher σ contribution (69.3–75.3%) and comparatively weak π contribution (8.5–20%). The π contribution of NHC and PMe3 substituted species is less compared to cAAC substituted species. This can be attributed to the poor π accepting ability of NHC and PMe3 ligands. The previous synthetic reports on NHC and cAAC stabilized Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P–Ar (D–E)5,6 [Ar = Mes* or Tip] having bulky aryl group on P-atom, suggest the importance of steric bulk of the Ar-group to prevent the Si
P–Ar (D–E)5,6 [Ar = Mes* or Tip] having bulky aryl group on P-atom, suggest the importance of steric bulk of the Ar-group to prevent the Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P bond from further reacting with each other. The electronic and steric effects of the ligands are required in n-Cl/n-F compounds.
P bond from further reacting with each other. The electronic and steric effects of the ligands are required in n-Cl/n-F compounds.
Conclusion
In conclusion, the quantum chemical calculations on four cAAC–PSi(Cl)–L (1-Cl to 4-Cl) and four cAAC–PSi(F)–L compounds (1-F to 4-F) with L = cAACMe (1-Cl, 1-F), NHCMe (2-Cl, 2-F), PMe3 (2-Cl, 2-F) and aAAC (4-Cl, 4-F) shows significant increase in C–P–Si–C torsion angle on changing the substitution on Si from chlorine (14.7° in 2-Cl) to fluorine (29.2° in 2-F) in cAAC–PSi(Cl/F)–NHC compounds. The EDA-NOCV calculations predict the best bonding scenario of cAAC–PSi(Cl)–L bonds in 1-Cl, 4-Cl and 1-F as both electron sharing and dative with singly charged interacting fragments [(cAAC)L]+ and [P–Si(Cl)]− (Scheme 2; (4)). In 3-Cl and 3-F, the best bonding as σ and π electron sharing bonds and other σ and π dative bonds from the interaction of neutral [(cAAC)L] and P–Si(Cl/F) fragments in triplet electronic state (Scheme 2; (2)). While, in 2-Cl the best bonding can be described with singly charged interacting fragments [(cAAC)L]+ and [P–Si(Cl)]− forming both electron sharing and dative bonds (Scheme 2; (4)). In contrast, the best bonding of 2-F comes from the interaction of neutral [(cAAC)L] and P–Si(Cl/F) fragments in triplet electronic states, forming σ- and π-electron sharing bonds and other σ- and π-dative bonds (Scheme 2; (2)). The bonding situation in 4-F can be best described with two possibilities (Scheme 2; (4) and (5)); one, in terms of mixture of electron sharing and the other as dative bonds (4), as well as all electron sharing bonds (5). The HOMOs of cAAC/aAAC ligand are significantly higher in energy than those of NHC and PMe3 ligands. This crucial difference makes L-containing (L = cAAC) complexes to possess different bonding in compounds 1-Cl, 4-Cl and 1-F, 4-F compared to other compounds. The P–Si bonding in all compounds can be best described by the interaction of neutral cAAC-P and Si(Cl/F)–L fragments in doublet state, forming electron sharing and dative bonds. The quantum chemical calculations and bonding analysis reveals that the single ligand-stabilized species, like L–PSi(Cl/F) and L–Si(Cl/F)P are less stable and reactive, hence, difficult to isolate. Finally, it can be stated that the reasonably high endergonic nature of dissociation, high singlet–triplet energy gaps and high HOMO–LUMO energy gaps supports the synthetic viability of hetero ligand-stabilized illusive PSi(Cl/F) species. The steric crowding of the ligands is also required to have the synthetic success of this class of molecules.Conflicts of interest
Authors do not have any conflict of interest.Acknowledgements
We thank Prof. Gernot Frenking for providing computational facilities. S. M. also thank Dr S. Pan. K. C. M. thanks Prof. K. M. S. for providing QTAIM facility. S. M. and M. F. thank CSIR for their respective SRF and JRF. K. C. M. and S. R. thank SERB for their respective ECR grants (ECR/2016/000890 for KCM; ECR/2016/000733 for SR).References
- R. Graf, Chlorosulfonyl Isocyanate, Org. Synth., 1966, 46, 23 CrossRef CAS.
- J. E. Huheey, E. A. Keiter and R. L. Keiter, Inorganic Chemistry: Principles of Structure and Reactivity, Pearson Education Asia, 4th edn, 1999, ch. 2, pp. 10–45 Search PubMed.
- V. Nesterov, N. C. Breit and S. Inoue, Advances in Phosphasilene Chemistry, Chem.–Eur. J., 2017, 23, 12014 CrossRef CAS.
- G. Becker, G. Gresser and W. Uhl, Acyl-und Alkylidenphosphane, XV 2.2-Dimethylpropylidinphosphan, eine stabile Verbindung mit einem Phosphoratom der Koordinationszahl 1/Acyl- and Alkylidenephosphines, XV 2,2-Dimethylpropvlidynephosphine, a Stable Compound with a Phosphorus Atom of Coordination Number 1, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1981, 36, 16 Search PubMed.
- D. Geiß, M. I. Arz, M. Straßmann, G. Schnakenburg and A. C. Filippou, Si=P Double Bonds: Experimental and Theoretical Study of an NHC-Stabilized Phosphasilenylidene, Angew. Chem., Int. Ed., 2015, 54, 2739 CrossRef.
- S. Roy, B. Dittrich, T. Mondal, D. Koley, A. C. Stückl, B. Schwederski, W. Kaim, M. John, S. K. Vasa, R. Linser and H. W. Roesky, Carbene Supported Dimer of Heavier Ketenimine Analogue with P and Si Atoms, J. Am. Chem. Soc., 2015, 137, 6180 CrossRef CAS.
- R. Pietschnig and A. Orthaber, Towards Heteronuclear Triple Bonds Involving Silicon or Germanium, Phosphorus, Sulfur Silicon Relat. Elem., 2011, 186, 1361 CrossRef CAS.
- (a) C.-H. Chen and M.-D. Su, Theoretical Design of Silicon–Phosphorus Triple Bonds: A Density Functional Study, Eur. J. Inorg. Chem., 2008, 1241 CrossRef CAS; (b) C.-H. Lai, M.-D. Su and S.-Y. Chu, Effects of First-Row Substituents on Silicon−Phosphorus Triple Bonds, Inorg. Chem., 2002, 41, 1320 CrossRef CAS; (c) K. J. Dykema, T. N. Truong and M. S. Gordon, Studies of silicon-phosphorus bonding, J. Am. Chem. Soc., 1985, 107, 4535 CrossRef CAS.
- (a) G. Frenking and R. Tonner, Divalent carbon(0) compounds, Pure Appl. Chem., 2009, 81, 597 CAS; (b) D. Himmel, I. Krossing and A. Schnepf, Dative or Not Dative?, Angew. Chem., Int. Ed., 2014, 53, 6047 CrossRef CAS; (c) R. Tonner and G. Frenking, Divalent Carbon(0) Chemistry, Part 2: Protonation and Complexes with Main Group and Transition Metal Lewis Acids, Chem.–Eur. J., 2008, 14, 3273 CrossRef CAS; (d) R. Tonner, G. Heydenrych and G. Frenking, First and Second Proton Affinities of Carbon Bases, ChemPhysChem, 2008, 9, 1474 CrossRef CAS; (e) S. Klein, R. Tonner and G. Frenking, Carbodicarbenes and Related Divalent Carbon(0) Compounds, Chem.–Eur. J., 2010, 16, 10160 CrossRef CAS; (f) C. Esterhuysen and G. Frenking, Distinguishing Carbones from Allenes by Complexation to AuCl, Chem.–Eur. J., 2011, 17, 9944 CrossRef CAS; (g) S. Klein and G. Frenking, Carbodiylides C(ECp*)2 (E=B–Tl): Another Class of Theoretically Predicted Divalent Carbon(0) Compounds, Angew. Chem., Int. Ed., 2010, 49, 7106 CrossRef CAS; (h) C. Esterhuysen and G. Frenking, Complexation behavior of two-coordinated carbon compounds containing fluorenyl ligands, Dalton Trans., 2013, 42, 13349 RSC; (i) O. Kaufhold and F. E. Hahn, Carbodicarbenes: Divalent Carbon(0) Compounds, Angew. Chem., Int. Ed., 2008, 47, 4057 CrossRef CAS; (j) A. K. Phukan and A. K. Guha, Stabilization of cyclic and acyclic carbon(0) compounds by differential coordination of heterocyclic carbenes: a theoretical assessment, Dalton Trans., 2012, 41, 8973 RSC; (k) D. Himmel, I. Krossing and A. Schnepf, Dative Bonds in Main-Group Compounds: A Case for Fewer Arrows!, Angew. Chem., Int. Ed., 2014, 53, 370 CrossRef CAS; (l) G. Frenking, Dative Bonds in Main-Group Compounds: A Case for More Arrows!, Angew. Chem., Int. Ed., 2014, 53, 6040 CrossRef CAS.
- (a) G. Frenking, M. Hermann, D. M. Andrada and N. Holzmann, Donor–acceptor bonding in novel low-coordinated compounds of boron and group-14 atoms C–Sn, Chem. Soc. Rev., 2016, 45, 1129 RSC; (b) Y. Xiong, S. Yao, S. Inoue, J. D. Epping and M. Driess, A Cyclic Silylone (“Siladicarbene”) with an Electron-Rich Silicon(0) Atom, Angew. Chem., Int. Ed., 2013, 52, 7147 CrossRef CAS; (c) G. Frenking, R. Tonner, S. Klein, N. Takagi, T. Shimizu, A. Krapp, K. K. Pandey, P. Parameswaran and P. Parameswaran, New bonding modes of carbon and heavier group 14 atoms Si–Pb, Chem. Soc. Rev., 2014, 43, 5106 RSC; (d) B. Niepçtter, R. Herbst-Irmer, D. Kratzert, P. P. Samuel, K. C. Mondal, H. W. Roesky, P. Jerabek, G. Frenking and D. Stalke, Experimental Charge Density Study of a Silylone, Angew. Chem., Int. Ed., 2014, 53, 2766 CrossRef; (e) Y. Xiong, S. Yao, G. Tan, S. Inoue and M. Driess, A Cyclic Germadicarbene (“Germylone”) from Germyliumylidene, J. Am. Chem. Soc., 2013, 135, 5004 CrossRef CAS; (f) H. Braunschweig, R. D. Dewhurst, K. Hammond, J. Mies, K. Radacki and A. Vargas, Ambient-Temperature Isolation of a Compound with a Boron-Boron Triple Bond, Science, 2012, 336, 1420 CrossRef CAS; (g) A. Sidiropoulos, C. Jones, A. Stasch, S. Klein and G. Frenking, N-Heterocyclic Carbene Stabilized Digermanium(0), Angew. Chem., Int. Ed., 2009, 48, 9701 (Angew. Chem., 2009, 121, 9881) CrossRef CAS; (h) C. Jones, A. Sidiropoulos, N. Holzmann, G. Frenking and A. Stasch, An N-heterocyclic carbene adduct of diatomic :Si=Sn:, Chem. Commun., 2012, 48, 9955 Search PubMed; (i) R. Appel and R. Schçllhorn, Triphenylphosphineazine Ph3P=N−N=PPh3, Angew. Chem., Int. Ed. Engl., 1964, 3, 805 CrossRef; (j) Y. Wang, Y. Xie, P. Wei, R. B. King, H. F. Schaefer III, P. v. R. Schleyer and G. H. Robinson, Carbene-Stabilized Diphosphorus, J. Am. Chem. Soc., 2008, 130, 14970 CrossRef CAS; (k) M. Y. Abraham, Y. Wang, Y. Xie, P. Wei, H. F. Schaefer III, P. v. R. Schleyer and G. H. Robinson, Carbene Stabilization of Diarsenic: From Hypervalency to Allotropy, Chem.–Eur. J., 2010, 16, 432 CrossRef CAS; (l) R. Kinjo, B. Donnadieu and G. Bertrand, Isolation of a Carbene-Stabilized Phosphorus Mononitride and Its Radical Cation (PN+.), Angew. Chem., Int. Ed., 2010, 49, 5930 CrossRef CAS.
- (a) V. Lavallo, Y. Canac, C. Präsang, B. Donnadieu and G. Bertrand, Stable Cyclic (Alkyl)(Amino)Carbenes as Rigid or Flexible, Bulky, Electron-Rich Ligands for Transition-Metal Catalysts: A Quaternary Carbon Atom Makes the Difference, Angew. Chem., Int. Ed., 2005, 44, 5705 CrossRef CAS; (b) D. Martin, M. Melaimi, M. Soleilhavoup and G. Bertrand, A Brief Survey of Our Contribution to Stable Carbene Chemistry, Organometallics, 2011, 30, 5304 CrossRef CAS; (c) O. Back, M. Henry-Ellinger, C. D. Martin, D. Martin and G. Bertrand, 31P NMR Chemical Shifts of Carbene–Phosphinidene Adducts as an Indicator of the π-Accepting Properties of Carbenes, Angew. Chem., Int. Ed., 2013, 52, 2939 CrossRef CAS.
- F. Ramirez, N. B. Desai, B. Hansen and N. McKelvie, Hexaphenylcarbodiphosphorane, (C6H5)3PCP(C6H5), J. Am. Chem. Soc., 1961, 83, 3539 CrossRef CAS.
- R. Tonner, F. Öxler, B. Neumüller, W. Petz and G. Frenking, Carbodiphosphoranes: The Chemistry of Divalent Carbon(0), Angew. Chem., Int. Ed., 2006, 45, 8038 CrossRef CAS.
- (a) N. V. Sidgwick, The Electronic Theory of Valency, Clarendon, Oxford, 1927 Search PubMed; (b) Y. S. Varshavskii, Russ. J. Gen. Chem., 1980, 50, 406 Search PubMed; (c) Y. S. Varshavskii, Attempt to Describe Some Reactions of Organic Molecules Containing the R1R2C group in Terms of Donor-Acceptor Interaction, Zh. Obshch. Khim., 1980, 50, 514 CAS.
- (a) A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS; (b) J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef; (c) S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS; (d) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef; (e) F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC; (f) F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- M. J. Frisch, et al., Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- (a) F. Weinhold and C. Landis, Valency and Bonding, A Natural Bond Orbital Donor – Acceptor Perspective, Cambridge University Press, Cambridge, 2005 Search PubMed; (b) C. R. Landis and F. Weinhold, The NBO View of Chemical Bonding, in The Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik. Wiley, 2014, pp. 91–120 Search PubMed.
- K. B. Wiberg, Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane, Tetrahedron, 1968, 24, 1083 CrossRef CAS.
- E. D. Glendening, C. R. Landis and F. Weinhold, NBO 6.0: Natural bond orbital analysis program, J. Comput. Chem., 2013, 34, 1429 CrossRef CAS.
- T. Ziegler and A. Rauk, On the calculation of bonding energies by the Hartree Fock Slater method, Theor. Chim. Acta, 1977, 46, 1 CrossRef CAS.
- (a) M. Mitoraj and A. Michalak, Donor–Acceptor Properties of Ligands from the Natural Orbitals for Chemical Valence, Organometallics, 2007, 26, 6576 CrossRef CAS; (b) M. Mitoraj and A. Michalak, Applications of natural orbitals for chemical valence in a description of bonding in conjugated molecules, J. Mol. Model., 2008, 14, 681 CrossRef CAS.
- (a) ADF2017, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed; (b) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- (a) E. van Lenthe and E. J. Baerends, Optimized Slater-type basis sets for the elements 1–118, J. Comput. Chem., 2003, 24, 1142 CrossRef CAS; (b) E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic regular two-component Hamiltonians, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS; (c) E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic total energy using regular approximations, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS.
- (a) G. Frenking and F. M. Bickelhaupt, The Chemical Bond 1. Fundamental Aspects of Chemical Bonding, Wiley-VCH, Weinheim, 2014, ch. The EDA Perspective of Chemical Bonding, vol. 121 CrossRef; (b) L. M. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 1345 Search PubMed; (c) L. Zhao, M. Hermann, W. H. E. Schwarz and G. Frenking, The Lewis electron-pair bonding model: modern energy decomposition analysis, Nat. Rev. Chem., 2019, 3, 48 CrossRef CAS; (d) L. Zhao, S. Pan, N. Holzmann, P. Schwerdtfeger and G. Frenking, Chemical Bonding and Bonding Models of Main-Group Compounds, Chem. Rev., 2019, 119, 8781 CrossRef CAS; (e) J. Andrés, P. W. Ayers, R. A. Boto, R. Carbó-Dorca, H. Chermette, J. Cioslowski, J. Contreras-García, D. L. Cooper, G. Frenking, C. Gatti, F. Heidar-Zadeh, L. Joubert, Á. Martín Pendás, E. Matito, I. Mayer, A. J. Misquitta, Y. Mo, J. Pilmé, P. L. A. Popelier, M. Rahm, E. Ramos-Cordoba, P. Salvador, W. H. E. Schwarz, S. Shahbazian, B. Silvi, M. Solà, K. Szalewicz, V. Tognetti, F. Weinhold and É. L. Zins, Nine questions on energy decomposition analysis, J. Comput. Chem., 2019, 40, 2248 CrossRef; (f) W. Yang, K. E. Krantz, L. A. Freeman, D. Dickie, A. Molino, G. Frenking, S. Pan, D. J. D. Wilson and R. J. Gilliard, Jr, Persistent Borafluorene Radicals, Angew. Chem., Int. Ed., 2020, 59, 3850–3854 CrossRef CAS; (g) G. Deng, S. Pan, G. Wang, L. Zhao, M. Zhou and G. Frenking, Side-On Bonded Beryllium Dinitrogen Complexes, Angew. Chem., Int. Ed., 2020, 59, 10603 CrossRef CAS; (h) S. Pan and G. Frenking, Comment on “Realization of Lewis Basic Sodium Anion in the NaBH3−Cluster”, Angew. Chem., Int. Ed., 2020, 59, 8756 CrossRef CAS; (i) L. Zhao, S. Pan, M. Zhou and G. Frenking, Response to Comment on “Observation of alkaline earth complexes M(CO)8 (M = Ca, Sr, or Ba) that mimic transition metals”, Science, 2019, 365, eaay5021 CrossRef CAS; (j) R. Saha, S. Pan, P. K. Chattaraj and G. Merino, Filling the void: controlled donor–acceptor interaction facilitates the formation of an M–M single bond in the zero oxidation state of M (M = Zn, Cd, Hg), Dalton Trans., 2020, 49, 1056 RSC.
- (a) A. Kulkarni, S. Arumugam, M. Francis, P. G. Reddy, E. Nag, S. M. N. V. T. Gorantla, K. C. Mondal and S. Roy, Solid-State Isolation of Cyclic Alkyl(Amino) Carbene (cAAC)-Supported Structurally Diverse Alkali Metal-Phosphinidenides, Chem.–Eur. J., 2021, 27, 200 CrossRef CAS; (b) S. Roy, K. C. Mondal, S. Kundu, B. Li, C. J. Schürmann, S. Dutta, D. Koley, R. Herbst-Irmer, D. Stalke and H. W. Roesky, Two Structurally Characterized Conformational Isomers with Different C−P Bonds, Chem.–Eur. J., 2017, 23, 12153 CrossRef CAS; (c) S. Kundu, S. Sinhababu, A. V. Luebben, T. Mondal, D. Koley, B. Dittrich and H. W. Roesky, Reagent for Introducing Base-Stabilized Phosphorus Atoms into Organic and Inorganic Compounds, J. Am. Chem. Soc., 2018, 140, 151 CrossRef CAS.
- S. Kundu, S. Sinhababu, M. M. Siddiqui, A. V. Luebben, B. Dittrich, T. Yang, G. Frenking and H. W. Roesky, Comparison of Two Phosphinidenes Binding to Silicon(IV)dichloride as well as to Silylene, J. Am. Chem. Soc., 2018, 140, 9409 CrossRef CAS.
- K. C. Mondal, H. W. Roesky, B. Dittrich, N. Holzmann, M. Hermann, G. Frenking and A. Meents, Formation of a 1,4-Diamino-2,3-disila-1,3-butadiene Derivative, J. Am. Chem. Soc., 2013, 135, 15990 CrossRef CAS.
- R. S. Ghadwal, H. W. Roesky, S. Merkel, J. Henn and D. Stalke, Lewis Base Stabilized Dichlorosilylene, Angew. Chem., Int. Ed., 2009, 48, 5683 CrossRef CAS.
- Y. Wang, Y. Xie, P. Wei, R. B. King, H. F. Schaefer III, P. v. R. Schleyer and G. H. Robinson, A Stable Silicon(0) Compound with a Si=Si Double Bond, Science, 2008, 321, 1069 CrossRef CAS.
- S. Roy, P. Stollberg, R. Herbst-Irmer, D. Stalke, D. M. Andrada, G. Frenking and H. W. Roesky, Carbene-Dichlorosilylene Stabilized Phosphinidenes Exhibiting Strong Intramolecular Charge Transfer Transition, J. Am. Chem. Soc., 2015, 137, 150 CrossRef CAS.
- S. Kundu, B. Li, J. Kretsch, R. Herbst-Irmer, D. M. Andrada, G. Frenking, D. Stalke and H. W. Roesky, An Electrophilic Carbene-Anchored Silylene-Phosphinidene, Angew. Chem., Int. Ed., 2017, 56, 4219 CrossRef CAS.
- (a) Q. Zhang, W.-L. Li, C. Xu, M. Chen, M. Zhou, J. Li, D. M. Andrada and G. Frenking, Formation and Characterization of the Boron Dicarbonyl Complex [B(CO)2]−, Angew. Chem., Int. Ed., 2015, 54, 11078 CrossRef CAS; (b) D. M. Andrada and G. Frenking, Stabilization of Heterodiatomic SiC Through Ligand Donation: Theoretical Investigation of SiC(L)2 (L=NHCMe, CAACMe, PMe3), Angew. Chem., Int. Ed., 2015, 54, 12319 CrossRef CAS; (c) C. Mohapatra, S. Kundu, A. N. Paesch, R. Herbst-Irmer, D. Stalke, D. M. Andrada, G. Frenking and H. W. Roesky, The Structure of the Carbene Stabilized Si2H2 May Be Equally Well Described with Coordinate Bonds as with Classical Double Bonds, J. Am. Chem. Soc., 2016, 138, 10429 CrossRef CAS; (d) L. T. Scharf, M. Andrada, G. Frenking and V. H. Gessner, The Bonding Situation in Metalated Ylides, Chem.–Eur. J., 2017, 23, 4422 CrossRef CAS; (e) M. Hermann and G. Frenking, Carbones as Ligands in Novel Main-Group Compounds E[C(NHC)2]2 (E=Be, B+, C2+, N3+, Mg, Al+, Si2+, P3+): A Theoretical Study, Chem.–Eur. J., 2017, 23, 3347 CrossRef CAS; (f) D. C. Georgiou, L. Zhao, D. J. D. Wilson, G. Frenking and J. L. Dutton, NHC-Stabilised Acetylene—How Far Can the Analogy Be Pushed?, Chem.–Eur. J., 2017, 23, 2926 CrossRef CAS; (g) Z. Wu, J. Xu, L. Sokolenko, Y. L. Yagupolskii, R. Feng, Q. Liu, Y. Lu, L. Zhao, I. Fernández, G. Frenking, T. Trabelsi, J. S. Francisco and X. Zeng, Parent Thioketene S-Oxide H2CCSO: Gas-Phase Generation, Structure, and Bonding Analysis, Chem.–Eur. J., 2017, 23, 16566 CrossRef CAS; (h) W. Petz, D. M. Andrada, M. Hermann, G. Frenking and B. Neumüller, A C2 Fragment as Four-Electron σ Donor, Z. Anorg. Allg. Chem., 2017, 643, 1096 CrossRef CAS; (i) D. M. Andrada, J. L. Casalz-Sainz, A. M. Pendás and G. Frenking, Dative and Electron-Sharing Bonding in C2F4, Chem.–Eur. J., 2018, 24, 9083 CrossRef CAS; (j) R. Saha, S. Pan, G. Merino and P. K. Chattaraj, Unprecedented Bonding Situation in Viable E2(NHBMe)2 (E=Be, Mg; NHBMe=(HCNMe)2B) Complexes: Neutral E2 Forms a Single E−E Covalent Bond, Angew. Chem., Int. Ed., 2019, 58, 8372 CrossRef CAS; (k) Q. Wang, S. Pan, Y. Wu, G. Deng, G. Wang, L. Zhao, M. Zhou and G. Frenking, Transition-Metal Chemistry of Alkaline-Earth Elements: The Trisbenzene Complexes M(Bz)3 (M=Sr, Ba), Angew. Chem., Int. Ed., 2019, 58, 17365 CrossRef CAS; (l) T. Yang, D. M. Andrada and G. Frenking, Dative versus electron-sharing bonding in N-imides and phosphane imides R3ENX and relative energies of the R2EN(X)R isomers (E = N, P; R = H, Cl, Me, Ph; X = H, F, Cl), Mol. Phys., 2019, 117, 1306 CrossRef CAS; (m) S. M. N. V. T. Gorantla, S. Pan, K. C. Mondal and G. Frenking, Stabilization of Linear C3 by Two Donor Ligands: A Theoretical Study of L-C3-L (L=PPh3, NHCMe, cAACMe), Chem.–Eur. J., 2020, 26, 14211 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra10338a |
| This journal is © The Royal Society of Chemistry 2021 |