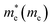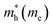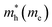Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
In-depth first-principle study on novel MoS2 polymorphs†
Håkon Eidsvåg *a,
Murugesan Rasukkannua,
Dhayalan Velauthapillaia and
Ponniah Vajeestonb
*a,
Murugesan Rasukkannua,
Dhayalan Velauthapillaia and
Ponniah Vajeestonb
aDepartment of Computing, Mathematics and Physics, Western Norway University of Applied Sciences, Inndalsveien 28, Box 5063, Bergen, Norway. E-mail: heid@hvl.no
bCenter for Materials Science and Nanotechnology, Department of Chemistry, University of Oslo, Box 1033 Blindern N-0315, Oslo, Norway
First published on 19th January 2021
Abstract
Molybdenum disulphide (MoS2) is a rising star among transition-metal dichalcogenides in photovoltaics, diodes, electronic circuits, transistors and as a photocatalyst for hydrogen evolution. A wide range of MoS2 polymorphs with varying electrical, optical and catalytic properties is of interest. However, in-depth studies on the structural stability of the various MoS2 polymorphs are still lacking. For the very first time, 14 different MoS2 polymorphs are proposed in this study and in-depth analysis of these polymorphs are carried out by employing first-principle calculations based on density functional theory (DFT). In order to investigate the feasibility of these polymorphs for practical applications, we employ wide range of analytical methods including band structure, phonon and elastic constant calculations. Three of the polymorphs were shown to be unstable based on the energy volume calculations. Among the remaining eleven polymorphs (1T1, 1T2, 1H, 2T, 2H, 2R1, 2R2, 3Ha, 3Hb, 3R and 4T), we confirm that the 1T1, 1T2, 2R2 and 3R polymorphs are not dynamically stable based on phonon calculations. Recent research suggests that stabilising dopants (e.g. Li) are needed if 1T polymorphs to be synthesised. Our study further shows that the remaining seven polymorphs are both dynamically and mechanically stable, which make them interesting candidates for optoelectronics applications. Due to high electron mobility and a bandgap of 1.95 eV, one of the MoS2 polymorphs (3Hb-MoS2) is proposed to be the most promising candidate for these applications.
Introduction
Recent research has established transition-metal dichalcogenides (TMDs) as a promising material within several fields.1 This is due to their unique optical, electronic and structural properties, which are dependent on the layered structure of the TMDs.2–4 Molybdenum disulphide (MoS2) is perhaps the most well-known TMD with an indirect electronic bandgap of 1.2 eV (experimental value for bulk MoS2),5 which is surprising as it has a graphene-like polymorph. This is mainly because the electronic properties for TMDs are based on filling the d orbitals, in contrast to graphene and silicon where it is the hybridization of s and p orbitals that lays the foundation for the electronic properties.6 In addition to the low bandgap, MoS2 is a low-cost material; it has a high surface-to-volume ratio and an abundance of active sites making it attractive in several fields.7 Currently, MoS2 is known for its properties as a lubricant8 and lately in photovoltaic (PV) cells,9 as a photocatalyst for hydrogen evolution,10 as gas or biosensors11,12 and as a transistor that can operate at room temperature.4 Especially within photocatalytic water splitting MoS2 is seen as the potential successor to TiO2 photocatalysts due to the tuneable bandgaps, its high charge carrier mobility, high transparency and excellent chemical stability.7The MoS2 polymorphs consists of a layer of Mo (transition metal) sandwiched between two layers of S (chalcogens) and strong covalent bonds are present within the sandwich, while the interlayer bonds between two layers are van der Waals bonds.13 Depending on the coordinate configuration MoS2 can exist in different phases including 2H, 3R, 1T, 1T′, 1T′′, etc.14,15 Amongst these, two phases stand out in terms of favourable structural properties: 2H MoS2 is a thermodynamically stable phase with A–B–A sandwich layers that occurs at ambient pressure conditions, this is also the most commonly used phase. 1T is a metastable phase, A–B–C layers, and has not been strictly determined due to a lack of a strict structural refinement. Another important distinction between the two phases is that 1T is metallic while 2H is a semiconductor/insulator.11
An alternative to adding dopants to transform materials from insulators to metals is utilising high pressure during the synthesis. It is well known that bilayer sheets of MoS2 go through a semiconductor–metal transition upon vertical compressive pressure. Early research suggests that bulk MoS2 could metallize under pressure as they found that the bandgap shrinks due to a negative pressure coefficient of resistivity, dEG/dP < 0.16 Unfortunately, the structural transition is unknown, and it requires further research.
Most of the work done on MoS2 by the research community so far is experimental with focus on synthesis, characterization and application of the material as a photocatalyst.7,11,12,17–20 However, over the last years, we have seen a rise in computational work,21 including a pioneering work by Byskov et al.22 As the MoS2 structure can easily be modified by changing the stacking sequence and/or the layer distance, a variety of MoS2 polymorphs could be synthesised. However, a fundamental understanding of how these modifications will affect the structural stability of the material is still lacking. This knowledge is of utmost importance as different configurations have different properties, making them viable for a diverse range of applications. So far, the challenges have been to synthesise MoS2 polymorphs and to identify the stacking sequences. In this study, we propose as many as 14 different MoS2 polymorphs and carry out in-depth theoretical analysis on their properties based on DFT calculations. We verify analytically how the different layers and coordinate configuration of MoS2 affect the stability and electronic properties of the bulk material. For the very first-time, direct comparison between calculated Raman and IR spectra for pure 1T-MoS2 and 2H-MoS2. The main objective of this study is to explore the possible metastable phases of MoS2 and their relative stability.
Method of calculations
All the calculations were performed within the periodic density functional theory framework, as it is implemented in the VASP code.23–27 The interaction between the core (Mo: [Kr] 4d5 5s1, and S: [Ne] 3s2 3p4) and the valence electrons were described using the projector-augmented wave (PAW) method.26,28 In order to speed up our structural optimisation process, the initial structures were optimised with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.27 The obtained PBE level optimised structures were further optimised with the DFT/vdW-DF2 method and based on this, the energy volume curves were generated.29–31 Our previous calculations suggested32 that structural parameters in oxides could be reliably predicted only by using large energy-cut off to guarantee basis-set completeness. Hence, we have used a cut-off of 600 eV. The atoms were deemed to be relaxed when all atomic forces were less than 0.02 eV Å−1 and the geometries were assumed to get optimized when the total energy converged to less than 1 meV between two consecutive geometric optimization steps. The electronic properties were computed by using the screened hybrid functional as proposed by Heyd, Scuseria and Ernzerhof (HSE06) for the polymorphs optimized at the PBE level.33 If not specified differently, we used a Monkhorst–Pack 9 × 9 × 9 k-mesh for the structural optimization and the electronic polymorph studies. Band polymorphs were computed by solving the periodic Kohn–Sham equation on ten k-points along each direction of high symmetry of the irreducible part of the first Brillouin zone.The supercell method is used for phonon calculations.34 The VASP code is used to calculate the real space force constants of supercells, and the PHONOPY35 code is used to calculate the phonon frequencies from the force constants on a supercell consisting of at least 32 atoms in all systems. In order to get the force-constant matrices for each binary system, every atom is displaced by a finite displacement of 0.01 Å in x-, y- and z-direction. Strict energy convergence criteria of (10−8 eV) and 4 × 4 × 4 k-points were used for the force constant calculations. After getting the force-constant matrices, the dynamical matrix is built for different q vectors in the Brillouin zone. The eigenvalues of phonon frequencies and eigenvectors of phonon modes are found by solving the dynamical matrix. The thermodynamic properties require summations over the phonon eigenvectors which is implemented in the PHONOPY code. We have checked the dynamical stability of all systems, and no imaginary modes are observed in the polymorphs. The thermal properties, including heat capacity, free energy and entropy, were obtained from the calculated PhDOS. The phonon band polymorphs figures for all the studied systems have also been added to the ESI under SI3 and SI4.† Our study is then completed by evaluating the mechanical stability by computing the single-crystal elastic constants. A set of strains (−0.015 −0.010 −0.005 0.000 0.005 0.010 0.015) is applied to the crystal cell, and the stress tensor is calculated. The elastic constants are then evaluated by linear fitting of the stress–strain curve using VASPKIT.36
Results and discussion
Structural stability and optimization
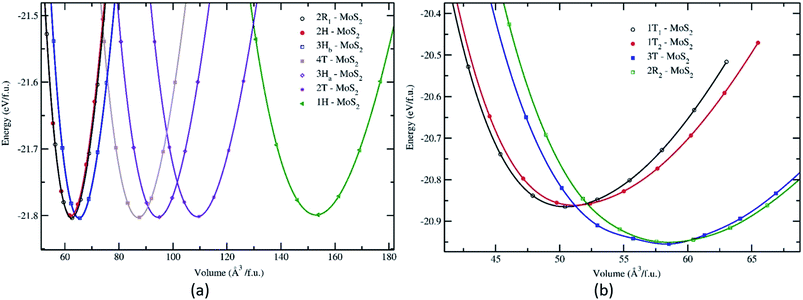
Structurally, MoS2 can be regarded as strongly bonded two-dimensional S–Mo–S layers or sandwiches which are loosely coupled to one another by relatively weak van der Waals-type forces. Within a single S–Mo–S sandwich, the Mo and S atoms create two-dimensional hexagonal arrays. Depending on the relative alignment of the two S-atom sheets within a single S–Mo–S sandwich, two distinct two-dimensional crystal polymorphs are obtained. In one, the metal atoms are octahedrally coordinated by six neighbouring S atoms, whereas in the other, the coordination of the metal atoms is trigonal prismatic. Variations in the stacking sequence and registry of successive S–Mo–S sandwiches along the hexagonal c axis lead to a large number of crystal polymorphs or polytypes in three dimensions. These are referred to as the 1T, 2H, 3R, 4Ha, 4Hb and 6R phases. In this abbreviated notation, the integer indicates the number of S–Mo–S sandwiches per unit cell along the hexagonal c axis and T, H, and R denote trigonal, hexagonal, and rhombohedral symmetries, respectively. Variations in the stacking sequence like A, A′, B, B′, C, C′′, etc. (for more details see Fig. 3) and variation in the layer–layer distances means we can tune these compounds into several modifications. In order to understand the relative stability of these modifications, we have considered the following 14 polymorphs and they have been used as starting inputs in the structural optimization calculations (number of formula units; and Materials Project ID are given in parenthesis; low energy polymorph identified this work is highlighted as bold letters): R3m (1, 1434, 2R1), P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (4, 1027525, 4T), P63/mmc (2, 2815, 2H); P
m1 (4, 1027525, 4T), P63/mmc (2, 2815, 2H); P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 (3, 1025874, 3Ha), P
m2 (3, 1025874, 3Ha), P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (3, 1023939, 2T), P63/mmc (6, 1018809, 3Hb), P
m1 (3, 1023939, 2T), P63/mmc (6, 1018809, 3Hb), P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 (1, 1023924, 1H), Pmmn (18, 990083), F
m2 (1, 1023924, 1H), Pmmn (18, 990083), F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (4, 11780), R
3m (4, 11780), R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (1, 558544, 3T), P
m (1, 558544, 3T), P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (1, 1238797, 2R2), I
m1 (1, 1238797, 2R2), I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d (2, 1042086), P
2d (2, 1042086), P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (1, 1T2) and P
(1, 1T2) and P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (1, 1T1). However, the following polymorphs Pmmn (18, 990083), F
m1 (1, 1T1). However, the following polymorphs Pmmn (18, 990083), F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (4, 11780) and I
3m (4, 11780) and I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d (2, 1042086) are omitted from the rest of the analysis. This is because their energy-volume data are far away from the others as presented in Fig. 1, they are also unstable compared to the other polymorphs.
2d (2, 1042086) are omitted from the rest of the analysis. This is because their energy-volume data are far away from the others as presented in Fig. 1, they are also unstable compared to the other polymorphs.
The structural stability of the several different phases of MoS2 has been studied to find the most stable phase and polymorph for further investigation and research. Our first step was to perform a total energy calculation as a function of volume for all the phases. Based on this calculation we divided the phases into two different groups (according to the energetics), group A and group B. The polymorphs in group A, shown in Fig. 1a, are (space group and space group number are given in the parenthesis): 2R1-MoS2 (P3m1; 156), 2H-MoS2 (P63/mmc; 194), 3Hb-MoS2 (P63/mmc; 194), 4T-MoS2 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1; 164), 3Ha-MoS2 (P
m1; 164), 3Ha-MoS2 (P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2; 187), 2T-MoS2 (P
m2; 187), 2T-MoS2 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1; 164), and 1H-MoS2 (P
m1; 164), and 1H-MoS2 (P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2; 187). In group B, as shown in Fig. 1b, we have placed the following polymorph models: 1T1-MoS2 (P
m2; 187). In group B, as shown in Fig. 1b, we have placed the following polymorph models: 1T1-MoS2 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ; 164), 1T2-MoS2 (P
; 164), 1T2-MoS2 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1; 164), 3T-MoS2 (R
m1; 164), 3T-MoS2 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m; 166) and 2R2-MoS2 (P
m; 166) and 2R2-MoS2 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1; 164). It should be noted that the 2H and 3R variants the Mo–S coordination is trigonal prismatic and the layers stacking sequence are significantly different (see Fig. 2).37 On the other hand, the 1T variants consist of MoS2 layers with almost perfectly ordered MoS6 octahedra.37
m1; 164). It should be noted that the 2H and 3R variants the Mo–S coordination is trigonal prismatic and the layers stacking sequence are significantly different (see Fig. 2).37 On the other hand, the 1T variants consist of MoS2 layers with almost perfectly ordered MoS6 octahedra.37
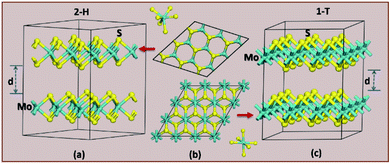 | ||
| Fig. 2 The difference in crystal structure for 2H (a) and 1T (c) MoS2 polymorphs. (b) Shows a top-down look on the hexagonal polymorph of 2H (top) and 1T (bottom). | ||
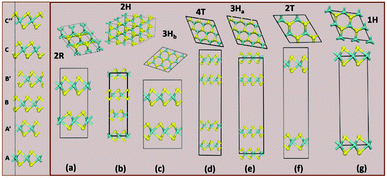 | ||
| Fig. 3 The column on the left shows the various stacking sequences (A, A′, B, B′, C, C′′) for MoS2. On the right side, we see how the group A polymorphs are stacked. | ||
As shown in Fig. 1, the total energy curves clearly show that group A is energetically favoured over group B with an energy difference of 0.8 eV. In general, we see that our first principle calculations coincide well with experimental results.38–41 Interestingly, we observe in Fig. 1a that the various polymorphs in group A seem to have the same minimum energy, although with a varying range of volume. Which indicates that MoS2 can easily be found in any of these variants. The calculated positional and lattice constants of different polymorphs are presented in Table 1. From the space group numbers and names, we see that all group B polymorphs and three of the group A polymorphs are trigonal, while the last four group A polymorphs are hexagonal. From Fig. 1 it is clear that the hexagonal polymorphs have a wider spread in volume than the trigonal polymorphs. However, the involved energy difference in group A is small, and it is hard to conclude whether trigonal or hexagonal polymorphs are more energetically favourable. Regarding the group B polymorphs, three of them are trigonal crystal systems and of them 3T-MoS2 has the lowest energy. Another point of interest is how the volume affects the energy of the unit cell. For group A there is little difference between the energies and all the polymorphs could be synthesised (based on Fig. 1). However, for group B it appears that the two larger polymorphs (with regards to volume) are more energy favourable compared to the smaller ones.
Nonetheless, Fig. 1 only gives an indication of which polymorphs MoS2 prefers to be in, which is why we calculated the elasticity constants and phonon densities.
| Polymorph | Cell constants (Å) | Coordinates |
|---|---|---|
| 2R1-MoS2 (P3m1; 156) | a = 3.1887, b = 3.1887, c = 21.3444 | Mo1 (1a): 0, 0, 0 |
| Mo2 (1a): 2/3, 1/3, 1/3 | ||
| Mo3 (1a): 1/3, 2/3, 2/3 | ||
| S1 (1a): 0, 0, 0.5928 | ||
| S2 (1a): 2/3, 1/3, 0.9271 | ||
| S3 (1a): 1/3, 2/3, 0.2604 | ||
| S4 (1a): 0, 0, 0.7400 | ||
| S5 (1a): 2/3, 1/3, 0.0733 | ||
| S6 (1a): 1/3, 2/3, 0.4067 | ||
2T-MoS2 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1; 164) m1; 164) |
a = 3.1891, b = 3.1891, c = 24.8987 | Mo (2d): 1/3, 2/3, 0.8505 |
| S1 (2d): 1/3, 2/3, 0.2122 | ||
| S2 (2d): 1/3, 2/3, 0.0868 | ||
4T-MoS2 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1; 164) m1; 164) |
a = 3.1889, b = 3.1889, c = 39.7944 | Mo1 (2d): 1/3, 2/3, 0.0936 |
| Mo2 (2d): 1/3, 2/3, 0.7193 | ||
| S1 (2d): 1/3, 2/3, 0.3199 | ||
| S2 (2d): 1/3, 2/3, 0.9457 | ||
| S3 (2d): 1/3, 2/3, 0.2414 | ||
| S4 (2d): 1/3, 2/3, 0.8672 | ||
1H-MoS2 (P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2; 187) m2; 187) |
a = 3.1881, b = 3.1881, c = 17.4639 | Mo (1a): 0, 0, 0 |
| S (2h): 1/3, 2/3, 0.0894 | ||
3Ha-MoS2 (P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2; 187) m2; 187) |
a = 3.1890, b = 3.1890, c = 32.3461 | Mo1 (2h): 1/3, 2/3, 0.7698 |
| Mo2 (1e): 2/3, 1/3, 0 | ||
| S1 (2h): 1/3, 2/3, 0.0483 | ||
| S2 (2i): 2/3, 1/3, 0.2785 | ||
| S3 (2i): 2/3, 1/3, 0.8181 | ||
| 3Hb-MoS2 (P63/mmc; 194) | a = 3.1890, b = 3.1890, c = 14.8916 | Mo (2d): 2/3, 1/3, 1/4 |
| S (4f): 2/3, 1/3, 0.8549 | ||
| 2H-MoS2 (P63/mmc; 194) | a = 3.1779, b = 3.1779, c = 14.1156 | Mo (2b): 0, 0, 1/4 |
| S (4f): 2/3, 1/3, 0.3608 | ||
2R2-MoS2 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1; 164) m1; 164) |
a = 3.1798, b = 3.1798, c = 6.5738 | Mo (1b): 0, 0, 1/2 |
| S (2d): 2/3, 1/3, 0.2575 | ||
3T-MoS2 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m; 166) m; 166) |
a = 3.2060, b = 3.2060, c = 19.7232 | Mo (3a): 1/3, 2/3, 2/3 |
| S (6c): 0, 0, 0.2534 | ||
1T1-MoS2 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ; 164) ; 164) |
a = 3.1900, b = 3.1900, c = 5.9450 | Mo (1a): 0, 0, 0 |
| S (2d): 1/3, 2/3, 0.2488 | ||
1T2-MoS2 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1; 164) m1; 164) |
a = 3.1900, b = 3.1900, c = 5.9450 | Mo (1a): 0, 0, 0 |
| S (2d): 1/3, 2/3, 0.2488 |
Band structure
In order to verify which of these polymorphs are viable for e.g. photocatalytic processes, photovoltaic cells or in transistors we carry out in depth electronic calculations. Materials with semiconducting properties could be used to absorb visible light, while metals could be used as conductors. Our HSE06 bandgap calculations, presented in Fig. 4, clearly states that the group B polymorphs are metallic, which is in line with previous findings.42 However, the polymorphs in group A are semiconductors with indirect bandgaps as the valence band is at the Γ point, while the conduction band minimum is although accurate in its band polymorph description, underestimates the bandgap value. GGA calculations are less accurate than HSE06 (ref. 43 and 44) but they are cheaper in computing time, making them excellent for first-time investigations and gives an idea about the bandgap configuration. This is confirmed when the GGA results are compared to the HSE06 calculations, which are also presented in Table 2. Our HSE06 results coincide well with the experimentally found bandgaps for MoS2 which are within the range of 1.2–1.9 eV.7 The valence bands and conduction bands for the polymorphs in both groups are derived from Mo-d and S-p states.21 This shows that the group A MoS2 is well suited for photovoltaic solar cell and photocatalytic water splitting applications.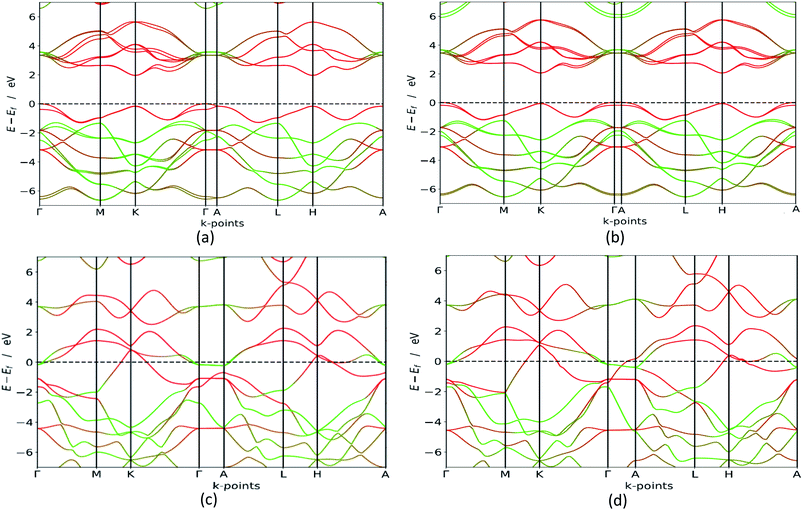 | ||
| Fig. 4 HSE06 band structure (colour code: green line – S, red line – Mo) for 3Hb in (a), 1H in (b), 2R2 in (c) and 1T1 in (d). We see that the group A polymorphs are semiconductors with a bandgap between 1.8 and 2.1 eV, while the group B polymorphs are metallic. The other polymorphs are seen in the ESI.† | ||
| Name | GGA band gap (eV) | HSE06 band gap (eV) | The effective mass of electrons in K–Γ directions | Effective mass of holes in K–Γ direction | Effective mass of hole in Γ–A and Γ–M directions | Type of bandgap |
|---|---|---|---|---|---|---|
| 2R1-MoS2 | 1.41 | 1.87 | 0.50 | 0.57 | 0.92 (Γ–A) | Indirect |
| 2H-MoS2 | 1.42 | 1.94 | 0.51 | 0.55 | 0.86 (Γ–A) | Indirect |
| 3Hb-MoS2 | 1.45 | 1.95 | 0.22 | 0.03 | 1.01 (Γ–A) | Indirect |
| 4T-MoS2 | 1.48 | 1.96 | 0.48 | 0.56 | 1.82 (Γ–M) | Indirect |
| 3Ha-MoS2 | 1.50 | 1.98 | 0.47 | 0.56 | 1.89 (Γ–M) | Indirect |
| 2T-MoS2 | 1.54 | 2.04 | 0.47 | 0.56 | 2.32 (Γ–M) | Indirect |
| 1H-MoS2 | 1.64 | 2.12 | 0.47 | 0.56 | 2.96 (Γ–M) | Indirect |
| MoS2 (ref. 48) | 1.58 (LDA) | 2.48 (G0W0) | 0.55 | 0.53 | NA | NA |
The electron effective mass is an indication of the mass of the structure/particle when it responds to forces. It can be used to calculate electron mobility and diffusion constants. We used Fonari and Sutton's effective mass calculator for our calculations.45 The higher curvature of the conduction band minimum compared to the valence band minimum indicates a higher hole effective mass than the electron effective mass. This indicates that MoS2 has higher electron mobility, compared to the hole mobility, due to the lower electron effective mass.
We calculated the effective masses for the semiconductor (group A) polymorphs to confirm the findings in the band structures. In general, the effective masses of electrons and holes are relevant for the mobility, electrical resistivity, quantum confinement,46,47 and free-carrier optical response in semiconductor materials. For the first time, effective masses are presented for seven different polymorphs of MoS2 and are shown in Table 2. We have compared them to a 2H-MoS2 polymorph from Rasmussen et al. to get an indication of how our polymorphs measure up against previously studied polymorphs, and we see that our values are lower for electrons.48 This is due to the different approximations (G0W0) used in the calculations.
For photocatalytic processes, the transfer of carriers to the reactive sites is easier with smaller effective masses.49 Compared to 2H-TiO2 (1.4me and 5mh)48 and 1T-TiO2 (8.2me and 1.1mh)48 the electron mobility in MoS2 is better than that of TiO2. This combined with a much lower bandgap (3.2 eV for TiO2 (ref. 50)) clearly show that MoS2 is a better photocatalyst than TiO2.
Further research on carrier transport characteristics is needed as the presence of valleys and defects in the polymorph, charge carrier scattering, reduced mean free path and elastic scattering time all influence the carrier mobility in the crystal.
Phonon calculations
In order to understand the dynamical stability of the studied polymorphs we carried out phonon calculations. In addition to the total phonon density of states (PDOS), we calculated the phonon dispersion curves, at the equilibrium volume, along the high symmetry direction of the Brillouin zone for all the polymorphs and these variations are presented in Fig. 5 with their corresponding PDOS. None of the group A polymorphs displays any soft/negative modes, which means that they should be dynamically stable. Whereas the group B polymorphs show the presence of negative modes, making them dynamically unstable. This shows that going from 2H polymorphs to 1T polymorphs creates a less stable polymorph, which is supported by experimental findings.51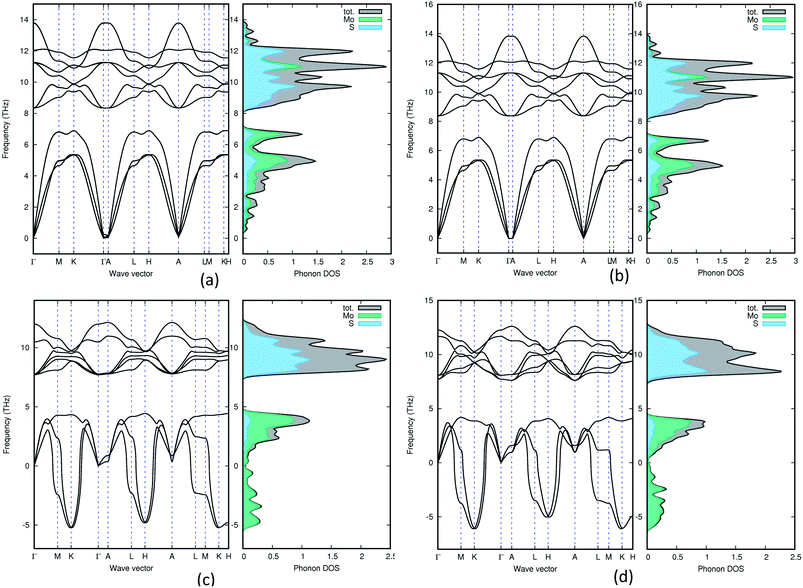 | ||
| Fig. 5 Phonon density of states for 3Hb (a), 1H (b), 2R2 (c) and 1T1 (d). Both group B polymorphs (2R2 and 1T1) contains negative frequencies, which means that they are dynamically unstable. | ||
The total phonon density of states is calculated at the equilibrium volumes for the different polymorphs of MoS2. From Fig. 5 we observe that the two group B polymorphs (all four can be found in SI 4a–d†) contains unstable (imaginary) phonon modes while for the two group A (SI 3a–g† for the remaining polymorphs) polymorphs we only have stable (real) modes. These findings indicate that the group A polymorphs are dynamically stable, while the group B polymorphs are dynamically unstable. All group A polymorphs have a similar PDOS, this combined with the low energy difference between phases indicates that one can easily modify one polymorph into another using temperature or pressure. This explains why depending on different synthesis routes it is possible to stabilise different MoS2 polymorphs.7 Not surprisingly we find that 1T2-MoS2 and 1T1-MoS2 have very similar wave vectors, PDOS and partial PDOS, as they are both trigonal and share the same lattice parameters (see Table 1) although they are in different space groups. Comparing 3T-MoS2 to 2R2-MoS2 there is a slight difference in where the maximum peaks are, this could be explained by the difference in the volume of the unit cell. For group A, they all seem quite similar, except for 2H-MoS2 which have a slightly different distribution in the higher frequency area compared to the others. Indicating that it has fewer occupied states in the 11 THz regions compared to the others.
The partial PDOS are included in Fig. 5 as well and it is clear that the smaller atom S dominates the higher frequencies (above 8 THz), while the heavier Mo atom dominates the lower frequencies. However, some S modes appear in the low-frequency region and for the 2H polymorphs, a few Mo modes appear above 10 THz.
Mechanical stability
We have computed the single-crystal elastic constants to help us understand the mechanical stability of the investigated MoS2 phases. The elastic constants of a material describe how the material responds to an applied force, as either applied strain or the required stress to maintain a certain deformation. Both stress and strain have three tensile and three shear components. Due to this, the elastic constants of a crystal can be described using a 6 × 6 symmetric matrix, having 27 components where 21 of those are independent. Naturally, we can reduce the number of components by utilising any existing symmetry in the polymorph. The 6 × 6 matrix is known as Cij, the stiffness matrix, and it can be used to calculate properties as the bulk modulus, Poisson coefficient and Lame constants. Previous studies show that the accuracy of the DFT elastic constant is within 10% of the experimental values.63 Hence, we can safely use our results to predict the elastic constant for our MoS2 polymorphs.For trigonal polymorphs the mechanical stability criteria of the elastic constants are:64
| BT1 = C11 − C12 > 0 |
| BT2 = (C11 + C12)C33 > 2C132 |
| BT3 = (C11 − C12)C44 > 2C142 |
| BT4 = C44 > 0 |
For the hexagonal polymorphs the stability criteria are:64
| BH1 = C11 >|C12| |
| BH2 = (C11 + C12)C33 > 2C132 |
| BH3 = C44 > 0 |
| BH4 = C66 > 0 |
As seen in Table 3, only 1T2-MoS2 is found to be mechanically unstable since it does not fulfil the Born criteria. Even though group B polymorphs fulfil the Born criteria this does not imply that these could be synthesised as they were found to be dynamically unstable based on the phonon analysis. In general, if a compound is found to be dynamically stable, it indicates that it has either a stable phase or a possible metastable phase. All A group materials are both dynamically and mechanically stable, so these polymorphs can be synthesised experimentally. Since the B group materials are dynamically unstable, but mechanically stable (except 1T2-MoS2) we could conclude that these polymorphs have metastable phases. This explains why monovalent elements/nanoparticles/nanoobjects have been added to stabilise group B polymorphs.29,65–67
| Polymorph | 2R1-MoS2 | 2T-MoS2 | 4T-MoS2 | 1H-MoS2 | 3Ha-MoS2 | 3Hb-MoS2 | 2H-MoS2 | 2R2-MoS2 | 3T-MoS2 | 1T1-MoS2 | 1T2-MoS2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Crystal system | Trigonal | Trigonal | Trigonal | Hexagonal | Hexagonal | Hexagonal | Hexagonal | Trigonal | Trigonal | Trigonal | Trigonal |
| C11 | 105 | 132 | 75 | 123 | 176 | 190 | 140 | 177 | 187 | 195 | |
| C12 | 27 | 34 | 19 | 31 | 45 | 48 | 8 | −4 | 37 | 44 | |
| C13 | 0.1 | 0.40 | 0.1 | 0.5 | 0.6 | 2 | 10 | 14 | 30 | 58 | |
| C14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C33 | 0.3 | 1 | 0.3 | 1 | 2 | 7 | 14 | 29 | 10 | 12 | |
| C44 | 39 | 49 | 28 | 0.4 | 66 | 71 | 66 | 90 | 75 | 75 | |
| C66 | 0.2 | 0.42 | 0.1 | 46 | 0.3 | 0.21 | 4 | 6 | 31 | −82 | |
| Born | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | No | |
| BV | 29 | 37 | 21 | 35 | 50 | 55 | 39 | 48 | 64 | 80 | |
| BR | 0.3 | 1 | 0.3 | 1 | 2 | 7 | 14 | 26 | 4 | −125 | |
| BH | 15 | 19 | 11 | 18 | 26 | 31 | 26 | 37 | 34 | −23 | |
| GV | 20 | 72 | 14 | 24 | 34 | 37 | 32 | 44 | 104 | −2 | |
| GR | 0.4 | 1 | 0.2 | 1 | 0.8 | 1 | 4 | 12 | 5 | −41 | |
| GH | 10 | 36 | 7 | 12 | 17 | 19 | 18 | 28 | 55 | −21 | |
| νV | 0.22 | −0.09 | 0.22 | 0.22 | 0.22 | 0.23 | 0.18 | 0.15 | −0.03 | 0.51 | |
| νR | 0.08 | 0.19 | 0.25 | 0.23 | 0.35 | 0.46 | 0.36 | 0.30 | 0.01 | 0.35 | |
| νH | 0.22 | −0.08 | 0.22 | 0.22 | 0.23 | 0.25 | 0.22 | 0.20 | −0.02 | 0.14 | |
| EV | 49 | 131 | 35 | 58 | 83 | 90 | 76 | 102 | 203 | −5 | |
| ER | 0.9 | 2 | 0.5 | 2 | 2 | 2 | 11 | 31 | 10 | −110 | |
| EH | 25 | 66 | 18 | 30 | 43 | 47 | 45 | 68 | 106 | −48 |
To investigate how the polymorphs would react to applied mechanical forces, we calculated the Voigt (V), Reuss (R) and Hill (H) modulus through the elastic stiffness moduli, Cij. These were then used to calculate the bulk modulus B, shear modulus G, Young's modulus E and Poisson's ratio ν. The calculated values are found in Table 3.
The Hill average young modulus for 1T2-MoS2 (−48 GPa) is negative, which indicates that the atoms are stretched instead of being compressed. For 2T-MoS2 (25 GPa), 4T-MoS2 (66 GPa), 1H-MoS2 (18 GPa), 3Ha-MoS2 (30 GPa), 3Hb-MoS2 (43 GPa), 2H-MoS2 (47 GPa), 2R2-MoS2 (45 GPa), 3T-MoS2 (68 GPa) and 1T1-MoS2 (106 GPa) the atoms are compressed due to the positive value. We see that there is spread in the stiffness of the polymorphs varying from 1H-MoS2 with 18 GPa (like peptide nanotubes68,69) up to 1T1-MoS2 at 106 GPa (like bronze, brass and some titanium alloys70).
Looking at the Poisson's ratio, we see that 4T-MoS 2 and 1T1-MoS2 have negative values, −0.08 and −0.02, which makes them auxetic materials. This means that when the materials are subjected to a positive strain along a longitudinal axis, the transverse strain would increase the cross-sectional area. MoS2 is known for being among crystalline materials that have polymorphs with negative Poisson's ratio,71 and 1T polymorphs are the more common auxetic polymorphs.72 Auxetic materials are expected to have mechanical properties such as high energy absorption and fracture resistance.
The other materials vary from a Poisson's ratio of 0.14 (1T2-MoS2) up to 0.25 (2H-MoS2), which is a range from foam-like compressibility to cast iron. The average of our polymorphs seems to be 0.2, which is around cast iron. In addition to Youngs' modulus and Poisson's ratio, we can also calculate shear modulus over bulk modulus (G/B), a value that will determine if the material is ductile or brittle. The critical value for high (low) G/B that separates ductile and brittle materials is 0.5.73 Our calculated G/B values are below 0.5, implying that all the polymorphs have brittle characteristics except 3Ha-MoS2 which has a G/B value of 0.97. 3Ha-MoS2 is thus expected to be a ductile material.
Raman and IR spectra
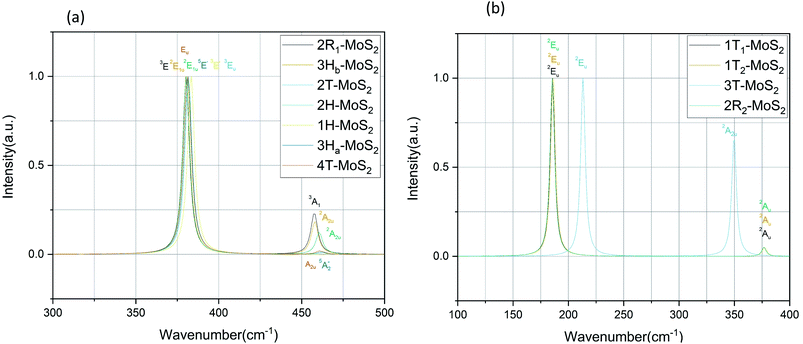
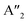 plus E′ correspond to single layer, and A2u and Eu are active IR modes for double layer MoS2.52 Based on the calculated IR spectra for the group B polymorphs shown in Fig. 6b, we see that 3T-MoS2 is a double-layer polymorph (due to comparatively larger intermediate distance between the layers), while 1T1-MoS2 and 1T2-MoS2 contain the 2Eu from double-layer polymorphs in addition to much softer 2Au mode. Our results clearly show that the group B polymorphs are only metastable, and this may the reason for lack of other theoretical IR studies in the literature on these polymorphs. This makes it difficult to verify this result due to lack of literature data. Further theoretical and experimental studies are needed on this aspect.
plus E′ correspond to single layer, and A2u and Eu are active IR modes for double layer MoS2.52 Based on the calculated IR spectra for the group B polymorphs shown in Fig. 6b, we see that 3T-MoS2 is a double-layer polymorph (due to comparatively larger intermediate distance between the layers), while 1T1-MoS2 and 1T2-MoS2 contain the 2Eu from double-layer polymorphs in addition to much softer 2Au mode. Our results clearly show that the group B polymorphs are only metastable, and this may the reason for lack of other theoretical IR studies in the literature on these polymorphs. This makes it difficult to verify this result due to lack of literature data. Further theoretical and experimental studies are needed on this aspect.
| Polymorph | Raman active modes | IR active modes |
|---|---|---|
| a From ref. 58.b From ref. 59.c From ref. 60.d From ref. 49.e From ref. 61.f From ref. 62.g From ref. 54. | ||
| 2R1-MoS2 | 3E: 286, 381. 3A1: 405 | 3E: 380. 3A1: 457 |
| 2H-MoS2 | 2E2g: 30, 382. 1E1g: 283. 1A1g: 404 | 2E1u: 380. 2A2u: 460 |
| 3Hb-MoS2 | 2E2g: 36, 380. 1E1g: 284. 1A1g: 403 | 2E1u: 380. 2A2u: 458 |
| 4T-MoS2 | Eg: 14, 33, 282, 283, 380. A1g: 22, 53, 401, 403, 461, 463 | Eu: 26, 281, 283, 380. A2u: 43, 399, 402, 463 |
| 3Ha-MoS2 | 4E′′: 19. 5E′: 283, 381. 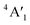 : 398, 461 : 398, 461 |
5E′: 381. 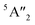 : 461 : 461 |
| 2T-MoS2 | 3A1g: 40, 400. 3Eg: 284, 382 | 3Eu: 382 |
| 1H-MoS2 | 1E′′: 284. 2E′: 383 | 3E′: 384 |
| 1T1-MoS2 | 1Eg: 274. 1A1g: 386 | 2Eu: 186. 2Au: 377 |
| 1T2-MoS2 | 1Eg: 275. 1A1g: 386 | 2Eu: 186. 2Au: 377 |
| 3T-MoS2 | 1Eg: 258. 1A1g: 398 | 2Eu: 213. 2A2u: 350 |
| 2R2-MoS2 | 1Eg: 274. 1A1g: 386 | 2Eu: 185. 2Au: 376 |
| Bulk 2H-MoS2 | E12g: 384a, 382b, 384c. A1g: 408a, 408b, 408c | E1u: 382e, 384f, 384g. A2u: 468f, 470g |
| Mono 2H-MoS2 | E′: 384d, 385c. 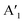 : 403d, 404c : 403d, 404c |
|
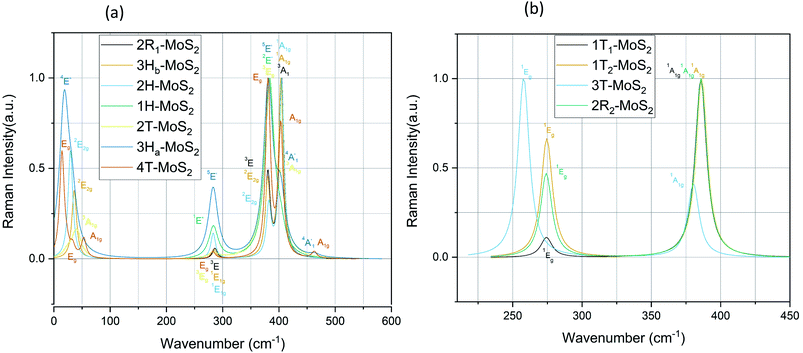
Regarding the group A polymorphs, we clearly notice the presence of 2E1u and 2A2u active modes for 3Hb-MoS2 and 2H-MoS2 indicating that they are MoS2 bulk polymorphs. 4T-MoS2 has Eu and A2u as active modes, which is also an indication of a bulk polymorph. Due to the presences of the E′ and 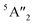 modes (due to comparatively larger intermediate distance between the layers) we find 3Ha-MoS2 to be a single layer. The Eu modes seen for 2T-MoS2 confirms that this a double layer polymorph, while the E′ mode for 1H-MoS2 makes it a single layer polymorph. 2R1-MoS2 on the other hand shows E modes and A1, neither of these modes have previously been reported as active IR modes for MoS2. This could be an artefact from the calculation method, although the historical known accuracy speaks against this. However, it could also be a result of the interlayer distance and van der Waals forces making it harder to differentiate between the MoS2 layers of the polymorph. Another possible explanation is that the polymorphs are tilted slightly, and therefore exist in a state between 2H and 1T. This would change the crystal symmetry enough to introduce previously unseen modes.
modes (due to comparatively larger intermediate distance between the layers) we find 3Ha-MoS2 to be a single layer. The Eu modes seen for 2T-MoS2 confirms that this a double layer polymorph, while the E′ mode for 1H-MoS2 makes it a single layer polymorph. 2R1-MoS2 on the other hand shows E modes and A1, neither of these modes have previously been reported as active IR modes for MoS2. This could be an artefact from the calculation method, although the historical known accuracy speaks against this. However, it could also be a result of the interlayer distance and van der Waals forces making it harder to differentiate between the MoS2 layers of the polymorph. Another possible explanation is that the polymorphs are tilted slightly, and therefore exist in a state between 2H and 1T. This would change the crystal symmetry enough to introduce previously unseen modes.
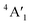 mode (∼460 cm−1) for 3Ha-MoS2 are due to strong electron–phonon couplings and could come from a second-order process involving the longitudinal acoustic phonons at M point (LA(M)).56 We also note that the E1g and A1g are redshifted compared to the Raman modes of group B polymorphs. Raman spectra can be used to verify the crystallinity of a material. The Raman spectra for crystalline materials contain sharper peaks or long-range correlations, while amorphous materials only have short-range ordering.57 Raman spectra indicates clearly that the MoS2 polymorphs considered in this study are shown to have crystalline characteristics.
mode (∼460 cm−1) for 3Ha-MoS2 are due to strong electron–phonon couplings and could come from a second-order process involving the longitudinal acoustic phonons at M point (LA(M)).56 We also note that the E1g and A1g are redshifted compared to the Raman modes of group B polymorphs. Raman spectra can be used to verify the crystallinity of a material. The Raman spectra for crystalline materials contain sharper peaks or long-range correlations, while amorphous materials only have short-range ordering.57 Raman spectra indicates clearly that the MoS2 polymorphs considered in this study are shown to have crystalline characteristics.
For the sake of checking the validity of our approach, we have tabulated experimental as well as other theoretical findings on 2H-MoS2 polymorph. Based on our knowledge, there are still no studies reported on 1T polymorphs due to the synthesis and stability challenges of these polymorphs. We see that in general, we have the same major peaks around 380 cm−1 and 405 cm−1 for group A polymorphs as reported in the literature. The same is observed with the IR modes, which are in good agreement with reported literature data.
Conclusion
For the very first time 14 different MoS2 polymorphs are proposed and studied using DFT total-energy calculations, band structure analysis, phonon density of states and elastic constants calculations. The in-depth study shows.• Three of the polymorphs were omitted from the study because their energy-volume data were far away from the data for other polymorphs, which indicates that these polymorphs are unstable.
• Polymorphs in group B (1T1-MoS2, 1T2-MoS2, 3T-MoS2 and 2R2-MoS2) are all metallic and lacked dynamical stability. 1T2-MoS2 is neither dynamical stable nor mechanical stable.
• Group A (2R1-MoS2, 3Hb-MoS2, 2H-MoS2, 1H-MoS2, 2T-MoS2, 3Ha-MoS2 and 4T-MoS2) polymorphs are semiconductors with an indirect bandgap, the range for the seven polymorphs is 1.87 eV to 2.12 eV. They are all dynamically and mechanically stable.
• 2R1-MoS2 has the lowest bandgap of 1.87 eV.
• 4T-MoS2 stands out due to being auxetic, which means it has a high level of fracture resistance.
• 3Hb-MoS2 has the lowest effective electron mass (0.22me vs. for example 1.4me for 2H-TiO2, which is widely used in PV and photocatalytic applications).
Our theoretical analysis show that the candidates in group A can be readily synthesised. Here further experimental verification is needed. The bandgap range of 1.87 eV to 2.12 eV makes the group A polymorphs viable for photovoltaic and photocatalytic applications. Out of the seven polymorphs in group A, 3Hb-MoS2, with its high electron mobility and with the bandgap of 1.95 eV, is the most promising candidate for photovoltaic and photocatalytic applications. MoS2 has recently shown promise as electron and/or hole-transport layer in perovskite solar cells, and the high carrier mobility of 3Hb-MoS2 makes it a promising candidate for this use.
The group B polymorphs were only found to be metastable phases (except 1T2-MoS2) and cannot be synthesised. Due to the transitions of metastable phases in 1T polymorphs, more research on these polymorphs is needed such that the synthesis of a pure 1T-MoS2 single-layer polymorph is viable.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the Research Council of Norway for providing the computer time (under the project number NN2875k and NN2867k) at the Norwegian supercomputer clusters.References
- D. Voiry, A. Goswami, R. Kappera, C. d. C. C. e. Silva, D. Kaplan, T. Fujita, M. Chen, T. Asefa and M. Chhowalla, Nat. Chem., 2014, 7, 45 CrossRef.
- Z. Yin, H. Li, H. Li, L. Jiang, Y. Shi, Y. Sun, G. Lu, Q. Zhang, X. Chen and H. Zhang, ACS Nano, 2012, 6, 74–80 CrossRef CAS.
- M. Xu, T. Liang, M. Shi and H. Chen, Chem. Rev., 2013, 113, 3766–3798 CrossRef CAS.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147–150 CrossRef CAS.
- K. K. Kam and B. A. Parkinson, J. Phys. Chem., 1982, 86, 463–467 CrossRef CAS.
- D. Voiry, A. Mohite and M. Chhowalla, Chem. Soc. Rev., 2015, 44, 2702–2712 RSC.
- C. Wu, J. Zhang, X. Tong, P. Yu, J. Y. Xu, J. Wu, Z. M. Wang, J. Lou and Y. L. Chueh, Small, 2019, 15, e1900578 CrossRef.
- M. Dallavalle, N. Sändig and F. Zerbetto, Langmuir, 2012, 28, 7393–7400 CrossRef CAS.
- M.-L. Tsai, S.-H. Su, J.-K. Chang, D.-S. Tsai, C.-H. Chen, C.-I. Wu, L.-J. Li, L.-J. Chen and J.-H. He, ACS Nano, 2014, 8, 8317–8322 CrossRef CAS.
- Z. Li, X. Meng and Z. Zhang, J. Photochem. Photobiol., C, 2018, 35, 39–55 CrossRef CAS.
- M. Donarelli and L. Ottaviano, Sensors, 2018, 18(11), 3638 CrossRef.
- S. Barua, H. S. Dutta, S. Gogoi, R. Devi and R. Khan, ACS Appl. Nano Mater., 2017, 1, 2–25 CrossRef.
- N. Bandaru, R. S. Kumar, D. Sneed, O. Tschauner, J. Baker, D. Antonio, S.-N. Luo, T. Hartmann, Y. Zhao and R. Venkat, J. Phys. Chem. C, 2014, 118, 3230–3235 CrossRef CAS.
- Y.-C. Lin, D. Dumcenco, Y.-s. Huang and K. Suenaga, Nat. Nanotechnol., 2014, 9, 391–396 CrossRef CAS.
- A. Enyashin, L. Yadgarov, L. Houben, I. Popov, M. Weidenbach, R. Tenne, M. Bar-Sadan and G. Seifert, J. Phys. Chem. C, 2011, 115, 24586 CrossRef CAS.
- L. Hromadová, R. Martoňák and E. Tosatti, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 144105 CrossRef.
- S. Ahmad and S. Mukherjee, Graphene, 2014, 3, 52–59 CrossRef.
- B. Han and Y. H. Hu, Energy Sci. Eng., 2016, 4, 285–304 CrossRef CAS.
- J. Sun, X. Li, W. Guo, M. Zhao, X. Fan, Y. Dong, C. Xu, J. Deng and Y. Fu, Crystals, 2017, 7, 198 CrossRef.
- M. R. Vazirisereshk, A. Martini, D. A. Strubbe and M. Z. Baykara, Lubricants, 2019, 7, 57 CrossRef.
- O. V. Yazyev and A. Kis, Mater. Today, 2015, 18, 20–30 CrossRef CAS.
- L. S. Byskov, J. K. Nørskov, B. S. Clausen and H. Topsøe, J. Catal., 1999, 187, 109–122 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- L. Andrinopoulos, N. D. M. Hine and A. A. Mostofi, J. Chem. Phys., 2011, 135, 154105 CrossRef.
- P. L. Silvestrelli, Phys. Rev. Lett., 2008, 100, 053002 CrossRef.
- P. L. Silvestrelli, J. Phys. Chem. A, 2009, 113, 5224–5234 CrossRef CAS.
- P. Ravindran, R. Vidya, A. Kjekshus, H. Fjellvåg and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 224412 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. van de Walle and G. Ceder, Rev. Mod. Phys., 2002, 74, 11–45 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- V. Wang, N. Xu, J. C. Liu, G. Tang and W.-T. Geng, 2019, arXiv:1908.08269.
- W. Zhao, J. Pan, Y. Fang, X. Che, D. Wang, K. Bu and F. Huang, Chem.–Eur. J., 2018, 24, 15942–15954 CrossRef CAS.
- Z. Xia, Y. Tao, Z. Pan and X. Shen, Results Phys., 2019, 12, 2218–2224 CrossRef.
- C. Lane, D. Cao, H. Li, Y. Jiao, B. Barbiellini, A. Bansil and H. Zhu, Condens. Matter, 2019, 4, 53 CrossRef CAS.
- M. Kan, J. Y. Wang, X. W. Li, S. H. Zhang, Y. W. Li, Y. Kawazoe, Q. Sun and P. Jena, J. Phys. Chem. C, 2014, 118, 1515–1522 CrossRef CAS.
- A. N. Enyashin, L. Yadgarov, L. Houben, I. Popov, M. Weidenbach, R. Tenne, M. Bar-Sadan and G. Seifert, J. Phys. Chem. C, 2011, 115, 24586–24591 CrossRef CAS.
- H. Huang, Y. Cui, Q. Li, C. Dun, W. Zhou, W. Huang, L. Chen, C. A. Hewitt and D. L. Carroll, Nano Energy, 2016, 26, 172–179 CrossRef.
- P. Borlido, T. Aull, A. W. Huran, F. Tran, M. A. L. Marques and S. Botti, J. Chem. Theory Comput., 2019, 15, 5069–5079 CrossRef CAS.
- J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, 174101 CrossRef.
- A. Fonari and C. Sutton, Effective Mass Calculator, 2012 Search PubMed.
- L. A. Cipriano, G. Di Liberto, S. Tosoni and G. Pacchioni, Nanoscale, 2020, 12, 17494–17501 RSC.
- C. Liang, X. Sui, A. Wang, J. Chang, W. Wang, Z. Chen, W. Jiang, Y. Ma, J. Zhang, X. Liu and Y. Zhang, Adv. Mater. Interfaces, 2020, 7, 2001130 CrossRef CAS.
- F. A. Rasmussen and K. S. Thygesen, J. Phys. Chem. C, 2015, 119, 13169–13183 CrossRef CAS.
- X. Li, Y. Dai, M. Li, W. Wei and B. Huang, J. Mater. Chem. A, 2015, 3, 24055–24063 RSC.
- C. Dette, M. A. Pérez-Osorio, C. S. Kley, P. Punke, C. E. Patrick, P. Jacobson, F. Giustino, S. J. Jung and K. Kern, Nano Lett., 2014, 14, 6533–6538 CrossRef CAS.
- S. Jayabal, J. Wu, J. Chen, D. Geng and X. Meng, Mater. Today Energy, 2018, 10, 264–279 CrossRef.
- X. Zhang, X.-F. Qiao, W. Shi, J.-B. Wu, D.-S. Jiang and P.-H. Tan, Chem. Soc. Rev., 2015, 44, 2757–2785 RSC.
- L. Liang and V. Meunier, Nanoscale, 2014, 6, 5394–5401 RSC.
- T. J. Wieting and J. L. Verble, Phys. Rev. B: Condens. Matter Mater. Phys., 1971, 3, 4286–4292 CrossRef.
- J. M. Chen and C. S. Wang, Solid State Commun., 1974, 14, 857–860 CrossRef CAS.
- H. Li, Q. Zhang, C. C. R. Yap, B. K. Tay, T. H. T. Edwin, A. Olivier and D. Baillargeat, Adv. Funct. Mater., 2012, 22, 1385–1390 CrossRef CAS.
- A. Z. Samuel, Spectrochim. Acta, Part A, 2020, 224, 117431 CrossRef CAS.
- C. Lee, H. Yan, L. E. Brus, T. F. Heinz, J. Hone and S. Ryu, ACS Nano, 2010, 4, 2695–2700 CrossRef CAS.
- B. P. Majee, S. Mishra, R. K. Pandey, R. Prakash and A. K. Mishra, J. Phys. Chem. C, 2019, 123, 18071–18078 CrossRef CAS.
- K. Gołasa, M. Grzeszczyk, K. P. Korona, R. Bożek, J. Binder, J. Szczytko, A. Wysmołek and A. Babiński, Acta Phys. Pol., A, 2013, 124, 849–851 CrossRef.
- X. Guo, H. Chen, X. Wen and J. Zheng, J. Chem. Phys., 2015, 142, 212447 CrossRef.
- Q. C. Sun, X. S. Xu, L. I. Vergara, R. Rosentsveig and J. L. Musfeldt, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205405 CrossRef.
- P. Ravindran, L. Fast, P. A. Korzhavyi, B. Johansson, J. Wills and O. Eriksson, J. Appl. Phys., 1998, 84, 4891–4904 CrossRef CAS.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- Z. Lei, J. Zhan, L. Tang, Y. Zhang and Y. Wang, Adv. Energy Mater., 2018, 8, 1703482 CrossRef.
- Q. Liu, Q. Fang, W. Chu, Y. Wan, X. Li, W. Xu, M. Habib, S. Tao, Y. Zhou, D. Liu, T. Xiang, A. Khalil, X. Wu, M. Chhowalla, P. M. Ajayan and L. Song, Chem. Mater., 2017, 29, 4738–4744 CrossRef CAS.
- P. Luo, F. Zhuge, Q. Zhang, Y. Chen, L. Lv, Y. Huang, H. Li and T. Zhai, Nanoscale Horiz., 2019, 4, 26–51 RSC.
- N. Kol, L. Adler-Abramovich, D. Barlam, R. Z. Shneck, E. Gazit and I. Rousso, Nano Lett., 2005, 5, 1343–1346 CrossRef CAS.
- L. Niu, X. Chen, S. Allen and S. J. B. Tendler, Langmuir, 2007, 23, 7443–7446 CrossRef CAS.
- E. Toolbox, Young's Modulus - Tensile and Yield Strength for common Materials, https://www.engineeringtoolbox.com/young-modulus-d_417.html, accessed 06.08.2020 Search PubMed.
- R. V. Goldstein, V. A. Gorodtsov and D. S. Lisovenko, Dokl. Phys., 2011, 56, 602–605 CrossRef CAS.
- L. Yu, Q. Yan and A. Ruzsinszky, Nat. Commun., 2017, 8, 15224 CrossRef CAS.
- S. F. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra10443d |
| This journal is © The Royal Society of Chemistry 2021 |