Electronic structure and mechanism for the uptake of nitric oxide by the Ru(III) antitumor complex NAMI-A

Abstract

Nitric oxide (NO) has well known vasodilation effects in living organisms and its participation in the metastasis of cancer cells through the angiogenesis process has been demonstrated experimentally. Therefore, the uptake of NO has become one focus of investigation to produce anti-metastatic drugs. In this article we have investigated the uptake of NO by the ruthenium based metallodrug trans-tetrachloride(dimethylsulfoxide)imidazole ruthenate(III) [Im]trans-[RuCl₄(Im)(DMSO)], known as New Anti-tumor Metastasis Inhibitor-A (NAMI-A). Electronic structure calculations using Density Functional Theory, DFT, and State-Averaged Complete Active Space Self Consistent Field, SA-CASSCF, with second order perturbation theory corrections, NEVPT2 were carried out to investigate the mechanism involved in the uptake of NO by the Ru-based anticancer metallodrug NAMI-A. The calculations revealed that the reaction takes place at the triplet potential energy surface, with the singlet surface being ∼15 kcal mol⁻¹ shifted to higher energies, and there is a surface crossing to form the most stable singlet product after the reaction takes place at the triplet surface. The spin pairing and electron transfer from the nitric oxide to the metallic fragment takes place at the region of the minimum energy crossing point between the two surfaces. The Ru–NO bond in the {Ru–NO}⁶ product has ∼10% of the Ru^III–NO⁰ character. The SA-CASSCF/NEVPT2 calculations revealed that the uptake of NO by NAMI-A has a small energy barrier of ∼8 kcal mol⁻¹ and, therefore a rate constant of 11.3 × 10⁶ s⁻¹ at 300 K. In addition, the reaction is thermodynamically favorable, with a Gibbs free energy of ∼30 kcal mol⁻¹. These results show that the uptake of nitric oxide by the NAMI-A complex is kinetically and thermodynamically feasible in biological medium and, therefore, gives support to the anti-angiogenesis theory associated to the mode of action of NAMI-A and other related compounds.

---

1. Introduction

Ruthenium complexes have been investigated as anti-cancer drugs which may be a viable alternative to traditional platinum-based drugs because of their lower toxicity.^1–7 Among the large group of ruthenium complexes synthesized, the trans-tetrachloride(dimethylsulfoxide)imidazole ruthenate(III), [Im]trans-[RuCl₄(Im)(DMSO)], known as New Anti-tumor Metastasis Inhibitor-A (NAMI-A), stood out due to its anti-metastatic activity and low cytotoxicity. On average, this compound is more than 1000 times less cytotoxic compared to cisplatin, a well-known reference anti-cancer metallodrug.⁸ NAMI-A demonstrated excellent and selective activity against lung metastases of several solid metastatic tumors in mice, including a mouse-grafted NSCLC (non-small-cell lung carcinoma) of human origin.^9–11 By virtue of these properties, NAMI-A was the first compound to be tested in humans and became a landmark in the field of anticancer metal compounds.¹² However, despite numerous investigations, NAMI-A molecular target and why NAMI-A is inactive in primary tumors are still unknown. While first studies have suggested that biological effects are related to the binding of the ruthenium complex to extracellular matrix collagen and surface cell integrins, which increases adhesion and reduces the invasiveness of cancer cells,¹³ later ones attributed NAMI-A activity against already developed metastases to its anti-angiogenic properties, which have been confirmed in membranes of chicken and rabbit eye cornea.^14–16 To the present date, the drug is no longer in clinical trials due to its side effects and antitumor activity lesser than expected.⁶

In the angiogenesis new capillary vessels are formed from existing blood vessels, increasing tumor growth and favoring the process of metastasis.¹⁶ Thus, angiogenesis is responsible for the growth of primary tumors from their metastasis and, therefore, identified as a target for pharmacological control of malignant tumors.^17–19 Nitric Oxide (NO) is expected to participate in the angiogenesis process due to its well-known vasodilation effects, which are of primary importance in the regulation of blood pressure. This participation was first demonstrated by Pipili-Synetos and co-authors^20,21 and since then several studies have been dedicated to understand the mechanism involved in the formation of new capillaries and showing that NO is directly involved in the angiogenesis.^22–27 Tumor and inflammatory cells produce NO in response to cytokines or other stimuli and under the control of endogenous NO, the same cells can produce and release angiogenic or modulating factors, which act on endothelial cells, leading to angiogenesis.²⁸ Due to the involvement of NO in the various events that contribute to tumor progression and the ability of ruthenium complexes to interact with NO, a theory that this signaling molecule is one of the targets of NAMI-A antimetastatic activity has been proposed.^14,15

The in vitro angiogenic process was investigated by Castellarin et al.²⁹ using endothelial cell lines EA.hy926. The authors showed that NAMI-A reduces the production and release of nitric oxide (NO) by EA.hy926 and consequently inhibits its invasive capacity. It also strongly inhibits angiogenesis in Matrigel/sponges implanted subcutaneously in healthy mice. These data support the anti-angiogenic activity of the tested ruthenium compound and contribute to the selective activity of NAMI-A against solid tumor metastases, the tumor compartment in which angiogenesis is strongly involved. Oszajca et al.³⁰ studied the reactivity of NAMI-A to NO in aqueous solution and under physiological conditions revealing that NAMI-A can interfere on the NO metabolism through the formation of the [Ru^II–NO⁺] complex which cannot release nitric oxide via electron reduction due to the relatively low reduction potential of the NO⁺ coordinated to the Ru^II center (−0.69 V).³⁰

In a detailed recent work, Li and co-workers³¹ investigated the mechanism for the nitrosylation reaction of NAMI-A mono-hydrolysate complexes in the singlet and triplet states, in aqueous solution, using QM/MM methods. Their results showed the possible coexistence of the singlet and triplet spin states in the ruthenium nitrosyl complex in aqueous solution leading to a competitive interaction between spin states. According to their results the ligand exchange reactions involving NO can occur not only in the singlet spin state but also in the triplet spin and, therefore, the reaction does not always occur with an electron transfer. However, in this study, the nitrosylation reaction was investigated on only one potential energy surface (singlet or triplet) and did not address the possible mechanistic route in which the singlet and triplet potential energy curves may intersect at one or more points. This can be a possible route since both NO (S = 1/2) and the [RuCl₃(H₂O)(Im)(DMSO)] complex (S = 1/2) have each an unpaired electron. Although we can think of these reactions occurring on either surface, the spin multiplicity of the final product will preferably be singlet, since it is significantly more stable and the only one experimentally verified.^29,30,32 In other words, the reaction can involve at least one surface crossing point. Indeed, we have shown employing Density Functional Theory calculations and Monte Carlo statistical mechanical simulations that the ligand exchange reaction between NO and water, involved in the formation of the [Ru(NH₃)₅(NO)]³⁺ complex in its most stable singlet state can occur through at least two singlet-triplet surface crossings.³³ This type of non-radiative transition between electronic states with two different spin multiplicities can be adequately investigated using the non-adiabatic transition state theory (NA-TST).³⁴

The NAMI-A complex is known to be rather susceptible to many structural transformations in biological environment.^9,35–39 Therefore, a NO capture may compete with other processes such as the exchange of ligands for water, reduction of the metallic center from Ru^III to Ru^II and interactions with other biomolecules. The ligand exchange reactions are fairly dependent on pH and it was shown experimentally that the DMSO is released in more extent in moderately acid pH's (∼6) while its related product, [trans-RuCl₄(H₂O)(Him)]⁻, is the predominant species together with the original NAMI-A molecule in pH < 6.^9,35 In physiological pH (7.4) the DMSO release is observed but the predominant reaction is the subsequent hydrolysis of two chloride ions and further formation of oxo products.^9,35,38 Lastly, the literature shows that imidazole exchange reactions do not happen in physiological or even lower pH conditions for NAMI-A and other very similar antitumoral Ru complexes like the trans-[RuCl₄(Him)₂] (KP418).⁴⁰ Imidazole NH group acidity (pK_a = 14.9)⁴¹ is also too weak to consider a deprotonation and its further implications in physiological environment. Therefore, the mechanistic proposal studied here considers that the dominant reaction taking place before the NO uptake is the hydrolysis of one chloride, which is also essential for the following nitrosylation process. This proposition was the one demonstrated experimentally in the work of Oszajca et al.³⁰ under physiological-like conditions (pH = 7.4, [NaCl] = 0.1 M, T = 37 °C).

In this paper, we use quantum chemical calculations at the Density Functional Theory (DFT) and Complete Active Space Self Consistent Field (CASSCF) levels to investigate the mechanism for the uptake reaction of NO by the NAMI-A complex in its mono-hydrolyzed form. As we shall see, in contrast with previously reported, the reaction takes place in the triplet spin state surface and there is a surface crossing to generate the most stable singlet nitrosylated complex. The singlet spin surface, despite having a lower energy barrier, is shifted at least 15 kcal mol⁻¹ to higher energies when compared with the triplet surface.

2. Computational details

For the sake of clarity, the NAMI-A ([Ru(Cl)₄(Im)(DMSO)]⁻) derivate complexes [Ru(Cl)₃(Im)(DMSO)(H₂O)] (first hydrolysis product) and [Ru(Cl)₃(Im)(DMSO)(NO)] (nitrosylated product) will hereafter be called NAMI–H₂O and NAMI–NO, respectively.

Gas-phase geometry optimizations of the complexes were carried out at the Density Functional Theory (DFT) level,⁴² using the hybrid B3LYP exchange–correlation functional^43,44 and the Ahlrichs full electron def2-TZVP basis set⁴⁵ for all atoms. Vibrational analyses were carried out on the optimized structures to verify the nature of the stationary point (minima or first-order transition state). Resolution of the identity (RI)⁴⁶ was used in all calculations for the coulomb, and the chain of sphere approach (COS)⁴⁷ for the exchange part of the Fock matrix, employing the def2-TZVP/J auxiliary basis set.⁴⁸ The open-shell structures were treated within the unrestricted Hartree–Fock (UHF) or Kohn–Sham (UKS) formalism.⁴²

The potential energy surfaces (PES) for the reactions involving NO and the NAMI–H₂O complex, both in the singlet and triplet spin states, were first explored using the coordinate-driven minimum-energy approach, where we choose the Ru–NO distance as the main geometric parameter that drives the reaction and kept it fixed along with the reaction and all other internal coordinates are fully optimized. For the nitrosylation reaction, the NO molecule was approached to the NAMI–H₂O complex, varying the Ru–NO distance from 3.8 to 2.0 Å in 10 equally spaced steps, which were maintained fixed. These calculations were also performed with the same B3LYP functional and a smaller def2-SV(P) basis set.⁴⁵ The most stable structure of NAMI–H₂O has low spin configuration and, as a result, nitric oxide and the NAMI–H₂O complex each have an unpaired electron, thus the reaction can take place either in the singlet or triplet state. Here, we will try to unveil more aspects of these mechanisms focusing on the nature of the electronic structure of the systems. As we have shown³³ for the exchange reaction of NO with water in the complex [Ru(NH₃)₅(H₂O)]³⁺, the singlet and triplet surfaces can cross each other and this crossing may be relevant for the mechanism of NO uptake. The minimum energy crossing points (MECP's) between the singlet and triplet potential energy surfaces were obtained using the method suggested by Harvey et al.^34,49 and implemented in the ORCA program.^50,51

Complete active space self-consistent field (CASSCF),^52,53 with second-order perturbation theory corrections, NEVPT2,^54–56 calculations were performed at the optimized DFT structures, to obtain a better description of not only the electronic states but also of static and dynamic electron correlation effects along the reaction coordinate. The CASSCF active space was constructed performing fractional occupation density (FOD)⁵⁷ calculations where orbitals with fractional occupation between 1.98 and 0.02 were selected as active space. The FOD calculations were done with ORCA default settings, which uses DFT with the TPSS⁵⁸ functional and def2-TZVP basis set. CASSCF calculations are not usually straightforward, even for a set of similar systems. Therefore, despite using the initial approach to choose the active spaces based on the FOD results, this not always led to convergence and adjustments in the active spaces of the calculations had to be done individually (more details can be checked in the Table S3 of ESI†). The basis sets used for the CASSCF calculations were the all-electron def2-TZVP basis set, with second-order scalar-relativistic corrections performed according to the Douglas–Kroll–Hess (DKH) Hamiltonian.⁵⁹ Spin–orbit coupling (SOC) effects⁶⁰ were also taken into account as implemented in ORCA using 10 singlet and 10 triplet roots in a SA-CASSCF(8,8) calculations. To select the number of roots and active space we carried SOC calculations up to the point that the SOC between the first triplet and first singlet became somewhat constant (results are shown in ESI†). When included, solvent effects (in water) were accounted for by the implicit solvation method C-PCM⁶¹ in conjunction with the SMD model corrections.⁶² All quantum chemical calculations reported in this work were performed using the ORCA program package.^50,51

3. Results and discussion

Fig. 1 shows the B3LYP/def2-TZVP optimized structures for the isolated complexes NAMI-A, NAMI–H₂O and NAMI–NO in the singlet and triplet spin states. Besides, the main geometrical parameters for this species are quoted in Table 1.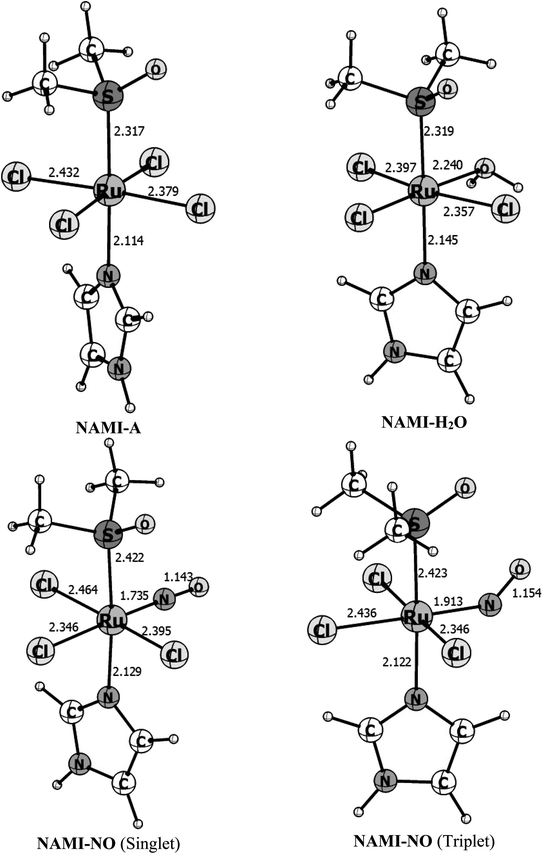

Fig. 1 Gas phase B3LYP/def2-TZVP optimized parameters for the complexes NAMI-A, NAMI–H₂O and NAMI–NO in the singlet and triplet states. Bond distances in Å and bond angles in degrees.

Table 1 Gas phase B3LYP/def2-TZVP optimized parameters for the complexes NAMI-A, NAMI–H₂O and NAMI–NO in the singlet (S) and triplet (T) states. Bond distances in Å and bond angles in degrees

Parameter	[RuCl4(DMSO)Im]^1− (NAMI-A)^a	[RuCl3(H2O)(DMSO)Im] (NAMI–H2O)	[RuCl3(NO)(DMSO)Im] (NAMI–NO)
			S	T
a Experimental values (in parenthesis) taken from ref. 32 for the analogous sodium salt of NAMI-A.
r(Ru–S)	2.317(2.30)	2.318	2.422	2.423
r(Ru–Im)	2.114(2.08)	2.145	2.129	2.122
r(Ru–Cl)avg.	2.406(2.34)	2.348	2.402	2.377
r(Ru–H2O)	—	2.239	—	—
r(Ru–NO)	—	—	1.735	1.913
∠(Ru–N–O)	—	—	177.8	141.1

---

As can be seen, these Ru(III) complexes exhibit distorted octahedral geometry and replacing the chlorine ligand by water have very subtle changes in the equatorial Ru–Cl bonds. However, when we replace water by nitric oxide the changes are more pronounced. The coordination mode of nitric oxide to a metal center is dependent on its formal oxidation state. Thus, if NO is coordinated as NO˙ or NO⁻, we should expect angular-type coordination in order to maximize HOMO/SOMO interaction.^63,64 For the formal NO⁺ oxidation state linear coordination is expected.^65,66 Usually, the {RuNO}ⁿ complex, with n = 6, where n is the sum of d-orbital electrons of Ru and the NO π-electrons, the ground state exhibits linear coordination and singlet spin multiplicity.⁶⁷ In the triplet spin state, these complexes usually assume angular coordination (∠Ru–N–O < 180°) due to the donation of electron density to the π* orbitals of NO. As a general case, {RuNO}⁶ complexes do not undergo NO substitution reactions under normal thermodynamic conditions, and this should be accomplished by chemical or photochemical reducing processes.^65–67 In Fig. 3 we can see that the complex in the singlet spin state shows linear coordination, with ∠Ru–N–O = 178°, consistent with Ru^II–NO⁺ coordination while in the triplet spin state the ∠Ru–N–O = 141° is consistent with Ru^III–NO coordination. At the B3LYP/def2-TZVP the structure obtained with the singlet spin state is 21.5 kcal mol⁻¹ more stable than the triplet structure. This is in line with the experimental fact that only the linear structure (singlet spin) is observed experimentally.⁶⁷ That is, at normal conditions of temperature and pressure, only the singlet structure is obtained.

To become an active species in the biological environment, NAMI-A undergo hydrolysis reaction due to the difference in concentration of chloride ions, in the blood plasma and the cytoplasm of the cells, providing a coordination site for other exchange reactions in the biological medium.^1–7 The potential energy surface for the uptake of NO by the mono-hydrolysate NAMI-A complex, eqn (1), was first explored at the B3LYP/def2-SV(P) level including the solvent effects with the SMD solvation model, using the procedure described earlier. Both the singlet and triplet surfaces were explored and, the potential energy curves are shown in Fig. 2.

[RuCl₃(H₂O)(Im)(DMSO)] + NO → [RuCl₃(NO)(Im)(DMSO)] + H₂O (1)

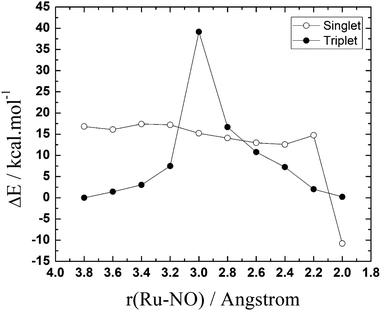Fig. 2 Potential energy surfaces (PES) for the NO–H₂O exchange reaction [RuCl₃(H₂O)(Im)(DMSO)] + NO → [RuCl₃(NO)(Im)(DMSO)] + H₂O, in the singlet and triplet spin states.

As can be seen, the reactants in the triplet surface are about 17 kcal mol⁻¹ more stable than the singlet reactants. The singlet product, on the other hand, is ∼11 kcal mol⁻¹ more stable than the triplet product. The peaks appearing in the curves indicates the possible transition states regions. This initial PES exploration shows that the triplet surface has exceedingly high activation energy (∼39 kcal mol⁻¹) compared with the almost barrierless singlet surface. What is interesting is that the results show that there may be three crossing points between the singlet and triplet surfaces, one before the triplet transition state and two others after, in the singlet product region.

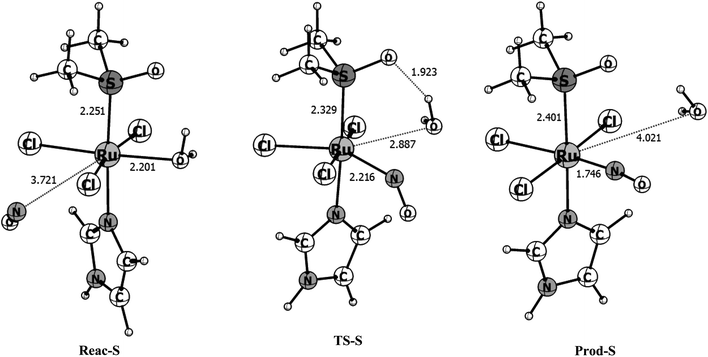
To have a clearer picture of the reaction mechanism, the points close to the reactants, transition states and products were fully reoptimized at the B3LYP/def2-TZVP level of theory, removing the Ru–NO distance constraint. The optimized structures of the stationary points found in the singlet and triplet surfaces are shown in Fig. 3 and 4, respectively. The singlet surface is characterized by a transition state (TS) with an imaginary frequency of 122.6i cm⁻¹. The nuclear movement associated with this frequency involves the breaking of the Ru–H₂O bond and the formation of the Ru–NO bond. Following the singlet reaction pathway, the r(Ru–H₂O) bond increases from 2.201 Å in the reactants to 2.887 Å in the TS while the r(Ru–NO) bond decreases from 3.721 Å in the reactants to 2.216 Å at the transition state. In the final product, the water molecule is completely dissociated with r(Ru–H₂O) = 4.021 Å and the NO molecule bonds to the ruthenium atom with r(Ru–NO) = 1.746 Å. The final optimized ∠RuNO = 170° is characteristic of a Ru^II–NO⁺ type of coordination, resulted from an intramolecular electron transfer from the NO to the ruthenium upon coordination, which leads to a reduction of the formal oxidation state of ruthenium. The nature of this interaction will be further discussed with the CASSCF calculations. Based on the mentioned distances changes we calculated 31% of the Ru–H₂O bond breaking (compared with the Ru–H₂O distance in the reactant) and 73% of the Ru–NO bond formation (compared with the Ru–NO bond in the product) at the transition state for the singlet surface, indicating a reaction mechanism with a tight transition state and associative character. The Gibbs free energies obtained for the singlet reaction pathway in gas phase and water solution are shown in Table 2. The calculated free energy of activation for this singlet process is 4.03 kcal mol⁻¹ and the total free energy of reaction is −38.05 kcal mol⁻¹ characterizing a very exergonic and favorable reaction. With the inclusion of solvent effects through the C-PCM(SMD) protocol previously described, the activation energy increases to 7.44 kcal mol⁻¹ while the total free energy of reaction becomes ∼1.5 kcal mol⁻¹ more exergonic. This implies that in solution the reaction rate should slightly decrease. In the chemical sense, this is expected since a large “concentration” of water in solution displace the reaction equilibrium towards the reactants, where the water is coordinated.

Fig. 3 B3LYP/Def2-TZVP optimized structures for the reactant (Reac-S), transition state (TS-S) and product (Prod-S) obtained along the singlet potential energy surface. Bond distances are given in angstrom.

Fig. 4 B3LYP/Def2-TZVP optimized structures for the reactant (Reac-T), transition state (TS-T) and product (Prod-T) obtained along the triplet potential energy surface. Bond distances are given in angstrom.

Table 2 Gibbs free energy variation in gas phase (ΔG_g) and in solution (ΔG_solution) for the uptake of nitric oxide by the NAMI-A complex, relative to the most stable (triplet) reactant and the Ru–NO bond distance (in Å) for each species^a

Parameter	Reactant	TS	Product
a Absolute energy values can be found in Table S1 of the ESI.
Singlet surface
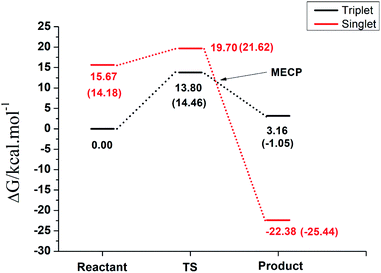
ΔGg (kcal mol^−1)	15.67	19.70	−22.38
ΔGsolution (kcal mol^−1)	14.18	21.62	−25.44
r(Ru–NO)	3.721	2.216	1.746
Triplet surface
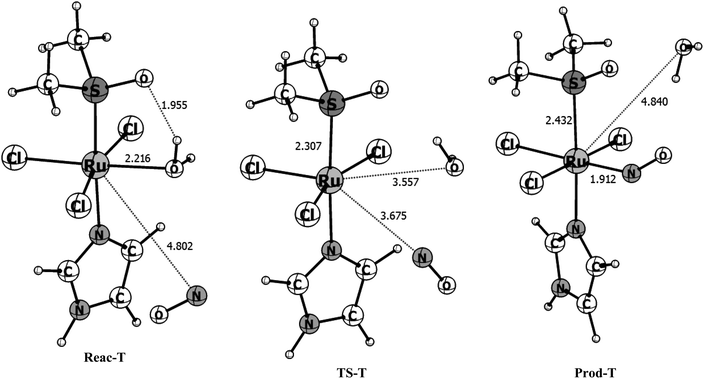
ΔGg (kcal mol^−1)	0.00	13.80	3.16
ΔGsolution (kcal mol^−1)	0.00	14.46	−1.05
r(Ru–NO)	4.801	3.675	1.912

---

The triplet reaction pathway has a transition state with an imaginary frequency of 71.0i cm⁻¹ and the distances of the leaving and entering group are 3.557 and 3.675 Å, respectively. From the reactants to the TS the r(Ru–H₂O) bond stretches from 2.216 to 3.557 Å while the r(Ru–NO) shortens from 4.802 to 3.675 Å, respectively. In the products, the water molecule is released and r(Ru–NO) = 1.912 Å which is, as expected, much longer than in the more stable singlet product. Also, different from the singlet product, the ∠RuNO angle of 141° is far from linearity due to the presence of the unpaired electron in the antibonding orbital of the NO ligand. In the transition state obtained for the triplet pathway the Ru–H₂O bond is 61% broken, compared with the reactants and the Ru–NO bond is only 8% formed, indicating a loose transition state and characterizing a dissociative mechanism, in contrast with what is found for the singlet surface. The B3LYP/def2-TZVP activation free energy computed for this pathway is 13.80 kcal mol⁻¹ (see Table 2) which is more than three times higher than for the singlet pathway, but it is still relatively low for a chemical reaction. The overall Gibbs free energy of reaction shows that the reaction is slightly unfavorable thermodynamically in the gas phase with ΔG_r = 3.16 kcal mol⁻¹. However, the inclusion of solvent effects makes the reaction slightly favorable thermodynamically, with ΔG_r = −1.05 kcal mol⁻¹. The solvent effects increase the energy barrier by only 0.7 kcal mol⁻¹.

From the three singlet-triplet possible crossing points initially located in Fig. 2, fully optimization of the MECP using the suggestions of Harvey et al.^34,49 and implemented in the ORCA program, lead to three crossing point structures within 5 × 10⁻⁴ eV of energy difference between the singlet and triplet surfaces (see Table S2† for the energetic data on the MECP's). However, only one of the MEPCs found seems likely to be the surface's crossing point. The first one, which happens before both the transition states is 30 kcal mol⁻¹ higher in energy than the triplet reactants and it is way out of the energy range. This probably happened because the MECPs were reoptimized at a different level of theory than that used for the PES exploration (Fig. 2). The second MECP is closer to the triplet transition state and it is around 2 kcal mol⁻¹ higher in energy than the later. Since the calculated spin–orbit coupling for this point is quite small, ∼5 cm⁻¹, if we assume a Landau–Zener hopping probability^68–70 it is very unlike that the crossing will happen at this point when we consider that the third optimized MECP structure (see Fig. 5) has a Ru–NO distance of 1.975 Å, the ∠RuNO angle of 141°, a strong SOC in the order of 450 cm⁻¹ (see Table S5†), and occurs after the transition state region of both surfaces, being 3.10 kcal mol⁻¹ higher in energy than the triplet reactant. Therefore, we will consider that this last MECP is the only one available for the reaction to take place.

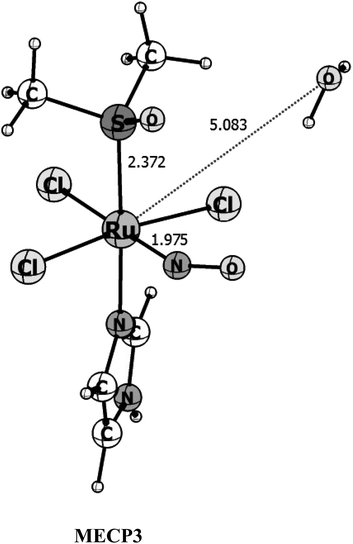Fig. 5 B3LYP/Def2-TZVP optimized structures for the Minimum Energy Crossing Point (MECP3) between the singlet and triplet surfaces. Bond distances are given in angstrom.

The overall free energy profile for the reactions is shown in Fig. 6. The analysis of the reaction on the singlet and triplet spin multiplicities individually revealed that the reaction can take place in both spin states with favorable Gibbs free energy differences. However, when the results are plotted on the same graph an overall picture of the process emerges.

Fig. 6 Overall energy profile in aqueous solution, computed at the B3LYP/def2-TZVP(SMD) for the NO–H₂O exchange reaction [RuCl₃(H₂O)(Im)(DMSO)] + NO → [RuCl₃(NO)(Im)(DMSO)] + H₂O, in the singlet and triplet spin states. Values in parenthesis were obtained in aqueous solution.

First, despite having a higher energy barrier, the reaction must take place at the triplet surface since the reactants in the singlet surface are ∼15 kcal mol⁻¹ higher in energy, which is the energy penalty for the electron pairing. Under normal physiological conditions, the reaction will follow the triplet pathway and the singlet pathway will take place only with the necessary input of energy. In other words, despite both pathways being thermodynamically favorable in aqueous solution, the reaction will take place in the triplet surface, with an energy barrier of 14.46 kcal mol⁻¹, leading to a rate constant of 1.82 × 10² s⁻¹. In order to generate the singlet product, which is the one observed experimentally, there must be a hoping from the triplet to the singlet surface through the MECP, which takes place after the transition state region and is 3.10 kcal mol⁻¹ higher in energy than the triplet reactant. Since this MECP occurs after the transition state, it will not interfere on the kinetics of the reaction and the crossing from the triplet to the singlet surface, to generate the most stable product, will have a close to unit transition probability assuming a Landau–Zener hopping probability, since the energies will be above the energy of the crossing region.

As the results suggest, the uptake of NO by the [RuCl₃(H₂O)(Im)(DMSO)] complex should occur on the triplet potential energy surface and, at some point along with the PES, the unpaired electron on the NO molecule should be transferred to the metallic center to generate the most stable [RuCl₃(NO)(Im)(DMSO)] singlet product. The apparent question that arises is when along with the PES this electron transfer process will occur. In order to investigate this process, we carried out CASSCF(4,4) and state averaged SA-CASSCF(4,4) on the B3LYP/def2-TZVP optimized structures obtained on the singlet and triplet surfaces, with the inclusion of second-order perturbation theory with the NEVPT2 approach. For the SA-CASSCF(4,4) the calculations were performed with an equal weight of 50% for each of the singlet and triplet states. Since at this point the interest is on the energetics, we used only a single root for each multiplicity. The CASSCF energetic results are shown in Table S4 of the ESI.† As we can see, for the reactants the most stable electronic structure is best described by the triplet geometry with a wave function composed of the average of the singlet and triplet states. This is expected since, at long distances, the unpaired electrons on NO and the metallic fragment does not interact and, therefore, there should be no significant difference between singlet and triplet states. At the transition state, the situation is the same that is, the SA-CASSCF describes better the electronic structure of the system at the triplet geometry. This result suggests that the reaction takes place in the way that first there is an atomic rearrangement and formation of the transition state following the triplet surface so that with the proper orientation the singlet product can be formed with the coupling of the two unpaired electrons. The products, on the other hand, are best described by the pure singlet state, with the singlet geometry. This does not necessarily mean that the ground state of the products has no contribution from the triplet state, but only that its weight is much less than the singlet state. The SA-CASSCF energetic results with second-order perturbation theory correction on top of it, SA-CASSCF/NEVPT2, quoted on Table S4 of the ESI,† shows that the reaction proceeds with an activation barrier of 7.88 kcal mol⁻¹ and a reaction energy of −30.21 kcal mol⁻¹. Since the singlet-triplet crossing regions takes place after the transition state for the reaction, we can use conventional transition state theory using the activation energy obtained in the lowest energy triplet surface. The SA-CASSCF/NEVPT2 activation energy leads to a rate constant of 11.32 × 10⁶ s⁻¹ at 300 K, showing that the uptake of nitric oxide by the mono-hydrolyzed species of NAMI-A in the biological medium is indeed a fast reaction and can compete with enzymatic processes involving NO. This result is also consistent with some experimental data in the literature.^34,71,72

Fig. S1 and S2† shows the SA-CASSCF active orbitals containing the largest contribution from the π orbitals from NO and the d orbitals from ruthenium for the reactants and TS points located along the triplet potential energy surface. As we can see, for the reactants and transition state there are no combinations involving the unpaired electrons over the NO and the metallic center. The spin–orbit coupling constant computed for the reactants and transition state is 0.19 and 0.16 cm⁻¹ respectively. Therefore, the entire system is composed of NO⁰ and Ru^III and the atomic rearrangement takes place before the coupling of the spins. As the Ru–NO distance decreases to 1.97 Å at the MECP (see Fig. 5) the computed spin–orbit coupling constant increases to ∼450 cm⁻¹. At this point, there is a considerable mixing involving the π* orbitals of NO and the d orbitals of the ruthenium, (see Fig. S3†). Therefore, the coupling of the electronic spins of the fragments occurs at the MECP, with concomitant NO → Ru electron transfer. At the most stable singlet product, as can be seen in Fig. S4,† the major contribution to the HOMO and HOMO-1 orbitals comes from the d(Ru)–π*(NO) interacting orbitals forming a Ru–NO bonding orbital, in a Ru^II–NO⁺ type of interaction. However, orbitals LUMO and LUMO+1, which have contributions from the π*(NO) and the d(Ru) orbitals with Ru–NO antibonding character (Ru^III–NO⁰), have combined occupation of 0.2. Compared with the combined occupation of 1.8 from both bonding orbitals HOMO and HOMO−1, indicates that there is 7% of the contribution from the Ru^III–NO⁰ character to the Ru–NO. That is, in the singlet state the Ru–NO bond in {Ru–NO}⁶ compounds cannot be view as composed of 100% of the Ru^II–NO⁰ character. This same observation was found for other ruthenium nitrosyl complexes.^73–75

4. Conclusions

In this work, we have carried out electronic structure calculations at the Density Functional Theory, DFT, and State-Averaged Complete Active Space Self Consistent Field, SA-CASSCF, with second-order perturbation theory corrections, NEVPT2, to investigate the NO scavenging mechanism by the Ru-based anticancer metallodrug NAMI-A. From the theoretical point of view, the calculations revealed that the reaction takes place at the triplet potential energy surface, with the singlet surface being ∼15 kcal mol⁻¹ shifted to higher energies. There is a surface crossing to form the most stable singlet product after the reaction takes place at the triplet surface. The spin pairing and electron transfer from the nitric oxide to the metallic fragment take place at the region of the minimum energy crossing point between the two surfaces. The Ru–NO bond in the {Ru–NO}⁶ product formed cannot be viewed as 100% composed of the Ru^II–NO⁺ configuration, as is usually assumed, since the CASSCF calculations revealed that in the product there is ∼10% of Ru^III–NO⁰ character. The main finding that can help to understand the possible role of the NAMI-A anticancer activity is the fact our SA-CASSCF/NEVPT2 calculations revealed that the uptake of NO by NAMI-A has a small energy barrier of ∼8 kcal mol⁻¹ and, therefore a rate constant of 11.3 × 10⁶ s⁻¹ at 300 K. In addition, the reaction is thermodynamically favorable with a Gibbs free energy of ∼30 kcal mol⁻¹. These results show that the uptake of nitric oxide by the NAMI-A complex is kinetically and thermodynamically feasible in biological medium and, this complex can indeed reduce the concentration of NO, reducing the angiogenesis and avoiding the tumor growth. The results obtained in this work, therefore, give support to the anti-angiogenesis theory associated with the mode of action of NAMI-A and other related compounds. However, we emphasize that our results and conclusions only consider the previously mentioned biological conditions where the first chloride hydrolysis is the predominant initial reaction for NAMI-A before the nitrosylation. Thus, we cannot guarantee that our proposed mechanism will not change in biological conditions that may favor other NAMI-A ligand-exchange competitive processes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico, INCT-Catálise) and FAPEMIG (Fundação de Amparo à Pesquisa do Estado de Minas Gerais) for the financial support and research grants. The authors would also like to gratefully acknowledge the free of charge availability of the ORCA package for academic purposes.

References

1. M. J. Clarke, Coord. Chem. Rev., 2002, 232, 69–93.
2. E. Alessio, G. Mestroni, A. Bergamo and G. Sava, Curr. Top. Med. Chem., 2004, 4, 1525–1535.
3. M. Melchart and P. J. Sadler, in Bioorganometallics: Biomolecules, Labeling, Medicine, 2006, pp. 39–64.
4. E. S. Antonarakis and A. Emadi, Cancer Chemother. Pharmacol., 2010, 66, 1–9.
5. A. Bergamo, C. Gaiddon, J. H. M. Schellens, J. H. Beijnen and G. Sava, J. Inorg. Biochem., 2012, 106, 90–99.
6. E. Alessio, Eur. J. Inorg. Chem., 2017, 1549–1560.
7. C. Jiang, H. Yang, P. Di, W. Li, Y. Tang and G. Liu, J. Appl. Toxicol., 2019, 39, 844–854.
8. D. Pluim, R. C. A. M. van Waardenburg, J. H. Beijnen and J. H. M. Schellens, Cancer Chemother. Pharmacol., 2004, 54, 71–78.
9. G. Sava, A. Bergamo, S. Zorzet, B. Gava, C. Casarsa, M. Cocchietto, A. Furlani, V. Scarcia, B. Serli, E. Iengo, E. Alessio and G. Mestroni, Eur. J. Cancer, 2002, 38, 427–435.
10. G. Sava, S. Zorzet, C. Turrin, F. Vita, M. Soranzo, G. Zabucchi, M. Cocchietto, A. Bergamo, S. DiGiovine, G. Pezzoni, L. Sartor and S. Garbisa, Clin. Cancer Res., 2003, 9, 1898–1905.
11. B. Gava, S. Zorzet, P. Spessotto, M. Cocchietto and G. Sava, J. Pharmacol. Exp. Ther., 2006, 317, 284–291.
12. S. Leijen, S. A. Burgers, P. Baas, D. Pluim, M. Tibben, E. van Werkhoven, E. Alessio, G. Sava, J. H. Beijnen and J. H. M. Schellens, Invest. New Drugs, 2015, 33, 201–214.
13. J. B. Aitken, S. Antony, C. M. Weekley, B. Lai, L. Spiccia and H. H. Harris, Metallomics, 2012, 4, 1051–1056.
14. A. Vacca, M. Bruno, A. Boccarelli, M. Coluccia, D. Ribatti, A. Bergamo, S. Garbisa, L. Sartor and G. Sava, Br. J. Cancer, 2002, 86, 993–998.
15. L. Morbidelli, S. Donnini, S. Filippi, L. Messori, F. Piccioli, P. Orioli, G. Sava and M. Ziche, Br. J. Cancer, 2003, 88, 1484–1491.
16. M. Ziche and L. Morbidelli, J. Neuro-Oncol., 2000, 50, 139–148.
17. D. Hanahan and J. Folkman, Cell, 1996, 86, 353–364.
18. A. Giacomini, P. Chiodelli, S. Matarazzo, M. Rusnati, M. Presta and R. Ronca, Pharmacol. Res., 2016, 107, 172–185.
19. Y. Zhao and A. A. Adjei, Oncologist, 2015, 20, 660–673.
20. E. Pipili-Synetos, E. Sakkoula and M. E. Maragoudakis, Br. J. Pharmacol., 1993, 108, 855–857.
21. E. Pipili-Synetos, E. Sakkoula, G. Haralabopoulos, P. Andriopoulou, P. Peristeris and M. E. Maragoudakis, Br. J. Pharmacol., 1994, 111, 894–902.
22. D. Fukumura, S. Kashiwagi and R. K. Jain, Nat. Rev. Cancer, 2006, 6, 521–534.
23. D. Wink, Y. Vodovotz, J. Cook, M. Krishna, S. Kim, D. Coffin, W. DeGraff, A. Deluca, J. Liebmann and J. Mitchell, Biochemistry, 1998, 802–809.
24. B. Bonavida, S. Baritaki, S. Huerta-Yepez, M. I. Vega, A. R. Jazirehi and J. Berenson, in Nitric Oxide (NO) and Cancer, 2010, pp. 459–477.
25. D. E. Koshland, Science, 1992, 258, 1861.
26. P. Pacher, J. S. Beckman and L. Liaudet, Physiol. Rev., 2007, 87, 315–424.
27. D. Basudhar, L. A. Ridnour, R. Cheng, A. H. Kesarwala, J. Heinecke and D. A. Wink, Coord. Chem. Rev., 2016, 306, 708–723.
28. M. R. Kapadia, J. W. Eng, Q. Jiang, D. A. Stoyanovsky and M. R. Kibbe, Nitric Oxide, 2009, 20, 279–288.
29. A. Castellarin, S. Zorzet, A. Bergamo and G. Sava, Int. J. Mol. Sci., 2016, 17, 1254.
30. M. Oszajca, E. Kuliś, G. Stochel and M. Brindell, New J. Chem., 2014, 38, 3386–3394.
31. H. Li, D. Wang, X. Zhao, L. N. Lu, C. Liu, L. D. Gong, D. X. Zhao and Z. Z. Yang, J. Comput. Chem., 2018, 40, 1141–1150.
32. E. Alessio, G. Balducci, A. Lutman, G. Mestroni, M. Calligaris and W. M. Attia, Inorg. Chim. Acta, 1993, 203, 205–217.
33. G. L. S. Rodrigues and W. R. Rocha, J. Phys. Chem. B, 2016, 120, 11821–11833.
34. J. N. Harvey, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 1–14.
35. M. Bacac, A. C. G. Hotze, K. Van Der Schilden, J. G. Haasnoot, S. Pacor, E. Alessio, G. Sava and J. Reedijk, J. Inorg. Biochem., 2004, 98, 402–412.
36. A. Casini, G. Mastrobuoni, M. Terenghi, C. Gabbiani, E. Monzani, G. Moneti, L. Casella and L. Messori, J. Biol. Inorg Chem., 2007, 12, 1107–1117.
37. S. Ciambellotti, A. Pratesi, M. Severi, G. Ferraro, E. Alessio, A. Merlino and L. Messori, Dalton Trans., 2018, 47, 11429–11437.
38. M. I. Webb and C. J. Walsby, Dalton Trans., 2011, 40, 1322–1331.
39. J. C. Toledo, B. Dos Santos Lima Neto and D. W. Franco, Coord. Chem. Rev., 2005, 249, 419–431.
40. N. Cetinbas, M. I. Webb, J. A. Dubland and C. J. Walsby, J. Biol. Inorg Chem., 2010, 15, 131–145.
41. National Center for Biotechnology Information, PubChem Compound Summary for CID 795, Imidazole, https://pubchem.ncbi.nlm.nih.gov/compound/Imidazole, accessed 2 February 2021.
42. R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, Dordrecht, 1989.
43. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
44. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
45. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
46. F. Neese, J. Comput. Chem., 2003, 24, 1740–1747.
47. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
48. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
49. J. N. Harvey, M. Aschi, H. Schwarz and W. Koch, Theor. Chem. Acc., 1998, 99, 95–99.
50. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
51. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
52. P. E. M. Siegbahn, J. Almlöf, A. Heiberg and B. O. Roos, J. Chem. Phys., 1981, 74, 2384–2396.
53. B. J. Neves, R. F. Dantas, M. R. Senger, C. C. Melo-Filho, W. C. G. Valente, A. C. M. de Almeida, J. M. Rezende-Neto, E. F. C. Lima, R. Paveley, N. Furnham, E. Muratov, L. Kamentsky, A. E. Carpenter, R. C. Braga, F. P. Silva-Junior and C. H. Andrade, J. Med. Chem., 2016, 59, 7075–7088.
54. C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305.
55. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252.
56. C. Angeli, R. Cimiraglia and J. P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153.
57. S. Grimme and A. Hansen, Angew. Chem., Int. Ed., 2015, 54, 12308–12313.
58. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
59. T. Nakajima and K. Hirao, Chem. Rev., 2012, 112, 385–402.
60. F. Neese, J. Chem. Phys., 2005, 122, 034107.
61. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
62. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
63. P. C. Ford, J. C. M. Pereira and K. M. Miranda, Struct. Bonding, 2013, 154, 99–136.
64. W. Kaim, in Advances in Inorganic Chemistry, 2015, vol. 67, pp. 295–313.
65. J. H. Enemark and R. D. Feltham, J. Am. Chem. Soc., 1974, 96, 5002–5004.
66. R. D. Feltham and J. H. Enemark, in Topics in Stereochemistry, John Wiley & Sons, Inc., 2007, vol. 12, pp. 155–215.
67. F. Bottomley, Coord. Chem. Rev., 1978, 26, 7–32.
68. J. R. Rubbmark, M. M. Kash, M. G. Littman and D. Kleppner, Phys. Rev. A, 1981, 23, 3107–3117.
69. C. Zener, Proc. R. Soc. London, Ser. A, 1933, 140, 660–668.
70. C. Wittig, J. Phys. Chem. B, 2005, 109, 8428–8430.
71. M. R. A. Blomberg and P. Ädelroth, Biochim. Biophys. Acta, Bioenerg., 2018, 1859, 1223–1234.
72. J. Tejero, A. P. Hunt, J. Santolini, N. Lehnert and D. J. Stuehr, J. Biol. Chem., 2019, 294, 7904–7916.
73. L. Freitag and L. González, Inorg. Chem., 2014, 53, 6415–6426.
74. L. Freitag, S. Knecht, S. F. Keller, M. G. Delcey, F. Aquilante, T. Bondo Pedersen, R. Lindh, M. Reiher and L. González, Phys. Chem. Chem. Phys., 2015, 17, 14383–14392.
75. A. P. De Lima Batista, A. G. S. De Oliveira-Filho and S. E. Galembeck, Phys. Chem. Chem. Phys., 2017, 19, 13860–13867.

---

Footnotes

† Electronic supplementary information (ESI) available: B3LYP/def2-TZVP optimized cartesian coordinates of all species investigated in this work, absolute and relative energy values obtained, details of the CASSCF calculations (active spaces and energies obtained), example of the ORCA input files used for the SA-CASSCF and MECP calculations and SA-CASSCF orbital analysis for the species studied. See DOI: 10.1039/d0ra10622d

‡ Present address: Department of Physics, Albanova University Center, Stockholm University, 10691 Stockholm, Sweden.

---