Open Access Article
Open Access ArticleCore growth of detonation nanodiamonds under high-pressure annealing
Denis Bogdanova,
Alexander Bogdanova,
Vladimir Plotnikova,
Sergey Makarova,
Alexander Yelisseyevb and
Aleksei Chepurov *b
*b
aAltai State University, Pr. Lenina 61a, Barnaul, 656049, Russia
bV.S. Sobolev Institute of Geology and Mineralogy SB RAS, Koptyuga Ave. 3, Novosibirsk, 630090, Russia. E-mail: achepurov@igm.nsc.ru
First published on 6th April 2021
Abstract
The present paper reports the results of a study of the X-ray and Raman spectra of detonation nanodiamonds after high-pressure–high-temperature (HPHT) annealing at different temperatures. The experiments were carried out using a multi-anvil high-pressure apparatus of the “split-sphere” type (BARS) at 5 GPa and 1100–1500 °C. It was found that HPHT annealing at 1500 °C led to the growth of nanodiamond cores sized from 4.2 to 6.9 nm. It was determined that transformation of the detonation nanodiamond particles includes the formation of both a new diamond phase as well as ordered graphite around the initial diamond core. It was suggested that the gasification of adsorbed impurities from the nanodiamond shell results in the formation of a supercritical fluid that stimulates the growth of the diamond phase. The appearance of newly formed graphite led to covering the exposed areas of the nanodiamond core capable of contacting with neighboring nanodiamonds during annealing, which explains the earlier established heterogeneity of the hardness increase within the sample volume after HPHT sintering.
1. Introduction
Nanocrystals of diamonds produced by detonation synthesis (DND) are an attractive material for the production of composites, mainly because of their low cost in mass production. At the same time, their use is limited mainly due to the presence of a shell around the diamond core as “onion-like” structures, consisting of carbon as well as impurities captured from the starting materials.1 Different approaches have been used to affect the core–shell microstructure, and the one we used is by annealing at high pressure and high temperature (HPHT), which changes the properties of both natural and synthetic diamonds.2,3 The growth of detonation diamond nanocrystals under HPHT is obviously related to the phase transformation of graphite into diamond. The transition of carbon atoms from the sp2 to sp3 state during the annealing of detonation diamonds in a hydrogen atmosphere is well known, with the graphite-to-diamond transition resulting in nanocrystals growth up to the micron size.4 The growth of detonation diamond crystals after a high-pressure and high-temperature process has an impact on the Raman scattering spectra.5 As is known, the first-order spectrum in a perfect monocrystal of natural diamond consists of a single narrow symmetric line at 1332.5 cm−1 with a full-width at half-maximum (FWHM) of about 1.5 cm−1, associated with scattering at triply degenerated phonons TO(X) with the F2g symmetry.6 DNDs have demonstrated a considerably weaker and asymmetric Raman line at about 1324 cm−1 broadened up to 30 cm−1,7 where the broadening effect is due to a size factor and size-related change of the phonon spectrum in nanocrystals.7 The Raman spectra of nanodiamonds commonly contain broad bands at about 1350 and 1580 cm−1. The latter is associated with crystalline graphite (G band), while the 1350 cm−1 band is related to disordered or nanocrystalline graphite, disordered glass-like carbon, sp2-hybridized carbon phases, or microcrystalline defect graphite.8 Bands with maxima at 1550 and 1630 cm−1 related to the fluctuations of links C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C
C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and O–H are also present in the Raman spectra of detonation diamonds.8–10 The Raman spectra of detonation diamonds also contain broad bands in the 400–800 cm−1 range as well as a peak near 1050 cm−1.11
O, and O–H are also present in the Raman spectra of detonation diamonds.8–10 The Raman spectra of detonation diamonds also contain broad bands in the 400–800 cm−1 range as well as a peak near 1050 cm−1.11
After annealing at 940–1600 °C, reflections of the graphite phase are present in the X-ray diffraction patterns of detonation diamonds, alongside the diamond reflections (111), (220), and (311). At the same time, the intensity of graphite lines increases as the annealing temperature increases, while the diamond reflections weaken. Also, X-ray diffraction patterns show a decrease in the reflections' intensity and an increase in their asymmetry, which proves the emerging diffusion scattering at the fluctuations of a long-range order. Such fluctuations may be related to the appearance of graphite flakes on diamond crystals. In contrast, the growth of nanoparticles even up to a micron-size was reported as a result of annealing in the hydrogen environment at temperatures of 700–800 °C,4 or after sintering the detonation diamond at a pressure of 7 GPa and a temperature of up to 1600 °C,12 with some diamond crystals reaching the sizes of 100–750 μm without any visible graphitization of the nanodiamond. Moreover, carbon transition from sp2 to sp3 was observed followed by weakening of the 1350 cm−1 band in the Raman spectra.11 Therefore, the available literature data presents evidence for a significant increase in the size of detonation diamond nanoparticles under high-pressure conditions, but the mechanism of this process remains unclear. The present paper reports on the growth of the core of detonation nanodiamonds both in the form of graphite and diamond phases after annealing at a pressure of 5 GPa and temperatures of 1100 °C, 1200 °C, 1300 °C, 1400 °C, and 1500 °C, based on X-ray diffraction and Raman spectroscopy data.
2. Experimental
The powder of a detonation nanodiamond fabricated under Specification 84-1124-87 of the Federal State Unitary Enterprise “Federal Research & Production Center ALTAI” was used.13,14 Starting samples were prepared by pressing the nanodiamond powder using a hydraulic press with a force of 2000 kg. In order to study the annealing impact at atmospheric pressure, the samples were treated in vacuum at a temperature of 1000 °C. High-pressure experiments were performed using a multi-anvil apparatus of the “split-sphere” type (BARS) at the Institute of Geology and Mineralogy of the Siberian Branch of Russian Academy of Sciences according to the state assignment. The high-pressure cell was made from refractory oxide ZrO2. A graphite heater was used in the experiments. The initial nanodiamond powder was pressed in the form of with a diameter of 8 mm that matched the size of the samples for hardness testing. The thermocouple was placed near the reaction zone (as in Fig. 1 of ref. 15). The pressure in the cell was calibrated at room temperature with the reference substances Bi and PbSe.16 The temperature was measured with a PtRh30–PtRh6 thermocouple without a pressure correction. The temperature correction for pressure was determined by the melting curve of the pure metals Ag and Au.17 The measurement error was ±0.2 GPa and ±25 °C. The methodology was the same in all of the experiments. Heating of the samples was carried out after the pressurization. The short annealing time of 60 s was chosen to determine the changes that take place in very short runs, as demonstrated in our previous study.18 After the experiment, the samples were cooled by quenching. The details of the experimental procedures are described in our earlier works.19,20 The experiments were carried out at a pressure of 5 GPa and different temperatures: 1100 °C, 1200 °C, 1300 °C, 1400 °C, and 1500 °C (Table 1).| Experimental conditions | 2θ, degrees | (hkl) | d, Å | FWHM, degrees | β, degrees | I/I1200 ratio (111), % | Crystal size, nm |
|---|---|---|---|---|---|---|---|
| P = 0 GPa, T = 25 °C (initial powder) | 43.7 | 111 | 2.07 | 2.25 | 2.01 | — | 4.2 ± 0.2 |
| 75.3 | 220 | 1.26 | 2.92 | 2.68 | |||
| 91.3 | 311 | 1.07 | 3.03 | 2.79 | |||
| P = 0 GPa, T = 1000 °C | 43.8 | 111 | 2.07 | 2.23 | 1.99 | — | 4.2 ± 0.2 |
| 75.3 | 220 | 1.26 | 2.93 | 2.69 | |||
| 91.3 | 311 | 1.07 | 3.01 | 2.77 | |||
| P = 5 GPa, T = 1100 °C | 43.6 | 111 | 2.07 | 1.76 | 1.52 | — | 5.0 ± 0.3 |
| 75.2 | 220 | 1.26 | 2.41 | 2.17 | |||
| 91.3 | 311 | 1.07 | 2.95 | 2.71 | |||
| P = 5 GPa, T = 1200 °C | 43.7 | 111 | 2.07 | 1.67 | 1.43 | — | 5.3 ± 0.4 |
| 75.7 | 220 | 1.26 | 2.29 | 2.05 | |||
| 91.2 | 311 | 1.07 | 2.82 | 2.58 | |||
| P = 5 GPa, T = 1300 °C | 43.7 | 111 | 2.07 | 1.67 | 1.43 | 99 | 5.2 ± 0.4 |
| 75.2 | 220 | 1.26 | 2.38 | 2.14 | |||
| 91.4 | 311 | 1.07 | 2.89 | 2.65 | |||
| P = 5 GPa, T = 1400 °C | 43.7 | 111 | 2.07 | 1.66 | 1.42 | 97 | 5.2 ± 0.5 |
| 75.2 | 220 | 1.26 | 2.45 | 2.21 | |||
| 91.4 | 311 | 1.07 | 2.86 | 2.62 | |||
| P = 5 GPa, T = 1500 °C | 43.9 | 111 | 2.07 | 1.45 | 1.21 | 76 | 6.9 ± 0.5 |
| 75.7 | 220 | 1.26 | 1.79 | 1.55 | |||
| 91.4 | 311 | 1.07 | 2.07 | 1.83 |
X-ray diffraction studies of the samples were performed using the DRON-3 diffractometer with a copper anticathode of the X-ray tube. The X-ray diffraction patterns were obtained in the range of angles 2θ = 30°–110° in discreet scanning mode with a step of 0.01° and exposure during 3.6 seconds at each point. The Search-Match software package with powder diffraction database was used to identify the phases. Raman spectra were recorded at room temperature using a LabRAM HR800 Raman confocal microspectrometer with excitation from a He–Cd – gas laser (325 nm) and the second harmonic of a Nd:YAG diode pumped solid laser (532 nm).
3. Results
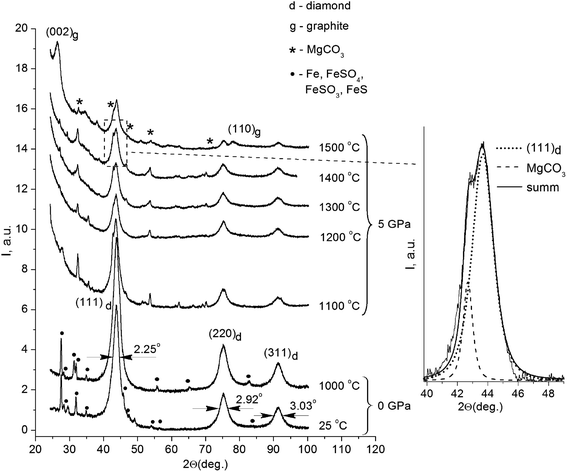
Fig. 1 displays the X-ray diffraction patterns of the initial powder of the detonation nanodiamond and data for the samples treated at high pressure and different temperatures.All the patterns were identified as a system of reflections from a carbon structure with a diamond crystalline lattice. The intensive symmetric reflections observed at angles of 2θ = 43.9°, 2θ = 75.3°, and 2θ = 91.3° correspond to the (111), (220), and (311) reflections from the diamond lattice (indicated in the picture). The diffractograms of the initial detonation nanodiamond powder (line 1 on Fig. 1) also demonstrated the presence of narrow maxima that correspond to the diffraction on large iron particles (Fe) and iron-containing compounds, such as FeS, FeSO4, and FeSO3. It should be noted that the effects of interaction between iron particles and diamond that usually take place at high temperatures21,22 could not be observed in the obtained run products. In samples annealed at high pressure, the X-ray line (111) of the diamond is located near the line of MgCO3, which does not show an anomalous broadening. Therefore, the reflex width cannot significantly exceed the instrumental broadening. In this case, the superposition method can be used to analyze the diffraction profile, and the results of the approximation are shown in Fig. 1.
Nanodiamond particles consist mainly of carbon, with its greatest part forming the diamond core, as well as a considerable amount of technology-related impurities. Previous investigations showed that detonation nanodiamonds contain oxygen (4.93 mas.%), iron (4.52 mas.%), sulfur (4.33 mas.%), calcium (1.92 mas.%), and aluminum (1.27 mas.%).23 During production procedures, strong acids are used, mainly sulfuric acid (H2SO4), to remove metallic impurities and carbon. This explains the presence of certain substances that are the products of interaction between the acids and the impurities in the X-ray diffraction patterns. It is noteworthy that the system of reflections corresponding to iron and iron-containing compounds is absolutely absent in the X-ray diffraction patterns of the samples annealed under high pressure. As for the samples annealed at high pressure, their X-ray diffraction patterns also showed reflections that belong to MgCO3. A small amount of Mg in the composites could be explained by the configuration of the high-pressure cell assembly with the MgO sleeve used.
The initial nanodiamond powder as well as the sintered samples demonstrated an anomalous broadening of the reflexes (Fig. 1), but the FWHM values of the reflections for the samples were different (Table 1). As for the FWHM value of the (111) reflection in the initial nanodiamond, this was 2.25°. The nanodiamonds after annealing in vacuum showed no substantial changes in the reflection's FWHM value compared to that of the initial nanodiamond powder, showing a value of 2.23°. The HPHT annealing of nanodiamonds resulted in a decrease in the reflection's FWHM values. The sample sintered at 1500 °C showed the reflection width (111) of 1.45°, which was 0.8° less than the reflection width (111) of the initial nanodiamond sample.
The width of the X-ray lines is determined by two parameters of the crystalline structure. First, by the size of the coherent scattering areas (the sizes of the areas of the crystal with an ideal crystalline structure). Second, by the microstresses in the crystalline structure, determined by atomic displacements from the nodes of the crystalline structure.24 The analysis of the reflections broadening make it possible to define the sizes of the diamond nanocrystals in the samples. However, the width of the X-ray lines in the X-ray diffraction patterns is determined not only by the physical factors (micro-stress and a small value of CDS), but also by the radiation heterogeneity and geometrical conditions of the patterns recording (aperture sizes, divergence, and non-monochromaticism of the X-rays primary beam, absorption within the sample, etc.). Actually, the X-ray line can be performed as a ‘sum’ of instrumental broadening of b and physical broadening of β. Therefore, in order to find the value of the CDS and micro-stress, it was necessary to subtract the constituents, such as radiation heterogeneity-bound and recording-geometry-based, from the experimentally determined total FWHM value for the X-ray line.
A summary of the X-ray diffraction measurements of the reflection positions and broadening, as well as the values of interplanar distances for crystals of the detonation nanodiamond before and after the sintering, are given in Table 1. The determination of the interplanar distances dhkl of the lattice was carried out by measuring the Wulff–Bragg's angle θ with the application of Wulff–Bragg's formula:
2dhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl = nλ. θhkl = nλ.
| (1) |
The ratio I25/I1000 between the integral reflections intensities (111) of the initial nanodiamonds and one sintered in vacuum at 1000 °C without external pressure had a value of 0.73. A value less than one indicates the increase of the portion of the diamond phase in the sample after sintering. This result is very plausible, because the nanodiamond particles lost up to 20 mas.% of volatile compounds from their surface during annealing.23 In this case, the increase in the portion of the diamond phase in the samples was most probably due to the impurity release. An opposite result was observed for the samples sintered under high pressure and high temperatures (Fig. 1). Thus, the correlation between the reflections of the integral intensities (111) for the samples sintered at 1300 °C and 1400 °C with the reflection intensity (111) for the sample sintered at 1200 °C corresponded to I1300/I1200 = 0.99 and I1400/I1200 = 0.97, respectively. It should be noted that a slight decrease in the diffraction maxima intensities was observed as the temperature increased. The value of this ratio being close to one suggests that no significant phase transformation of the diamond crystalline lattice occurred after sintering below 1400 °C. In the sample annealed at 1500 °C, this ratio was I1500/I1200 = 0.76 and the X-ray diffraction patterns showed a significant decrease in the reflection intensity (111). It is supposed that the reduction of the I1500/I1200 ratio was due to the diamond-to-graphite phase transition of the nanodiamond core during the HPHT process.
As has been mentioned above (Table 1), all the reflections of the detonation diamond showed a considerable broadening, which could be attributed to the small size of the particles and an increase in the micro-stress of the second type. The value of the lattice microdeformation-based broadening is defined by the Δd/d ratio value, where d is an interplanar distance for an ideal crystal and Δd is an average value of the interplanar distance shift. The Δd/d value in covalent crystals cannot be large because of the great modules of diamond elasticity.25 That is why it is the small-sized diamond crystals that contribute greatly to the reflections' broadening. Also, in order to determine the crystal size, a Selyakov–Scherrer simplified equation can be applied,26 and that shows that the physical broadening of the β X-rays lines is linked only to a dispersity effect expressed by the formula:
β = λ/(D × cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) θ)
| (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is a cosine of the diffraction angle of the X-rays. The calculated sizes of the nanodiamond crystals are presented in the right column of Table 1.
θ is a cosine of the diffraction angle of the X-rays. The calculated sizes of the nanodiamond crystals are presented in the right column of Table 1.
The data obtained confirm that the size of the detonation nanodiamond crystals prior to HPHT treatment was near 4.2 nm which is in good agreement with the published data.27,28 High-temperature processing in the vacuum was not followed by any visible structural changes of the nanodiamond core, and the size of diamond nanocrystals remain unchanged after the annealing at 0 GPa (4.2 nm). On the contrary, annealing under high pressure and high temperatures was followed by an increase in the diamond nanocrystals size; whereby the size of the nanodiamond crystals annealed at 5 GPa and 1100 °C reached 5 nm. Further increases of the annealing temperature were accompanied by the gradual growth of nanocrystals, and for the sample annealed at 1500 °C, this was determined to be more than 2.6 nm, resulting in a nanocrystal size of 6.9 nm (Table 1).
It should be noted, that the sample sintered at the temperature of 1500 °C showed wide, pronounced maxima at the angles 2θ = 26.5° and 2θ = 77.6°, which corresponded well with the diffraction at the (002) and (110) planes of graphite. Evaluation of the sizes of these structures along with the analysis of the reflection half-width was made using a similar method as in our previous work,18 and it gave an average value of the graphite-like structures of 7.8 nm. The calculated value of interplanar distance was d(002) = 3.36 Å, which agreed well with the period of neighboring graphene layers in a perfect crystalline structure of graphite.29 The correlation of the diamond (111) and (002) reflection integral intensities with that of graphite for the given sample equaled ID/IG = 4/3, and roughly corresponded to a 60 wt% diamond phase in the sample. Most probably, the size of the carbon inclusions cannot be associated with the diffraction by carbon particles of a similar size. In our case, the appeared graphite phase could be located only on the surface of the diamond nanocore, and the value of 7.8 nm corresponded to the size of the whole complex: inside it, there was a 6.9 nm diamond nanocrystal surrounded by carbon structures that did not have a three-dimensional symmetry. The thickness of the carbon shell was about 0.9 nm, which corresponded to the three enclosed in each other's carbon spheres consisting of graphene layers located at a distance of d(002) = 3.36 Å from each other.
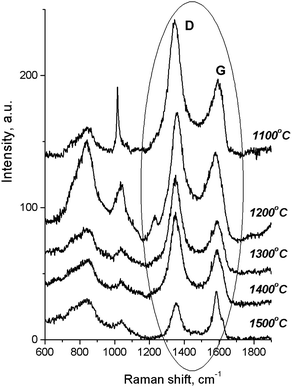
According to the Raman spectra of the HPHT-annealed detonation diamond (Fig. 2), the intensity of G and D peaks decreased as the sintering temperature increased. Here G is a peak related to the graphite lattice, while the D peak is caused by disordered graphite. It can be seen that the 1322 cm−1 line characteristic of detonation diamond was not observed in the Raman spectra.
4. Discussion
The results of the study demonstrated that the increase in the nanocrystals of detonation diamond after HPHT annealing could be a result of the transition of the carbon present on the surface of the nanodiamond core into the diamond phase. On the one hand, X-ray diffraction analysis did not identify any carbon forms other than diamond. On the other hand, the sample sintered at 1500 °C demonstrated well-pronounced maxima corresponding to the diffraction on the (002) and (110) planes of graphite.It is known that graphite crystal consists of a system of mutually parallel hexagonal planes where carbon atoms are located in the corners of a hexagon. Each plane is turned at 60° toward the neighboring plane, and the layers alternation matches the type ab ab.29 According to the X-ray diffraction patterns of a crystalline carbon, the reflections of the 00l type determine the periodicity of the layers and the interplanar distance, as the regular ab ab is characterized by peaks of the (hlk) type.30 However, in our case there were no general (hlk) reflections on the sample X-ray diffraction patterns. According to Warren,31 crystals with a hexagonal structure are built from separate layers of graphite (onion-like structures).1 The layers are parallel to each other at equal distances, but their rotations around the normal are random. Annealing at 1300–1700 °C changed their position, and led to an ordering of the “onion-like” structures, which finally affected the Raman spectra. As a result, the X-ray diffraction patterns demonstrated only crystalline reflections of the (00l) and (hk0) types. The presence of only (00l) and (hk0) reflections with the absence of (hkl) reflections indicated the absence of a 3D periodical arrangement of carbon atoms in the graphite structure. Similar peculiarities were discovered for multi-layer carbon nanotubes32–34 and “onion-like” carbons presenting closed, nested one-inside-another carbon spheres. Later on, similar closed graphitic spheres were discovered on the surface of high-temperature-processed diamond nanocrystals.35–38 The structural transformation of the nanodiamonds start from the particle surface and result in the formation of an external graphite-like shell. The process continues toward the nanodiamond center, while the diamond plane (111) turns into a graphitic plane (001).39,40
X-ray diffraction patterns of the other samples contained no (002) reflections of graphite. However, this did not mean that the surface of the nanodiamond core bore no carbon with a graphitic structure. Diamond nanoparticles are known to have a complex arrangement of a carbon layer on the surface of the diamond nanocrystal.41 It is considered that the layer consists of disordered, non-closed “onion-like” graphitic carbon nanoplates. The thickness of such a layer depends on the synthesis conditions and can reach 2.5 nm. The intense 002 peak corresponding to the graphite structure requires a natural laying of graphene sheets, but its absence indicates the presence of irregularly arranged graphene layers only.42 Annealing at higher temperatures facilitates the arrangement and structuring of graphene layers on the surface of the diamond nanocrystal. In this respect, the observed growth of diamond nanocrystals is most probably related to the transition of the carbon shell into a diamond phase that had possibly been rearranged into an ordered graphite crystalline structure. At lower annealing temperatures, the crystallization of the graphite shell is less expressed. The formation of the new crystalline phase is accompanied by the appearance of the reflection system in the X-ray diffraction pattern of the sintered sample. This results in reducing the intensity of the diamond reflections (I1500/I1200).
At the same time, in the Raman spectra, the most well-repeated bands are designated as D and G bands (Fig. 2), and these are due to graphite. It is commonly accepted that the band of about 1586 cm−1 in the optical mode of the stretching symmetry E2g (G-mode) reflects a well-arranged, defect-free crystalline graphite. In the current case, it was shifted toward 1600 cm−1, because of the disordering in graphite43 (Fig. 3c). In natural crystalline graphite, this band is rather narrow: the FWHM value is about 13 cm−1 (Fig. 3b). A broadening to values of 60–80 cm−1 is commonly explained by the occurrence of glass-like graphite. The D band near 1354 cm−1 is associated with disordered graphite. This was first described by Tuinstra and Koening44 and was related to a breathing mode of symmetry A1g with a phonon near the border of the k-zone: this mode is absent in perfect graphite. The band position varies in the range of 1310–1450 cm−1, whereas the FWHM values are within the interval of 80–400 cm−1. The D-peak intensity changes depending on a number of aromatic rings in graphitic clusters. Although Raman spectra are not a specific criteria to measure sp3- or sp2-hybridizations' contribution, some parameters in these spectra, such as the position of the G peak or the ID/IG ratio, can be informative. For instance, a high-energy shift of the G peak and an increase of the ID/IG ratio indicates the increase of sp2 π–π*-binding and otherwise, the decrease of diamond-like sp3 hybridization.45 The intensity distribution in graphite bands at D = 1354 cm−1 and G = 1586 cm−1 support the domination of graphite phonon lines in the spectra of thermobarically sintered samples of the detonation nanodiamond. Comparing the obtained Raman spectra and the spectrum of the initial detonation nanodiamond, it can be seen that the diamond line with the maximum at 1322 cm−1 can be clearly identified (Fig. 3c). In that case, an intense G band of graphite is located near 1616 cm−1, whereas the much weaker D band has its maximum near 1443 cm−1 (Fig. 3c).
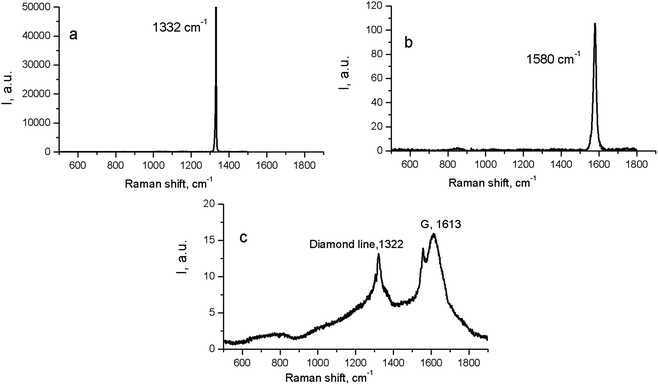 | ||
| Fig. 3 Raman spectra for natural crystalline cubic diamond (a), graphite (b), and the initial (untreated) detonation nanodiamond (c). | ||
On the contrary, the Raman spectra of the HPHT-sintered detonation nanodiamond contained only G and D bands of sp2-linked carbon (graphite). At the same time, the X-ray diffraction (Fig. 1 and Table 1) results demonstrated the presence of a diamond phase in our samples. It may look as if these two methods give conflicting results, but this contradiction can be easily explained: it is well known that the high symmetry of the diamond lattice determines the simplicity of the oscillating spectrum. The Raman spectrum of diamond contains only a line near 1332.5 ± 0.5 cm−1 corresponding to triply-degenerated fundamental oscillation in the structurally perfect diamond lattice.46 The width of this peak grows when passing to a nanocrystalline diamond, and the peak then disappears completely in tetragonal and structureless films.46 It should be emphasized that the Raman spectrum of nanocrystals of detonation diamond (Fig. 3c) contained a wide line near 1322 cm−1 with an FWHM value of about 80 cm−1, which can easily be hidden inside the D band (Fig. 2). Fig. 2 also shows the manifestation of a number of other features in the low-energy range in the Raman spectra of detonation nanodiamond after HPHT treatment; for example, in the form of broad bands of about 800 and 1000 cm−1. These features are supposed to originate from the violation of the selection rules and are said to be characteristic of the vibrational density of the states of diamond.47 Concerning the broad band near 1000 cm−1, there are some other alternative explanations for this, such as the surface plasmon modes47 or trans-polyacetylene (t-PA) structures on the particle surface.48
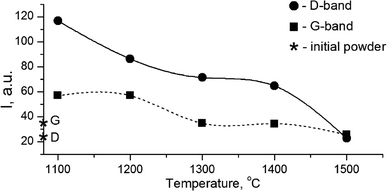
The growth of the nanocrystals of detonation diamond during HPHT sintering evidently occurred due to the phase transition of carbon from a non-diamond phase (sp2) into the sp3-state. Comparing the dependence of the integral intensity of D- and G-spectral bands on the sintering temperature (Fig. 4), it is evident that the integral intensity monotonically decreased as the HPHT temperature increased.
It is known that annealing above 1000 °C leads to an increase in the intensity of D and G bands and a decrease in their width, which indicates a decrease in the defectiveness in the graphitic layers, while their intensity increase demonstrates the graphitization of diamond nanoparticles. The latter is considered as evidence of sp3 → sp2 transition in the hybridization of carbon atoms to form onion-like carbon nanoparticles.8 However in our case, the sintering at a pressure of 5 GPa and temperatures of 1100–1500 °C was accompanied by a transformation of graphite into diamond as well. It should be emphasized that, simultaneous to the sp2 → sp3 phase transition, the reduction of the FWHM values for D and G bands occurs, as shown in Fig. 5. This fact illustrates the growing structural quality of the graphite phase, which was especially noticeable in the sample sintered at 1500 °C.
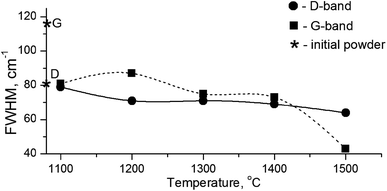 | ||
| Fig. 5 FWHM values for D- and G-bands in the Raman spectra depending on the annealing temperature. Diamond symbols correspond to the graphite and diamond lines in the initial powder. | ||
The experimental results are in agreement with the phonon confinement model (PCM),49,50 which argues for the appearance of additional phonon modes in the spectrum of phonon vibrations of diamond according to the expression 0 < q < 1/L, where q is the wave vector and L is the nanoparticle size. As a result, the Raman spectrum is broadened and shifted toward low wavenumbers, while the intensity of the 1322 cm−1 lines essentially decreases. It should be added that the broadening of the 1332 cm−1 line and its intensity decrease is due to the small size of the detonation diamond particles. This elucidates the absence of the 1322 cm−1 line in the Raman spectrum of the HPHT-treated detonation diamond due to its hiding within a rather intense signal from the graphite D-band. It can also be suggested that the HPHT effect changes the content of phonon modes, because, taking into account the high Debye temperature for diamond (1910 K), the high P–T experimental conditions (5 GPa and 1100–1500 °C) cause changes in the phonon spectrum of the diamond nanocrystals. Therefore, the X-ray diffraction and Raman spectroscopy analyses enable establishing the temperature at which the graphitization of the nanodiamond core does not negatively affect the structure and properties of the thermobarically sintered diamond matrix.
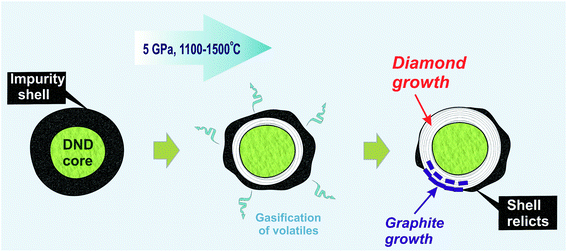
The data obtained in the present work elucidate the process of nanodiamond transformation. Annealing under a pressure of 5 GPa and at temperatures in the range of 1100–1500 °C is followed by graphitization, which occurs with the formation of multi-layer graphitic shells on the surface of diamond nanocrystal from the initially present atoms of sp2-bound carbon. The distance between the separate layers corresponds to the distance between graphite layers, that is 3.36 Å. The thickness of the whole shell is about 1 nm. At the same time, due to the structuring of the layers, and through the competitive sp2 → sp3 transition, the growth of nanodiamond core occurs and most intensively takes place at 1500 °C, demonstrated by the increase from 4.2 to 6.9 nm (Table 1).
Based on the results of the study, it is possible to make an assumption about the mechanism of synthesis of the diamond phase as well as the growth of the diamond layer during HPHT annealing. On the one hand, under the experimental conditions (5 GPa and 1100–1500 °C), a direct transition of graphite to diamond by the solid-to-solid mechanism is not possible, since it requires significantly higher pressures: graphite → diamond transition is known to occur at a pressure of 9 GPa and temperature of 2200–2300 °C,51 although the synthesis most typically occurs at higher pressures.52 On the other hand, for the catalytic transformation of graphite into diamond at the given P–T parameters, the presence of transition metals (Fe, Ni, Co) is necessary.53,54 However, no metal melt was identified in the products in our experiments. A possible factor that stimulates diamond synthesis under the conditions of our experiments was most probably the fluid phase.55,56 As was shown earlier (see data in Table 3 from the article18), the significant amount of gases, which were initially present on the surface of the diamond nanocore, under HPHT annealing became a supercritical fluid phase, which led to a drastic decrease in O, S, and Fe within the nanodiamond particle. The role of the fluids on the complex composition in the processes of diamond crystallization has been widely discussed by geologists studying natural kimberlite diamonds and associated minerals.57,58 In addition, it is likely that a similar mechanism involving a fluid phase plays a significant role in the formation of specific types of natural diamond, such as the impact diamonds from Popigai astrobleme (Yakutia).59,60
In our earlier work, an increase in the hardness of nanodiamond composite after annealing at high pressure was demonstrated. The main reason for this was discussed in line with the effect of the gasification of volatiles from the shell due to thermal desorption,61 which resulted in the appearance of exposed diamond cores capable of interacting with those of neighboring diamonds.18 The data obtained in the present study significantly improve this model. It is suggested that during high-pressure annealing, two processes take place: (a) the process of gasification of impurities from the diamond shell, and (b) the formation of a new diamond phase as well as ordered graphite around the initial nanodiamond core (Fig. 6). The growth of graphite partially blocks the contact between neighboring nanodiamonds. This effect explains the earlier established heterogeneity of hardness increase within the samples annealed at high pressure.
5. Conclusions
The present study addresses the issues related to the use of HPHT process for the sintering of detonation nanodiamond powder. The implemented comparison of the X-ray data and Raman spectra of a high-pressure annealed detonation nanodiamond demonstrated that the structural changes in the nanocrystals were due to the phase transition of sp2 → sp3-bound carbon and the embedding of the latter into the lattice of the diamond nanocrystal core. Simultaneously with the growth of the diamond nanocore, the rearrangement of residual sp2-bonded carbon in the shell into a lamella structure occurred, which crystallographically corresponded to a graphite crystal, where the interplanar distance d(002) = 3.36 Å, which is in good agreement with the period of neighboring graphene layers in a perfect graphite lattice. The other important conclusion is that the newly formed graphite partially covered the exposed areas of the diamond core capable of contacting with that of neighboring diamond particles during annealing. That explains how the process can lead to an increase or decrease in the quality of the sintered nanodiamond composite.Author contributions
Bogdanov D. – writing an original draft, visualization; Bogdanov A. – resources; Plotnikov V. – conceptualization, data curation, project administration, writing an original draft; Makarov S. – supervision, writing an original draft; Yelisseyev A. – investigation, formal analysis, writing an original draft, funding acquisition; Chepurov A. – conceptualization, investigation, writing an original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The studies were performed with a financial support from the Ministry of Science and Higher Education of the Russian Federation grant no. 075-15-2020-781.References
- S. Tomita, M. Fujii, S. Hayashi and K. Yamamoto, Diamond Relat. Mater., 2000, 9, 856–860, DOI:10.1016/S0925-9635(99)00217-4.
- V. A. Nadolinnyi, O. P. Yur'eva, A. P. Yelisseyev, N. P. Pokhilenko and A. A. Chepurov, Dokl. Earth Sci., 2004, 399(9), 1268–1272 Search PubMed.
- A. I. Chepurov, A. P. Yelisseyev, E. I. Zhimulev, V. M. Sonin, I. I. Fedorov and A. A. Chepurov, Inorg. Mater., 2008, 44(4), 377–381, DOI:10.1134/S0020168508040092.
- A. E. Aleksenskii, M. V. Baidakova, A. Y. Vul, A. T. Dideikin, V. I. Siklitskii and S. P. Vul, Phys. Solid State, 2000, 42(8), 1575–1578, DOI:10.1134/1.1307073.
- S. V. Kidalov, F. M. Shakhov, A. V. Shvidchenko, A. N. Smirnov, V. V. Sokolov, M. A. Yagovkina and A. Y. Vul, Tech. Phys. Lett., 2017, 43, 53–56, DOI:10.1134/S1063785017010084.
- A. E. Aleksenskii, V. Y. Osipov, A. Y. Vul, B. Y. Ber, A. B. Smirnov, V. G. Melekhin, G. J. Adriaenssens and K. Iakoubovskii, Phys. Solid State, 2001, 43(1), 145–150, DOI:10.1134/1.1340200.
- S. N. Mikov, A. V. Igo and V. S. Gorelik, Phys. Solid State, 1995, 37, 1671–1673 Search PubMed.
- V. A. Popov, T. B. Sagalova, A. V. Egorov, S. V. Savilov, V. V. Lunin, A. N. Kirichenko, V. N. Denisov, V. D. Blank and O. M. Vyaselev, J. Surf. Invest.: X-Ray, Synchrotron Neutron Tech., 2013, 7(6), 1034–1043, DOI:10.1134/S1027451013060153.
- A. C. Ferrari and J. Robertson, Philos. Trans. R. Soc., A, 2004, 362, 2477–2512, DOI:10.1098/rsta.2004.1452.
- L. V. Daimay, N. B. Colthup, W. G. Fateley and J. G. Grasselli, The Handbook of Infrared and Raman Characteristic Frequencies of Organic Molecules, Acad. Press, St. Diego, USA, 1991 Search PubMed.
- A. E. Aleksenskii, M. V. Baidakova, A. Y. Vul', V. Y. Davydov and Y. A. Pevtsova, Phys. Solid State, 1997, 39, 1007–1015, DOI:10.1134/1.1129989.
- P. A. Vityaz and V. T. Senyut, Phys. Solid State, 2004, 46(4), 764–766, DOI:10.1134/1.1711470.
- A. I. Lyamkin, E. A. Petrov, A. P. Ershov, G. V. Sacovich, A. M. Staver and V. M. Titov, Sov. Phys. Dokl., 1988, 302(3), 705–706 Search PubMed.
- V. M. Titov, V. F. Anisichkin and I. Y. Mal'kov, Combust., Explos. Shock Waves, 1989, 25, 372–379, DOI:10.1007/BF00788819.
- V. M. Sonin, M. Leech, A. A. Chepurov, E. I. Zhimulev and A. I. Chepurov, Int. Geol. Rev., 2019, 61(4), 504–519, DOI:10.1080/00206814.2018.1435310.
- A. I. Turkin, High Temp. - High Pressures, 2003/2004, 35/36, 371–376 Search PubMed.
- E. Y. Tonkov and E. G. Ponyatovsky, in Phase Transformations of Elements Under High Pressure, ed. J. N. Fridlyander and D. G. Eskin, CRC Press, 2004 Search PubMed.
- D. Bogdanov, V. Plotnikov, A. Bogdanov, S. Makarov, V. Vins, A. Yelisseyev, V. Lin and A. Chepurov, Int. J. Refract. Met. Hard Mater., 2018, 71, 101–105, DOI:10.1016/j.ijrmhm.2017.10.026.
- I. I. Fedorov, A. I. Chepurov, V. M. Sonin, A. A. Chepurov and A. M. Logvinova, Geochem. Int., 2008, 46(4), 340–350, DOI:10.1134/S0016702908040034.
- E. I. Zhimulev, A. I. Chepurov, V. M. Sonin, K. D. Litasov and A. A. Chepurov, High Pressure Res., 2018, 38, 153–164, DOI:10.1080/08957959.2018.1458847.
- A. I. Chepurov, V. M. Sonin, A. A. Chepurov, E. I. Zhimulev, B. P. Tolochko and V. S. Eliseev, Inorg. Mater., 2011, 47(8), 864–868, DOI:10.1134/S0020168511070077.
- A. Chepurov, V. Sonin, D. Shcheglov, A. Latyshev, E. Filatov and A. Yelisseyev, Int. J. Refract. Met. Hard Mater., 2018, 76, 12–15, DOI:10.1016/j.ijrmhm.2018.05.011.
- D. G. Bogdanov, S. V. Makarov and V. A. Plotnikov, Tech. Phys. Lett., 2012, 38, 199–202, DOI:10.1134/S1063785012020198.
- B. K. Vainsthein, Fundamentals of Crystals: Symmetry, and Methods of Structural Crystallography, Springer-Verlag, Berlin, 1994, DOI:10.1007/978-3-662-02975-6.
- N. V. Novikov, J. A. Kocherzhinsky, L. A. Shulman, T. D. Ositinskaja, V. G. Malogolovets, A. V. Lysenko, V. I. Malnev, G. F. Nevstruev, E. A. Pugatch, G. P. Bogatyreva and A. S. Vishnevskii, Physical Properties of Diamond, Handbook, Naukova Dumka, Kiev, 1987 Search PubMed.
- N. V. Sharenkova, V. V. Kaminskii and S. N. Petrov, Tech. Phys., 2011, 56, 1363, DOI:10.1134/S1063784211090209.
- S. Osswald, A. Gurga, F. Kellogg, K. Cho, G. Yushin and Y. Gogotsi, Diamond Relat. Mater., 2007, 16, 1967–1973, DOI:10.1016/j.diamond.2007.09.012.
- S. Stelmakh, K. Skrobas, S. Gierlotka and B. Palosz, Diamond Relat. Mater., 2019, 93, 139–149, DOI:10.1016/j.diamond.2019.02.004.
- A. R. Ubbelode and F. A. Lewis, Graphite and Its Crystal Compounds, Clarendon Press, Oxford, 1960 Search PubMed.
- D. Reznik, C. H. Olk, D. A. Neumann and J. R. Copley, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52(1), 116–124, DOI:10.1103/physrevb.52.116.
- B. E. Warren, Phys. Rev., 1941, 59, 693–698, DOI:10.1103/PhysRev.59.693.
- Y. Saito, T. Yoshikawa, S. Bandow, M. Tomita and T. Hayashi, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 1907–1909, DOI:10.1103/PhysRevB.48.1907.
- Y. Q. Zhu, H. G. Zhang, J. H. Zhang, J. Liang, Z. D. Gao, B. Q. Wei, D. H. Wu and M. J. Hui, J. Mater. Sci. Lett., 1994, 13, 1104–1105, DOI:10.1007/BF00633527.
- A. Cao, C. Xu, J. Liang, D. Wu and B. Wei, Chem. Phys. Lett., 2001, 344(1–2), 13–17, DOI:10.1016/S0009-2614(01)00671-6.
- A. Rosenkranz, L. Freeman, S. Fleischmann, F. Lasserre, Y. Fainman and F. E. Talke, Carbon, 2018, 132, 495–502, DOI:10.1016/j.carbon.2018.02.088.
- S. Tomita, A. Burian, J. C. Dore, D. LeBolloch, M. Fujii and S. Hayashi, Carbon, 2002, 40, 1469–1474, DOI:10.1016/S0008-6223(01)00311-6.
- A. V. Gubarevich, J. Kitamura, S. Usuba, H. Yokoi, Y. Kakudate and O. Odawara, Carbon, 2003, 41, 2601–2606, DOI:10.1016/S0008-6223(03)00338-5.
- M. Zeiger, N. Jäckel, D. Weingarth and V. Presser, Carbon, 2015, 94, 507–517, DOI:10.1016/j.carbon.2015.07.028.
- V. L. Kuznetsov, A. L. Chuvilin, Y. V. Butenko, I. Y. Mal'kov and V. M. Titov, Chem. Phys. Lett., 1994, 222, 343–348, DOI:10.1016/0009-2614(94)87072-1.
- S. Tomita, M. Fujii, S. Hayashi and K. Yamamoto, Diamond Relat. Mater., 2000, 9(3–6), 856–860, DOI:10.1016/S0925-9635(99)00217-4.
- A. E. Aleksenskii, M. V. Baidakova, A. Y. Vul and V. I. Siklitskii, Phys. Solid State, 1999, 41(4), 668–671, DOI:10.1134/1.1130846.
- O. O. Mykhaylyk, Y. M. Solonin, D. N. Batchelder and R. Brydson, J. Appl. Phys., 2005, 97, 074302, DOI:10.1063/1.1868054.
- S. Bhargava, H. D. Bist, S. Sahli, M. Aslam and H. B. Tripathi, Appl. Phys. Lett., 1995, 67, 1706, DOI:10.1063/1.115023.
- F. Tuinstra and J. L. Koening, J. Chem. Phys., 1970, 53, 126, DOI:10.1063/1.1674108.
- J. R. Hardy and S. D. Smith, Philos. Mag., 1961, 6, 1163–1172, DOI:10.1080/14786436108239677.
- N. Dwivedi, S. Kumar and H. K. Malik, J. Appl. Phys., 2012, 112, 023518, DOI:10.1063/1.4739287.
- S. Prawer, K. W. Nugent, D. N. Jamieson, J. O. Orwa, L. A. Bursill and J. L. Peng, Chem. Phys. Lett., 2000, 332, 93–97, DOI:10.1016/S0009-2614(00)01236-7.
- L. Ginés, S. Mandal, A. Ahmed, C.-L. Cheng, M. Sowc and O. A. Williams, Nanoscale, 2017, 9, 12549, 10.1039/C7NR03200E.
- M. J. Lipp, V. G. Baonsa, W. J. Evans and H. E. Lorenzana, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56(10), 5978–5984, DOI:10.1103/PhysRevB.56.5978.
- J. W. Ager 3rd, D. K. Veirs and G. M. Rosenblatt, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43(8), 6491–6499, DOI:10.1103/physrevb.43.6491.
- S. I. Hirano, K. Shimoto and S. Naka, J. Mater. Sci., 1982, 17, 856–1862, DOI:10.1007/BF00540400.
- A. Onodera, K. Higashi and Y. Irie, J. Mater. Sci., 1988, 23, 422–428, DOI:10.1007/BF01174666.
- F. P. Bundy, H. T. Hall, H. M. Strong and R. H. Wentorf Jr, Nature, 1955, 176, 51–55, DOI:10.1038/176051a0.
- I. I. Fedorov, A. I. Chepurov, N. Y. Osorgin, A. G. Sokol and N. V. Sobolev, Dokl. Akad. Nauk SSSR, 1991, 320(3), 710–712 CAS.
- N. I. Osorgin, I. N. Palianov, N. V. Sobolev, I. P. Khokhriakova, A. I. Chepurov and N. A. Shugurova, Dokl. Akad. Nauk SSSR, 1987, 293(5), 1214–1217 CAS.
- A. Tomilenko, V. Sonin, T. Bul'bak and A. Chepurov, Carbon Lett., 2019, 29(4), 327–336, DOI:10.1007/s42823-019-00037-9.
- A. A. Chepurov, J.-M. Dereppe, A. I. Turkin and V. V. Lin, Neues Jahrb. Mineral., Abh., 2018, 195(1), 65–78, DOI:10.1127/njma/2018/0084.
- S. B. Shirey, P. Cartigny, D. J. Frost, S. Keshav, F. Nestola, P. Nimis, D. G. Pearson, N. V. Sobolev and M. J. Walter, Rev. Mineral. Geochem., 2013, 75, 355–421, DOI:10.2138/RMG.2013.75.12.
- A. Yelisseyev, V. Vins, V. Afanasiev and A. Rybak, Diamond Relat. Mater., 2017, 79, 7–13, DOI:10.1016/j.diamond.2017.08.012.
- A. P. Yelisseyev, V. P. Afanasiev, A. V. Panchenko, S. A. Gromilov, V. V. Kaichev and A. A. Saraev, Lithos, 2016, 265, 278–291, DOI:10.1016/j.lithos.2016.07.031.
- V. A. Plotnikov, D. G. Bogdanov, S. V. Makarov and A. S. Bogdanov, Izv. Vyssh. Uchebn. Zaved., Khim. Khim. Tekhnol., 2017, 60(9), 4–12, DOI:10.6060/tcct.2017609.1.
| This journal is © The Royal Society of Chemistry 2021 |