Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rotational excitation of C2H− anion in collision with H2†
Insaf Toumia,
Ounaies Yazidi *ab and
Faouzi Najar
*ab and
Faouzi Najar ac
ac
aLaboratoire de Spectroscopie Atomique, Moléculaire et Application, Faculté des Sciences, Université Tunis El Manar, Tunis 2092, Tunisia
bInstitut Préparatoire aux Etudes d'Ingénieurs de Tunis El Manar, Université de Tunis El Manar, Tunis 2092, Tunisia
cInstitut Préparatoire aux Etudes d'Ingénieurs de Tunis, Université de Tunis, Tunis 1007, Tunisia
First published on 13th April 2021
Abstract
The discovery of anions in the interstellar medium has shown that they are very reactive species. This gave them great importance in the modeling of the chemical and astrophysical evolution of the interstellar medium. The detection of the first anion C6H− followed by the other anions C4H−, C8H− and CN− in the interstellar medium has encouraged research on other detectable anions. The C2H− anion was observed for the first time in the circumstellar envelope of IRC+10216 and in TMC-1. In these cold and low-density regions, precise modeling of the chemical and physical conditions of the observed emission lines requires knowledge of the radiative and collisional excitation rates. We present here the first new two-dimensional Potential Energy Surface (PES) for C2H–H2 interaction. Rotational excitation of the anion by collision with para-H2(jH2 = 0) is investigated. The PES is obtained in the super-molecular approach based on a single and double excitation coupled cluster method with perturbative contributions from triple excitations (CCSD(T)). In all our calculations, all atoms were described using the augmented correlation-consistent triple zeta (aug-cc-pVTZ) basis sets and bond f unctions. Fully-quantum close-coupling calculations of inelastic integral cross sections are done on a grid of collision energies large enough to ensure converged state-to-state rate coefficients for the 16 first rotational levels of C2H− and for temperatures ranging from 5 to 120 K. For this collisional system, rate coefficients exhibit a strong propensity in favor of even Δj transitions.
1 Introduction
In the last two decades, anions have been intensively studied. These studies were framed by observations in the laboratory1–3 and some astrophysical observations.2,4–6 Among these species, mention is made of carbon chain anions C2nH−.6 The recent discovery of carbon chain anions C2nH− in interstellar and circumstellar media has been investigated by many theoretical and experimental works on these species.7,8 Their structures as well as the importance of their role in the interstellar chemistry and in gas phase ion–molecule reactions are the object of many recent studies.9–11 Although the existence of anions in astrophysical sources was first predicted theoretically and early considered in chemical models,12,13 the first negative hydrocarbon C6H− was detected in 2006 (ref. 2) solving the problem of the unidentified lines discovered by Kawaguchi et al.14 The C6H− identification was followed by the detection of other negatively charged species like C4H−, C8H−, C3N−, C5N− and CN−.15–23 Many of these species were first detected in IRC+10216.2,15,18 Hydrocarbon anions were also discovered later in other molecular clouds.17 In this set C2H− present a capital importance.Several observations in the laboratories have justified the detection of the C2H− anion. This experimental studies24 interest of the C2H− anion comes from the fact that the C2H− anion is the shortest in the sequence of carbon chain anions with a closed-shell electronic ground state, and the fact that gives the rest frequencies required for a radio astronomical search for this polar, astronomically plausible molecule.
From astrophysical observations, in 2007 J. Cernicharo et al.15,25 detected the 1–0 transition of the C2H− anion and calculated the abundance ratio C2H/C2H− = 12.5. Cernicharo et al. suggest that the 3–2 transition is strong enough to be detected. Later in 2010, the observations of M. Agùndez et al.26 found difficulties in detecting the 1–0 and 2–0 transitions of the anion. These difficulties are probably due to the very reactive natures of the C2H− anion.
We report in this work a first collisional study of C2H− with para-H2(jH2 = 0) at low temperatures trying to understand the particular behavior of negatively charged species during collisions and how they compare with neutral forms27,47 and the C2H− anion in collision with He.48 In the next section, we will present details of the ab initio calculations of the C2H–para-H2 potential Energy Surface (PES).In Section 3, some theoretical aspects of the scattering calculations are given, state-to-state collisional cross sections will be reported, the rate coefficients and the propensity rules will be showcased. In Section 4, comparative study between the rate coefficients of C2H−–para-H2 and C2H–He will be displayed. Concluding remarks are in Section 5.
2 Potential Energy Surface
This work primarily focuses on the rotational excitation of C2H− with para-H2 at low temperature; both monomers were considered as rigid species to deal with a reduced number of degrees of freedom. Accordingly, in our calculations, is considered to be linear, and both bond lengths are set at the CCSD/AV5Z theoretical values of rC–C = 1.250 Å and rC–H = 1.070 Å.28 For H2, we used the experimental bond length rH–H = 1.44876 bohr corresponding to the averaged value over the ground-state vibrational wave function for H2. The lowest bending mode of C2H− ν1 equal to 502.0 cm−1,28 is well above the energy of the highest C2H− rotational level considered in this work (j = 16, see Table 1). In addition, from QCT studies of rotational excitation of H2O by H2, it was shown29 that the coupling between the rotational excitation and the bending may be neglected for temperatures up to 5000 K. Moreover, it was also shown by Faure et al.,30 in the particular case of the H2O–H2 system, that the 5D-PES calculated at the experimental ground vibrational state geometry and the full 9D-PES averaged over the ground vibrational state are very similar. These results suggest that the use of a rigid body 2D-PES is sufficient as long as bending and vibrational excitations are not taken into consideration.| j | εj (cm−1) | j | εj (cm−1) |
|---|---|---|---|
| 0 | 0.0000000 | ||
| 1 | 2.7778579 | 15 | 333.1581888 |
| 2 | 8.3334960 | 16 | 377.5511276 |
| 3 | 16.6667590 | 17 | 424.7113668 |
| 4 | 27.7774142 | 18 | 474.6375867 |
| 5 | 41.6651509 | 19 | 527.3283902 |
| 6 | 58.3295811 | 20 | 582.7823022 |
| 7 | 77.7702390 | 21 | 640.9977702 |
| 8 | 99.9865812 | 22 | 701.9731640 |
| 9 | 124.9779866 | 23 | 765.7067757 |
| 10 | 152.7437566 | 24 | 832.1968200 |
| 11 | 183.2831149 | 25 | 901.4414338 |
| 12 | 216.5952076 | 26 | 973.4386763 |
| 13 | 252.6791032 | 27 | 1048.1865292 |
| 14 | 291.5337926 | 28 | 1125.6828966 |
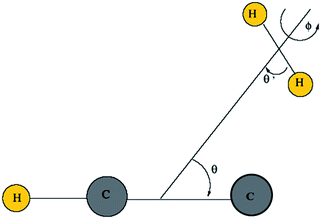
Then, we define the body-fixed coordinate system in Fig. 1. The geometry of C2H−–H2 collisional system with para-H2 and C2H− treated as rigid rotors is then characterized by three angles (θ, θ′, ϕ) and the distance R between the center of masses of H2 and C2H− (see Fig. 1). The polar angles of the C2H− and para-H2 molecules with respect to R are denoted θ and θ′ respectively, while ϕ denotes the dihedral angle, which is the relative polar angle between the C2H− and para-H2 bonds. For the solution of the close-coupling scattering equations, it is most convenient to expand, at each value of R, the interaction potential V(R,θ,θ′,ϕ) in angular functions. For the scattering of two linear rigid rotors, we used.31
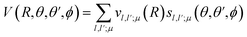 | (1) |
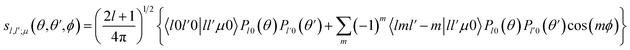 | (2) |
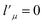 needs to be retained in the expansion of the interaction potential given in eqn (1). The resulting expansion then can be simplified to
needs to be retained in the expansion of the interaction potential given in eqn (1). The resulting expansion then can be simplified to
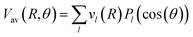 | (3) |
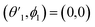 ,
, 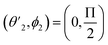 and
and 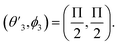 Thus, the C2H−–para-H2(jH2 = 0) is reduced to a two-dimensional Vav PES such as
Thus, the C2H−–para-H2(jH2 = 0) is reduced to a two-dimensional Vav PES such as
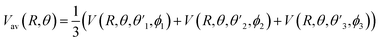 | (4) |
Such approximation has been shown to be reasonably accurate for relatively heavy molecule such as SiS,32 HCO+ (ref. 33) and C2.34 In the Cs point group, the ground electronic state of the C2H−–para-H2 van der Waals system is of A′ symmetry. The PES was calculated in the super-molecular approach based on a single and double excitation coupled cluster method with perturbative contributions from triple excitations (CCSD(T)).35,36 For the five atoms, we used the aug-cc-pVTZ basis set of Woon and Dunning.37 This basis set was further augmented by the additional 3s3p2d1f bond basis functions of Williams et al.38 and placed equidistant between the C2H− and H2 centers of mass. At all geometries, the Boys and Bernardi39 counterpoise procedure was used to correct for basis set superposition error (BSSE). All calculations were carried out using the MOLPRO 2010 package.40
The radial scattering coordinate R was assigned 36 values ranging from 3.0 to 50.0 bohr, the θ grid ranged from 0° to 180° in steps of 15°. This resulted in a total of 1404 geometries computed for the C2H−–para-H2(jH2 = 0) system.
An analytic representation of the present 2D PES suitable for dynamics calculations was obtained using the procedure described by eqn (12)–(16) of Werner et al.41 for the CN–He system. In order to perform the scattering calculations, this PES was expanded in terms of Legendre polynomials.
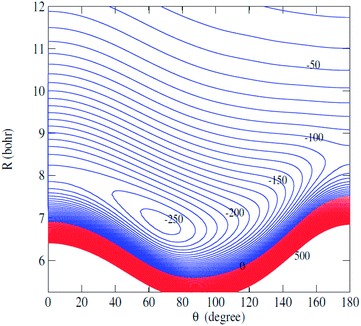
Fig. 2 displays the contour plot of the 2D V(R,θ) PES. For this van der Waals system, the global minimum was found to be 250.6 cm−1 at R = 7.20 bohr and θ = 76.0 degree.
3 Dynamical calculation
The fitted C2H−–para-H2 2D-PES was used to calculate state-to-state cross sections and rate coefficients. The full close coupling approach first introduced by Arthurs & Dalgarno42 was used for the calculations of the state-to-state cross sections between the 16 first rotational levels. The energies of the rotational levels were computed from the following C2H− spectroscopic constants: B0 = 1.3889354 cm−1 and D0 = 3.2345 10−6 cm−1.24 The scattering calculations were carried out with the MOLSCAT code.43 Calculations were performed for energies ranging from 3.0 to 1200.0 cm−1. The integration parameters and the sise of the basis set were chosen to ensure convergence of the cross sections over this range. At the highest considered total energy (1200.0 cm−1), the C2H− rotational basis included channels up to j = 28 to ensure convergence of the excitation cross sections for transitions including up to the j = 16 rotational level (see Tables 1 and 2).| jmax = 27 | jmax = 28 | jmax = 29 | jmax = 30 | jmax = 32 | |
|---|---|---|---|---|---|
| σ16–15 | 15.316 | 15.322 | 15.322 | 15.322 | 15.322 |
| σ16–14 | 6.666 | 6.665 | 6.665 | 6.665 | 6.663 |
| σ2–1 | 2.7937 | 2.7941 | 2.7941 | 2.7941 | 2.7941 |
We carefully spanned the energy grid to take into account the presence of resonances. The energy steps are 0.1 cm−1 below 100.0 cm−1, 0.2 cm−1 from 100.0 to 250.0 cm−1, 1.0 cm−1 between 250.0 and 300.0, 5.0 cm−1 between 300.0 and 400.0 cm−1, 10.0 cm−1 between 400.0 and 500.0 cm−1, 25.0 cm−1 between 500.0 and 700.0 cm−1 and 50.0 cm−1 between 700.0 and 1200.0 cm−1.
3.1 Integral cross sections
Fully-quantum close-coupling calculations of integral cross sections were carried out for values of total energies ranging from 3.0 to 1200 cm−1. The variation of integral cross sections for a few selected j → j′ rotational transitions with collision energy is shown in Fig. 3. For collisional energies below 300.0 cm−1 many resonances occur. This is a consequence of the attractive potential well with a depth of 252.6 cm−1. At low energy, the molecule can be temporarily trapped in quasi-bound states,44,45 which arise both from tunneling through the centrifugal barrier (shape resonances) and from excitation of C2H− to a higher rotational level which is energetically allowed in the well (Feshbach resonances). Some anisotropy appears around the well depth which may induce a different trend of the cross sections at lower energies.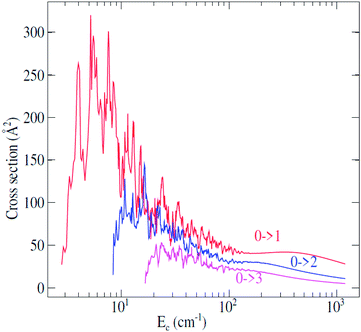 | ||
| Fig. 3 Rotational excitation j → j′ cross sections of C2H− in collision with para-H2(jH2 = 0) as a function of the relative kinetic energy. | ||
3.2 Rate coefficients
From the calculated cross sections, one can obtain the corresponding state-to-state rate coefficients by Boltzmann averaging:
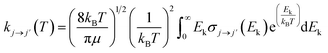 | (5) |
The complete set of de-excitation rate coefficients with j, j′ ≤ 16 will be available on-line from the BASECOL website (http://www.obspm.fr/basecol). Excitation rate coefficients can be easily obtained by detailed balance.
4 Comparison with C2H–He collisions
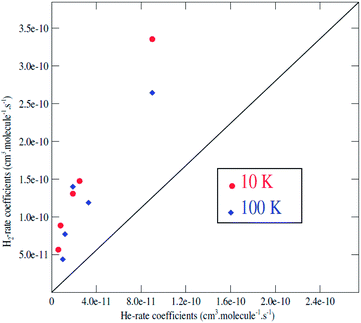
It is generally assumed that excitation rate coefficients associated with He as the collision partner can provide a first estimation for rate coefficients for collisions with para-H2(jH2 = 0) just applying a scaling factor which is equal to the square root of the ratio of the reduced masses of the two systems. For C2H−, this scaling factor tends to 1.4. Since rotational rate coefficients have been calculated previously for C2H− in collision with He,48 using the same methodology as the one employed in present work for C2H−–para-H2(jH2 = 0), the comparison between the two sets of rate coefficients can be used to assess the validity of such approximation.We report in Fig. 6 a comparison between the rate coefficients of the present study and those reported by Dumouchel et al.48 for the selected transitions (see Fig. 4 in ref. 48). The red circles and the blue diamond's reveal the rate coefficients of C2H−1–para-H2(jH2 = 0) vs. C2H−–He at kinetic temperatures T = 10.0 K and T = 100.0 K respectively. As shown above, the ratio between the rate coefficients clearly differs from the value of 1.4. These differences are due to the difference in interaction energies between the two systems. The ratios deviate clearly from 1.4 for all the transitions, by a factor varying from 3 to 11. The difference is more pronounced for the transitions with odd Δj. This is due to the difference in the interaction potential which is more symmetrical (with respect to the θ ↔ π − θ transformation) for the C2H−–He system than for C2H−1–para-H2(jH2 = 0). Then, the collision rates with corrected with the scale factor 1.4 do not always constitute a good approximation to model the rates with H2. This result is also found in the collisions with the neutral species C2H (see ref. 47).
5 Summary and conclusion
Quantum scattering calculations have been used to investigate energy transfer in collisions of C2H− with para-H2(jH2 = 0) molecule. The calculations are based on a new, highly correlated 2D PES calculated at the RCCSD(T) level using large AVTZ basis sets and a bend functions. Close coupling calculations were performed for collision energies ranging from 3.0 to 1200.0 cm−1. Rate coefficients for transitions involving the 16 first rotational levels of the C2H− anion were determined for temperature ranging from 5 to 120.0 K. The rate coefficients show a strong propensity for even Δj, mainly Δj = 2. The present set of rate coefficients can serve the modelling of C2H− emission lines in astrophysical environments. Finally, the resulting inelastic rate coefficients for collisions of C2H− with para-H2 will help in constraining astrophysical anion chemistry and also in accurately model regions containing anions such as IRC+10216. We encourage astrophysicists to use these new values in their next detection attempts in the IRC+10216. Future work will deal with calculations of C2H− in collision with both para- and ortho-H2 species using 4D PES approach in order to obtain rate coefficients for highly excited rotational states and higher temperatures. Detailed comparison with other systems, in particular carbon chain anions, will be studied in detail owing to its great interest for astrophysical modelling.Conflicts of interest
There are no conflicts to declare.Notes and references
- C. F. Lind Jabka, M. Polk, I. Zymak and W. D. Geppert, Phys. Chem. Chem. Phys., 2018, 20, 5377–5388 RSC.
- M. C. McCarthy, C. A. Gottlieb, H. Gupta and P. Thaddeus, Astrophys. J., 2006, 652, 141–144 CrossRef.
- H. Gupta, S. Brunken, F. Tamassia, C. A. Gottlieb, M. C. McCarthy and P. Thaddeus, Astrophys. J., 2007, 655, 57–60 CrossRef.
- S. Brunken, H. Gupta, C. A. Gottlieb, M. C. McCarthy and P. Thaddeus, Astrophys. J., 2007, 664, 43–46 CrossRef.
- Y. Kasai, E. Kagi and K. Kawaguchi, Astrophys. J., 2007, 661, 61–64 CrossRef.
- T. J. Millar, C. Walsh and A. Thomas, Field Chem. Rev., 2017, 117, 17651795 Search PubMed.
- M. A. Cordiner, T. J. Millar, C. Walsh, E. Herbst, D. C. Lis, T. A. Bell and E. Roueff, Organic Matter in Space, ed. S. Kwok and S. Sandford, Proceedings IAU Symposium no. 251, 2008 Search PubMed.
- M. A. Cordiner and T. J. Millar, Astrophys. J., 2009, 697, 68 CrossRef CAS.
- E. Herbst and Y. Osamura, Astrophys. J., 2008, 679, 1670 CrossRef CAS.
- C. Walsh, N. Harada, E. Herbst and T. J. Millar, Astrophys. J., 2009, 700, 752 CrossRef CAS.
- B. Eichelberger, T. P. Snow, C. Barckholtz and V. M. Bierbaum, Astrophys. J., 2007, 667, 1283 CrossRef CAS.
- A. Dalgarno and R. A. Mc Cray, Astrophys. J., 1973, 181, 95 CrossRef CAS.
- E. Herbst, Nature, 1981, 289, 656 CrossRef CAS.
- K. Kawaguchi, Y. Kasai, S. Ishikawa and N. Kaifu, Publ. Astron. Soc. Jpn., 1995, 47, 853 CAS.
- J. Cernicharo, M. Guélin and M. Agúndez, et al., Astron. Astrophys., 2007, 467, L37 CrossRef CAS.
- M. Agúndez, J. Cernicharo, M. Guelin, M. Gerin, M. C. McCarthy and P. Thaddeus, Astron. Astrophys., 2008, 478, L19 CrossRef.
- N. Sakai, T. Sakai and S. Yamamoto, Astrophys. J., 2008, 673, L71 CrossRef CAS.
- A. J. Remijan, J. M. Hollis and F. J. Lovas, et al., Astrophys. J., 2007, 664, L47 CrossRef CAS.
- K. Kawaguchi, et al., Publ. Astron. Soc. Jpn., 2007, 59, L47 CrossRef CAS.
- S. Brünken, H. Gupta and C. A. Gottlieb, et al., Astrophys. J., 2007, 664, L43 CrossRef.
- P. Thadeus, C. A. Gottlieb and H. Gupta, et al., Astrophys. J., 2008, 677, 1132 CrossRef.
- C. Walsh, N. Harada, E. Herbst and T. J. Millar, Astrophys. J., 2009, 700, 752 CrossRef CAS.
- M. Agúndez, et al., Astron. Astrophys., 2010, 517, L2 CrossRef.
- S. Brünken, C. A. Gottlieb and H. Gupta, et al., Astron. Astrophys., 2007, 464, L33 CrossRef.
- J. Cernicharo, M. Guélin and M. Agúndez, et al., Astrophys. J., 2008, 688, L83 CrossRef CAS.
- M. Agúndez, et al., Astron. Astrophys., 2010, 517, L2 CrossRef.
- A. Spielfiedel, N. Feautrier, F. Najar, D. Ben Abdallah, F. Dayou, M. L. Senent and F. Lique, Mon. Not. R. Astron. Soc., 2012, 421, 1891–1896 CrossRef CAS.
- X. Huang and T. J. Lee, J. Chem. Phys., 2009, 131, 1043 Search PubMed.
- A. Faure, Private Communication, 2011 Search PubMed.
- A. Faure, P. Valiron, M. W. L. Wiesenfeld, C. Rist, J. Noga and J. Tennyson, J. Chem. Phys., 2005, 122, 221201 CrossRef PubMed.
- T. S. Green, Astrophys. J., 1975, 201, 366 CrossRef.
- F. Lique and J. Klos, J. Chem. Phys., 2008, 128, 034306 CrossRef PubMed.
- O. Yazidi, D. Ben Abdallah and F. Lique, Mon. Not. R. Astron. Soc., 2014, 441, 664 CrossRef CAS.
- F. Najar and Y. Kalugina, RSC Adv., 2020, 10, 8580 RSC.
- C. Hampel, K. A. Peterson and H.-J. Werner, Chem. Phys. Lett., 1992, 190, 1 CrossRef CAS.
- J. D. Watts, J. Gauss and R. J. Bartlett, J. Chem. Phys., 1993, 98, 8718 CrossRef CAS.
- D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1994, 100, 2975 CrossRef CAS.
- H. L. Williams, E. M. Mas, K. Szalewicz and B. Jeziorski, J. Chem. Phys., 1995, 103, 7374 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- H.-J. Werner, et al., Molpro, a Package of Ab Initio Programs, 2010, Available at: http://www.molpro.net Search PubMed.
- H.-J. Werner, B. Follmeg, M. H. Alexander and D. Lemoine, J. Chem. Phys., 1989, 91, 5425 CrossRef CAS.
- A. M. Arthurs and A. Dalgarno, Proc. R. Soc. A, 1960, 256, 540 Search PubMed.
- J. M. Hutson and S. Green, MOLSCAT computer code, Version 14, Distributed by Collaborative Computational Project 6, Daresbury Laboratory, Warington, UK, 1995 Search PubMed.
- L. N. Smith, D. J. Malik and D. Secrest, J. Chem. Phys., 1979, 71, 4502 CrossRef CAS.
- K. M. Christoffel and J. M. Bowman, J. Chem. Phys., 1983, 78, 3952 CrossRef CAS.
- D. Ben Abdallah, F. Najar, N. Jaidane, F. Dumouchel and F. Lique, Mon. Not. R. Astron. Soc., 2012, 419, 2441 CrossRef CAS.
- F. Najar, D. Ben Abdallah, A. Spielfiedel, F. Dayou, F. Lique and N. Feautrier, Chem. Phys. Lett., 2014, 614, 251–257 CrossRef CAS.
- F. Dumouchel, A. Spielfiedel, M. L. Senent and N. Feautrier, Chem. Phys. Lett., 2012, 533, 6–9 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra00519g |
| This journal is © The Royal Society of Chemistry 2021 |