Open Access Article
Open Access ArticleStructural, elastic, and electronic properties of chemically functionalized boron phosphide monolayer†
Tuan V. Vu ab,
A. I. Kartamyshevab,
Nguyen V. Hieu*c,
Tran D. H. Dangd,
Sy-Ngoc Nguyene,
N. A. Poklonski
ab,
A. I. Kartamyshevab,
Nguyen V. Hieu*c,
Tran D. H. Dangd,
Sy-Ngoc Nguyene,
N. A. Poklonski f,
Chuong V. Nguyeng,
Huynh V. Phuch and
Nguyen N. Hieu
f,
Chuong V. Nguyeng,
Huynh V. Phuch and
Nguyen N. Hieu *ij
*ij
aDivision of Computational Physics, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: vuvantuan@tdtu.edu.vn
bFaculty of Electrical & Electronics Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam
cFaculty of Physics, University of Science and Education, The University of Danang, Da Nang, Vietnam. E-mail: nvhieu@ued.udn.vn
dTecStar, Macnica, Inc., 6-3 Shin-Yokohama, 222-8561, Japan
eDivision of Construction Computation, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam
fFaculty of Physics, Belarusian State University, Minsk, Belarus
gDivision of Theoretical Physics, Dong Thap University, Cao Lanh 870000, Vietnam
hDepartment of Materials Science and Engineering, Le Quy Don Technical University, Ha Noi 100000, Vietnam
iInstitute of Research and Development, Duy Tan University, Da Nang 550000, Vietnam
jFaculty of Natural Sciences, Duy Tan University, Da Nang 550000, Vietnam. E-mail: hieunn@duytan.edu.vn
First published on 24th February 2021
Abstract
Surface functionalization is one of the useful techniques for modulating the mechanical and electronic properties of two-dimensional systems. In the present study, we investigate the structural, elastic, and electronic properties of hexagonal boron phosphide monolayer functionalized by Br and Cl atoms using first-principles predictions. Once surface-functionalized with Br/Cl atoms, the planar structure of BP monolayer is transformed to the low-buckled lattice with the bucking constant of about 0.6 Å for all four configurations of functionalized boron phosphide, i.e., Cl–BP–Cl, Cl–BP–Br, Br–BP–Cl, and Br–BP–Br. The stability of functionalized BP monolayers is confirmed via their phonon spectra analysis and ab initio molecular dynamics simulations. Our calculations indicate that the functionalized BP monolayers possess a fully isotropic elastic characteristic with the perfect circular shape of the angle-dependent Young's modulus and Poisson's ratio due to the hexagonal symmetry. The Cl–BP–Cl is the most stiff with the Young's modulus C2D = 43.234 N m−1. All four configurations of the functionalized boron phosphide are direct semiconductors with a larger band gap than that of a pure BP monolayer. The outstanding stability, isotropic elastic properties, and moderate band gap make functionalized boron phosphide a very intriguing candidate for next-generation nanoelectromechanical devices.
1 Introduction
The physical properties of two-dimensional (2D) systems, including graphene, hexagonal boron nitride or boron phosphide, have been studied extensively during the past two decades.1,2 To serve a variety of purposes, scientists have sought to alter their physical and chemical properties. In addition to traditional methods such as the applications of deformation or electric field,3,4 placing on semiconductor substrates or the creation of heterostructures,5,6 recently, surface functionalization has emerged as one of the effective ways to alter the physical properties of 2D materials.7,8Physical properties of surface-functionalized 2D monolayers have been calculated using many different methods. Karlický and co-workers have demonstrated that the electronic properties of graphene are drastically changed when its surface is hydrogenated.9 Several configurations of hydrogenated graphene with outstanding mechanical properties have been reported, including boat-graphane with a negative Poisson ratio along both the zigzag and armchair axes of the honeycomb structure.10 Via density functional theory (DFT) calculations, chemically functionalization is predicted to make the 2D layered-nanomaterials more stable.11 Recently, the hydrogen-terminated germanium or germanane GeH has been successfully synthesized by experiment.12 By using the chemical vapor deposition method, Son and co-workers demonstrated experimentally that band gap of graphene can be tuned up to 3.9 eV by its surface-hydrogenation.13 Very recently, fully hydrogenated graphene or graphane has been synthesized and experimentally investigated.14 Along with the experimental works, a series of theoretical studies on surface functionalization of 2D materials, including DFT calculations, has been reported recently.8,15,16
Boron phosphide (BP) is not a common nanomaterial because there are many challenges in synthesizing process17 even though the single-crystal of BP has been synthesized long ago.18 BP monolayer, a hexagonal planar structure, is predicted to be a semiconductor with band gap of about 0.9 eV by DFT calculations.19,20 Experimental data for structural properties and also electronic characteristics of boron phosphide monolayer are not yet available, since it has not been successfully synthesized by experiments. BP monolayer possesses a low carrier effective mass and high mechanical stability.19,21 Particularly, the carrier mobility of BP monolayer is quite higher than that of monolayer MoS2 at room temperature.22 With the outstanding physicochemical properties, BP monolayer is predicted to be a perfect candidate for alkali metal-based batteries.20 Recently, adsorption properties of metal atoms on the BP monolayer have been investigated through the ab initio calculations.23 One showed that BP monolayer can strongly adsorb single atoms of group III transition metals on its surface with high adsorption energy.23 Yu and Guo have revealed that the haft-hydrogenated BP monolayer possesses incredible magnetic properties that do not exist in pure BP monolayer.24 Also, structural properties and electronic states of the fully hydrogenated and fluorinated BP monolayers have been investigated by DFT computations.25
Motivated by good achievements for the functionalization of 2D materials, in the present work, we investigate the functionalization of BP monolayer with Br and Cl atoms by using DFT calculations. The structural, elastic, and electronic properties of all possible four configurations of chemically functionalized BP with Br and Cl, i.e., Cl–BP–Cl, Cl–BP–Br, Br–BP–Cl, and Br–BP–Br. Also, the basic characteristics of pure BP monolayer are investigated for comparison purposes.
2 Computational details
We use Quantum Espresso package26 to perform the calculations in this study. DFT calculations with the projector augmented wave (PAW) method is used the present study. We use the Perdew–Burke–Ernzerhof (PBE) functional27 of the generalized gradient approximation (GGA) to describe the exchange-correlation interaction in Quantum ESPRESSO. The DFT-D2 method by Grimme28 is used to treat the long-range weak van der Waals interactions in the investigated systems. We sample the unit cell with a 15 × 15 × 1 k-point mesh. The cutoff of kinetic energy for the wave function expansion is set to 10−6 eV and the criterion for the force-convergence is to be 10−3 eV Å−1. To avoid any interactions between neighbor plates, we fix the vacuum region along the z direction being 20 Å. The density-functional perturbation theory (DFPT)29 is used for the calculations of the phonon spectrum of monolayers. To obtain accurate results, we use a large supercell of 4 × 4 × 1 for the phonon dispersion curves calculations. By using the ab initio molecular dynamics (AIMD) simulations, we also test the thermal stability of the monolayers at room temperature. The Born–Oppenheimer molecular dynamics30 simulations is used to calculate the thermal stability of the systems through the Nosé-thermostat algorithm.313 Results and discussion
3.1 Atomic structure and stability
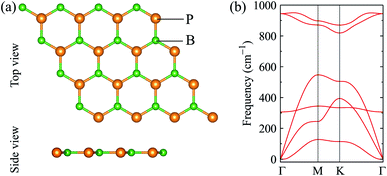
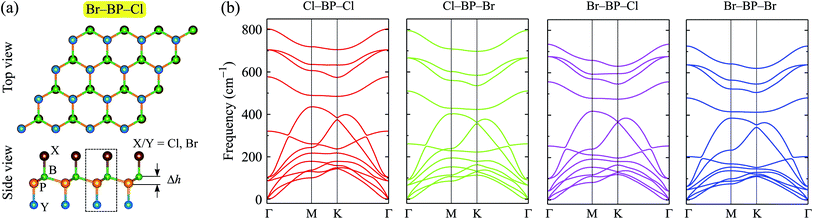
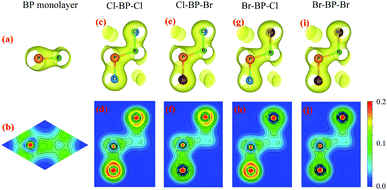
We first optimize the atomic structure of BP monolayer as depicted in Fig. 1(a). At equilibrium, BP monolayer has a planar hexagonal structure with the lattice constant of 3.210 Å. Our calculated results for the lattice constant are consistent with the previous DFT calculations.32 The unit cell of BP monolayer contains two atoms (one P atom and one B atom). Consequently, its phonon spectrum has six vibrational branches, including three optical branches and three acoustic branches as shown in Fig. 1(a). Our calculations demonstrate that there are no soft modes in the phonon dispersion curves of BP monolayer. It guarantees that BP monolayer is dynamically stable. Our calculated results are in good agreement with previous studies.24,33When the BP monolayer is functionalized with Br and/or Cl, our calculations reveal that the planar structure of BP monolayer is broken and surface-functionalized BP has a low-bucked structure with the bucking constant Δh depending on the species, i.e., Br or/and Cl. Here, we investigate four configurations of surface-functionalized BP with Br and Cl, including Cl–BP–Cl, Cl–BP–Br, Br–BP–Cl, and Br–BP–Br. Coordinates of atoms in atomic structure the functionalized BP monolayer with Br and Cl atoms are listed in Table S1 of ESI.† The low-bucked structure of surface-functionalized BP with Br and Cl is depicted in Fig. 2(a). Unit cell of the functionalized BP monolayer with Br and Cl atoms contains four atoms, including one B atom, one P atom, and two atoms of species, as presented in Fig. 2(a). The buckling constant of the surface-functionalized BP with Cl and Br is about 0.6 Å as listed in Table 1. The lattice constant of all four surface-functionalized configurations is longer than that of a pure BP monolayer. As listed in Table 1, the lattice constant of the Br–BP–Br is longest, being 3.467 Å. Also, the B–P bond length of the surface-functionalized BP is longer than that of pure BP monolayer. Our obtained results for the lattice constant for the surface-functionalized BP with Cl and Br is longer than that of the fully hydrogenated boron phosphide as reported by Ullah et al.25 More interestingly, the direct bond between the species (Cl/Br) to P atom dP–Cl/Br is longer than that between the species and B atom dB–Cl/Br. However, there is no significant difference between dB–Cl and dB–Br or between dP–Cl and dP–Br.
| a (Å) | dB–P (Å) | dB–Cl (Å) | dB–Br (Å) | dP–Cl (Å) | dP–Br (Å) | Δh (Å) | Eb (eV) | EPBEg (eV) | EHSEg (eV) | |
|---|---|---|---|---|---|---|---|---|---|---|
| BP | 3.210 | 1.853 | — | — | — | — | 0 | — | 0.887 | 1.399 |
| Cl–BP–Cl | 3.371 | 2.039 | 1.823 | — | 2.042 | — | 0.608 | −5.365 | 1.659 | 2.711 |
| Cl–BP–Br | 3.425 | 2.068 | 1.821 | — | 2.182 | — | 0.605 | −4.689 | 1.426 | 2.446 |
| Br–BP–Cl | 3.414 | 2.057 | — | 1.959 | — | 2.047 | 0.591 | −4.638 | 1.084 | 2.075 |
| Br–BP–Br | 3.467 | 2.087 | — | 1.958 | — | 2.187 | 0.591 | −3.980 | 1.055 | 2.032 |
To ensure that the material can exist in physical form, we need to check its dynamical stability first. The dynamical stability of the surface-functionalized BP monolayers can be checked via analysis of their phonon spectrum as presented in Fig. 2(b). Our calculations indicate that there are 12 vibrational modes in the phonon spectrum of the surface-functionalized BP monolayers. There is no gap between optical and acoustic modes. The coexistence of the acoustic and optical modes in the frequency range can cause these materials to have low thermal conductivity due to strong optical-acoustic scattering. In the phonon spectra of all four configurations, there is no negative frequency. It implies that the surface-functionalized BP monolayers with Br and Cl are dynamically stable.
Thermal stability is one of the most important characteristics to check to ensure that the material can be used in physical devices. By using AIMD simulations, the thermal stability of surface-functionalized BP monolayers is tested at room temperature (300 K) within 6 ps (6000 time-steps). The obtained results demonstrate that the fluctuations of the total energy and temperature are small. In all four configurations of the functionalized BP monolayer, the variation of the total energy is less than 0.5 eV. Also, the structures of surface-functionalized BP monolayers are only slightly distorted and still robust after 6 ps heating at 300 K. Neither structural reconstruction nor breaking of bonds takes place functionalized BP monolayers at 300 K. It implies that these structures are high thermal stability. The time-dependence of fluctuations of the total energy and temperature of the functionalized BP monolayers are depicted in Fig. S1 of the ESI.† Besides, the snapshots of atomic structures of the functionalized BP monolayers are presented in the ESI (see Fig. S2†).
The binding energy Eb of surface-functionalizated BP monolayers is calculated as
| Eb = Etotal − EBP − Especies, | (1) |
The calculated binding energy Eb of surface-functionalized BP monolayers is also provided in Table 1. Our obtained results demonstrate that the fully chlorinated boron phosphide configuration Cl–BP–Cl is the most stable model with the binding energy Eb = −5.365 eV and the fully brominated boron phosphide configuration Br–BP–Br is the least stable of the four configurations with Eb = −3.980 eV. There is no significant difference in the binding energy between Cl–BP–Br and Br–BP–Cl models. Previously, large binding energy is found for Ni or Co absorbed on BP monolayer.23
3.2 Elastic properties
For a more in-depth look at the issue of mechanical stability. We investigate the elastic properties of monolayers. For a 2D lattice, there are four independent parameters of the elastic constants, namely C11, C22, C12, and C66 (using the standard Voigt notation). The angular-dependent in-plane stiffness or 2D Young's modulus C2D(θ) and Poisson's ratio ν(θ) can be directly derived from the elastic constants Cij which can be obtained from DFT calculations34,35
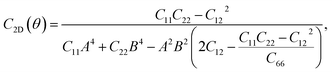 | (2) |
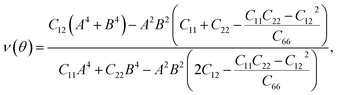 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and B = cos
θ and B = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ with θ being the angle relative to the x-direction.
θ with θ being the angle relative to the x-direction.
Due to the hexagonal symmetry of BP monolayer, there are only two elastic constants to be calculated being C11 and C12. The elastic constant C11 = C22 and C66 can be derived C11 and C12 as C66 = (C11 − C12)/2. The 2D Young's modulus C2D, 2D shear modulus G2D, and Poisson's ratio ν along the x/y-direction are given by36
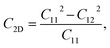 | (4) |
| G2D = C66, | (5) |
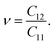 | (6) |
Our obtained results reveal that BP monolayer is mechanically stable similar to MoS2 (ref. 37) with the elastic constants being C11 = 146.285 (N m−1) and C12 = 38.753 (N m−1). These obtained values of the elastic constants of BP monolayer meet the Born criteria for mechanical stability.38 Our results for the elastic constants are consistent with the previous data.21 In Table 2, we listed our obtained results for the elastic properties of both pure BP and surface-functionalized BP monolayers. As presented in Table 2, we can see that the surface-functionalized BP with Br and Cl is less stiff than that of pure BP monolayer. This reduction in in-plane Young's modulus due to halogenated-functionalization has also been found in silicene.8 In our four functionalized configurations of BP monolayer, the Cl–BP–Cl is the most stiff with the Young's modulus C2D = 43.234 N m−1. In Fig. 3, we show the polar diagram for the in-plane Young's modulus C2D(θ) and Poisson's ratio ν(θ) of the surface-functionalized BP monolayers. We can see that all four configurations of the functionalized BP have perfect circular shape of the angle-dependent C2D(θ) and ν(θ). This implies that the functionalized BP monolayers possess a fully isotropic elastic characteristic due to the hexagonal symmetry.
| C11 | C12 | C2D | G2D | ν | |
|---|---|---|---|---|---|
| BP | 146.285 | 38.753 | 136.019 | 53.766 | 0.265 |
| Cl–BP–Cl | 104.858 | 18.373 | 101.639 | 43.243 | 0.175 |
| Cl–BP–Br | 102.896 | 19.457 | 99.216 | 41.719 | 0.189 |
| Br–BP–Cl | 101.503 | 26.531 | 94.568 | 37.486 | 0.261 |
| Br–BP–Br | 103.361 | 23.472 | 98.030 | 39.944 | 0.227 |
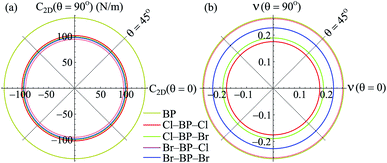 | ||
| Fig. 3 Polar diagram for Young modulus C2D (a) and Poisson ratio ν (b) of the surface-functionalized BP monolayers. | ||
3.3 Electronic structure
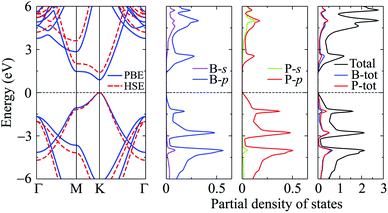
In this part, we investigate the electronic properties of the functionalized BP monolayers. To see the influence of the surface functionalization on the band structure of BP monolayer, we first calculate the band structure of the pure BP monolayer by using both PBE and HSE06 functionals. As presented in Fig. 4, we can see that at equilibrium, BP monolayer is a direct semiconductor in which both the conduction band minimum (CBM) and valence band maximum (VBM) are located at the K-point in the first Brillouin zone. The calculated band structures of BP monolayer at PBE and HSE06 levels are the same profile. However, the PBE functional is known to underestimate the energy gap of the semiconductors,39 and calculated energy gap by the hybrid functional such as HSE06 can yield more accurate results. Our calculated results reveal that the band gap of BP monolayer is 0.887 eV and 1.399 eV at the PBE and HSE06 levels, respectively. These results are consistent with the available data.20,22 In Fig. 4, we also present partial density of states (PDOS) of BP monolayer, which can help us estimate the contribution of atomic orbitals to the formation of electronic bands. Our calculations for the PDOS reveal that the electronic bands of BP monolayer are highly contributed by the B-p and P-p orbitals. The contributions of s-orbitals of both B and P to the conduction band are more prominent than their contributions to the valence band.When the boron phosphide monolayer is chemically functionalized with the halogen atoms Br and Cl, the functionalization of the surface not only changed its atomic structure (from planar to buckled structure), but also completely changed the electronic structure. Calculated band structures of the functionalized BP at the HSE06 level are presented in Fig. 5. We can see that all four configurations of the functionalized BP monolayer with Cl and Br are direct semiconductors. However, different from pure BP monolayer, the CBM and VBM of the functionalized BP lie at the Γ-point in the Brillouin zone. In Fig. 6, we present our calculations for the PDOS of the functionalized BP monolayers. We can see that the B-p and P-p orbitals contribute significantly to the formation of the electronic bands of the functionalized BP monolayers. Besides, the valence bands of the functionalized BP monolayers are significantly contributed from the p-orbitals of Br/Cl atoms.
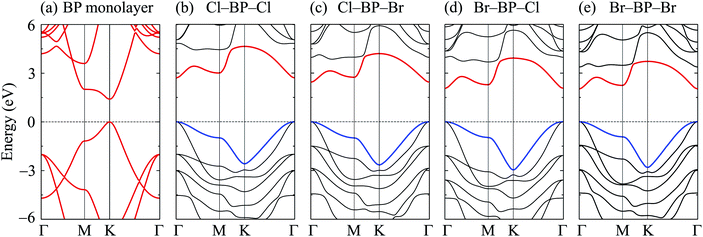 | ||
| Fig. 5 Calculated band structures of BP monolayer (a) and functionalized BP with Cl and Br (b–e) by the HSE06 method. | ||
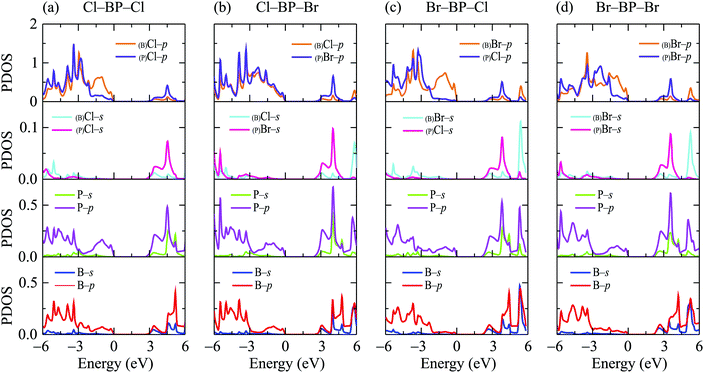 | ||
| Fig. 6 Partial density of states (PDOS) of the functionalized BP configurations: (a) Cl–BP–Cl, (b) Cl–BP–Br, (c) Br–BP–Cl, and (d) Br–BP–Br. | ||
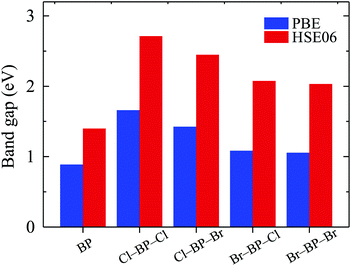
The band gaps of pure BP monolayer and functionalized BP monolayers are illustrated in Fig. 7. Our obtained results reveal that the band gaps of the functionalized BP monolayers are larger than that of pure BP monolayer. As presented in Fig. 7 and also listed in Table 1, the model of fully chlorinated boron phosphide Cl–BP–Cl possesses the largest band gap of 1.659 eV and 2.711 eV at the PBE and HSE06 levels, respectively. Meanwhile, the band gap of the fully brominated boron phosphide Br–BP–Br is found to be 1.055 eV/2.032 eV at the PBE/HSE06 level. The band gap of Br–BP–Br is the smallest compared to other functionalized configurations. Compared to other types of surface functionalization of boron phosphide, the band gap of Cl–BP–Cl is still less than that of the fully hydrogenated boron phosphide H–BP–H monolayer which is reported to be up to 4.80 eV by using the hybrid functional.25
To see the redistribution of charges after functionalization, we calculate the charge density of both pure BP and functionalized BP monolayers as shown in Fig. 8. In BP monolayer, the electron density is enriched around P atoms as presented in Fig. 8(b). After BP monolayer is functionalized with Br and Cl, the charge is strongly distributed in the species, especially the Cl species as illustrated in Fig. 8(d, f and h). The internal charge distribution is also investigated by using the Mulliken population analysis.40 Calculated results for the internal charge distribution in the functionalized BP monolayers and also charge transfer between BP and Br/Cl species are listed in Table 3. The total charges of B and P are −0.45e and +0.45e, respectively. From Table 3, we can see that there is the charge transfer from BP layer to the functionalized species Br/Cl. Due to the difference in the electronegativity of atoms, the amount of charge is transferred from the monolayer to the Br/Cl species in the functionalized configurations is different. Our calculated results demonstrate that the charge transferred from BP layer to the Cl species in the Cl–BP–Cl model is the largest (0.39e) and only 0.18e is transferred from BP layer to the Br species in the case of Br–BP–Br model. There is no difference in the charge transfer ΔQ from the BP layer and species in the cases of Cl–BP–Br and Br–BP–Cl models.
| Model | s | p | Total | Charge | ΔQ | |
|---|---|---|---|---|---|---|
| BP | B | 0.98 | 2.48 | 3.45 | −0.45 | — |
| P | 1.35 | 3.20 | 4.55 | +0.45 | ||
| Cl–BP–Cl | ClB | 1.91 | 5.24 | 7.15 | −0.14 | +0.39 |
| B | 0.99 | 2.26 | 3.25 | −0.25 | ||
| P | 1.49 | 2.87 | 4.36 | + 0.64 | ||
| ClP | 1.95 | 5.30 | 7.25 | −0.25 | ||
| Cl–BP–Br | ClB | 1.91 | 5.24 | 7.15 | −0.15 | +0.28 |
| B | 1.00 | 2.22 | 3.22 | −0.23 | ||
| P | 1.53 | 2.96 | 4.49 | +0.51 | ||
| BrP | 1.92 | 5.21 | 7.13 | −0.13 | ||
| Br–BP–Cl | BrB | 1.89 | 5.14 | 7.03 | −0.03 | +0.28 |
| B | 1.04 | 2.31 | 3.35 | −0.35 | ||
| P | 1.50 | 2.87 | 4.37 | +0.63 | ||
| ClP | 1.95 | 5.30 | 7.25 | −0.25 | ||
| Br–BP–Br | BrB | 1.90 | 5.14 | 7.04 | −0.03 | +0.18 |
| B | 1.05 | 2.27 | 3.32 | −0.32 | ||
| P | 1.55 | 2.95 | 4.50 | +0.50 | ||
| BrP | 1.93 | 5.21 | 7.14 | −0.14 |
4 Conclusion
In conclusion, the structural, elastic, and electronic properties of four configurations of the functionalized boron phosphide with Br and Cl atoms have been calculated by the DFT method. The functionalized boron phosphide monolayers exhibit high dynamical and thermal stability at room temperature. Upon the surface-functionalization, all four configurations Cl–BP–Cl, Cl–BP–Br, Br–BP–Cl, and Br–BP–Br have a low-buckled hexagonal structure with the lattice constant longer than that of pure BP monolayer. Our obtained results for the elastic constants satisfy Born's mechanical stability criteria. The surface-functionalization reduces the in-plane Young's modulus and Poisson's ratio of all four functionalized boron phosphide configurations was smaller than that of pure BP monolayer. The functionalized boron phosphide monolayers are direct semiconductors with the moderate gaps varying from 2.032 eV (Br–BP–Br) to 2.711 eV (Cl–BP–Cl) at the HSE06 level. The p orbitals of the Br/Cl species contribute greatly to the formation of the valence band of the functionalized BP monolayers and electron density is strongly enriched around the Cl species. The Mulliken population analysis has confirmed that the charge transfer in the fully chlorinated boron phosphide Cl–BP–Cl model. Our findings not only give a clear view of the possibility of modulating the physical properties of 2D materials by surface-functionalization but also open up a prospect of application of functionalized BP monolayers in nanoelectromechanical devices due to their excellent elastic and electronic properties.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Belarusian National Research Program “Convergence-2025”.References
- A. I. Siahlo, N. A. Poklonski, A. V. Lebedev, I. V. Lebedeva, A. M. Popov, S. A. Vyrko, A. A. Knizhnik and Y. E. Lozovik, Phys. Rev. Mater., 2018, 2, 036001 CrossRef CAS.
- N. A. Poklonski, S. A. Vyrko, A. I. Siahlo, O. N. Poklonskaya, S. V. Ratkevich, N. N. Hieu and A. A. Kocherzhenko, Mater. Res. Express, 2019, 6, 042002 CrossRef.
- T. V. Vu, V. T. T. Vi, C. V. Nguyen, H. V. Phuc and N. N. Hieu, J. Phys. D: Appl. Phys., 2020, 53, 455302 CrossRef CAS.
- H. T. T. Nguyen, V. V. Tuan, C. V. Nguyen, H. V. Phuc, H. D. Tong, S.-T. Nguyen and N. N. Hieu, Phys. Chem. Chem. Phys., 2020, 22, 11637–11643 RSC.
- C. V. Nguyen, M. Idrees, H. V. Phuc, N. N. Hieu, N. T. T. Binh, B. Amin and T. V. Vu, Phys. Rev. B, 2020, 101, 235419 CrossRef CAS.
- H. T. T. Nguyen, M. M. Obeid, A. Bafekry, M. Idrees, T. V. Vu, H. V. Phuc, N. N. Hieu, L. T. Hoa, B. Amin and C. V. Nguyen, Phys. Rev. B, 2020, 102, 075414 CrossRef CAS.
- R. Ruoff, Nat. Nanotechnol., 2008, 3, 10 CrossRef CAS.
- W.-B. Zhang, Z.-B. Song and L.-M. Dou, J. Mater. Chem. C, 2015, 3, 3087 RSC.
- F. Karlický, K. Kumara Ramanatha Datta, M. Otyepka and R. Zbořl, ACS Nano, 2013, 7, 6434 CrossRef.
- E. Cadelano, P. L. Palla, S. Giordano and L. Colombo, Phys. Rev. B, 2010, 82, 235414 CrossRef.
- Y. Jiao, F. Ma, J. Bell, A. Bilic and A. Du, Angew. Chem., Int. Ed., 2016, 55, 10292 CrossRef CAS.
- E. Bianco, S. Butler, S. Jiang, O. D. Restrepo, W. Windl and J. E. Goldberger, ACS Nano, 2013, 7, 4414 CrossRef CAS.
- J. Son, S. Lee, S. J. Kim, B. C. Park, H.-K. Lee, S. Kim, J. H. Kim, B. H. Hong and J. Hong, Nat. Commun., 2016, 7, 13261 CrossRef CAS.
- T. Pakornchote, Z. M. Geballe, U. Pinsook, T. Taychatanapat, W. Busayaporn, T. Bovornratanaraks and A. F. Goncharov, Carbon, 2020, 156, 549 CrossRef CAS.
- T. V. Vu, K. D. Pham, T. N. Pham, D. D. Vo, P. T. Dang, C. V. Nguyen, H. V. Phuc, N. T. T. Binh, D. M. Hoat and N. N. Hieu, RSC Adv., 2020, 10, 10731 RSC.
- A. Terentjevs, G. Cicero and A. Catellani, J. Phys. Chem. C, 2009, 113, 11323 CrossRef CAS.
- K. Woo, K. Lee and K. Kovnir, Mater. Res. Express, 2016, 3, 074003 CrossRef.
- K. Ananthanarayanan, C. Mohanty and P. Gielisse, J. Cryst. Growth, 1973, 20, 63 CrossRef CAS.
- H. Şahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Aktürk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453 CrossRef.
- H. R. Jiang, W. Shyy, M. Liu, L. Wei, M. C. Wu and T. S. Zhao, J. Mater. Chem. A, 2017, 5, 672 RSC.
- D. Çakir, D. Kecik, H. Sahin, E. Durgun and F. M. Peeters, Phys. Chem. Chem. Phys., 2015, 17, 13013 RSC.
- B. Zeng, M. Li, X. Zhang, Y. Yi, L. Fu and M. Long, J. Phys. Chem. C, 2016, 120, 25037 CrossRef CAS.
- N. Cakmak, Y. Kadioǧlu, G. Gökoǧu and O. Ü. Aktürk, Philos. Mag. Lett., 2020, 100, 116 CrossRef CAS.
- J. Yu and W. Guo, Appl. Phys. Lett., 2015, 106, 043107 CrossRef.
- S. Ullah, P. A. Denis and F. Sato, ACS Omega, 2018, 3, 16416 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
- D. Marx and J. Hutter, Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods, Cambridge University Press, Cambridge, 2009 Search PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511 CrossRef.
- B. Onat, L. Hallioglu, S. İpek and E. Durgun, J. Phys. Chem. C, 2017, 121, 4583 CrossRef CAS.
- M. Xie, S. Zhang, B. Cai, Z. Zhu, Y. Zou and H. Zeng, Nanoscale, 2016, 8, 13407 RSC.
- N. T. Hung, A. R. T. Nugraha and R. Saito, J. Phys. D: Appl. Phys., 2018, 51, 075306 CrossRef.
- L. Wang, A. Kutana, X. Zou and B. I. Yakobson, Nanoscale, 2015, 7, 9746 RSC.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- D. Çakir, F. M. Peeters and C. Sevik, Appl. Phys. Lett., 2014, 104, 203110 CrossRef.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- J. P. Perdew and M. Levy, Phys. Rev. Lett., 1983, 51, 1884–1887 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra00576f |
| This journal is © The Royal Society of Chemistry 2021 |