Predissociation resonances and accurate ab initio calculations of dication HF²⁺

Abstract

It is very interesting and challenging to investigate the electronic structures of diatomic dications, due to the nature of coulombic repulsive and bound attractive dissociation limits and their avoided diabatic interactions. Using the multi-reference configuration interaction approach, comprehensive ab initio calculations of the first 36 electronic states, corresponding to 15 dissociation limits, of dication HF²⁺ are reported. Good agreements for the vertical excitation energies and dissociation limits are achieved with the available references. Besides the common interesting quantities as adiabatic potential energy curves, dipole moments and spectral constants for the bound states, the nonadiabatic radial coupling matrix elements for the ^1,3Π states are also presented. A showcase for the diabatic potentials of ³Π states are presented and discussed. Furthermore, predissociation states from the nonadiabatic couplings or avoided crossing of potential energy curves, known as shape resonances in collisions, are also investigated by using the WKB and scattering methods.

---

I. Introduction

The studies of multiply charged ions and highly charged ions have been a long-standing interest due to their important participations in various dynamic processes as in astrophysics,^1–4 plasma physics,⁵ planetary ionospheres,⁶ interstellar chemistry,⁷ mass spectrometry⁸ and so on. In this work, we focus on the investigations of doubly charged diatomic dications, which have received much attention lying not only on their importance in diverse areas, but also on their interesting physical properties. Different from the highly charged and neutral systems, both Coulomb repulsive and chemical attractive interaction in diatomic dications play important roles, and avoided crossings between the potentials in short internuclear distances and metastable states could appear resulting from their diabatic interplay.^8–10 The metastable states of dications are of particular interest for both experiments and theories^11–15 as in absorption and emission spectroscopy,^16,17 fragmentations,^18,19 ion scatterings^20,21 and so on. Furthermore, the recently developed X-ray free-electron laser facilities can generate ultra-short and ultra-intense X-ray pulses,^22,23 and provide versatile Auger electron spectroscopy and kinetic energy release spectra to manipulate the nuclear dynamics of dications. These applications urgently ask for highly accurate electronic structures as potential energy curves (PEC) of dications,^24–26 which is also highly required for the charged transfer investigations in heavy ion collisions.³

As a typical diatomic dication, it is interesting that not too many works of HF²⁺ have been recorded. HF²⁺ can be obtained by kicking out two electrons of HF molecule, while HF gas can easily dissolve in water as extremely strong and caustic acid, very few related experiments have been performed.²⁷ This fact asks for much more investigations from the theoretical and computational aspects for HF²⁺ dication. The lowest PEC of HF²⁺ is a repulsive one, corresponding to the dissociation limit of ground-(F⁺ + H⁺). The ionization potentials (IP) of F⁺ ion and H atom are 35.970 eV and 13.598 eV, respectively. The first excited energy of H atom is 10.199 eV, so the HF²⁺ excited states with dissociation limits less than 31.571 eV (above the ground-(F⁺ + H⁺)) correspond to the repulsive ones-(F⁺* + H⁺) and attractive ones-(F²⁺* + H). For example, the dissociation limit of the lowest attractive curve is the ground-(F²⁺ + H), 21.372 eV above the ground-(F⁺ + H⁺). The Coulomb repulsion dominates the whole internuclear interactions of HF²⁺, interplayed by the excited attractive PECs. These facts lead to the difficulties to investigate the electronic structures and metastable states of dications by both theory and experiment.²⁸

The first comprehensive work about HF²⁺ electronic structures could be the measurements of Auger electron spectra of HF molecule excited by X-ray photoionization in 1975 by Shaw et.al.,²⁷ where most of the final states in HF²⁺ have been identified. Relevant theoretical investigations of the Auger electron spectra have been performed by Cederbaum's group^24,29 in 1990s, where the complete active space self-consistent field (CASSCF) method has been employed to calculate the repulsive electronic structures of HF²⁺. However, the correlations from the attractive states are not sufficiently introduced in the calculations and the PECs are restricted in the short internuclear distances of 0.4–2 Å. Up to now, the most advanced studies of HF²⁺ electronic structures could be the calculations by the multi-reference single- and double-excitation configuration interaction (MRDCI) method by Bruna et.al. in 2006, where the vertical transition energies up to the first bound state (1⁵Σ⁻) have been comprehensively calculated. Bearing in mind that the X-ray free-electron laser facilities have supplied more advanced degrees of freedom to investigate the dications. The present electronic structures of HF²⁺ are apparently far less and accurate enough. More comprehensive investigations for a broad internuclear distance and enough electronic states in high-level investigations are highly required.

In the present work, the highly accurate 36 potential energy curves of HF²⁺ are comprehensively investigated by the multi-reference configuration interaction approach (MRCI).³⁰ These states correspond to 12 repulsive dissociation limits (F⁺* + H⁺) and 3 attractive dissociation limits (F^2+* + H). The spectral constants of 9 bound states, transition dipole moments between the states, radial coupling matrix elements for ^1,3Π states are given. The diabatic potentials of ³Π states are also presented and discussed, and the position and decay width of predissociation states are jointly investigated by using the WKB³¹ and scattering methods.^32,33

II. Computation methods

A. Multi-reference configuration interaction calculations

All the calculations were performed using in the Molpro 2012 quantum chemistry ab initio package.^34,35 Different basis sets have been tested and finally the correlation-consistent aug-cc-pV5Z basis set^36–38 for F (15s9p5d4f3g2h → 7s6p5d4f3g2h) and H (9s5p4d3f2g → 6s5p4d3f2g) are employed. The irreducible representations of C_2v is used to describe the linear molecule of C_∞v as Σ⁺ = A₁, Σ⁻ = A₂, Π = B₁ + B₂ and Δ = A₁ + A₂. Since both states Δ and Σ⁺ share the same A₁, the unnatural avoid crossing or interplay in the PECs between A₁ of Δ and A₁ of Σ⁺ should be corrected; so do the PECs for states Σ⁻ and Δ.

To obtain more accurate PECs of HF²⁺, MRCI is adopted in the calculations for each internuclear distance, with the reference wave functions generated by a state averaged-CASSCF (SA-CASSCF) procedure.^39,40 In SA-CASSCF calculations, the initial molecular orbitals (MOs) are prepared by Hartree–Fock method, the active MOs for both singlet and triplet states are 5a₁, 3b₁ and 3b₂ (termed as (5330)), and the quintuplet states use the active MOs of (6220), all 8 electrons are active. The relativistic correction for the valance energies of F⁺ and F²⁺ is in the order of 0.01 eV,⁴¹ that the spin–orbit interaction could be safely ignored in the calculations.

Note that the key point for the application of multi-reference methods is the rational selections of active space. However, for dications, the conventional scheme of building active space according to the dissociation limit is not adequate enough than for the neutral diatomics. Due to the avoided crossing and interplay between repulsive and attractive adiabatic PECs, a low-lying excited state in the dissociation limit could result from a highly excited state at the small internuclear distance after interplaying several times. The avoided crossing changes the active space with the variations of internuclear distance, a larger active space would be expected for dications to provide consistent results for the whole internuclear region. After lots of preliminary checking, the large active space (5330) for the singlet and triplet sates, and (6220) for the quintuplet states are implemented to generate 36 accurate PECs of HF²⁺, corresponding to 15 dissociation limits.

B. Adiabatic to diabatic transformation

Generally speaking, the PECs are calculated in the adiabatic representation, and the nonadiabatic couplings are quite weak between PECs away from each other. When two adiabatic PECs of the same symmetry approach each other and even interplay as the avoided crossing in a narrow region, the diabatic couplings should be taken into account seriously.^3,42 For the PECs with strong diabatic couplings, it would be more convenient to transform the PECs into the diabatic representation.³³ Since in the adiabatic representation, the nonadiabatic radial coupling matrix A(R) would change rapidly and appear as sharp peaks in the avoided crossing regions, while the off-diagonal potential/Hamiltonian in the diabatic representation indicating the diabatic radial coupling evolve slowly with respect to the internuclear distance, bringing in less instabilities for the numerical investigations in molecular dissociation, ion collision and so on.³ The adiabatic PECs V^a can be transformed into the diabatic ones V^d by the unitary matrix C(R) as V^d = C^†V^aC. The transformation matrix C(R) satisfies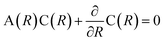 with C(R → ∞) → I.³

Practically, the radial coupling matrix elements can be calculated numerically by finite difference method as 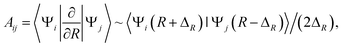^32,33 which can be implemented in MOLPRO with the subroutine OVERLAP,³⁵ and Δ_R = 0.001 a.u. in the present calculations. The important radial coupling matrix elements for ^1,3Π states have been calculated, and the diabatic potentials of ³Π states are transformed and discussed as a showcase.

C. Vibrational levels and spectroscopic constants

Once we get the potential energy curve of an electronic state, the vibrational energy levels can be obtained by numerically solving the radial Schrodinger equation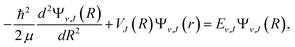 where μ is the reduced mass of the system, J is the rotational quantum number, R is the internuclear distance, and the rotationless (electronic) potential V(R) plus a centrifugal term forms the effective one-dimensional potential V_J(R). The piecewise exact power series expansions method⁴³ has been employed to efficiently solve the ro-vibrational levels in the present work. Generally speaking, the spectroscopic constants for a single bound state can be extracted from the numerical potential energy curves. For diatomic molecules, the potential energy curves of electronic states are simple and well-shaped, and the first few vibrational levels could be well represented by Morse potential.⁴⁴ Therefore, the parameters including the equilibrium distance (R_e), the well depth (D_e), the vertical transition energy (T_e), the harmonic frequency (ω_e), and the anharmonic constant (ω_eχ_e) can be obtained by fitting the vibrational levels. The other spectroscopic constants, such as rotational constant (B_e), can be generated by fitting the rovibrational levels as,^45,46 E_v,J = G(v) + B_v[J(J + 1)] − D_v[J(J + 1)]² + H_v[J(J + 1)]³ + … = ∑_m=0K_m(v)[J(J + 1)]^m, where G(v) is the vibrational energy level, B_v is rotational constant, D_v, H_v, … are anharmonicity.

D. Tunneling-predissociation states

When the PEC has a potential barrier above its dissociation limit, and the barrier is strong enough to temporally support localized states, these states will ultimately decay into the continuum through tunneling. These states are known as the tunneling-predissociation quasi-bound states, or shape resonances in particle collisions.^3,33,42 The state/resonance position and decay width are quite important to understand the predissociation dynamics of dications. For the tunneling states with very long lifetimes, the state levels could be well approximated as the bound levels within the potential barrier,⁴² and the classical WKB method³¹ can be efficiently employed to calculate the tunneling lifetime as τ = t_vib/ω, where t_vib is the oscillation period in the potential well, and ω is the probability per collision of tunneling through the barrier. Precisely,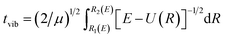 and 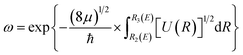, where E is the bound energy level, U(R) = V(R) + [J(J + 1)/R²](ℏ²/2μ) is the effective potential, μ is the reduced mass of the system, v and J are the vibration and rotation quantum numbers, respectively. R₁(E), R₂(E) and R₃(E) are the first three classical turning points.³¹ Note that the LEVEL program by Le Roy⁴⁷ has implemented the WKB method.

It has shown that the long-lived tunneling states close to the bottom of the potential well could be well studied by the WKB method, while for the states close to the barrier top, WKB calculations would introduce uncertainties up to 10% or more.^48–50 In such a case, an alternative quantum scattering method³ can be employed by treating the collisions of A⁺ + B⁺ in the potential of AB²⁺. The phase shift δ(E) of the free state fragments carries the information of scattering between A⁺ + B⁺, and the existence of resonance states would increase the phase shift by almost π,⁵¹ and the resonance position E_r and width Γ can be well extracted by fitting δ(E) using the Breit–Wigner formula^51,52 as 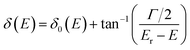. δ₀(E) is the background phase shift near the resonance, and varies slowly, so the resonance parameters can be efficiently calculated as 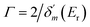, where 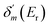is the maximum derivative value of the δ(E) with respect to the energy, and the corresponding energy is E_r as the resonance position.⁵³ Note that the electron potential scattering code RADIAL can be properly modified to efficiently calculate the particle scattering phases.^54,55

III. Results and discussion

With the help of Wigner–Witmer principle,⁵⁶ the electronic states of HF²⁺ can be determined by the atomic states in its corresponding dissociation limit, e.g., ⁴S_u + ²S_g = ⁵Σ⁻ and ³Σ⁻. With the data of energy levels (F⁺, F²⁺ and H) from NIST,⁴¹ the tens of dissociation limits including Rydberg series up to F²⁺(2s²2p³) + H(2s) are listed and shown in Table 1, the combinations between different excited F²⁺(2s²2p³) and H(1s) result into the 3 attractive dissociation limits, and the repulsive ones are from the interactions between F⁺* and H. Note that Rydberg states with dissociation limit F⁺(2s²2p³nl) + H⁺ below the limit F²⁺(2s²2p³) + H(2s) can not be precisely calculated, states up to 12 repulsive dissociation limits and all 3 attractive dissociation limits are carefully investigated in the present work. In the calculations, the energies of dissociation limits could be obtained as the energy differences from the ground state at large R₀ (50 a.u. in the present work) for the attractive states; while for the repulsive curves, such energy differences at large R₀ minus 1/R₀ produce the expected energies of dissociation limits, where 1/R₀ represents the left positive repulsive coulomb potential.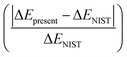

Table 1 The dissociation limits of HF²⁺ up to F²⁺(2s²2p³) + H(2s) with the corresponding 36 electronic states (states up to 5¹Σ⁺, 2¹Σ⁻, 6¹Π, 3¹Δ, 2³Σ⁺, 6³Σ⁻, 6³Π, 2³Δ, 3⁵Σ⁻ and 1⁵Π) calculated in the present MRCI. The relative excitation energies (eV, to states 1³Σ⁻) for the dissociation limits are compared with that of NIST,⁴¹ the ratio of differences are within 0.8%

Atomic state	Term	State	ΔENIST	ΔEpresent	Ratio of difference
F^+(2s^22p^4) + H^+	^3Pg	1^3Σ^−, 1^3Π	0	0	0
F^+(2s^22p^4) + H^+	^1Dg	1^1Σ^+, 1^1Π, 1^1Δ	2.588	2.572	0.61%
F^+(2s^22p^4) + H^+	^1Sg	2^1Σ^+	5.569	5.531	0.68%
F^+(2s2p^5) + H^+	^3Pu	1^3Σ^+, 2^3Π	20.432	20.460	0.14%
F^2+(2s^22p^3) + H(1s)	^4Su + ^2Sg	1^5Σ^−, 2^3Σ^−	21.371	21.198	0.81%
F^+(2s^22p^33s) + H^+	^5Su	2^5Σ^−	21.882	21.791	0.42%
F^+(2s^22p^33s) + H^+	^3Su	3^3Σ^−	22.672	22.594	0.34%
F^+(2s^22p^33s) + H^+	^5Pg	1^5Π, 3^5Σ^−	25.101	24.984	0.46%
F^2+(2s^22p^3) + H(1s)	^2Du + ^2Sg	2^1Δ, 2^1Π, 1^1Σ^−; 1^3Δ, 3^3Π, 4^3Σ^−	25.597	25.459	0.54%
F^+(2s^22p^33p) + H^+	^3Pg	4^3Π, 5^3Σ^−	25.751	25.701	0.19%
F^+(2s^22p^33s) + H^+	^3Du	5^3Π, 6^3Σ^−, 2^3Δ	26.268	26.190	0.30%
F^+(2s^22p^33s) + H^+	^1Du	3^1Π, 2^1Σ^−, 3^1Δ	26.665	26.584	0.30%
F^2+(2s^22p^3) + H(1s)	^2Pu + ^2Sg	4^1Π, 3^1Σ^+; 6^3Π, 2^3Σ^+	27.762	27.605	0.57%
F^+(2s^22p^33s) + H^+	^1Pu	4^1Σ^+, 5^1Π	28.173	28.187	0.04%
F^+(2s^22p^33s) + H^+	^3Pu	4^3Σ^+, 7^3Π	28.461	—	—
F^+(2s^22p^33d) + H^+	^3Du	8^3Π, 7^3Σ^−, 3^3Δ	28.772	—	—
F^+(2s^22p^34s) + H^+	^5Su	4^5Σ^−	29.155	—	—
F^+(2s^22p^33p) + H^+	^1Pg	3^1Σ^−, 6^1Π	29.216	29.383	0.57%
F^+(2s^22p^3nl) + H^+	—	—	—	—	—
F^2+(2s^22p^3) + H(2s)	^4Su + ^2Pu	^3,5Σ^−, ^3,5Π	31.569	—	—

---

In Table 1, the first and second column indicate different dissociation limits and its atomic terms. The corresponding molecular states is given in the third column. The fourth and fifth column are the NIST (ΔE_NIST) and present (ΔE_present) calculated excitation energies by MRCI with respect to the lowest dissociation limit F⁺(2s²2p⁴) + H⁺. The ratio of difference 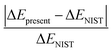is given in the last column. Practically, 15–17^th dissociation limits are not precisely calculated, the calculations show that very tiny improvement of the accuracy for states 7–9³Π requires huge active space and are very expensive, while such a small improvement of these states tiny affect other lower triplet states. Thus it turns much cheaper to lose the accuracy of the three dissociation limits and related states, and the accuracy for other dissociation limits and states can be properly achieved. Besides, such a treatment do not affect the 18^th dissociation limit of singlet states. So in Table 1, states up to 5¹Σ⁺, 2¹Σ⁻, 6¹Π, 3¹Δ, 2³Σ⁺, 6³Σ⁻, 6³Π, 2³Δ, 3⁵Σ⁻ and 1⁵Π, 36 electronic states in total corresponding to 15 dissociation limits are reported. As it shows, the present relative energies by MRCI for the dissociation limits agree quite well with that of the NIST data.⁴¹ The absolute difference and difference ratio are within 0.18 eV and 0.8%, respectively.

The corresponding adiabatic potential energy curves of HF²⁺ dication by MRCI for the 36 electronic states listed in Table 1, are presented in Fig. 1 in a broad internuclear distances of R = 0.7–50 a.u. The PECs in large internuclear distance (>10 a.u.) for states sharing the same dissociation limits almost overlap with each other, and the attractive and repulsive branches could interchange at large internuclear distances, such as the crossing around 30 a.u. between states 3¹Π and 4¹Π. The nonadiabatic coupling results into the interplay or avoided crossing between PECs, and the positions of these avoided crossings are listed in Table 2. The nonadiabatic coupling and avoided crossing play a very important role in the electron-nuclear correlated dynamics, such as the photoabsorption spectra, molecular dissociation yield, charge transfer in ion collisions and so on.^3,18,58 What is more, the related transition dipole moment (TDM) and permanent dipole moment (PDM) would surely be affected and even interchanged by the nonadiabatic couplings. The strength of nonadiabatic coupling is imprinted by the radial coupling matrix A(R), which must be firstly supplied to transform the PECs into diabatic representation. All these relevant quantities will be presented below.

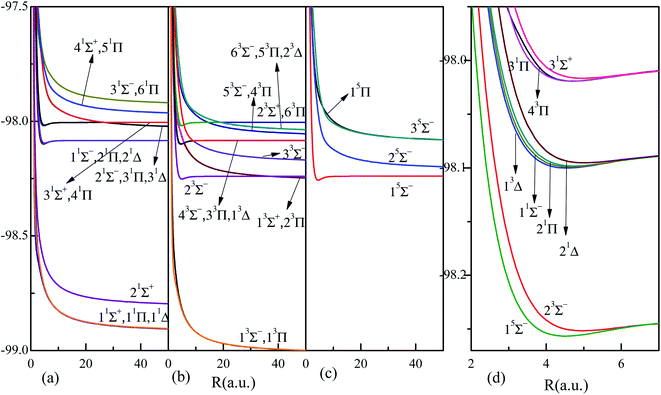Fig. 1 Highly accurate adiabatic potential curves of the 36 electronic states (states up to 5¹Σ⁺, 2¹Σ⁻, 6¹Π, 3¹Δ, 2³Σ⁺, 6³Σ⁻, 6³Π, 2³Δ, 3⁵Σ⁻ and 1⁵Π) of HF²⁺ dication by MRCI calculations, see Table 1 for more information of the states. Panels (a), (b) and (c) correspond to the 16 singlet, 15 triplet and 4 quintet states, respectively. The nine bound states are highlighted and given in panel (d).

Table 2 The positions R_c (a.u.) of avoided crossings between the adiabatic potential energy curves

States	Rc	States	Rc
2^3Π–3^3Π	5.75	3^1Π–4^1Π	1.85, 27
3^3Π–4^3Π	2.85	4^1Π–5^1Π	1.55, 3.55
4^3Π–5^3Π	1.5, 14.5	5^1Π–6^1Π	1.3
5^3Π–6^3Π	1.6, 19	3^3Σ^−–4^3Σ^−	9.1

---

Besides carefully checking of the convergence, the accuracy of the present PECs could also be roughly estimated from several points. The PECs smoothly vary with respect to R. The repulsive brunches (F⁺ + H⁺) in large R decrease as the coulombic potential 1/R and the attractive ones reach constant limits. The relative energies for the dissociation limits show very good agreements with that of NIST data,⁴¹ where the absolute differences are less than 0.1 eV for repulsive states and about 0.15 eV for attractive states (Table 1). Further more, the vertical excitation energies at R = 2.2 a.u. agree quite well with that of the available MRD-CI results by Pablo et.al.⁵⁷ shown in Table 3. The minor differences could be from different basis sets and different levels of calculations.

Table 3 Vertical excitation energies ΔE_v (eV) relative to 1³Σ⁻ at R = 2.2 a.u

	Present	MRD-CI data^57
1^1Δ	2.70	2.86
1^1Σ^+	4.23	4.39
1^3Π	2.22	2.29
1^1Π	4.72	4.92
2^1Σ^+	8.41	8.61
1^5Σ^−	17.37	17.33

---

To show the importance of including the dynamic electron correlations in the calculations, PECs of low-lying excited states by previous CASSCF²⁴ and present MRCI are shown in Fig. 2a. The CASSCF results of Pahl et.al.²⁴ include seven singlet states and two triplet states given at R = 1–4 a.u., the present MRCI results are matched at R = 4 a.u. for 1¹Δ state. As Fig. 2a shows, PECs of low-lying states (1¹Δ, 1¹Π, 1¹Σ⁺, and 2²Σ⁺) show excellent agreements between the previous CASSCF and present MRCI, however, significant discrepancies appear for higher excited states. The fact is that the dynamic electronic correlation is not fully considered in the CASSCF calculations, and such correlations should be more important for the description of highly excited states. Especially for the states involving nonadiabatic coupling and avoided crossing, more accurate descriptions of the dynamic electronic correlation are required. PECs of (1–6)³Π states by present CASSCF and MRCI are also presented in Fig. 2b and c, respectively, to further reveal the importance of including dynamic electron correlations. As it clearly shows, for these states with important nonadiabatic couplings, the inclusion of dynamic electron correlations shift back the avoided crossings into smaller internuclear region, therefore the electronic structures at small internuclear distances by CASSCF may be not reliable. CASSCF method could not be a proper choice to treat doubly charged HF²⁺ dications, especially for the states with nonadiabatic couplings. These features definitely indicate the importance of using high-level calculation methods instead of CASSCF method for dications.

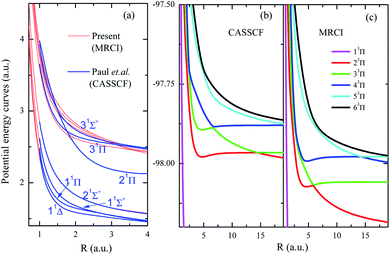Fig. 2 Panel (a) shows the PECs of some lowing excited states of HF²⁺ in the present MRCI level and the CASSCF level by Paul et al.;²⁴ the PECs of ³Π of HF²⁺ by present CASSCF and MRCI calculations are given in panels (b) and (c), respectively.

Fig. 1 also reveals nine shallow bound states, 1⁵Σ⁻, 2³Σ⁻, and 1¹Σ⁻, 2¹Δ, 2¹Π, 1³Δ, and 3¹Σ⁺, 3¹Π, 4³Π, locating at around 4.5 a.u., with binding energy of about 0.4 eV. The first two, the third to sixth, and the last three states are in the same dissociation limits F²⁺(2s²2p³)⁴S_u + H(1s)²S_g, F²⁺(2s²2p³)²D_u + H(1s)²S_g, and F²⁺(2s²2p³)²P_u + H(1s)²S_g, respectively. Detailed spectral constants of these nine bound states are presented in Table 4. About five vibrational states could be supported. The leading configuration and its weight around the equilibrium of each state are also given. It shows the configuration interactions are quite important for all these bound states. There are two leading configurations for both states 1⁵Σ⁻ and 2¹Π, while besides two leading configurations for states 3¹Σ⁺, 3¹Π and 4³Π, the listed additional 3% one also plays a very important role in MRCI calculations. Dynamic correlations are very important for the precise calculations.

Table 4 Spectral constants and leading configurations of nine bound states

States	Re/a.u.	ωe/cm^−1	De/eV	ωeχe/cm^−1	Be/cm^−1	Leading configuration and weight at R
1^5Σ^−	4.51	675	0.47	30	3.1	0.64 3σ4σ^05σ1π^2 + 0.34 3σ4σ1π^2 at R = 4.5 a.u.
1^5Σ^− (ref. 57)	4.34	670
2^3Σ^−	4.97	558	0.32	31	2.9	0.97 3σ4σ1π^2 at R = 5.0 a.u.
1^1Σ^−	4.62	639	0.41	30	3.0	0.97 3σ4σ1π^2 at R = 4.6 a.u.
2^1Δ	5.00	551	0.31	31	2.5	0.97 3σ4σ1π^2 at R = 5.0 a.u.
2^1Π	4.72	616	0.39	31	2.8	0.49 3σ^04σ1π^3 + 0.49 3σ^24σ^25σ1π^0 at R = 4.7 a.u.
1^3Δ	4.54	666	0.45	30	3.1	0.97 3σ4σ1π^2 at R = 4.5 a.u.
3^1Π	4.69	623	0.39	31	2.9	0.47 3σ^04σ1π^3 + 0.48 3σ^24σ1π + 0.03 2σ^03σ^24σ1π^3 at R = 4.7 a.u.
4^3Π	4.71	654	0.40	33	2.8	0.45 3σ^04σ1π^3 + 0.48 3σ^24σ1π + 0.03 2σ^03σ^24σ1π^3 at R = 4.7 a.u.
3^1Σ^+	4.97	562	0.32	31	2.5	0.47 3σ^04σ1π^3 + 0.47 3σ^24σ1π + 0.03 2σ^03σ4σ1π^4 at R = 5.0 a.u.

---

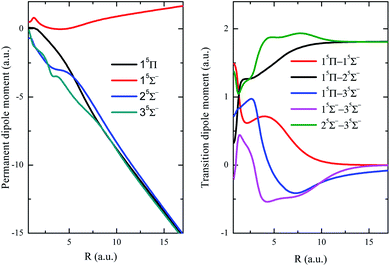
The permanent dipole moment (PDM), transition dipole moment (TDM), radial coupling matrix element (RCME) for the typical low-lying states are also presented in Fig. 3–5, based on the MRCI calculations. These molecular parameters are indispensable to describe the dynamic processes such as spontaneous emission (Einstein coefficient), photo excitation and dissociation, charge transfer in ion collisions and so on. Fig. 3 has shown the PDM and TDM for the quintet states of HF²⁺. The value of PDM depends on the reference point of coordinates for charged specifies,⁵⁹ the mass center of molecule is chosen as the reference point in this work, then the PDM at large R shows nearly linear behavior with respect to R, for the repulsive branches with one charge in each fragment. Similar features broadly appear in many systems with charged repulsive and even attractive branches.^60–62 Note that 1⁵Σ⁻ is the lowest quintet state, and its dipole spontaneous emission is forbidden, 1⁵Σ⁻ could be a long-lived stable candidate for HF²⁺. The leading configuration for 3⁵Σ⁻ is 0.99 1σ²2σ²3σ4σ⁰5σ⁰6σ1π², requiring the active orbitals up to at least 6a₁2b₁2b₂ in state-averaged CASSCF calculations.

Fig. 3 Permanent dipole moments and transition dipole moments of quintet states.

Both singlet and triplet Π states show avoided crossings, the PDM, TDM and RCME for states ^1,3Π are presented in Fig. 4 and 5. The linear behavior of the PDM at large R is apparently, the abrupt changes for PDM with respect to R correspond to the regions of avoided crossings (see Table 2), featured as significant peaks for RCME. Both PDM and TDM show much more complex variations compared with that of quintet states without nonadiabatic interactions (see Fig. 3). We would expect the nuclear wavepacket dynamics on excited Π states should seriously include the nonadiabatic couplings. Note that the main configurations for states 2³Π and 3³Π are 1σ²2σ3σ²1π³ and 0.49 1σ²2σ3σ⁰4σ1π³ + 0.48 1σ²2σ²3σ²4σ1π, respectively, indicating the importance of implementing the multi-configuration method.

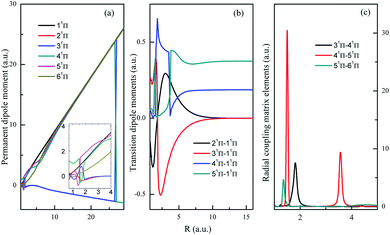Fig. 4 Permanent dipole moments, transition dipole moments and important radial coupling matrix elements between ¹Π states.

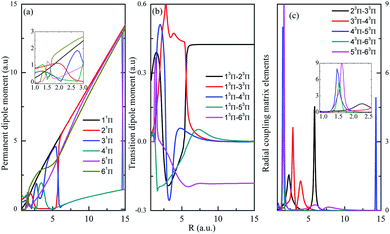Fig. 5 Same as in Fig. 4 but for ³Π.

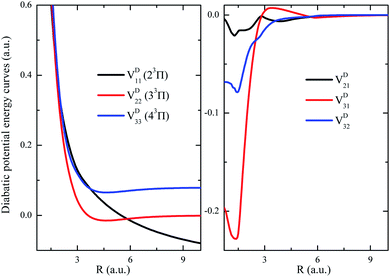
As a showcase for the treatments of nonadiabatic system in the diabatic representation, the strongly coupled (2, 3, 4)³Π states have been transformed into diabatic representation and their diabatic PECs (including off-diagonal couplings) are shown in Fig. 6. As it shows, the repulsive diabatic PEC V^D₁₁ crosses through both attractive ones V^D₂₂ and V^D₃₃, and the diabatic off-diagonal couplings evolve normally with respect to R. Such a transformation has depleted the difficulties induced by the sharp radical coupling matrix A(R) in the studies related to the nuclear wavepacket dynamics. It turns out that the diabatic representation is more suitable for system with intense nonadiabatic couplings.

Fig. 6 The diabatic potential energy curves from the transformations of adiabatic potential energy curves using the radial coupling matrix elements for showcase of ³Π states. (a) and (b) are the diabatic potential energy curves and off-diagonal diabatic interactions, respectively.

Finally, as a consequence of interchange between the PECs, tunneling-predissociation levels exist in this system. These states are also known as shape resonances or quasibound states in ion-atom collisions, they decay through the nonradiative tunneling process. As has mentioned in Sec. II, both WKB method and scattering method have been employed to calculate the predissociation level and width in a complementary way. Table 5 has shown the predissociation levels (relative to its dissociation limit) and widths for both states 3³Σ⁻ and 2³Π. Note that there are six and only one predissociation states for states 3³Σ⁻ and 2³Π, respectively. The WKB calculations show that the widths for ν = 5, 6 (3³Σ⁻) and ν = 0 (2³Π) are quite large, their positions and widths have been corrected by performing the scattering method. Typically, states ν = 6 (3³Σ⁻) and ν = 0 (2³Π) can tunneling decay as fast as in picosecond.

Table 5 The resonance parameters of the tunneling-predissociation levels with the rotation quantum number J = 0. WKB method has been employed to calculate the resonance parameters for states ν = 1–4 of 3³Σ⁻, and to be more accurately, the scattering method is used for 3³Σ⁻ states with ν = 5, 6 and the 2³Π states

ν	Position (eV)	Width (cm^−1)	Lifetime (s)
3^3Σ^−
0	2.45297	1.396 × 10^−23	1.521 × 10^12
1	2.52746	7.850 × 10^−18	2.706 × 10^6
2	2.59519	5.964 × 10^−13	3.560 × 10^1
3	2.6558	8.742 × 10^−9	2.430 × 10^−3
4	2.7089	2.820 × 10^−5	7.530 × 10^−7
5	2.75408	8.470 × 10^−3	1.254 × 10^−9
6	2.79094	1.164 × 10^0	9.117 × 10^−12
2^3Π
0	4.5129	4.566 × 10^0	2.325 × 10^−12

---

IV. Conclusion

In this work, accurate ab initio calculations have been implemented on the electronic structure of HF²⁺ dication. 36 potential energy curves, corresponding to 12 repulsive dissociation limits F⁺* + H⁺ and 3 attractive dissociation limits F²⁺ + H(1s), are obtained by multi-reference configuration interaction approach. Good agreement have been achieved with existing theoretical results with respect to dissociation limits and vertical excitation energies. Spectroscopic constants for bound states, dipole moments and the radial coupling matrix elements for typical showcases are also presented. Furthermore, the tunneling-predissociation levels, due to the nonadiabatic coupling or avoided crossing of PECs, are investigated by WKB method complemented by the scattering method. To achieve reliable results for dications, the dynamic electron correlations should be seriously taken into account, high-level calculations beyond CASSCF as MRCI are expected.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Grants from NSFC (No. 11934004, 11974230), the Science Challenge Program of China (TZ2018005) are acknowledged.

References

1. S. Butler and A. Dalgarno, Astrophys. J., 1980, 241, 838.
2. R. K. Janev, L. P. Presnyakov, and V. P. Shevelko, Physics of highly charged ions, vol. 13, Springer Science & Business Media, 2012.
3. B. H. Bransden and M. R. C. McDowell, Charge exchange and the theory of ion-atom collisions, Clarendon Press, 1992.
4. G. B. Rybicki and A. P. Lightman, Radiative processes in astrophysics, John Wiley & Sons, 2008.
5. T. V. Alves, W. Hermoso, K. Franzreb and F. R. Ornellas, Phys. Chem. Chem. Phys., 2011, 13, 18297.
6. R. Thissen, O. Witasse, O. Dutuit, C. S. Wedlund, G. Gronoff and J. Lilensten, Phys. Chem. Chem. Phys., 2011, 13, 18264.
7. D. K. Böhme, Phys. Chem. Chem. Phys., 2011, 13, 18253.
8. S. D. Price and J. Roithová, Phys. Chem. Chem. Phys., 2011, 13, 18251.
9. V. G. Nenajdenko, N. E. Shevchenko, E. S. Balenkova and I. V. Alabugin, Chem. Rev., 2003, 103, 229.
10. H. Sabzyan, E. Keshavarz and Z. Noorisafa, J. Iran. Chem. Soc., 2014, 11, 871.
11. A. S. Mullin, D. M. Szaflarski, K. Yokoyama, G. Gerber and W. Lineberger, J. Chem. Phys., 1992, 96, 3636.
12. D. Mathur, L. Andersen, P. Hvelplund, D. Kella and C. Safvan, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 3415.
13. H. Hogreve, Chem. Phys. Lett., 2004, 394, 32.
14. M. Kolbuszewski, J. S. Wright and R. J. Buenker, J. Chem. Phys., 1995, 102, 7519.
15. H. Sabzyan, E. Keshavarz and Z. Noorisafa, J. Iran. Chem. Soc., 2014, 11, 871.
16. U. Fano and J. W. Cooper, Phys. Rev., 1965, 137, A1364.
17. C. Ott, A. Kaldun, P. Raith, K. Meyer, M. Laux, J. Evers, C. H. Keitel, C. H. Greene and T. Pfeifer, Science, 2013, 340, 716.
18. E. F. Van Dishoeck, M. C. Van Hemert, A. C. Allison and A. Dalgarno, J. Chem. Phys., 1984, 81, 5709.
19. A. N. Heays, A. D. Bosman and E. F. Van Dishoeck, Astron. Astrophys., 2017, 602, A105.
20. B. Zygelman, A. Dalgarno, M. Kimura and N. F. Lane, Phys. Rev. A, 1989, 40, 2340.
21. Y. Wu, X. H. Lin, B. Yan, J. G. Wang and R. K. Janev, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 035203.
22. C. Bostedt, S. Boutet, D. M. Fritz, Z. Huang, H. J. Lee, H. T. Lemke, A. Robert, W. F. Schlotter, J. J. Turner and G. J. Williams, Rev. Mod. Phys., 2016, 88, 015007.
23. L. Young, K. Ueda, M. Gühr, P. H. Bucksbaum, M. Simon, S. Mukamel, N. Rohringer, K. C. Prince, C. Masciovecchio and M. Meyer, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 032003.
24. E. Pahl, H. Meyer, L. S. Cederbaum, D. Minelli and F. Tarantelli, J. Chem. Phys., 1996, 105, 9175.
25. S. Song, B. Ding, W. Xu, C. Nicolas, M. Patanen, S. Nandi, J. Bozek, C. Miron, Z. Xiao and X.-J. Liu, Phys. Rev. A, 2019, 99, 022511.
26. J. Ullrich, A. Rudenko and R. Moshammer, Annu. Rev. Phys. Chem., 2012, 63, 635.
27. R. W. Shaw and T. D. Thomas, Phys. Rev. A, 1975, 11, 1491.
28. M. Alagia, B. G. Brunetti, P. Candori, S. Falcinelli, M. Moix Teixidor, F. Pirani, R. Richter, S. Stranges and F. Vecchiocattivi, J. Chem. Phys., 2006, 124, 204318.
29. K. Zähringer, H. D. Meyer, L. S. Cederbaum, F. Tarantelli and A. Sgamellotti, Chem. Phys. Lett., 1993, 206, 247.
30. H. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803.
31. K. W. Ford, D. L. Hill, M. Wakano and J. A. Wheeler, Ann. Phys., 1959, 7, 239.
32. B. Zygelman, D. L. Cooper, M. J. Ford, A. Dalgarno, J. Gerratt and M. Raimondi, Phys. Rev. A, 1992, 46, 3846.
33. S. B. Zhang, Y. Wu and J. G. Wang, J. Chem. Phys., 2016, 145, 224306.
34. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242.
35. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, et al., see, http://www.molpro.net, 2012.
36. K. A. Peterson and T. H. Dunning Jr, J. Chem. Phys., 2002, 117, 10548.
37. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007.
38. R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
39. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259.
40. H. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053.
41. A. Kramida, Yu. Ralchenko and J. Reader and NIST ASD Team, NIST Atomic Spectra Database (ver. 5.7.1). National Institute of Standards and Technology, Gaithersburg, MD. 2019, [online]. available: https://physics.nist.gov/asd, 2020, July 14.
42. Y. K. Yang, Y. Cheng, Y. Wu, Y. Z. Qu, J. G. Wang and S. B. Zhang, New J. Phys., 2020, 22, 123022.
43. F. Salvat, J. Fernández-Varea and W. Williamson Jr, Comput. Phys. Commun., 1995, 90, 151.
44. P. M. Morse, Phys. Rev., 1929, 34, 57.
45. J. L. Dunham, Phys. Rev., 1932, 41, 721.
46. G. Herzberg, Molecular spectra and molecular structure. Vol.1: Spectra of diatomic molecules, 1950.
47. R. J. Le Roy, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 167.
48. R. J. Le Roy and R. B. Bernstein, J. Chem. Phys., 1971, 54, 5114.
49. R. J. Le Roy and W. Liu, J. Chem. Phys., 1978, 69, 3622.
50. R. J. Le Roy, Comput. Phys. Commun., 1989, 52, 383.
51. J. R. Taylor, Scattering theory: the quantum theory of nonrelativistic collisions, Courier Corporation, 2006.
52. H. Friedrich and H. Friedrich, Theoretical atomic physics, vol. 3, Springer, 2006.
53. S. B. Zhang, J. G. Wang and R. K. Janev, Phys. Rev. A, 2010, 81, 032707.
54. F. Salvat, J. Fernández-Varea and W. Williamson Jr, Comput. Phys. Commun., 1995, 90, 151.
55. Y. K. Yang, Y. Cheng, Y. G. Peng, Y. Wu, J. G. Wang, Y. Z. Qu and S. B. Zhang, J. Quant. Spectrosc. Radiat. Transfer, 2020, 254, 107203.
56. E. Wigner and E. E. Witmer, J. Appl. Phys., 1928, 51, 859.
57. P. J. Bruna and F. Grein, J. Phys. Chem. A, 2006, 110, 4906.
58. E. F. Van Dishoeck, J. Chem. Phys., 1987, 86, 196.
59. A. Buckingham, Q. Rev., Chem. Soc., 1959, 13, 183.
60. N. Khelifi, W. Zrafi, B. Oujia and F. X. Gadea, Phys. Rev. A, 2002, 65, 042513.
61. J. Senekowitsch, S. V. ONeil, H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1990, 93, 562.
62. N. Khelifi, J. Phys. Chem. A, 2009, 113, 8425.

---