Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural parameter-modulated nonlinear optical amplitude of acceptor–π–D–π–donor-configured pyrene derivatives: a DFT approach†
Muhammad Khalid *a,
Hafiza Munnazza Lodhia,
Muhammad Usman Khan
*a,
Hafiza Munnazza Lodhia,
Muhammad Usman Khan b and
Muhammad Imranc
b and
Muhammad Imranc
aDepartment of Chemistry, Khawaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan. E-mail: muhammad.khalid@kfueit.edu.pk; Khalid@iq.usp.br
bDepartment of Chemistry, University of Okara, Okara-56300, Pakistan
cDepartment of Chemistry, Faculty of Science, King Khalid University, P.O. Box 9004, Abha 61413, Saudi Arabia
First published on 15th April 2021
Abstract
In the present study, organic pyrene-based derivatives were selected for NLO investigation. The reference compound named methyl (E)-2-cyano-3-(5-(pyren-1-yl)thiophen-2-yl)-3-acrylate (MCPTR) was taken for the design of its derivatives, abbreviated from MCPTD1 to MCPTD8 compounds. The nonlinear optical (NLO) properties, frontier molecular orbitals (FMOs), natural bonding orbital (NBO), and UV-vis analyses of molecules (MCPTR–MCPTD8) were executed by M06 level with 6-31G(d,p) basis set. The UV-vis investigation showed that all designed compounds exhibited a redshift, and the maximum wavelength was studied in MCPTD7 (832.330 nm). The HOMO–LUMO band gaps of MCPTD1–MCPTD8 were found to be smaller as compared to those of MCPTR (3.210 eV). The global reactivity information was correlated with band gap values; MCPTD7, having a lower band gap, exhibited smaller hardness values (0.0321 Eh) with larger softness values (15.5763 Eh). The natural bond orbital analysis (NBO) helped to elucidate the hyper conjugative interactions, along with the stability and electron-transfer process. The dipole moment (μ), average polarizability 〈α〉, first hyperpolarizability (βvec) and second hyperpolarizability 〈γ〉 were computed for MCPTR–MCPTD8. Consequently, all designed compounds (MCPTD1–MCPTD8) possessed greater NLO responses than the reference compound (MCPTR). Interestingly, MCPTD7 showed a smaller energy gap and remarkable NLO response among MCPTD1–MCPTD8 compounds. The highest μtotal, 〈α〉, βvec and 〈γ〉 values for MCPTD7 were observed as 7.200, 2.40 × 10−22 esu, 2.84 × 10−27 esu and 8.6024 × 107 esu, respectively. Aptitude towards the NLO material relied upon the position of different groups, the conjugated system donor and acceptor regions. The high NLO response reveals the fact that this class of pyrene-based derivatives with a thiophene linker has remarkable contributions towards NLO technological applications.
Introduction
Organic compounds with donor–π-bridge–acceptor (D–π–A) configuration showed excellent nonlinear optical (NLO) properties employed in various areas of research like molecular switching, optical modulation/memory, laser, biophysics and surface interface science.1–3 Organic NLO compounds have advantages over the inorganic based on their enhanced electronic penetration, larger molecular polarizability and rapid response times.4 The π-based electronic delocalization permits organic compounds to exhibit rapid response times, resulting in promising NLO responses.5,6 The non-centrosymmetric π-conjugated spacer compounds boost the charge transfer process among electron-donors (D) and acceptors (A), accomplishing 1st, 2nd and 3rd order nonlinear amplitudes. The NLO materials have demonstrated large intramolecular charge transference (ICT), transmission of donor–acceptor π-clouds via π-linkers, higher ground electronic state dipole moments, along with excited transition states.7–9 In order to compute the structural and electronic characteristics, the HOMO and LUMO band gap greatly influenced the charge transfer in these compounds.10–12 The HOMO and LUMO properties of compounds can be changed by altering conjugation, and their NLO response may be improved with a reduction of the band gap. Appropriate donors, acceptors and π-linker arrangement play a significant role in the band gap reductions for the designed organic compound.13,14 Therefore, it is essential to establish such D–π–A-configured compounds containing promising NLO responses. DFT studies were executed to obtain a comprehensive understanding of the NBO, FMO and UV-vis analysis.The pyrene structure has a solid π-electron delocalization and fluorescent property because of its planar aromatic features. Its solid structure is based upon the two-dimensional geometry having a strong tendency toward π assembly, and the great variation in functional groups onto graphite, fullerenes15,16 and graphene17,18 make it attractive towards NLO applications.19 We have designed an appropriate donor–π-spacer–acceptor of pyrene-based molecules containing an acceptor (cyano vinyl ester) allied to pyrene centered by thienyl or phenyl conjugating linkers.19,20 These structural variations give promising NLO results towards pi spacer end capped donor–acceptor frameworks.21–24 These compounds may receive significant interest in their optoelectronic applications in the zone of photonic gadgets, sensors and optical exchanging.25 These computational methods have become a great curiosity in NLO containing a D–π–A system within pyrene-based compounds. The literature is overwhelmed with various structures, including donor–acceptor, donor–π-spacer–acceptor, acceptor–π-spacer–donor–π-linker–acceptor, donor–π-linker–acceptor–π-spacer–donor, donor–acceptor–π–acceptor and donor–donor–π–acceptor.26 The extent of π-conjugation and the nature of substituents strongly affect the NLO response of the molecules.26,27 Experimental and theoretical research studies enhanced the NLO response, which is created through participation of strong donor and acceptor groups on one of two sides of a suitable π-conjugated structure. The pyrene units embedded from both sides with electronegative substituents will lead to surprising bathochromic shifts in the optical transitions. After halogen substitution, a decline occurs in the pyrene transition energy because of uneven stabilization of the HOMO, exhibiting reduced orbital coefficients within the ring. The more strongly electron-withdrawing cyano entity is predicted to further red-shift the transitions of pyrene. Electronegative substitution impacts the electronic properties of the parent molecule to a much greater extent than assumed.28 The main objective towards NLO applications is the discovery of extremely active compounds with large second-order polarizabilities (β), and hyperpolarizability that relates with the intramolecular charge transference (ICT) of the compounds. The experimental and theoretical analyses revealed that excellent second order NLO properties arise because of the D–π–A system planarity, auxiliary donors, donors, and acceptor units, and the π-electron twisted model. These findings stimulated towards the second and third order NLO responses of pyrene-based compounds that are explored in the current findings. This is the first detailed DFT calculations, electronic, and NLO responses of D–π–A pyrene system compounds, and these finding may provide valuable outcomes in order to acquire new pyrene-based NLO compounds. The third-order NLO computations designed a remarkable series of pyrene derivatives with representative donor–π–acceptor structures.
Computational procedure
DFT calculations were executed to obtain the electronic properties, absorption spectra and NLO properties of pyrene-rooted compounds. In recent work, quantum chemical studies of MCPTR and designed compounds MCPTD1–MCPTD8 were done by M06/6-31G(d,p) level using the Gaussian 09 program package.29 The Gaussian 09 embedded NBO 3.1 program package was used for natural bond orbital (NBO) analysis by applying the aforesaid level of DFT and basis set. Similarly, M06/6-31G(d,p) level of TD-DFT was also employed for FMO analysis and UV-vis spectral analysis. It is used in determining photophysical properties. Gauss View 5.0 was used for organizing input files.30 Furthermore, Gauss View 5.0,30 Avogadro31 and Chemcraft32 were used for the interpretation of the output results. The dipole moment was calculated by eqn (1).33| μ = (μx2 + μy2 + μz2)1/2 | (1) |
The average polarizability 〈α〉 was determined with eqn (2).34
| 〈α〉 = 1/3(αxx + αyy + αzz) | (2) |
Analysis of the Gaussian output file yielded ten hyperpolarizability tensors oriented along the x, y, and z directions: βxxx, βxyy, βxzz, βyyy, βxxy, βyzz, βzzz, βxxz, βyyz, βxyz. The magnitude of the total first hyperpolarizability (βvec) was calculated with the help of eqn (3).34
| βvec = [(βxxx + βxyy + βxzz)2 + (βyyy + βyzz + βyxx)2 + (βzzz + βzxx + βxyz)2]1/2 | (3) |
The second hyperpolarizability was determined with the help of eqn (4).33
| 〈γ〉 = 1/5[γxxxx + γyyyy + γzzzz + 2(γxxxx + γyyyy + γzzzz)] | (4) |
Results and discussion
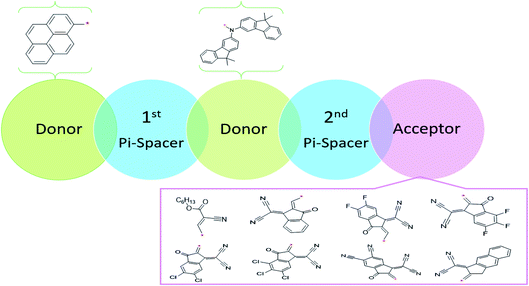
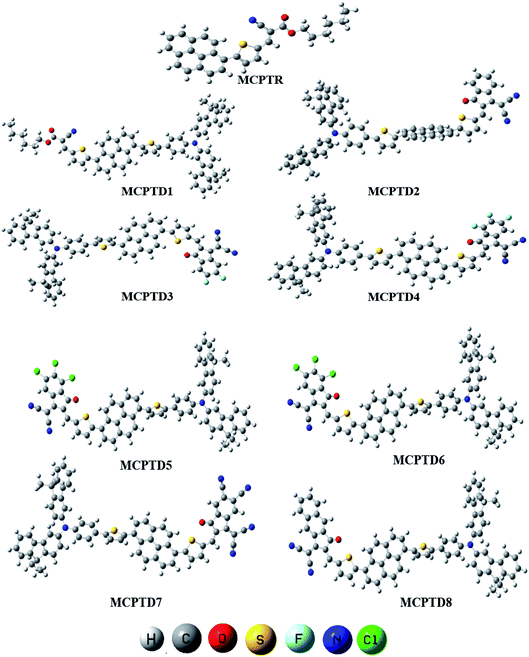
This NLO study was investigated using the theoretical designing of NLO-active pyrene-based derivatives with efficient configuration of D–π–D–π–A-type. The designed compounds have the following parts: acceptor (methyl cyano), π-conjugated linkers (thiophene), and donor (pyrene). The properties of the entitled chemical systems were altered by applying some structural modifications, such as acceptors and π-conjugated linkers. In particular, the following computed parameters: (i) linear polarizability (α), (ii) first hyperpolarizability (β), (iii) second hyperpolarizability (γ), (iv) absorption wavelength, (v) NBO transitions and (vi) HOMO–LUMO energies were obtained to a remarkable extent.Usually, theoretical and experimental investigations suggest that a significant NLO response can be achieved through the unification of strong donor and acceptor groups at the peripheral ends of a π-conjugated system.1 In the recent study, we used the original compound named methyl (E)-2-cyano-3-(5-(pyren-1-yl)thiophen-2-yl)acrylate with D–π–A configuration, which is abbreviated as MCPTR.19 The designed series of NLO-based compounds were developed by structural modeling of MCPTR by modification of the acceptor. First of all, we designed MCPTD1 from the parent molecule (MCPTR) by keeping the D–π part preserved, as taken from the parent molecule (MCPTR), and introducing a pyren-1-yl moiety as a donor and thiophen as π-spacer units before the acceptor. Furthermore, this MCPTD1 was used to design MCPTD2–MCPTD8 compounds by modulating the end acceptor (Scheme 1 and Fig. 1). Thus, the newly designed compounds consisted of IUPAC names and their abbreviations as hexyl (E)-3-(5-(6-(5-(4-(bis(9,9-dimethyl-9H-fluoren-3-yl)amino)phenyl) (MCPTD1), thiophen-2-yl)pyren-1-yl)thiophen-2-yl)-2-cyanoacrylate. (MCPTD2): (Z)-2-(2-((5-(6-(5-(4-(bis(9,9-dimethyl-9H-fluoren-3-yl)amino)phenyl)thiophen-2-yl)pyren-1-yl)thiophen-2-yl)methylene)-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile. (MCPTD3): (Z)-2-(2-((5-(6-(5-(4-(bis(9,9-dimethyl-9H-fluoren-3-yl)amino)phenyl)thiophen-2-yl)pyren-1-yl)thiophen-2-yl)methylene)-5,6-difluoro-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile. (MCPTD4): (Z)-2-(2-((5-(6-(5-(4-(bis(9,9-dimethyl-9H-fluoren-3-yl)amino)phenyl)thiophen-2-yl)pyren-1-yl)thiophen-2-yl)methylene)-4,5,6-trifluoro-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile. (MCPTD5): (Z)-2-(2-((5-(6-(5-(4-(bis(9,9-dimethyl-9H-fluoren-3-yl)amino)phenyl)thiophen-2-yl)pyren-1-yl)thiophen-2-yl)methylene)-5,6-dichloro-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile. (MCPTD6): (Z)-2-(2-((5-(6-(5-(4-(bis(9,9-dimethyl-9H-fluoren-3-yl)amino)phenyl)thiophen-2-yl)pyren-1-yl)thiophen-2-yl)methylene)-4,5,6-trichloro-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile. (MCPTD7): (Z)-2-((5-(6-(5-(4-(bis(9,9-dimethyl-9H-fluoren-3-yl)amino)phenyl)thiophen-2-yl)pyren-1-yl)thiophen-2-yl)methylene)-1-(dicyanomethylene)-3-oxo-2,3-dihydro-1H-indene-5,6-dicarbonitrile. (MCPTD8): (Z)-2-(2-((5-(6-(5-(4-(bis(9,9-dimethyl-9H-fluoren-3-yl)amino) phenyl)thiophen-2-yl)pyren-1-yl)thiophen-2-yl)methylene)-3-oxo-2,3-dihydro-1H-cyclopenta[b]naphthalen-1-ylidene)malononitrile. The chemical structures of these studied compounds (MCPTR, MCPTD1, MCPTD2, MCPTD3, MCPTD4, MCPTD5, MCPTD6, MCPTD7 and MCPTD8) are displayed in Fig. 1. It is expected that this work will trigger further research studies on their synthesis and analysis of their marvelous effects in terms of proficient NLO materials. Moreover, the optimized compounds are shown in Fig. 2.
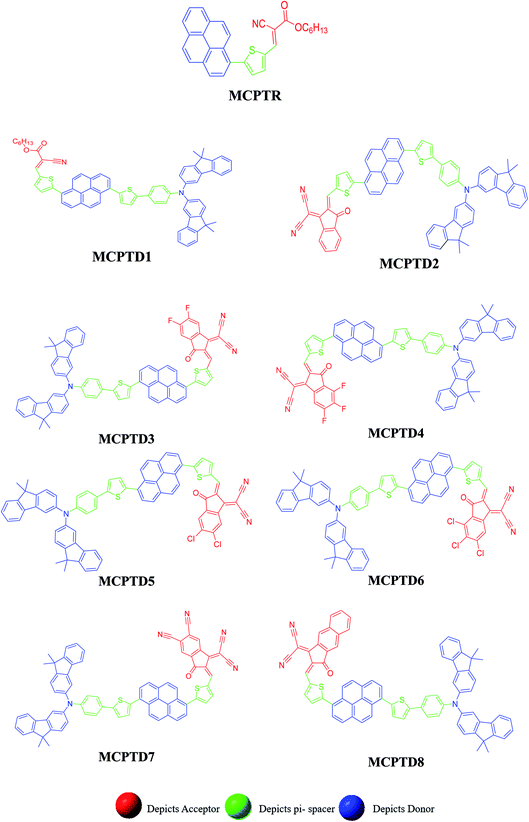 | ||
| Fig. 1 Structures of the reference (MCPTR)19 and designed compounds (MCPTD1–MCPTD8). | ||
Electronic structure
Frontier molecular orbitals (FMOs) contain two main orbitals; HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital).26 FMOs help in explaining the chemical affinity and interaction of the designed molecule with other moieties.35 It also helps us to deduce the reactive sites in any π-electron systems.17,36,37 The FMOs energy gap (Egap = ELUMO − EHOMO) elucidates the electron transference properties, reactivity, hardness and softness of the molecule.38 The higher value of Egap for molecules indicates more stability, less chemical affinity and greater hardness value, which means that they may cause a change in the electronic arrangement.12 In contrast, a molecule that is soft with high reactivity and low stability has a smaller Egap value. Moreover, the Egap is regarded as a basic characteristic for analyzing the NLO properties. The HOMO is located on such orbital having an electron-donating tendency, while the LUMO is considered as the orbital that is partially filled, having an electron-accepting tendency.19 The decreased HOMO–LUMO band gap, which can be highly polarizable, can elevate the NLO response.37,39 FMO analysis of MCPTR and MCPTD1–MCPTD8 was carried out, and the results are collected in Table 1.| Compounds | LUMO | HOMO | Band gap |
|---|---|---|---|
| a The experimental values in parentheses are from ref. 40. | |||
| MCPTR | −2.557(2.78)a | −5.767(−5.73)a | 3.210(2.95)a |
| MCPTD1 | −2.573 | −5.219 | 2.646 |
| MCPTD2 | −3.071 | −5.231 | 2.160 |
| MCPTD3 | −3.145 | −5.219 | 2.074 |
| MCPTD4 | −3.207 | −5.219 | 2.012 |
| MCPTD5 | −3.219 | −5.221 | 2.002 |
| MCPTD6 | −3.278 | −5.226 | 1.948 |
| MCPTD7 | −3.485 | −5.233 | 1.748 |
| MCPTD8 | −3.133 | −5.221 | 2.088 |
Table 1 shows that the parent molecule has calculated values of HOMO/LUMO at 2.557/−5.767 eV, which is in close accordance with the experimentally determined HOMO/LUMO values of −2.780/−5.730 eV.40 This good agreement points out that the implemented DFT computations, i.e., M06 level with 6-31G(d, p) basis set is apt to investigate MCPTD1–MCPTD8. The reference compound (MCPTR) has a larger band gap value, i.e., 3.210 eV, than all of its derivatives. This energy band gap is decreased to 2.646 eV in MCPTD1 due to the incorporation of the donor as N-(9,9-dimethyl-9H-fluoren-3-yl)-9,9-dimethyl-N-phenyl-9H-fluoren-3-amine and pi spacer (2-phenylthiophene) units, owing to enhancement of the conjugation and resonance factors. This band gap is further lowered in MCPTD2 as the stronger acceptor (Z)-2-(2-ethylidene-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile) is substituted with the former used acceptor in MCPTR and MCPTD1, thus, reducing the band gap value up to 2.160 eV due to the enhanced capability of the push–pull mechanism. Furthermore, the above mentioned band gap was reduced in MCPTD3 due to the incorporated one cyano and two fluoro moieties at the structure of acceptor as (2-(5,6-difluoro-2-methylene-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile), and one more fluoro moiety is introduced in the vicinity of the prior attached fluoro moieties at the structure of the acceptor in MCPTD4. Consequently, the electrons migrate towards the acceptor part in these molecules due to the strong accepting nature of the cyano and fluoro groups, which may be reason for the further reduction in their band gap values, such as 2.074 eV for MCPTD3 and 2.012 eV for MCPTD4. Further reduction in the band gap is examined, such as 2.002 and 1.948 eV for MCPTD5 and MCPTD6, respectively. In fact, the structure of MCPTD5 is designed via the replacement of the two fluoro groups with two chloro groups at the structure of the acceptor in the MCPTD3 molecule. In the same way, the structure of MCPTD6 is designed via replacement of the three fluoro groups with three chloro groups at the structure of the acceptor of MCPTD4. As it is expected, the greater electronegativity of the moieties will increase the movement of the electrons in the directions of the acceptor part because of the inductive electron withdrawal (F > Cl),41 as observed in MCPTD3 and MCPTD4. However, at the same time, the resonance effect may compete with the inductive effect. The F and Cl groups are electron-donating due to the resonance effect (Cl > F).39,41 The chloro groups at the structure of the acceptor are found in MCPTD5 and MCPTD6, which showed less inductive electron withdrawal as compared to the fluoro groups.42 However, a reduction in the band gap was observed in both molecules in comparison that of MCPTD3 and MCPTD4, which may be due to the (a) resonance effect, (b) better orbital matching, and (c) specific geometry of the acceptor moiety. A much lower HOMO–LUMO band gap was calculated at 1.748 eV in MCPTD7. This reduction in the band gap is due to the four substituted cyano (–CN) groups at the acceptor part having a larger (–I) effect than F and Cl. These four cyano groups can withdraw more electrons in the direction of the acceptor part. Subsequently, this factor enhances the charge transfer and reduces its band gap. This is the smallest value of Egap in the group of all investigated compounds. However, compound MCPTD8 was found with a larger value of Egap than MCPTD7 because it has just two substituted cyano (–CN) groups at the acceptor part, although one extra benzene ring was found in its acceptor part. Therefore, by structural tailoring of the donor, spacer and acceptor unit of MCPTR, the HOMO–LUMO energy gap was remarkably reduced in all investigated compounds.
In short, the HOMO–LUMO energy gap decreases in this order: MCPTR > MCPTD1 > MCPTD2 > MCPTD8 > MCPTD3 > MCPTD4 > MCPTD5 > MCPTD6 > MCPTD7. This order confirms that the designed compounds incorporating electronegative units would be a remarkable aspect to lower the Egap values, hence, significant the response of NLO.43
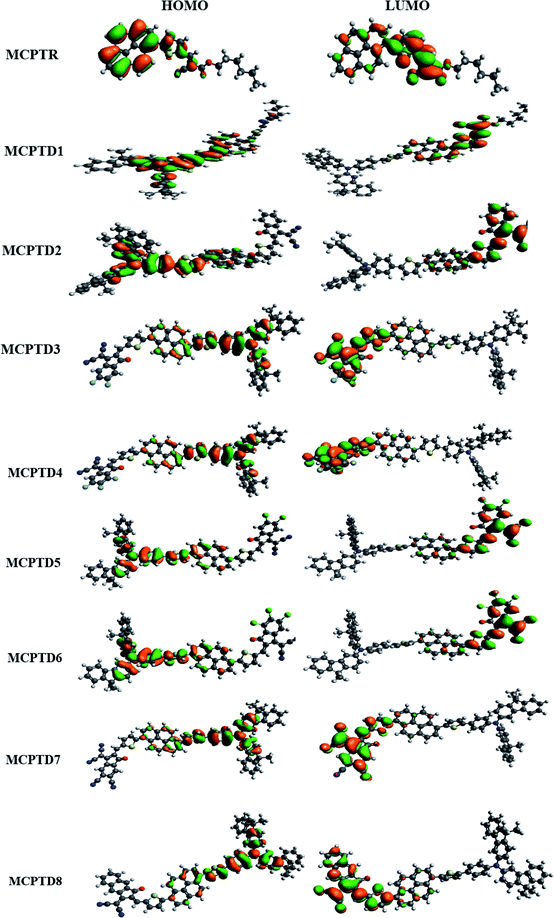
The magnitude of the band gap describes the experience of ICT from the donor to acceptor part facilitated via pi linkers, and provides information about the NLO structure related function associations.44–46 The contour sides of the frontier molecular orbitals (FMOs) are used to describe the transference of charges, as displayed in Fig. 3. In the reference compound (MCPTR), the charge density for HOMO is located over (N-(cyclohexa-1,5-dien-1-yl)-N-phenyl-4-(5-(pyren-1-yl)thiophen-2-yl)aniline), while the dominant portion of the acceptor part involved in the electronic distribution is methyl (E)-2-cyano-3(thiophen-2-yl)acrylate. In the designed compounds (MCPTD1–MCPTD8), the charge density for HOMO was predominantly present over (N-(cyclohexa-1,5-dien-1-yl)-N-phenyl-4-(5-(pyren-1-yl)thiophen-2-yl)aniline) and the minor charge density was located over the first pi-linker. The LUMO was concentrated partly on the second bridge moiety, and mainly on the acceptor moiety. Thus, a significant charge transfer in the entitled compounds was administered from the donor to an acceptor via π-linker. This assistance of the charge transference confirms that all of the investigated compounds should be proficient NLO substances. The designed compounds MCPTD1–MCPTD8 are more reactive, having larger wavelengths. Therefore, they are relatively readily polarizable compared to the reference compound.34 The other values of HOMO−1, LUMO+1, HOMO−2, and LUMO+2 are displayed in Table S10.† The pictographic display of HOMO−1, LUMO+1, HOMO−2, and LUMO+2 is shown in Fig. S1.†
UV-vis analyses
In order to gain insight into the absorption spectra for the excited states, TD-DFT calculations were executed via M06 level of theory and 6-31G(d,p) basis set combination. The TD-DFT investigation was executed with dichloromethane (DCM) as a solvent.47It is expected that the polar medium is involved in the stabilization of the π–π* state associated with the n–π* state by the use of an appropriate electronic level.39 Usually, the energy of the interactions of the compound in dichloromethane is controlled by non-covalent interactions (NCIs) and polarity effects.42 This factor defines the dipolar interactions and hydrogen bond performing a major part, while stabilizing the first singlet electronic level of the molecules.48 As the solvent polarity is increased, the molecule shifts to red shift. The excited state is regarded as more polar than the ground state; hence, the excited state is more stabilizing as compared to the ground state in DCM.42
Our results revealed that all molecules (reference MCPTR and designed MCPTD1–MCPTD8) display absorbance in the visible region (Table 2). The results discussed in Table 2 shows that the largest absorption peak of MCPTR was found at 481.21 nm, which is comparable to their corresponding experimental λmax of 424 nm. The designed molecules MCPTD1–MCPTD8 cover the absorption range from 547.050 nm to 832.330 nm. Generally, the λmax values of the designed MCPTD1–MCPTD8 molecules were detected to be greater in measure than the value of MCPTR (Table 2). It can be seen that the λmax values are greatly influenced by the end-capped electron acceptor motifs, which in turn push the absorption spectra to move towards a red shift.49–52 The computed maximum absorption peak for MCPTR was obtained at 481.212 nm with 2.577 eV transition energy and oscillator strength (0.619), showing 99% molecular orbital contributions from HOMO to LUMO. The introduction of the donor as N-(9,9-dimethyl-9H-fluoren-3-yl)-9,9-dimethyl-N-phenyl-9H-fluoren-3-amine and pi spacer (2-phenylthiophene) in the MCPTD1 molecule effectively increased the λmax value to 547.050 nm with 2.266 eV transition energy. Furthermore, the λmax value of MCPTD2 was observed as 664.505 nm, which is higher than that for MCPTD1. This is because of the stronger acceptor as (Z)-2-(2-ethylidene-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile). For MCPTD3, the maximum absorption wavelength was further enhanced and the transition energy was reduced due to incorporation of two fluoro groups in the structure of the acceptor as (2-(5,6-difluoro-2-methylene-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile). Additionally, in MCPTD4, the absorption wavelength was further moved to red shift, and the transition energy was reduced to 1.722 eV. The alteration in the above parameters for MCPTD4 might be due to one extra fluoro moiety, which was submitted in the neighborhood of the antecedent attached fluoro moieties in the structure of the acceptor. The calculated maximum wavelengths for MCPTD5 and MCPTD6 were obtained at 724.286 and 743.667 nm with 1.712 and 1.667 eV transition energies showing 91% (HOMO to LUMO) and 92% (HOMO−1 to LUMO), respectively. Similarly, for MCPTD7 and MCPTD8, the maximum wavelengths were calculated at 832.330 and 691.600 nm with 1.490 and 1.793 eV transition energies and oscillator strengths as 0.277 and 0.488. The best efficacy for the acceptor in MCPTD7 induces the highest red shifting in accordance with the lowering of the band gap results, as discoursed above. The λmax values of all molecules are found in the subsequent decreasing order: MCPTR < MCPTD1 < MCPTD2 < MCPTD8 < MCPTD3 < MCPTD4 < MCPTD5 < MCPTD6 < MCPTD7. The lowest excitation energy value as 1.490 eV is disclosed in MCPTD7, owing to the influence of the strong electron withdrawing acceptor entity and conjugation. The increasing order of the excitation energy values is as follows: MCPTR > MCPTD1 > MCPTD2 > MCPTD8 > MCPTD3 > MCPTD4 > MCPTD5 > MCPTD6 > MCPTD7. Moreover, some absorption values of MCPTR–MCPTD8 are shown in S14–S22.† The enhancement in the wavelengths and lower transition energy values uncovered that the MCPTD1–MCPTD8 molecules demonstrated larger charge transport facility. Subsequently, an easy excitation may occur between HOMO and LUMO. A former HOMO–LUMO study of MCPTD1–MCPTD8 supports the UV-vis data with respect to the minimum transition energy and higher λmax values, which guide them to enhance their photoelectric effects.
| Compounds | DFT λ (nm) | E (eV) | f | MO contributions |
|---|---|---|---|---|
| a MO = molecular orbital; H = HOMO, L = LUMO.b Exp. value in parentheses.19 | ||||
| MCPTR | 481.212(424)b | 2.577 | 0.619 | H → L (99%) |
| MCPTD1 | 547.050 | 2.266 | 0.074 | H → L (82%) |
| MCPTD2 | 664.505 | 1.866 | 0.456 | H → L (87%) |
| MCPTD3 | 697.123 | 1.779 | 0.454 | H → L (90%), H−1 → L (8%) |
| MCPTD4 | 720.205 | 1.722 | 0.430 | H → L (91%), H−1 → L (8%) |
| MCPTD5 | 724.286 | 1.712 | 0.438 | H → L (91%), H−1 → L (8%) |
| MCPTD6 | 743.667 | 1.667 | 0.388 | H−1 → L (92%), |
| MCPTD7 | 832.330 | 1.490 | 0.277 | H → L (94%), H−1 → L (4%) |
| MCPTD8 | 691.600 | 1.793 | 0.488 | H → L (89%), H−1 → L (10%) |
To sum things up, MCPTD7 has the capacity for the lower most transition energy, minimum band gap and largest λmax value, which may be contemplated like an appropriate material for using its optoelectronic properties in the NLO field.
Global reactivity parameters
The strength of FMOs (Egap = ELUMO − EHOMO) is valuable to discover the global reactivity, such as the ionization potential (IP), global softness (σ), global hardness (η), global electrophilicity index (ω), electron affinity (EA),43 electronegativity (X), and the chemical potential (μ).38,53–56 The IP and EA are calculated by utilizing the following equations.| IP = −EHOMO | (5) |
| EA = −ELUMO | (6) |
The chemical hardness (η), chemical potential (μ), electronegativity (X), global softness (σ), and electrophilicity index (ω) were determined by utilizing Koopmans's theorem.57
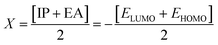 | (7) |
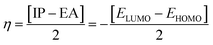 | (8) |
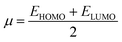 | (9) |
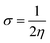 | (10) |
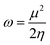 | (11) |
The ionization potential expressed the electron-accepting and electron donating abilities, and this equals the energy compulsory to extract one electron from HOMO. The reactivity and stability of the compounds are also related to the chemical potential of the species.50 The chemical potential, energy gaps, hardness, and stability of the compound are directly related, whereas the relation is inverse in the case of the reactivity.50 Hence, the molecule with greater energy gap is considered to be a harder molecule, and has low reactivity and more kinetic stability.
The electronegativity of the substituent controls the stabilization of the molecules. The position of the molecule holding the electronegative substituent plays a role in its stability.58 The electronegativity explicates the capability of a representative compound to attract electrons to it. The molecule manifests more stability, lesser chemical reactivity and greater hardness if the band gap becomes higher.
The examined hardness value gradually decreased through MCPTR–MCPTD8. The hardness value calculated in MCPTD1 is 0.0486 Eh, which falls to a value of 0.0397 Eh in MCPTD2 and further decreases to 0.0321 Eh in MCPTD7. In the same manner, the chemical potential was found to decrease, as explained in Table 3. Hence, the trend of the calculated hardness values across the designed molecules was absolutely the same as the order of the decrease of Egap. The decreasing order of the hardness and chemical potential of the investigated molecules was: MCPTR > MCPTD1 > MCPTD2 > MCPTD3 > MCPTD4 > MCPTD5 > MCPTD6 > MCPTD8 > MCPTD7. However, the softness is another factor that reveals the reactivity of the molecules as directly related to their polarizability. The value of the softness expanded in the designed compounds from the MCPTR softness (8.4818 Eh) to MCPTD7 (15.5763 Eh). Interestingly, MCPTD7 shows the highest softness value, and it is regarded as the most polarizable species among all designed compounds. The higher softness values indicated that all designed compounds are polarizable. Consequently, these molecules may hold potential NLO findings. Moreover, all global reactivity information of the studied compounds is correlated with the band gap values of MCPTR–MCPTD8. The molecules with lower band gaps exhibited smaller values of hardness and chemical potential with larger values of softness.
| Compounds | IP | EA | X | η | μ | ω | σ |
|---|---|---|---|---|---|---|---|
| a Units in hartree Eh. | |||||||
| MCPTR | 0.2119 | 0.0940 | 0.1530 | 0.0589 | −0.1530 | 0.1984 | 8.4818 |
| MCPTD1 | 0.1918 | 0.0946 | 0.1432 | 0.0486 | −0.1432 | 0.2110 | 10.2881 |
| MCPTD2 | 0.1922 | 0.1129 | 0.1526 | 0.0397 | −0.1526 | 0.2935 | 12.6103 |
| MCPTD3 | 0.1918 | 0.115.6 | 0.1537 | 0.0381 | −0.1537 | 0.3100 | 13.1234 |
| MCPTD4 | 0.1918 | 0.1178 | 0.1548 | 0.0370 | −0.1548 | 0.3238 | 13.5135 |
| MCPTD5 | 0.1919 | 0.1183 | 0.1551 | 0.0368 | −0.1551 | 0.3268 | 13.5869 |
| MCPTD6 | 0.1920 | 0.1205 | 0.1563 | 0.0358 | −0.1563 | 0.3415 | 13.9860 |
| MCPTD7 | 0.1923 | 0.1281 | 0.1602 | 0.0321 | −0.1602 | 0.3998 | 15.5763 |
| MCPTD8 | 0.1919 | 0.1151 | 0.1535 | 0.0384 | −0.1535 | 0.3068 | 13.0208 |
Natural bond orbital (NBO) analysis
NBO analysis is recognized as the most accurate framework to achieve insights into the electron-transfer process, bond interaction and elucidation of the hyper conjugative interaction among the nucleophile and electrophile.59 The study of NBO can be useful in the interpretation of the steady image formation in donor–π–acceptor architectures, charge density transitions from fully occupied, bonded or a donor to partially-filled, non-bonded type NBOs.60 Delocalizing reactions were evaluated by a second order perturbation access. For every transition donor (i) and acceptor (j), the stabilization energy E(2) accompanied with delocalization i → j was measured by the following equation:
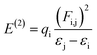 | (12) |
| Compound | Donor (i) | Type | Acceptor (j) | Type | E(2) | E(j) E(i) | F(i → j) |
|---|---|---|---|---|---|---|---|
| MCPTR | C53–C54 | π | C26–C28 | π* | 26.91 | 0.31 | 0.083 |
| C56–C58 | π | C56–C58 | π* | 0.67 | 0.3 | 0.013 | |
| C26–H27 | σ | C53–S55 | σ* | 7.79 | 0.74 | 0.068 | |
| C44–C47 | σ | C47–H52 | σ* | 0.51 | 1.04 | 0.021 | |
| O33 | LP(2) | C31–O32 | π* | 51.37 | 0.36 | 0.123 | |
| S55 | LP(1) | C17–H18 | σ* | 0.54 | 1.13 | 0.022 | |
| MCPTD1 | C52–C53 | π | C25–C27 | π* | 26.79 | 0.31 | 0.082 |
| C85–C86 | π | C77–C79 | π* | 0.53 | 0.29 | 0.011 | |
| C25–H26 | σ | C52–S54 | σ* | 7.73 | 0.74 | 0.067 | |
| C129–H132 | σ | C95–C129 | σ* | 0.50 | 0.89 | 0.019 | |
| O32 | LP(2) | C30–O31 | π* | 51.37 | 0.36 | 0.123 | |
| O32 | LP(1) | C34–C37 | σ* | 0.60 | 1.01 | 0.022 | |
| MCPTD2 | C25–C103 | π | C104–C110 | π* | 25.63 | 0.3 | 0.079 |
| C49–C50 | π | C41–C43 | π* | 0.54 | 0.29 | 0.011 | |
| C25–H26 | σ | C27–S29 | σ* | 9.04 | 0.73 | 0.073 | |
| C30–C32 | σ | C27–S29 | σ* | 0.51 | 0.93 | 0.019 | |
| S29 | LP(2) | C30–C32 | π* | 26.44 | 0.27 | 0.077 | |
| S29 | LP(1) | C16–H17 | σ* | 0.59 | 1.12 | 0.023 | |
| MCPTD3 | C27–C28 | π | C25–C103 | π* | 30.08 | 0.31 | 0.087 |
| C111–N112 | π | C109–N110 | π* | 0.69 | 0.46 | 0.016 | |
| C25–H26 | σ | C27–S29 | σ* | 9.05 | 0.73 | 0.073 | |
| C28–H31 | σ | C25–H26 | σ* | 0.50 | 0.97 | 0.02 | |
| N40 | LP(1) | C119–C123 | π* | 28.94 | 0.29 | 0.085 | |
| S29 | LP(1) | C16–H17 | σ* | 0.63 | 1.13 | 0.024 | |
| MCPTD4 | C27–C28 | π | C25–C103 | π* | 30.68 | 0.31 | 0.087 |
| C110–N111 | π | C108–N109 | π* | 0.70 | 0.46 | 0.016 | |
| C25–H26 | σ | C27–S29 | σ* | 9.11 | 0.73 | 0.073 | |
| C84–H87 | σ | C61–C84 | σ* | 0.50 | 0.89 | 0.019 | |
| N40 | LP(1) | C118–C122 | π* | 28.90 | 0.29 | 0.085 | |
| F113 | LP(2) | C100–C101 | σ* | 0.52 | 0.98 | 0.02 | |
| MCPTD5 | C27–C28 | π | C25–C103 | π* | 30.59 | 0.31 | 0.087 |
| C110–N111 | π | C108–N109 | π* | 0.69 | 0.46 | 0.016 | |
| C25–H26 | σ | C27–S29 | σ* | 9.07 | 0.73 | 0.073 | |
| C118–H122 | σ | N40–C120 | σ* | 0.52 | 0.97 | 0.02 | |
| N40 | LP(1) | C116–C120 | π* | 28.86 | 0.29 | 0.085 | |
| F113 | LP(2) | C100–C101 | σ* | 0.52 | 0.98 | 0.02 | |
| MCPTD6 | C27–C28 | π | C25–C103 | π* | 31.15 | 0.3 | 0.088 |
| C49–C50 | π | C41–C43 | π* | 0.70 | 0.29 | 0.013 | |
| C25–H26 | σ | C27–S29 | σ* | 9.22 | 0.73 | 0.073 | |
| C118–H122 | σ | N40–C120 | σ* | 0.52 | 0.97 | 0.02 | |
| N40 | LP(1) | C116–C120 | π* | 28.79 | 0.29 | 0.085 | |
| Cl125 | LP(2) | C97–C98 | σ* | 0.57 | 0.92 | 0.02 | |
| MCPTD7 | C27–C28 | π | C25–C103 | π* | 32.49 | 0.3 | 0.089 |
| C110–N111 | π | C108–N109 | π* | 0.68 | 0.46 | 0.016 | |
| C25–H26 | σ | C27–S29 | σ* | 9.23 | 0.73 | 0.073 | |
| C28–H31 | σ | C25–H26 | σ* | 0.50 | 0.97 | 0.02 | |
| S29 | LP(2) | C30–C32 | π* | 29.41 | 0.27 | 0.077 | |
| S29 | LP(1) | C16–H17 | σ* | 0.75 | 1.13 | 0.026 | |
| MCPTD8 | C27–C28 | π | C25–C103 | π* | 29.53 | 0.31 | 0.086 |
| C49–C50 | π | C41–C43 | π* | 0.60 | 0.29 | 0.012 | |
| C25–H26 | σ | C27–S29 | σ* | 9.12 | 0.73 | 0.073 | |
| C30–C32 | σ | C27–S29 | σ* | 0.51 | 0.93 | 0.02 | |
| S29 | LP(2) | C30–C32 | π* | 26.58 | 0.27 | 0.077 | |
| N40 | LP(1) | C49–C50 | π* | 3.08 | 0.84 | 0.049 |
The overlapping of the orbitals causes the hyper conjugative type events to occur from σ → σ*, π → π*, LP → σ* and LP → π*. These transitions are imperative for the intramolecular charge transfer and results in system stabilization. In π → π* transitions, the charge transfer taking place within the molecule is more dominant as compared to σ → σ*. In MCPTR, the important π → π* electronic transition, which expressed the highest value of stabilization energy (26.91 kcal mol−1), is for π (C53–C54) → π* (C26–C28). In contrast, π (C56–C58) →π* (C56–C58) was of the lowest energy transition, having 0.67 kcal mol−1 energy. Moreover, the σ → σ* transition as σ (C26–H27) → σ* (C53–S55) had 7.79 kcal mol−1 as highest energy and σ (C44–C47) → σ* (C47–H52) having 0.51 kcal mol−1 lowest energy transitions. Furthermore, other transitions such as LP → π* had the highest value at 51.37 kcal mol−1 for the LP2 (O33) → π* (C31–O32) transition, and LP → σ* had the lowest stabilization energy value of 0.54 kcal mol−1 for the LP1 (S55) → σ* (C17–H18) transition. A bunch of transitions exhibiting conjugation are demonstrated in Table S23.†
For MCPTD1, the π → π* electronic transition with the highest value of stabilization energy (26.79 kcal mol−1) was of π (C52–C53) →π* (C25–C27). In contrast, π (C85–C86) → π* (C77–C79) was of the lowest energy transition having 0.53 kcal mol−1 energy. Furthermore, the σ → σ* transition, like σ (C25–H26) → σ* (C52–S54), had 7.73 kcal mol−1 as the highest energy and σ (C129–H132) → σ* (C95–C129) having 0.50 kcal mol−1 as the lowest energy. The other LP → π* had the highest value of 51.37 kcal mol−1 for the transition from LP2 (O32) → π* (C30–O31), while the lowest value observed in the LP1 (O32) to σ* (C34–C37) transition was 0.60 kcal mol−1. A bunch of transitions in MCPTD1 exhibiting conjugation are established in Table S24.†
In MCPTD2, the π → π* transition with the highest value of stabilization energy (25.63 kcal mol−1) was of π (C25–C103) → π* (C104–C110) and π (C49–C50) → π* (C41–C43) having 0.54 kcal mol−1 lowest energy. Furthermore, the σ → σ* transition σ (C25–H26) → σ* (C27–S29) had 9.04 kcal mol−1 as the highest energy. The σ (C30–C32) → σ* (C27–S29) transition was with the lowest energy at 0.51 kcal mol−1 value. The other LP → π* had the highest value of 26.44 kcal mol−1 for the LP2 (S29) → π* (C30–C32) transition, while the lowest value observed in LP1 (S29) → σ* (C16–H17) transition was 0.59 kcal mol−1. Other transitions exhibiting conjugation are demonstrated in Table S25.†
In the chemical structure of MCPTD3, the π → π* electronic transition exhibiting the highest value of stabilization energy (30.08 kcal mol−1) was π (C27–C28) → π* (C25–C103). In contrast, the transition π (C111–N112) → π* (C109–N110) exhibited the lowest energy as 0.69 kcal mol−1. The highest energy from the σ → σ* transition σ (C25–H26) → σ* (C27–S29) was found as 9.05 kcal mol−1. In contrast, the lowest energy in σ (C28–H31) → σ* (C25–H26) was uncovered as 0.50 kcal mol−1. Furthermore, LP1 → π* had the highest value of 28.94 kcal mol−1 in LP1 (N40) → (C119–C123), while the lowest value (0.63 kcal mol−1) was observed in LP1 → π* as the LP1 (S29) → (C16–H17) transition. Other transitions exhibiting established conjugation are summarized in Table S26.†
In the framework of MCPTD4, the π → π* transition had the highest value of stabilization energy (30.68 kcal mol−1) for π (C27–C28) → π* (C25–C103). In contrast, π (C110–N111) → π* (C108–N109) was found to have the lowest energy as 0.70 kcal mol−1. The σ → σ* transition σ (C25–H26) → σ* (C27–S29) had 9.11 kcal mol−1 as the highest energy. The σ (C84–H87) → σ* (C61–C84) consisted of the lowest energy, having 0.50 kcal mol−1. The other LP → π* had the highest value at 28.90 kcal mol−1 for the transition LP1 (N40) → π* (C118–C122) and the lowest value (0.52 kcal mol−1) was for the LP2 (F113) → σ* (C100–C101) transition. Other transitions exhibiting conjugation are shown in Table S27.†
For MCPTD5, the π → π* transition that has the highest value of stabilization energy was of π (C27–C28) → π* (C25–C103) with 30.59 kcal mol−1. The π (C110–N111) → π* (C108–N109) was of the lowest energy, having 0.69 kcal mol−1. The σ → σ* transition as σ (C25–H26) → σ* (C27–S29) had 9.07 kcal mol−1. The σ (C118–H122) → σ* (N40–C120) transition was of the lowest energy, having 0.52 kcal mol−1. LP → π* had the high value of 28.86 kcal mol−1 for LP1 (N40) → π* (C116–C120), and the lowest value (0.52 kcal mol−1) was observed for the LP2 (F113) → σ* (C100–C101) transition. Other transitions exhibiting conjugation can be seen in Table S28.†
In MCPTD6, the π → π* transition having the highest value of stabilization energy at 31.15 kcal mol−1 was for the π (C27–C28) → π* (C25–C103) transition, and the π (C49–C50) → π* (C41–C43) was of the lowest energy, having 0.70 kcal mol−1. The σ → σ* transition as σ (C25–H26) → σ* (C27–S29) had 9.22 kcal mol−1 as the highest energy. The σ (C118–H122) → σ* (N40–C120) had the lowest energy at 0.52 kcal mol−1. The LP → π* transition had the highest value at 28.79 kcal mol−1 for LP1 (N40) → π* (C116–C120), and the lowest value (0.57 kcal mol−1) was observed for the LP2 (Cl125) → σ* (C97–C98) transition. Other transitions exhibiting conjugation are listed in Table S29.†
For MCPTD7, the π → π* transition having the highest value of stabilization energy was for π (C27–C28) → π* (C25–C103) as 32.49 kcal mol−1, whereas π (C110–N111) → π* (C108–N109) consisted of the lowest energy as 0.68 kcal mol−1. The σ → σ* transition: σ (C25–H26) → σ* (C27–S29) had 9.23 kcal mol−1 as the highest value, and σ (C28–H31) → σ* (C25–H26) comprised the lowest energy at 0.50 kcal mol−1. Moreover, LP → π* had the highest value at 29.41 kcal mol−1 for LP2 (S29) → π* (C30–C32), while the lowest value (3.08 kcal mol−1) was observed for the LP1 (N40) → σ* (C49–C50) transition. The remaining transitions exhibiting conjugation are listed in Table S30.†
For MCPTD8, the π → π* transition contained the highest value of stabilization energy at 29.53 kcal mol−1 for π (C27–C28) → π* (C25–C103). However, the lowest energy (0.60 kcal mol−1) was uncovered for π (C49–C50) → π* (C41–C43). Furthermore, the σ → σ* transition, such as σ (C25–H26) → σ* (C27–S29), comprised the highest energy at 9.12 kcal mol−1. The σ (C30–C32) → σ* (C27–S29) was found to have the lowest energy at 0.51 kcal mol−1. Furthermore, LP → π* has the highest value at 26.58 kcal mol−1 due to LP2 (S29) → π* (C30–C32), while the lowest value observed in LP1 (N40) → σ* (C49–C50) was the 3.08 kcal mol−1 transition. Many transitions exhibiting conjugation are listed in Table S31.†
Among all the entitled compounds, MCPTD7 had the highest stability due to the extended hyper-conjugation with 32.49 kcal mol−1. All of the entitled compounds exhibited more stability in comparison with the reference compound. The overall stability order is as follows: MCPTD7 > MCPTD6 > MCPTD5 > MCPTD4 > MCPTD3 > MCPTD8 > MCPTD1 > MCPTR > MCPTD2. Therefore, NBO analysis of these compounds entails that the extended hyper conjugation and robust intramolecular transference of the charge play a remarkable role in stabilizing these compounds, and signify the charge transfer properties that are important for NLO properties.
Nonlinear optical (NLO) properties
The electronic characteristics of the designed compounds were measured for the optical analyses, such as linear response: polarizability (α) and nonlinear responses: first hyper polarizability (β) and second hyper polarizability (γ).61 An applied external electric field interacts with the electronic densities of the extended conjugated systems. Consequently, it changes their dipole moments.62 The delocalization strength of the electrons in any system can be enhanced using substituents (electron donor and acceptor) at reasonable places of the conjugated system.43,63 This enhancement in the asymmetric distribution of the electrons can be a reason for the promising nonlinear optical phenomena of molecules.62 In compounds MCPTD1–MCPTD8, the resonance of the π-electrons between the phenyl rings has been increased, and the C–C π-bond is not positioned. Therefore, it takes part in the extended conjugation of the two or more phenylic rings.64 So, the delocalization increased from MCPTD1–MCPTD8 through the addition of the chlorine, fluorine and cyano groups as a substituent, which drifts electrons marvelously. Thus, introducing a pi-spacer to link different appropriate acceptor parts is effective to decrease the Egap, and thus to increase polarizabilities.62 Moreover, the polarity has a significant impact on the dipole moment (μ) by enhancing their NLO values.43 Dipole moments are produced from electronegativity differences. The larger the difference in the electronegativity, the larger the dipole moment.65 The dipole moment (μ) can be seen by the results mentioned in Table 5. The dipole moment (μ), average polarizability 〈α〉, second-order polarizability (βvec), and second-order hyperpolarizability 〈γ〉 values of the entire compound are calculated in esu units,66 and are listed in Table 5, while their major contributing tensors are discussed in detail in S11–S13.†| Systems | μtotal | 〈α〉 (a.u) | 〈α〉 (esu) ×106 | βvec (a.u) | βvec (esu) | 〈γ〉 |
|---|---|---|---|---|---|---|
| MCPTR | 3.512 | 559.1 | 8.29 × 10−23 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 943.1 943.1 |
2.07 × 10−28 | 2.1452 × 106 |
| MCPTD1 | 3.432 | 1307.8 | 1.94 × 10−22 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 488.5 488.5 |
6.35 × 10−28 | 1.3209 × 107 |
| MCPTD2 | 4.071 | 1476.0 | 2.19 × 10−22 | 152![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 679.8 679.8 |
1.32 × 10−27 | 3.02404 × 107 |
| MCPTD3 | 4.756 | 1502.1 | 2.23 × 10−22 | 191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755.3 755.3 |
1.66 × 10−27 | 4.1097 × 107 |
| MCPTD4 | 4.411 | 1515.5 | 2.25 × 10−22 | 215![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 171.0 171.0 |
1.86 × 10−27 | 4.7632 × 107 |
| MCPTD5 | 5.002 | 1563.4 | 2.32 × 10−22 | 221![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 788.6 788.6 |
1.92 × 10−27 | 4.9960 × 107 |
| MCPTD6 | 4.669 | 1583.3 | 2.35 × 10−22 | 234![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130.8 130.8 |
2.02 × 10−27 | 5.4032 × 107 |
| MCPTD7 | 7.200 | 1621.0 | 2.40 × 10−22 | 328![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 177.0 177.0 |
2.84 × 10−27 | 8.6024 × 107 |
| MCPTD8 | 4.163 | 1596.5 | 2.37 × 10−22 | 192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 391.8 391.8 |
1.66 × 10−27 | 4.180 × 107 |
The reference molecule (MCPTR) had the lowest average polarizability. The strong acceptor moiety with stronger electron-withdrawing groups caused the highest value of average polarizability. Therefore, MCPTD7 had the predominant value of the dipole moment as 7.200 a.u. The decreasing order of the dipole moment values was observed for the designed compounds with the reference as MCPTD7 > MCPTD5 > MCPTD6 > MCPTD3 > MCPTD4 > MCPTD8 > MCPTD2 > MCPTR > MCPTD1. The addition of the electronegative atom pulled the electron density to that atom; in this way, it rendered the other parts of the molecule as a result of this increased linear polarizability.67 The trend for the average linear polarizability values of the designed compounds with the reference was observed as: MCPTD7 > MCPTD8 > MCPTD6 > MCPTD5 > MCPTD4 > MCPTD3 > MCPTD2 > MCPTD1 > MCPTR. Similar to the dipole moment, the highest value of the average polarizability was observed for the designed compound MCPTD7 due to the presence of four cyano groups, which enhanced the electron density towards the A unit and made it more electron-withdrawing. Hence, a remarkable increase in its value was observed, i.e., 2.40 × 10−22 esu. Furthermore, a systematic relationship was obtained between the molecular structures and β values. The β parameter usually increased with the strength of the acceptor substituents attached with MCPTR, like the fluoro, chloro and cyano groups, which contribute to the molecular nonlinearity. Moreover, the contribution of the extension of the conjugated system to β is dominant too as the substitutions take place. Thus, the βvec value for all designed compounds decreased in the following order: MCPTD7 > MCPTD6 > MCPTD5 > MCPTD4 > MCPTD8 > MCPTD3 > MCPTD2 > MCPTD1 > MCPTR. Moreover, MCPTD7 has been shown to possess the highest value of βvec as 2.84 × 10−27 esu compared to the other designed compounds. However, MCPTD1 and MCPTD2 showed minimal βvec values, owing to the poor ICT. The introduction of a fluorine (electron acceptor) in MCPTD3 and MCPTD4 enhanced the accepting power on the opposite end. MCPTD3 has an effectively high NLO value due to the strong accepting tendency of the two fluorine atoms attached to it. There is the phenyl ring as a donor moiety and three atoms of the fluoro (–F) moiety competing on the opposite end in the case of MCPTD4. Thus, the βvec value was boosted from 1.66 × 10−27 esu of MCPTD3 to 1.86 × 10−27 esu in MCPTD4. The installation of a chlorine electron acceptor onto the phenyl ring in MCPTD5 and MCPTD6 enhances the accepting power again. MCPTD5 has a high NLO value because of the strong accepting ability of the chlorine. There is the phenyl ring as a donor moiety and three atoms of the chloro (–Cl) moiety competing on the other end. Thus, the βvec value is shifted from 1.92 × 10−27 esu in MCPTD5 to 2.02 × 10−27 esu in MCPTD6. MCPTD7 has the highest NLO value of all because it consists of four cyano (–CN) groups. In these molecules, the maximum and minimum NLO responses can be ascribed to the proficiency of the charge transfer from the donor to acceptor through their corresponding π-linked interactions. Moreover, upsurges in the hyperpolarizability values in the molecules discussed here arise in association with the delocalization of the π-electrons. This delocalization decreases the HOMO–LUMO energy difference. The calculated values of the average polarizability and second-order polarizability of the investigated molecules are significantly greater than that for urea (βvec (urea) = 0.372 × 10−30 esu), a standard molecule for the analysis of the NLO response.68 The hyperpolarizability values of MCPTR, MCPTD1, MCPTD2, MCPTD3, MCPTD4, MCPTD5, MCPTD6, MCPTD7, and MCPTD8 were determined to be 557, 1709, 3551, 4459, 5004, 5158, 5445, 7632 and 4474 times larger than the second-order polarizability value of urea, respectively.
The first hyperpolarizability values of all designed compounds were uncovered with the opposite order of the Egap between the HOMO–LUMO orbitals. The abovementioned factors affect the second hyper polarizability 〈γ〉 amplitudes for MCPTD1–MCPTD8 too.69 The maximum 〈γ〉 amplitude (8.6024 × 107 esu) was also found in MCPTD7. Overall, the decreasing trend of all of the studied compounds was observed as: MCPTD7 > MCPTD6 > MCPTD5 > MCPTD4 > MCPTD8 > MCPTD3 > MCPTD2 > MCPTR > MCPTD1. It may be deduced from the aforementioned discussion that the electron-withdrawing nature of the acceptors with the pi-conjugation and thienyl moieties played a pivotal role and yielded remarkable NLO amplitudes.69
Conclusion
A series of structurally related molecules (MCPTD1–MCPTD8) were designed from the pyrene-based synthesized compound (MCPTR). The influence of different acceptors of MCPTD1–MCPTD8 was carefully explored for the NLO properties. These results revealed the fact that the acceptors have promising influence over the donor–π–acceptor structures, and strongly tuned the entire features of the designed compounds over the synthesized compound. MCPTD1–MCPTD8 showed the highest wavelength with low transitional energy, a broader extent of orbital formation, and oscillating strength values compared to MCPTR. The larger red shifted spectrum value (λmax = 832.330 nm) was found for MCPTD7. The FMO-based investigation indicates that HOMOs are located over the donor moiety and its nearby π-linker, while LUMOs are settled on the acceptor in all of the molecules. The HOMO–LUMO energy-gap was reduced from 3.210 eV to −2.088 eV for MCPTR–MCPTD8, respectively. Interestingly, the HOMO–LUMO energy-gap of MCPTD7 was decreased by up to 1.748 eV. Contrarily, the NLO values have been enhanced from 2.07 × 10−28 esu to 1.66 × 10−27 esu for MCPTR–MCPTD8. Surprisingly, the 〈α〉, βvec and 〈γ〉 values were found to be 2.40 × 10−22, 2.84 × 10−27 and 8.6024 × 107 esu, respectively, for MCPTD7, which was greater than the reference (MCPTR) and MCPTD1–MCPTD8. Experimental researchers may be attracted to our designed compounds owing to the impressive NLO results. We could enlist the promising abilities of our designed compounds for establishing the better and responsive NLO. The larger NBO and NLO response in MCPTD7 was produced as a consequence of the delocalization of the π-system. Delocalization lessens the HOMO–LUMO band gap and ensures stability of the molecules. Thus, it can exhibit excellent material properties in photoresponsive compounds.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. Imran express appreciation to the Deanship of Scientific Research at King Khalid University Saudi Arabia for funding through research groups program under grant number R.G.P. 2/28/42.References
- M. G. Papadopoulos, A. J. Sadlej and J. Leszczynski, Non-linear optical properties of matter, Springer, 2006 Search PubMed.
- D. N. Christodoulides, I. C. Khoo, G. J. Salamo, G. I. Stegeman and E. W. Van Stryland, Adv. Opt. Photonics, 2010, 2, 60–200 CrossRef CAS.
- D. F. Eaton, Nonlinear Optical Materials, ACS Publications, 1991 Search PubMed.
- B. Ivanova and M. Spiteller, Cryst. Growth Des., 2010, 10, 2470–2474 CrossRef CAS.
- E. Knill, R. Laflamme and G. J. Milburn, Nature, 2001, 409, 46–52 CrossRef CAS PubMed.
- J. D. Feng, L. K. Yan, Z. M. Su, Y. H. Kan, Y. Q. Lan, Y. Liao and Y. L. Zhu, Chin. J. Chem., 2006, 24, 119–123 CrossRef CAS.
- S. Haid, M. Marszalek, A. Mishra, M. Wielopolski, J. Teuscher, J. E. Moser, R. Humphry-Baker, S. M. Zakeeruddin, M. Grätzel and P. Bäuerle, Adv. Funct. Mater., 2012, 22, 1291–1302 CrossRef CAS.
- V. Srinivasan, M. Panneerselvam, N. Pavithra, S. Anandan, K. Sundaravel, M. Jaccob and A. Kathiravan, J. Photochem. Photobiol., A, 2017, 332, 453–464 CrossRef CAS.
- S. Smith, Nature, 1985, 316, 319–324 CrossRef.
- P. S. Halasyamani and W. Zhang, Am. Chem. Soc., 2017, 12077–12085 CAS.
- G. Berkovic, Y. Shen and M. Shadt, Mol. Cryst. Liq. Cryst., 1987, 150, 607–616 Search PubMed.
- A. J. Garza, O. I. Osman, N. A. Wazzan, S. B. Khan, A. M. Asiri and G. E. Scuseria, Theor. Chem. Acc., 2014, 133, 1–8 Search PubMed.
- M. R. S. A. Janjua, Z. H. Yamani, S. Jamil, A. Mahmood, I. Ahmad, M. Haroon, M. H. Tahir, Z. Yang and S. Pan, Aust. J. Chem., 2016, 69, 467–472 CrossRef CAS.
- R. Mahmood, M. R. S. A. Janjua and S. Jamil, J. Cluster Sci., 2017, 28, 3175–3183 CrossRef CAS.
- S. Yamashita, J. Lightwave Technol., 2011, 30, 427–447 Search PubMed.
- L. Guo, Z. Guo and X. Li, J. Mater. Sci.: Mater. Electron., 2018, 29, 2577–2584 CrossRef CAS.
- R. D. Fonseca, M. G. Vivas, D. L. Silva, G. Eucat, Y. Bretonnière, C. Andraud, L. De Boni and C. R. Mendonça, J. Phys. Chem. C, 2018, 122, 1770–1778 CrossRef CAS.
- P.-H. Sung and T.-F. Hsu, Polymer, 1998, 39, 1453–1459 CrossRef CAS.
- M. I. Nan, E. Lakatos, G.-I. Giurgi, L. Szolga, R. Po, A. Terec, S. Jungsuttiwong, I. Grosu and J. Roncali, Dyes Pigm., 2020, 181, 108527 CrossRef CAS.
- J. Zyss, Quantum Electronics—Principles and Applications, Academic Press, Inc, New York, 1987, pp. 222–223 Search PubMed.
- P.-T. T. Pham, V. G. Young and M. M. Bader, CrystEngComm, 2018, 20, 128–132 RSC.
- P.-T. T. Pham and M. M. Bader, Cryst. Growth Des., 2014, 14, 916–922 CrossRef CAS.
- M. M. Bader, P.-T. T. Pham and E. H. Elandaloussi, Cryst. Growth Des., 2010, 10, 5027–5030 CrossRef CAS.
- M. M. Bader, P.-T. T. Pham, B. R. Nassar, H. Lin, Y. Xia and C. D. Frisbie, Cryst. Growth Des., 2009, 9, 4599–4601 CrossRef CAS.
- C. Carati, N. Gasparini, S. Righi, F. Tinti, V. Fattori, A. Savoini, A. Cominetti, R. Po, L. Bonoldi and N. Camaioni, J. Phys. Chem. C, 2016, 120, 6909–6919 CrossRef CAS.
- M. Wielopolski, J.-H. Kim, Y.-S. Jung, Y.-J. Yu, K.-Y. Kay, T. W. Holcombe, S. M. Zakeeruddin, M. Grätzel and J.-E. Moser, J. Phys. Chem. C, 2013, 117, 13805–13815 CrossRef CAS.
- D. Fichou, T. Watanabe, T. Takeda, S. Miyata, Y. Goto and M. Nakayama, Jpn. J. Appl. Phys., Part 2, 1988, 27, L429 CrossRef CAS.
- D.-W. Lee, T. Kim and M. Lee, Chem. Commun., 2011, 47, 8259–8261 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., Gaussian09, Revision A, Gaussian Inc., Wallingford CT, 2009, pp. 150–166 Search PubMed.
- N. M. O'boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17 Search PubMed.
- G. Zhurko, Chemcraft, http://www.chemcraftprog.com, 2014, p. 22 Search PubMed.
- C. Valverde, S. A. d. L. e Castro, G. R. Vaz, J. L. de Almeida Ferreira, B. Baseia and F. A. Osório, Acta Chim. Slov., 2018, 65, 739–749 CrossRef CAS PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Tammer, Colloid Polym. Sci., 2004, 235–235 CrossRef CAS.
- M. R. S. A. Janjua, M. U. Khan, B. Bashir, M. A. Iqbal, Y. Song, S. A. R. Naqvi and Z. A. Khan, Comput. Theor. Chem., 2012, 994, 34–40 CrossRef CAS.
- M. R. S. A. Janjua, M. Amin, M. Ali, B. Bashir, M. U. Khan, M. A. Iqbal, W. Guan, L. Yan and Z. M. Su, Eur. J. Inorg. Chem., 2012, 705–711 CrossRef CAS.
- P. K. Chattaraj, S. Giri and S. Duley, Chem. Rev., 2011, 111, PR43–PR75 CrossRef PubMed.
- W. Rahmalia, J.-F. Fabre, T. Usman and Z. Mouloungui, Spectrochim. Acta, Part A, 2014, 131, 455–460 CrossRef CAS PubMed.
- M. I. Nan, E. Lakatos, G.-I. Giurgi, L. Szolga, R. Po, A. Terec, S. Jungsuttiwong, I. Grosu and J. Roncali, Dyes Pigm., 2020, 181, 108527 CrossRef CAS.
- S. Namuangruk, R. Fukuda, M. Ehara, J. Meeprasert, T. Khanasa, S. Morada, T. Kaewin, S. Jungsuttiwong, T. Sudyoadsuk and V. Promarak, J. Phys. Chem. C, 2012, 116, 25653–25663 CrossRef CAS.
- M. J. Kamlet, J. L. Abboud and R. Taft, J. Am. Chem. Soc., 1977, 99, 6027–6038 CrossRef CAS.
- K. Fukui, Science, 1982, 218, 747–754 CrossRef CAS PubMed.
- P.-T. Pham, Y. Xia, C. D. Frisbie and M. M. Bader, J. Phys. Chem. C, 2008, 112, 7968–7971 CrossRef CAS.
- X. Cai, M. W. Burand, C. R. Newman, D. A. da Silva Filho, T. M. Pappenfus, M. M. Bader, J.-L. Brédas, K. R. Mann and C. D. Frisbie, J. Phys. Chem. B, 2006, 110, 14590–14597 CrossRef CAS PubMed.
- M. M. Bader, R. Custelcean and M. D. Ward, Chem. Mater., 2003, 15, 616–618 CrossRef CAS.
- M. U. Khan, M. Khalid, M. Ibrahim, A. A. C. Braga, M. Safdar, A. A. Al-Saadi and M. R. S. A. Janjua, J. Phys. Chem. C, 2018, 122, 4009–4018 CrossRef CAS.
- M. Adeoye, A. Adeogun, S. Adewuyi, S. Ahmed, N. Odozi and N. Obi-Egbeedi, Sci. Res. Essays, 2009, 4, 107–111 Search PubMed.
- M. Ans, K. Ayub, S. Muhammad and J. Iqbal, Comput. Theor. Chem., 2019, 1161, 26–38 CrossRef CAS.
- M. Khalid, A. Ali, R. Jawaria, M. A. Asghar, S. Asim, M. U. Khan, R. Hussain, M. F. ur Rehman, C. J. Ennis and M. S. Akram, RSC Adv., 2020, 10, 22273–22283 RSC.
- M. R. McLean, M. Bader, L. R. Dalton, R. L. Devine and W. H. Steier, J. Phys. Chem., 1990, 94, 4386–4387 CrossRef CAS.
- C. W. Spangler, T. J. Hall, K. O. Havelka, M. Badr, M. R. McLean and L. R. Dalton, Nonlinear Optical Properties of Organic Materials II, 1990, pp. 149–156 Search PubMed.
- R. G. Parr, L. v. Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- N. Kovačević and A. Kokalj, Corros. Sci., 2011, 53, 909–921 CrossRef.
- N. Sheela, S. Muthu and S. Sampathkrishnan, Spectrochim. Acta, Part A, 2014, 120, 237–251 CrossRef CAS PubMed.
- T. Koopmans, Physica, 1934, 1, 104–113 CrossRef.
- S. He, Y. Tan, X. Xiao, L. Zhu, Y. Guo, M. Li, A. Tian, X. Pu and N.-B. Wong, J. Mol. Struct.: THEOCHEM, 2010, 951, 7–13 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- M. Szafran, A. Komasa and E. Bartoszak-Adamska, J. Mol. Struct., 2007, 827, 101–107 CrossRef CAS.
- W. Sun, M. M. Bader and T. Carvalho, Opt. Commun., 2003, 215, 185–190 CrossRef CAS.
- B. S. Mendis and K. N. de Silva, J. Mol. Struct.: THEOCHEM, 2004, 678, 31–38 CrossRef.
- C. James, A. A. Raj, R. Reghunathan, V. Jayakumar and I. H. Joe, J. Raman Spectrosc., 2006, 37, 1381–1392 CrossRef CAS.
- A. Dulcic, C. Flytzanis, C. Tang, D. Pepin, M. Fetizon and Y. Hoppilliard, J. Chem. Phys., 1981, 74, 1559–1563 CrossRef CAS.
- H. S. Nalwa, T. Watanabe, S. Miyata and J. Rabek, Progress in photochemistry and photophysics, 1992, vol. 5, pp. 103–185 Search PubMed.
- M. M. Bader, T. Hamada and A. Kakuta, J. Am. Chem. Soc., 1992, 114, 6475–6479 CrossRef CAS.
- J. P. Remington, The Practice of Pharmacy, JB Lippincott Company, 1917 Search PubMed.
- D. R. Kanis, M. A. Ratner and T. J. Marks, Chem. Rev., 1994, 94, 195–242 CrossRef CAS.
- A. Saeed, S. Muhammad, S.-u. Rehman, S. Bibi, A. G. Al-Sehemi and M. Khalid, J. Mol. Graph. Model., 2020, 100, 107665 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra00876e |
| This journal is © The Royal Society of Chemistry 2021 |