Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electric control of ionic transport in sub-nm nanopores†
Anping Ji ab and
Yunfei Chen*a
ab and
Yunfei Chen*a
aSchool of Mechanical Engineering, Jiangsu Key Laboratory for Design and Manufacture of Micro-Nano Biomedical Instruments, Southeast University, Nanjing, 211189, China. E-mail: ji-anping@sanxiau.edu.cn
bSchool of Mechanical Engineering, Chongqing Three Gorges University, Chongqing, 404100, China
First published on 13th April 2021
Abstract
The ion transport behavior through sub-nm nanopores (length (L) ≈ radius (R)) on a film is different from that in nanochannels (L ≫ R), and even more different from the bulk behavior. The many intriguing phenomena in ionic transport are the key to the design and fabrication of solid-state nanofluidic devices. However, ion transport through sub-nm nanopores is not yet clearly understood. We investigate the ionic transport behavior of sub-nm nanopores from the perspective of conductance via molecular dynamics (MD) and experimental methods. Under the action of surface charge, the average ion concentration inside the nanopore is much higher than the bulk value. It is found that 100 mM is the transition point between the surface-charge-governed and the bulk behavior regimes, which is different from the transition point for nanochannels (10 mM). Moreover, by investigating the access, pores, surface charge, electroosmosis and potential leakage conductance, it is found that the conductive properties of the nanopore at low bulk concentration are determined by the surface charge potential leaks into the reservoir. Specifically, there is a huge increase in cation mobility through a cylindrical nanopore, which implies potential applications for the fast charging of supercapacitors and batteries. Sub-nm nanopores also show a strong selectivity toward Na+, and a strong repellence toward Cl−. These conclusions presented here will be useful not only in understanding the behavior of ion transport, but also in the design of nanofluidic devices.
1. Introduction
Due to many intriguing phenomena in ionic transport, for example, ion selectivity,1,2 the ionic field-effect,3 and ionic current rectification,4 the design and fabrication of solid-state nanofluidic devices have elicited increasing attention in both the scientific and engineering communities.5–7 Electric control of ionic transport is of primary importance for the design of novel nanofluidic devices, such as sensing devices,8 water desalination,9 and energy conversion.10 Many studies have shown that ionic transport in nanoconfinement is mainly controlled by the following factors: (1) geometry, (2) surface charge, (3) chemical composition, (4) wettability, (5) environmental pH, (6) electrolyte concentration gradient, (7) ion mobility, and (8) electric field strength.11 Factors 1–4 are determined by the design and fabrication of nanopores, while factors 5–8 can be tuned in the electrolyte solutions. Determining how to exploit these factors in subtle ways is key to the design of nanofluidic devices.Ion transport is the result of steric interactions (range, 0.1–2 nm), van der Waals forces (range, 0.1–50 nm) and electrostatic forces (range, 1–100 nm).3,12 Ion dynamics in a charged nanopore with dimensions comparable to the Debye length (sub-nm nanopore) deviate from the bulk values.13,14 Similar phenomena, referred to as charge overspill,15 and electroneutrality breakdown,16 have been extensively reported. Furthermore, the fluid mechanics in nanoscale conduits have not been fully explored, as they are difficult to measure due to their tiny scale.17
It has always been a goal of scientists to manipulate ion transport like that in biological channels (sub-nm), but the scaling behavior18 of ion transport is the theoretical basis for this pursuit. Although the continuum theory cannot describe the results perfectly for many experiments, it still has great significance for the modulation of parameters in the design of nanofluidic devices, such as graphene–Al2O3 nanopore sensors for the detection of DNA.19 However, these scaling behaviors18–24 have not been evaluated in an in-depth analysis of the nanopore conductance composition. The roles of access conductance, potential leakage conductance, surface potential conductance, nanopore conductance and electroosmotic conductance still need to be further explored. In this paper, we have investigated the ionic transport behavior of sub-nm nanopores from the perspective of conductance using the molecular dynamics (MD) and experimental methods. It is found that the nanopore conductive properties at low bulk concentration are determined by the surface charge potential leaks into the reservoir. At low ionic concentrations, the ion concentration is controlled by the surface charge, and the ion mobility is much higher than in the bulk.
2. Methods
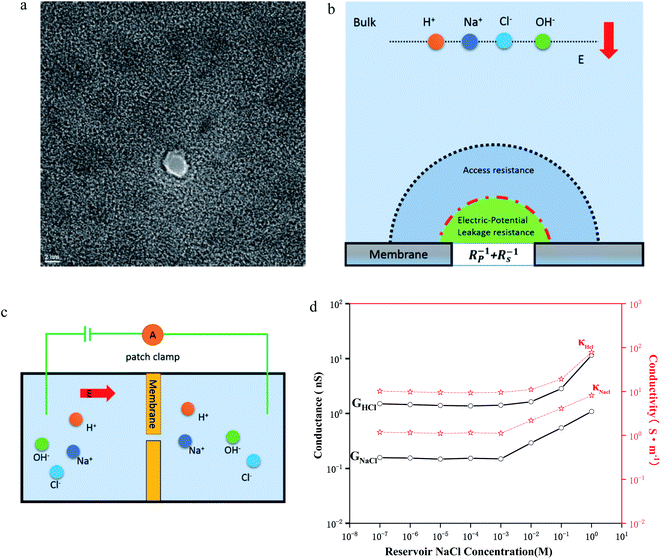
First, a 100 nm thick Si3N4 membrane was grown on a silicon wafer using low-pressure chemical vapor deposition. Then, a window on the other side of the wafer was opened using a wet etching process to expose the silicon nitride thin film. After the etching process, the silicon nitride film was exposed to a focused ion beam with high energy to reduce the film thickness to 20 nm. In the last step, a nanopore was drilled with a transmission electron microscope (TEM) using a tightly focused electron beam (Fig. 1a). To probe the electrodynamic properties of the ions, we must first investigate the composition and role of the nanopore conductance (Fig. 1b). Experimentally, the pore current is measured by inserting two electrodes into the aqueous cis and trans chambers (Fig. 1c). Using Ohm's law, the conductance can be obtained (Fig. 1d, see ESI†).In order to investigate the concentration of nanopores (R ≫ L) in extremely thin films, we used molecular dynamics to simulate the passage of water and NaCl through graphene nanopores under an electric field. Based on the simulation results, we calculated the concentration distribution of ions along the radial and axial directions to compare with the bulk behavior. In order to investigate the effect of the electric field on the rearrangement of water molecules, we also calculated statistics for the electric potential distribution of pure water along the axis (see ESI†). The mutual confirmation of the experiment and simulation helped us to understand the transport function of ions inside the nanopore.
3. Results and discussion
3.1. Ensemble averaged concentration inside the nanopore
In a cylindrical pore, we can also simply express the conductance as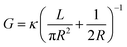 , where G and κ are the conductance and conductivity of an electrolyte inside the pore, respectively; R and L are the radius and the length of a nanopore, respectively. The conductivity can be written as
, where G and κ are the conductance and conductivity of an electrolyte inside the pore, respectively; R and L are the radius and the length of a nanopore, respectively. The conductivity can be written as 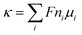 , where ni and ui are the concentration and the electrophoretic mobility of an ion of the ith species, respectively; F is the Faraday constant. Intuitively, the migration behavior of ions is determined by (6) the electrolyte concentration gradient and (7) ion mobility, but factors 6 and 7 are controlled by (5) the environmental pH and (8) electric field strength. Both theoretical studies25–27 using molecular dynamics and experimental nuclear magnetic resonance studies16 show that the ion concentration deviates from the bulk values. Various power-law relations between the conductance and ion concentration (G ∝ n0α) have been widely studied, which has also been verified in our experiments (Fig. 1d). Conductivity exhibits a similar phenomenon. Moreover, the conductivity of NaCl solution is always an order of magnitude lower than that of HCl solution, which is similar to the bulk behavior.
, where ni and ui are the concentration and the electrophoretic mobility of an ion of the ith species, respectively; F is the Faraday constant. Intuitively, the migration behavior of ions is determined by (6) the electrolyte concentration gradient and (7) ion mobility, but factors 6 and 7 are controlled by (5) the environmental pH and (8) electric field strength. Both theoretical studies25–27 using molecular dynamics and experimental nuclear magnetic resonance studies16 show that the ion concentration deviates from the bulk values. Various power-law relations between the conductance and ion concentration (G ∝ n0α) have been widely studied, which has also been verified in our experiments (Fig. 1d). Conductivity exhibits a similar phenomenon. Moreover, the conductivity of NaCl solution is always an order of magnitude lower than that of HCl solution, which is similar to the bulk behavior.
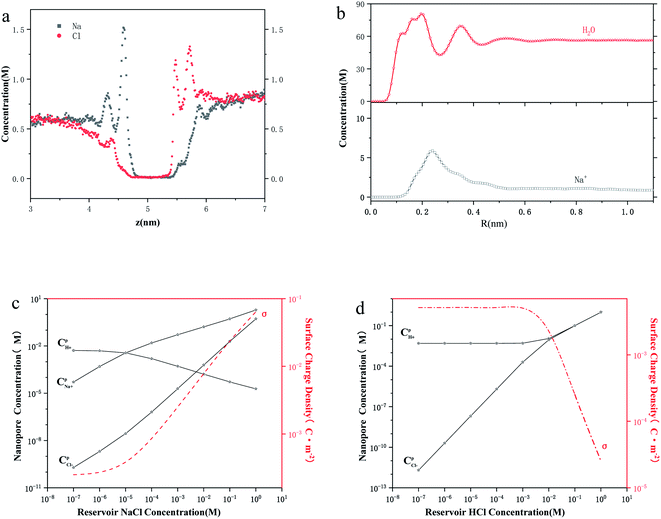
As shown in Fig. 2a, both sodium ions and chloride ions formed concentration polarization layers on either side of the thin-film nanopore, which is similar to the density profiles reported by Titus27 and Hu.25 In the polarization zone, the peak sodium ion and chloride ion concentrations are 1.55 and 1.33 times the bulk values. This difference may be caused by the difference in surface charge and ion hydration. The radial distribution of ions and water in Fig. 2b shows that a water and ion layer is formed inside the nanochannel, and two water layers surround the ion layer. The difference between the size-constraint effect28,29 of pure water passing through the nanochannel is that the peak concentration of water occurs close to the center of the hole, rather than the peak concentration of water being close to the wall in the nanochannel like in pure water. This behavior is obviously a consequence of the fact that the cations can optimize their hydration shell and quickly pass through the nanochannel. It is worth noting that the peak concentration of cations is five times the bulk value. These phenomena all imply that the ion concentration inside the nanochannel is different from the bulk concentration.
To further understand the role of concentration in the ion transport behavior, we use the model of ref. 12 to estimate the ion concentration inside the nanochannel. Here, we define the ensemble average concentration as the average concentration of all ions in the access conductance,30 surface conductance, potential leakage conductance,31 and nanopore conductance regions (Fig. 1b). nOH−/nCl−/nH+/nNa+ are used to represent the concentrations of OH−/Cl−/H+/Na+, which are different from the bulk concentration n0. For a given surface charge density σ, the ion concentration inside the nanopore must satisfy a certain relationship due to the quasi-electroneutrality condition, as suggested by earlier works:12 σ/eR = nOH− + nCl− − nH+ − nNa+. As we performed the measurements under ambient conditions, the pH of the electrolyte solution was 5 due to CO2 absorption.12,32 By using the Donnan equilibrium condition to relate the electric potentials and Poisson–Boltzmann theory, we can obtain the ion concentration results (Fig. 2c and d). As shown in Fig. 1d and 2c, the ion concentration in the 2 nm nanopore changes drastically until the bulk concentration reaches 1 mM, although there is no change in the conductance value. The complete ion transport operation means that an ion can only be emitted when the ion is trapped in the channel. In this region, although the concentration of the pore increases rapidly, the surface charge also increases just as quickly, so that the ions are always in a state of depletion to maintain electrical neutrality and the conductance cannot be increased. In the interval from 1 mM to 100 mM, the proton concentration drops rapidly, resulting in an increase in surface charge,12,33,34 while the Na+/Cl− concentration also increases rapidly with the increase of bulk concentration. Part of the Na+ participates in maintaining the electrical neutrality of the nanopore, and part of it is used for transportation. The increase in the concentration of chloride and sodium ions also leads to a power-law increase in conductance (G ∝ n0α).
To explore the role of the Na+ and H+ concentrations on the conductance, we performed the experiment using HCl alone to measure the transport through nanopore for comparison with the NaCl solution (Fig. 2d). This experiment shows that when the bulk concentration is higher than 1 mM, the surface charge drops rapidly, and the Cl− and H+ concentrations are almost the same. A similar phenomenon has been reported, which is consistent with our conclusion that there is no surface charge below pH 2 due to the complete protonation of the silica surface.35 However, in Fig. 2c, it can be observed that Na+ concentration is at least one order of magnitude higher than that of Cl− until the bulk concentration reaches 100 mM. Even if the bulk concentration reaches 1 M, the Na+ concentration (1.9 M) in the NaCl solution is almost four times the Cl− concentration (0.53 M), while Cl− and H+ concentrations (1 M) in the HCl solution are the same as the bulk concentration. Moreover, the Na+/H+ concentration in the NaCl/HCl solution is always higher than the bulk concentration. In contrast, the Cl− concentration is always less than or equal to the bulk concentration. These phenomena show that the charged nanopores are ion-selective.
3.2. Ionic conductance
In many experiments that study ion dynamics in micron-sized channels, the ionic conductance measurement (for neutral pores) is estimated as33,36
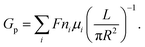 | (1) |
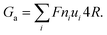 The ionic conductance of ions can be theoretically predicted through a combination of access resistance and pore resistance as suggested by earlier works:30,38,40,42
The ionic conductance of ions can be theoretically predicted through a combination of access resistance and pore resistance as suggested by earlier works:30,38,40,42
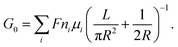 | (2) |
For a charged nanopore, the surface conductance makes an additional contribution to the overall conductance, as the nanopore requires counterions to screen the surface charge and maintain electrical neutrality.3,43 The surface conductance (Gs) can be expressed as 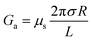 , where μs is the mobility of the counterions of a charged pore surface.30 The overall conductance (G0) can be written as G0−1 = Ga−1 + (Gs + Gp)−1. By combining eqn (1) and (2), the total conductance can be expressed as31
, where μs is the mobility of the counterions of a charged pore surface.30 The overall conductance (G0) can be written as G0−1 = Ga−1 + (Gs + Gp)−1. By combining eqn (1) and (2), the total conductance can be expressed as31
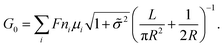 | (3) |
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/char_e10d.gif) is the ratio of the net charge concentration required in the pore and the charge concentration of the bulk solution, which is a dimensionless coefficient. For the experimental system in which a 1
is the ratio of the net charge concentration required in the pore and the charge concentration of the bulk solution, which is a dimensionless coefficient. For the experimental system in which a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solution is placed in a cylindrical pore with a homogeneous charge distribution,
1 solution is placed in a cylindrical pore with a homogeneous charge distribution, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/char_e10d.gif) can be written as
can be written as 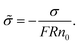
A large number of experiments have shown the failure of the principle of electrical neutrality inside the nanopore region, such as charge overspill, end effects, surface-electric-potential leakage and electroneutrality breakdown, but the entire nanopore system retains electroneutrality.16,31,44–46 The reason for these phenomena is that the surface charge potential leaks into the reservoir and the net charge inside the pores is insufficient. This potential leakage is different from the effect of surface charges, which enhances the counterion transport and weakens the co-ion transport. Taking the electric potential leakage conductance (Gl) into consideration, the electrophoretic conductance (Gph) can be expressed as
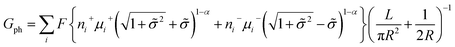 | (4) |
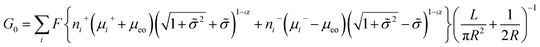 | (5) |
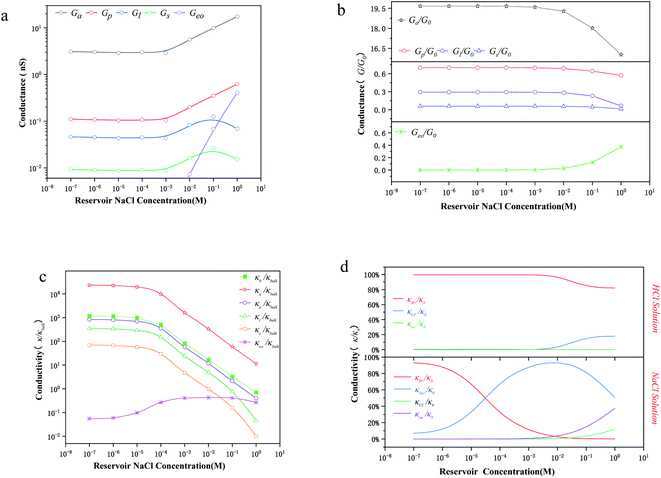
Fig. 3a shows the conductance values based on the experimental results (Fig. 1c). When the bulk concentration is less than 10 mM, the conductance values follow the order Ga > Gp > Gl > Gs > Geo, and an increase in the bulk concentration also leads to a power-law increase in conductance (Ga, Gp, Gl, Gs ∝ n0α). Furthermore, the most conductive part is the access resistance, which is 1–2 orders of magnitude higher than the other parts. At the same time, it can be seen from Fig. 3b that the access conductance is 16–20 times the total conductance. This situation indicates that ions queue up for entrance into the nanopore and wait to pass through the nanopore, which results in a concentration polarization phenomenon, in accordance with the MD conclusion (Fig. 2a). For the nanopore itself, the pore conductance (Gp), surface conductance (Gs) and electric potential leakage conductance (Gl) constitute the overall conductance of the nanopore (Gnc), and the sum of these three partial values (Gp, Gl, Gs) is close to the total conductance (G0) below 10 mM in Fig. 3b. This conclusion shows that Gnc is key to the conductive properties of the nanopore (G0). This is because in a series resistor, the larger the resistance value, the greater the voltage drop it bears. Moreover, the additional conductance (Gl, Gs) affected by the surface charge reaches half of the pore conductance (Gp), which indicates that ionic transport through a charged nanopore at low ionic concentration is governed by the surface charge, consistent with earlier reports.3,47–49 At the same time, we also observed that the surface potential leakage conductance is about six times the surface conductance below 100 mM, which provides ideas for increasing the ion selectivity of the nanopore and accelerating ions in energy conversion devices. Slightly different from in Duan's12 report of a rectangular 2 nm nanochannel, the effect of the electroosmotic flow on the conductance starts at 10 mM instead of 100 mM in a cylindrical pore. This is because Ga, Gl, and Gs have an increased influence on the total conductance, which enhances ion transport and leads to an increase in electroosmotic flow. Research indicates that the two obvious characteristics of conductance inside the nanopore are the surface-charge-governed regimes at low ion concentrations and the bulk behavior regimes at high ion concentrations.12,47 Fig. 3a illustrates that the additional conductance (Gl, Gs) affected by the surface charge reaches a peak value at 100 mM, which indicates that the leading role of the surface charge has begun to decrease, and that the role of electroosmotic flow has become stronger. In other words, 100 mM is the transition point between the surface-charge-governed and the bulk behavior regimes.
To further investigate the transition point, we removed the geometric factors and studied the difference between the nanopore conductivity (κ0) and NaCl solution conductivity(κbulk). Fig. 3c illustrates that 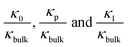 decrease from 103 to 100 as the concentration is increased to 100 mM, which shows that the enhancement effect of surface charge on ion transport almost disappears after the transition point is exceeded. Moreover, these curves have a similar arrangement to the conductance distribution curve in Fig. 3a
decrease from 103 to 100 as the concentration is increased to 100 mM, which shows that the enhancement effect of surface charge on ion transport almost disappears after the transition point is exceeded. Moreover, these curves have a similar arrangement to the conductance distribution curve in Fig. 3a 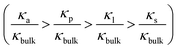 , and such a result is expected due to the relationship between conductance and conductivity. The access, pore and potential leakage conductivity (κa, κp, κl) are 102 to 104 times the conductivity of the NaCl solution (κbulk) below 10−4 M, while these values quickly drop to 100 at concentrations of 10−4 M to 10−1 M. This different performance is caused by the different concentration and ion mobility behavior in the two regions (Fig. 2c and 4a): (1) at ∼10−4 M, the ionic concentration inside the pore increases rapidly due to the surface charge and the ion mobility inside the pore is much higher than the ion mobility in the NaCl solution; (2) between 10−4 M and 10−1 M, the increase in the ion concentration inside the pore is slower than the increase in the bulk concentration, and this increase in concentration also leads to a decrease in ion mobility.
, and such a result is expected due to the relationship between conductance and conductivity. The access, pore and potential leakage conductivity (κa, κp, κl) are 102 to 104 times the conductivity of the NaCl solution (κbulk) below 10−4 M, while these values quickly drop to 100 at concentrations of 10−4 M to 10−1 M. This different performance is caused by the different concentration and ion mobility behavior in the two regions (Fig. 2c and 4a): (1) at ∼10−4 M, the ionic concentration inside the pore increases rapidly due to the surface charge and the ion mobility inside the pore is much higher than the ion mobility in the NaCl solution; (2) between 10−4 M and 10−1 M, the increase in the ion concentration inside the pore is slower than the increase in the bulk concentration, and this increase in concentration also leads to a decrease in ion mobility.
Fig. 3d illustrates that the contribution of protons to the conductance exceeds 80% in HCl solution, even at a bulk concentration of 1 M. This is because the mechanism of proton transfer is tunneling, and its exceptionally large mobility produces a very high conductivity, which is different from metal ions.5,12 Therefore, in HCl solution, the electroosmotic flow contributes less than 20% to the conductivity, which can be ignored at low ion concentration. In NaCl solution, the conductivity in a charged nanopore at ∼10−5 M is governed by H+, and the transition to being dominated by Na+ occurs from 10−4 M to 10−2 M, but the conductivity is a collective effect of electroosmotic flow, H+ and Na+ when the ion concentration is higher than 10−2 M.
3.3. Ion mobility
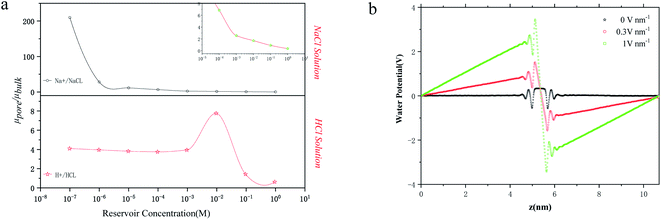
Another important factor in ion transport is ion mobility. Using eqn (5), we compared the cation mobility in the sub-nm cylindrical nanopore with the bulk mobility (μbulk) based on the experimental results. In HCl solution, the proton mobility of the nanopore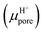 was found to be four times the bulk proton mobility
was found to be four times the bulk proton mobility 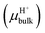 until the bulk concentration reached 10−3 M; this conclusion is consistent with earlier reports12 (Fig. 4a). Moreover, we also found that the proton mobility reached a peak of seven times the bulk proton mobility at 10−2 M, and then quickly dropped below the bulk mobility value. The proton transport method first involves the formation of hydrate ions, and then tunneling for transport. Therefore, the ion mobility in this way is determined by the speed of rearrangement of water molecules.5,50 Obviously, an external electric field can strengthen the rearrangement of water, which is conducive to proton transmission. Our simulation results (Fig. 4b) also proved that the stronger the electric field, the more violent the orderly changes of the water potential, which reflects the relationship between the rearrangement of water molecules and the electric field. In the measured nanopore system, the voltage drop is mainly concentrated on the nanopore, which makes the electric field intensity in the nanopore particularly high (>107 V m−1). This strengthening effect of the rearrangement increases the proton mobility, making it greater than the bulk mobility. As there is no surface charge below pH 2 due to the full protonation of the silica surface (Fig. 2d), the electrostatic interaction exerted by the electric double layer on the counterions disappears, so that the ion mobility reaches the peak value at 10−2 M (Fig. 4a). After the ion concentration exceeds 10−2 M, the Cl− concentration (Fig. 2d) and its contribution to the conductance (Fig. 3d) increase to be comparable to those of the protons, and the transport of Cl− has a destructive effect on the rearrangement of water molecules, causing the proton mobility to decrease.
until the bulk concentration reached 10−3 M; this conclusion is consistent with earlier reports12 (Fig. 4a). Moreover, we also found that the proton mobility reached a peak of seven times the bulk proton mobility at 10−2 M, and then quickly dropped below the bulk mobility value. The proton transport method first involves the formation of hydrate ions, and then tunneling for transport. Therefore, the ion mobility in this way is determined by the speed of rearrangement of water molecules.5,50 Obviously, an external electric field can strengthen the rearrangement of water, which is conducive to proton transmission. Our simulation results (Fig. 4b) also proved that the stronger the electric field, the more violent the orderly changes of the water potential, which reflects the relationship between the rearrangement of water molecules and the electric field. In the measured nanopore system, the voltage drop is mainly concentrated on the nanopore, which makes the electric field intensity in the nanopore particularly high (>107 V m−1). This strengthening effect of the rearrangement increases the proton mobility, making it greater than the bulk mobility. As there is no surface charge below pH 2 due to the full protonation of the silica surface (Fig. 2d), the electrostatic interaction exerted by the electric double layer on the counterions disappears, so that the ion mobility reaches the peak value at 10−2 M (Fig. 4a). After the ion concentration exceeds 10−2 M, the Cl− concentration (Fig. 2d) and its contribution to the conductance (Fig. 3d) increase to be comparable to those of the protons, and the transport of Cl− has a destructive effect on the rearrangement of water molecules, causing the proton mobility to decrease.
Unlike the proton transport in HCl solution, the Na+ mobility in NaCl solution shows a downward trend, but it is always higher than the maximum value of bulk Na+ mobility (μNa+ at infinite dilution is 5.19 × 10−8 m2 V−1 s−1) until a concentration of 10−2 M. The reason for this phenomenon is that the electric field strength inside the nanopore (2 × 107 V m−1 in this experiment) is higher than the critical electric field of the Wien effect (107 V m−1), which causes the Wien effect when ions pass through the nanopore.50
3.4. Ion selectivity
There is a significant difference in the ion exchange ability of the pore to pass/reject the two ion types, and this characteristic can be defined as the ion selectivity of the pore.51,52 Nanochannels/nanopores have shown the ability to replicate and mimic the characteristics for use in a range of applications, including ultra-sensitive ion detection and antimicrobial agents.2,53 The stronger the ion selectivity, the more ions will be used for transport through the nanopore, which leads to a greater contribution to the conductance. Therefore, the ion selectivity can be expressed as31
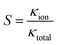 | (6) |
In HCl solution, the Na+ selectivity is always less than 50% at ∼10−5 M, and it reached a peak of 95.69% at 10−2 M as the bulk concentration was increased. In the concentration region below 10−2 M, it is the surface charge that plays the active role, which repels the ions of the co-ion (Cl−) and attracts the counterions (Na+) at the same time, thereby enhancing the Na+ selectivity. In the concentration region above 10−2 M, the Na+ selectivity decays, as the role of electroosmotic flow is beginning to manifest and its physical occupation hinders ion selectivity. Because surface charge and electroosmotic flow both reduce the selectivity toward chloride ions, the selectivity toward chloride ions is always at a low level.
4. Conclusions
In summary, we have investigated the ionic transport of a sub-nm nanopore from the perspective of conductance using MD and experimental methods. The results show that the ion transport behavior through the sub-nm nanopores (L ≈ R) on the film is different from that in the nanochannel (L ≫ R), and is even more different from the bulk behavior. Under the action of surface charge, the average ion concentration inside the nanopore is much higher than the bulk value. It is found that 100 mM is the transition-point between the surface-charge-governed and the bulk behavior regimes. Moreover, it is found that the conductive properties of the nanopore at low bulk concentration are determined by the surface charge potential leaks into the reservoir, based on investigation of the access, pores, surface charge, electroosmosis and potential leakage conductance. The results also exhibited up to a four-fold increase in proton mobility in HCl solution, and we concluded that this result is caused by the extremely high electric field strength accelerating the rearrangement rate of the water molecules. At the same time, in NaCl solution, there is a huge increase in Na+ mobility due to the Wien effect. The nanopores also showed a strong selectivity toward Na+ and a strong repellence for Cl− due to the effect of surface charge and electroosmosis. These conclusions may help to provide a new understanding of the design of nanofluidic devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful for the financial support from Chongqing Education Commission (Grants No. yjg182037, KJQN201801204), Chongqing Science and Technology Bureau (Grants No. cstc2017jcyjA1543) and Chongqing Engineering Technology Research Center for Light Alloy and Processing (Grants No. GCZX201702).References
- Y. Kang, Z. Zhang, H. Shi, J. Zhang, L. Liang, Q. Wang, H. Agren and Y. Tu, Nanoscale, 2014, 6(18), 10666–10672 RSC
.
- T. Yang, Q. Liu, B. Kloss, R. Bruni, R. C. Kalathur, Y. Guo, E. Kloppmann, B. Rost, H. M. Colecraft and W. A. Hendrickson, Science, 2014, 346(6207), 355–359 CrossRef CAS PubMed
.
- Y. F. Chen, Z. H. Ni, G. M. Wang, D. Y. Xu and D. Y. Li, Nano Lett., 2008, 8(1), 42–48 CrossRef CAS
.
- L. Cao, Q. Wen, Y. Feng, D. Ji, H. Li, N. Li, L. Jiang and W. Guo, Adv. Funct. Mater., 2018, 28(39), 1–8 CrossRef
.
- K. Gopinadhan, S. Hu, A. Esfandiar, M. Lozada-Hidalgo, F. C. Wang, Q. Yang, A. V. Tyurnina, A. Keerthi, B. Radha and A. K. Geim, Science, 2019, 363(6423), 145–148 CrossRef CAS PubMed
.
- S. Sahu and M. Zwolak, Phys. Chem. Chem. Phys., 2018, 20(7), 4646–4651 RSC
.
- T. Mouterde, A. Keerthi, A. R. Poggioli, S. A. Dar, A. Siria, A. K. Geim, L. Bocquet and B. Radha, Nature, 2019, 567(7746), 87–90 CrossRef CAS PubMed
.
- Z. Zhang, L. Wen and L. Jiang, Chem. Soc. Rev., 2018, 47, 322–356 RSC
.
- G. Amy, N. Ghaffour, Z. Li, L. Francis, R. V. Linares, T. Missimer and S. Lattemann, Desalination, 2017, 401, 16–21 CrossRef CAS
.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7(11), 845–854 CrossRef CAS PubMed
.
- W. Guo, Y. Tian and L. Jiang, Acc. Chem. Res., 2013, 46(12), 2834–2846 CrossRef CAS PubMed
.
- C. Duan and A. Majumdar, Nat. Nanotechnol., 2010, 5(12), 848 CrossRef CAS PubMed
.
- A. Gupta, P. J. Zuk and H. A. Stone, Phys. Rev. Lett., 2020, 125(7), 076001 CrossRef CAS PubMed
.
- A. Davoodabadi, M. Nazari, D. Huang, T. Luo and H. Ghasemi, ACS Nano, 2020, 14(12), 16348–16391 CrossRef PubMed
.
- J. D. Sherwood, M. Mao and S. Ghosal, Langmuir, 2014, 30(31), 9261–9272 CrossRef CAS PubMed
.
- Z. X. Luo, Y. Z. Xing, Y. C. Ling, A. Kleinhammes and Y. Wu, Nat. Commun., 2015, 6, 6358 CrossRef CAS PubMed
.
- W. Chen, Q. Zhang, Y. Qian, W. Xin and L. Wen, ACS Cent. Sci., 2020, 6(11), 2097–2104 CrossRef CAS PubMed
.
- E. Secchi, A. Niguès, L. Jubin, A. Siria and L. Bocquet, Phys. Rev. Lett., 2015, 116(15), 154501 CrossRef PubMed
.
- B. M. Venkatesan, D. Estrada, S. Banerjee, X. Jin, V. E. Dorgan, M. H. Bae, N. R. Aluru, E. Pop and R. Bashir, ACS Nano, 2012, 6(1), 441–450 CrossRef CAS PubMed
.
- Z. Siwy and A. Fulinski, AIP Conf. Proc., 2003, 665(1), 273 CrossRef CAS
.
- D. C. Martins, V. Chu and J. P. Conde, Biomicrofluidics, 2013, 7(3), 47 CrossRef PubMed
.
- W. Nonner, D. P. Chen and B. Eisenberg, J. Gen. Physiol., 1999, 113(6), 773–782 CrossRef CAS PubMed
.
- M. Queralt-Martín, M. López, M. Aguilella-Arzo, V. M. Aguilella and A. Alcaraz, Nano Lett., 2018, 18(10), 6604–6610 CrossRef PubMed
.
- Y. C. Yao, A. Taqieddin, M. A. Alibakhshi, M. Wanunu and A. Noy, ACS Nano, 2019, 13(11), 12851–12859 CrossRef CAS PubMed
.
- G. Hu, M. Mao and S. Ghosal, Nanotechnology, 2012, 23, 395501 CrossRef PubMed
.
- M. E. Suk and N. R. Aluru, J. Chem. Phys., 2014, 140, 084707 CrossRef PubMed
.
- T. A. Beu, J. Chem. Phys., 2010, 132(16), 56 CrossRef PubMed
.
- T. A. Pascal, W. A. Goddard and Y. Jung, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(29), 11794–11798 CrossRef CAS PubMed
.
- L. Meng, Q. Li and Z. Shuai, J. Chem. Phys., 2008, 128(13), 56 CrossRef PubMed
.
- L. Binquan, Nanotechnology, 2015, 26(5), 055502 CrossRef PubMed
.
- Y. Noh and N. R. R. Aluru, ACS Nano, 2020, 14, 10518–10526 CrossRef CAS PubMed
.
- d. H. Van, H. J. Frank, D. Stein and C. Dekker, Phys. Rev. Lett., 2005, 95(11), 116104 CrossRef PubMed
.
- R. M. M. Smeets, U. F. Keyser, D. Krapf, M. Y. Wu, N. H. Dekker and C. Dekker, Nano Lett., 2006, 6(1), 89–95 CrossRef CAS PubMed
.
- J. N. Israelachvili and B. Chu, J. Colloid Interface Sci., 1987, 116(1), 77 Search PubMed
.
- R. Fan, S. Huh, R. Yan, J. Arnold and P. Yang, Nat. Mater., 2008, 7(4), 303–307 CrossRef CAS PubMed
.
- M. Tsutsui, Y. He, M. Furuhashi, S. Rahong, M. Taniguchi and T. Kawai, Sci. Rep., 2012, 2, 394 CrossRef PubMed
.
- S. Garaj, W. Hubbard, A. Reina, J. Kong, D. Branton and J. A. Golovchenko, Nature, 2010, 467(7312), 190–193 CrossRef CAS PubMed
.
- C. Hyun, R. Rollings and J. Li, Small, 2012, 8(3), 385–392 CrossRef CAS PubMed
.
- S. Sahu and M. P. Zwolak, Biophys. J., 2018, 114(3), 493a CrossRef
.
- A. Alcaraz, M. Lidón López, M. Queralt-Martí and V. M. Aguilell, ACS Nano, 2017, 11(10), 10392–10400 CrossRef CAS PubMed
.
- J. E. Hall, J. Gen. Physiol., 1975, 66(4), 531–532 CrossRef CAS PubMed
.
- M. E. Suk and N. R. Aluru, J. Chem. Phys., 2014, 140(8), 1–7 CrossRef PubMed
.
- S. Chaudhury, A. Bhattacharyya and A. Goswami, Ind. Eng. Chem. Res., 2014, 53(21), 8804–8809 CrossRef CAS
.
- A. Gupta, S. Shim, L. Issah, C. Mckenzie and H. A. Stone, Soft Matter, 2019, 15(48), 9965–9973 RSC
.
- S. M. H. Hashemi Amrei, S. C. Bukosky, S. P. Rader, W. D. Ristenpart and G. H. Miller, Phys. Rev. Lett., 2018, 121(18), 1–6 CrossRef PubMed
.
- D. E. Jiang, Z. Jin and J. Wu, Nano Lett., 2011, 11(12), 5373–5377 CrossRef CAS PubMed
.
- S. Derek, Phys. Rev. Lett., 2004, 93, 035901 CrossRef PubMed
.
- A. Siria, P. Poncharal, A. L. Biance, R. Fulcrand, X. Blase, S. T. Purcell and L. Bocquet, Nature, 2013, 494, 455–458 CrossRef CAS PubMed
.
- B. Radha, A. Esfandiar, F. C. Wang, A. P. Rooney, K. Gopinadhan, A. Keerthi, A. Mishchenko, A. Janardanan, P. Blake and L. Fumagalli, Nature, 2016, 538, 222–225 CrossRef CAS PubMed
.
- M. M. Collinson, J. Am. Chem. Soc., 1999, 121(36), 8413 CrossRef CAS
.
- L.-H. Yeh, C. Hughes, Z. Zeng and S. Qian, Anal. Chem., 2014, 86(5), 2681–2686 CrossRef CAS PubMed
.
- M. Thomas, B. Corry and T. A. Hilder, Small, 2014, 10(8), 1453–1465 CrossRef CAS PubMed
.
- T. Dudev and C. Lim, Sci. Rep., 2015, 5, 7864 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra01089a |
| This journal is © The Royal Society of Chemistry 2021 |