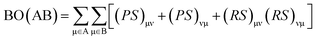Open Access Article
Open Access ArticleWhether planar or corrugated graphitic carbon nitride combined with titanium dioxide exhibits better photocatalytic performance?
Nguyen Thi Thu Ha a,
Pham Thi Beab,
Phung Thi Lana,
Nguyen Thi Moa,
Le Minh Cama and
Nguyen Ngoc Ha*a
a,
Pham Thi Beab,
Phung Thi Lana,
Nguyen Thi Moa,
Le Minh Cama and
Nguyen Ngoc Ha*a
aFaculty of Chemistry, Hanoi National University of Education, 136 Xuan Thuy Str., Hanoi, Vietnam. E-mail: hann@hnue.edu.vn
bFaculty of Natural Science and Technology, Taynguyen University, Daklak, Vietnam
First published on 5th May 2021
Abstract
The density functional theory method was performed to study the electronic structures of planar (pGN), corrugated (cGN) graphitic carbon nitride and their interactions with titanium dioxide cluster (TiO2)7. The transfer of photoinduced electrons was analyzed and electronic excitations were calculated. The obtained results show that cGN is thermodynamically more stable than pGN. cGN chemically interacts with titanium dioxide clusters, while the interaction between pGN and the cluster is assigned to physical nature. The combination of cGN and pGN with (TiO2)7 reduces the energy of the first excited states compared to that of the pure substances. The photocatalytic activities were estimated based on hypotheses on the location of the reduction and oxidation sites, the distance between the photoinduced holes and electrons and the electron density of molecular orbitals involved in the excitation. cGN/TiO2 is predicted to have a higher photocatalytic activity than pGN/TiO2.
Introduction
Graphitic carbon nitride (g-C3N4) is a relatively new type of carbon-based material that is being researched in the last few decades. g-C3N4 possesses many unique properties such as non-toxicity, high thermal and chemical stability, simplicity of fabrication techniques, moderate band gap, which make it a promising candidate in electronic, catalytic and energetic applications.1,2 In particular since Wang and his co-workers first discovered the photocatalytic H2 and O2 evolution by water splitting over g-C3N4 in 2009,3 g-C3N4 has gained tremendous attention as an organic semiconductor metal-free photocatalyst. Recently, g-C3N4 has been widely investigated for the photodegradation of organic pollutants,4–6 water splitting,7,8 CO2 conversion,9–11 etc. However, high electron–hole pair recombination rate and insufficient visible absorption are principal drawbacks of g-C3N4. Many efforts have been devoted to overcoming these two deficiencies by modifying the electronic band structure of g-C3N4 through methods such as metal ion doping,12 non-metal doping,13 noble metal-loading9,14 or creating heterojunction structures with other semiconductors.10,11,15,16 The latter has been shown to be an effective method for improving photocatalytic performance through better charge separation at the interface between two semiconductors since valence and conduction bands (VB and CB) of one semiconductor are located at higher energy levels compared to those of other coupling semiconductors. The popular semiconductor widely used for coupling with g-C3N4 is a traditional photocatalyst – titanium dioxide (TiO2). The combination of g-C3N4 and TiO2 (g-C3N4/TiO2) has shown to exhibit higher photocatalytic activity compared to that of pure materials in many reactions due to the efficient separation of the photogenerated electron–hole pairs.15,17–22 However, the inside mechanism of electron transfer in the g-C3N4/TiO2 combination and the interaction between components are still rarely discussed in the literature. Wang et al. studied TiO2–C3N4 hybrid microspheres21 and found that this hybrid material exhibited superior photocatalytic activity compared to TiO2–C3N4 composites prepared by traditional physical mixing methods. In the FTIR spectrum of the hybrid material, some location shifts of C3N4 characteristic bands were observed, suggesting the presence of chemical interaction or a synergistic effect between TiO2 and C3N4. Fagan et al. studied photocatalytic properties of g-C3N4/TiO2 heterojunctions22 and reported a substantial up-field shift in Raman spectra upon the addition of g-C3N4 to TiO2, indicating the formation of new bonds or bond modifications. Therefore, the authors suggested that g-C3N4 was probably incorporated into the TiO2 system rather than existing as a component of the mixture of the two.19The structural and optical properties of the g-C3N4/TiO2 system have also been intensively investigated in various theoretical studies.15,19,20,23,24 Lin et al. studied the electronic and optical properties of g-C3N4/TiO2(101) heterostructure using spin-polarized DFT+U calculations.15 Based on the calculated equilibrium distance between g-C3N4 and anatase TiO2(101) (1.94 Å) and the binding energy (24 meV Å−2), the g-C3N4/TiO2(101) composite material was assigned to the van der Waals heterostructure. The authors also noticed that the electrons can migrate from the g-C3N4 monolayer to anatase TiO2 (101) surface, which leads to oxidation and redox reactions occurring on g-C3N4 and TiO2, respectively. A similar charge transfer was reported in the work of Liu et al.20 The interaction between TiO2 and g-C3N4 results in the formation of a built-in electric field at the interface, which encourages the separation of electron–hole pairs.15,19,20 Gao et al. suggested that electron transition from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO) promoted the separation of electrons and holes.19
Obviously, the interaction between TiO2 and g-C3N4 plays a crucial role in the photocatalytic performance of the combined material. It is also has been reported in various studies that the structure of the material, including deficient structures of g-C3N4, significantly influences its catalytic activity.25–28 Lei et al. studied a TiO2/g-C3N4 composite photocatalyst with an inverse opal structure and heterojunction28 and showed that the inverse opal TiO2/g-C3N4 degraded Rhodamine B 2.7 times faster than the normal TiO2/g-C3N4, owing to the interaction between inverse opal g-C3N4 and TiO2 creating more interfaces for the efficient transfer of photogenerated electron–hole pairs.29 Ren et al. studied stabilities, electronic properties, and nitrogen reduction activity of planar and corrugated conformations of g-C3N4 (ref. 25) and showed the distortion conformation could activate more n → π* transitions of g-C3N4, promoting separation efficiency of photoinduced carriers in g-C3N4. The stability of the corrugated geometry of g-C3N4 compared to the planar geometry was highlighted in several theoretical studies. The corrugation was proved to minimize the electronic repulsion experienced by the N lone pairs located in their structural holes.29,30 It was suggested that the corrugation enhances the catalytic performance of g-C3N4 for the selective production of CO/CH3OH.30
In this work, we investigate the interaction between the planar and corrugated g-C3N4 with titanium dioxide cluster and clarify the mechanism of the transfer of photogenerated electrons using a combination of different theoretical methods.
Models and computational methods
In both, constructed corrugated and planar models, the peripheral atoms were saturated by hydrogen atoms. cGN and pGN consist of 200 atoms and have a molecular formula of C75N100H20.
Titanium dioxide cluster (TiO2)7 was chosen due to the comparable stability among small (TiO2)n clusters (n = 1–9) in terms of cluster formation energy per TiO2 unit.32 The initial geometry of the (TiO2)7 cluster was created from the anatase structure of the bulk.
UV-Vis spectra were calculated using time-dependent-density functional theory (TD-DFT) at CAM-B3LYP/6-31G(d,p) level of theory. This method is implemented in the ORCA code.36,37 The energy threshold up to which configuration state functions (CSFs) included is 8 eV.
Results and discussions
Electronic structures of cGN, pGN and (TiO2)7
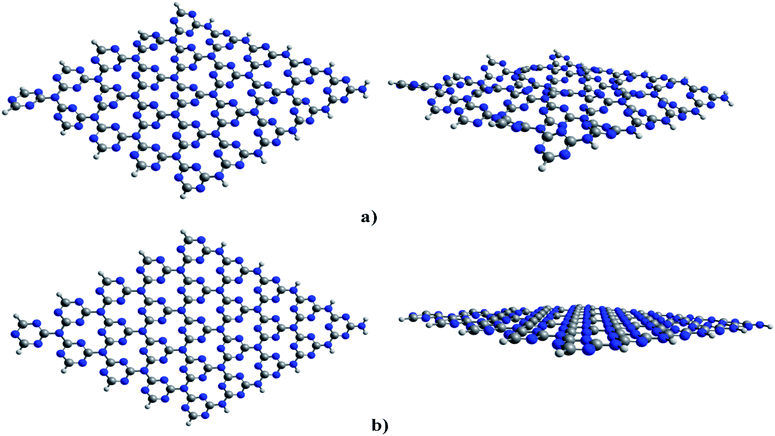 | ||
| Fig. 1 Optimized structures of cGN (a) and pGN (b); colours: grey-carbon, blue-nitrogen; key distances are in Å. | ||
The calculated results show that cGN has an energy of 9.2 eV, lower than that of pGN. In other words, cGN is more stable than pGN in terms of the formation energy. The corrugation in the structure of cGN is attributed to the strong repulsion between nitrogen atoms, which are in the sp2 hybridization state and contain valence electron pairs in the xOy plane.30 This finding is consistent with previous studies.29,30
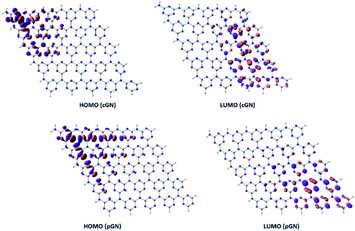
Analysis of HOMO and LUMO provides useful information about the photogenerated electrons. Fig. 2 illustrates HOMO and LUMO of cGN and pGN. Notably, the multiplicity of both cGN and pGN is 1, implying that the systems do not have unpaired electrons.
The distribution of HOMO and LUMO of cGN and pGN is very similar. In cGN, as well as in pGN, HOMO is mainly located on the nitrogen atoms in the triazine heterocycles (denoted as N1 atoms), while the three-coordinated (linked) nitrogen atoms (denoted as N2 atoms) almost do not contribute to HOMO. The LUMO is primarily supported by N1 and carbon atoms in the heterocycles. It is noted that LUMO is perpendicular to the molecular plane.
When a molecule absorbs light with appropriate energy, electrons can be excited from the occupied molecular orbitals (H) to the unoccupied molecular orbitals (L) to form photogenerated holes (h+) and electrons (e*), as illustrated in the following scheme:
| H − e → h+ | (1a) |
| L + e → e* | (1b) |
The h+–e* pair will play the critical role of an oxidant and a reductant in photocatalysis reactions.
An effective photocatalyst is a material that satisfies the following two requirements: (i) the recombination rate of h+ and e* is low and (ii) h+ and e* can be generated under visible light irradiation.
Starting from the first requirement, we propose three hypotheses for the explanation of an effective separation of h+ and e*:
(i-a): The reduction and oxidation sites are located separately to facilitate photocatalytic reactions,
(i-b): The greater the distance between h+ and e* is, the more efficient the separation is,
(i-c): The electron density of H (where h+ is formed) as well as L (where e* is generated) in narrow space results in high densities of h+ and e*, which would be more effective for the electron transfer process.
The HOMO and LUMO of the cGN system (Fig. 2) are located in different spatial areas and spread across many atoms. As a result, the photogenerated electrons and holes are far apart from each other, leading to their efficient separation and slow recombination. A similar picture is observed for the pGN system. These specific structural features along with the moderate band gap properly contribute to the photocatalytic activity of g-C3N4.
To study the nature of the excitation of g-C3N4, TD-DFT calculations were performed. The results are summarized in Table 1. Fig. 3 and 4 illustrate molecular orbitals involved in the first excitation of cGN and pGN. The excitation energy of the first excited state was used instead of the bandgap to evaluate the photocatalytic activity. In principle, a photocatalytic process is initiated with the photon absorption of the photocatalyst to generate the first excited state. The calculation results show that cGN has 2070 roots (excitations) and pGN has 2190 roots. The excitation energies of the first excited states of gCN and pCN were determined to be 4.185 eV and 3.769 eV, respectively. It is also noted that the theoretical band gap is strongly dependent on the model size due to the quantum confinement effect.38,39 Hence, using the energy of the first excited state is meaningful for the same size of the g-C3N4 model used.
| Excitation energy, eV | Oscillator strength f × 104 | The amplitude of MO transition | |||
|---|---|---|---|---|---|
| cGN | 4.185 | 9.93 | 0.07 (HOMO−4 → LUMO) | 0.06 (HOMO−4 → LUMO+3) | 0.06 (HOMO−1 → LUMO+1) |
| pGN | 3.769 | 7.07 | 0.11 (HOMO−1 → LUMO+12) | 0.08 (HOMO → LUMO+22) | 0.06 (HOMO → LUMO+15) |
 | ||
| Fig. 3 Molecular orbitals involved in the first excitation of cGN depicted at an isovalue of 0.03 e Å−3. | ||
 | ||
| Fig. 4 Molecular orbitals involved in the first excitation of pGN depicted at an isovalue of 0.03 e Å−3. | ||
H and L involved in the first excitation of cGN are distributed in a narrower space than those of pGN. Although the excitation energy of the first excited state of cGN is slightly larger than that of pGN, according to the above-proposed hypothesis (i-c), cGN form is predicted to have higher photocatalytic activities than the pGN form. This finding is consistent with the previous studies.25,30
To estimate the photoexcitation probability, fractional occupation density (FOD) was calculated and analyzed. The FOD analysis provides meaningful information about the static correlated electrons, viz. active electrons in a molecule.40,41 The fractional occupation number weighted electron density (ρFOD) at r position is defined as:
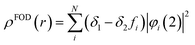 | (2) |
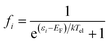 | (3) |
The larger the FOD of an atom is, the more active is the atom considered. From the results of FOD calculations for cGN at Tel = 12500 K, it can be seen that the nitrogen and carbon atoms in the triazine heterocycles are more active with FOD equal to 0.32 and 0.20 e per bohr3, respectively. Meanwhile, the linked three coordinated nitrogen atoms outside the ring have a FOD value of only about 0.10 e per bohr3. These results are consistent with the above-discussed contribution of atoms of g-C3N4 into HOMOs and LUMOs. Thus, photoinduced electrons are likely to come from N and C atoms in the heterocycles.
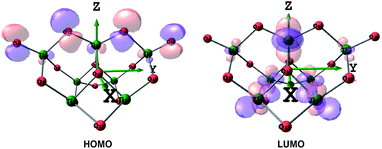 | ||
| Fig. 5 HOMO and LUMO of the (TiO2)7 cluster depicted at an isovalue of 0.05 e Å−3, colours: red-oxygen, green-titanium. | ||
Thus, when TiO2 absorbs photons, electrons will transfer from O atoms contributing to HOMO to Ti atoms, contributing to LUMO. It is noted that in the Frontier HOMO and LUMO of the TiO2 cluster, contributions of O atoms at different positions to HOMO (and similarly for Ti atoms to LUMO) are different, which is attributed to the different mobility of the atoms.
The excitation energy of the first excited state of (TiO2)7 is 4.738 eV. The calculation results for the first excited state of (TiO2)7 are tabulated in Table 2.
| Excitation energy (eV) | Oscillator strength f × 104 | The amplitude of MO transition | |||
|---|---|---|---|---|---|
| (TiO2)7 | 4.738 | 7.67 | 0.88 (HOMO → LUMO) | 0.03 (HOMO → LUMO+12) | 0.03 (HOMO → LUMO+3) |
Thus, for the (TiO2)7 cluster, the transition from HOMO to LUMO primarily contributes to the first excitation. Unlike g-C3N4, TiO2 is typically considered chemically inert, i.e., it does not react with other substances and is, therefore, a stable substance that can be used in many different industries and in a variety of applications. This is an important property contributing to the broad practical application of TiO2. However, the drawback of using anatase in photocatalytic applications lies in its large bandgap. Therefore, the combination of TiO2 with g-C3N4 is expected to decrease the band gap compared to that in pure substances.
Combination of g-C3N4 and TiO2
The interaction between cGN and pGN with (TiO2)7 cluster is characterized by the interaction energy (ΔintE), which is defined as follows:
| ΔintE = E(gC3N4/TiO2) − E(gC3N4) − E(TiO2) |
The interaction energy determined for cGN/TiO2 and pGN/TiO2 was −355.9 kJ mol−1 and −185.0 kJ mol−1, respectively. Thus, the formation of g-C3N4/TiO2 systems is energetically favorable. To evaluate the nature of the interaction between g-C3N4 and TiO2 cluster, Mayer bond order (BO) was calculated and analyzed using the following definition:
The computed BO, distances between atoms (d) and Hirshfeld net atomic charge (q) for cGN/TiO2 and pGN/TiO2 are presented in Table 3.
| Parameters | cGN/TiO2 | pGN/TiO2 |
|---|---|---|
| BO | BO(Ti1–N) = 0.386 | BO(Ti–N) = 0.015–0.071 |
| BO(Ti2–N) = 0.384 | BO*(Ti–N) = 0.183 | |
| BO(Ti3–N) = 0.362 | ||
| d, Å | d(Ti1–N) = 2.235 | d(Ti–N) = 3.200 |
| d(Ti1–N) = 2.243 | ||
| d(Ti1–N) = 2.327 | ||
| q(TiO2)7, e | −1.019 | −0.741 |
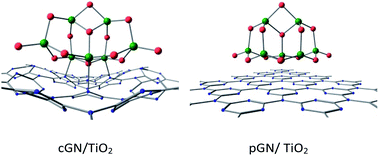
It can be seen that, for the cGN/TiO2 combination, the distances between Ti and N atoms are slightly larger than the sum of the atomic radius of Ti and N (2.05 Å). This finding is consistent with the reasonable values of BO between Ti atoms and N atoms, which are smaller than 1. A significant charge transfer from cGN to (TiO2)7 is observed. Thus, the interaction between cGN and TiO2 clusters is considered to have a chemical nature.
For the pGN/TiO2 combination, the minimum distance between Ti atoms of the TiO2 cluster and N atoms of g-C3N4 was determined to be 3.2 Å, which is significantly larger than the sum of the atomic radii of Ti and N. The BO between Ti and N atoms is quite small and ranges from 0.015 to 0.071 and the total BO between Ti and N atoms is only 0.183. The charge transfer from pGN to (TiO2)7 is less than from cGN to (TiO2)7. Therefore, it can be suggested that the interaction between the TiO2 cluster and pGN is primarily governed by physical interactions. These findings are in good agreement with the work of Lin et al., who reported that the interaction between g-C3N4 and anatase TiO2 (101) is assigned to the van der Waals heterostructure.15 This can make the photocatalytic performance of pGN/TiO2 very different compared to that of the cGN/TiO2 combination.
| Excitation energy (eV) | Oscillator strength f × 104 | The amplitude of MO transition | ||||
|---|---|---|---|---|---|---|
| cGN/TiO2 | 3.712 | 7.67 | 0.34 (HOMO → LUMO+1) | 0.10 (HOMO−7 → LUMO+1) | 0.08 (HOMO−6 → LUMO+1) | |
| pGN/TiO2 | 2.206 | 2.25 | 0.16 (HOMO−5 → LUMO) | 0.15 (HOMO−3 → LUMO) | 0.11 (HOMO−2 → LUMO) | |
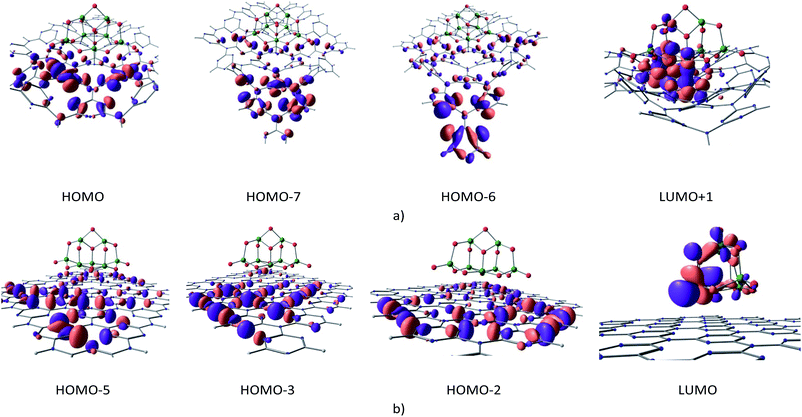 | ||
| Fig. 7 Molecular orbitals involved in the first excitation of cGN/TiO2 (a) and pGN/TiO2 (b) depicted at an isovalue of 0.03 e Å−3. | ||
The calculation results show that the first excitation of cGN/TiO2 is primarily determined by the transfer of photogenerated electrons from the HOMOs (HOMO, HOMO−7, HOMO−6), mainly located on g-C3N4 to the LUMO+1 orbital principally contributed from d orbitals of Ti and 2pz orbitals of N atoms. Electrons from cGN/TiO2 could be photogenerated by photons with an energy of 3.712 eV, which is much lower than the case of pure cGN and the TiO2 clusters. Moreover, HOMOs and LUMO+1 orbitals of cGN/TiO2 are distributed in different spatial areas. When photogenerated electrons are assigned to TiO2, their density is higher as compared to the distribution of these electrons on the large cGN surface and, thus, makes the electron transfer process more favorable.
The calculated HOMO and LUMO energy levels are −10.575 and −2.406 eV, and, −7.964 and −1.054 eV for the TiO2 cluster and cGN, respectively. There is an important issue that will be clarified: how do electrons transfer from g-C3N4 to TiO2 when photogenerated? If the interaction between g-C3N4 and TiO2 is just physical, electrons cannot migrate because both g-C3N4 and TiO2 are non-metal. If there is a strong chemical interaction, the electronic structure of each substance will be changed, leading to photocatalytic deactivity.
For the cGN/TiO2 system, the interaction between TiO2 and cGN is considered as a weak chemical interaction expressed through a small BO and the atomic distances and, thus, the LUMO+1 orbital of the cGN/TiO2 system contains both 2pz orbitals of N atoms and 3d orbitals of Ti atoms. Therefore, the electron transition in cGN/TiO2 can be described as follows: cGN, due to the lower energy of the first excited state as compared to TiO2, when photogenerated, electrons transfer from the hybrid orbitals containing electron pairs of the N atoms in HOMOs (H) to the 2pz orbitals of N atoms in (LUMO+1) orbitals. This transition is the same as described for g-C3N4 (Fig. 2), but the difference is that electrons transfer only to 2pz orbitals of N atoms bound to Ti atoms. Both the 2pz orbitals of N atoms and the 3d orbitals of Ti atoms are involved in the (LUMO+1) orbital, so in this case, the electron transition is almost instantaneous.
For the pGN/TiO2 system, the LUMO system consists of only orbitals of the TiO2 cluster. Because there is no chemical interaction between pGN and the TiO2 cluster, there is no electron transfer from pGN to TiO2. Thus, for the pGN/TiO2 system, although the energy of the first excited state is reduced, the photocatalytic efficiency of the combined system is not significantly improved compared to the pure substances.
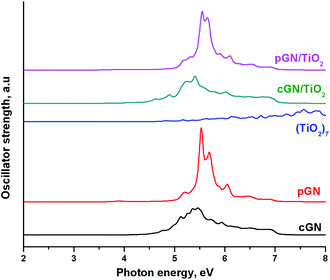
The calculated UV-Vis spectra for (TiO2)7, cGN, pGN compared with UV-Vis of cGN/TiO2 and pGN/TiO2 are illustrated in Fig. 8. The relative total peak areas (S) in the photon energy region of 2–5 eV for the studied systems are shown in Table 5.
| System | (TiO2)7 | cGN | pGN | cGN/TiO2 | pGN/TiO2 |
| S | 1.0 | 91.4 | 32.2 | 117 | 38.8 |
The UV-Vis of pGN/TiO2 is not different from the parent pGN, proving that there is no chemical interaction between (TiO2)7 and pGN. Meanwhile, the spectrum of cGN/TiO2 has a significant shift to the lower energy photon region. This is attributed to the above-mentioned interaction between (TiO2)7 and cGN. Besides, cGN/TiO2 exhibits a larger total peak area than that of the pure components and thus, more transitions are appearing in the photon energy region of 2–5 eV. The combination between TiO2 and cGN improved the light absorption ability of the component due to the synergistic effect. Concerning the idea of using corrugated and planar models of g-C3N4 that characterize the thickness of the material (see section Models), our calculation results confirm that exfoliated g-C3N4 nanosheets exhibit higher photocatalytic performance than bulk C3N4. These findings are in good agreement with the experimental study of Gao et al. on the enhancement of the photocatalytic activity of ZnO/g-C3N4 composites by regulating the stacked thickness of g-C3N4 nanosheets.45 Their results showed that ZnO/g-C3N4 with the middle thickness shows the highest photocatalytic performance.
Conclusions
The interactions between planar g-C3N4 (pGN) and corrugated g-C3N4 (cGN) with the (TiO2)7 cluster were investigated using the DFT method. The obtained findings show that the cGN chemically interacts with the titanium cluster, while the interaction between pGN and the cluster is assigned to physical nature. The combination of both cGN and pGN with (TiO2)7 reduces the energy of the first excited state. The photocatalytic activities were estimated based on hypotheses on the location of the reduction and oxidation sites, the distance between the photoinduced holes and electrons and the electron density of the molecular orbitals involved during excitation. cGN/TiO2 is predicted to have a higher photocatalytic activity than pGN/TiO2 due to the synergistic effect.Author contributions
Conceptualization: Nguyen Ngoc Ha; data curation: Nguyen Thi Thu Ha, Pham Thi Be, formal analysis: Nguyen Thi Thu Ha, Phung Thi Lan, Nguyen Thi Mo and Pham Thi Be, investigation: Nguyen Thi Thu Ha, Nguyen Ngoc Ha, Phung Thi Lan, Nguyen Thi Mo and Pham Thi Be; methodology: Nguyen Ngoc Ha, Le Minh Cam and Nguyen Thi Thu Ha; project administration: Nguyen Ngoc Ha; visualization: Phung Thi Lan, Nguyen Thi Mo and Pham Thi Be; writing – original draft: Nguyen Thi Thu Ha, Pham Thi Be, Phung Thi Lan and Nguyen Thi Mo; writing – review & editing: Nguyen Ngoc Ha and Le Minh Cam.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 05/2018/TN.Notes and references
- A. Wang, C. Wang, L. Fu, W. Wong-Ng and Y. Lan, Nano-Micro Lett., 2017, 9, 1–21 CrossRef PubMed.
- G. Dong, Y. Zhang, Q. Pan and J. Qiu, J. Photochem. Photobiol., C, 2014, 20, 33–50 CrossRef CAS.
- X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76–80 CrossRef CAS.
- Z. Chen, S. Zhang, Y. Liu, N. S. Alharbi, S. O. Rabah, S. Wang and X. Wang, Sci. Total Environ., 2020, 731, 139054 CrossRef CAS PubMed.
- Y. Wei, Q. Zou, P. Ye, M. Wang, X. Li and A. Xu, Chemosphere, 2018, 208, 358–365 CrossRef CAS PubMed.
- P. Wang, S. Sun, X. Zhang, X. Ge and W. Lü, RSC Adv., 2016, 6, 33589–33598 RSC.
- H. Ma, J. Feng, F. Jin, M. Wei, C. Liu and Y. Ma, Nanoscale, 2018, 10, 15624–15631 RSC.
- S. Ye, R. Wang, M. Z. Wu and Y. P. Yuan, in Applied Surface Science, Elsevier B.V., 2015, vol. 358, pp. 15–27 Search PubMed.
- W. J. Ong, L. L. Tan, S. P. Chai and S. T. Yong, Dalton Trans., 2014, 44, 1249–1257 RSC.
- Y. He, Y. Wang, L. Zhang, B. Teng and M. Fan, Appl. Catal., B, 2015, 168–169, 1–8 CAS.
- J. Wang, C. Qin, H. Wang, M. Chu, A. Zada, X. Zhang, J. Li, F. Raziq, Y. Qu and L. Jing, Appl. Catal., B, 2018, 221, 459–466 CrossRef CAS.
- S. Wojtyła, K. Śpiewak and T. Baran, J. Inorg. Organomet. Polym. Mater., 2020, 30, 3418–3428 CrossRef.
- W. Xing, G. Chen, C. Li, Z. Han, Y. Hu and Q. Meng, Nanoscale, 2018, 10, 5239–5245 RSC.
- X. B. Qian, W. Peng and J. H. Huang, Mater. Res. Bull., 2018, 102, 362–368 CrossRef CAS.
- Y. Lin, H. Shi, Z. Jiang, G. Wang, X. Zhang, H. Zhu, R. Zhang and C. Zhu, Int. J. Hydrogen Energy, 2017, 42, 9903–9913 CrossRef CAS.
- S. Adhikari and D. H. Kim, Appl. Surf. Sci., 2020, 511, 145595 CrossRef CAS.
- M. A. Alcudia-Ramos, M. O. Fuentez-Torres, F. Ortiz-Chi, C. G. Espinosa-González, N. Hernández-Como, D. S. García-Zaleta, M. K. Kesarla, J. G. Torres-Torres, V. Collins-Martínez and S. Godavarthi, Ceram. Int., 2020, 46, 38–45 CrossRef CAS.
- R. Acharya and K. Parida, J. Environ. Chem. Eng., 2020, 8, 103896 CrossRef CAS.
- H. Gao, J. Jia, F. Guo, B. Li, D. Dai, X. Deng, X. Liu, C. Si and G. Liu, J. Photochem. Photobiol., A, 2018, 364, 328–335 CrossRef CAS.
- J. Liu, B. Cheng and J. Yu, Phys. Chem. Chem. Phys., 2016, 18, 31175–31183 RSC.
- W. Wang, Y. Liu, J. Qu, Y. Chen, M. O. Tadé and Z. Shao, ChemPhotoChem, 2017, 1, 35–45 CrossRef CAS.
- R. Fagan, D. E. McCormack, S. J. Hinder and S. C. Pillai, Materials, 2016, 9, 286 CrossRef PubMed.
- B. Zhu, B. Cheng, L. Zhang and J. Yu, Carbon Energy, 2019, 1, 32–56 CrossRef CAS.
- H. Gao, B. Lu, D. Li, F. Guo, D. Dai, C. Si, G. Liu and X. Zhao, RSC Adv., 2016, 6, 65315–65321 RSC.
- C. Ren, Y. Zhang, Y. Li, Y. Zhang, S. Huang, W. Lin and K. Ding, J. Phys. Chem. C, 2019, 123, 17296–17305 CrossRef CAS.
- H. Gao, R. Cao, S. Zhang, H. Yang and X. Xu, ACS Appl. Mater. Interfaces, 2019, 11, 2050–2059 CrossRef CAS PubMed.
- A. Dandia, S. L. Gupta, P. Saini, R. Sharma, S. Meena and V. Parewa, Curr. Opin. Green Sustain. Chem., 2020, 3, 100039 CrossRef.
- J. Lei, B. Chen, W. Lv, L. Zhou, L. Wang, Y. Liu and J. Zhang, Dalton Trans., 2019, 48, 3486–3495 RSC.
- D. T. Vodak, K. Kim, L. Iordanidis, P. G. Rasmussen, A. J. Matzger and O. M. Yaghi, Chem.–Eur. J., 2003, 9, 4197–4201 CrossRef CAS PubMed.
- L. M. Azofra, D. R. MacFarlane and C. Sun, Phys. Chem. Chem. Phys., 2016, 18, 18507–18514 RSC.
- L. Zhang, Z. Jin, H. Lu, T. Lin, S. Ruan, X. S. Zhao and Y. J. Zeng, ACS Omega, 2018, 3, 15009–15017 CrossRef CAS PubMed.
- A. Zheng-wang Qu and G.-J. Kroes, J. Phys. Chem. B, 2006, 110(18), 8998–9007 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425–1428 CrossRef CAS.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- ORCA Forum – Portal, https://orcaforum.kofo.mpg.de/app.php/portal, accessed 13 February 2021.
- S. Furukawa and T. Miyasato, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 5726–5729 CrossRef CAS PubMed.
- J. Liu, Y. Nie, W. Xue, L. Wu, H. Jin, G. Jin, Z. Zhai and C. Fu, J. Mater. Res. Technol., 2020, 9, 8020–8028 CrossRef CAS.
- S. Grimme and A. Hansen, Angew. Chem., Int. Ed., 2015, 54, 12308–12313 CrossRef CAS PubMed.
- C. A. Bauer, A. Hansen and S. Grimme, Chem.–Eur. J., 2017, 23, 6150–6164 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- X. Gao, B. Yang, W. Yao, Y. Wang, R. Zong, J. Wang, X. Li, W. Jin and D. Tao, Environ. Pollut., 2020, 257, 113577 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2021 |