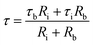Open Access Article
Open Access ArticleCrossover of positive and negative magnetoconductance in composites of nanosilica glass containing dual transition metal oxides†
Subha Samanta ab,
Anupam Maity
ab,
Anupam Maity ac,
Alorika Chatterjeeb,
Saurav Giri
ac,
Alorika Chatterjeeb,
Saurav Giri b and
Dipankar Chakravorty
b and
Dipankar Chakravorty *a
*a
aSchool of Materials Science, Indian Association for the Cultivation of Science, 2A and 2B Raja S.C. Mallick Road, Kolkata 700032, India. E-mail: mlsdc@iacs.res.in; Fax: +91 33 2473 2805; Tel: +91 33 2473 4971 (Ext 1580)
bSchool of Physical Science, Indian Association for the Cultivation of Science, 2A and 2B Raja S.C. Mallick Road, Kolkata 700032, India
cDepartment of Physics, Jadavpur University, 188 Raja S.C. Mallick Road, Kolkata 700032, India
First published on 30th April 2021
Abstract
A facile sol–gel approach to prepare composites of nanosilica glass containing dual transition metal oxides with compositions xCoO·(20 − x)NiO·80SiO2 comprising x values 5 (NC-1), 10 (NC-2) and 15 (NC-3) within hexagonal pores of SBA-15 template has been demonstrated. The synergistic effect of dual transition metal oxide ions on MD properties and crossover of positive and negative magnetoconductance phenomena were observed in these nanocomposite systems. The physical origin of magnetoconductance switching is explained based on the factors: nanoconfinement effect, wave-function shrinkage and spin polarized electron hopping. DFT calculations were performed to understand the structural correlation of the nanoconfined system. The static (dc) and dynamic (ac) responses of magnetization revealed the spin-glass behaviour of the investigated samples. Both scaling law and Vogel–Fulcher law provide a satisfactory fit to our experimental results which are considered as a salient feature of the spin-glass system. Our studies indicate the possibilities of fabricating magnetically controlled multifunctional devices.
1. Introduction
Multiferroic materials have attracted scientific and technological interest over the past few decades because of their multifunctional properties.1–7 The coupling between electric and magnetic field in multiferroic materials has been the cause of a myriad of technological revolutions in the development of magnetoelectronic devices. Researchers have developed multiferroic composites that allow co-existence of ferroelectric and ferromagnetic phases in nickel-zinc ferrite8 and barium titanate.9 Room temperature dielectric properties along with magnetodielectric (MD) and magnetoresistance (MR) effects have been reported in various systems.10–13 Magnetic-field induced electric and dielectric properties for double perovskite materials, usually La2MMnO6 (M = Co and Ni), were investigated because of their unique structural features.10,11 Transition metal oxides provide an interesting area of research because of their efficiency of structural evolution with different oxidation states and electronic configurations.14–16 Several investigations revealed the promising application of transition metal oxides in giant magnetoresistance17 and energy-storage devices.18The progressive demand for electronic component minimization has spurred the search of new-generation multiferroic materials with lower dimensionality in a more affordable manner. Nanostructured materials are an integral part of rapidly emerging field of nanoscience and nanotechnology.19–22 The enhanced surface-to-volume ratio in nanostructured materials impart an indelible interest and provide a platform to tailor novel functionalities which will aid in the development of future multifunctional devices. Much exploration has taken place in designing nanostructured materials for their potential applications in nanodevices.23 The unique features of nanostructured materials have emanated from the quantum effects at nanoscale.21,24,25 The generation of surfaces and interfaces with the reduced dimensionality play a pivotal role in imparting useful magnetic behaviour to the nanomaterials.21 Therefore, substantial research effort is on to synthesize transition metal oxide nanomaterials with the objective to achieve a high magnetodielectric effect.26 Magnetodielectric effect of CoFe2O4–BaTiO3 nanocomposite in the core–shell form was attributed to the presence of magnetostrictive and magnetoresistive behaviour associated with the Maxwell–Wagner effect.27 Magnetic studies of BaTiO3/ZnFe2O4 core/shell nanoparticles revealed that the strain/lattice mismatch near the interface of the core BaTiO3 and the shell ZnFe2O4 materials is responsible for the appearance of MD effect.28 In the presence of 1 T external magnetic field, a change in dielectric constant of 1.3% was obtained in this system at a frequency of 1 MHz. The nanoparticle size-dependent magneto–dielectric properties of Fe3O4/polymer composites were extensively investigated.29
In nanostructured materials magnetoresistance (MR) has a significant impact on the magneto–transport property which is governed by the response of electron in a suitably oriented magnetic field.30 Bismuth nanoparticles exhibited positive MR effect owing to their layer structure and finite-size effect.31 The magnetic field dependent variable range hopping (VRH) conduction process induces a positive MR effect in Fe3Se4 nanowires at temperatures below 100 K.22 Besides, the semiconducting 2H phase WTe2 nanosheets also achieved a high room-temperature positive magnetoresistance (16.2% at 300 K, 9 T).32 Several research findings revealed that MR can have negative values as well.26,33 In disordered systems, spin–orbit interaction plays influential role in governing the sign of MR.34–36 Interplay between magnetism and electrical properties was explored in BaTiO3–SrFe12O19 nanocomposites.37 Positive and negative MD effect depending on frequency and temperature was observed in these nanocomposites which may be attributed to the induced internal magnetic field and space charge/interfacial polarization respectively. The co-existence of positive and negative MD effect has been reported in the system of double perovskite Pr2CoMnO6.3 Substitution with Ni impurity leads to crossover of different regimes in FeSi.38 The correlation between MR sign with temperature and bias current was revealed in La0.7Ce0.3MnO3–SrTiO3–Nb heterojunctions.39 A crossover from negative to positive MR sign was observed in the junction with increasing temperature and bias current. Moreover, positive and negative magnetoresistance switching phenomena is evident in magnetic electrospun polyacrylonitrile-based carbon nanocomposite fibers and explained considering the influential impact of variable range hopping electron transportation model, electron quantum interference and spin-dependent scattering effects.40 Therefore, a great deal of effort is needed to achieve the desired functionality in nanosystems.
In this work, we have elucidated the synergistic effect of dual transition metal oxide ions in silica based nanoglass system and their influential impact on predicting the MR parameter. The obtained MD results are interpreted on the basis of Catalan's model. We explained the experimental probe through theoretical modelling using density function theory (DFT) simulation and represented the optimised geometric model of the investigated systems. In addition, we have explored the time-dependent density function theory (TDDFT) properties in these systems which agree well with the experimental results. The dc magnetization and ac susceptibility measurements were executed and analyzed further considering dynamic scaling law and Vogel–Fulcher law.
2. Experimental procedure
2.1. Materials
The starting materials were cobalt(II) nitrate hexahydrate (Co(NO3)2·6H2O), nickel(II) nitrate hexahydrate ((Ni(NO3)2·6H2O)). Tetraethyl orthosilicate (TEOS) was used as silica source and tri-block copolymer pluronic P-123 [HO(CH2CH2O)20(CH2CH(CH3)O)70(CH2CH2O)20H] was used as pore-directing agent to obtain mesoporous SBA-15 template. All the chemicals with purity 99.99% were supplied by Sigma Aldrich and used without further purification. A simple sol–gel approach was adopted for the synthesis of nanocomposites with uniform microstructures and high degree of dispersion between the template matrix and auxiliary phases. The investigated compositions of the nanocomposites were xCoO·(20 − x)NiO·80SiO2 comprising of x values 5 (NC-1), 10 (NC-2) and 15 (NC-3) respectively.2.2. Synthesis
The method for synthesizing surfactant–modified SBA-15 (Santa Barbara Amorphous-15) was similar to the method in the literature reported earlier.41 To fabricate the target composition xCoO·(20 − x)NiO·80SiO2, three different solutions were prepared by mixing ethanol with the calculated proportions of cobalt nitrate, nickel nitrate and TEOS and stirred separately for 1 hour at ambient temperature. All these solutions were mixed and then stirred vigorously at ambient temperature for 6 hours to obtain a homogenous sol.The typical pellet, having diameter ∼10 mm and thickness ∼0.8 mm, was obtained from SBA-15 powder after subjecting to a hydraulic press operated at a uniaxial pressure of 5 tons. Prior to the soaking process, the as–prepared pellets were heated at 450 K for 6 hours in an autoclave to remove the volatile layer at the surface and enhance the porosity of the template. The resulted pellets were soaked into the above-prepared sol and kept under static condition for another 19 hours to adhere the sol within the nanopores. Afterwards, pellets were removed from the sol followed by the cleaning process and heating at an elevated temperature (333 K) for 72 hours to execute the gelation process. The derived pellets were calcined in a furnace at 523 K for additional 150 min to obtain the final nanocomposite material.
2.3. Computational method
Density function theory (DFT) and time-dependent density functional theory (TDDFT) are reliable computational methods for unveiling transitions between electronic states based upon photo-properties of the systems. Electron density distribution, obtained through DFT and TDDFT calculations, play a fundamental role in governing the molecular properties of the system. Density function theory (DFT) calculation was performed for theoretical modelling of ground state level. Among various exchange correlation functional, Becke, 3-parameter, Lee–Yang–Parr (B3LYP)42,43 hybrid functional was used to evaluate associated energy values of the systems. Computational parameters were obtained using 6-31G** Gaussian Orbital as basis set and RIJCOSX as auxiliary basis function in the Orca v4.2 package.44 Avogadro v1.2 program45 were involved for the visualization of the entire structural units and to simulate the prior portions of the absorption UV-Vis spectra. The geometry of the system was optimized without any symmetry constraint delineating the absence of any imaginary frequency. Time-dependent density functional theory (TDDFT) was implemented to investigate the excited state energies and electronic transitions generating UV-Vis spectra of the systems.46 Empirical dispersion correction47 was implemented in search for intermolecular interaction within the system. During geometry optimization, no constrains upon symmetry, bonds, angles, or dihedral angles were imposed. The optimized geometry is used as the input for further calculations to obtain molecular orbitals. In Orca program, the better precision value through TDDFT approach47,48 was achieved by implementing resolution-of-identity technique RIJCOSX,49 where the chain of spheres (COSX) approximation for the Hartree–Fock exchange term is integrated with the Split-RI-J method for the Coulomb term.492.4. Characterizations
The X-ray diffraction (XRD) patterns were recorded on a Bruker XRD SWAX diffractometer with Cu Kα1 radiation (λ = 1.54056 Å) in the Bragg angles (2θ) ranging from 0.6–5° and 10–80° for small and wide angles, respectively at a step size of 0.02°.Textural properties of the samples were investigated by N2 adsorption–desorption analysis. For the analysis of the specific surface area of the materials, N2 adsorption and desorption isotherms at 77 K were obtained by means of the Brunauer–Emmet–Teller (BET) multipoint method50 within the relative pressure (P/P0) range between 0.05 and 0.3 using Autosorb-iQ, version 1.11 (Quantachrome Instruments). The total pore volume was evaluated from the adsorbed amount at a relative pressure ∼1. The pore size distribution curves were determined using the NLDFT model.51 The studied samples were outgassed at 473 K for 3 hours prior to testing.
The microstructural features of the samples were estimated from the field emission transmission electron microscopy (FEG-TEM) analysis using JEOL JEM 2100F microscope at an accelerating potential of 200 kV. Well-resolved TEM images were acquired with Gatan Orius SC200D (2k × 2k) diffraction camera in conjunction with high-resolution (Cs = 1.0 mm) pole piece. A Schottky FEG source and a JEOL SDD energy-dispersive X-ray detector helped to achieve the information of elemental composition by means of energy-dispersive spectrometry (EDS) measurements. A trace of sample powder was suspended in high-purity acetone solvent and vigorously sonicated at room temperature for 30 min to disperse the particles. Afterwards, a uniform thin film of sample was drop-casted on a carbon-coated copper grid and allowed to dry at 313 K thoroughly before imaging.
The characteristic X-ray photoelectron spectroscopy (XPS) data for each constituent element were taken at an Omicron nanotechnology spectrometer (serial no. 0571) equipped with a monochromatic Al Kα radiation (1486.6 eV) source for excitation under the operational voltage 15 kV and current 5 mA. The spectrometer was calibrated against the Ag 3d5/2 peak with a binding energy (BE) of 84.0 eV. The estimated errors in the measured values were found to be ±0.1 eV. C–C peak with BE at 284.8 eV is considered for charge correction reference. Prior to the measurement, the powdered oxide samples were carefully mounted on sample stub by means of a copper based adhesive tape followed by the placement in the preparative chamber of the instrument. No further sample treatment was used to avoid the problems of sample surface reduction. The experiment was carried out under the chamber pressure of ∼10−10 mbar. The obtained data were fitted and deconvoluted for searching peaks and identifying oxidation states utilizing PeakFit software (v4.12).
The chemical identity of bare template (SBA-15) and the nanocomposites were examined by Fourier transform infrared spectroscopy (FTIR, Shimadzu FTIR-8400S spectrometer). During data acquisition, the optimal alignment was stable and a consistent reproducible spectrum was ensured. The samples were mixed with KBr and the spectra were recorded in the wavenumber range between 400 and 4000 cm−1.
Perkin-Elmer Lambda 25 UV-Vis spectrometer was employed to study the optical characteristics of the investigated materials. The UV-Vis spectra were recorded using 1 cm quartz cuvettes over the wavelength range of 350–700 nm. In a typical measurement, the solutions were prepared by dispersing the powdered sample in distilled water (concentration of 500 μM) with sonication at room temperature for 30 min. UV WinLab ES software was used to identify the position and intensity of the peak maximum.
Magnetodielectric property measurements were carried out by placing the sample between the pole pieces of an electromagnet (supplied by M/S Control System & Devices, Mumbai, India). The dielectric parameter data were collected at different frequencies ranging between 20 Hz and 1 MHz using an Agilent E4980AL LCR meter operated at an AC signal with a 1 V amplitude. All measurements were carried out on the entire series of nanocomposites. The obtained results were consistent indicating reproducibility of data.
The dc and ac magnetization properties were studied in a commercial superconducting quantum interference device (SQUID) magnetometer (Quantum Design MPMS, evercool).
3. Results and discussions
3.1. Structural properties
XRD data were utilized to extract the information about the structural details of the studied samples. The small-angle XRD (SAXS) patterns for all the samples are illustrated in Fig. 1. For both filled (nanocomposite) and unfilled (SBA-15) template, a well-resolved pattern was obtained with a pronounced peak at 2θ = 1.1° attributed to (100) plane and two other peaks at 2θ = 1.62° and 1.8° associated with (110) and (200) planes, respectively.52 Based on the position of the diffraction peaks, the presence of ordered hexagonal porous structure with P6mm symmetry group is evident for all samples.53 The peak positions remain unaltered for both unfilled and filled template whereas a broadening of peak with reduced intensity is observed due to the incorporation of nanoglass phase. The above observations indeed suggest that the ordered hexagonal porous structure of sample is maintained throughout the experiments. To affirm the amorphous nature of the samples, they were further inspected under wide-angle XRD measurement and the obtained pattern is demonstrated in the inset of Fig. 1. The absence of any significant diffraction peak implies the existence of an amorphous (glassy) phase throughout the sample.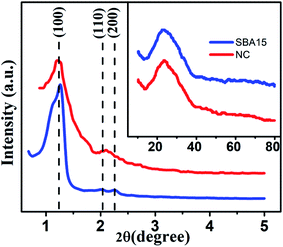 | ||
| Fig. 1 Typical small-angle X-ray scattering data of SBA-15 and NC. Inset shows the corresponding wide-angle X-ray diffraction pattern. | ||
To enable more precise visualisation of nanoconfinement effect, it is required to quantify the amount of nanoglass loading into the pores of SBA-15 template and is estimated from N2 adsorption–desorption analysis. Fig. 2 illustrates the typical N2 adsorption-desorption isotherm of both SBA-15 template and nanocomposite. From Fig. 2(a) it is clearly seen that SBA-15 template exhibited a typical type IV isotherm with H1 type hysteresis loop at high relative pressure whereas a modified suppressed isotherm exists for the nanocomposite sample as shown in Fig. 2(b). This results in a lower specific surface area (49.839 m2 g−1) for the nanocomposites compared to the SBA-15 template (770.442 m2 g−1). The corresponding pore size distribution curves are represented in the inset of Fig. 2(a) and (b) for SBA-15 and nanocomposite respectively. The pore size distribution curves show one distinct peak suggesting that pore size uniformity is maintained in the samples and the average pore diameter of ∼5 nm and 1.6 nm for SBA-15 and nanocomposite respectively was obtained by BJH method. Nevertheless, noticeably lower pore volume was obtained for nanocomposite compared to SBA-15 template which substantiates the incorporation of nanoglass within the nanochannels of SBA-15. From above observations it is estimated that the nanoglass phase takes part in filling ∼95% pores within the template. Table 1 summarizes mesopore parameters of all studied samples and the impact of incorporation of nanoglass phase on the BET specific surface areas and pore volumes.
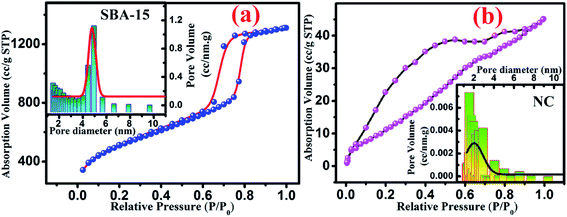 | ||
| Fig. 2 Typical nitrogen adsorption–desorption isotherm curve for (a) SBA-15 and (b) NC. Inset shows the pore size distribution of each sample where solid line represents the Gaussian fit. | ||
| Samples | Specific surface area (m2 g−1) | Average pore diameter (nm) | Pore volume (cm3 g−1) |
|---|---|---|---|
| SBA-15 | 770.44 | 4.94 | 1.497 |
| NC | 49.84 | 1.57 | 0.071 |
The typical TEM micrograph shown in Fig. 3 provides microstructural insight of the investigated samples. In the micrographs, the well-ordered nanochannel structure can be clearly observed for both SBA-15 and nanocomposite sample in Fig. 3(a) and (b) respectively. Owing to the weak contrast between silica-based nanoglass and silica frameworks of SBA-15, the imaging of nanoglass is not pronounced from TEM. Nevertheless, the incorporation of the nanoglass within the nanopores occludes the irradiation of electron beam and resulted in imaging of porous wall with greater thickness for the nanocomposite. The nanochannels within the framework of SBA-15 are shown in Fig. 3(a) during the beam direction perpendicular to the pore surface whereas the inset of Fig. 3(a) reveals the porous arrangement inherent in the SBA-15 considering the beam direction parallel to the pore direction. The corresponding selected area electron diffraction (SAED) pattern obtained from nanocomposite is illustrated in the inset of Fig. 3(b). The obtained pattern without any distinct spot substantiates the amorphous nature of the sample.
 | ||
| Fig. 3 Typical TEM images of (a) SBA-15 and (b) NC. Inset shows (a) magnified porous arrangement of SBA-15 and (b) SAED pattern of NC. | ||
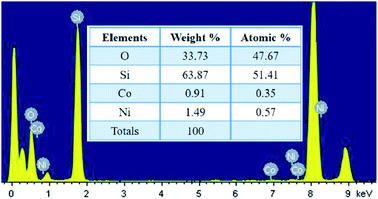
The localized elemental compositions for NC-2 were recognized by energy-dispersive X-ray analysis (EDAX) and the corresponding spectra is outlined in Fig. 4. Data acquisition was carried out from arbitrary areas and the obtained contribution ratios of the elements are analogous affirming well-distribution of each species throughout the sample.
The oxidation states of transition metal species incorporated within SBA-15 nanopores are considered as the influential component because it directly affects the magnetodielectric behaviour of the system. The existence of various oxidation states of cobalt and nickel species was analysed quantitatively by XPS measurement and the well-resolved spectra of such states are illustrated in Fig. 5. As shown in Fig. 5(a), (c) and (e), Co 2p spectra were fitted and thereby deconvolution resulted in two peaks at 780.3 eV and 781.9 eV associated with the two oxidation states of Co2+ and Co3+ respectively.26 Similarly, two deconvoluted Ni 2p spectra with peak centred at 854.6 eV and 855.8 eV were assigned to Ni2+ and Ni3+ respectively33 as revealed in Fig. 5(b), (d) and (f). Based on the degeneracy of each spin state, each peak possess a specific area which gives a measure of the contribution of each ionic species. The calculated areal proportion is tabulated in Table 2 which is utilized to properly identify the influential role of each constituents effecting the magnetodielectric properties.
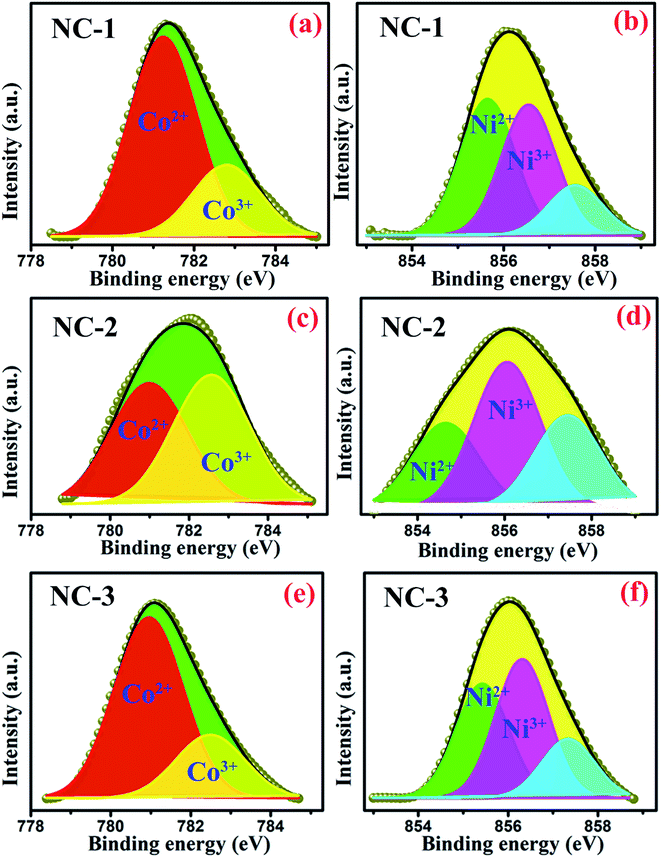 | ||
| Fig. 5 Deconvoluted XPS spectra of Co 2p3/2 for (a) NC-1, (c) NC-2, (e) NC-3 and Ni 2p3/2 for (b) NC-1, (d) NC-2, (f) NC-3. | ||
| Oxidation states | Peak position (eV) | % area | ||
|---|---|---|---|---|
| NC-1 | NC-2 | NC-3 | ||
| Ni2+ | 854.6 | 42.94 | 55 | 36.54 |
| Ni3+ | 855.7 | 41.27 | 45 | 44.55 |
| Co2+ | 780.3 | 73.63 | 49 | 74.07 |
| Co3+ | 781.9 | 26.37 | 50 | 25.93 |
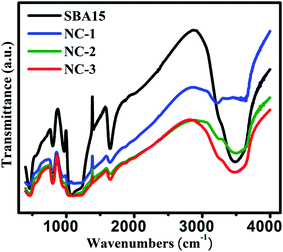
In order to extract the information on the vibrational properties of the chemical bonds of constituent species in SBA-15 template and nanocomposite samples, their FTIR spectra have been recorded under absorption of IR radiation and depicted in Fig. 6. Typical Si–O–Si symmetric and antisymmetric stretching vibrational modes are reflected by a bending band at 800 cm−1 and 1080 cm−1 respectively. A peak at 460 cm−1 was originated due to internal vibration between Si–O–Si tetrahedral structures of SBA-15. A peak at 1630 cm−1 corresponds to O–H stretching vibration mode whereas wide intense peak at 3500–3300 cm−1 represents the O–H bending vibration mode of the surface water molecules. The stretching vibration of silanol groups give rise to a peak at 960 cm−1 whose relative intensity gradually weakened for the nanocomposites compared to bare SBA-15 template. This could be attributed to the loading of the nanoglass within the nanochannels of the SBA-15 template. However, there was no alteration in original positions of those characteristic peaks suggesting invariable structural configuration of the samples.52,54–56
Optical properties of the prepared samples were investigated through UV-Vis spectroscopy within the wavelength range of 350–700 nm and the obtained absorption spectra are represented in Fig. 7. Due to the coexistence of cobalt and nickel ions, an intricate spectra have been observed in silicate nanoglasses containing dual transition ions. From Fig. 7, it is clearly seen that the absorption spectra consist of multiple absorption peaks within the UV-Visible region. The peaks positioned at 379 nm and 520 nm are assigned to Ni2+ and Ni3+ respectively57,58 whereas the peak appearing at 582 nm and 408 nm are arising due to the Co2+ and Co3+ species59 respectively.
This study is extended further to examine the electronic transitions corresponding to the obtained UV-Vis peaks using theoretical density function theory (DFT) simulations. Nanoconfinement have significant impact on all electronic transitions that rely on separating distance between silicon atom and transition metal ions. Therefore, calculations were performed to develop an optimized model considering energy minimization. A number of theoretical investigations have been carried out for amorphous SiO2, derived from TEOS.60–62 The DFT calculations were performed considering a self-consistent reaction field (SCRF) as the conductor-like polarizable continuum model (CPCM),63,64 where the interaction between the solute with the surrounding continuum dielectric medium was investigated considering point charge distribution and GEnerating POLyhedra (GEPOL) algorithm.62,64,65
Numerous investigations have implemented B3LYP functional and 6-31G* basis set in performing DFT simulations.66,67 To enhance the computational efficiency and precise understanding of the contribution coming from respective transition metal ions by DFT approach, a smaller size cluster approximation was considered.68 For this aspect, a structural unit was adopted comprising of silicon, oxygen, hydrogen atom and neighboring transition metal ions as shown in Fig. 7. Initially, the SiO2 structure was successfully generated followed by the interaction study between transition metal ion and SiO2 was obtained. During the geometry optimization, the self-consistent convergence of the total energy was about 1.0 × 10−8 eV per atom. The optimized SiO2 structure is shown in ESI Fig. S1.†
For the sake of completeness, we performed individual investigations on four different interactions among SiO2 and each constituent transition metal ion species (Ni2+, Ni3+, Co2+, Co3+) followed by analysing the corresponding energy transitions which generated absorption peak in UV-Vis spectra.
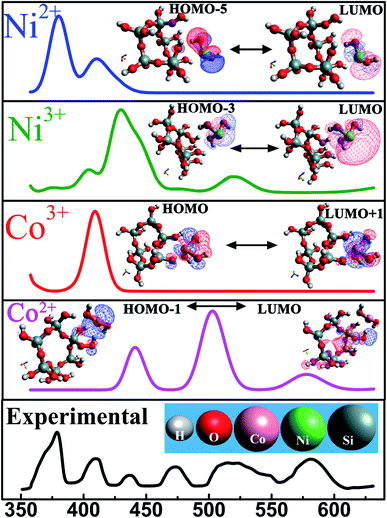
This calculation predicts that at equilibrium a transition metal ion is located at a close proximity (∼4 Å) of the silicon atom. The geometry optimized models were validated further by exclusion of any imaginary frequencies. This classical DFT approach deals with ground stationary state of the material. Electronic excited states, obtained from UV-Vis spectroscopy, were substantiated by time-dependent density functional theory (TD-DFT). TD-DFT formalism furnish an efficient pathway to evaluate the excitation energies. Transitions from highest occupied molecular orbital (HOMO) to lowest unoccupied molecular orbital (LUMO) give rise to each peak in absorption spectra and the energies corresponding to each transition are tabulated in table-3. The theoretically derived absorption spectra were in satisfactory agreement with the experimental values as demonstrated in Fig. 7. Inset reveals the possible HOMO ↔ LUMO transitions of these systems. Excited state geometry optimization reveals that an excited state charge transfer process occurs between the two neighbouring atoms which is shown in Fig. 7. In this figure, the positive and negative charge distributions are represented by the red and blue coloured iso-surfaces respectively. The electronic configuration of Co2+ and Co3+ are [Ar]3d7 and [Ar]3d6. Owing to their electronic configuration, Co3+ possesses more stable configuration than Co2+ resulting in higher excitation energy values.59 In similar fashion, Ni3+ requires lower excitation energy compared to Ni2+ which is clearly visible in Table 3. Therefore, it is entrenched with conjuncture of theoretical and experimental results that oxidation state of each transition metal ion governs the optical response of each material.
| Elements | UV peak position (nm) | Transitions | Excitation energy (eV) |
|---|---|---|---|
| Ni2+ | 378 | HOMO−5 → LUMO | 3.31 |
| Ni3+ | 520 | HOMO−3 → LUMO | 2.38 |
| Co2+ | 580 | HOMO → LUMO+1 | 2.26 |
| Co3+ | 409 | HOMO−1→ LUMO | 3.03 |
3.2. Magnetodielectric properties
Meanwhile, we focused on the impact of the re-orientation of ionic species at nanoscale regime in the presence of magnetic field as it is expected to alter the magnetodielectric (MD) behaviour of the materials. In this regard, investigations were performed on room temperature MD properties representing the magnetic field induced variation in dielectric permittivity. The MD parameter is determined from the following formula| MD = (εH′/ε0′ − 1) | (1) |
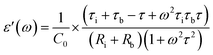 | (2) |
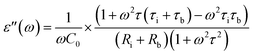 | (3) |
τb = CbRb; Cb corresponds to capacitance of SBA-15 template,
τi = CiRi; Ci corresponds to capacitance of nanoglass,
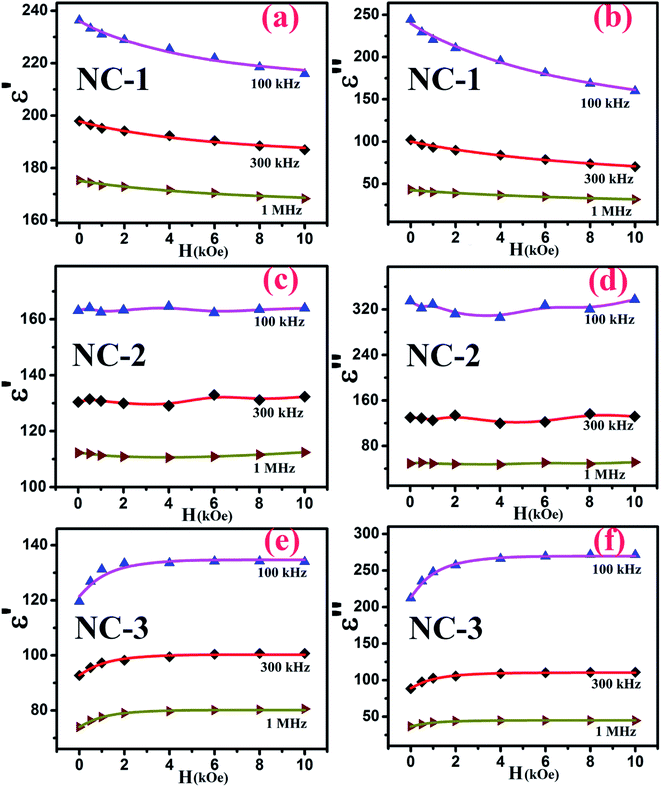
Accordingly, the plot revealing the variation of real (ε′) and imaginary (ε′′) part of magnetodielectric permittivity values as a function of applied magnetic field at various frequencies is shown in Fig. 8(a–f) for NC-1, NC-2 and NC-3 respectively. The solid line represents the theoretical fits to Catalan's model. The real part (ε′) signifies the degree of polarization whereas imaginary part (ε′′) corresponds to dielectric loss factor.
Fig. 9(a–c) displays the variation of dissipation factor as function of frequency at various magnetic field for NC-1, NC-2 and NC-3 respectively. In Fig. 9, the trend of magnetic field dependent peak shift and peak intensity variation is notable and reflects resistive origin.5 Magnetoresistance (MR) is the reciprocal of magnetoconductance.
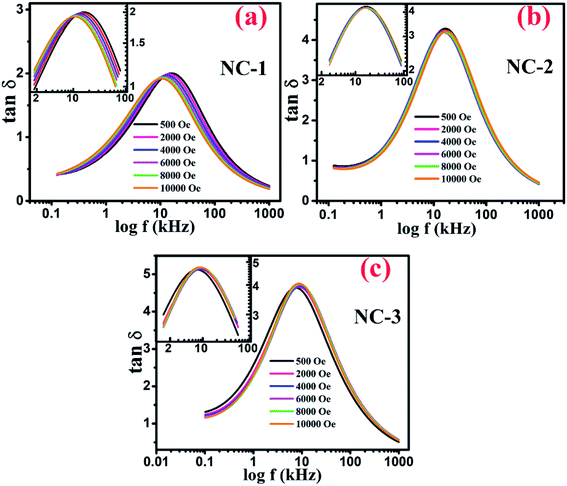 | ||
Fig. 9 Variation of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ as a function of frequency at various applied magnetic field for (a) NC-1, (b) NC-2, (c) NC-3. Inset shows the magnified view around the peak position. δ as a function of frequency at various applied magnetic field for (a) NC-1, (b) NC-2, (c) NC-3. Inset shows the magnified view around the peak position. | ||
In Fig. 10(a) (for NC-1), eqn (2) and (3) were used to fit the experimental data considering a positive MR in the nanoglass phase with the variation in magnetic field expressed as,
| RH = Ri − Rfexp(−H/Hs) | (4) |
On contrary, the experimental data for NC-3, as depicted in Fig. 10(b), exhibited an entirely new exchange coupling where the data were fitted accordingly to eqn (2) and (3) considering a negative MR in the nanoglass phase with the variation in magnetic field expressed as,
| RH = Ri + Rfexp(−H/Hs). | (5) |
The solid lines in Fig. 10(b) represent the theoretical fits. This negative MR can be attributed to the hopping of electrons between Co2+/Ni2+ and Co3+/Ni3+. This exchange becomes further easier with the application of magnetic field, therefore spin polarized electron hopping between the localized states is enhanced.26 This phenomenon is responsible for the presently observed large MD effect in NC-3.
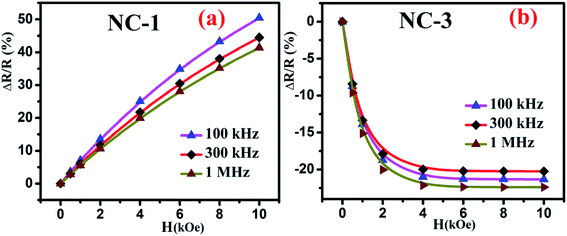
Fig. 10 shows the percentage change of magnetoresistance with applied magnetic field extracted by using eqn (5) for all the investigated nanocomposites. These theoretical results were in satisfactory agreement with the experimental data obtained by direct measurement of magnetoresistance of the specimen and is shown in Fig. 11. Table 4 delineates the magnetic field induced percentile change of MD and MR at various frequencies.
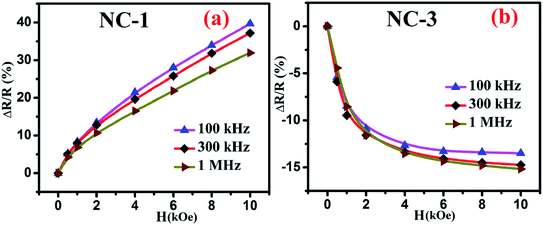 | ||
| Fig. 11 Magnetic field dependent variation of directly measured values of MR for (a) NC-1 and (b) NC-3. | ||
| Sample | Frequency (kHz) | MD% | MR% |
|---|---|---|---|
| NC-1 | 100 | 8 | +51 |
| 300 | 5 | +45 | |
| 1000 | 3 | +41 | |
| NC-2 | 100 | Negligible | Negligible |
| 300 | |||
| 1000 | |||
| NC-3 | 100 | 12 | −21 |
| 300 | 7 | −20 | |
| 1000 | 9 | −23 |
It is quite probable that for NC-2 with nanoglass composition having an equal proportion of CoO and NiO, the MD change as a function of magnetic field would be small. This has indeed been noticed for NC-2 as depicted in Fig. 8(c and d). The scatter nature of the data points imply that the dielectric permittivity change is not accountable and thereby no change in MR of the nanoglass.
In order to infer the MR contribution on to the MD properties of nanocomposites, impedance spectroscopy measurements were executed in absence and presence of magnetic field for NC-1 and NC-3 samples. Accordingly, the Nyquist plot of real (Z′) and imaginary (Z′′) part of impedance is shown in Fig. 12(a and b) for NC-1 and NC-3 respectively. The experimental data were fitted and analysed using equivalent circuit model consisting two R–C circuits connected in series as shown in inset of Fig. 12. The solid lines in Fig. 12 represent the theoretical fits. The circuit confers a cumulative effect of diffusion and kinetic process engenders polarization.
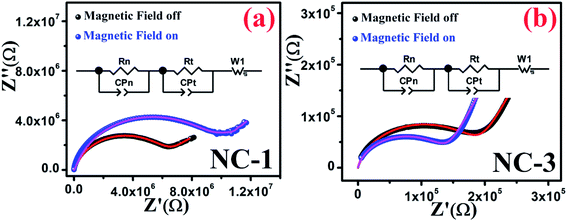 | ||
| Fig. 12 Nyquist plots in the presence and absence of magnetic field for (a) NC-1 and (b) NC-3. Inset shows the equivalent circuit diagram. | ||
In the circuit model, the contribution of nanoglass leads to the formation of resistance Rn and capacitance CPn whereas Rt and CPt are associated with the template contribution. Table 5 represents the contributions of the corresponding circuit components present in the sample. The value of Rt and CPt remain unaltered under the application of magnetic field due to the diamagnetic nature of SBA-15 template which indicates the absence of any extrinsic MD effect. With the application of magnetic field, the values of Rn increase for NC-1 and decrease for NC-3 which substantiates our findings related to Catalan's model with positive MR and negative MR respectively. In the higher frequency region, only nanoglass (grain) contribution is expected because of quenched hopping charge transport. In the low-frequency region, a Warburg impedance is used to describe the diffusion characteristics. Noteworthy, the detailed investigations revealed that MR effect emerges solely due to the contribution originated from nanoglass phase and an intrinsic MD effect was detected. On the account of MD and MR analysis, it is recognized that the extent of disorder and subsequent variation in the proportion of transition ions will have explicit influence on the magnetic properties.
| Sample | Magnetic field | Rn (MΩ) | CPn (μF) | Rt (MΩ) | CPt (μF) |
|---|---|---|---|---|---|
| NC-1 | Off | 5.5 | 0.10 | 8.0 | 100 |
| On | 8.5 | 0.15 | 8.0 | 100 | |
| NC-3 | Off | 0.18 | 1.35 | 8.0 | 100 |
| On | 0.13 | 1.15 | 8.0 | 100 |
3.3. DC magnetization
To extract fundamental information on the characteristic features of the magnetic state of these nanocomposites, the temperature dependence behaviour of magnetization [M(T)] were investigated by ZFC and FC measurements. During the ZFC measurements, the system was cooled down to a low temperature in the absence of magnetic field followed by magnetization data acquisition during gradual heating. On the other hand, in case of FC measurements cooling protocol was performed in the presence of magnetic field. Fig. 13(a) and (b) reveal the thermal response of ZFC and FC magnetization curves for NC-1 and NC-3 measured at 20 Oe magnetic field (H). The magnified view of the curves at low temperature region are depicted in the inset of the Fig. 13. The ZFC and FC curves separate from each other around 80 K and 60 K for NC-1 and NC-3 respectively and the bifurcation increases significantly with the reduction in temperature. The splitting of ZFC and FC curves at higher temperature (Tirr) is attributed to characteristic signature of disordered system.71 In the inset of Fig. 13, ZFC curve exhibited a pronounced peak at 7.04 K and 3.97 K for NC-1 and NC-3 respectively, which corresponds to the freezing temperature (Tg). Below Tirr temperature, the FC curve increases gradually upto 20 K followed by a sharp increase to the lowest measured temperature without any significant peak. The acute increasing tendency of FC magnetization below Tg is typical for cluster-spin-glass (CSG) arising due to the existence of finite range of inhomogeneous state around a quasi-critical temperature.71,72 Beyond Tirr temperature, there is no noticeable differences between ZFC and FC curves which may be assigned to the thermal excitation arising from paramagnetic nature of the sample.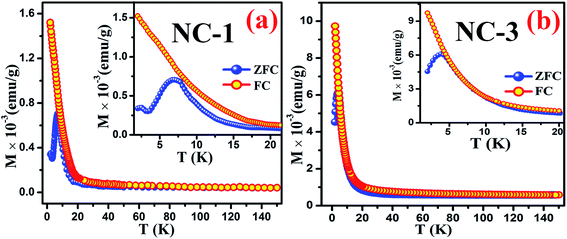 | ||
| Fig. 13 Thermal response of ZFC and FC magnetization curves for (a) NC-1 and (b) NC-3. Inset shows the magnified view of the curves at low temperature regime. | ||
To explore the magnetic behaviour at low temperature region, the variation of magnetization as a function of applied field (within the range between −50 kOe and +50 kOe) was measured at different temperatures for NC-1 and NC-3 which are illustrated in Fig. 14(a) and (b) respectively. From Fig. 14, the magnetic hysteresis (M–H) loop exhibit S-shaped structure suggesting typical CSG nature of our systems at low temperature domain.71 The enlarged view of M–H loops at low field region are highlighted in the insets of Fig. 14. The simultaneous presence of M–H loop at lower field domain as well as lack of magnetization saturation at higher field region account for the spin-glass behaviour.73,74
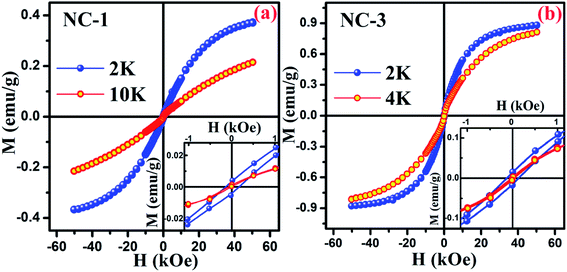 | ||
| Fig. 14 Magnetic hysteresis loop for (a) NC-1 and (b) NC-3. Inset shows the enlarged view of the curves at low field region. | ||
Magnetic relaxation along with memory effect in the dc magnetization are the essential tools used to analyse such CSG systems.75 The investigation on memory effect under ZFC protocol (ZFCM) manifests assured experimental validation of spin-glass behaviour.75 Under the strategy of ZFCM, the system is cooled down from reference temperature Tr = 16 K (Tr ≫ Tg) to measurement temperature Tm = 4 K at 1 K min−1 rate without any field followed by system relaxing in zero-magnetic field for 7670 s (tw) and subsequently cooled down to the lowest measurement temperature of 2 K. After attaining steady state at 2 K, system is gradually heated up to Tr = 16 K at a certain rate in 20 Oe field along with magnetization data acquisition. The brief schematic of the protocol is shown in the inset of Fig. 15(b). The ZFCM and ZFC curves for NC-3 are represented in the Fig. 15(a). The thermoremanent magnetization is defined as the difference between the pairs of ZFCM and ZFC curves and is expressed as, ΔM = MZFCM ∼ MZFC. In the Fig. 15(b), the temperature dependent ΔM plot for NC-3 displays a pronounced ‘dip’ at 4 K, which is identical with system relaxation temperature during cooling step. Similar characteristics are also obtained for NC-1. This ‘dip’ arises as a consequence of spin–spin interaction and elucidates that the system, upon gradual heating schedule, can fetch the details of relaxation segment in the cooling step. Such phenomenon validates that our system exhibits memory effect which is a salient aspect of spin-glass behaviour.
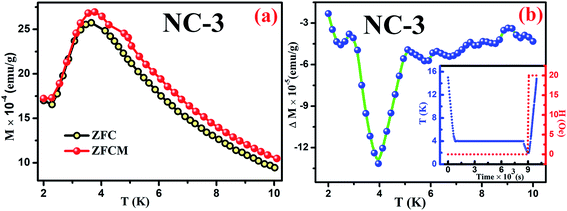 | ||
| Fig. 15 (a) ZFC and ZFCM curves for NC-3, (b) Plot of ΔM variation as a function of temperature for NC-3. Inset of (b) shows the experimental protocol. | ||
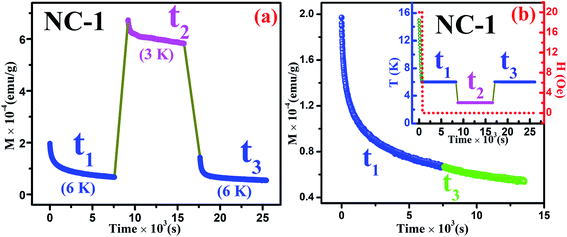
In addition to the above ZFC protocol, memory effect was also established through magnetic relaxation dynamics which correlates the influence of applied field on dipolar interaction.76,77 Relaxation dynamics study for NC-1 was carried out by recording time-dependent magnetization using the protocol as mentioned in the inset of Fig. 16(b). Initially, the system was cooled down from reference temperature Tr = 16 K (Tr ≫ Tg) to measurement temperature Tm = 6 K at 1 K min−1 rate under 20 Oe magnetic field. At steady condition, the applied field is switched off and time-dependent magnetization decay was recorded for time span of t1. The system temperature is further quenched to 3 K followed by relaxation data recording for another time span of t2. After t2, the system is shifted back to its previous state (6 K) and subsequently relaxation data acquisition is performed for time span of t3. The complete relaxation dynamics for total time span of (t1 + t2 + t3) is depicted in the Fig. 16(a). The magnetization enhancement in t2 time span may be attributed to the reduced thermal agitation. From the Fig. 16(b), it is noteworthy that the magnetic relaxation of t3 resumes from the end value of t1 and a continuous relaxation curve was obtained which essentially substantiates the memory effect of the system. The phenomenon may be interpreted based on paradigm of the droplet theory.78,79
3.4. AC magnetization
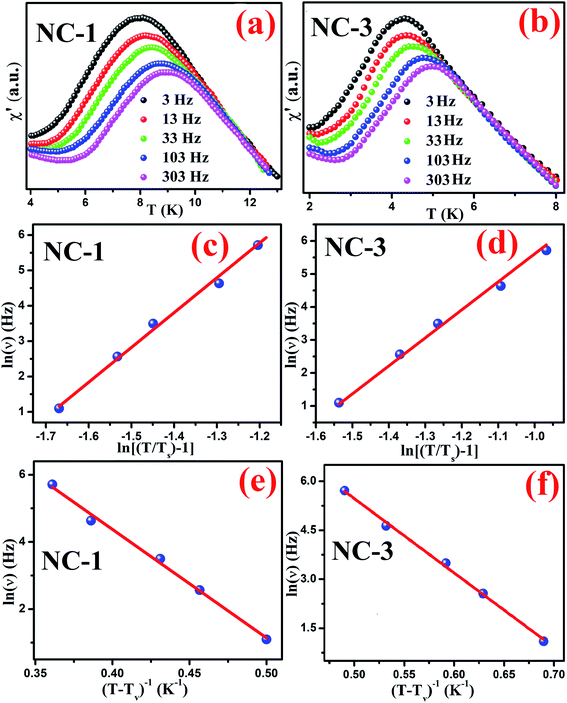
We further performed AC magnetization measurements to realize the origin of spin-glass behaviour. Therefore AC susceptibility (χac) measurement with varying frequency at low temperature region (close to Tg) was carried out for NC-1 and NC-3. Fig. 17(a) and (b) show the temperature variation of the real part (χ′) of AC susceptibility at different frequencies for NC-1 and NC-3 respectively. Each curve exhibited a well-pronounced peak around Tg. Interestingly, when the frequency value (ν) is increased, the peak intensity around Tg is reduced monotonically whereas peak position is shifted towards higher temperature. The existence of frequency-dependent χ′(T) is an evident aspect of spin-glass behaviour. The relation between frequency and shift of Tg is governed by a dynamic scaling theory80 as,
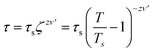 | (6) |
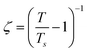 is the correlation length and z is the dynamic critical exponent. In the Fig. 17(c) and (d), the plot of ln(ν) vs.
is the correlation length and z is the dynamic critical exponent. In the Fig. 17(c) and (d), the plot of ln(ν) vs.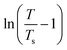 represents a satisfactory linear fit using scaling theory for NC-1 and NC-3 respectively considering Ts = 6.90 K and 3.58 K. Table 6 summarizes all the obtained fitting parameters for all studied samples. The extracted values of τs and zν′ support the typical characteristics of CSG.81–84
represents a satisfactory linear fit using scaling theory for NC-1 and NC-3 respectively considering Ts = 6.90 K and 3.58 K. Table 6 summarizes all the obtained fitting parameters for all studied samples. The extracted values of τs and zν′ support the typical characteristics of CSG.81–84
| Sample | Ts (K) | zν′ | τs (s) | Tv (K) | τv (s) |
|---|---|---|---|---|---|
| NC-1 | 6.9 | 9.85 | 2.27 × 10−8 | 6.2 | 3.13 × 10−8 |
| NC-3 | 3.58 | 8.48 | 7.52 × 10−7 | 2.9 | 4.8 × 10−8 |
The existence of CSG is further analysed considering Vogel–Fulcher (VF) law defined as,
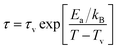 | (7) |
4. Conclusions
In summary, we have successfully synthesized composites of nanosilica glass containing dual transition metal oxide with compositions xCoO·(20 − x)NiO·80SiO2 within hexagonal pores of SBA-15 template via facile sol–gel method. The structural information of the investigated samples were derived from the XRD studies. BET investigation revealed 95% loading of the nanoglass within SBA-15 template. TEM imaging coupled with EDAX mapping gave the microstructural insight of sample with uniform distribution of constituent elements. The presence of Co2+/Co3+ and Ni2+/Ni3+ oxidation states were affirmed by XPS analysis. These nanocomposites exhibited significant MD effect with the magnetodielectric parameter having values in the ranges of 3% to 8% and 9% to 12%, respectively, for NC-1 and NC-3 respectively. MR shows strong dependence on dual transition metal ions owing to the nanoconfinement effect in these materials leading a positive (51%) and a negative (23%) magnetoresistance for NC-1 and NC-3 respectively. It is believed that the phenomenon of positive magnetoresistance may be attributed to the wave-function shrinkage whereas enhanced spin polarized electron hopping between the localized states give rise to negative magnetoresistance. The synergistic effect of dual transition metal oxides on MD properties can be utilized to a great extent on switching MR properties by suitable selection of constituent species. The magnetization responses of our samples under static and dynamic condition were investigated and analysed. Magnetic memory effect and frequency dependency of ac susceptibility yield an influential insight towards spin-glass nature. The shift of Tg was found to be in accordance with both dynamic scaling law and Vogel–Fulcher law. Therefore, it is expected that these nanocomposite systems will lead to a fascinating area of research in the field of multifunctional devices.Authors contributions
Subha Samanta: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, writing – original draft. Anupam Maity: data curation, formal analysis, funding acquisition, resources, software, writing – original draft. Alorika Chatterjee: formal analysis, software. Saurav Giri: supervision, validation, writing – review & editing. Dipankar Chakravorty: conceptualization, project administration, supervision, validation, visualization, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. Samanta acknowledges the award of INSPIRE fellowship by Department of Science and Technology, New Delhi. A. Maity acknowledges the award of NFSC, University Grants Commission, New Delhi. D. Chakravorty thanks Indian National Science Academy, New Delhi for giving him an Emeritus Scientist position.References
- W. Eerenstein, N. D. Mathur and J. F. Scott, Nature, 2006, 442, 759–765 CrossRef CAS PubMed.
- Y. Shi and Y. Wang, Materials, 2019, 12, 260 CrossRef CAS PubMed.
- L. Y. Wang, Q. Li, Y. Y. Gong, D. H. Wang, Q. Q. Cao and Y. W. Du, J. Am. Ceram. Soc., 2014, 97, 2024–2026 CrossRef CAS.
- P. Jain, Q. Wang, M. Roldan, A. Glavic, V. Lauter, C. Urban, Z. Bi, T. Ahmed, J. Zhu, M. Varela, Q. X. Jia and M. R. Fitzsimmons, Sci. Rep., 2015, 5, 9089 CrossRef CAS PubMed.
- G. Catalan, Appl. Phys. Lett., 2006, 88, 102902 CrossRef.
- H. Schmid, Ferroelectrics, 1994, 162, 317–338 CrossRef.
- I. H. Lone, J. Aslam, N. R. E. Radwan, A. H. Bashal, A. F. A. Ajlouni and A. Akhter, Nanoscale Res. Lett., 2019, 14, 142 CrossRef PubMed.
- H. Zhang, S. W. Or and H. L. W. Chan, Mater. Res. Bull., 2009, 44, 1339–1346 CrossRef CAS.
- G. Sreenivasulu, V. H. Babu, G. Markandeyulu and B. S. Murty, Appl. Phys. Lett., 2009, 94, 112902 CrossRef.
- N. S. Rogado, J. Li, A. W. Sleight and M. A. Subramanian, Adv. Mater., 2005, 17, 2225–2227 CrossRef CAS.
- Y. Q. Lin and X. M. Chen, J. Am. Ceram. Soc., 2011, 94, 782–787 CrossRef CAS.
- M. A. Subramanian, T. He, J. Chen, N. S. Rogado, T. G. Calvarese and A. W. Sleight, Adv. Mater., 2006, 18, 1737–1739 CrossRef CAS.
- N. Hur, S. Park, P. A. Sharma, S. Guha and S.-W. Cheong, Phys. Rev. Lett., 2004, 93, 107207 CrossRef CAS PubMed.
- B. Raveau, J. Eur. Ceram. Soc., 2005, 25, 1965–1969 CrossRef CAS.
- T. K. Mandal and M. Greenblatt, in Functional Oxides, John Wiley & Sons, Ltd, Chichester, UK, 2010, pp. 257–293 Search PubMed.
- J. L. Hubisz, Phys. Teach., 2014, 52, 574 Search PubMed.
- C. N. R. Rao and A. K. Cheetham, Science, 1996, 272, 369–370 CrossRef CAS.
- C. Yuan, H. Bin Wu, Y. Xie and X. W. D. Lou, Angew. Chem., Int. Ed., 2014, 53, 1488–1504 CrossRef CAS PubMed.
- S. Chaturvedi, P. Shyam, R. Bag, M. M. Shirolkar, J. Kumar, H. Kaur, S. Singh, A. M. Awasthi and S. Kulkarni, Phys. Rev. B, 2017, 96, 024434 CrossRef.
- P. Poizot, S. Laruelle, S. Grugeon, L. Dupont and J. Tarascon, Nature, 2000, 407, 496–499 CrossRef CAS PubMed.
- R. Singh, J. Magn. Magn. Mater., 2013, 346, 58–73 CrossRef CAS.
- D. Li, J. J. Jiang, W. Liu and Z. D. Zhang, J. Appl. Phys., 2011, 109, 07C705 CrossRef.
- A. Barman, S. Mondal, S. Sahoo and A. De, J. Appl. Phys., 2020, 128, 170901 CrossRef CAS.
- A. Maity, S. Samanta, S. Chatterjee, R. Maiti, D. Biswas, S. K. Saha and D. Chakravorty, J. Phys. D: Appl. Phys., 2018, 51, 245301 CrossRef.
- S. Samanta, A. Maity, S. Chatterjee, R. Maiti, D. Biswas, S. Giri and D. Chakravorty, Trans. Indian Inst. Met., 2019, 72, 1963–1969 CrossRef CAS.
- A. Maity, S. Samanta, R. Maiti, S. Chatterjee, D. Biswas and D. Chakravorty, J. Magn. Magn. Mater., 2019, 491, 165633 CrossRef CAS.
- M. M. Selvi, P. Manimuthu, K. S. Kumar and C. Venkateswaran, J. Magn. Magn. Mater., 2014, 369, 155–161 CrossRef CAS.
- S. Singh, N. Kumar, R. Bhargava, M. Sahni, K. Sung and J. H. Jung, J. Alloys Compd., 2014, 587, 437–441 CrossRef CAS.
- T.-I. Yang, R. N. C. Brown, L. C. Kempel and P. Kofinas, J. Magn. Magn. Mater., 2008, 320, 2714–2720 CrossRef CAS.
- M. Wołoszyn, B. J. Spisak, P. Wójcik and J. Adamowski, Phys. E, 2016, 83, 127–134 CrossRef.
- J. Wang, G. Cao and Y. Li, Mater. Res. Bull., 2003, 38, 1645–1651 CrossRef CAS.
- S. Li, F. Lei, X. Peng, R. Wang, J. Xie, Y. Wu and D. Li, Inorg. Chem., 2020, 59, 11935–11939 CrossRef CAS PubMed.
- S. Chatterjee, R. Maiti and D. Chakravorty, RSC Adv., 2020, 10, 13708–13716 RSC.
- S. Hikami, A. I. Larkin and Y. Nagaoka, Prog. Theor. Phys., 1980, 63, 707–710 CrossRef.
- H. Fukuyama and K. Hoshino, J. Phys. Soc. Jpn., 1981, 50, 2131–2132 CrossRef CAS.
- B. J. Spisak, A. Paja and G. J. Morgan, Phys. Status Solidi, 2005, 242, 1460–1475 CrossRef CAS.
- M. Stingaciu, P. G. Reuvekamp, C.-W. Tai, R. K. Kremer and M. Johnsson, J. Mater. Chem. C, 2014, 2, 325–330 RSC.
- M. Krishnan, A. Mishra, D. Singh, S. Yadam, R. Venkatesh, M. Gangrade and V. Ganesan, J. Magn. Magn. Mater., 2018, 448, 257–261 CrossRef CAS.
- Z. G. Sheng, W. H. Song, Y. P. Sun, J. R. Sun and B. G. Shen, Appl. Phys. Lett., 2005, 87, 032501 CrossRef.
- J. Zhu, M. Chen, H. Qu, H. Wei, J. Guo, Z. Luo, N. Haldolaarachchige, D. P. Young, S. Wei and Z. Guo, J. Mater. Chem. C, 2014, 2, 715–722 RSC.
- S. Samanta, A. Maity, S. Chatterjee, S. Giri and D. Chakravorty, J. Phys. Chem. Solids, 2020, 142, 109470 CrossRef CAS.
- J. K. Perry, J. Tahir-Kheli and W. A. Goddard, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 144510 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- Y. Dong, J. Wen, F. Pang, Z. Chen, J. Wang, Y. Luo, G. Peng and T. Wang, Appl. Surf. Sci., 2014, 320, 372–378 CrossRef CAS.
- A. A. Safonov, A. A. Bagaturyants and V. A. Sazhnikov, J. Mol. Model., 2017, 23, 164 CrossRef CAS PubMed.
- A. G. Martynov, J. Mack, A. K. May, T. Nyokong, Y. G. Gorbunova and A. Y. Tsivadze, ACS Omega, 2019, 4, 7265–7284 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- J.-F. Pommaret, in Partial Differential Equations and Group Theory, Springer Netherlands, Dordrecht, 1994, vol. 407, pp. 61–80 Search PubMed.
- J. Jagiello and W. Betz, Microporous Mesoporous Mater., 2008, 108, 117–122 CrossRef CAS.
- Z. Y. Wu, Q. Jiang, Y. M. Wang, H. J. Wang, L. B. Sun, L. Y. Shi, J. H. Xu, Y. Wang, Y. Chun and J. H. Zhu, Chem. Mater., 2006, 18, 4600–4608 CrossRef CAS.
- S. Samanta, A. Maity, S. Roy, S. Giri and D. Chakravorty, J. Phys. Chem. C, 2020, 124, 21155–21169 CrossRef CAS.
- L. Chen, J. Hu, Z. Qi, Y. Fang and R. Richards, Ind. Eng. Chem. Res., 2011, 50, 13642–13649 CrossRef CAS.
- B. K. Ghosh, S. Hazra, B. Naik and N. N. Ghosh, Powder Technol., 2015, 269, 371–378 CrossRef CAS.
- X. Zhang, H. Yang, Y. Huo, J. Li, J. Ma and J. Ma, Dalton Trans., 2016, 45, 8972–8983 RSC.
- A. Martucci, N. Bassiri, M. Guglielmi, L. Armelao, S. Gross and J. C. Pivin, J. Sol-Gel Sci. Technol., 2003, 26, 993–996 CrossRef CAS.
- J. Hernández-Torres and A. Mendoza-Galván, J. Non-Cryst. Solids, 2005, 351, 2029–2035 CrossRef.
- J. Ndalamo, A. F. Mulaba-Bafubiandi and B. B. Mamba, Int. J. Miner., Metall. Mater., 2011, 18, 260–269 CrossRef CAS.
- R. M. Nor, S. N. M. Halim, M. F. M. Taib and M. K. Abd-Rahman, Solid State Phenom., 2017, 268, 92–96 Search PubMed.
- Y. Cheng, D. Ren, H. Zhang and X. Cheng, J. Non-Cryst. Solids, 2015, 416, 36–43 CrossRef CAS.
- L. Fernandez, I. Tuñón, J. Latorre, C. Guillem, A. Beltrán and P. Amorós, J. Mol. Model., 2012, 18, 3301–3310 CrossRef CAS PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- J. L. Pascual-Ahuir and E. Silla, J. Comput. Chem., 1990, 11, 1047–1060 CrossRef CAS.
- P. A. Denis, J. Phys. Chem. C, 2009, 113, 5612–5619 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 720–723 CrossRef.
- G.-M. Rignanese, J. Phys.: Condens. Matter, 2005, 17, R357–R379 CrossRef CAS.
- R. Menon, C. O. Yoon, D. Moses and A. J. Heeger, Handb. Conduct. Polym., 1998, 27–84 Search PubMed.
- B. I. Shklovskii and A. L. Efros, Electronic Properties of Doped Semiconductors, Springer Berlin Heidelberg, Berlin, Heidelberg, 1984, p. 45 Search PubMed.
- S. Nair and A. Banerjee, Phys. Rev. Lett., 2004, 93, 117204 CrossRef PubMed.
- A. Kumar, R. P. Tandon and V. P. S. Awana, J. Appl. Phys., 2011, 110, 043926 CrossRef.
- Y.-Q. Liang, N. Di and Z. Cheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 134416 CrossRef.
- F. Du, Z.-F. Huang, C.-Z. Wang, X. Meng, G. Chen, Y. Chen and S.-H. Feng, J. Appl. Phys., 2007, 102, 113906 CrossRef.
- M. Sasaki, P. E. Jönsson, H. Takayama and H. Mamiya, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 104405 CrossRef.
- J.-Y. Ji, P.-H. Shih, T.-S. Chan, Y.-R. Ma and S. Y. Wu, Nanoscale Res. Lett., 2015, 10, 243 CrossRef PubMed.
- A. Chatterjee, S. Majumdar, S. Chatterjee, A.-C. Dippel, O. Gutowski, M. V. Zimmermann and S. Giri, J. Alloys Compd., 2019, 778, 30–36 CrossRef CAS.
- H. Takayama and K. Hukushima, J. Phys. Soc. Jpn., 2004, 73, 2077–2080 CrossRef CAS.
- M. Bandyopadhyay and S. Dattagupta, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 214410 CrossRef.
- J. A. Mydosh, Spin Glasses: An Experimental Introduction, Taylor & Francis, London, 1993 Search PubMed.
- S. Pakhira, C. Mazumdar, R. Ranganathan, S. Giri and M. Avdeev, Phys. Rev. B, 2016, 94, 104414 CrossRef.
- V. K. Anand, D. T. Adroja and A. D. Hillier, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 014418 CrossRef.
- T. Mori and H. Mamiya, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 214422 CrossRef.
- P. Bag, P. R. Baral and R. Nath, Phys. Rev. B, 2018, 98, 144436 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra02215f |
| This journal is © The Royal Society of Chemistry 2021 |