Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structure, phase transition and properties of the one-dimensional antiferromagnet Cu(2,6-dimethylpyrazine)Br2†
Fei Dinga,
Chuanlu Yanga,
Xiangnan Gongb,
Hui Zhengc,
Xiaoyu Zhoua,
Lingli Lia,
Lichun Zhanga,
Dehua Wanga and
Bingying Pan *a
*a
aSchool of Physics and Optoelectronic Engineering, Ludong University, Yantai, Shandong 264025, China. E-mail: bypan@ldu.edu.cn
bAnalytical and Testing Center, Chongqing University, Chongqing, 401331, China
cSchool of Chemistry and Materials Science, Ludong University, Yantai, Shandong 264025, China
First published on 25th June 2021
Abstract
We report the crystal structure and properties of the one-dimensional S = 1/2 antiferromagnet Cu(2,6-dimethylpyrazine)Br2 with strong intra-chain exchange. At room temperature, its linear spin chains are formed by Cu2+ ions via the non-bonding Br⋯Br contacts. Interestingly, a phase transition from Pmmn to P21/n structure occurs at TS ≈ 248 K below which the [CuBr2]n spin chains become non-linear and the magnetic susceptibility abruptly increases, reflecting the weakening of antiferromagnetic exchange strength. This result evidences the Goodenough–Kanamori rules which claim that a linear super-exchange pathway produces stronger antiferromagnetic coupling. From magnetic susceptibility measurements we find the average intra-chain exchange strength is J/kB ≈ −88.18 K in the low temperature phase. Both magnetic and specific measurements show the absence of magnetic ordering down to 2 K, implying the excellent magnetic one-dimensionality of Cu(2,6-dimethylpyrazine)Br2. We also performed ultra-violet (UV) absorption and photoluminescence measurements which give a semiconducting band gap Δ ≈ 2.79 eV which is consistent with theoretical calculations.
Introduction
The synthesis and physical properties of coordination polymer complexes with the chemical formula LCuX2 (L = organic ligand, X = halide ions) is an important subject of inorganic chemistry, because these materials play a crucial role for understanding the pathway of magnetic interactions. Especially, for the quantum antiferromagnets, the superexchange pathways are highly relevant to the specific structure of the compound.1–3 The Cu2+ ion with one unpaired electron in coordination polymers exhibits the smallest spin number (S = 1/2) and strongest quantum fluctuations, and thus is widely used to study quantum magnetism. Depending on the organic ligand species and coordination environment of the Cu2+ ions, various superexchange pathways and magnetic behaviors can form in different coordination polymers.3One-dimensional (1D) magnetic systems have been continuously drawing research interests for their novel quantum states, excitations, and strong quantum fluctuations.4 In the past decades, various copper(II) coordination complexes have been reported as material realizations of 1D quantum spin models.1–3 The properties of 1D magnets are directly affected by the superexchange pathways which are dependent on the concrete crystalline structure. Especially, the non-bonding contacts between halide ions (Cu–X ⋯X–Cu, X = Br, Cl) represents an important type of superexchange pathways and have been widely studied.1,3 The sign and strength of the magnetic interaction via such a two-halide bridge depend on various parameters such as the geometry of the chains and the distance of the bridging halide ions.1,5 In fact, all related variables in the coordination environment have potential influence on the properties of 1D magnetism.1 For example, studies show that the Br⋯Br contacts propagate stronger exchanges than their Cl⋯Cl counterparts in all cases.6–8 Upon to date, a full description on the magnetic interaction via the two-halide bridge is still lacking.
The pyrazine-based compound Cu(pyrazine)(NO3)2 is a model 1D Heisenberg antiferromagnet and has been extensively studied by neutron scattering,9 muon-spin relaxation (μSR),10 nuclear magnetic resonance (NMR) spectroscopy,11,12 and thermal transport.13 Substituting pyrazine with related ligands such as phenazine, quinoxaline, methylpyrazine, and chloropyrazine also result in a variety of linear spin chains, but the magnetic super-exchange through pyrazine ring is weak with J/kB smaller than −10.3 K.14 By using Br as anions, a derivative 1D antiferromagnet Cu(2,5-dimethylpyrazine)Br2 exhibit a exceptionally strong exchange with J/kB = −234 K and the authors demonstrate the dominate antiferromagnetic exchange propagate through the non-bonding Cu–Br ⋯Br–Cu pathway.15 Such strong exchange is also very unusual among the 1D magnets mediated by the two bromide contacts.1 It is of great interest to investigate related compounds in order to explore the mechanism of enhanced superexchange in this two-halide bridged spin chain system.
Cu(2,6-dimethylpyrazine)Br2 (1) is an analog compound of Cu(2,5-dimethylpyrazine)Br2 but its structure has not been reported in literature. The preliminary magnetic susceptibility of 1 was reported by Inman et al. in 1972 on powder sample and the data was explained by an antiferromagnetic spin chain model with J = −47.5 K.2 However, no magnetic susceptibility data is available in a wide temperature range above 100 K, leaving large uncertainty on the data fitting result.2
In this work, we report the structure, phase transition, magnetism, specific heat and optical properties of 1. At room temperature, 1 is featured by [CuBr2]n spin chains, similar to Cu(2,5-dimethylpyrazine)Br2. Surprisingly, an unique phase transition from Pmmn to P21/n structure occurs at TS = 248 K, resulting in significant deformation of the spin chains at the low temperature (LT) phase. This structural transition is accompanied by a sharp jump in magnetic susceptibility across TS, indicative of the weakening of the intra-chain exchange strength once entering the LT phase. By fitting the LT susceptibility data by a uniform spin chain model we find the average exchange strength is −88.18 K, this strength is comparable to that of Cu(2,5-dimethylpyrazine)Br2. The specific heat data do not show any feature of magnetic ordering down to 2 K, indicating excellent 1D magnetism of 1. Our work reveals 1 is an unique 1D system that shows linear to non-linear transition in spin chains which has not been found in other copper(II) coordination complexes at ambient pressure. This system thus provides a novel platform to study the mechanism of spin chain geometry on the two-halide bridge mediated magnetic superexchange.
Experimental
Synthesis
Single crystals of Cu(2,6-dimethylpyrazine)Br2 were synthesized by conventional diffusion method. 4 mmol 2,6-methylpyrazine (>99%, Adamas-beta) and 4 mmol copper bromide (>99%, Adamas-beta) were loaded into the 250 mL and 50 mL beakers, respectively. The 50 mL beaker was put inside the larger one and alcohol was slowly introduced till the alcohol level is far up beyond the edge of the 50 mL beaker. After about one week, black single crystals were formed. The typical single crystal size is 3 mm × 0.25 mm × 0.1 mm. Anal. calc.: C, 21.72%; H, 2.41%; N, 8.45%; found: C, 21.76%; H, 2.62%; N, 8.44%.X-ray diffraction
We used the three-circle diffractometer (Mo Kα radiation, λ = 0.71073 Å) for the X-ray diffraction of Cu(2,6-dimethylpyrazine)Br2 single crystal. High quality diffraction data were collected at 300 and 240 K and the crystal structures were solved by the direct method and refined via full-matrix least-square techniques using the Olex2 and SHELXL program package.16,17 The resulted cell parameters, selective atomic coordinates, bond lengths and bond angles are listed in Tables 1 and 2. Crystallographic data of Cu(2,6-dimethylpyrazine)Br2 have been deposited at the Cambridge Crystallographic Data Center (CCDC No. 2070208 (T = 300 K) and 2070209 (T = 240 K)).| Temperature (K) | 300(2) | 240(2) |
| Empirical formula | (C6H8N2)CuBr2 | (C6H8N2)CuBr2 |
| Formula weight | 331.50 | 331.50 |
| Space group | Pmmn | P21/n |
| Crystal system | Orthorhombic | Monoclinic |
| Wavelength | 0.71073 Å | 0.71073 Å |
| Lattice parameters | a = 8.3552(9) Å | a* = 10.2576(5) Å |
| b = 8.5782(11) Å | b* = 8.3613(5) Å | |
| c = 6.6959(7) Å | c* = 11.2178(5) Å | |
| α = β = γ = 90° | α* = γ* = 90° | |
| β* = 102.982(2)° | ||
| Z | 2 | 4 |
| μ (mm−1) | 10.541 | 10.791 |
| θmin/θmax (°) | 6.808/77.732 | 4.866/70.382 |
| Independent reflections | 1468 | 4262 |
| Rint | 0.0552 | 0.0649 |
| F(000) | 314.0 | 628.0 |
| Restraints/parameters | 0/37 | 0/105 |
| Goodness-of-fit on F2 | 1.023 | 1.051 |
| R1/wR2 [I ≥ 2σ(I)] | 0.0395/0.0795 | 0.0551/0.1340 |
| Largest diff. peak/hole (e Å−3) | 1.39/−0.97 | 1.46/−1.30 |
| 300 K | 240 K | |
|---|---|---|
| Bond lengths | ||
| Cu1–Br1 | 2.3813(5) Å | 2.37(1) Å |
| Br1–Br2 | 3.593(2) Å | 3.80(1) Å |
| Cu2–Br2 | 2.3813(5) Å | 2.38(6) Å |
| Cu2–Br3 | 2.3813(5) Å | 2.37(1) Å |
| Br3–Br4 | 3.593(2) Å | 3.80(1) Å |
| Cu3–Br4 | 2.3813(5) Å | 2.38(6) Å |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Bond angles | ||
| Cu1–Br1–Br2 | 180.0° | 156.51(2)° |
| Br1–Br2–Cu2 | 179.84(9)° | 167.20(6)° |
| Br2–Cu2–Br3 | 179.69(4)° | 175.09(9)° |
| Cu2–Br3–Br4 | 180.0° | 156.51(1)° |
| Br3–Br4–Cu3 | 179.84(9)° | 167.20(6)° |
Elemental analysis, photoluminescence, and UV absorption measurements
Elemental analysis were determined on an Vario EL cube analyzer. Photoluminescence (PL) measurements were conducted with a 325 nm He-Cd laser as the pump source (Kimmon Electric, Ltd., Saitama, Japan) and a monochromator (SR-500i-A, Andor Technology, Belfast, UK) working at room temperature. The characteristic absorption peak was measured by a Shimadzu UV-2550 spectrophotometer.Magnetic susceptibility and specific heat measurements
The magnetic susceptibility properties were measured by a MPMS SQUID magnetometer (Quantum Design) with magnetic field up to 7 T. The measured temperature range is from 300 to 2 K. Specific heat was measured by a Physical Property Measurement System (PPMS, Quantum Design) down to 2 K.Results and discussion
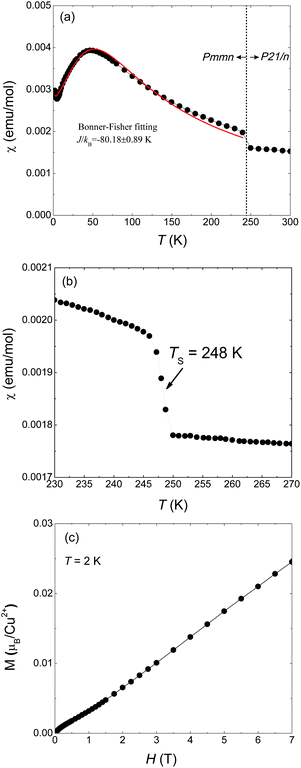
Magnetic susceptibility of 1 on powder sample was measured under 1000 Oe from 300 to 2 K (Fig. 1(a)). A abrupt jump in χ appears around TS = 248 K which corresponds to a phase transition from high temperature (HT) phase to a low temperature (LT) phase. Fig. 1(b) is a detailed measurement around TS. Such a discontinuous jump at TS can not be attributed to a second-order transition but arises from a first-order structural transition, as also evidenced by our X-ray diffraction results which will be shown later. At lower temperatures a maximum appears at around 50 K and then decreases, a typical behavior for one-dimensional magnets. The maximum temperature is consistent with the results of Inman et al. which is 47 K.2 We used the Bonner–Fisher formula for a Heisenberg magnetic chain to approximately describe the magnetic susceptibility of the LT phase.18 The fitting is represented by the red solid line in Fig. 1(a) which gives JL/kB = −88.18 ± 0.89 K and g = 2.40 ± 0.01.The magnetization at 2 K as a function of applied field is shown in Fig. 1(c) in which M varies quasi-linearly with H up to 7 T. Especially, the measured magnetization at 7 T is only 0.25 μB/Cu2+, far smaller than the spin-only saturated value 1.73 μB/Cu2+ of Cu2+ with spin −1/2. This behavior again indicates strong antiferromagnetic coupling in 1.
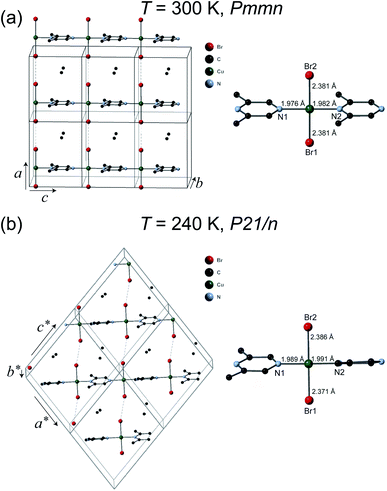
The crystal structures of 1 were solved at 300 K and 240 K. The refinement results are listed in Table 1. The chemical formula of 1 is (C6H8N2)CuBr2 which can also be verify by the thermogravimetric analysis measurement (see ESI†) and elemental analysis. As can be seen in Fig. 2(a), at 300 K the space group of 1 is Pmmn with the lattice parameters a = 8.3552(9) Å, b = 8.5782(11) Å, and c = 6.6959(7) Å. The structure of 1 is similar to its analogous coordination compound Cu(2,5-dimethylpyrazine)Br2 (ref. 15) with –Cu–2,6-dimethylpyrazine–Cu– infinite structure along the c axis. The copper(II) atom is tetrahedrally coordinated by two bromide atoms and two N atom from the 2,5-dimethylpyrazine ring. The Cu–Br bond length is 2.381 Å, and the Cu–N bond lengths are 1.976–1.982 Å (right panel of Fig. 2(a)). The linear Cu–Br⋯Cu magnetic chains propagate along the a axis with the non-bonding two-halide contacts (Br⋯Br length dBr⋯Br = 3.593 Å, Cu–Br⋯Br angle = 180.0°). The mean plane of 2,6-dimethylpyrazine ring perpendicular to the chain direction. In view that dBr⋯Br = 3.632 Å in Cu(2,5-dimethylpyrazine)Br2,15 both compounds should also have similar intra-chain super-exchange strength.
However, the structure of 1 at 240 K dramatically changes to the monoclinic type with P21/n structure. At the LT phase, the Cu–N and Cu–Br2 bond lengths were enlarged to 1.989–1.991 and 2.386 Å, respectively. Only the Cu–Br1 bond length was shortened to 2.371 Å. The 2,6-dimethylpyrazine rings also display rotation around the N1–Cu–N2 axis (right panel of Fig. 2(b)). The two-halide contacts are obviously distorted to form a non-linear spin chain (Br⋯Br length dBr⋯Br = 3.80(1) Å, Cu–Br⋯Br angle = 156.51(2)°). These large lattice distortions across TS make the [CuBr2]n magnetic chains substantially twisted, rendering the crystal to a lower symmetry. The [CuBr2]n chain structure and its detailed length/angle parameters at 300 and 240 K are shown in Fig. 3 and Table 2.
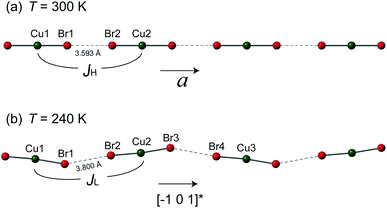 | ||
| Fig. 3 The [CuBr2]n magnetic chains at (a) 300 K and (b) 240 K. The antiferromagnetic super-exchanges between neighboring copper ions through the Br⋯Br non-bonding contact are denoted as JH and JL for the HT and LT phases, respectively. The detailed bond lengths and bond angles of the spin chains are listed in Table 2. | ||
The observation of structural phase transition in 1 is surprising because it has never been found in its analog compounds like Cu(2,5-dimethylpyrazine)Br2, Cu(2,6-dimethylpyrazine)(NO3)2, or other pyrazine-based coordination complexes at ambient pressure.2,15,19–21 The linear to non-linear structural transition of [CuBr2]n chains bring substantial change in the coordination environment and should have considerable impact on its 1D magnetism.
It is known that superexchange through the pyrazine ring pathway arises from the weak coupling π mechanism and the strength is less than J/kB = −10.3 K is all cases.14 For example, the 2,6-dimethylpyrazine bridged exchange strength in Cu(2,6-dimethylpyrazine)(NO3)2 is only J = −4.0 ± 0.1 K,14 far smaller than the exchange strength in 1. So the dominate exchange in 1 through the –Cu–2,6-dimethylpyrazine–Cu– pathway is unlikely. Butcher et al. investigated the structure and magnetic behavior of Cu(2,5-dimethylpyrazine)Br2 combined with quantum Monte Carlo simulations.15 They found the strong antiferromagnetic exchange J = −234 K is through the Cu–Br⋯Br–Cu pathway, whereas the Cu–2,5-dimethylpyrazine–Cu pathway only generates a much weaker strength J′ = −12 K. In sight its similar structure to 1, it is appropriate to attribute the propagation of JL to the Cu–Br⋯Br–Cu pathway.
The buckling of [CuBr2]n spin chain in 1 across TS offers an unprecedented opportunity to investigate the relation of chain geometry with 1D magnetism. In the HT phase, the closest Br⋯Br is 3.593 Å which is very short in comparison with the chain structure in strong coupled tetrabromocuprate compounds.1,22 Together with the linear chain structure, the Cu–Br⋯Br–Cu pathway is expected to propagate strong antiferromagnetic exchange. At the LT phase, the Cu–Br⋯Br angle and the Cu–Br⋯Br–Cu dihedral angle all significantly deviate from 180°. According to the Goodenough–Kanamori rules, non-linear pathway propagate weaker superexchange.23 Also, the Br⋯Br contact distance is enlarged to 3.800 Å, this would further reduce the intra-chain exchange strength.1 The analysis is evidenced by the jump at TS in Fig. 1(a). However, a qualitative theory should consider all geometric variables in the chain structure which is not currently available.
Fig. 4 is the specific heat data from 100 to 2 K at zero field. C monotonously decreases with lowering temperature. The absence of any anomaly in the measured temperature range verifies the broad peak around 50 K in χ (Fig. 1(a)) is purely from one-dimensional magnetism, not magnetic ordering. There is also no sign of magnetic ordering transition down to 2 K in specific heat data (inset of Fig. 4).
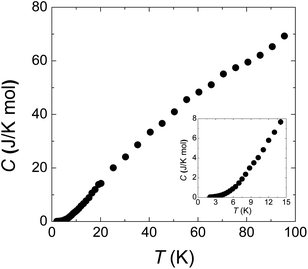 | ||
| Fig. 4 Specific heat from 2 to 100 K. The inset panel shows the data below 15 K. The smooth curve indicates the absence of long range spin ordering down to 2 K. | ||
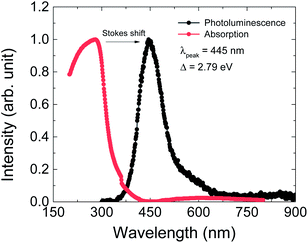
The optical properties were investigated by PL and UV-vis absorption spectra measurements (Fig. 5). The PL spectrum was excited by a 325 nm laser source and the maximum wavelength is at 445 nm, as shown by the black dots in Fig. 6. This PL peak wavelength corresponds to an electron band gap of 2.79 eV. The PL emission peak of 445 nm can be assigned to the π–π* transition of between the organic ligand. The UV-vis absorption spectrum shows an obvious Stokes shift effect with a maximum appearing at around 280 nm.
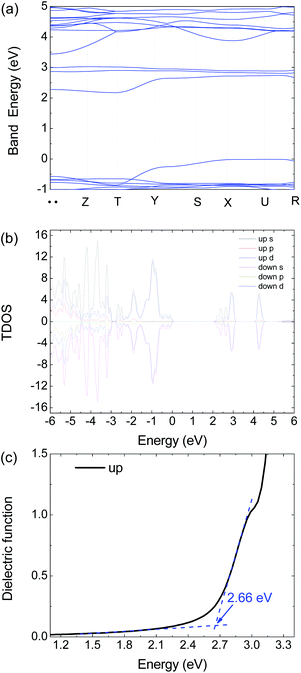 | ||
| Fig. 6 Calculated (a) electronic band structure, (b) TDOS and (c) dielectric function of 1 by HSE06 with an antiferromagnetism model. | ||
To get further insight on its electric and optical properties, we theoretically calculated the electronic structure and optical properties of 1 by using the Vienna ab initio simulation package (VASP) 6.1.2 code with a projector-augmented-wave pseudopotential.24–26 The exchange–correlation functional for describing the electron interactions is the generalized gradient approximation with Perdew–Burke–Ernzerh of parametrization (GGA-PBE).27 The Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional28 is adopted to calculate the electronic properties, optical properties, and mobility calculations because of the GGA-PBE functional usually underestimate the band energy gap.
There are 38 atoms in the unit cell with the Pnmn structure. The 3 × 3 × 3 Γ-centered k-mesh of Brillouin zone (BZ) are employed in integration, but the band structure are calculated with additional 7 special k points including 71 points. The energy cutoff the plane-wave basis sets is 500 eV to ensure the calculations to reach convergence. The energy convergent criterion is 10−6 eV. In the relaxation calculation, all the force is smaller than 0.01 eV Å−1 for the equilibrium structures.
The optical absorption coefficient α(ω) is used to quantitatively describe the response-ability of 1. α(ω) can be determined by the imaginary part ε2(ω) of the complex dielectric function ε(ω) = ε1(ω) + iε2(ω). In the present work ε2(ω) is calculated by the following equation29–31
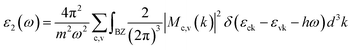 | (1) |
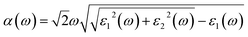 | (2) |
Conclusions
In summary, we synthesized single crystalline Cu(2,6-dimethylpyrazine)Br2 and successively solved its structure. The linear [CuBr2]n chains demonstrate strong one-dimensional antiferromagnetism via the two-halide exchange pathway, similar to its analog compound Cu(2,5-dimethylpyrazine)Br2. However, Cu(2,6-dimethylpyrazine)Br2 experiences a special phase transition from Pmmn to P21/n structure at TS = 248 K. The [CuBr2]n spin chains are non-linear and the average antiferromagnetic exchange strength get weakened after transition to the low temperature phase. Thus our experiments reveal a novel one-dimensional antiferromagnet with linear to non-linear structural transition in the spin chains and provide an example compound in the study of two-halide exchange mechanism.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 11804137, 62075092, 11874192) and the Natural Science Foundation of Shandong Province (Grant No. ZR2020YQ03, ZR2018BA026,ZR2019MA066).Notes and references
- M. M. Turnbull, C. P. Landee and B. M. Wells, Coord. Chem. Rev., 2005, 249, 2567–2576 CrossRef CAS.
- G. W. Inman and W. E. Hatfield, Inorg. Chem., 1972, 11, 3085–3090 CrossRef CAS.
- C. P. Landee and M. M. Turnbull, Eur. J. Inorg. Chem., 2013, 2266–2285 CrossRef CAS.
- H.-J. Mikeska and A. K. Kolezhuk, Lect. Notes Phys., 2004, 645, 1–83 CAS.
- K. K. Sharma, R. Singh, N. Fahmi and R. Singh, J. Coord. Chem., 2010, 63, 3071–3082 CrossRef CAS.
- R. Block and L. Jansen, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 148–153 CrossRef CAS.
- P. Straatman, R. Block and L. Jansen, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 1415–1418 CrossRef CAS.
- L. O. Snively, G. F. Tuthill and J. E. Drumheller, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 5349–5355 CrossRef CAS.
- M. B. Stone, D. H. Reich, C. Broholm, K. Lefmann, C. Rischel, C. P. Landee and M. M. Turnbull, Phys. Rev. Lett., 2003, 91, 037205 CrossRef CAS PubMed.
- T. Lancaster, S. J. Blundell, M. L. Brooks, P. J. Baker, F. L. Pratt, J. L. Manson, C. P. Landee and C. Baines, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 020410 CrossRef.
- H. Kühne, A. A. Zvyagin, M. Günther, A. P. Reyes, P. L. Kuhns, M. M. Turnbull, C. P. Landee and H.-H. Klauss, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 100407 CrossRef.
- H. Kühne, H.-H. Klauss, S. Grossjohann, W. Brenig, F. J. Litterst, A. P. Reyes, P. L. Kuhns, M. M. Turnbull and C. P. Landee, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045110 CrossRef.
- A. V. Sologubenko, K. Berggold, T. Lorenz, A. Rosch, E. Shimshoni, M. D. Phillips and M. M. Turnbull, Phys. Rev. Lett., 2007, 98, 107201 CrossRef CAS PubMed.
- H. W. Richardson and W. E. Hatfield, J. Am. Chem. Soc., 1976, 98, 835–839 CrossRef CAS.
- R. T. Butcher, J. J. Novoa, J. Ribas-Ariño, A. W. Sandvik, M. M. Turnbull, C. P. Landee, B. M. Wells and F. F. Awwadi, Chem. Commun., 2009, 1359–1361 RSC.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2010, 42, 339–341 CrossRef.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- J. C. Bonner and M. E. Fisher, Phys. Rev., 1964, 135, A640–A658 CrossRef.
- B. R. Jones, P. A. Varughese, I. Olejniczak, J. M. Pigos, J. L. Musfeldt, C. P. Landee, M. M. Turnbull and G. L. Carr, Chem. Mater., 2001, 13, 2127–2134 CrossRef CAS.
- F. F. Awwadi, C. P. Landee, M. M. Turnbull, B. Twamley and B. M. Wells, Polyhedron, 2005, 24, 2153–2159 CrossRef CAS.
- J. C. Monroe, C. P. Landee, M. M. Turnbull, M. Polson and J. L. Wikaira, Polyhedron, 2019, 171, 344–352 CrossRef CAS.
- J. L. Wikaira, L. Li, R. Butcher, C. M. Fitchett, G. B. Jameson, C. P. Landee, S. G. Telfer and M. M. Turnbull, J. Coord. Chem., 2010, 63, 2949–2964 CrossRef CAS.
- J. B. Goodenough, Magnetism and the Chemical Bond, Wiley, New York, 1963 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- S. Saha, T. P. Sinha and A. Mookerjee, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8828–8834 CrossRef CAS.
- X. Zhang, X. Zhao, D. Wu, Y. Jing and Z. Zhou, Adv. Sci., 2016, 3, 1600062 CrossRef PubMed.
- P. Li, C. wen Zhang, J. Lian, M. juan Ren, P. ji Wang, X. hong Yu and S. Gao, Opt. Commun., 2013, 295, 45–52 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2070208 and 2070209. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1ra02318g |
| This journal is © The Royal Society of Chemistry 2021 |