Open Access Article
Open Access ArticleEffect of manganese doping on the hyperthermic profile of ferrite nanoparticles using response surface methodology†
Ruby Gupta,
Ruchi Tomar,
Suvankar Chakraverty and
Deepika Sharma *
*
Institute of Nano Science and Technology, Knowledge City, Phase 81, Mohali-140306, Punjab, India. E-mail: deepika@inst.ac.in
First published on 7th May 2021
Abstract
Magnetic hyperthermia-based cancer therapy mediated by magnetic nanomaterials is a promising antitumoral nanotherapy, owning to its power to generate heat under the application of an alternating magnetic field. However, although the ultimate targets of these treatments, the heating potential and its relation with the magnetic behavior of the employed magnetic nanomaterials are rarely studied. Here we provide a bridge between the heating potential and magnetic properties such as anisotropy energy constant and saturation magnetization of the nano-magnets by simultaneous investigation of both hyperthermia and magnetism under a controlled set of variables given by response surface methodology. In the study, we have simultaneously investigated the effect of various synthesis parameters like cation ratio, reaction temperature and time on the magnetic response and heat generation of manganese-doped ferrite nanomaterials synthesized by a simple hydrothermal route. The optimum generation of heat and magnetization is obtained at a cationic ratio of approximately 42 at a temperature of 100 °C for a time period of 4 h. The optimized nanomaterial was then evaluated for in vitro magnetic hyperthermia application for cancer therapy against glioblastoma in terms of cell viability, effect on cellular cytoskeleton and morphological alterations. Furthermore, the correlation between the magnetic properties of the synthesized nanomaterial with its hyperthermia output was also established using K.V.Ms variable where K, V and Ms are the anisotropy energy constant, volume, and saturation magnetization of the nanomaterial respectively. It was found that the intensity of heat generation decreases with an increase in K.V.Ms value, beyond 950 J emu g−1.
1. Introduction
Magnetic nanoparticles (MNPs) depending on their properties, namely their crystallite size, structure, composition, and physicochemical properties, are being widely investigated for a range of biomedical applications such as magnetic resonance imaging, drug delivery, and hyperthermia.1–3 Hyperthermia is a therapeutic technique based upon the generation of localized heat at the tumor site which induces alterations in numerous cellular processes triggering tumor cell death.2,3 It can be achieved via various modes including radiation, microwave, ultrasound, or magnetic hyperthermia mediated by MNPs.4 The application of magnetic hyperthermia therapy for cancer treatment is known as magnetic hyperthermia-mediated cancer therapy (MHCT)5,6 and was first attempted by Gilchrist in 1957.7 It is based upon exposure of MNPs to an alternating magnetic field (AMF), that raises the temperature from 37 °C to 42–45 °C locally at the tumor site, inducing death of cancerous cells while the healthy cells remain unaffected.8,9Owning to its advantages of high tumor penetration with negligible non-specific toxicity, MHCT is been evaluated for various clinical trials for prostrate and glioblastoma.10 However, certain factors limits realization of its complete potential for treatment of inoperable solid tumors like glioblastomas. These include, lack of in-depth understanding of the interaction mechanism of hyperthermia treatment with the cancer cells at the sub-cellular level, incapability of the nanomaterials to generate enough heat inside the cellular compartments to achieve the desired therapeutic effect and presence of biological barriers like the blood–brain barrier, that limits the delivery of the required minimum dose of MNPs at the tumor site.4 Besides these limitations, the heat dissipated from the nano-systems is dependent upon various physical factors of the MNPs including its size, morphology and composition along with the physical parameters of the magnetic field applied including the AMF strength and duration of exposure.11,12 Thus, with an ultimate goal to maximize the hyperthermia output, MNPs with varied characteristics by altering their synthesis route or reaction parameters, morphology or composition. Table 1 represents summary of some of the nano-systems investigated for in vitro magnetic hyperthermia-mediated glioblastoma therapy, either used alone or in combination with other adjuvant therapies like chemotherapy and photothermal therapy.
| MNP system | Size (nm) | AMF parameters | ΔT (°C) | SAR (W g−1 MNP) | Therapy system | Tumor inhibition achieved (%) | Ref. | |
|---|---|---|---|---|---|---|---|---|
| f (kHz) | H (Oe) | |||||||
| SPIONS (superparamagnetic iron oxide NPs) | 15.8 | 473.5 | 168 | 12 | 113 | MHCT | 60 | 13 |
| Co0.1Fe2.9O4 | 7.1 | 112.6 | 250 | 4 | 13.8 | MHCT | 40 | 14 |
| MnxFe3−xO4 | 34 | 405 | 168 | 10.8 | 600 | MHCT-photothermal therapy | 70 | 15 |
| SPIONS | 20 | 753 | 200 | 4–5 | — | MHCT-chemotherapy | 99.8 | 16 |
| SPIONS | 75 | 780 | 12.5 | 6–7 | — | MHCT-chemotherapy | 49.6 | 17 |
| Zn-SPIONS | 15 | 522 | 104 | — | 743.8 | MHCT | 50 | 18 |
| Fe3O4 | 3 | 405 | 168 | 13 | 80 | MHCT | 66 | 19 |
| Fe(salen) | — | 280 | 335 | 5–6 | — | MHCT-chemotherapy | 30 | 20 |
| Fe3O4 | — | 473 | 150 | — | 265 | MHCT | 80–90 | 21 |
| Zn0.9Fe2.1O4 | 11 | 700 | 34.4 | 4 | 36 | MHCT | 20 | 22 |
As discussed, for unfolding the complete potential of MHCT for solid tumors like glioblastomas, development of new nanomaterials with higher and tunable functionality is very crucial. In this regard, strategy to dope ferrite nanoparticles with other metal atoms has been pursued to achieve high and tunable hyperthermic nanomagnetic systems.23–25 For example, a study reports that ferrite nanoparticles simultaneously doped with other metal ions exhibit approximately four-fold higher hyperthermia output as compared to that of conventional iron oxide nanoparticles.26 Also, various studies have reported the hyperthermia output to be highly dependent on magnetic relaxation processes and roughly proportional to the saturation magnetization (Ms) value of the nanomaterials.27,28 For nanoparticles, the magnetic properties are very sensitive to the synthesis technique.29 Response surface methodology (RSM) has been significantly used for nanoparticle synthesis for various applications.30–34 RSM is an optimizing tool mainly used for evaluating effect of multiple process variables simultaneously as fewer experimental runs are required as compared to investigation of each variable independently. Also, it allows identification and quantification of significant interactions between the variables.
In this paper, we have focused on the effect of manganese (Mn) doping on saturation magnetization and magnetic hyperthermia of ferrite nanoparticles. We have investigated the simultaneous effect of Mn doping by varying synthesis parameters including cation ratio, reaction temperature, and reaction time on magnetic and hyperthermic responses of these samples by RSM technique. The optimum reaction conditions were then deduced to obtain a nanosystem with higher saturation magnetization and hyperthermic efficiency which was further tested for its efficacy in in vitro magnetic hyperthermia-based glioblastoma therapy. Further, we have also studied an empirical relation between the magnetic properties of the nanomaterials with their heat generating capabilities that may open a new window in the field of magnetic hyperthermia-based cancer therapy.
2. Experimental section
2.1 Materials
To synthesize the nanoparticles, analytical grade iron chloride hexahydrate (FeCl3·6H2O), manganese chloride tetrahydrate (MnCl2·4H2O) from Sigma Aldrich were used as initial precursors. Ammonium hydroxide solution (NH4OH solution; 25%) from Sigma Aldrich was used as the reducing agent.For cellular studies, normal murine fibroblasts cell line (L929) and human glioma cell line (U87-MG) were purchased from NCCS, Pune, India. The cells were cultured in Dulbecco's Modified Eagles Medium (Hyclone) supplemented with 10% heat-inactivated fetal bovine serum (FBS; Gibco) and 1% antibiotic–antimycotic solution (Lonza). The cell cultures were grown at 37 °C under 5% CO2.
2.2 Synthesis of MnxFe3−xO4 nanoparticles
The Mn-doped nanoparticles (MnxFe3−xO4) were synthesized by hydrothermal synthesis route35 with varying cationic ratio (Fe3+/Mn2+), reaction temperature and time. Different concentrations of FeCl3·6H2O and MnCl2·4H2O salts (according to stoichiometric ratio of each run) were magnetically dispersed in 11.5 mL deionized water (Table S1†). Then 2.5 mL of NH4OH as a reducing agent was added into the mixture and air stirred for 10 min. The mixture was then sonicated for 15 min and then added to 23 mL Teflon-lined stainless steel pressure vessel at varying conditions of temperature and time (as per Table S1†). After cooling the reaction mixture to room temperature, the black precipitate obtained was washed with several centrifugation–dispersion cycles with water and ethanol. The final dispersion in water was freeze-dried to obtain the desired MnxFe3−xO4 nanoparticle powder.2.3 Design of experiments
In this study, the RSM technique was used by DESIGN EXPERT software (V 11.0) to evaluate the effects of different parameters for the synthesis of MnxFe3−xO4 nanoparticles for magnetic hyperthermia-based applications. The design of experiments was done by central composite design (CCD) which is based on 5 defined levels of influential parameters (factors) such as −α, −1, 0, +1, and +α. The effect of three independent variables, namely cation ratio of Fe3+ and Mn2+ ions in the reaction mixture (A), reaction temperature (B) and reaction time (C), were studied on the saturation magnetization (R1) and total degree rise in temperature on AMF application (R2). Based on the preliminary work done, the range of independent variables chosen are 0.5–60 (cation ratio), 60–200 °C (reaction temperature) and 2–12 h (reaction time).For a three-factor system,36 a second-order quadratic equation as given below was fitted to the data by multiple regression procedure:
| Y = β0 + β1A + β2B + β3C + β11A2 + β22B2 + β33C2 + β12AB + β13AC + β23BC | (1) |
The predicted (using equations obtained for the individual responses) and experimental results for both saturation magnetization (R1) and total degree rise in temperature (R2) are presented in Table S1 (ESI file†). The statistical significance of the regression coefficients was evaluated by student's test, and then, the analysis of variance (ANOVA) was performed using only the statistically significant experimental terms. The optimum doping conditions were obtained by response surface and point prediction using Design Expert software.
To verify the optimal conditions and to check the correlation between predicted and measured values, synthesis of Mn-doped ferrite nanoparticles was carried out using the optimal reaction parameters given by the software i.e. cationic ratio of approximately 42 at 100 °C for 4 h. Under these conditions, the synthesized nanoparticles were predicted to have saturation magnetization of 75 emu g−1 and 6 °C rise in temperature on AMF application. The optimal nanoparticles were also coated in situ with polyethylene glycol (PEG-2000) under identical conditions. To do so, 0.13 M PEG-2000 was initially magnetically stirred into 11.5 mL water for 1 h followed by the same protocol as described earlier for synthesis of Mn-doped nanomaterials.
2.4 Characterization of nanoparticles
Next, to determine Fe and Mn content in the nanoparticles, ICP-MS was done. Briefly, 50 mg of the MNPs were digested with ICP grade HNO3 and heated at 80 °C until a clear solution was formed. The volume of the sample was made upto 50 mL with deionized water. The samples were then analyzed with the help of Agilent 7700 series ICP-MS system (Santa Clara, California, USA). X-ray photoelectron spectroscopy (XPS) was further done to confirm the elemental composition of the optimally synthesized Mn-doped Ferrite MNPs using Nexsa base spectrophotometer (ThermoFisher Scientific, Waltham, Massachusetts, USA). The PEG-2000 coating onto the surface layer of optimal MNPs was further confirmed by Agilent Fourier transform infrared (FTIR) 600 series spectrometer (Santa Clara, California, USA).
The parametric dependence of magnetic parameters of a nanomaterial, namely anisotropy energy constant, saturation magnetization on its thermal profile when exposed to an alternating magnetic field was further studied. To calculate the anisotropy energy constant for all the samples, time dependent magnetization was measured at room temperature. In the process, relaxation of magnetization was measured as a function of time after the externally applied magnetic field was switched off. The relaxation time constant was calculated using the following equation:
| M(t) = Moe−t/τ | (2) |
Then the anisotropy energy constant was calculated by using the following equation:
| τ = τoeKV/TKB | (3) |
2.5 Magnetic hyperthermia measurements
The calorimetric magnetic hyperthermia efficiency of the synthesized magnetic MnxFe3−xO4 nanoparticles was calculated using the DM2 equipped DM100 nanomagnetic heating system by nB nanoscale Biomagnetics (Zaragoza, Spain). The aqueous nanoparticle dispersions were subjected to an AC magnetic field (f) at 405 kHz with a field amplitude (H) of 168 Oe for 1200 s to determine the increase in temperature. A fluoro-optic thermometer fiber probe was used to probe the temperature every 0.2 s after switching on the magnetic field.The hyperthermia output was investigated in terms of the specific absorption rate (SAR), which is defined as the power dissipation per unit mass of nanoparticle (W g−1), calculated by using the following equation:
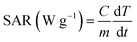 | (4) |
However, due to the existence of discrepancies in SAR value owning to its strong dependence on magnetic field parameters, the hyperthermia output was further evaluated in terms of intrinsic loss power (ILP) given as:
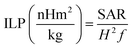 | (5) |
2.6 Cellular studies
The biocompatibility of the optimal MNPs (0–1000 μg mL−1), both bare and PEG-coated, were determined on L929 cell lines for a period of 24 h using MTT assay. The cytotoxic effect of the hyperthermic treatment in presence of optimal PEG-MNPs was then evaluated on U87-MG cell line by MTT assay. The treatment controls were established as follows: (a) untreated cells; (b) cells treated with heat alone for 20 min; (c) cells treated with MNPs alone for 20 min; (d) cells analyzed immediately after heat treatment for 20 min in the presence of MNPs, (e) cells analyzed post-24 h of heat treatment for 20 min in the presence of MNPs.The effect of heat treatment on cytoskeleton of glioma cells was also analyzed by confocal microscopy. For the experiment, PEG-MNPs was conjugated to Rhodamine 6G (R6G; Invitrogen) by incubating 500 μg mL−1 MNPs with 50 μg mL−1 R6G at RT for 12 h. After heat treatment in presence of R6G-PEG-MNPs, U87-MG cells were fixed with 4% paraformaldehyde for 5 min at RT. The cells were then stained with Hoechst-33342 (5 μg mL−1) for 5 min followed by cytoskeletal staining with Fluorescein Phalloidin (Invitrogen) for 20 min. The cells were rinsed with PBS and mounted on a glass slide to visualize under Zeiss LSM880 confocal microscope (Carl Zeiss, Thornwood, New York).
The changes in cellular morphology were further determined by using a JEOL JSM-IT300 scanning electron microscope (Akishima, Tokyo, Japan).15 For the analysis, glioma cells were grown to confluency on coverslips in 35 mm tissue culture Petri-plates. Post-heat treatment for 20 min, cells were fixed with 2.5% glutaraldehyde containing 0.1 M phosphate buffer for 60 min at 4 °C. Following incubation, samples were serially dehydrated using graded ethanolic solutions (10%, 25%, 50%, 75% and 100%) for 20 min each. After air-drying, samples were sputter coated with gold–palladium before SEM analysis.
3. Results and discussion
3.1 Physical properties of the MNPs
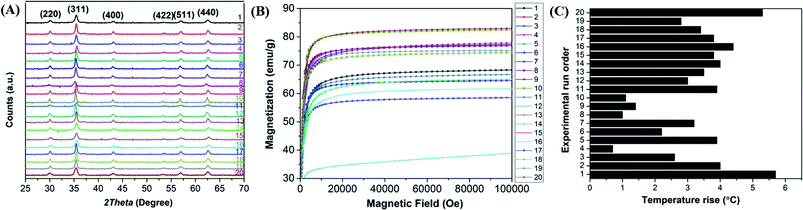
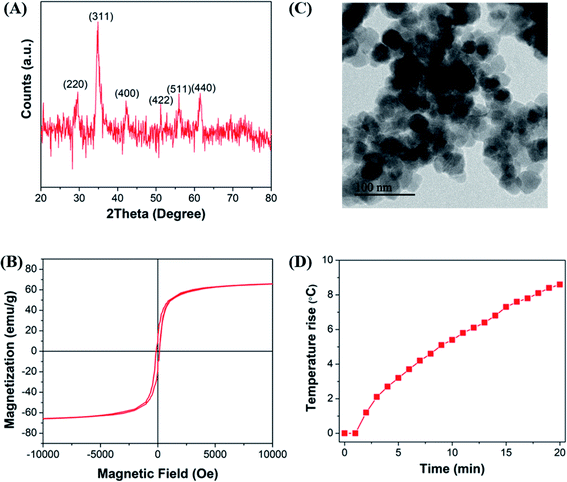
The crystallite structure of the Mn-doped ferrite nanoparticles was determined by X-ray diffraction (Fig. 1(A)). No traces of other iron oxide phases were found which suggest the formation of single phase MnxFe3−xO4 nanoparticles. The relative intensity and position of all peaks match well with the standard magnetite (Fe3O4) crystal.37 Further characterizations including the estimation of crystallite size, lattice constant, hydrodynamic size, surface charge and dopant value (x) of all the nanomaterials generated in the study were done to determine the nature and composition of all the nanomaterials synthesized in each reaction (ESI file; Table S2†). The lattice parameter obtained for all the synthesized nanoparticles correlates well with the reported values for that of Mn-ferrite nanomaterials.15,37 The variation in lattice constant observed in comparison to the reported value for Fe3O4 MNPs (0.836 nm),38 further indicates successful doping of Mn ions into ferrite structure.15Fig. 1(B) shows the MH curve at room temperature for all the synthesized magnetic nanoparticles suggesting that the saturation magnetization of the particles was found to vary between 40–83 emu g−1 with change in the selected factors. The graph shows that the run order 12 corresponding to maximum doping shows minimum Ms of 41 emu g−1 and the one corresponding to minimum doping (run order 19) shows a higher Ms of 75 emu g−1. While the maximum value of Ms (83 emu g−1) was observed for medium level doped NPs (run order 9 and 10). This is consistent with the various studies, which report that magnetic properties of the nanoparticles are affected by the doping percentage.39,40 Table S3† lists the magnetic properties of all the synthesized nanosystems.
The magnetization as a function of temperature for the nanoparticles exhibiting maximum magnetization (run order 9) and maximum degree rise in temperature (run order 1) are shown in ESI Fig. S2(A) and (B),† respectively.
The hyperthermia profile of all the MnxFe3−xO4 nanoparticles was determined on application of AMF (405 kHz and 168 Oe) for 20 min (Fig. 1(C)). The results indicated that the maximum temperature rise (5.7 °C) was achieved for nanoparticles synthesized at the lower cationic ratio at low temperature (run order 1) while the minimum temperature rise (0.7 °C) was observed for nanoparticles synthesized using higher cationic ratio at a higher temperature (run order 4). The SAR and ILP values obtained for all the MNPs are presented in Table S3 (ESI file†). As observed in the table, the SAR values obtained for the synthesized nano-systems are lower than that obtained for some of the reported systems41–43 but are also in accordance with other reported systems used for applications in nano-theranostic-based cancer therapy.44–47 A micromode ferrofluid (size ∼7 nm) is one such example of magnetic nano-systems employed for commercial purposes despite of lower ILP of 0.15–0.37 nHm2 kg−1.48 Thus, indicating that the MNPs generated in the study can be used for hyperthermia therapy.
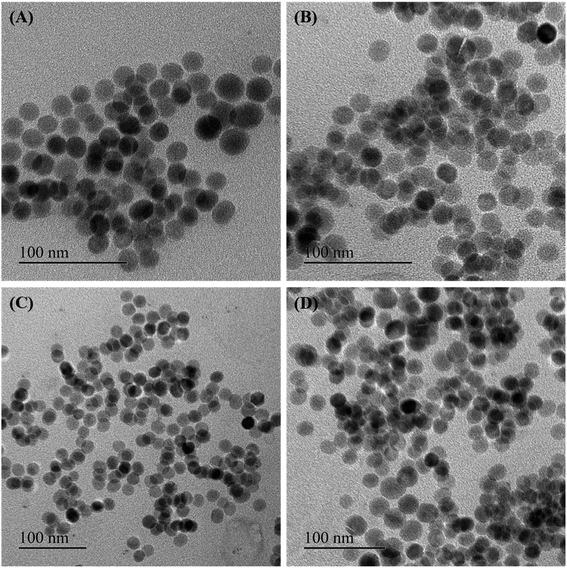
Some of the as-synthesized MnxFe3−xO4 nanoparticles corresponding to run orders 7, 2, 6 and 1, were observed under TEM to determine the crystallite size of the nanomaterials (Fig. 2). The crystallite sizes obtained for these nanomaterials were determined to be 28.3 ± 1.7 nm, 25.1 ± 0.9 nm, 16.7 ± 1.1 nm and 17.5 ± 2 nm, respectively. The results indicate the generation of nearly spherical nanoparticles with size differences due to synthesis under different reaction conditions. With lower Mn doping, the crystallite size of the nanoparticles were observed to be greater (∼25 nm) than that obtained for higher Mn doped nanoparticles (∼17 nm). In accordance with this finding, various other studies have also reported changes in crystallite size of the nanoparticles on introducing dopants in the lattice structure of the material.15,37
A brief description of the electronic properties of Mn-doped Fe3O4 nanoparticles studied theoretically is given below. Sharifi et al. performed density functional theory (DFT) simulations to check changes in the geometrical and electronic properties of MnFe2O4.49 For this study, they considered both normal and inverse spinel structures and all of them were ferrimagnetic. To confirm, they further computed the XRD patterns optimized by DFT calculations and concluded that its XRD pattern is a combination of normal and inverse spinel structures. Electronic band structures and atom-projected density of states of the considered structures suggest that the normal spinel MnFe2O4 is an insulator whereas the inverse spinel MnFe2O4 is predicted to be conducting in nature which has not been observed experimentally. The lattice constants, spin-up gap, and spin-down gap of the considered structures calculated by DFT are listed in Table 2 given below. According to the atom-projected DOS of normal and inverse MnFe2O4 spinel structures, they suggested that MnFe2O4 is a combination of 20% inverse and 80% normal spinel structures. It was also seen that the density of states near the Fermi level of MnFe2O4 is higher. Brabers et al. have shown that two types of cation migration take place in MnxFe3−xO4.50 At 200 °C, the cation exchange between the octahedral and tetrahedral sublattices occurs in the entire system and the octahedral Mn3+ clustering occurs only in that part of the system rich in manganese. As observed, MnxFe3−xO4 shows two crystal structures at room temperature i.e., cubic spinel structure when x < 1.9 and tetragonally deformed spinal structure when x > 1.9.
| a (Å) | c (Å) | Spin up gap (eV) | Spin down gap (eV) | |
|---|---|---|---|---|
| Normal spinel | 6.14 | 8.68 | 1.4 (indirect) | 4.5 (direct) |
| Inverse spinel | 5.96 | 8.71 | 0 | 0 |
As for the magnetic properties of MnxFe3−xO4, Miao et al. have shown that its magnetization increases first up to some value of x (≤0.37) and above this value of x, it starts decreasing.51 As known, MnFe2O4 has a mixed spinel structure with the Mn ions predominantly occupying tetrahedral sites. Mn2+ has five unpaired electrons, which is the same number as in Fe3+, and one more than in Fe2+. For MnxFe3−xO4 with small x values, the Mn2+ dopant can replace Fe2+ to give a magnetic moment of (4 + x) μB per formula unit, resulting in an enhanced magnetic moment in comparison with [Fe3+]Td[Fe2+Fe3+]OhO4. However, as the doping level further increases, the magnetization gradually decreases (x = 1.57) due to the weakening of the Td–Oh interaction when Fe3+ is replaced by Mn2+ in the Td site.52–54
3.2 Central composite design (CCD) and response surface analysis
The fitted model equation to determine the saturation magnetization (R1) of the nanomaterials can be defined as follows:| R1 = 74.22 + 7.20A + 2.53B − 1.08C − 0.6738AB + 2.32AC − 0.0113BC − 4.17A2 + 2.67B2 − 2.13C2 | (6) |
For testing the fit of the model, the regression equation and determination of coefficient (R2) were evaluated. The model presented a high determination of coefficient value (R2 = 0.7831) which suggests that 78.31% of the variables; cation ratio, reaction temperature and time were supported by the response.55,56 The corresponding ANOVA analysis of the fitted model for saturation magnetization (R1) is presented in Table S4.† The ANOVA of quadratic regression model as presented from the Fisher's F-value of 4.01 with P-value corresponding to 0.0205 (<0.05) demonstrated that the model was significant. As seen in Table S4,† the linear effect of cationic ration (A) and its squared term had the maximum effect on the response with the cation ratio variable (A) being the most significant factor in determining the outcome of the model (P < 0.005).
The fitted model equation for the total degree rise in temperature, represented by R2, is as follows:
| R2 = 3.73 − 0.1857A − 0.8730B − 0.0972C − 0.4250AB − 0.1000AC + 1.15BC − 0.2973A2 − 0.6686B2 + 0.1623C2 | (7) |
The model presented a high determination of coefficient (R2 = 0.8800) suggesting that 88% of the variables were also supported by the response. The corresponding ANOVA analysis of the fitted model for total degree rise in temperature (R2) is presented in Table S5.† The Fisher's F-value of 8.15 with P-value corresponding to 0.0015 (<0.005) of the model demonstrated that the model was significant. As seen in Table S5,† the linear effect of reaction temperature (B), the interaction of reaction temperature (B) and time (C), and the squared effect of reaction temperature (B2) forms the most significant factors in determining the outcome of the model (P < 0.005) with the first two terms being highly significant model terms (P < 0.0005).
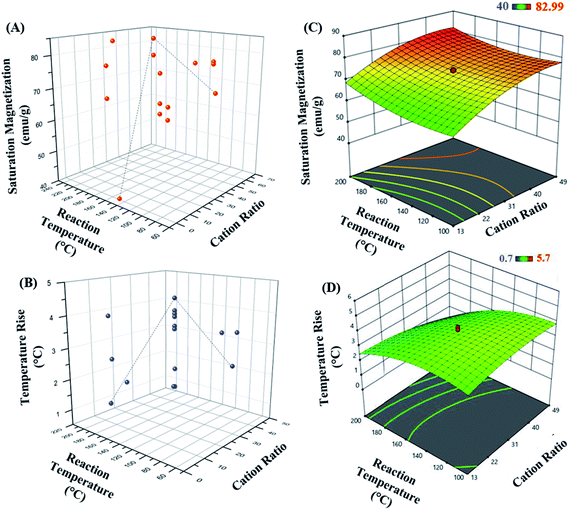
The 3D response surface plots represent graphical description of the regression equation to determine the optimum values of the variables taken within the ranges considered, such that the response is maximized.57 The respective plots for both responses, saturation magnetization and hyperthermic rise are presented in Fig. 3. Fig. 3(A and B) represent the saturation magnetization and the temperature rise (hyperthermia output), respectively as a function of both cation ratio and reaction temperature for all the 20 experimental runs. Each contour curve at the base of the 3D response curves, constitutes of an infinite number of combinations of two test variables with the third variable maintained at its respective zero level. Elliptical shape of the contours represents perfect interaction between the independent variables.58–60 Thus, the elliptical nature of the contours suggests that the variables chosen in the study directly influence the outcome of the responses.
Further, as seen in Fig. 3(C and D), the response surface graphs obtained for both responses were elliptical in the entire region. The maximum response values are achieved at the point of intersection of major and minor axes of the ellipse. The cation ratio acts as one of the key variables affecting the magnetic property of the MnxFe3−xO4 nanoparticles.
The set of experiments in the RSM resulted in an optimum set of independent variables in order to obtain the higher levels of saturated magnetization with maximum total degree rise in temperature on AMF application. The regression coefficient (R2) value of 0.783 (in case of R1; saturation magnetization) and 0.880 (for R2; hyperthermia output) showed a good fitting of the model with the experimental data obtained, and the model predicted accurately the maximum point of saturation magnetization of the optimal nanoparticle synthesized.
3.3 Effect of magnetic properties on hyperthermia profile
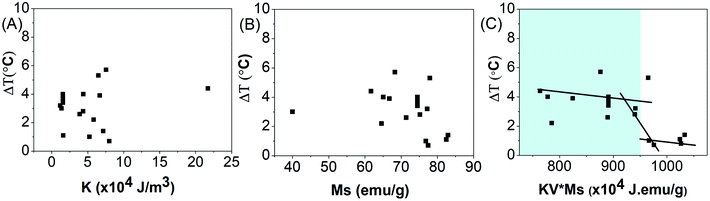
The parametric dependence of magnetic parameters of a nanomaterial, namely anisotropy energy constant, saturation magnetization and the thermal profile of the nanoparticles when exposed to an alternating magnetic field was further studied.Fig. 4(A and B) show the total degree rise in temperature as a function of anisotropy energy constant and saturation magnetization, suggesting no correlation between them.
The total degree rise in temperature was then plotted as a function of the K.V.Ms value which suggests that on increasing K.V.Ms, initially ΔT decreases slowly until it reaches approximately 950 J emu g−1. Beyond this, ΔT decreases rapidly with further increase in K.V.Ms value (Fig. 4(C)).
The magnetic measurements combined with magnetic hyperthermia suggest that a nanoparticle with K.V.Ms value lying in the region shaded blue (K.V.Ms < 950 J emu g−1) in Fig. 4(C) will exhibit superior heat generating capabilities for successful use in biomedical applications. Hence, the K.V.Ms value for the magnetic nanoparticles can be considered as a good measure of magnetic parameter regarding hyperthermic effect.
3.4 Verification of optimum conditions
To confirm aforementioned results, the synthesis of Mn-doped ferrite nanoparticles was conducted under the optimum conditions calculated by response surface analysis to achieve optimal amounts of both saturation magnetization (R1) and total degree rise in temperature (R2). According to the software, synthesizing MNP using cation ratio (Fe3+/Mn2+) of 42 at 100 °C for 4 h as the reaction temperature and time, respectively would yield Mn0.07Fe2.93O4 nanoparticles with saturation magnetization of 75 emu g−1 and 6 °C degree rise in temperature on AMF application. Based on these results, the nanoparticles with higher magnetic properties and heat generation capabilities were generated at the higher Fe3+/Mn2+ ratio, lower temperature and shorter duration of time.The crystallite structure of the optimal Mn-doped ferrite samples synthesized was confirmed by X-ray diffraction (Fig. 5(A)). The average particle size of the synthesized nanoparticle was found to be 19.2 ± 2.3 nm with spherical morphology as obtained by TEM image analysis using Digital Micrograph software (Fig. 5(B)). The size distribution profile is shown in ESI Fig. S1.† Fig. 5(C) represents the DC hysteresis loops of the optimal sample synthesized at 300 K. As shown in the graph, negligible hysteresis is observed which indicates the superparamagnetic behavior of the nano-systems. The Ms obtained for the sample is 73 emu g−1 which is very similar to that predicted by RSM (75 emu g−1). The magnetic properties of the particle as a function of temperature when 100 Oe field is applied is shown in ESI Fig. S2(C).†
Fig. 5(D) shows the hyperthermia profile of the nanoparticles when exposed to an AMF of strength 405 kHz and 168 Oe for 20 min. Though RSM predicted rise in temperature on AMF application to be about 5.5 °C, we observed a total degree rise of 8.4 °C in temperature on AMF application Fig. 5(D).
The results demonstrate that the correlation between predicted and measured value of these experiments verified the validity of the response model and the existence of an optimum point.
Overall, in this study, the RSM technique proved to be a powerful tool for optimizing the magnetic behavior by manganese doping. In the present work, all variables were positively significant factors, the proposed model equations and the optimum condition results illustrate the interaction between the factors in case of R1 (saturation magnetization).
The investigation of the elemental composition of the optimally synthesized Mn-ferrite MNPs was further done using XPS in the 0–1300 eV region. The survey spectrum (Fig. 6(A)) indicates the presence of all Fe, Mn and O in the nanomaterial indicating successful doping of Mn ions in the ferrite structure.15 The high-resolution XPS spectra of Fe 2p, Mn 2p and O 1s respectively of the MNPs, is represented in Fig. 6(B–D). The presence of doublet characteristic peaks of Fe3+ and Fe2+ in the Fe 2p spectra (Fig. 6(B)) confirms the formation of Fe3O4.61 Further, deconvolution of the Mn 2p electron peaks presented three valence states of Mn atoms corresponding to Mn2+, Mn3+, and Mn4+ in the ferrite structure (Fig. 6(C)). The presence of these Mn valence states validates interaction of Mn ions with oxygen atoms.62 The deconvolution of O 1s photoelectron spectrum into two O2− chemical state characteristic peaks corresponding to O and O1− further confirms formation of Fe3O4 based nanomaterial (Fig. 6(D)).63 The structure coordinates of the synthesized nanosystem is presented in Table S6.†
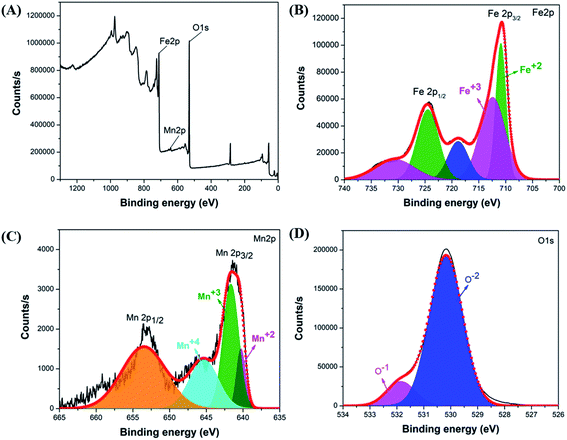 | ||
| Fig. 6 (A) Survey scan of optimal Mn-ferrite MNPs, XPS spectra of (B) Fe 2p, (C) Mn 2p and (D) O 1s of the MNPs. | ||
After confirmation of generation of optimal Mn-doped Fe3O4 nanoparticles, the MNPs was further coated with PEG to be applied for magnetic hyperthermia-mediated cancer therapy (MHCT) against glioma cells. Surface functionalization of the MNPs with PEG was confirmed by FTIR analysis (ESI Fig. S3†). Before starting with the in vitro experiments, the PEG-coated Mn-doped Fe3O4 nanoparticles (PEG-MNPs) were investigated for their capability to generate heat as a function of variable AMF frequency and field strength (Fig. 7).
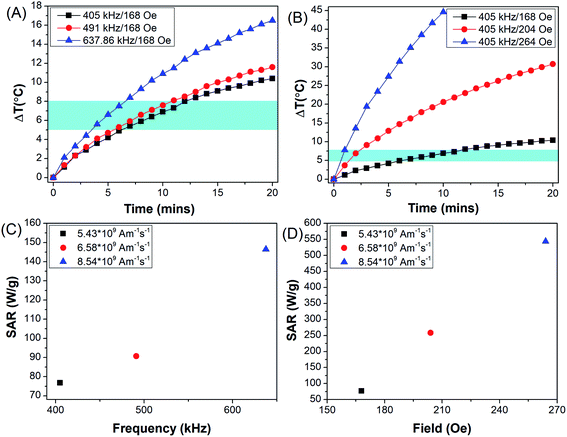
Fig. 7(A) represents rise in temperature (ΔT) achieved when PEG-MNPs were subjected to AMF of field strength 168 Oe and frequency ranging from 405–637.6 kHz. While Fig. 7(B) represents rise in temperature achieved on exposure of PEG-MNPs to variable field strength (168–264 Oe) with fixed AMF frequency of 405 kHz. The frequency (f) and field (H) were varied such that the product Hf remains the same in both graphs (Fig. 7(A and B)). As seen in the graphs, hyperthermia output in terms of ΔT increased with increasing frequency and field, respectively. Fig. 7(C and 6D) further represent the SAR value obtained when the MNPs were subjected to the variable frequency and field, respectively. The inset values corresponds to the Hf product value obtained respectively by varying the AMF frequency and field accordingly. As the PEG-MNPs demonstrate the capability to achieve the desired hyperthermia window (ΔT = 5–8 °C) even at the lowest AMF parameters, i.e. H = 168 Oe and f = 405 kHz, the synthesized MNPs were further evaluated for their potential to be employed as theranostic agents for in vitro magnetic hyperthermia applications against solid tumors like glioma.
3.5 In vitro magnetic hyperthermia
Even though the understanding of how MHCT interacts with cancer cells causing their cell death is limited, it is known to be dependent upon the temperature achieved and the duration of AMF exposure.64 Localized heat generation has been shown to be responsible for any alterations in cellular processes that causes magneto-thermal stress in cells inducing tumor cell death. One of the possible modes of action of hyperthermia on reduced cell viability includes induction of protein denaturation as stability of the proteins is greatly influenced by thermal changes.65 Thus, this affects the processing of various downstream signaling pathways66,67 like progression through the cell cycle, DNA repair mechanisms, activation of immune cells and effect on protein synthesis.68–70 Furthermore, the magneto-thermal stress can also be conducive to an adverse impact on the cellular cytoskeleton structure, membrane integrity, intracellular transport, mitochondrial membrane potential, and RNA processing.15,19,71 In addition, elevated temperatures have also been shown to cause temporary disruption of the biological barriers including blood–brain barrier, leading to increased permeability of therapeutic payloads into the brain tissues for treatment of brain disorders.72,73 Besides these interactive mechanisms, the cells surviving hyperthermia treatment activate their defense mechanism by increasing expression levels of certain chaperone proteins known as heat shock proteins, which are majorly responsible for rendering tumor cells thermo-resistance.74,75Despite the multitude of MHCT interaction mechanisms with tumour cells, its clinical translation is limited, mainly due to reduced heat generating capability of nanosystems inside cellular environment and the induction of thermotolerance which renders MHCT less effective. Hence, optimization of nanoparticle design is required to develop highly efficient heat generating systems to achieve the desired therapeutic outcomes.
For this, the nanoparticles corresponding to the optimized synthesis parameters for maximum hyperthermia output and high magnetization, were then evaluated for their potential to be used as hyperthermia agents for glioblastomas.
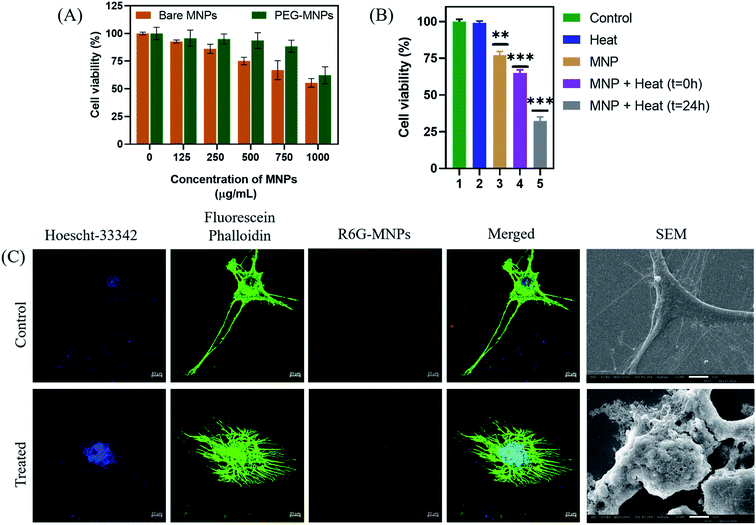
The optimal Mn-doped ferrite nanomaterial coated with PEG-2000 (PEG-MNPs) was observed to be non-toxic till concentration of 750 μg mL−1 while the bare MNPs were observed to be biocompatible till the concentration of 500 μg mL−1 when tested on murine L929 cells (Fig. 8(A)) suggesting the surface functionalization of the MNPs with PEG to be attributed for the enhanced biocompatibility observed. All the in vitro cytotoxicity assays were performed using 500 μg mL−1 concentration of PEG-MNPs.
After determining the biocompatibility of the material, in vitro cytotoxic assay was performed (Fig. 8(B)). The results demonstrated that exposure of cells to heat in the presence of the synthesized nanomaterial (500 μg mL−1) resulted in decrease in percentage cell viability to ∼60% as compared to cell viability observed nearly 75% in presence of MNPs alone. Moreover, re-culturing the cells for 24 h after heat exposure in presence of MNPs further resulted in decrease in cell viability to ∼30%. This demonstrates the long-term effect of heat treatment on glioma cells using the synthesized nanomaterial. The control cells, both untreated and exposed to heat alone, maintained their viabilities ∼100%, suggesting that heat alone has no cytotoxic effect on cancer cells. As described earlier, this reduced cell viability of glioma cells on hyperthermia treatment could be attributed to the effect of heat generated on various cellular processes like protein denaturation, enhanced oxidative stress and DNA damage.70,71
Besides the above suggested causes of glioma cell death, the effect of hyperthermia treatment on cellular cytoskeleton (Fig. 8(C)) and cellular morphology (Fig. 8(D)) was further investigated by confocal microscopy and SEM analysis, respectively and compared to that of the untreated control glioma cells. As seen in the figure, exposure of glioma cells to heat stress caused evident cellular damage that ultimately resulted in cancer cell death. Our results suggests that MHCT in the presence of the optimally synthesized nano-magnetic system generated enough heat to cause plasma membrane disruption that altered various cellular processes, inducing magneto-thermal stress in cells as exhibited by the distorted cytoskeleton also, causing remarkable glioma cell death. Thus, our study indicates the potential of the synthesized manganese ferrite nanosystem to be employed as hyperthermic agent for treatment of solid tumors.
4. Conclusion
Realizing the “good-parameter” that controls magnetic hyperthermia efficiently and systematically is a long-standing issue. We have performed a systematic case study on ferrite magnetic nanoparticles using response surface methodology resulted in an optimum set of independent variables to obtain the desired levels of magnetic hyperthermia output. Our result indicated that the value of saturation magnetization observed for the optimal sample was 73 emu g−1 and the temperature rise achieved on AMF application was 8.4 °C by optimized condition given by RSM. Our experiments on this test material revealed that a product of magnetic anisotropy energy, volume of the nanoparticles and saturation magnetization could be regarded as a “good-parameter” rather than Ms alone to predict and design efficient and desirable magnetic hyperthermic materials. Our method is not restricted to any particular system and can be extended to any material.Conflicts of interest
The authors have no conflict to declare.Acknowledgements
This work was supported by the DST-SERB [grant number ECR/2017/000049]; DST Nanomission [grant number SR/NM/NS-1007/2015(G)] (for PPMS magnetometer facility at Institute of Nano Science and Technology (INST), Mohali).Notes and references
- K. Hayashi, Y. Sato, W. Sakamoto and T. Yogo, ACS Biomater. Sci. Eng., 2017, 3, 95–105 CrossRef CAS PubMed.
- S. Liébana-Viñas, K. Simeonidis, U. Wiedwald, Z.-A. Li, Z. Ma, E. Myrovali, A. Makridis, D. Sakellari, G. Vourlias, M. Spasova, M. Farlea and M. Angelakeris, RSC Adv., 2016, 6, 72918 RSC.
- S. Laurent, S. Dutz, U. O. Häfeli and M. Mahmoudi, Adv. Colloid Interface Sci., 2011, 166, 8–23 CrossRef CAS.
- R. Gupta and D. Sharma, ACS Chem. Neurosci., 2019, 10, 1157–1172 CrossRef CAS PubMed.
- A. Jordan, R. Scholz, P. Wust, H. Fähling and R. Felix, J. Magn. Magn. Mater., 1999, 201, 413–419 CrossRef CAS.
- R. Hergt, S. Dutz, R. Müller and M. Zeisberger, J. Phys.: Condens. Matter, 2006, 18, S2919–S2934 CrossRef CAS.
- R. K. Gilchrist, R. Medal, W. D. Shorey, R. C. Hanselman, J. C. Parrott and C. B. Taylor, Ann. Surg., 1957, 146, 596–606 CrossRef CAS PubMed.
- H. Kenneth, M. D. Luk, R. M. Hulse and T. L. Phillips, West. J. Med., 1980, 132, 179–185 Search PubMed.
- J. R. Oleson, S. K. Calderwood, C. T. Coughlin, M. W. Dewhirst, L. E. Gerweck, F. A. Gibbs and D. S. Kapp, Am. J. Clin. Oncol., 1988, 11, 368–380 CrossRef CAS PubMed.
- B. Thiesen and A. Jordan, Int. J. Hyperthermia, 2008, 24, 467–474 CrossRef CAS PubMed.
- N. R. Datta, S. Krishnan, D. E. Speiser, E. Neufeld, N. Kuster, S. Bodis and H. Hofmann, Cancer Treat. Rev., 2016, 50, 217–227 CrossRef CAS.
- X. Liu, Y. Zhang, Y. Wang, W. Zhu, G. Li, X. Ma, Y. Zhang, S. Chen, S. Tiwari, K. Shi, S. Zhang, H. M. Fan, Y. X. Zhao and X. J. Liang, Theranostics, 2020, 10, 3793–3815 CrossRef CAS.
- L. Dallet, D. Stanicki, P. Voisin, S. Miraux and E. J. Ribot, Sci. Rep., 2021, 11, 3286 CrossRef CAS PubMed.
- A. G. Leonel, A. A. P. Mansur, S. M. Carvalho, L. E. F. Outon, J. D. Ardisson, K. Krambrock and H. S. Mansur, Nanoscale Adv., 2021, 3, 1029–1046 RSC.
- R. Gupta and D. Sharma, ACS Appl. Nano Mater., 2020, 3, 2026–2037 CrossRef CAS.
- C. Pucci, D. De Pasquale, A. Marino, C. Martinelli, S. Lauciello and G. Ciofani, ACS Appl. Mater. Interfaces, 2020, 12, 29037–29055 CrossRef CAS PubMed.
- A. Bazzazzadeh, B. F. Dizaji, N. Kianinejad, A. Nouri and M. Irani, Int. J. Pharm., 2020, 587, 119674 CrossRef CAS PubMed.
- P. Das, L. Salvioni, M. Malatesta, F. Vurro, S. Mannucci, M. Gerosa, M. Antonietta Rizzuto, C. Tullio, A. Degrassi, M. Colombo, A. M. Ferretti, A. Ponti, L. Calderan and D. Prosperi, J. Colloid Interface Sci., 2020, 579, 186–194 CrossRef CAS PubMed.
- R. Gupta and D. Sharma, Int. J. Hyperthermia, 2019, 36, 302–312 CrossRef PubMed.
- M. Ohtake, M. Umemura, I. Sato, T. Akimoto, K. Oda, A. Nagasako, J. H. Kim, T. Fujita, U. Yokoyama, T. Nakayama, Y. Hoshino, M. Ishiba, S. Tokura, M. Hara, T. Muramoto, S. Yamada, T. Masuda, I. Aoki, Y. Takemura, H. Murata, H. Eguchi, N. Kawahara and Y. Ishikawa, Sci. Rep., 2017, 7, 42783 CrossRef CAS PubMed.
- G. Hemery, C. Genevois, F. Couillaud, S. Lacomme, E. Gontier, E. Ibarboure, S. Lecommandoux, E. Garanger and O. Sandre, Mol. Syst. Des. Eng., 2017, 2, 629–639 RSC.
- A. Hanini, L. Lartigue, J. Gavard, K. Kacem, C. Wilhelm, F. Gazeau, F. Chau and S. Ammar, J. Magn. Magn. Mater., 2016, 416, 315–320 CrossRef CAS.
- J. W. Strohbehn and E. B. Douple, IEEE Trans. Biomed. Eng., 1984, 31, 779–787 CAS.
- Y. W. Jun, J. H. Lee and J. Cheon, Angew. Chem., Int. Ed., 2008, 47, 5122–5135 CrossRef CAS PubMed.
- Y. Qu, J. Li, J. Ren, J. Leng, C. Lin and D. Shi, ACS Appl. Mater. Interfaces, 2014, 6, 16867–16879 CrossRef CAS PubMed.
- M. Zhang, Y. Cao, L. Wang, Y. Ma, X. Tu and Z. Zhang, ACS Appl. Mater. Interfaces, 2015, 7, 4650–4658 CrossRef CAS PubMed.
- J. T. Jang, H. Nah, J. H. Lee, S. H. Moon, M. G. Kim and J. Cheon, Angew. Chem., Int. Ed., 2009, 48, 1234–1238 CrossRef CAS PubMed.
- A. G. Kolhatkar, A. C. Jamison, D. Litvinov, R. C. Willson and T. R. Lee, Int. J. Mol. Sci., 2013, 14, 15977–16009 CrossRef PubMed.
- R. E. Rosensweig, J. Magn. Magn. Mater., 2002, 252, 370–374 CrossRef CAS.
- M. Wegmann and M. Scharr, Synthesis of Magnetic Iron Oxide Nanoparticles, in Precision Medicine, ed. H.-P. Deigner and M. Kohl, Academic Press, Furtwangen University, Villingen-Schwenningen, Germany, 2018, ch. 8, pp. 145–181 Search PubMed.
- M. R. Ghazanfari, M. Kashefi and M. R. Jaafari, J. Magn. Magn. Mater., 2016, 405, 88–96 CrossRef CAS.
- A. Tamilvanan, K. Balamurugan, T. Mohanraj, P. Selvakumar and B. Madhankumar, Mater. Today: Proc., 2020 DOI:10.1016/j.matpr.2020.02.801.
- E. Cheraghipour and M. Pakshir, J. Environ. Chem. Eng., 2021, 9, 104883 CrossRef CAS.
- Z. Ciğeroğlu, G. Küçükyıldız, B. Erim and E. Alp, J. Mol. Struct., 2021, 1224, 129182 CrossRef.
- S. Ge, X. Shi, K. Sun, C. Li, J. R. Baker, M. M. Banaszak Holl and B. G. Orr, J. Phys. Chem. C, 2009, 113, 13593–13599 CrossRef CAS PubMed.
- M. Z. Alam, P. Jamal and M. M. Nadzir, World J. Microbiol. Biotechnol., 2008, 24, 1177–1185 CrossRef CAS.
- I. Elahi, R. Zahira, K. Mehmood, A. Jamil and N. Amin, J. Basic Appl. Sci., 2012, 6, 1–5 CAS.
- X. Liu, J. Liu, S. Zhang, Z. Nan and Q. Shi, J. Phys. Chem. C, 2016, 120, 1328–1341 CrossRef CAS.
- W. Montha, W. Maneeprakorn, I. M. Tang and W. Pon-On, RSC Adv., 2020, 10, 40206–40214 RSC.
- S. Chakrabarty, A. Dutta and M. Pal, J. Alloys Compd., 2015, 625, 216–223 CrossRef CAS.
- R. Ludwig, M. Stapf, S. Dutz, R. Müller, U. Teichgräber and I. Hilger, Nanoscale Res. Lett., 2014, 9, 602 CrossRef PubMed.
- P. T. Phong, P. H. Nam, D. H. Manh and I. J. Lee, J. Magn. Magn. Mater., 2017, 433, 76–83 CrossRef CAS.
- E. Mazarío, J. Sánchez-Marcos, N. Menéndez, M. Cañete, A. Mayoral, S. Rivera-Fernández, J. M. de la Fuente and P. Herrasti, J. Phys. Chem. C, 2015, 119, 6828–6834 CrossRef.
- M. Ma, Y. Wu, J. Zhou, Y. Sun, Y. Zhang and N. Gu, J. Magn. Magn. Mater., 2004, 268, 33–39 CrossRef CAS.
- C. L. Dennis, A. J. Jackson, J. A. Borchers, R. Ivkov, A. R. Foreman, J. W. Lau, E. Goernitz and C. Gruettner, J. Appl. Phys., 2008, 103, 07A319 CrossRef.
- M. E. de Sousa, M. B. Fernández van Raap, P. C. Rivas, P. Mendoza Zélis, P. Girardin, G. A. Pasquevich, J. L. Alessandrini, D. Muraca and F. H. Sánchez, J. Phys. Chem. C, 2013, 117, 5436–5445 CrossRef CAS.
- M. E. F. Brollo, J. M. Orozco-Henao, R. López-Ruiz, D. Muraca, C. S. B. Dias, K. R. Pirota and M. Knobel, J. Magn. Magn. Mater., 2016, 397, 20–27 CrossRef CAS.
- M. Kallumadil, M. Tada, T. Nakagawa, M. Abe, P. Southern and Q. A. Pankhurst, J. Magn. Magn. Mater., 2009, 321, 1509–1513 CrossRef CAS.
- S. Sharifi, A. Yazdani and K. Rahimi, Sci. Rep., 2020, 10, 10916 CrossRef CAS PubMed.
- V. A. M. Brabers, J. Phys. Chem. Solids, 1971, 32, 2181–2191 CrossRef CAS.
- Y. Miao, Q. Xie, H. Zhang, J. Cai, X. Liu, J. Jiao, S. Hu, A. Ghosal, Y. Yang and H. Fan, Theranostics, 2019, 9, 1764–1776 CrossRef CAS PubMed.
- L. Yang, L. Ma, J. Xin, A. Li, C. Sun, R. Wei, B. W. Ren, Z. Chen, H. Lin and J. Gao, Chem. Mater., 2017, 29, 3038–3047 CrossRef CAS.
- X. Lasheras, M. Insausti, J. M. de la Fuente, I. G. de Muro, I. Castellanos-Rubio, L. Marcano, M. L. Fernández-Gubieda, A. Serrano, R. Martín-Rodríguez, E. Garaio, J. A. García and L. Lezama, Dalton Trans., 2019, 48, 11480–11491 RSC.
- K. Vamvakidis, M. Katsikini, G. Vourlias, M. Angelakeris, E. C. Paloura and C. Dendrinou-Samara, Dalton Trans., 2015, 44, 5396–5406 RSC.
- S. Basu, S. K. M. Hossain, D. Chakravorty and M. Pal, Curr. Appl. Phys., 2011, 11, 976–980 CrossRef.
- S. Akhnazaroza and V. Kefarov, Experiment optimization in chemistry and chemical engineering, Mir Publishers, Moscow and Chicago, 1982, p. 312 Search PubMed.
- A. I. Khuri and J. A. Cornell, Response surfaces: designs and analysis, CRC Press, New York, 2nd edn, 1987 Search PubMed.
- M. S. Tanyildizi, D. Ozer and E. Elibiol, Process Biochem., 2005, 40, 2291–2296 CrossRef CAS.
- Y. Wu, S. W. Cui, J. Tang and X. Gu, Food Chem., 2007, 105, 1599–1605 CrossRef CAS.
- M. J. Dalvand, S. S. Mohtasebi and S. Rafiee, Food Sci. Nutr., 2014, 2, 758–767 CrossRef PubMed.
- A. S. Basaleh and S. M. Sheta, Anal. Bioanal. Chem., 2020, 412, 3153–3165 CrossRef CAS PubMed.
- S. M. Sheta, S. M. El-Sheikh, M. M. Abd-Elzaher, M. L. Ghanemc and S. R. Salem, RSC Adv., 2019, 9, 20463–20471 RSC.
- M. Alhaddad and S. M. Sheta, ACS Omega, 2020, 5, 28296–28304 CrossRef CAS PubMed.
- D. Chang, M. Lim, J. Goos, R. Qiao, Y. Y. Ng, F. M. Mansfeld, M. Jackson, T. P. Davis and M. Kavallaris, Front. Pharmacol., 2018, 9, 831 CrossRef PubMed.
- P. Leuenberger, S. Ganscha, A. Kahraman, V. Cappelletti, P. J. Boersema, C. Von Mering, M. Claassen and P. Picotti, Science, 2017, 355, eaai7825 CrossRef PubMed.
- T. Feng, L. Zhou, Z. Wang, C. Li, Y. Zhang, J. Lin, D. Lu and P. Huang, Biomaterials, 2020, 232, 119709 CrossRef CAS PubMed.
- L. Beola, L. Asín, C. Roma-Rodrigues, Y. Fernández-Afonso, R. M. Fratila, D. Serantes, S. Ruta, R. W. Chantrell, A. R. Fernandes, P. V. Baptista, J. M. de la Fuente, V. Grazú and L. Gutiérrez, ACS Appl. Mater. Interfaces, 2020, 12, 43474–43487 CrossRef CAS PubMed.
- J. R. Lepock, Int. J. Hyperthermia, 2005, 21, 681–687 CrossRef CAS PubMed.
- M. Payne, S. H. Bossmann and M. T. Basel, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2020, 12, e1638 Search PubMed.
- S. Piehler, L. Wucherpfennig, F. L. Tansi, A. Berndt, R. Quaas, U. Teichgraeber and I. Hilger, Nanomedicine, 2020, 28, 102183 CrossRef CAS.
- P. de Andrade Mello, S. Bian, L. Savio, H. Zhang, J. Zhang, W. Junger, M. R. Wink, G. Lenz, A. Buffon, Y. Wu and S. C. Robson, Oncotarget, 2017, 8, 67254–67268 CrossRef PubMed.
- S. N. Tabatabaei, M. S. Tabatabaei, H. Girouard and S. Martel, Int. J. Hyperthermia, 2016, 32, 657–665 CrossRef CAS PubMed.
- J. Estelrich and M. A. Busquets, Magnetic Nanoparticles as Delivery Systems to Penetrate the Blood-Brain Barrier, in Nanomedicines for Brain Drug Delivery, ed. J. O. Morales and P. J. Gaillard, Humana, New York, NY, 2021, vol. 1, p. 157 Search PubMed.
- E. M. Scutigliani, Y. Liang, H. Crezee, R. Kanaar and P. M. Krawczyk, Cancers, 2021, 13, 1243 CrossRef PubMed.
- T. J. Carter, G. Agliardi, F. Y. Lin, M. Ellis, C. Jones, M. Robson, A. Richard-Londt, P. Southern, M. Lythgoe, M. Zaw Thin, V. Ryzhov, R. T. M. de Rosales, C. Gruettner, M. R. A. Abdollah, R. B. Pedley, Q. A. Pankhurst, T. L. Kalber, S. Brandner, S. Quezada, P. Mulholland, M. Shevtsov and K. Chester, Small, 2021, 17, e2005241 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra02376d |
| This journal is © The Royal Society of Chemistry 2021 |