Open Access Article
Open Access ArticleElectronic effects on polypyridyl Co complex-based water reduction catalysts†
Xusheng Guoab,
Chao Lia,
Weibo Wanga,
Baowen Zhanga,
Yuanjun Hou*a,
Xuesong Wang *ab and
Qianxiong Zhou
*ab and
Qianxiong Zhou *a
*a
aKey Laboratory of Photochemical Conversion and Optoelectronic Materials, Technical Institute of Physics and Chemistry, Chinese Academy of Science, Beijing 100190, P. R. China. E-mail: houyuanjun@mail.ipc.ac.cn; xswang@mail.ipc.ac.cn; zhouqianxiong@mail.ipc.ac.cn
bUniversity of Chinese Academy of Science, Beijing 100049, P. R. China
First published on 12th July 2021
Abstract
Three new isomeric cobalt complexes of TPA (tris(2-pyridylmethyl)amine) based on methoxy substitution at the ortho, meta and para positions, respectively, were constructed and their photocatalytic proton reduction efficiencies were compared. It was found that there are good linear correlations with the Hammett constants of the substituents for the computed Co–N bond lengths, redox potentials of CoII/I and CoI/0 events, and the photocatalytic activities of the complexes. The ortho-substituted Co complex distinguished itself from the others remarkably in all these comparisons, demonstrating the presence of a steric effect besides the electronic effect. For other examined complexes, a stronger electron-donating substituent may lead to a higher hydrogen evolution efficiency, suggesting that the formation of a Co(III) hydride intermediate is the rate-limiting step.
Introduction
Sustainable energy sources and carriers are the key to overcoming the approaching global energy crisis and climate change.1,2 Thanks to its high energy density and clean combustion, hydrogen has become one of the most suitable energy carriers.3–5 Photocatalytic water splitting makes the production of hydrogen also a carbon-free process, and therefore has received enthusiastic attention.6–9 Progress has been made in the past decades in the pursuit of efficient, robust and low-cost water reduction catalysts.10–14 Among all these catalysts, the polypyridyl cobalt complexes are particularly attractive due to their easy-to-tune ligands and remarkable stability,15–20 and have become a perfect platform to build the bridge between structure and catalytic activity.21–23In spite of the diverse molecular structures of the cobalt complexes, their mechanisms for catalytic hydrogen evolution are very similar,24–26 in which two key intermediates are inevitable, i.e. the low valence Co(I) and Co(III) hydride intermediates.27–37 However, a full understanding of how electronic effects of the ligands contribute to the overall catalytic activity is still lacking.38–40 Opposite conclusions could be drawn in different studies, for example, electron-withdrawing substituents brought a higher catalytic activity in some cases40–42 while contrary results were obtained in others.43–46 In these studies, different substituents were generally utilized. Besides electronic effects, these substituents may also elicit different interactions with solvents and substrates, and complicate the underlying mechanisms. It occurred to us that a substituent may has a varied Hammett constants in terms of its substitution positions,47 which may reveal the real electronic effect while ruling out the unwanted interferences. Bearing this idea in mind, we herein introduced a methoxy group into a TPA (tris(2-pyridylmethyl)amine) ligand-supported cobalt complex (C1), a catalyst has been intensively explored in CO2 reduction,48,49 water oxidation50 and water reduction.51 A methyl substituted analogue (C5) was also prepared for comparison (Scheme 1). By varying the substitution position from para to meta, the role of the methoxy group may change from an electron donor to an acceptor.47 Along with this change, the photocatalytic hydrogen evolution efficiencies of these complexes showed a close correlation with the Hammett constants of the substituents. Interestingly, the ortho-substituted complex (C2) behaved abnormally, hinting at an involvement of a steric effect.
Results and discussion
Synthesis and characterization
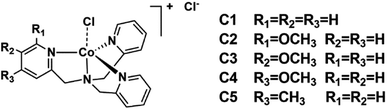
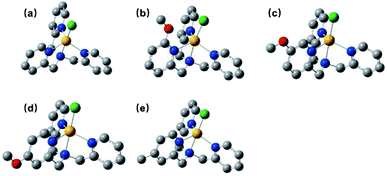
The ligands L2–L5 were obtained by the reaction between N,N-bis(2-pyridinylmethyl)amine and methoxy- or methyl-substituted 2-pyridinecarboxaldehyde according to the literatures,52 which were subsequently combined with equivalent cobalt chloride hexahydrate to give four complexes C2–C5. All complexes were characterized by 1H NMR (Fig. S3†), IR (Fig. S12†), ESI-MS (Fig. S8–S11†), UV-vis absorption spectroscopy (Fig. S13†), elemental analysis and cyclic voltammetry.The 1H NMR spectra for all complexes were broaden up to 155 ppm which is consistent with a paramagnetic high-spin state species as previously reported.40 It is somewhat interesting that there was a proton signal at −3 ppm for C2, which may be attributed to the methoxy group in a shielding region of the Co center.53 The ortho-position substitution should account for this result, which allows the methoxy group to be in close proximity to Co. For UV-vis absorption spectra, all the complexes exhibited d–d transitions in the region of 450–700 nm in acetonitrile, consistent with the reported analogous cobalt complexes.51,54 The molar extinction coefficients of these d–d transitions at their absorption maxima ranged from 159 to 214 (Table S1†), suggesting a five-coordination configuration for all the Co(II) complexes in acetonitrile.48,55 Therefore, the DFT structure optimization of all the complexes began with a five-coordination configuration, and ended up in a most stable trigonal-bipyramidal geometry as presented in Fig. 1. The optimized structure of C1 is in good agreement with the crystal data (CCDC 1529343) of an analogue [Co(TPA)Cl]ClO4 (Table S5†).49 The Gibbs free energies of possible spin states of all the complexes were calculated and compiled in Table S6,† in which the high-spin states show lower energy and therefore may be true conditions of the Co center. The Co–N bond lengths of all the complexes are also in line with other high spin Co(II) complexes.40,43,56 It is worth noting that the Co–N1 bond lengths have a close correlation with the Hammett constants of the substituents (Fig. 2). The Hammett constants of meta-methoxy, para-methoxy and para-methyl substituents are 0.12, −0.27, and −0.17, respectively.47 It should be noted that the determination of accurate Hammett constants of ortho substituents are difficult due to the steric effect. We set the Hammett constant of ortho-methoxy as −0.27, a value similar to that of para-methoxy just for clarity when compared with other complexes. An electron-donating substituent would build a more basic ligand to bind the metal center more strongly, leading to a shorter Co–N1 bond. Surprisingly, though C2 carries the same substituent compared with C3 and C4, the Co–N1 bond length of C2 is much longer than them and the other two complexes (C1 and C5) as well (Table S7†), but in the optimized Co(II) species in which the chloride atom is taken out (Fig. S33†), the Co–N1 bond length in C2 becomes nearly the same as that in C4 (2.01187 Å vs. 2.01102 Å). Besides, we also noticed that the N1–Co–Cl angle of C2 is much larger than the rest (Table S7†), suggesting a strong steric hindrance between the axial chloride atom and the ortho-methoxy group. The following studies show that such a steric effect had also a great impact on the hydrogen evolution catalytic activity.
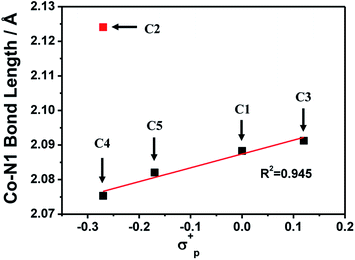 | ||
| Fig. 2 A linear correlation between the optimized Co–N1 bond lengths and the Hammett constants of the R substituents in [Co(R-TPA)Cl]Cl (N1 is the N atom of the R-substituted pyridine). | ||
Electrochemistry studies
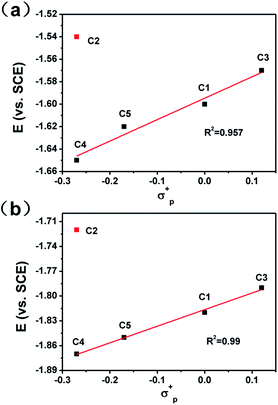
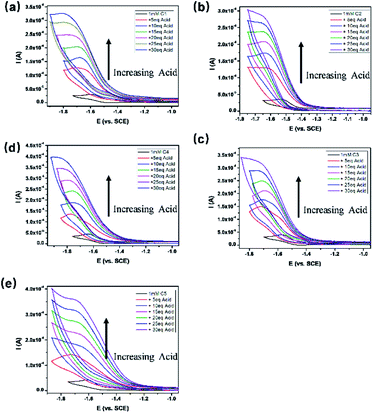
To get a clear picture of redox processes involved in photocatalytic proton reduction, cyclic voltammetry (CV) experiments were performed in argon-saturated anhydrous acetonitrile for all the complexes. A quasi-reversible wave and another more negative irreversible wave were found in all the cathodic scans (Fig. S19†) which may be assigned to the CoII/I and CoI/0 events, respectively.48,49 The peak currents of all the CoII/I redox waves increased linearly with the square root of the scan rate, consistent with a diffusion-controlled process (Fig. S14–S18†). A linear correlation between these reduction potentials of C1–C5 and the Hammett constants of the substituents was also observed as shown in Fig. 3. As expected, an electron-donating substitution as in the cases of C4 and C5, signaled by a negative Hammett constant of the substituent, may destabilize the low valent states of the central metal ions, leading to a more negative reduction potential with respect to C1. In contrast, once placed at the meta-position (C3), the methoxy group plays an electron-withdrawing role as revealed by a positive Hammett constant, and results in an easy reduction of the Co center. Interestingly, the redox potentials of C2 were recorded at −1.54 V for CoII/I and −1.73 V for CoI/0, both deviates far away from the Hammett plots of its counterparts. This abnormal behavior may be attributable to the steric effect also, which gives rise to a much longer Co–N1 bond length as mentioned above and thus weakens the electron-donating ability of the ligand remarkably and eases the reduction of the Co center greatly.All the complexes exhibited a current enhancement near the CoII/I couple with the addition of acetic acid as a proton source (Fig. 4), demonstrating that proton reduction started from the formation of Co(I) species followed by an instant formation of Co(III)–H species and ends up with hydrogen evolution. There was only a minor current increase without the complexes as shown in the control experiments (Fig. S20†), revealing the source of the catalytic current. The control potential electrolysis experiments were performed at −1.9 V (vs. SCE) in acetonitrile for 1 h, the hydrogen in the cell was analyzed by GC and all the complexes gave Faraday efficiencies close to 90% (Table S2†). The rinse test (Fig. S21†) proved that there was no deposition of catalytically active particles at the surface of glassy carbon working electrode.
Photocatalytic H2 evolution
The photocatalytic hydrogen evolution with C1 to C5 was evaluated under argon atmosphere in a solution of CH3CN/H2O using a blue LED as light source. We chose [Ir(ppy)2(dtbpy)]Cl (ppy = 2-phenylpyridine, dtbpy = 4,4′-di-tert-butyl-2,2′-bipyridine) as photosensitizer (PS) and triethylamine (TEA) as a sacrificial electron donor (SD). The gas at headspace of the reaction vessel was analyzed by gas chromatography to monitor the gaseous product. Based on a series of optimization experiments (Fig. S22 and S23†), an out-standing condition of 0.2 mM PS, 0.3 M SD, and 10 μM cobalt complex in CH3CN/H2O (8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
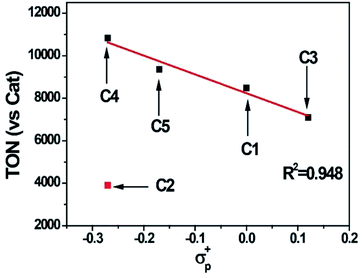
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, v/v) was chosen for photocatalytic reactions. Control experiments indicated all components were required as presented in Table S3.† All the cobalt complexes exhibited photocatalytic activity under these conditions and followed the order C4 > C5 > C1 > C3 ≫ C2 (Fig. 5). The TONs of C1, C3, C4 and C5 showed a linear relation again with the Hammett constant of the substituents (Fig. 6), in which the catalytic activities would be enhanced by an electron-donating substitution. As discussed above, an electron donor may shift the reduction of the Co center to a more negative potential, seems to be unfavorable for hydrogen evolution. On the other hand, the electron donor may facilitate Co(III)–H formation by enhancing the electron density of the Co center and thus its protonation. The Hammett correlation shown in Fig. 6 suggests that the formation of Co(III)–H is most likely the rate-determining step in catalytic hydrogen evolution. C2 has the least negative reduction potentials among the examined complexes, however, its photocatalytic activity fall far behind others, demonstrating again the important role of the Co(III) formation. The behind reason may also lie in the steric effect of the meso-methoxy group, which may hinder the approaching of a proton towards the Co center, just like its conflict with the axial Cl ligand mentioned above.
2, v/v) was chosen for photocatalytic reactions. Control experiments indicated all components were required as presented in Table S3.† All the cobalt complexes exhibited photocatalytic activity under these conditions and followed the order C4 > C5 > C1 > C3 ≫ C2 (Fig. 5). The TONs of C1, C3, C4 and C5 showed a linear relation again with the Hammett constant of the substituents (Fig. 6), in which the catalytic activities would be enhanced by an electron-donating substitution. As discussed above, an electron donor may shift the reduction of the Co center to a more negative potential, seems to be unfavorable for hydrogen evolution. On the other hand, the electron donor may facilitate Co(III)–H formation by enhancing the electron density of the Co center and thus its protonation. The Hammett correlation shown in Fig. 6 suggests that the formation of Co(III)–H is most likely the rate-determining step in catalytic hydrogen evolution. C2 has the least negative reduction potentials among the examined complexes, however, its photocatalytic activity fall far behind others, demonstrating again the important role of the Co(III) formation. The behind reason may also lie in the steric effect of the meso-methoxy group, which may hinder the approaching of a proton towards the Co center, just like its conflict with the axial Cl ligand mentioned above.
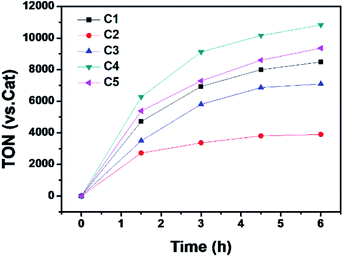 | ||
Fig. 5 Photocatalytic H2 production profiles of the multi-component systems containing 0.2 mM [Ir(ppy)2(dtbpy)]Cl, 0.3 M TEA, 10 μM Co complex in Ar-saturated CH3CN/H2O (8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, v/v). 2, v/v). | ||
After 6 h irradiation, the hydrogen evolution stagnated in all cases, only the addition of PS could restore the catalytic activity (Fig. S24†), which indicates the inactivation originated from the decomposition of PS. The mercury poisoning experiments were performed to identify the catalytic activity stems from the cobalt complexes instead of their decomposition products as the mercury could adsorb or amalgamate with metal-particles.57 No significant decays were found in all the control experiments (Fig. S25†), and no metal-particles were observed in dynamic light scattering (DLS) measurements (Fig. S26†), demonstrating all these photocatalytic reactions are homogeneous.
Catalytic mechanism
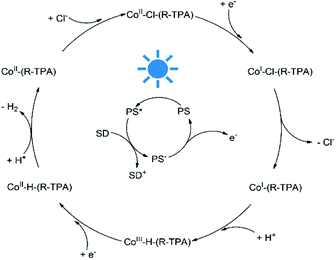
To better understand the mechanism of photocatalytic H2 evolution, luminescence quenching experiments were performed to investigate the electron transfer process, and DFT calculations were used to analyze the intermediates for a rationalized and complete catalytic cycle. As shown in Fig. S27–S32,† an emission peak of the PS centered at 597 nm upon excitation at 420 nm were quenched by all the complexes efficiently, with a bimolecular quenching constant an order of magnitude higher than that of TEA (Table S4†). However, the concentration of TEA was much higher (0.3 M vs. 10 μM) than the complexes, thus the PS* was quenched by TEA mostly and underwent a reductive quenching process as shown in Scheme 2. After the formation of PS* upon irradiation, the PS* is quenched by TEA first and gets an electron to transform into PS−, a highly active species58 which could provide an electron to reduce Co(II) to a Co(I) species. Then the chloride ligand of the unstable Co(I) species may dissociate and leave an open axial coordination site for proton access as demonstrated by the elongated Co–Cl bond length (Table S8†) and irreversible CoII/I reduction peaks, and the Co–Cl bond dissociation would lower the energy. In contrast, if a pyridyl arm dissociates from Co(I), no Gibbs free energy reduction will be observed as shown in Table S9.† The following protonation brings another important intermediate, the Co(III) hydride species which exhibits a trigonal-bipyramidal geometry (Fig. S34†). Subsequently, the Co(III) hydride would be reduced into Co(II) hydride, accompanying the combination with another proton to form H–H bond and then release of a H2 molecule. Finally, the returning of a chloride ligand regenerates the initial complex and complete the catalytic cycle.Based on this mechanism, we calculated the Gibbs free energy changes of the key intermediates for complex C1 and presented an outline in Fig. S35.† The reduction from Co(II)–Cl to Co(I)–Cl and the subsequent dissociation of the chloride ligand (−2.04 kJ mol−1) are both downhill in energy and therefore a thermodynamically allowed process. In sharp contrast, the following protonation of the Co(I) species is an energy uphill process (8.03 kJ mol−1) and thus most likely the rate-limiting step. As a result, we compared the energy changes occurred in the Co(III) hydride formation of all the complexes. As shown in Table S10,† the Gibbs energy change or the net energy barrier of this step may be reduced more efficiently with a stronger electron-donating substituent, which on one hand can enhance electron density of the Co center and thus facilitate proton contact and on the other hand can stabilize the high valent Co(III) state. In the case of C2, both the less negative CoII/I reduction potential and the longer Co–N1 bond length lead to a poor electron-donating ability of L2. Besides, the unusual N1–Co–H angle in its Co(III) hydride intermediate (Table S11†) indicates that there is a steric hindrance between the axial H atom and the ortho-methoxy group, which makes the protonation of the Co(I) species more difficult and results in the lowest catalytic activity of C2.
Conclusions
In summary, except for the steric effect found in C2, the overall hydrogen evolution catalytic activities of other examined complexes follow a clear electronic effect of the substituents, i.e. stronger the electron-donating ability of a substituent, higher the catalytic activity of the corresponding complex is. Such a rule is obviously in operation when the formation of Co(III) hydride is the rate-limiting step.Experimental section
Materials
TBAPF6 (tetrabutylammonium hexafluorophosphate) used as supporting electrolyte was purchased from Adamas-Beta, prior to use, it was recrystallized from cold ethanol and then dried under vacuum overnight. Water used in all experiments was Milli-Q ultrapure water. All the other reagents were purchased form InnoCHEM and used without further purification.Instruments
1H NMR and 13C NMR spectra were obtained on a Bruker DMX-400 MHz spectrometer. ESI-MS spectra were taken on a Brucker APEX IV(7.0T) FT_MS. Elemental analysis results were obtained on a vario MICRO cube. UV-vis absorption spectra were recorded on a Shimadzu UV-2450 spectrophotometer. Fluorescence emission spectra were run on a Hitachi F-4600 fluorescence spectrophotometer. IR data was collected on Varian Excalibur 3100.Photocatalytic H2 evolution
Hydrogen production experiments were performed in a home-made reactor. Typically, a 5 mL of CH3CN/H2O (8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, v/v) solution containing 0.2 mM [Ir(ppy)2(dtbpy)]PF6, 10 μM cobalt complex, and 0.3 M TEA was irradiated by an LED light source (λ = 455 nm ± 10 nm, 40 W) after bubbling with argon for 25 min to remove the oxygen and 3 mL of methane was injected as the internal standard. The headspace samplings were monitored and quantified by GC-2014 gas chromatography equipped with a thermal conductivity detector (TCD) and a TDX-01 packed column, argon gas as carrier.
2, v/v) solution containing 0.2 mM [Ir(ppy)2(dtbpy)]PF6, 10 μM cobalt complex, and 0.3 M TEA was irradiated by an LED light source (λ = 455 nm ± 10 nm, 40 W) after bubbling with argon for 25 min to remove the oxygen and 3 mL of methane was injected as the internal standard. The headspace samplings were monitored and quantified by GC-2014 gas chromatography equipped with a thermal conductivity detector (TCD) and a TDX-01 packed column, argon gas as carrier.
Electrochemistry experiments
All the cyclic voltammetry measurements were performed in a home-made three-neck electrode cell at temperature of 30 °C with a standard three-electrode system on an EG&G model 283 potentiostat/galvanostat, where a 3 mm glassy carbon working electrode, a 1 × 1 × 0.1 cm platinum-plate counter electrode, and a SCE (saturated calomel electrode) reference electrode were placed in 10 mL argon-saturated dry CH3CN containing 0.1 M n-Bu4NPF6 as the supporting electrolyte. Controlled potential electrolysis (CPE) were performed under same conditions with stirring during the experiments.Luminescence quenching experiments
A CH3CN/H2O (8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, v/v) solution containing 10 μM [Ir(ppy)2(dtbpy)]Cl was degassed with argon for 25 min. Fluorescence spectra were collected when 0 to 250 μL of solutions containing calibrated amounts of quenchers were added. The bimolecular quenching rate kq constant was calculated by the luminescence intensities of the solution in the absence or presence of quencher according to the Stern–Volmer equation.
2, v/v) solution containing 10 μM [Ir(ppy)2(dtbpy)]Cl was degassed with argon for 25 min. Fluorescence spectra were collected when 0 to 250 μL of solutions containing calibrated amounts of quenchers were added. The bimolecular quenching rate kq constant was calculated by the luminescence intensities of the solution in the absence or presence of quencher according to the Stern–Volmer equation.| I0/I = 1 + kqτ0[Q] | (1) |
In this equation, I0 and I are the emission intensities of the Ir complex without or with the quencher. The triplet excited state lifetime of the Ir complex is 0.557 μs,59 [Q] is the concentration of the quencher.
DFT calculations
The main text of the article should appear here with headings as appropriate. The DFT calculations were performed with the Gaussian 09 (G09)60 using the B3LYP61,62 density functional. The LANL2DZ63–65 basis set was used for cobalt atom and the 6-31+g(d) basis set was used for H, C, N, O and Cl atoms. All the optimized structures were characterized by vibrational frequency analysis calculations using the same level of theory to confirm as minima. The 6-311+g(d,p) basis set was used for all the atoms to obtain more accurate single-point energy calculation results. The solvent effect of water was evaluated using the SMD continuum solution model.66 The London interactions are considered through Grimme-D3 dispersion correction.67The Gibbs free energy changes were calculated by eqn (2), in which Gsol designates the Gibbs free energy in the aqueous sphere while Ggas is Gibbs free energy in the gas sphere. The ΔGsolv is solvation free energies from 1 M gas sphere (24.5 L mol−1 at 1 atm, 298.15 K) to 1 M in water solution. The ΔG0/* is the correction for the free energy change from the standard state gas phase (1 atm, 298.15 K) to the standard state aqueous phase which was calculated as ΔG0/* = 1.89 kcal mol−1. The Gibbs free energies of proton and electron were obtained from previously reported values.68
| Gsol = Ggas + ΔGsolv + ΔG0/* | (2) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by National Key R&D Program of China (2018YFC1602204), NSFC (21390400, 21571181 and 21773277) and the Strategic Priority Research Program of China Academy of Sciences (XDB17000000). We also appreciated the funding and technical support from the Shanghai Supercomputer Center in theoretical calculations.Notes and references
- B. Zhang and L. Sun, Chem. Soc. Rev., 2019, 48, 2216–2264 RSC.
- A. Kätelhön, R. Meys, S. Deutz, S. Suh and A. Bardow, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 11187 CrossRef.
- L. Schlapbach, Nature, 2009, 460, 809–811 CrossRef CAS.
- L. Schlapbach and A. Züttel, Nature, 2001, 414, 353–358 CrossRef CAS PubMed.
- I. Staffell, D. Scamman, A. Velazquez Abad, P. Balcombe, P. E. Dodds, P. Ekins, N. Shah and K. R. Ward, Energy Environ. Sci., 2019, 12, 463–491 RSC.
- Y. He and D. Wang, Chem, 2018, 4, 405–408 CAS.
- I. Roger, M. A. Shipman and M. D. Symes, Nat. Rev. Chem., 2017, 1, 3 CrossRef CAS.
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. X. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS.
- J. Qi, W. Zhang and R. Cao, Adv. Energy Mater., 2018, 8, 16 Search PubMed.
- T. R. Cook, D. K. Dogutan, S. Y. Reece, Y. Surendranath, T. S. Teets and D. G. Nocera, Chem. Rev., 2010, 110, 6474–6502 CrossRef CAS.
- D. Lips, J. M. Schuurmans, F. Branco dos Santos and K. J. Hellingwerf, Energy Environ. Sci., 2018, 11, 10–22 RSC.
- M. S. Dresselhaus and I. L. Thomas, Nature, 2001, 414, 332–337 CrossRef CAS PubMed.
- K. E. Dalle, J. Warnan, J. J. Leung, B. Reuillard, I. S. Karmel and E. Reisner, Chem. Rev., 2019, 119, 2752–2875 CrossRef CAS.
- L. P. Tong, L. L. Duan, A. J. Zhou and R. P. Thummel, Coord. Chem. Rev., 2020, 402, 22 CrossRef.
- E. Joliat-Wick, N. Weder, D. Klose, C. Bachmann, B. Spingler, B. Probst and R. Alberto, Inorg. Chem., 2018, 57, 1651–1655 CrossRef CAS.
- Y. Sun, J. P. Bigi, N. A. Piro, M. L. Tang, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2011, 133, 9212–9215 CrossRef CAS.
- S. Fukuzumi, Y.-M. Lee and W. Nam, Coord. Chem. Rev., 2018, 355, 54–73 CrossRef CAS.
- P. Du and R. Eisenberg, Energy Environ. Sci., 2012, 5, 6012–6021 RSC.
- V. Artero, M. Chavarot-Kerlidou and M. Fontecave, Angew. Chem., Int. Ed., 2011, 50, 7238–7266 CrossRef CAS.
- S. Losse, J. G. Vos and S. Rau, Coord. Chem. Rev., 2010, 254, 2492–2504 CrossRef CAS.
- N. Queyriaux, R. T. Jane, J. Massin, V. Artero and M. Chavarot-Kerlidou, Coord. Chem. Rev., 2015, 304–305, 3–19 CrossRef CAS.
- S. Schnidrig, C. Bachmann, P. Muller, N. Weder, B. Spingler, E. Joliat-Wick, M. Mosberger, J. Windisch, R. Alberto and B. Probst, ChemSusChem, 2017, 10, 4570–4580 CrossRef CAS.
- X. Zhao, P. Wang and M. Long, Comments Inorg. Chem., 2016, 37, 238–270 CrossRef.
- S. C. Marinescu, J. R. Winkler and H. B. Gray, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15127–15131 CrossRef CAS PubMed.
- A. Rodenberg, M. Orazietti, B. Probst, C. Bachmann, R. Alberto, K. K. Baldridge and P. Hamm, Inorg. Chem., 2015, 54, 646–657 CrossRef CAS PubMed.
- D. Moonshiram, C. Gimbert-Surinach, A. Guda, A. Picon, C. S. Lehmann, X. Zhang, G. Doumy, A. M. March, J. Benet-Buchholz, A. Soldatov, A. Llobet and S. H. Southworth, J. Am. Chem. Soc., 2016, 138, 10586–10596 CrossRef CAS.
- E. S. Wiedner and R. M. Bullock, J. Am. Chem. Soc., 2016, 138, 8309–8318 CrossRef CAS PubMed.
- W. M. Singh, M. Mirmohades, R. T. Jane, T. A. White, L. Hammarström, A. Thapper, R. Lomoth and S. Ott, Chem. Commun., 2013, 49, 8638–8640 RSC.
- Z. J. Li, F. Zhan, H. Xiao, X. Zhang, Q. Y. Kong, X. B. Fan, W. Q. Liu, M. Y. Huang, C. Huang, Y. J. Gao, X. B. Li, Q. Y. Meng, K. Feng, B. Chen, C. H. Tung, H. F. Zhao, Y. Tao and L. Z. Wu, J. Phys. Chem. Lett., 2016, 7, 5253–5258 CrossRef CAS.
- S. Varma, C. E. Castillo, T. Stoll, J. Fortage, A. G. Blackman, F. Molton, A. Deronzier and M.-N. Collomb, Phys. Chem. Chem. Phys., 2013, 15, 17544–17552 RSC.
- S. Mandal, S. Shikano, Y. Yamada, Y. M. Lee, W. Nam, A. Llobet and S. Fukuzumi, J. Am. Chem. Soc., 2013, 135, 15294–15297 CrossRef CAS PubMed.
- N. Elgrishi, D. A. Kurtz and J. L. Dempsey, J. Am. Chem. Soc., 2017, 139, 239–244 CrossRef CAS PubMed.
- K. Walaijai, S. A. Cavill, A. C. Whitwood, R. E. Douthwaite and R. N. Perutz, Inorg. Chem., 2020, 59, 18055–18067 CrossRef CAS PubMed.
- A. Lewandowska-Andralojc, T. Baine, X. Zhao, J. T. Muckerman, E. Fujita and D. E. Polyansky, Inorg. Chem., 2015, 54, 4310–4321 CrossRef CAS PubMed.
- T. Lazarides, T. McCormick, P. Du, G. Luo, B. Lindley and R. Eisenberg, J. Am. Chem. Soc., 2009, 131, 9192–9194 CrossRef CAS PubMed.
- B. Probst, M. Guttentag, A. Rodenberg, P. Hamm and R. Alberto, Inorg. Chem., 2011, 50, 3404–3412 CrossRef CAS PubMed.
- E. Deponti, A. Luisa, M. Natali, E. Iengo and F. Scandola, Dalton Trans., 2014, 43, 16345–16353 RSC.
- B. Shan, T. Baine, X. A. Ma, X. Zhao and R. H. Schmehl, Inorg. Chem., 2013, 52, 4853–4859 CrossRef CAS.
- W. K. Lo, C. E. Castillo, R. Gueret, J. Fortage, M. Rebarz, M. Sliwa, F. Thomas, C. J. McAdam, G. B. Jameson, D. A. McMorran, J. D. Crowley, M. N. Collomb and A. G. Blackman, Inorg. Chem., 2016, 55, 4564–4581 CrossRef CAS PubMed.
- A. Call, F. Franco, N. Kandoth, S. Fernández, M. González-Béjar, J. Pérez-Prieto, J. M. Luis and J. Lloret-Fillol, Chem. Sci., 2018, 9, 2609–2619 RSC.
- Y. Sun, J. Sun, J. R. Long, P. Yang and C. J. Chang, Chem. Sci., 2013, 4, 118–124 RSC.
- A. Mahammed, B. Mondal, A. Rana, A. Dey and Z. Gross, Chem. Commun., 2014, 50, 2725–2727 RSC.
- R. S. Khnayzer, V. S. Thoi, M. Nippe, A. E. King, J. W. Jurss, K. A. El Roz, J. R. Long, C. J. Chang and F. N. Castellano, Energy Environ. Sci., 2014, 7, 1477–1488 RSC.
- M. Nippe, R. S. Khnayzer, J. A. Panetier, D. Z. Zee, B. S. Olaiya, M. Head-Gordon, C. J. Chang, F. N. Castellano and J. R. Long, Chem. Sci., 2013, 4, 3934–3945 RSC.
- S. Aroua, T. K. Todorova, V. Mougel, P. Hommes, H. U. Reissig and M. Fontecave, ChemCatChem, 2017, 9, 2099–2105 CrossRef CAS.
- X. Hu, B. S. Brunschwig and J. C. Peters, J. Am. Chem. Soc., 2007, 129, 8988–8998 CrossRef CAS.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- S. L. Chan, T. L. Lam, C. Yang, S. C. Yan and N. M. Cheng, Chem. Commun., 2015, 51, 7799–7801 RSC.
- J. W. Wang, H. H. Huang, J. K. Sun, T. Ouyang, D. C. Zhong and T. B. Lu, ChemSusChem, 2018, 11, 1025–1031 CrossRef CAS PubMed.
- H. Y. Wang, E. Mijangos, S. Ott and A. Thapper, Angew. Chem., Int. Ed., 2014, 53, 14499–14502 CrossRef CAS.
- J. Wang, C. Li, Q. Zhou, W. Wang, Y. Hou, B. Zhang and X. Wang, Catal. Sci. Technol., 2016, 6, 8482–8489 RSC.
- S. Kim, C. Saracini, M. A. Siegler, N. Drichko and K. D. Karlin, Inorg. Chem., 2012, 51, 12603–12605 CrossRef CAS.
- G. L. Miessler, P. J. Fishcer and D. A. Tarr, Inorganic Chemistry, Prentice Hall, 5 edn, 2013 Search PubMed.
- S. L.-F. Chan, T. L. Lam, C. Yang, J. Lai, B. Cao, Z. Zhou and Q. Zhu, Polyhedron, 2017, 125, 156–163 CrossRef CAS.
- O. Seneque, M. Campion, M. Giorgi, Y. Le Mest and O. Reinaud, Eur. J. Inorg. Chem., 2004, 9, 1817–1826 CrossRef.
- A. L. Ward, L. Elbaz, J. B. Kerr and J. Arnold, Inorg. Chem., 2012, 51, 4694–4706 CrossRef CAS PubMed.
- J. A. Widegren and R. G. Finke, J. Mol. Catal. A: Chem., 2003, 198, 317–341 CrossRef CAS.
- E. D. Cline, S. E. Adamson and S. Bernhard, Inorg. Chem., 2008, 47, 10378–10388 CrossRef CAS PubMed.
- F. De Angelis, S. Fantacci, N. Evans, C. Klein, S. M. Zakeeruddin, J.-E. Moser, K. Kalyanasundaram, H. J. Bolink, M. Grätzel and M. K. Nazeeruddin, Inorg. Chem., 2007, 46, 5989–6001 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 19 CrossRef.
- Z. Marković, J. Tošović, D. Milenković and S. Marković, Comput. Theor. Chem., 2016, 1077, 11–17 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: 1H-NMR, ESI-MS spectra, UV-visible absorption spectrum, photochemistry, electrochemistry, Stern–Volmer plots and computational details. See DOI: 10.1039/d1ra02435c |
| This journal is © The Royal Society of Chemistry 2021 |