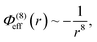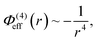Open Access Article
Open Access ArticleDensity functional theory of confined ionic liquids: the influence of power-law attractions on molecule distributions and surface forces
Adrian L. Kiratidis and
Stanley J. Miklavcic
and
Stanley J. Miklavcic *
*
Phenomics and Bioinformatics Research Centre, UniSA STEM, University of South Australia, Mawson Lakes, SA, Australia. E-mail: stan.miklavcic@unisa.edu.au
First published on 14th May 2021
Abstract
Interaction energies and density profiles for two model ionic liquids, [C4mim+][BF4−] and [C4mim+][TFSI−], confined between charged planar walls are studied within a density functional theory framework. The results of these simulations are also compared with results assuming a simpler linear hexamer–monomer, cation–anion system. We focus attention on the effect on the atom site distributions and the surface forces of an additional, specific attractive potential between oppositely charged molecules. We consider both short- and long-ranged attractive potentials in order to span the degree to which the ionic counterions associate. Independent of its strength, we interpret the results found with the short-ranged potential to be a manifestation of limited molecular association. In contrast, depending on its strength, the results found with the long-ranged potential suggest a much stronger and possibly longer ranged associations of ionic groups. Both potentials are found to influence the behavior of the surface force at small separations, while the long-ranged attractive potential has the greater influence of the two on the long-ranged behavior of the surface force.
1. Introduction
In a recent paper1 we reported on a density functional theory (DFT) study of the behavior of adsorbing room temperature ionic liquids (RTILs) confined between two rigid surfaces. We investigated a range of conditions, with some emphasis on the responses of the RTILs and the inter-surface force to increases in the strength of the surface adsorption potential. Although a wide range of conditions were considered, we did not find any evidence of a long range, exponentially decaying surface interaction of the character of an electrical double layer force. Such forces have been detected with some IL systems in labs using the surface force apparatus (SFA).2–7 The experimental finding was unexpected given the exceptionally high charge screening ability of the organic RTILs. It has been put forward that such measured forces arise as a consequence of a high but incomplete pairing of oppositely charged molecular ions, leaving a high enough concentration of free, unpaired ions to mimic a weak electrolyte confined between two charged walls.In our model system1 we did not entertain any specific pairing or clustering of the ions; the generic Coulomb interactions between partial charged atoms, and the non-specific dispersion attractive forces superimposed on hard sphere repulsion between all atoms that we included were clearly not sufficient to generate specific pairs. On the other hand, in closely related works by Forsman, Woodward, Ma and co-workers,8–11 who first implemented independently a DFT model, a mechanism through which ion clusters were present was added. These authors introduced additional molecular species in their IL model to differentiate clustered from un-clustered molecules. The authors manually controlled the molar proportion of clustered to un-clustered molecules to see what effect this would have on the resulting surface force. Indeed, it was found that a long range, exponentially decaying force did appear at an extremely high concentration ratio of clustered to un-clustered molecules.10 This was in qualitative agreement with the postulated explanation offered by the experimental researchers. Nevertheless, the manner employed to bring about clustering10,11 was artificial. Although demonstrative, the approach taken leaves open the questions of what intermolecular mechanism could bring about ion pairing, and how pairing is affected by external conditions and other system variables. Addressing these questions is one of the aims of this paper.
The molecular manifestation of ion pairing or clustering must obviously go beyond the level to which generic attractive Lennard-Jones dispersion interactions between all atoms and electrostatic attractions between oppositely charged molecules are treated in the DFT model. Presumably, the pairing of oppositely charged macromolecules is due either to an additional attractive interaction of non-electrostatic origin, or to an attractive electrostatic contribution beyond that captured in a mean-field, DFT description. In the theoretical studies of Kjellander,12–14 it was proposed that clustering could be a consequence of strong nonlocal electrostatic or ion correlation effects arising in high density ionic liquids. Kjellander argued that “anions and cations may partially associate due to strong electrostatic attractions, specific interactions and/or effects of ion correlations”, which “may lead to the formation of ion pairs that are electroneutral entities”.14 Furthermore, Kjellander argued that although it is tempting to create classes of RTIL molecules, associated and free, as was the approach taken by Forsman, Woodward, Ma and co-workers,10,11 any ion association arising specifically from ion correlations should actually emerge automatically. Confirmation of these ideas emerged from his dressed ion model.
Whether due to strong ion correlations or a specific, non-electrostatic interaction it would seem instructional to determine the explicit physical consequences of such an effective attractive potential on ion distributions and on surface forces, especially for small and intermediate surface separations (Kjellander's study did not explicitly include non-electrostatic intermolecular interactions, and only considered a bulk liquid, arguing correctly that asymptotic behavior of surface forces is dictated by bulk solution properties). Kjellander12–14 suggested that the “dressing” of ions by a polarized ion cloud (dominated by counterions) may be likened to the inclusion of multipole contributions: dipole, quadrupole moments, etc. This perspective suggests looking to familiar intermolecular potentials as candidates for case studies. In this work we consider two models for an effective attractive potential. The first effective potential is based on a Boltzmann-weighted, angle-averaged dipole–quadrupole interaction,15
which is longer ranged than the dispersion interaction. Both are shorter ranged than the Coulomb attraction between the opposite charged oligomers, r−1. In our model the potentials are assumed to act only between specific atoms on oppositely charged molecules. To be precise, the potentials act between the central atoms in a given charge grouping (see Section 2).
Our aim with considering these functional dependencies is two-fold. Firstly, we seek to explore the contrasting influences of the functions – their short versus long range influences – on the molecular distributions between the surfaces and the overall effect on the surface forces. The more specific second aim is to see if in either case the surface force tends in character to the long-ranged exponential force measured experimentally.
In the next section we summarize the contributions included in the model, paying particular attention to the new attractive potentials. This is followed by a brief description of the density functional theory model itself and the numerical solution procedure. After a presentation of our main findings in the Results and discussion section, we offer some closing statements and suggestions of future work in the Conclusions section.
2. Ionic liquid systems and intermolecular potentials
2.1 RTIL systems
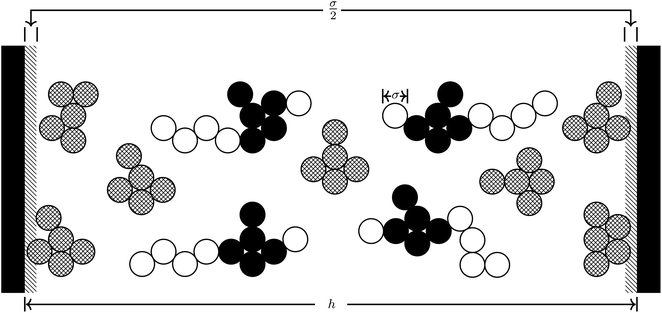
In this work we consider three explicit model molecular systems, and study their behavior under confinement. In parallel we study the response of the force between the confining surfaces to changes in molecular distribution resulting from the action of the pairing potential. Two RTILs systems have the same imidazolium cation, [C4mim+], one with the anion bis(trifluoromethane)sulfonimide ([TFSI−]) and one with the anion tetrafluoroborate ([BF4−]). The third RTIL is somewhat simpler but intended to capture the core features of the other two model RTILs. The RTIL molecules [C4mim+] and [BF4−], on the one hand, and [C4mim+] and [TFSI−] on the other, are compared with a model RTIL comprised of a hexamer cation, [HEX+], and a monomeric anion, [A−]. The [HEX+] cation mimics [C4mim+] in the sense that it has five neutral atoms and one positively charged end atom, arranged linearly. The monomeric anion, [A−], is more representative of [BF4−] than the much bulkier [TFSI−], with a unit negative charge at the centre of a single sphere. The molecular structures and associated hard sphere models of these oligomers are presented in Fig. 1.As in previous work, we utilize the well-established course grained approach9–11,17 in which only large constituent atoms (e.g., the carbon atom on the CH2 molecule) are modeled as single hard spheres. All atoms have a common hard sphere diameter, σ. Once again we concern ourselves with the behavior of RTILs between neutral and charged solid surfaces; the atomic hard sphere centers have a closest approach distance of σ/2. A schematic representation of the ionic liquid [C4mim+][BF4−] confined between two planar surfaces separated by a distance h is shown in Fig. 2.
2.2 Generic potentials
As with our previous work, each constituent atom interacts with every other atom through a Sutherland model potential,15
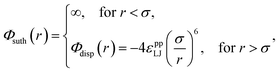 | (1) |
Electrostatic interactions are again quantified using the Coulomb potential
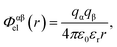 | (2) |
All atoms interact with the confining walls via steric and electrostatic forces. The former case is manifested in a closest approach distance σ/2. In the latter case, this contribution appears as a 2D integral (per surface) of the Coulomb potential between a charged oligomer atom and an element of surface charge.
In contrast with our previous calculations and to simplify the present investigation, we assume no atom-wall dispersion interaction that was featured in Kiratidis and Miklavcic.1
2.3 Additional effective potential
In addition to the foregoing generic potentials we now introduce our effective potentials, Φeff(r). We consider two forms motivated by higher-order, thermodynamic-averaged intermolecular interactions, and modelled directly on the asymptotic form of the thermodynamically weighted, angle-averaged, dipole–quadrupole interaction potential,15 and the asymptotic form of the thermodynamically weighted, angle-averaged, charge-dipole interaction potential:15,16
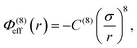 | (3) |
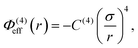 | (4) |
Note that because of the difference in the distance dependencies and their strengths, in what follows it is not reasonable to simply compare numerical values of C(8) and C(4); the same numerical value still implies a difference in the influences of the effective potentials. For [TFSI−], [HEX+], and the monomeric anion, [A−], the interaction sites for these potentials are simply the single charged atoms on those oligomers (Fig. 1). For [C4mim+] and [BF4−], on the other hand, the potential acts between the central atoms of the respective groups of atoms possessing partial charges.
We make two further remarks before proceeding.
In reality, eqn (3) and (4) would be temperature dependent. Despite this we do not explore any influence of temperature. Nevertheless, the effect of temperature would represent a worthwhile investigation given the results of previous experimental work by Rutland and co-workers on the temperature dependence of surface forces across RTILs.19,20
Secondly, although the effective potentials have been motivated by higher order multipole potentials they are not here attributed any such properties. Hence, we ignore any perceived issue with over counting of charge interactions through the use of these multipole-like potentials, and focus instead on exploring the physical consequences of these additional interactions.
Further comments are made in Section 4.
3. Density functional theory
In a classical density functional theory (DFT) of molecular liquids, the free energy is expressed as a functional of distributions,9–11,17
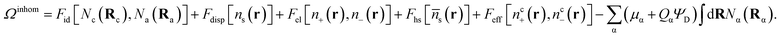 | (5) |
In eqn (5), Fid, Fdisp, Fel and Fhs denote, respectively, the configuration, dispersion, electrostatic and hard sphere contributions to the free energy functional. Feff is a contribution arising from the supra-dispersive effective potential. Equilibrium properties are found by minimizing this free energy functional with respect to the distribution functions. The total atom density ns(r) is the sum of the charged and neutral atom densities,
| ns(r) = n+(r) + n0(r) + n−(r), | (6) |
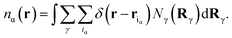 | (7) |
The ideal chain contribution, of an entropy term and a molecular connectivity term, is
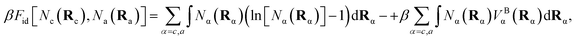 | (8) |
The electrostatic free energy functional contribution is
| Fel[n+ (r), n− (r)] = Fppel[n+ (r), n− (r)] + Fpwel[n+ (r), n− (r)], | (9) |
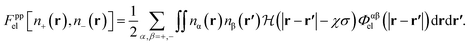 | (10) |
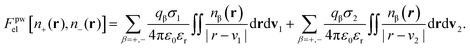 | (11) |
The factor χσ denotes the radius of the “hard Coulomb hole” with the value χ = 0.71. v1 and v2 are surface vectors.
The hard sphere contribution is treated as in ref. 1 and accounts somewhat for the excluded volume interactions between all pairs of hard sphere atoms. This is a functional of the weighted density,
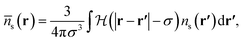 | (12) |
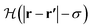 is the Heaviside step function.
is the Heaviside step function.
The dispersion contribution considered in this work comprises only the interaction between atoms,
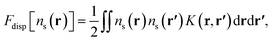 | (13) |
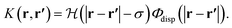 | (14) |
The interatomic Lennard-Jones interaction potential, Φdisp(r), is given by the dispersion contribution in eqn (1).
Finally, the new contribution to the total functional, Feff, involves an integration of interacting specific core atom site distributions,
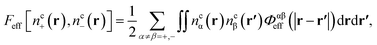 | (15) |
Equilibrium properties are obtained from the grand potential by first minimizing eqn (5) with respect to the oligomeric densities,
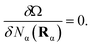 | (16) |
Through an application of the chain rule this results in the formal expression for the equilibrium atom densities,
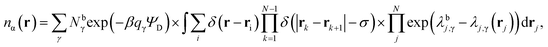 | (17) |
Note that as the values of λj,γ(rj) themselves depend on nα(r), eqn (17) must be solved self-consistently via an iterative method.
The implementation details of our iterative scheme, and the procedure by which densities are updated throughout this work are identical to those reported previously. A detailed discussion can be found in ref. 1. The interaction free energy is calculated as described in ref. 1. All results shown here have been subjected to a testing for thermodynamic self-consistency and accuracy based on application of the contact theorem.1,10,21
4. Results and discussion
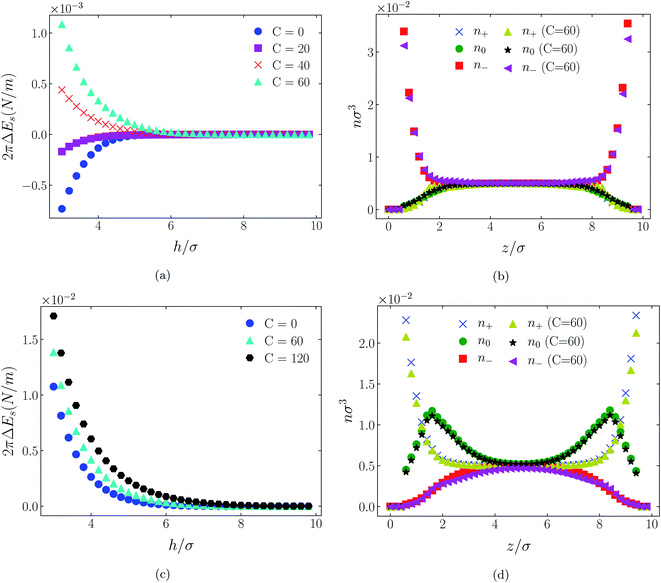
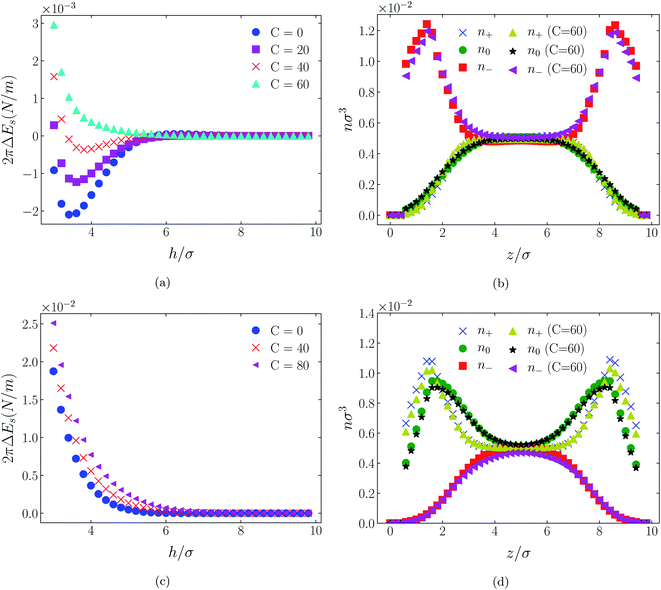
The influence of an (additional) attractive potential between central atoms on oppositely charged cations and anions of an ionic liquid is greatly dependent on the effective range of the potential. This is the most significant of all factors. To demonstrate this influence we compare in Fig. 3 through 11 atom distributions and surface forces generated by the attractive interaction potentials, eqn (3) and (4), between positive and negative charge centres of the cationic and anionic molecules. We also compare the responses of the two molecular ionic liquids, [C4mim+][BF4−] and [C4mim+][TFSI−], with the response of a simpler model ionic liquid comprising hexamer cation [HEX+] and monomeric anion, [A−]. As already mentioned, the latter cation is representative of [C4mim+] in that it has five neutral atoms and one positively charged atom, arranged linearly. As the monomeric anion is more representative, albeit imperfectly, of [BF4−], with a unit negative charge at the centre of a single sphere, it should be anticipated that the cause of any significant difference between [TFSI−] and either of [BF4−] or its model anion [A−] lies in the former ion's considerably larger size due to a larger number of neutral atoms.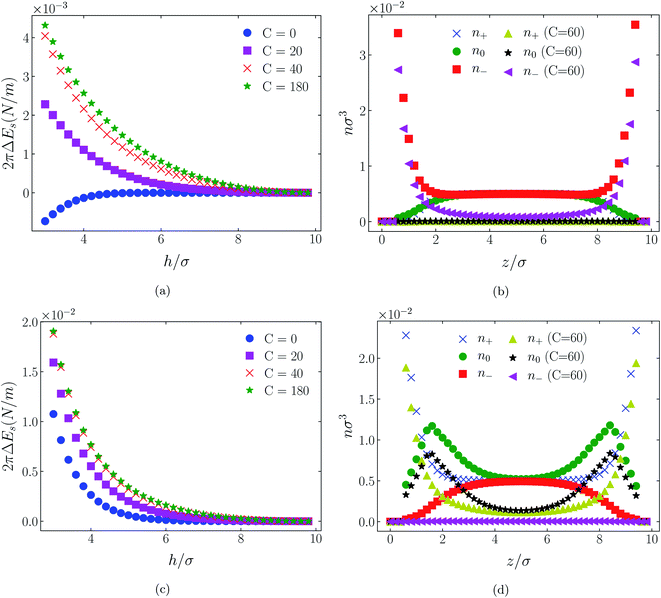 | ||
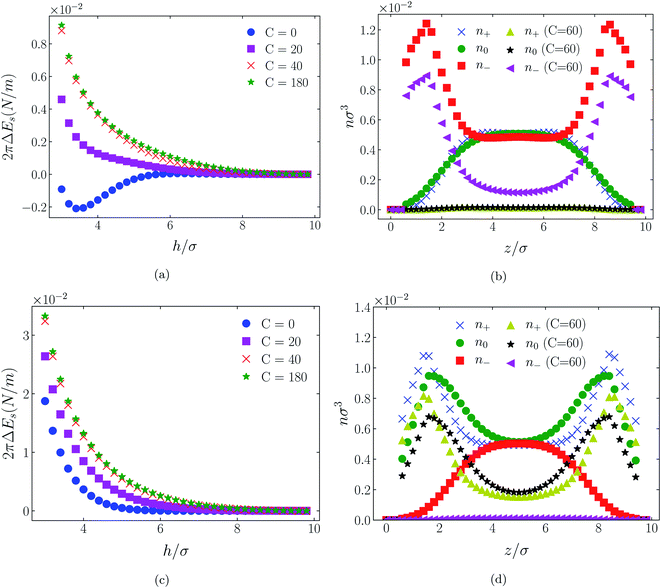
| Fig. 3 Interaction energies ((a) & (c)) and scaled atom densities ((b) & (d)) plots for [HEX+][A−] at various C(4) values. In (a) & (b) the surfaces were positively charged σ1 = σ2 = +1/320e Å−2, while in plots (c) and (d) the surfaces were negatively charged, σ1 = σ2 = −1/320e Å−2. In this and all subsequent figures, the normalised bulk RTIL density was nblkσ3 = 0.005. The cation center-anion center effective potential was −C(4)/r4. In this figure and Fig. 4 through 11, the blue crosses, green circles and red squares in subplots (b) & (d) correspond to the C = 0 case. | ||
 | ||
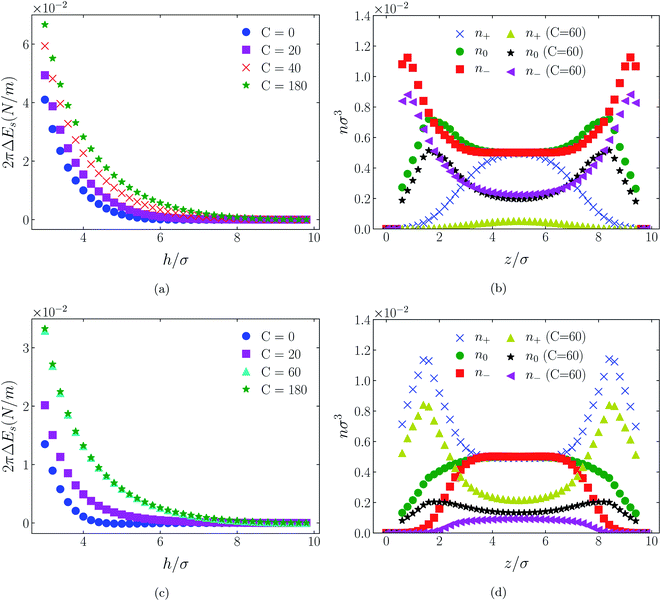
| Fig. 4 Interaction energies and scaled atom densities as in Fig. 3, except that the cation center-anion center effective potential was −C(8)/r8. | ||
 | ||
| Fig. 6 Interaction energies and scaled atom densities as in Fig. 5, except that the cation center-anion center effective potential was −C(8)/r8. | ||
 | ||
| Fig. 8 Interaction energies and scaled atom densities as in Fig. 7, except that the cation center-anion center effective potential was −C(8)/r8. | ||
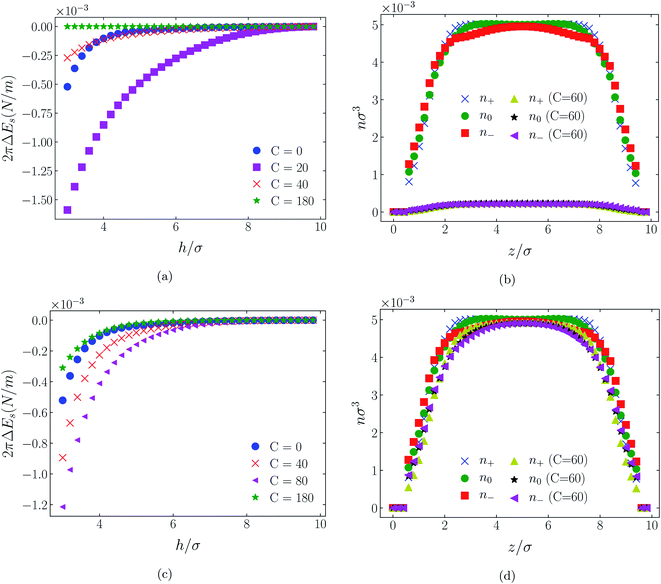 | ||
| Fig. 10 Interaction energies and scaled atom densities as in Fig. 9, except for [C4mim+][BF4−]. | ||
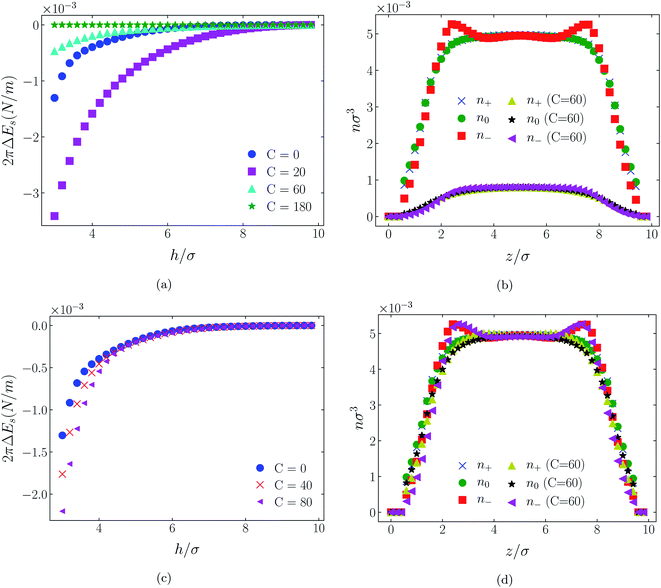 | ||
| Fig. 11 Interaction energies and scaled atom densities as in Fig. 9, except for [C4mim+][TFSI−]. | ||
Our findings are most naturally presented as a summary of results for charged surfaces, where the positive and negative surface charges exhibit a certain reciprocity, and a summary of results for the case of neutral surfaces, which shows distinctly different behavior.
It should be recalled that in the cases considered here a particle-wall dispersive interaction1 has not been included. Consequently, no atom experiences any preferential attraction to either wall. Although this is unlikely to reflect the state of a real system, the exclusion has the advantage of simplifying the analysis and of not confounding the interpretation of cation–anion coupling effects.
4.1 Symmetrically charged surfaces
In all cases discussed here, the benchmarks are those results for which no additional (effective) potential is present. That is, the reference state is the result obtained when either C(4) = 0 or C(8) = 0 (i.e. the same benchmark for both). In addition, to engender a balanced comparison between molecular species, the density profiles shown in the figures below have been scaled according to the numbers of like atoms in the molecule. For example, the nondimensional number density of negative atoms, n−σ3, for the case of [BF4−] has been divided by five, since we have assigned a partial charge of −0.2e to each of the five atoms in the [BF4−] molecule. Analogous scaling has been done for neutral and positive atoms.In Fig. 3 and 4 we present the interaction free energies, panels (a) and (c), and scaled, normalized atom densities, panels (b) and (d), for our model ionic liquid, [HEX+][A−], system. Corresponding results for the [C4mim+][BF4−] and [C4mim+][TFSI−] systems are shown in Fig. 5, 6, 7 and 8, respectively.
In each of the cases explored in this section, the interaction free energy responds monotonically to increasing strength of the effective potential, irrespective of the sign of the surface charge, or the range of the potential, or the molecular nature of the cation and anion molecule. Moreover, the tendency with increasing effective potential strength is uniformly toward an increasing repulsion between the surfaces. In other words, increasing the strength of the effective potential between the oppositely charged oligomers results in a more unfavorable energetic state of the system at one and the same separation.
Looking at the difference between positive and negative surface charges one notes that – relative to their respective benchmarks – all systems tend not only to have a reduced coion concentration, they also have a reduced counterion concentration.22 The latter result is presumably a consequence of the reduced need to balance the net charge between the surfaces caused by the depletion of the coions. The shapes of the counterion profiles reflect the geometric differences in molecular structures of the counterions.
In the case of positively charges surfaces, the single spherical anions, [A−], are distributed in the shape that is characteristic of simple ionic double layers. The [BF4−] counterions, with all five partial charged hard sphere atoms, are not only prevented from approaching closer than a hard sphere radius to each surface, they exhibit a peak in the density profile at about 1.5σ from each wall. If we acknowledge that the partial charges configure themselves so as to minimize the molecular self energy, we find that [BF4−] takes a 3D tetrahedral shape so the negative charge distribution peaks at a distance of approximately 1.5σ – the distance of the centre the molecule from a wall. In contrast, the [TFSI−] model possesses just the single unit negative charge atom, the profile exhibits a peak at around one σ from a surface, while the neutral atom distribution peaks further out by approximately another half radius. Since the neutral atoms have no energetic preference for the wall this suggests that these oligomers are oriented on average with their molecular plane approximately parallel to the surface.
When the surfaces are negatively charged, the counterions are the cationic hexamer [HEX+] and [C4mim+]. In the former case the combination of a peak in the positive atom distribution at σ/2 from each wall (and monotonic decay thereafter), and a neutral atom distribution that peaks further out suggests that the hexamers are oriented on average at a finite angle to the surfaces, with their tails dangling into solution. The bulkier charged head of [C4mim+] has a non-monotonic profile near the surfaces but then decays monotonically thereafter. The neutral distributions in Fig. 5 and 6 are attributed to the neutral tails of [C4mim+], the atoms of which are distributed in synchronicity with the positive atoms. In Fig. 7 and 8, the neutral atom distribution contains contributions from atoms on both ionic oligomers, especially the heavily laden [TFSI−] (14 neutral atoms), which explains the oft-appearing mono-modal shape of the distributions which peak at the centre of the gap between the surfaces. Exceptions, however, arise in some cases of the nonzero effective potential in Fig. 7.
The distinction between Fig. 3, 5, and 7 on the one hand, and Fig. 4, 6, and 8 on the other, lies in the long range nature of the potential, Φ(4)eff compared with Φ(8)eff. A close inspection shows that the response of all profiles is qualitatively similar for both the longer ranged Φ(4)eff (Fig. 3, 5, and 7), and the shorter ranged Φ(8)eff potential (Fig. 4, 6, and 8). However, it is clear that the considerably longer ranged potential has a much more dramatic quantitative effect on the ion distributions. Moreover, Φ(4)eff has a marked effect on the surface force. Principally, the stronger potential Φ(4)eff effectively drives coions out from between the charged walls leaving, in every case, the counterions to the surfaces alone to balance the surface charges. The greater the value of C(4), the stronger the effect. The end result is reminiscent of the double layer systems studied in the 1980's by the Swedish and Australian groups who studied counterion-only electrical double layers. Jönsson, Wennerström and co-workers,23–26 performing Monte Carlo simulations, and Kjellander, Marčelja and Attard,26–29 performing continuum (hypernetted chain) statistical mechanical calculations, showed that in the case of the counterion-only electrical double layer, repulsive surface interactions are to be found for monovalent ions. The similarity is suggestive.
While other mechanisms may be put forward,30 the results can be explained by, and are consistent with, a strong association of oppositely charged oligomers. Although the potential between oppositely charged atoms (the central atoms in the case of [C4mim+] and [BF4−]) acts between every pair it is not homogeneously efficacious. Rather than Φ(4)eff forcing coions, originally in the diffuse region midway between the walls, to pair with counterions in a less entropically favorable and more energetically unfavorable condition close to the like-charged walls, the associated ions are removed to the bulk, leaving only free counterions to screen the surface charges. It would seem that a counterion-only scenario is a less unfavorable free energy state for the system. Only in the case of Φ(8)eff is there some evidence of both coions and an excess of counterions existing between the walls, as evident from Fig. 4, 6 and 8, most notably in the case of [HEX+][A−], Fig. 4(b).
That the Φ(8)eff potential is less effective in altering the density distributions is not surprising. To achieve with the shorter ranged potential a magnitude equivalent to that achieved at a distance R by Φ(4)eff, the atoms would need to be within a distance of
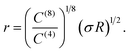 | (18) |
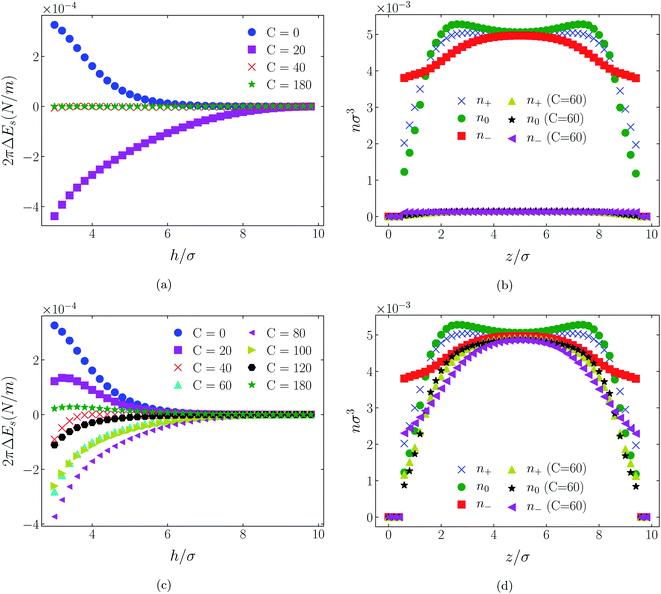
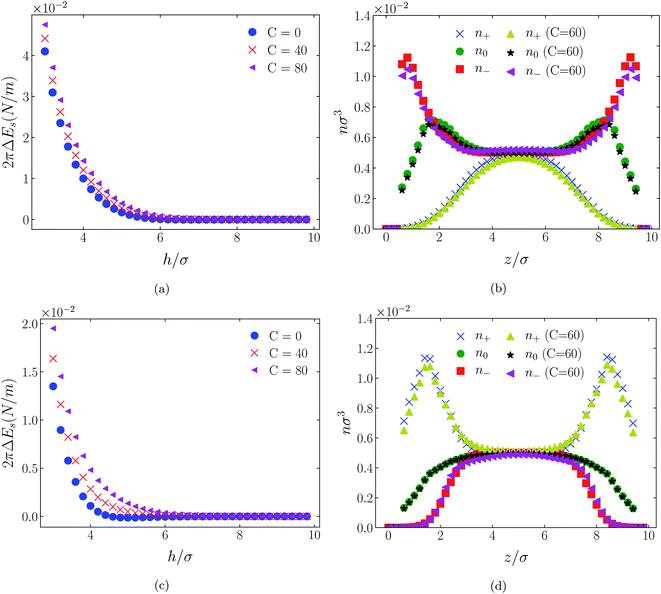
4.2 Neutral surfaces
While it is not clear that the surfaces involved in, say, surface force experiments with ionic liquids were uncharged, it is worth completing the study with a consideration of neutral surfaces. For this state our results are shown in Fig. 9, 10, and 11 for the [HEX+][A−], [C4mim+][BF4−], and [C4mim+][TFSI−] systems, respectively. In each of these figures, panels (a) and (b) show the interaction energies and scaled atom densities found with the Φ(4)eff potential. Panels (c) and (d) show corresponding quantities found with the Φ(8)eff potential.The neutral surface case shows a distinctly different response to the effective potential compared with either of the charged surface cases. The features that remain true, however, are that the Φ(8)eff-based results are again in qualitative agreement with the Φ(4)eff-based results. Secondly, the extent of the response is again stronger in the case of Φ(4)eff, compared with Φ(8)eff. Other traits, however, bear no similarity to the cases of charged surfaces. The most significant difference being that the interaction free energy responds non-monotonically to increasing strength of potential. Significantly, the initial trend is toward an increased attraction rather than repulsion, from either an initially (C = 0) attractive interaction or an initially repulsive interaction, and the magnitude of attraction diminishes with increasing C(8) or C(4). Another related difference is that with the longer ranged Φ(4)eff, the gap between the surfaces becomes all but devoid of oligomers! Having no preferential surface interaction (such as an attractive atom-wall dispersion potential) both molecule types gain entropy by withdrawing to the bulk.
4.3 Decay behavior of surface forces
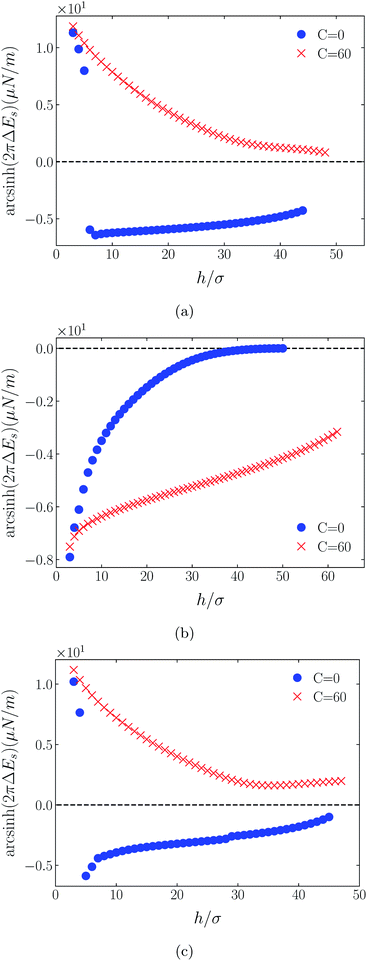
Shown on a sinh−1-linear scale in Fig. 12 and 13 are the long-range interaction energies (equivalent to the normalized forces between a plane and a sphere of radius, R, or between two crossed cylinders, F/R31) between symmetrically charged surfaces (panels (a) and (c)) and between neutral surfaces (panel (b)) across a thin film of an RTIL: [C4mim+][TFSI−] in Fig. 12 and [C4mim+][BF4−] in Fig. 13. The figures are detailed and extended versions of those interaction energies shown in Fig. 7, 5, 10 and 11, respectively. The focus of interest here is on the changes in the long-range character of the surface force as a consequence of effective attraction between the oligomers. For brevity we present results only for Φ(4)eff.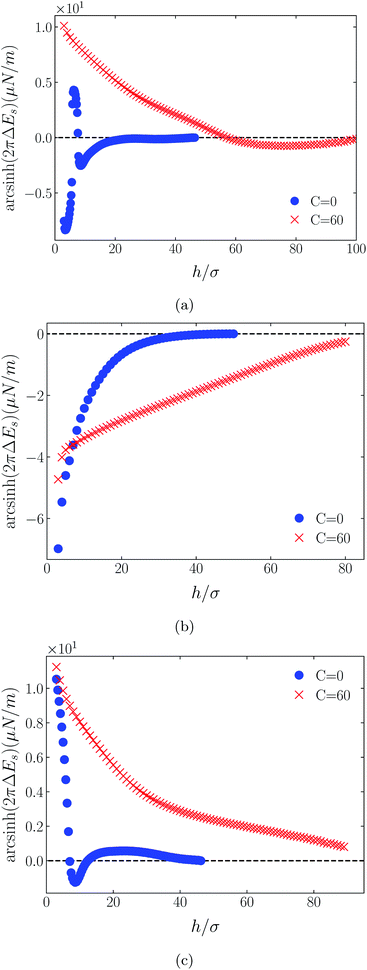 | ||
| Fig. 13 Detailed plots of scaled interaction free energies as in Fig. 12, but for the case [C4mim+][BF4−]. | ||
Two cases are shown: the benchmark case C(4) = 0; and the strong association case of C(4) = 60. As suggested by earlier results for charged surfaces, intermediate results are found with intermediate values of C(4). As the interaction energies (normalized forces) can be repulsive or attractive depending on system conditions, we have plotted the energies on an sinh−1 scale to reflect both their sign and their decay character. Given that the two RTILs give rise to qualitatively similar behavior in the surface forces, our discussion will cover just the generic findings.
Although the conditions under which our simulations were conducted differ from those of Ma et al.,11 the response to increased C(4) (and increased degree of oligomer attraction) is consistent with the latter group's results. In all cases, the increased degree of intermolecular attraction gives rise to a longer ranged and more repulsive force in the case of similarly charged surfaces, and a longer ranged and more attractive force in the case of neutral surfaces. In fact, assuming no atom-wall dispersion interaction, the surface forces in the C(4) = 0 benchmark models are asymptotically all attractive compared with those scenarios where the additional attraction is present. In the latter cases, the axis scales highlight an exponential decay which is characteristic too of measured repulsive forces. However, it is interesting that the asymptotic attractions between neutral walls for the nonzero C(4) cases also show roughly exponential decay, over some range of separations.
With no other differentiating factors, the quantitative differences between the force profiles in the two RTIL systems obviously reflect the differences in the anions, [TFSI−] in Fig. 12 and [BF4−] in Fig. 13. When an intermolecular attractive potential is applied, the bulkier [TFSI−] gives rise to both a greater repulsion between positively charged surfaces and a greater attraction between neutral surfaces, than are generated with the smaller [BF4−] anion.
5. Concluding statements
In this work we have continued our earlier efforts to understand the behavior of ionic liquids in confined geometries, and their influence on the forces between the macroscopic surfaces that confine them. The focus of attention was on an added attractive intermolecular interaction between oppositely charged ionic molecules. An equilibrium between free cations and anions and associated molecules, orchestrated by this pair potential (Φ(8)eff or Φ(4)eff) has consequences for the molecular ion distributions as well as the forces between the surfaces. This has been studied with a density functional theory of ionic liquids.1 Admittedly, as with similar statistical mechanical treatments of complex liquids, the overall scheme is based on the assumption of pairwise interactions. Many-body effects are not included, but are likely to be significant in fluids of higher density.From our numerical results it would seem that the long range attractive pair potential, Φ(4)eff, which decays intermediately between the Coulomb and the dispersion potentials, inspires a significant degree of molecular association of ionic liquid molecules. This stronger coupling of oppositely charged oligomers has the effect of inducing a counterion-only state to exist between charged surfaces, and a near absence of all molecules between neutral surfaces. In contrast the shorter ranged Φ(8)eff, has limited ability to induce association. In this case, although the molecular distributions between the surfaces are not significantly affected, the surface force is still appreciatively modified.
With the DFT model it is nigh impossible to quantify explicitly the degree of ion association resulting from the additional effective potentials. It is only possible to draw qualitative inferences from the atom distributions. Whatever the degree of macromolecular association and irrespective of the origin of the effective attractive potential responsible for it, there can be no argument that the intermolecular attractive potential does makes a significant difference to the state of the system and specifically to the force between the surfaces. Moreover, the trend in the surface force with increasing strength of the attractive pair potential is in the direction of measured forces2–7 and is then also consistent with the findings of the different DFT cluster model of Forsman, Ma, Woodward and co-workers.8–11 This indicates that an effective intermolecular attraction is present in the physical system. What is needed is a verification of the origin of the attraction as either a consequence of strong ion correlations12–14 or of non-electrostatic causes.
On this same line of thought we make two further comments. Firstly, the DFT attempts to go beyond a mean-field approach by taking some account of steric and charge correlations, which are known to be absent from the mean-field, Gouy-Chapman theory of simple electrolytes.31 However, we acknowledge that the DFT approach too is limited compared with more accurate, integral equation theories, such as the hypernetted chain model.28 Just how accurate (or inaccurate) the DFT model is for a system of such complex ionic liquid molecules is likely only possible to determine through a comparison with Monte Carlo simulations. While non-trivial, we are pursuing such calculations in our ongoing work. Secondly, another drawback of the DFT approach is its inability to provide explicit quantitative information on specific cluster concentrations. While it is implicit from our results that intermolecular association occurs, quantifying the extent to which association occurs (pairing or higher order clustering) is beyond the DFT model. It has been suggested to us32 that an approach along the lines of a statistical associating fluid theory (SAFT),33–35 based on Wertheim's thermodynamic perturbation theory for associating fluids,36,37 might be the more appropriate route follow in order to divulge this information. We shall be considering this approach in future efforts.
Finally, we reiterate that two interesting topics to explore in other future studies are the temperature dependence of the system, adopting a temperature-dependent effective potential, and that of invoking a charge-dipole pair potential that includes the effect of dipole alignment in the field of the charge at short separations, transitioning to a freely rotating dipole at large separations.16 The latter study is likely to be pertinent to the adopted model of RTIL [C4mim+][TFSI−] which currently assumes a single charge on [TFSI−] interacting with a distribution of point charges on [C4mim+].
6. Appendix: electrostatic contributions to the functional
It has been discussed in the literature that modelling electrostatic correlations requires the use of different functionals in order to differentiate between electrostatic interactions between like atoms and those between unlike species. Typically, the functionals corresponding to the like (l) and unlike (ul) atom–atom electrostatic interactions are given by
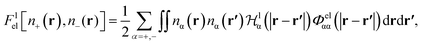 | (19) |
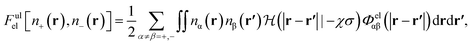 | (20) |
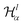 describes a soft exponential Coulomb hole. That is,
describes a soft exponential Coulomb hole. That is,
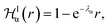 | (21) |
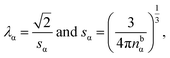 | (22) |
The differentiated contribution is to be contrasted with the model implemented in ref. 1 where the electrostatic interaction between charged atoms was treated uniformly using
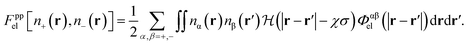 | (23) |
While there is a formal difference between these two approaches, the former approach being the case implemented for this work, we have not noted any significant difference in our results using the two methods.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Department for Innovation and Skills (formerly the Department of State Development), South Australian Government (Grant No: IRGP 22) is gratefully acknowledged.References
- A. Kiratidis and S. J. Miklavcic, Density functional theory of confined ionic liquids: A survey of the effects of ion type, molecular charge distribution and surface adsorption, J. Chem. Phys., 2019, 150, 184502 CrossRef PubMed.
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Ionic liquids behave as dilute electrolyte solutions, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(24), 9674–9679 CrossRef CAS PubMed.
- M. A. Gebbie, H. A. Dobbs, M. Valtiner and J. N. Israelachvili, Long-range electrostatic screening in ionic liquids, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(24), 7432–7437 CrossRef CAS PubMed.
- A. M. Smith, A. A. Lee and S. Perkin, The electrostatic screening length in concentrated electrolytes increases with concentration, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- C. Fung, R. Sedev, S. J. Miklavcic and J. N. Connor, Influence of electric field on the structure of a nanoconfined concentrated electrolyte, Chemeca 2016: Chemical Engineering – Regeneration, Recovery and Reinvention, 2016, pp. 391–399 Search PubMed.
- M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Long range electrostatic forces in ionic liquids, Chem. Commun., 2017, 53, 1214–1224 RSC.
- S. J. Miklavcic and C. Fung, Quantifying the force between mercury and mica across an ionic liquid using whilte light interferometry, J. Colloid Interface Sci., 2019, 218–227 CrossRef CAS PubMed.
- J. Forsman, C. E. Woodward and M. Trulsson, A classical density functional study of ionic liquids, J. Phys. Chem. B, 2011, 115, 4606–4612 CrossRef CAS PubMed.
- M. Turesson, R. Szparaga, K. Ma, C. E. Woodward and J. Forsman, Classical density functional theory & simulations on a coarse-grained model of aromatic ionic liquids, Soft Matter, 2014, 10, 3229–3237 RSC.
- K. Ma, J. Forsman and C. E. Woodward, Influence of ion pairing in ionic liquids on electrical double layer structures and surface force using classical density functional approach, J. Chem. Phys., 2015, 142(17), 174704 CrossRef PubMed.
- K. Ma, J. Forsman and C. E. Woodward, A classical density functional study of clustering in ionic liquids at electrified interfaces, J. Phys. Chem. C, 2017, 121(3), 1742–1751 CrossRef CAS.
- R. Kjellander, Nonlocal electrostatics in ionic liquids: The key to an understanding of the screening decay length and screened interactions, J. Chem. Phys., 2016, 145, 124503 CrossRef PubMed.
- R. Kjellander, Decay behavior of screened electrostatic surface forces in ionic liquids: the vital role of non-local electrostatics, Phys. Chem. Chem. Phys., 2016, 18, 18985 RSC.
- R. Kjellander, Focus article: Oscillatory and long-range monotonic exponential decays of electrostatic interactions in ionic liquids and other electrolytes: The significance of dielectric permittivity and renormalized charges, J. Chem. Phys., 2018, 148, 193701 CrossRef PubMed.
- J. O. Hirschfelder, C. F. Curtiss and R. B. Bird, Molecular Theory of Gases and Liquids, John Wiley & Sons, New York, 1954 Search PubMed.
- S. J. Miklavic, Effective dipole potentials after angle averaging, Phys. Rev. E, 1997, 56, 1142–1147 CrossRef.
- H. Lu, S. Nordholm, C. E. Woodward and J. Forsman, A classical density functional theory for the asymmetric restricted primitive model of ionic liquids, J. Chem. Phys., 2018, 148(19), 193814 CrossRef PubMed.
- M.-M. Huang, Y. Jiang, P. Sasisanker, G. W. Driver and H. Weingärtner, Static relative dielectric permittivities of ionic liquids at 25°C, J. Chem. Eng. Data, 2011, 56(4), 1494–1499 CrossRef CAS.
- N. Hjalmarsson, R. Atkin and M. W. Rutland, Is the boundary layer of an ionic liquid equally lubricating at higher temperature, Phys. Chem. Chem. Phys., 2016, 18, 9232–9239 RSC.
- N. Hjalmarsson, R. Atkin and M. W. Rutland, Switchable long-range double layer force observed in a protic ionic liquid, Chem. Commun., 2017, 53, 647–650 RSC.
- S. J. Miklavic and C. E. Woodward, The osmotic pressure in polyelectrolyte solutions: Exact and mean-field results, J. Chem. Phys., 1990, 93(2), 1369–1375 CrossRef CAS.
- The reference to counterion and coion is with respect to the surface charge. So, if the surfaces were negatively charged the counterion would be the cation, and the coion would be the anion, and vice versa for positively charged surfaces.
- B. Jönsson, H. Wennerström and B. Halle, Ion distributions in lamellar liquid crystals. a comparison between results from Monte Carlo simulations and solutions of the Poisson-Boltzmann equation, J. Phys. Chem., 1980, 84, 2179–2185 CrossRef.
- D. Bratko, B. Jönsson and H. Wennerström, Electrical double layer interactions with image charges, Chem. Phys. Lett., 1986, 128(5), 449–454 CrossRef CAS.
- T. Åkesson and B. Jönsson, Monte Carlo simulations of colloidal stability - beyond the Poisson-Boltzmann approximation, Electrochim. Acta, 1991, 36, 1723–1727 CrossRef.
- R. Kjellander, T. Åkesson, B. Jönsson and S. Marcelja, Double layer interactions in mono- and divalent electrolytes: a comparison of the anisotropic hypernetted chain theory and Monte Carlo simulations, J. Chem. Phys., 1992, 97, 1424–1431 CrossRef CAS.
- R. Kjellander and S. Marcelja, Correlation and image charge effects in electrical double layers, Chem. Phys. Lett., 1984, 112, 49–53 CrossRef CAS.
- R. Kjellander and S. Marcelja, Double-layer interaction in the primitive model and the corresponding Poisson-Boltzmann description, J. Phys. Chem., 1986, 90, 1230–1232 CrossRef CAS.
- P. Attard, D. J. Mitchell and B. W. Ninham, Beyond Poisson-Boltzmann: Images and correlations in the electrical double layer. i. counterions only, J. Chem. Phys., 1988, 88(8), 4987–4996 CrossRef CAS.
- One reviewer suggested the mathematically legitimate proposal that in a planar geometry the 1/r4 interaction converts to a 1/z2 dependence which increases the chemical potential of all oligomers in the thin film. This must then be counteracted by a lower internal density in order to maintain chemical equilibrium with bulk molecules.
- E. Verwey and J. T. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier, Amsterdam, 1948 Search PubMed.
- We thank one independent reviewer for this suggestion.
- W. G. Chapman, K. E. Gubbins, G. Jackson and M. Radosz, Saft-equation of state solution model for associating fluids, Fluid Phase Equilib., 1989, 52, 31–38 CrossRef CAS.
- W. G. Chapman, K. E. Gubbins, G. Jackson and M. Radosz, New reference equation of state for associating liquids, Ind. Eng. Chem. Res., 1990, 29(8), 1709–1721 CrossRef CAS.
- E. A. Muller and K. E. Gubbins, Molecular-based equations of state for associating liquids: A review of saft and related approaches, Ind. Eng. Chem. Res., 2001, 40(10), 2193–2211 CrossRef.
- M. S. Wertheim, Fluids with highly directional attractive forces. i. statistical thermodynamics, J. Stat. Phys., 1984, 35(1/2), 19–34 CrossRef.
- M. S. Wertheim, Fluids with highly directional attractive forces. ii. thermodynamic perturbation theory and integral equations, J. Stat. Phys., 1984, 35(1/2), 35–47 CrossRef.
| This journal is © The Royal Society of Chemistry 2021 |