Chemical dynamics simulations of energy transfer in CH₄ and N₂ collisions

Abstract

Chemical dynamics simulations have been performed to study the energy transfer from a hot N₂ bath at 1000 K to CH₄ fuel at 300 K at different bath densities ranging from 1000 kg m⁻³ to 30 kg m⁻³. At higher bath densities, the energy transfer from the bath to the fuel was rapid and as the density was decreased, the energy transfer rate constant decreased. The results show that in combustion systems with CH₄ as a prototype fuel, the super pressure regimes control the fuel heating and combustion processes.

---

Introduction

Combustion is an important process which involves synchronized multiphase fluid dynamics, chemical kinetics, heat transfer and the chaotic mixing of different species.¹ Among these processes, heat transfer is very crucial because of its strong relation to the energy utilization efficiency of the system during combustion. On a microscopic scale, energy transfer between a molecule and its surroundings takes place depending on the degrees of freedom of the molecule and the nature of the surroundings.^2,3 In order to simulate the energy transfer processes, N₂ gas is used as a surrounding gas, since the contribution of N₂ is large in the ambient air. Further, N₂ has been shown to be a dominant collision partner in lean combustion flames.^4–6 Since, practical fuels are complex mixtures of hydrocarbons, understanding the energy transfer between the hydrocarbons and the surrounding gas is vital to evaluate the energy utilization efficiency of fuels. Further, energy transfer efficiency is measured in terms of the degree of vibrational excitation and the nature of the deactivating collision partner.^7,8 The combustion of fuel in a dense supercritical fluid at high pressures^9–11 has potential applications in jet propulsion, tertiary oil and gas recovery, toxic waste treatment etc. In high-pressure combustion devices such as propellant rocket motors, the comportment of fuel in dense fluids and the associated chemical kinetics play a vital role in determining the efficacy of combustion processes.¹²

To develop a high-performance aircraft, fuel is the main heat sink and prior to combustion, the temperature of jet fuel rises. The most heat generating combustion reaction is with CH₄, the most abundant natural gas with reaction enthalpy of −890.7 ± 0.4 kJ mol⁻¹.¹³ As such, heating of CH₄ by the surrounding gas to increase combustion efficiency will be of interest in the context of energy utilization. In the present work, CH₄ is used as a model fuel and is heated from 300 to 1000 K in N₂ bath at pressures from the binary collision regime and the super pressure regime by means of chemical dynamics simulations. The energy transfer process between thermalized N₂ bath (1000 K) and CH₄ (300 K) is determined by crucial factors such as energy and temperature difference between CH₄ and N₂ bath as well as the energy and temperature difference of CH₄ before and after complete equilibration with the bath. A unified protocol for simulating liquid and gas phase intermolecular energy transfer was reported in our earlier work⁷ and applied for energy transfer from a hot N₂ bath to cold C₆F₆ molecule.¹⁴ This simulation procedure will be followed in the present work to study the intermolecular energy transfer of the system of CH₄ in the thermalized N₂ bath at 1000 K.

Computational methodology

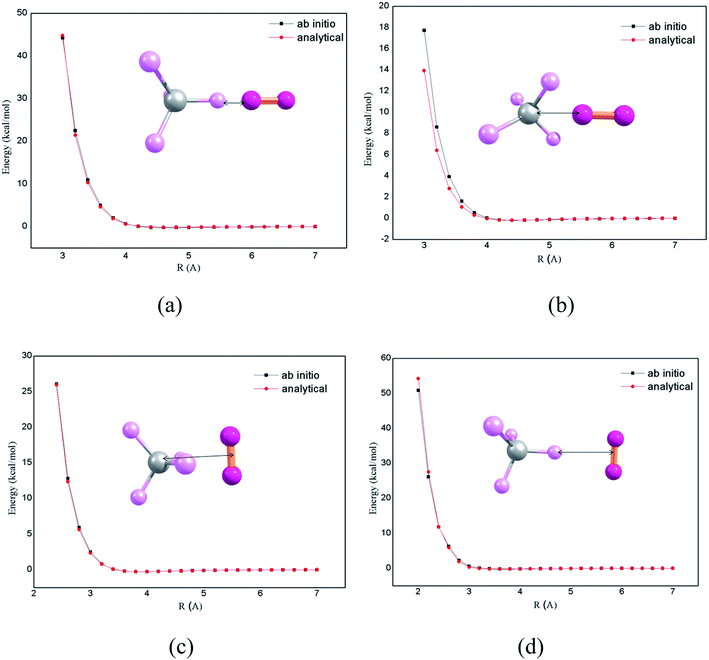
The chemical dynamics simulations can be accurately performed by the use of proper potential energy function. In previous works,^7,8 it was shown that there is an overall very good agreement of theoretical studies of intermolecular energy transfer by chemical dynamics simulation with the accurate intermolecular potentials, compared with experimental studies. The potential energy function for the CH₄ + N₂ system is expressed as a sum of intramolecular and intermolecular potentials. In CH₄–N₂ bath, the intermolecular pair potentials such as CH₄–CH₄, N₂–N₂ and CH₄–N₂ determine the properties of the system. The intramolecular potential for CH₄ is obtained in terms of stretching and bending coordinates. The intermolecular potential for N₂–N₂ was presented and described in previous publications^7,8 and is used in the current simulations. The CH₄–N₂ intermolecular potential is calculated by performing electronic structure calculations at CCSD(T)/aug-cc-pVTZ level of theory. The ab initio potential energy curves along with the analytic potential fitted using two body potentials according to Buckingham potential using genetic algorithm¹⁵ are presented in Fig. 1. In order to obtain the intermolecular potential of CH₄–N₂, the electronic structure calculations for four orientations were performed, as shown in Fig. 1. In the panel (a), N₂ molecule approaches along C–H bond axis. In the panel (b), the N₂ molecule approaches bisecting the H–C–H angle of CH₄. In panels (c) and (d), the midpoint of N₂ molecule approaches the carbon atom directly and along the C–H bond axis perpendicularly, respectively. The V₀ and R₀ by ab initio calculation for a–d are 0.02 kcal mol⁻¹ and 4.1 Å, −0.02 kcal mol⁻¹ and 3.9 Å, −0.01 kcal mol⁻¹ and 3.5 Å, and −0.01 kcal mol⁻¹ and 3.2 Å. The parameters obtained from potential energy function were used for chemical dynamics simulations.

Fig. 1 CH₄–N₂ interaction potential energy for four different orientations. The ab initio curves are calculated at CCSD(T)/aug-cc-pVTZ level. The analytical curves are generated by fitting the ab initio potential to the two body potentials according to Buckingham potential.

The simulations were performed by considering CH₄ at a temperature of 300 K and placing the N₂ bath with 1000 N₂ molecules at 1000 K temperature and collisional energy transfer takes place from N₂ bath to CH₄, thereby heating the “cold” CH₄. The simulations were studied at different densities ranging from 1000 kg m⁻³ to 30 kg m⁻³. Classical microcanonical sampling is used for the simulations accounting for the initial vibrational energy of 5.3 kcal mol⁻¹ for CH₄ at 300 K as implemented in the condensed phase version of VENUS chemical dynamics program.^7,16,17 The initial translational and rotational energies of CH₄ are chosen from their thermal distributions at 300 K. Also, the initial translational, vibrational and rotational energy of N₂ molecules were prepared by their thermal distribution at 1000 K. The procedure for choosing the initial conditions for the molecule and the bath are described in our earlier studies.^14,18,19 Collisional activation of CH₄ in N₂ bath was simulated by placing CH₄ at the center of a cubical box and CH₄ was surrounded by thermally equilibrated N₂ bath at 1000 K. The simulations were performed using periodic boundary conditions (PBCs) and a neighbour list algorithm with a cut-off distance of 15 Å. A set of 100 trajectories with random initial conditions for both CH₄ and N₂ bath were calculated. For the densities, 800 and 1000 kg m⁻³, the trajectories were integrated upto 6000 ps and for the remaining densities, the trajectories were integrated upto 8000 ps, with 2 fs of integration step size.

Results and discussion

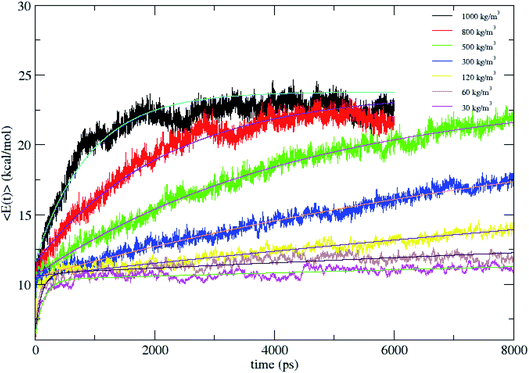
The average total energy of CH₄, 〈E(t)〉 versus time for N₂ bath densities of 30, 60, 120, 300, 500, 800 and 1000 kg m⁻³ averaged over 100 trajectories is shown in Fig. 2. The 〈E(t)〉 are fit by a biexponential function given in eqn (1) and the fitting parameters are tabulated in Table 1.

〈E(t)〉 = [E(∞) − E(0)](1 − f₁ exp(−k₁t) − f₂ exp(−k₂t)) + E(0) (1)

where f₁ + f₂ = 1, E(0) and E(∞) are the initial and final energies of CH₄, k₁ and k₂ are the rate constants.

Fig. 2 Average energy of CH₄ versus time for N₂ bath densities of 1000, 800, 500, 300, 120, 60, and 30 kg m⁻³ and this was fit to biexponential equation. The energies were averaged over 100 trajectories.

Table 1 Parameters for fits to 〈E(t)〉 for various bath densities

ρ (kg m^−3)	E(∞) (kcal mol^−1)	f1	f2	k1 (s^−1)	k2 (s^−1)	C1	C2
1000	23.8	0.3185	0.6815	1.42559	0.00103835	0.001426	1.04 × 10^−6
800	23.8	0.3095	0.6904	1.22559	0.00049534	0.001532	6.19 × 10^−7
500	23.8	0.3090	0.6910	0.9315	0.0002331	0.001863	4.66 × 10^−7
300	23.8	0.3078	0.6921	0.7315	7.13296 × 10^−5	0.002438	2.38 × 10^−7
120	23.8	0.2965	0.7034	0.010821	0.109 × 10^−5	9.02 × 10^−5	9.08 × 10^−9
60	23.8	0.2987	0.7012	0.005499	0.57 × 10^−6	9.17 × 10^−5	9.5 × 10^−9
30	23.8	0.2930	0.7069	0.002939	2.80 × 10^−7	9.8 × 10^−5	9.33 × 10^−9

---

Since from statistical mechanics, the final energy of fully equilibrated CH₄ at 1000 K which includes translational, rotational and vibrational energy should be 23.8 kcal mol⁻¹, all the energy curves in Fig. 2 are fit to this energy value. E(∞) is fixed with the value for the fitting. 〈E(t)〉 is highly non-exponential and the fluctuations in the energy curve are due to the relatively small size of the molecule and there is a strong oscillation between the kinetic and potential energy. As given in Table 1, as the density decreases, the weight of the larger rate constant component (k₁) decreases. That is, at high pressures frequent collisions in the bath populate molecular vibrational states and lead to intramolecular processes in nearly equilibrium ensembles which are rate determining.²⁰ As the solvent density is lowered, the energy transfer dynamics enters the independent, single collision limit.^14,18,19 Here, the rate constants k₁ and k₂ are proportional to the bath density, ρ with proportionality constants C₁ and C₂ defined by k₁ = C₁ × ρ and k₂ = C₂ × ρ, with the criterion for single collision limit being C₁ and C₂ becoming independent. The proportionality constant C₁ is same for the densities 120, 60 and 30 kg m⁻³, with C₂ also showing the same trend. Thus C₁ and C₂ become independent of density between 120 and 30 kg m⁻³, suggesting that the simulation in the 120 kg m⁻³ is in the single collision limit as predicted in earlier studies.^14,18,19

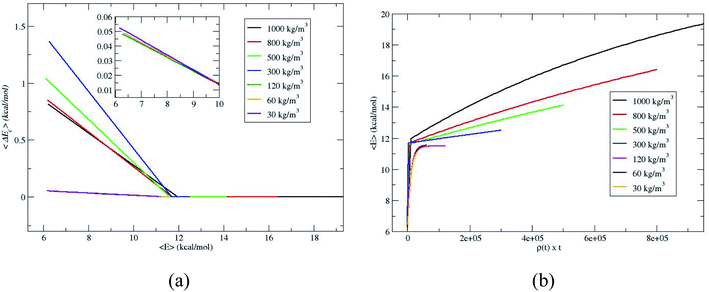
To further verify whether the C₁ and C₂ are identical for the densities 120, 60 and 30 kg m⁻³, the average energy transfer per collision is calculated.^14,18,19 The average energy transfer per unit time for the value of 〈E(t)〉 in eqn (1) is obtained by differentiating with respect to time, d〈E(t)〉/dt. In the single collision limit, the average energy transfer per collision is obtained by dividing d〈E(t)〉/dt by the collision frequency, ω, i.e.,

〈ΔE_c〉 = [d〈E(t)〉/dt]/ω (2)

The collision frequency of ω = 2.8 × 10⁸ s⁻¹ is used in the calculation of 〈ΔE_c〉. Thus using eqn (2) and 〈E(t)〉 in Fig. 2 and the collision frequency, the average energy transferred per collision, 〈ΔE_c〉 as a function of 〈E〉 for the different densities is shown in Fig. 3. 〈ΔE_c〉 is a composite of energy transfer from and to CH₄, i.e. 〈ΔE^up_c〉 and 〈ΔE^down_c〉, respectively. At large 〈E〉,〈ΔE^up_c〉 dominates and at long times, when equilibrium is attained, 〈ΔE^up_c〉 and 〈ΔE^down_c〉 are same and 〈ΔE_c〉 equals zero. The curves for 120, 60 and 30 kg m⁻³ are nearly identical, coinciding with the identical proportionality constants for 120, 60 and 30 kg m⁻³. The slopes of 〈ΔE_c〉 versus 〈E〉 plots become identical at or below ρ for single collision limit as shown in the inset of Fig. 3a. These discussions reveal that ρ = 30 kg m⁻³ is the good depiction of single collision limit and the collisional activation rate constant is directly proportional to the density. A plot of 〈E〉 versus ρ × t is shown in Fig. 3b to illustrate the single collision regime more clearly. The curves at densities 120, 60 and 30 kg m⁻³ coincide depicting that the system is in or near the single collision regime for these densities.

Fig. 3 Average energy transferred per collision, 〈ΔE_c〉, for the simulations.

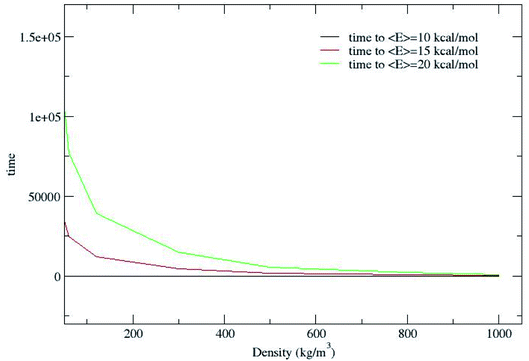
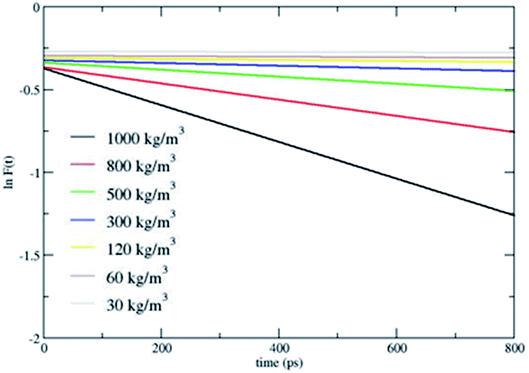
Fig. 2 shows that CH₄ is heated at relatively lesser time at higher densities 1000 and 800 kg m⁻³ and as the density is decreased, energy transfer from the bath to CH₄ is very moderate. A more precise plot illustrating the time required for each density to reach average energies of 10, 15 and 20 kcal mol⁻¹ is presented in Fig. 4. The energy transfer of 10 kcal mol⁻¹ from N₂ bath to CH₄ is instantaneous independent of the density of the bath. The time required to transfer 15 and 20 kcal mol⁻¹ energy from the bath to CH₄ is relatively shorter for densities 500, 800 and 1000 kg m⁻³ densities, whereas at low densities relatively longer time is required to transfer energy from N₂ bath to heat CH₄ and equilibration of the system. The plot shown in Fig. 4 is tantamount to assume that the fuels are heated rapidly at higher bath pressures. The dynamics of energy transfer from the bath to CH₄ can thus be expressed as ln F(t) versus time for each density for clarity purpose, where ln F(t) = ln[(f₁) − k₁T] or ln[(f₂) − k₂T] as shown in Fig. 5. The energy transfer rate constant plots show linear behaviour and at the single collision regime, the magnitude of the collisional activation rate constant, k is similar and the collisional activation is remarkably sensitive to the high pressures.

Fig. 4 Time (ps) to reach average energies of 10, 15 and 20 kcal mol⁻¹ for each density.

Fig. 5 ln F(t) versus time. ln F(t) = ln[(f₁) − k₁T] or ln[(f₂) − k₂T].

Conclusions

To summarize, in the present study the energy transfer from a thermalized 1000 K N₂ bath to CH₄ at 300 K is studied using classical chemical dynamics simulations. The simulations were performed for different N₂ bath densities ranging from 1000 kg m⁻³ to 30 kg m⁻³. The average energy of the ensemble of CH₄, 〈E〉 versus time is well fit by the biexponential eqn (1) and the fitting parameters f₁ is smaller and f₂ is larger and the longer time activation rate constant k₂ is smaller than k₁. The average energy transfer per collision 〈ΔE_c〉, is obtained and 〈ΔE_c〉 versus 〈E〉 is plotted. The plots are similar for 120, 60 and 30 kg m⁻³ densities indicating the single collision regime, whereas at higher densities 〈ΔE_c〉 decreases with the increase in density. The average energy transferred from the bath to CH₄ per collision is 〈ΔE^up_c〉 = 0.02 kcal mol⁻¹ at the initial CH₄ temperature of 300 K. The energy transfer from the bath to CH₄ is comparatively faster at higher bath densities than at the lower densities. The collisional activation rate constant decreases as the density is decreased. Thus, the heating of fuels is largely determined by high pressures and the combustion processes is controlled at these high pressures. The density dependence reveals that over wide density ranges from low pressure gases to highly compressed gases, various factors influence the intermolecular energy transfer and the diffusion control induced by the surrounding medium at high densities is one of the major factors. At supercritical pressures, the combustion mechanism is diffusion controlled and the rate will increase with pressure. Incorporation of diffusion controlled rate in the intramolecular dynamics of N₂ bath has more impact at gas/liquid phase transition.^20,21 In the diffusion controlled range, bimolecular reactions pre-dominate. Hence, the diffusion control is expected not to have much influence on the collisional activation rate constant for intermolecular energy transfer process in the current study. To conclude, in combustion systems the fuel is heated rapidly at super pressure regimes than at binary collision regimes and the energy transfer from the bath at pressures higher than the supercritical pressures to the fuels will be of future interest.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research reported here is based upon work supported by the Air Force Office of Scientific Research (AFOSR) under Grant No. FA9550-17-1-0119 and the Robert A. Welch Foundation under Grant No. D-0005. The simulations were performed on the Quanah computer cluster of the High Performance Computing Center (HPCC) of Texas Tech University and the Chemdynm computer cluster of the Hase Research Group.

References

1. M. Janbozorgi, K. E. Far and H. Metghalchi, Combustion Fundamentals in Handbook of Combustion, Fundamentals and Safety, ed. M. Lackner, F. Winter, and A. K. Agarwal, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2010, vol. 1.
2. D. C. Tardy and B. S. Rabinovitch, Intermolecular vibrational energy transfer in thermal unimolecular systems, Chem. Rev., 1977, 77, 369–408.
3. I. Oref and D. C. Tardy, Energy transfer in highly excited large polyatomic molecules, Chem. Rev., 1990, 90, 1407–1445.
4. R. A. Copeland, M. L. Wise and D. R. Crosley, Vibrational energy transfer and quenching of OH (A²∑⁺, v' = 1), J. Phys. Chem., 1988, 92, 5710–5715.
5. P. H. Paul, A model for temperature-dependent collisional quenching of OH A²∑⁺, J. Quant. Spectrosc. Radiat. Transfer, 1994, 51, 511–524.
6. P. H. Paul, Vibrational energy transfer and quenching of OH A²∑⁺ (v' = 1) measured at high temperatures in a shock tube, J. Phys. Chem., 1995, 99, 8472–8476.
7. A. K. Paul, S. C. Kohale, S. Pratihar, R. Sun, S. W. North and W. L. Hase, A unified model for simulating liquid and gas phase, intermolecular energy transfer: N₂ + C₆F₆ collisions, J. Chem. Phys., 2014, 140, 194103.
8. A. K. Paul, S. C. Kohale and W. L. Hase, Bath model for N₂ + C₆F₆ gas-phase collisions. details of the intermolecular energy transfer dynamics, J. Phys. Chem. C, 2015, 119, 14683–14691.
9. W. Schilling and E. U. Franck, Combustion and diffusion flames at high pressures to 2000 bar, Ber. Bunsen-Ges. Phys. Chem, 1988, 92, 631.
10. E. U. Franck, High pressure combustion and flames in supercritical water, Proc. Znt. Symp. Supercritical Fluids, 1991, p. 91.
11. J. Zhang, S. Wang, M. Ren, J. Lu, S. Chen and H. Zhang, Effect mechanism of auxiliary fuel in supercritical water: a review, Ind. Eng. Chem. Res., 2019, 58(4), 1480–1494.
12. P. E. Savage, S. Gopalan, T. I. Mizan, C. J. Martino and E. E. Brock, Reactions at supercritical conditions: applications and fundamentals, AIChE J., 1995, 41, 1723–1778.
13. D. A. Pittam and G. Pilcher, Measurements of heats of combustion by flame calorimetry. Part 8.-methane, ethane, propane, n-butane and 2-methylpropane, J. Chem. Soc., Faraday Trans., 1972, 68, 2224–2229.
14. A. K. Paul, D. Donzis and W. L. Hase, Collisional intermolecular energy transfer from a N₂ bath at room temperature to a vibrationally “Cold” C₆F₆ molecule using chemical dynamics simulations, J. Phys. Chem. A, 2017, 121, 4049–4057.
15. J. M. C. Marques, V. F. Prudente, F. B. Pereira, M. M. Almeida, A. M. Maniero and C. E. Fellows, A new genetic algorithm to be used in the direct fit of potential energy curves to ab initio and spectroscopic data, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 085103.
16. W. L. Hase, R. J. Duchovic, X. Hu, A. Komornicki, K. F. Lim, K. D. –H. Lu, G. H. Peslherbe, K. N. Swamy, S. R. Vande Linde, A. Varandas, et al., VENUS96: A General Chemical Dynamics Computer Program, Texas Tech University, Lubbock, TX, 2005.
17. X. Hu, W. L. Hase and T. Pirraglia, Vectorization of the general monte carlo classical trajectory program VENUS, J. Comput. Chem., 1991, 12, 1014–1024.
18. H. Kim, A. K. Paul, S. Pratihar and W. L. Hase, Chemical dynamics simulations of intermolecular energy transfer: azulene + N₂ collisions, J. Phys. Chem. A, 2016, 120, 5187–5196.
19. H. Kim, H. N. Bhandari, S. Pratihar and W. L. Hase, Chemical dynamics simulation of energy transfer: propylbenzene cation and N₂ collisions, J. Phys. Chem. A, 2019, 123, 2301–2309.
20. J. Troe, Elementary reactions in compressed gases and liquids: from collisional energy transfer to diffusion control, J. Phys. Chem., 1986, 90, 357–365.
21. H. Hippler, V. Schubert and J. Troe, A low-pressure extension of the Stokes–Einstein relationship, Ber. Bunsen-Ges. Phys. Chem, 1985, 89, 760–763.

---

Footnote

† Deceased.

---