Open Access Article
Open Access ArticleAn online optimization strategy for a fluid catalytic cracking process using a case-based reasoning method based on big data technology†
Peng Nia,
Bin Liub and
Ge He *b
*b
aChina University of Petroleum, Beijing 102249, China
bLanzhou Petro of PetroChina Company Limited, Lanzhou 730060, China. E-mail: 877157304@qq.com; hege@scu.edu.cn
First published on 24th August 2021
Abstract
Rigorous mechanistic models of refining processes are often too complex, which results in long modeling times, low model computational efficiencies, and poor convergence, limiting the application of mechanistic-model-based process optimization and advanced control in complex refining production processes. To address this problem and take advantage of big data technology, this study used case-based reasoning (CBR) for process optimization. The proposed method makes full use of previous process cases and reuses previous process cases to solve production optimization problems. The proposed process optimization method was applied to an actual fluid catalytic cracking maximizing iso-paraffins (MIP) production process for industrial validation. The results showed that the CBR method can be used to obtain optimization results under different optimization objectives, with a solution time not exceeding 1 s. The CBR method based on big data technology proposed in this study provides a feasible solution for fluid catalytic cracking to achieve online process optimization.
1 Introduction
In recent years, as crude oil has become increasingly heavy and inferior, the market demand for clean fuels and low-carbon olefins has been on the rise, and the targets for safety and environmental protection have been increasingly stringent. However, given the slowdown in the growth of refined oil consumption and the challenges brought by the rapid development of new energy fields, international competition for petrochemical products has become increasingly fierce, thereby putting forward new requirements for modern oil refining production.1 To address this problem, intelligent manufacturing provides an effective solution path by optimizing the refinery production process and the supply network through vertical, horizontal, and end-to-end integration.2 This improves the operational agility of the production process, and, in the face of internal and external disturbances, allows the rapid detection of, adaptation to, and handling of new situations, such as changes in oil properties and product prices. The development of intelligent manufacturing for refinery production necessarily includes soft measurements,1,3 scheduling and management,4,5 advanced process control (APC), and real-time optimization (RTO),6 all of which are based on mathematical models.7 However, the applications of rigorous mechanistic models (based on first principles), especially the industrial applications of APC, are mainly limited to heat transfer and separation processes, such as heat exchangers and distillation columns, while they are rarely applied in the reaction sections of complex refinery production units, such as fluid catalytic cracking and continuous reforming.8 This is because their reaction mechanisms are too complex and are not yet fully understood. In addition, the construction of mechanistic models is time consuming, and the resulting models have a low computational speed and poor convergence. In addition, the calibration data used for modeling are likely to deviate from the original range of model adaptations as the process changes. All these factors have reduced or even limited the application of mechanistic model-based process optimization in complex refinery production processes.Big data technology directly mines patterns from massive production data and retrieves and extracts useful information. The analysis process can reduce the reliance on complex process mechanisms. The application of cutting-edge data analysis technologies, such as big data and artificial intelligence, to the field of unit optimization can further improve the unit control, enhance the operating efficiency of the unit in the optimal operating range, increase the target product yield, improve product quality, reduce the energy consumption and production costs, improve safety, control environmental indicators, improve production efficiency, and increase economic benefits from multiple dimensions. As an alternative to APC and RTO, extracting reliable solutions from historical data sets based on mechanistic models is a feasible approach without any requirements for first-principles models.8
Based on the above discussion and the requirements of intelligent process manufacturing, we propose a data-model-based optimization method for fluid catalytic cracking units in this paper. This method is a general strategy of distributed reasoning based on historical cases, i.e., case-based reasoning (CBR). CBR mimics human reasoning by reusing data and solutions from similar problems in the past to solve new problems. It is an excellent tool for reusing previously acquired experience and is widely used to build design automation or decision support systems,9 such as production scheduling,10 processing,11,12 and fault diagnosis.13 In this paper, we first process the accumulated data sets of industrial refineries and high-fidelity simulation activities to form a case base with a determined structure. We then use a fuzzy matching method to extract cases from the case base that are similar to the new cases. The CBR method proposed in this paper is essentially a variable correlation algorithm, which can intelligently select variables that are strongly correlated with the target variables from a large number of the laboratory information management system (LIMS) and distributed control system (DCS) variables, thereby minimizing the model complexity and allowing the model to exhibit high computational speeds, fast convergence, and strong adaptability while ensuring reliability. Thus, it can be used to guide real-time online optimization.14–16
The rest of this article is organized as follows. Section 2 briefly reviews the method and applications of CBR. The method of CBR in the optimization of the fluid catalytic cracking process is presented specifically in Sections 3. Section 4 focuses on the validation of the effectiveness of the model with cases, and the article is concluded with the main findings.
2 Research progress of CBR method in refining and chemical field
CBR is a problem-solving and learning method that has received extensive attention in recent years. Aamodt and Plaza17 overviewed the foundational issues of CBR and described some of the leading methodological approaches in this field. Regarding the case extraction, Kolodner18 proposed three basic steps of extraction: (1) find the corresponding features, (2) calculate the similarity of each feature, and (3) finally multiply the partial similarity by the corresponding coefficient and compute the sum to obtain the overall similarity. Xia19 developed the dynamic CBR (DCBR) in view of the dynamics of process operation support systems. Aiming at the adaptation problem of case reuse, Koiranen et al.20 proposed a hybrid adaptation system, the main components of which are based on fuzzy logic and neural networks.CBR has been used in many aspects of the refining industry, mainly in chemical process synthesis, design analysis, and fault diagnosis. (1) The following research progress has been made in the application of CBR in chemical process synthesis and design analysis. In 2001, Pajula et al.21 proposed a CBR-based approach for chemical process synthesis and demonstrated the application of CBR in separation systems with cases. Avramenko et al.22 in 2004 used the CBR method as a design support tool for the pre-selection of the packing type for reactive distillation columns. In 2005, Seuranen et al.23 presented a new CBR-based approach for separation process synthesis and selection of single separations. Lopez-Arevalo et al.24 in 2007 proposed an approach for managing the complexity in the redesign/retrofitting of chemical processes. This approach uses model-based reasoning (MBR) to automatically generate alternative representations of an existing chemical process at multiple levels of abstraction. In the overall process, the hierarchical representation leads to sets of equipment and sections organized according to their functions and purposes. In 2009, Robles et al.25 proposed an approach for accelerating the inventive preliminary design for chemical engineering by coupling CBR with the TRIZ (theory of inventive problem solving) theory to achieve an extension of the CBR method from routine design to inventive design. Stephane et al.26 in 2010 attempted to improve the retrieval step of the CBR-based preliminary design of chemical engineering units. (2) The following research progress has been made in the application of CBR in process monitoring and fault diagnosis. Zhao et al.27 integrated CBR and ontology to develop a new learning hazard and operability analysis (HAZOP) expert system to improve the learning capability of the expert system. Zhao et al.13 proposed an improved CBR method to predict the status of the Tennessee Eastman (TE) process. Yan et al.28 proposed a case retrieval method based on a learning pseudo-metric (LPM) to replace the distance measure retrieval method and established a CBR-based fault diagnosis model for the TE process.
Zhang et al.8 applied the CBR method for the first time to optimize the refinery production process. First, the accumulated data sets from the industrial plants as well as high-fidelity simulation activities were processed to form a case base with a determined structure. Fuzzy matching was employed to evaluate the similarity, and an optimization model was established for the parameters of the fuzzy membership function. The application to an industrial fluid catalytic cracking unit was performed as an example for validation.
3 Case-based reasoning (CBR)-based process optimization model
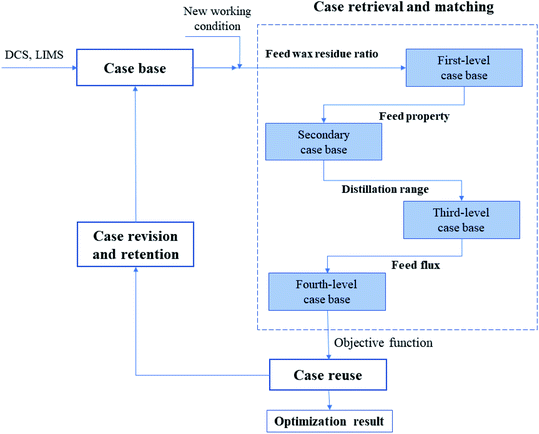
CBR method is essentially a process of database case extraction and reuse. The optimization process is to discretize the continuous operating variables (that represent the operation conditions), and then interpolate and match the operating variables to obtain the optimal operating variables. In addition to the establishment of case base, process optimization using CBR can be described by the following four processes: case extraction, case reuse, case revision and retention. Fig. 1 shows the technical route of the CBR method.• Retrieve: With the feed composition of the current case, including wax/residue ratio, residual carbon, sulfur contents, distillation temperature range and the feeding rate, etc., using the distance similarity to calculate the similarities between the operation conditions of the current case with historical cases, and then perform the comparison on four levels. The target is to find the historical cases with the most similar operation conditions.
• Reuse: The solution resulting from the retrieved cases is used as a suggested solution to the target problem. By matching the feed compositions to find the candidates from the case base, and arrange these candidates in descending order regarding the total liquid yield (or the gasoline yield, the coke yield). Then the optimal solution is the first one with the highest total liquid yield (or the highest gasoline yield, the lowest coke yield).
• Revise: If the actual product yield and the total liquid yield under the recommended conditions did not conform to the calculation results in the corresponding case base, then such case base would be modified, then the above operation was repeated to obtain the process optimization results.
• Retain: The process model or the simulation software was used to simulate different operating conditions, and a large number of cases representing various operating conditions were obtained. The generated cases were added to the case base to complete its expansion. On the other hand, due to the process transformation, the cases that did not appear were then eliminated.
3.1 Case base establishment
Before using CBR for process optimization, a historical case base must be established. First, the historical production data of DCS and LIMS of the unit are collected to establish a standard database of production data. The database format is standardized, and indexing rules are established to facilitate querying, addition, and extraction at a later stage. The variables used in the modeling are extracted from the standard database for pre-processing to prepare for the subsequent establishment of the case base. The pre-processing includes deleting invalid data, interpolating and fitting the missing values, eliminating the effects of noise signals and outliers with data smoothing techniques, and classifying variables. Linear interpolation is chosen as the interpolation method, and wavelet decomposition is used as the data smoothing technique to eliminate the effects of high-frequency noise signals and outliers during data analysis.The case base should be established to cover all possible problems and variable sets in the application field.29 The variables are divided into feed variables, influencing variables, and product variables. The case model is expressed as follows:
| Ck = {(Ik,Pk) → Sk} | (1) |
| Ik = (Ik,1,Ik,2, …, Ik,11) = (r, ρ, σ, ξ, Tini, T5%, T10%, T30%, T50%, T70%, Qm) | (2) |
| Pk = (Pk,1,Pk,2, …, Pk,m) = (Ydrygas, YLPG, Ygasoline, Ydiesel, Yslurry, Ycoke…) | (3) |
3.2 Case extraction
After the case base is established, the case with the highest similarity and its corresponding solution are extracted from the case base by means of case similarity calculations to complete the case extraction.9 In this study, we adopted the distance similarity. Assuming that a variable in the case corresponding to the current operating condition is x, the similarity between x and the corresponding variable xk of the case in the case base is calculated as follows:
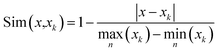 | (4) |
Four-level matching of the feed information was conducted based on the established case base using a distributed reasoning algorithm, which is shown by the steps in the rounded box in Fig. 1, as described in detail below:
(1) The cases that meet the upper and lower limits of the wax residue ratio are selected, and the resulting number of cases is denoted as n1. The similarity Sim(I1,Ik,1) between the wax residue ratio I1 of the current feed and the wax residue ratio Ik,1 in the case base is calculated using eqn (4). The first n2(n2 ≤ n1) cases greater than 0.9 are selected from the results ranked in descending order as the first-level case base.
(2) The weighted similarity D1 of the density, residual carbon, and sulfur content between the current feed and the feed in the case base in the first-level case base is calculated, and they are assigned different weights. The first n3(n3 ≤ n2) cases greater than 0.85 are selected according to the D1 results ranked in descending order as the second-level case base. D1 is calculated as follows:
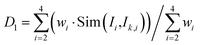 | (5) |
(3) The weighted similarity D2 of the boiling range temperatures (including the initial boiling point and the 5%, 10%, 30%, 50%, and 70% boiling range temperatures) between the current feed and the feed in the case base in the second-level case base is calculated, different weights are assigned to boiling range temperatures. The first n4(n4 ≤ n3) cases greater than 0.8 are selected according to the D2 results ranked in descending order as the third-level case base. D2 is calculated as follows:
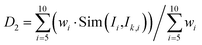 | (6) |
(4) The similarity Sim(I11,Ik,11) of the flow rate between the current feed and the feed in the historical base in the third-level case base is calculated. The first n5(n5 ≤ n4) cases greater than 0.7 are selected according to the results ranked in descending order as the fourth-level case base.
3.3 Case reuse
The case reuse of the process optimization is realized by optimizing the objective function.(1) If the maximization of the total liquid yield Fk is used as the objective of the process optimization, the operating condition corresponding to the maximum value of Fk in the fourth-level case base is the optimal operating condition ST:
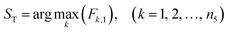 | (7) |
| Fk,1 = Pk,2 + Pk,3 + Pk,4 | (8) |
(2) If the maximization of the gasoline yield Fk,2 is used as the objective of the process optimization, the operating condition corresponding to the maximum value of Fk,2 in the fourth-level case base is the optimal operating condition ST:
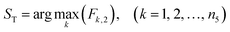 | (9) |
| Fk2 = Pk,3 | (10) |
(3) If the minimization of the coke yield Fk,3 is used as the objective of the process optimization, the operating condition corresponding to the minimum value of Fk,3 in the fourth-level case base is the optimal operating condition ST:
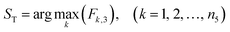 | (11) |
| Fk3 = Pk,6 | (12) |
3.4 Case revision and retention
If the product yield and total liquid yield actually obtained under the recommended operating conditions do not match the product calculation results in the corresponding case base, the case base is revised, and then the above operations are repeated to obtain the process optimization results.Case expansion provide enough cases to ensure the reliability of results and broad applicability of model. There are two methods of case expansion: one is industrial historical data (actual data), and the other is the prediction results of the process model or the simulation software. In addition, regarding some hidden parameters such as the mass transfer performance of the unit change slowly with time, so regular updates can ensure the timeliness of the model. There are two methods of case update: one is to update the expansion regularly, and the other is to expand immediately when the process is modified or the operating conditions continue to change significantly. During the case update, the new production data are added to the data set while part of the oldest data are eliminated, and the new data set is used to adapt to the new operating conditions.
4 Industrial application
4.1 Description of fluid catalytic cracking process
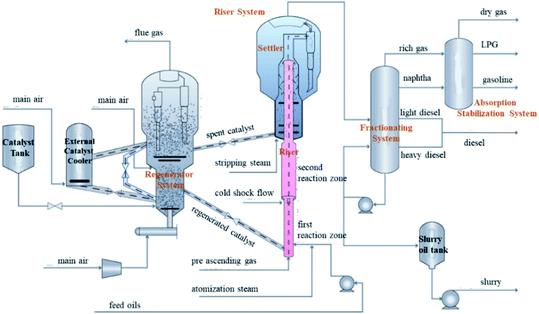
Fig. 2 shows the maximizing iso-paraffins (MIP) process flow of the fluid catalytic cracking process. The reaction regeneration process of the core section is described as follows. The raw material enters the first reaction zone of the riser reactor, comes into contact with the regenerated catalyst from the regenerator, and immediately gasifies and reacts, with the heat of gasification of the raw material and the heat of reaction provided by the high-temperature regenerated catalyst. The reaction oil and gas have a short residence time in the first reactor and then enter the expanded second reactor with the catalyst. After the oil and gas carries the catalyst through the cyclone fast separator at the outlet of the riser, the oil and gas with a small amount of catalyst enters the top cyclone separator for further separation, and the separated oil and gas goes to the fractionation column and absorption stabilization system.The MIP process of a fluid catalytic cracking unit in a refinery in northwest China was modeled for industrial validation. This unit has a production load of 300 million tons per annum, and its calibrated operating conditions were as follows: wax oil feed rate, 250 t h−1; residue oil feed rate, 140 t h−1; catalyst–oil ratio, 6.5; inlet temperature of the second reactor, 502 °C; inlet temperature of the first reactor, 512 °C; outlet temperature of the second reactor, 501 °C; settler top pressure, 0.18 MPa; riser pressure drop, 50 kPa; and regenerator pressure, 0.22 MPa.
The production data from October 2019 to May 2020 were collected, and a case base was created according to the method presented in Section 3.1, including 42 DCS items and 9 LIMS analysis indices. The description of these variables is given in Appendix A, Tables S1 and S2.†
4.2 Discussion of process optimization results under different optimization objectives
The selected feed composition and physical properties were as follows: wax oil feed rate, 227.90 t h−1; residual oil feed rate, 176.53 t h−1; and the corresponding physical property data of the feed are shown in Table 1.| No. | Type | Name | Value | Unit |
|---|---|---|---|---|
| 1 | General properties | Density (20 °C) | 913.5 | kg m−3 |
| 2 | Residual carbon | 3.1 | Wt% | |
| 3 | Slag mixing ratio | 0.436 | Dimensionless | |
| 4 | Boiling range temperature | Initial boiling point | 219 | °C |
| 5 | 5% distilled temperature | 324 | °C | |
| 6 | 10% distilled temperature | 348 | °C | |
| 7 | 30% distilled temperature | 400 | °C | |
| 8 | 50% distilled temperature | 435 | °C | |
| 9 | 70% distilled temperature | 489 | °C | |
| 10 | Element content | Sulfur | 0.35 | Wt% |
In this study, 22 important DCS items were selected as the influencing variables for optimization, and the process optimization calculation was carried out with the selected feed for different optimization objectives, including the maximum gasoline yield, the maximum total liquid yield, and the minimum coke yield, to obtain the results of the influencing variables. Specifically, the product yield distribution of three different working conditions (optimal, suboptimal and third best) under three different optimization objectives is given. See Table 2 for specific data results. The calculated optimal chemical parameters are given with the best gasoline yield as an example, as shown in Table 3.
| Optimization objective and value (wt%) | Product | Yield under optimal condition (wt%) | Yield under second optimal condition (wt%) | Yield under third optimal condition (wt%) |
|---|---|---|---|---|
| Maximization of gasoline yield, 52.50% | Total liquid | 86.01 | 87.07 | 85.49 |
| Gasoline | 52.5 | 52.16 | 52.02 | |
| Diesel | 16.63 | 17.36 | 16.66 | |
| Dry gas | 3.65 | 3.77 | 3.58 | |
| LPG | 16.88 | 17.55 | 16.81 | |
| Slurry | 3.53 | 3.81 | 3.81 | |
| Coke | 6.81 | 5.35 | 7.12 | |
| Maximization of total liquid yield, 87.07% | Total liquid | 87.07 | 86.06 | 86.01 |
| Gasoline | 52.16 | 51.45 | 52.5 | |
| Diesel | 17.36 | 17.06 | 16.63 | |
| Dry gas | 3.77 | 3.71 | 3.65 | |
| LPG | 17.55 | 17.55 | 16.88 | |
| Slurry | 3.81 | 4.05 | 3.53 | |
| Coke | 5.35 | 6.18 | 6.81 | |
| Minimization of coke yield, 5.35% | Total liquid | 87.07 | 86.06 | 85.94 |
| Gasoline | 52.16 | 51.45 | 51.44 | |
| Diesel | 17.36 | 17.06 | 17.01 | |
| Dry gas | 3.77 | 3.71 | 3.7 | |
| LPG | 17.55 | 17.55 | 17.49 | |
| Slurry | 3.81 | 4.05 | 4.08 | |
| Coke | 5.35 | 6.18 | 6.28 |
| No. | Item | Optimal condition | Second optimal condition | Third optimal condition |
|---|---|---|---|---|
| 1 | TI3106B | 506.48 | 503.86 | 506.34 |
| 2 | TI3106A | 511.82 | 509.48 | 511.8 |
| 3 | TI3111 | 676.02 | 679.39 | 677.46 |
| 4 | FIC3105 | 1.53 | 1.49 | 1.52 |
| 5 | FIC3208 | 168.66 | 176.88 | 170.99 |
| 6 | FIC3209 | 216.92 | 237.64 | 213.65 |
| 7 | FIC3109 | 2.25 | 2.26 | 2.25 |
| 8 | PdI3122 | 69.47 | 68.11 | 69.34 |
| 9 | PdIC3103 | 52.23 | 54.45 | 48.87 |
| 10 | DI3102 | 32.47 | 50.11 | 31.23 |
| 11 | TIC3101 | 496.73 | 495.49 | 496.02 |
| 12 | TIC3204 | 197.67 | 193.59 | 197.5 |
| 13 | FIC3111 | 7.5 | 5.01 | 7.5 |
| 14 | FIC3110 | 3 | 5.5 | 3 |
| 15 | PI3106 | 0.23 | 0.23 | 0.23 |
| 16 | TIC3125 | 694.58 | 694.91 | 697.21 |
| 17 | TI3131A | 669.51 | 671.82 | 669.75 |
| 18 | TI3126A | 699.97 | 699.98 | 703.64 |
| 19 | TIC3102 | 691.88 | 693.73 | 700.38 |
| 20 | PI3110 | 0.3 | 0.31 | 0.3 |
| 21 | DI3112 | 419.34 | 415.17 | 437.66 |
| 22 | FIC3122 | 2524.2 | 2629.98 | 2374.71 |
MATLAB 2014b (MathWorks, Inc.) was used to modeling for process optimization. Computer configuration: processor: Intel (R) Xeon (R) Gold 5117 CPU @ 2.00 GHz (dual processor); memory: 32.0 GB; operating system type: 64-bit. The optimization calculation process, including case extraction and case reuse, was controlled to be completed within 1 s.
4.3 Effectiveness validation and benefit calculation of process optimization
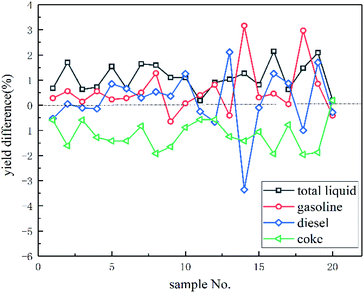
A total of 20 sets of operating conditions were taken to validate the effectiveness of the process optimization. The differences between the actual and optimized values calculated by the CBR method using the maximization of the total liquid yield as the objective are shown in Fig. 3. After optimization, the total liquid yield, liquefied petroleum gas yield, and gasoline yield increased by 1.10%, 0.36%, and 0.57%, respectively, on average, and the coke yield decreased by 1.17% on average.The benefits were calculated with the following considerations. The energy consumption was based on the relevant Chinese national standard. The energy consumption for processing heavy raw oil should be less than 85 kg of standard oil per ton, and the product with increased yield was multiplied by an energy consumption coefficient of 0.085. Coke was processed by the regenerator to provide energy for the unit at no cost. The maximization of the total liquid yield was the objective for optimization. The yield change and profit calculation of each product are shown in Table 4. The profit change was calculated as follows:
| Material flow | Yield change (%) | Average price (yuan per ton) | Average profit (yuan per ton) |
|---|---|---|---|
| Dry gas | 0.08 | 2000 | 200 |
| Liquefied petroleum gas | 0.36 | 3500 | 350 |
| Catalytic gasoline | 0.57 | 5000 | 500 |
| Catalytic diesel | 0.17 | 4000 | 400 |
| Slurry | −0.01 | 2500 | 250 |
| Coke | −1.17 | 0 | — |
It is estimated that the use of the optimized system can bring about a profit improvement of approximately 13.52 million yuan per year for a 3 million ton/year fluid catalytic cracking unit.
5 Conclusion
Modeling, optimization, and control of fluid catalytic cracking processes are all important aspects of the refining industry. However, the complexity of the process and the uncertainty of the raw materials and product markets pose a challenge for achieving timely control optimization based on models. To address this problem, this study proposes a CBR-based process optimization method based on big data technology, which ensures both the accuracy of the optimization results and satisfactory computational efficiency to effectively support industrial applications of complex refinery production processes. Taking the MIP process of the fluid catalytic cracking unit as an example, effective optimization results were obtained by the CBR method under different optimization objectives. Furthermore, the feasibility of the method was verified through optimization tests under 20 sets of operating conditions. Therefore, the optimization of the process operating conditions by the CBR method based on the big data technology proposed in this paper can lead to more reasonable product quality control and product yield distribution in fluid catalytic cracking units, which is significant for improving the product structure, performing real-time adjustments to external changes, and improving refinery efficiency. The method proposed in this paper can also be combined with APC systems to achieve fine optimization and control in real time.Although the application of real-time operation and optimal control based on rigorous mechanistic models in complex production processes is still in its infancy, the CBR method used in this paper is advantageous in terms of data models. The fusion of the two technical methods will become an important research topic and direction in the future. In particular, the development of plant-wide process optimization in real time using mechanism-based big data technology may be achieved.
Conflicts of interest
There are no conflicts of interest to declare.References
- P. K. Dasila, I. R. Choudhury, D. N. Saraf, V. Kagdiyal, S. Rajagopal and S. J. Chopra, Estimation of FCC feed composition from routinely measured lab properties through ANN model, Fuel Process. Technol., 2014, 125, 155–162 CrossRef CAS.
- G. He, Y. Dang, L. Zhou, Y. Dai, Y. Que and J. Xu, Architecture model proposal of innovative intelligent manufacturing in the chemical industry based on multi-scale integration and key technologies, Comput. Chem. Eng., 2020, 141, 106967 CrossRef CAS.
- J. Michalopoulos, S. Papadokonstadakis, G. Arampatzis and A. Lygeros, Modelling of an industrial fluid catalytic cracking unit using neural networks, Chem. Eng. Res. Des., 2001, 79(A2), 137–142 CrossRef CAS.
- K. Pashikanti and Y. A. Liu, Predictive Modeling of Large-Scale Integrated Refinery Reaction and Fractionation Systems from Plant Data. Part 2: Fluid Catalytic Cracking (FCC) Process, Energy Fuels, 2011, 25(11), 5298–5319 CrossRef CAS.
- F. D. Mele, A. Espuna and L. Puigjaner, Supply chain management through dynamic model parameters optimization, Ind. Eng. Chem. Res., 2006, 45(5), 1708–1721 CrossRef CAS.
- A. A. Alaradi and S. Rohani, Identification and control of a riser-type FCC unit using neural networks, Comput. Chem. Eng., 2002, 26(3), 401–421 CrossRef CAS.
- M. Heitzig, G. Sin, M. Sales-Cruz, P. Glarborg and R. Gani, Computer-Aided Modeling Framework for Efficient Model Development, Analysis, and Identification: Combustion and Reactor Modeling, Ind. Eng. Chem. Res., 2011, 50(9), 5253–5265 CrossRef CAS.
- Z. Zhang, D. Chen, Y. Feng, Z. Yuan, B. Chen, W. Qin, S. Zou, S. Qin and J. Han, A strategy for enhancing the operational agility of petroleum refinery plant using case based fuzzy reasoning method, Comput. Chem. Eng., 2018, 111, 27–36 CrossRef CAS.
- S. Dong, B. Habib, B. Li, W. Yu and B. Young, Organic Rankine Cycle Systems Design Using a Case-Based Reasoning Approach, Ind. Eng. Chem. Res., 2019, 58(29), 13198–13209 CrossRef CAS.
- T. Kocsis, S. Negny, P. Floquet, X. Meyer and E. Rév, Case-Based Reasoning system for mathematical modelling options and resolution methods for production scheduling problems: Case representation, acquisition and retrieval, Comput. Ind. Eng., 2014, 77, 46–64 CrossRef.
- A. Y. Sheikh and A. G. Jones, Crystallization process optimization via a revised machine learning methodology, AIChE J., 1997, 43(6), 1448–1457 CrossRef CAS.
- Y. Li, X. Wang, Z. Liu, X. Bai and J. Tan, A data-based optimal setting method for the coking flue gas denitration process, Can. J. Chem. Eng., 2019, 97(4), 876–887 CrossRef CAS.
- H. Zhao, J. Liu, W. Dong, X. Sun and Y. Ji, An improved case-based reasoning method and its application on fault diagnosis of Tennessee Eastman process, Neurocomputing, 2017, 249, 266–276 CrossRef.
- H. J. L. Van Can, H. A. B. Te Braake, S. Dubbelman, C. Hellinga, K. C. A. M. Luyben and J. J. Heijnen, Understanding and applying the extrapolation properties of serial gray-box models, AIChE J., 1998, 44(5), 1071–1089 CrossRef CAS.
- W. H. AlAlaween, M. Mahfouf and A. D. Salman, Integrating the physics with data analytics for the hybrid modeling of the granulation process, AIChE J., 2017, 63(11), 4761–4773 CrossRef CAS.
- M. Hinchliffe, G. Montague, M. Willis and A. Burke, Hybrid approach to modeling an industrial polyethylene process, AIChE J., 2003, 49(12), 3127–3137 CrossRef CAS.
- A. Aamodt and E. Plaza, Case-Based Reasoning: Foundational Issues, Methodological Variations, and System Approaches, AI Commun., 2001, 7, 39–59 Search PubMed.
- J. Kolodner, Case-based reasoning, Morgan Kaufmann Publishers Inc., 1993 Search PubMed.
- Q. J. Xia and M. Rao, Dynamic case-based reasoning for process operation support systems, Eng. Appl. Artif. Intell., 1999, 12(3), 343–361 CrossRef.
- T. Koiranen, T. Virkki-Hatakka, A. Kraslawski and L. Nystrom, Hybrid, fuzzy and neural adaptation in case-based reasoning system for process equipment selection, Comput. Chem. Eng., 1998, 22, S997–S1000 CrossRef CAS.
- E. Pajula, T. Seuranen, T. Koiranen and M. Hurme, Synthesis of separation processes by using case-based reasoning, Comput. Chem. Eng., 2001, 25(4–6), 775–782 CrossRef CAS.
- Y. Avramenko, L. Nystrom and A. Kraslawski, Selection of internals for reactive distillation column - case-based reasoning approach, Comput. Chem. Eng., 2004, 28(1–2), 37–44 CrossRef CAS.
- T. Seuranen, M. Hurme and E. Pajula, Synthesis of separation processes by case-based reasoning, Comput. Chem. Eng., 2005, 29(6), 1473–1482 CrossRef CAS.
- I. Lopez-Arevalo, R. Banares-Alcantara, A. Aldea, A. Rodriguez-Martinez and L. Jimenez, Generation of process alternatives using abstract models and case-based reasoning, Comput. Chem. Eng., 2007, 31(8), 902–918 CrossRef CAS.
- G. C. Robles, S. Negny and J. M. Le Lann, Case-based reasoning and TRIZ: A coupling for innovative conception in Chemical Engineering, Chem. Eng. Process., 2009, 48(1), 239–249 CrossRef.
- N. Stephane, R. Hector and L. L. J. Marc, Effective retrieval and new indexing method for case based reasoning: Application in chemical process design, Eng. Appl. Artif. Intell., 2010, 23(6), 880–894 CrossRef.
- J. Zhao, L. Cui, L. Zhao, T. Qiu and B. Chen, Learning HAZOP expert system by case-based reasoning and ontology, Comput. Chem. Eng., 2009, 33, 371–378 CrossRef CAS.
- A.-j. Yan, Y.-j. Wang and D.-h. Wang, Fault diagnosis method using learning case-based reasoning for Tennessee-Eastman process, Control Theory Appl., 2017, 34(9), 1179–1184 Search PubMed.
- T. Farkas, Y. Avramenko, A. Kraslawski, Z. Lelkes and L. Nyström, Selection of a Mixed-Integer Nonlinear Programming (MINLP) Model of Distillation Column Synthesis by Case-Based Reasoning, Ind. Eng. Chem. Res., 2006, 45(6), 1935–1944 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra03228c |
| This journal is © The Royal Society of Chemistry 2021 |