DOI:
10.1039/D1RA03527D
(Paper)
RSC Adv., 2021,
11, 27499-27511
Analysing cation-modified magnetic perovskites A2SnFeO6 (A = Ca, Ba): a DFT study
Received
6th May 2021
, Accepted 19th July 2021
First published on 13th August 2021
Abstract
Self-consistent DFT-based structural optimizations for understanding the cation effect on various properties of A2SnFeO6 (A = Ca, Ba) perovskites have been figured out in this study. The two-dimensional spin-polarized band structures, along with their corresponding density of states within the mix of two calculation schemes Perdew–Burke–Ernzerhof Generalized Gradient Approximation (PBE-GGA) and Hubbard correlation correction (PBE + U), strongly appeals its half-metallic nature, which has been discussed in detail. The perfect occurrence of the half-metallic nature with high-spin subsystem corresponds to a metal-type spectrum and in contrast to the opposite-spin claims semiconducting behaviour. The effect of significant spin-polarisation creates a ferromagnetism of total 4 (μB) mostly arising at (Fe). The induced magnetism of oxygen atoms is due to the overlapping between Fe-3d-O-2p orbitals. The mechanical strength is characterized from cubic elastic parameters that decide the capability of these materials against various external distortion forces displaying brittle nature. Apart from this, the semi-classical Boltzmann transport theory embedded in BoltzTraP package has been keenly addressed to turn out Seebeck coefficients, electrical and lattice thermal conductivities. The overall study creates a significant momentum in connection with the development of unlocking spintronics, spin dynamics and energy harvesting applications.
1 Introduction
In the present era, the perovskite field has become a point of prestige for the scientific community due to their multi-dimensional applications in the fields of spintronics, as an electrode material for a solid oxide fuel cell, in thermoelectrics as an active material for the conversion of squandered heat into usable electrical energy.1–3 More likely, these materials are striking novel applicants due to their environment-friendly nature, high-temperature stability, and better oxidation resistance.4–6 Searching for better and smarter materials retains the promising capabilities to meet the challenges for new technological applications. Highly spin-based magnetic materials have scored forthcoming applications thanks to density functional theory (DFT), which had simulated these materials and are considered be the most prominent to become replacements for various conventional materials.7–11 Besides, to their intriguing advancements, they have the ability to display the characteristic feature of half-metallicity near the Fermi level which results the 100% spin-polarization within these compounds.12–14 The highly spin-polarized materials are recognized as having their one spin channel metallic and semiconducting in another spin direction. However, the occurrence of half-metallicity along with efficient thermoelectric performance has shown the double perovskites to be applicable in spin-electronics, power technology sources, and energy harvesting technologies.15–17 Apart from this, the perovskite structure holding transition elements in their corresponding lattices could result in enhancing the simultaneous ordering of magnetism, ferroelectricity, magnetodielectric coupling and electric field-controlled magnetic sensors.18 On further exploring these materials in terms of their structural stability, the Goldschmidt tolerance factor (t)19 lies in the cubic range 0.99–1.0 and defines the cubic structural stability. The discovery of perovskites in the ancient era was substantially laid by Russian mineralogist and crystallographer Gustav Rose amd got the name in the honour of Lev-Perovski.20 The simple and double perovskite compounds generally are characterized by ABO3 and A2(BB′)O6 respectively, where A is the rare-earth or alkaline earth metal residing in the center of the dodecahedral structure, B and B′ are transition elements with open dn shells (1 ≤ n ≤ 9), and O is an sp (main group) element.21 The enhancement in their chemical and physical properties can be altered by changing the A-site, B site, and B′ site, leading to a change in the double exchange and super exchange mechanisms.22 On the contrary, the double perovskite structure with BO6 and B′O6 octahedra are alternatively arranged in a three-dimensional space, resulting in different space groups, such as Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, I4/m, and P4/nmc.23 The possibilities of tailoring the applications in such systems have increased the resurgent interests in these compounds with the advent of time. However, a large number of experimental and theoretical studies are going on to expand the properties of these compounds. Therefore, we have carried this piece of work to discuss the main highlights regarding the main theme of the present study. The survey of the literature reveals that the compositional analysis of both these materials belongs to the cubic unit cell structures, along with the space group orientation of Fm
m, I4/m, and P4/nmc.23 The possibilities of tailoring the applications in such systems have increased the resurgent interests in these compounds with the advent of time. However, a large number of experimental and theoretical studies are going on to expand the properties of these compounds. Therefore, we have carried this piece of work to discuss the main highlights regarding the main theme of the present study. The survey of the literature reveals that the compositional analysis of both these materials belongs to the cubic unit cell structures, along with the space group orientation of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with ferromagnetic parallel spin ordering. Similar prototype perovskites Sr2SnMnO6 and Sr2SnFeO6 were also predicted within the strict and rigorous DFT simulation techniques, showing a satisfactory thermoelectric and spintronic response. The present report is confined to explore the basic understandings of A2SnFeO6 (A = Ca, Ba) double perovskites above and beyond 100% spin polarization, which may be fruitful to meet the requirements in future situations.
m with ferromagnetic parallel spin ordering. Similar prototype perovskites Sr2SnMnO6 and Sr2SnFeO6 were also predicted within the strict and rigorous DFT simulation techniques, showing a satisfactory thermoelectric and spintronic response. The present report is confined to explore the basic understandings of A2SnFeO6 (A = Ca, Ba) double perovskites above and beyond 100% spin polarization, which may be fruitful to meet the requirements in future situations.
2 Calculation and simulation
We have also performed our calculations to determine these perovskites A2SnFeO6 (A = Ca, Ba) for their potential in thermoelectric technology and future spintronic applications. Relaxation of the lattice constant, atomic positions, optimized volume, and so forth was obtained via full potential linearized augmented plane wave (FP-LAPW), as installed in the WIEN2k program.24 The density functional theory (DFT) calculations have been conveniently performed in the version of PBE-GGA25 parameterization for dealing with the exchange–correlation potential. This is because the PBE-GGA formulism has wide anomalies when defining the electronic structure, particularly the underestimation of the band gap in correlated d/f systems, due to the insufficient potential for highly localized states and also the self-interaction error between the electrons, which fails to produce the accurate band profiles. Therefore, a useful approach that provides satisfactory results for such systems known as the strong correlation correction (GGA + U)26 was employed, in which the total energy is expressed by the equation written as:| |
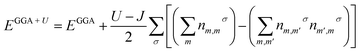 | (1) |
Here, in the abovementioned equation, m and σ represent the d-orbital and spin index, respectively. The parameters U and J are coupled into a spherically averaged, single effective interaction parameter, U–J.27 It should be mentioned here that the optimization of the Hubbard (U) parameter is an alternative approach to describe the results near the experimental values. The optimization of the U parameter is achieved theoretically by making the calculations converge for the total energy, bulk electronic and magnetic properties. In the present set of calculations, we have adopted the effective potential Ueff = U − J, where U defines the on-site Coulomb interaction, which was calibrated to 0.45 Ry and 0.50 Ry on the Fe-3d orbitals. This difference may be attributed to the size difference of Ca and Ba in both crystal structures because the bigger atom tends to increase the lateral strain, and the decreased bond length makes the electronic wave functions superimpose the larger accounts. Keeping the magnetic properties in mind, we have not kept J constant; i.e., we make use of both Hubbard correction to the electronic correlation and the exchange correction (J) varied from (0 to 0.04 eV) in order to know the spin magnetic interaction among the various constituents of atoms in the A2SnFeO6 (A = Ca, Ba) compounds. The muffin-tin potential for the basis set defined as a product of Rmt × Kmax = 7, where Rmt represents the smallest muffin tin sphere radii and Kmax is the largest k-value, has been selected in a proper way to prevent electron hopping, as well as charge leakage from the interstitial regions. The valence electronic configuration of each atomic species has been written as Ca/Ba: 4s2/5s25p66s2, Sn: 4d105s25p2, Fe: 3d64s2 and O: 1s22s22p4. The valence and deep-lying core electrons are separated by a cut-off energy of −7.0 Ry. For the Brillouin zone (BZ) integration in momentum space, a mesh of 1000 k points was used. The crystal potential and charge density are expanded up to an orbital quantum number ‘lmax’ = 10. The self-consistent field (SCF) for calculating the electronic ground state density can be determined until the charge and energy convergence reaches the specific values 10−4 a. u.3 and 10−4 Ry, respectively. The computation on the elastic constants associated with the second-order change of the internal energy is determined from cubic-elastic package. Finally, the transport and thermodynamical properties have been established from their respective packages.
3 Results and discussions
The refined lattice constants of A2SnFeO6 (A = Ca, Ba) derived from their cubic unit cell structures within the ferromagnetic spin configurations decide the various physical properties of these compounds debated, as below:
3.1 Structural properties
Under normal conditions, the double perovskite compounds A2SnFeO6 (A = Ca, Ba) having the stoichiometric formula A2(BB′)O6 crystallizes in a cubic geometry possessing the space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225) with four distinct elements (A, B, B, and X) in the ratio of 2
m (225) with four distinct elements (A, B, B, and X) in the ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. The constituents (atoms) occupy their positions at their corresponding cites. The position of the larger cation A (Ca, Ba) with 12-fold coordination resides at the body-centered cubic system having a Wyckoff site at (0.25, 0.25, 0.25). The remaining B and B′ (Fe) atoms are located in the centre having fractional coordinates (0.5, 0.5, 0.5). In addition, the B and B′ atoms are inside the cages surrounded by the O atoms having crystallographic site at the corner positions (0.25, 0, 0), forming alternate BO6 and B′O6 octahedrons, respectively, and are shown in Fig. 1. Furthermore, the accuracy of the relaxed lattice constants is well established from Birch Murnaghan's equation of state.28,29 From the literature survey and graphical plot as shown in Fig. 2, it is visualized that the lowest ground state energy from both alloys is released in the ferromagnetic phase, and is hence thermodynamically stable. However, the stability curve for both oxides displays essential parameters, including the lattice constant a0 (Å), volume in (a. u.3), bulk modulus (B), derivative of the bulk modulus (B′) and crystal-free minimum energy (Ry), as presented in Table 1. In addition, understanding the bond lengths shown in Table 2 describes a crucial role in defining the structural stability, as well as the tolerance factor (t) of these perovskites.19 The tolerance factor varies between crystal structures; henceforth, it is mentioned that if the value of t lies in the interval range of 0.9–1.0, this means that all of the atoms are ideally fit at individual positions, resulting in an ideal cubic structure. When t = 0.71–0.9, the 12-folded cation is so small that it cannot fit its position, resulting in an orthorhombic or rhombohedral structure. However, if t > 1, the A-site cations are oversized to fit their positions, resulting in hexagonal structures. For t < 0.71, different structures are formed. The present study reveals that A2SnFeO6 (A = Ca, Ba), with their tolerance factor values within the cubic range, defines the structural stability in the Fm
6. The constituents (atoms) occupy their positions at their corresponding cites. The position of the larger cation A (Ca, Ba) with 12-fold coordination resides at the body-centered cubic system having a Wyckoff site at (0.25, 0.25, 0.25). The remaining B and B′ (Fe) atoms are located in the centre having fractional coordinates (0.5, 0.5, 0.5). In addition, the B and B′ atoms are inside the cages surrounded by the O atoms having crystallographic site at the corner positions (0.25, 0, 0), forming alternate BO6 and B′O6 octahedrons, respectively, and are shown in Fig. 1. Furthermore, the accuracy of the relaxed lattice constants is well established from Birch Murnaghan's equation of state.28,29 From the literature survey and graphical plot as shown in Fig. 2, it is visualized that the lowest ground state energy from both alloys is released in the ferromagnetic phase, and is hence thermodynamically stable. However, the stability curve for both oxides displays essential parameters, including the lattice constant a0 (Å), volume in (a. u.3), bulk modulus (B), derivative of the bulk modulus (B′) and crystal-free minimum energy (Ry), as presented in Table 1. In addition, understanding the bond lengths shown in Table 2 describes a crucial role in defining the structural stability, as well as the tolerance factor (t) of these perovskites.19 The tolerance factor varies between crystal structures; henceforth, it is mentioned that if the value of t lies in the interval range of 0.9–1.0, this means that all of the atoms are ideally fit at individual positions, resulting in an ideal cubic structure. When t = 0.71–0.9, the 12-folded cation is so small that it cannot fit its position, resulting in an orthorhombic or rhombohedral structure. However, if t > 1, the A-site cations are oversized to fit their positions, resulting in hexagonal structures. For t < 0.71, different structures are formed. The present study reveals that A2SnFeO6 (A = Ca, Ba), with their tolerance factor values within the cubic range, defines the structural stability in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m lattice symmetry.
m lattice symmetry.
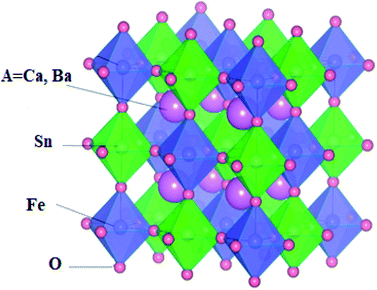 |
| | Fig. 1 Polyhedral unit cell structure of crystalline A2SnFeO6 (A = Ca, Ba) compounds. | |
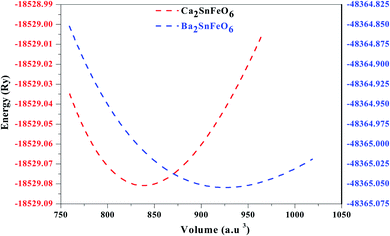 |
| | Fig. 2 Calculated energy (Ry) vs. volume (a. u.3) structural optimisation of A2SnFeO6 (A = Ca, Ba) in the ferromagnetic spin configurations. | |
Table 1 Several physical properties of A2SnFeO6 (A = Ca, Ba) in the face-centered cubic lattice structure
| Parameter |
Ca2SnFeO6 |
Ba2SnFeO6 |
| a0 (Å) |
7.92 |
7.99 (ref. 30) others |
7.85 |
7.81 (ref. 30) |
| V0 (a. u.3) |
838.28 |
925.64 |
| B (GPa) |
151.95 |
135.44 |
| B′ |
4.63 |
4.91 |
| Energy (Ry) |
−18529.08 |
−48365.05 |
Table 2 Estimated bond lengths (Å) and tolerance factor (t) of the A2SnFeO6 (A = Ca, Ba) oxides
| Materials |
Ca2SnFeO6 |
Ba2SnFeO6 |
| Bond lengths (Å) |
| Ca–O/Ba–O |
5.29 |
5.46 |
| Sn–O |
3.74 |
3.86 |
| Fe–O |
3.74 |
2.04 |
| Tolerance factor (t) |
0.99 |
0.99 |
3.2 Elasto-mechanical constants
Self-consistent simulations have proven to be an alternative and highly reliable approach for the experimental determination of elastic constants. The elastic constants determine the strength of a material to external strains, and thus aids their performance in various technological and industrial-based applications. For the present study, the calculations have been carried out by means of ground-state total energies to furnish the elastic constants (Cij; C11, C12, C44) for both A2SnFeO6 (A = Ca, Ba) compounds, as shown in Table 3. The number of elastic constants is directly related to the symmetry of the crystal structure. This means that a lower number of elastic constants is required to define the mechanical properties of a system from materials of higher symmetry. To investigate them, we used rhombohedral and tetragonal distortions on the cubic lattices under volume-conserving constraints. In addition to this, these elastic constants must follow the Born–Haung stability criterion, as the existence of the given crystal structures is not possible in the stable or metastable phase unless these constants obey the below-mentioned stability condition, which is C11 > 0, C12 > 0, C44 > 0, C11 + 2C12 > 0, C11 − C12 > 0.31–33 The abovementioned elastic constants completely satisfy the above conditions, indicating that both A2SnFeO6 (A = Ca, Ba) compounds are elastically stable. Thus, the elastic constants (Cijs) with the help of certain mathematical equations are used to reproduce the other essential parameters, such as the bulk modulus (B), shear (G), Young's moduli (Y), anisotropy factor (A) and others, which decide their mechanical strength. In order to determine the mechanical stability of these representative perovskites, the polycrystalline mechanical parameters were predicted using the Voigt (V), Reuses (R) and Hill (H) formula:34,35| |
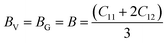 | (2) |
Table 3 PBE calculated elastic constants and mechanical properties of A2SnFeO6 (A = Ca, Ba)
| Materials |
Ca2SnFeO6 |
Ba2SnFeO6 |
| C11 |
320.90 |
234.85 |
| C12 |
65.56 |
85.45 |
| C44 |
136.43 |
106.93 |
| B (GPa) |
150.67 |
135.25 |
| G (GPa) |
132.85 |
92.61 |
| Y (GPa) |
199.27 |
226.20 |
| B/G |
1.13 |
1.46 |
| C′′ = C12 − C44 |
−70.87 |
−21.48 |
| A |
1.06 |
1.43 |
| ECoh |
5.25 |
5.23 |
| Ef |
−2.42 |
−2.65 |
Shear modulus (G) as:
| |
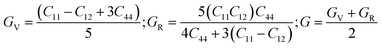 | (3) |
and, the Young's modulus (
Y) and anisotropy factor (
A) are considered, respectively, as:
| |
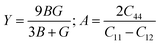 | (4) |
Here, we discuss how the bulk modulus ‘
B’ measures the resistance of the volumetric change caused by the external pressure of a given material. The calculated value of ‘
B’ from the elastic parameters of these typical materials is 142.67 and 135.25 in the units of GPa respectively, signifying the strong bonding strength among the various constituents of the atoms. The estimated value of the bulk modulus of A
2SnFeO
6 (A = Ca, Ba) foretells that the atoms in Ca
2SnFeO
6 offers low volumetric change (incompressibility) in comparison to Ba
2SnFeO
6 due to its smaller atomic size. The strong nature of bonding also gets confirmed from their cohesive energy values. On the contrary, the change of shape of a solid surely depends on its shear modulus
G, which also displays a crucial role in predicting the material's hardness. The reported value of
G is given in
Table 3. In addition, the Young's modulus (
Y) defines the relationship of stress and strain, providing a better piece of evidence about the stiffness of a material. The calculated values of (
Y) of both perovskite systems determine the stiffness character. Apart from this, for most of the practical applications, a material must be categorized as either ductile or brittle. To describe the characteristics of the materials, the Pugh's ratio
36 is defined as the
B/
G of the index value 1.75. According to this formula, a material acts as a ductile if the value of Pugh's ratio surpasses the critical value, and exhibits brittle character below this critical value. The calculated values of the Pugh's ratio lie below the critical value, demonstrating the brittle nature of both compounds. Furthermore, on determining the Cauchy
's discrepancy
C′′ = (
C12 −
C44),
37 this differentiates the nature of the materials as either ductile or brittle. If the value of the Cauchy pressure is negative, the material is labelled as brittle; otherwise, a positive value hints at the ductile character. Since,
C′′ = (
C12 −
C44) is negative in both compounds, they are considered to be brittle. At last, the universal anisotropic factor denoted by ‘
A’ is an another indicator that is also used in practice to clarify the ductile and brittle nature of these crystals. If ‘
A’ = 1, the material is perfectly isotropic; otherwise, it is considered to be anisotropic.
38 The values of A for both complex perovskites are 1.06 and 1.43, respectively, referring to the brittle nature of both materials. Therefore, the compounds A
2SnFeO
6 (A = Ca, Ba), in accordance with the above mentioned parameters, support the brittle characteristics. In addition, by using the ground state parameters, we have established the chemical stability using the cohesive energy (
ECoh) analysis. The depiction of large cohesive energy values potentially facilitates the stability, as well as retention of the ground state structures upon the implementation of external forces. We have computationally formulated the formation energy of these materials by DFT technique. The outcome values of the formation energy are −2.42 eV and −2.65 eV, respectively, which address the probability of these perovskites forming experimentally, and also ensures that these compounds do not decompose spontaneously into other binary or elemental phases.
Due to the anisotropic behavior of these materials, it is quite interesting to determine the elastic sound velocities of A2SnFeO6 (A = Ca, Ba). The cubic symmetry of these corresponding oxides certifies that the pure modes of elastic waves are strongly dependent on the propagation directions [100], [110] and [111]. The respective transverse velocity (νt) and longitudinal along (νl) with mean velocity (νm) have also been calculated and are presented in Table 4.
| |
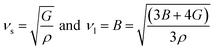 | (5) |
| |
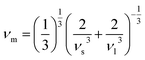 | (6) |
Table 4 Calculated sound waves in different directions of A2SnFeO6 (A = Ca, Ba)
| [100] |
[110] |
[111] |
νt |
vl |
vm |
θD |
| vl |
vt1 |
vt2 |
vl |
vt1 |
vt2 |
vl |
vt1 |
vt2 |
| 8280 |
5399 |
5399 |
7474 |
7386 |
5399 |
8429 |
5282 |
5282 |
5320 |
8360 |
5880 |
753 |
| 5960 |
4022 |
4022 |
5684 |
4754 |
4022 |
6482 |
3595 |
3595 |
3740 |
6250 |
4140 |
596 |
These above quantities are quite beneficial in predicting the Debye temperature (θD) of the ASnFeO6 (A = Ca, Ba) oxides by classical method using the mean sound velocity,39 and is closely related to the melting temperature, elastic constants, specific heat and other parameters.
| |
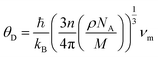 | (7) |
The Debye temperature is found to be large for both materials, A2SnFeO6 (A = Ca). The higher value of θD in Ca2SnFeO6 compared to that of Ba2SnFeO6 is due to its lower value of lattice thermal conductivity, and therefore suggests the lower involvement of the phonon vibrations below this temperature.
3.3 Origin of half-metallicity and magnetism
First-principles calculations on the electronic structure play a pivotal role in understanding the possible applications of the materials in various subject areas of research regarding their excellent properties. In this systematic report, we have chosen exact and accurate relaxed lattice constants from their structural unit cell optimizations to forecast and justify the electronic nature in the A2SnFeO6 (A = Ca, Ba) perovskite systems. The present study provides a superb description on the electronic properties of these alloys. The description of the electronic nature of both of these complex oxides within the entirely PBE-GGA and PBE + U functionals illustrates that the half-metallic band characters with spin-up channels form a metal-type spectrum. Furthermore, the presence of a gap demonstrates the semiconducting nature in the spin-dn channel, as displayed in Fig. 3 and 4. Separately, from the majority-up channels in the case of Ca2SnFeO6, the valence band (top) and conduction band (bottom) in both of the functional schemes are located at the Γ and X symmetry directions of the Brillouin zone with an indirect bandgap of 0.81 eV and 1.51 eV, respectively. Similarly, from the band structures of Ba2SnFeO6, the conduction band (bottom) and valence band (top) reside at X and Γ within the two calculated functional schemes PBE-GGA and GGA + U, describing the character of the resulting direct bandgap with approximate values of 0.81 eV and 1.44 eV, respectively. Here, in both materials, the shifting of the energy levels can be seen from the Fermi level on the employment of the PBE + U correction. In turn, this increases the band gap of these materials. The presence of a forbidden gap in both schemes prevails its half-metallic nature in the present alloys. However, a previous study divulges that these materials are reported theoretically as semimetal ferromagnetic perovskites through the LDA approximation.30 Now showing the feature of the band structures of these compounds in terms of the total density of states (TDOS) shown in Fig. 5(a and b), it can be seen that they also incorporate a half-metallic nature in the mentioned exploited schemes. The half-metallic nature of these materials can also be viewed from the neighboring material investigated in the recent past by others.40 Hence, these results evidence the half-metallic nature of the A2SnFeO6 compounds. In addition, in order to understand the elemental activeness of various energy states of these materials at the Fermi level, the partial density of states (pDOS) has been executed as shown in Fig. 5(c and d). Gaining insight towards the (pDOS) of the A2SnFeO6 (A = Ca, Ba) compounds, the crystal fields associated with the FeO6 cage that are generated by the Coulomb interactions are responsible for the splitting of the 3d degenerate state of Fe into the non-degenerate states, dxy, dyz, and dzx, called the eg states, and dx2−y2, dz2 are the dt2g states. From the projected density of states for both materials, it can be clearly seen that the presence of the Fe-deg and O-p states, being of their strong hybridization occupancy at the Fermi level, is responsible for showing the metallic behavior in all up-spin cases and semiconducting behavior in spin-down cases. However, the low-lying states Ca-s, Ba-s, Sn-s, p, which are far away from the Fermi level, depict negligible appearance. Hence, the partial density of states exclusively portrays a clear environment of states (being active or inactive) at the Fermi-level, and also designates that the p–d hybridization is predominant in both chemical systems. Next, we tried to describe the magnetism, which is also an another important property directly linked to their structures, especially the electronic configuration. Within this study, two exchange–correlation approximations, GGA and PBE + U, have been incorporated to gain appropriate knowledge among the interactions between the various constituents, which therefore displays the magnetic character in these oxide-based compounds. Here, we can see from Table 5 that the magnetism is found to be the integral value equivalent to 4.00 μB, which mainly arises from the Fe atoms in both of these perovskite systems. The materials that are of particular interest to display the same quantity of magnetism are Sr2SnFeO6, Sr2MnTaO6 and others.40,41 Later, the spin orbit coupling (SOC) was additionally employed to determine the magnetism of these alloys, and found to be the same. The obtained values of the magnetic moment of various atoms (Ca, Ba, Sn, Fe and O) are positive, which hints at the positive alignment of spins (ferromagnetic interaction) between the various constituents of these alloys. The half-metallicity, along with 100% spin polarization and quantized magnetism of these alloys, projects a better position towards the spin filters, high-performance electronic devices, spin injectors and others to meet the necessary demands of the new spin-based technologies.
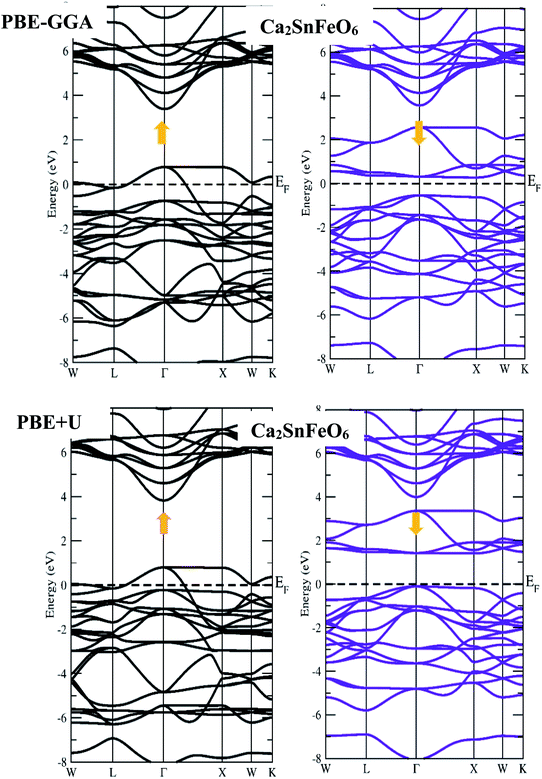 |
| | Fig. 3 Spin-up and spin-down band profiles of Ca2SnFeO6 within the PBE-GGA and PBE + U schemes. | |
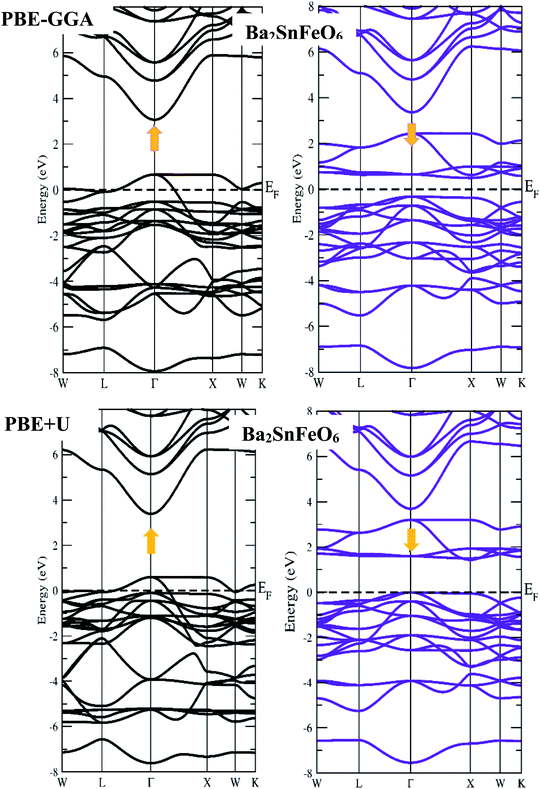 |
| | Fig. 4 Spin-up and spin-down band profiles of Ba2SnFeO6 within the PBE-GGA and PBE + U schemes. | |
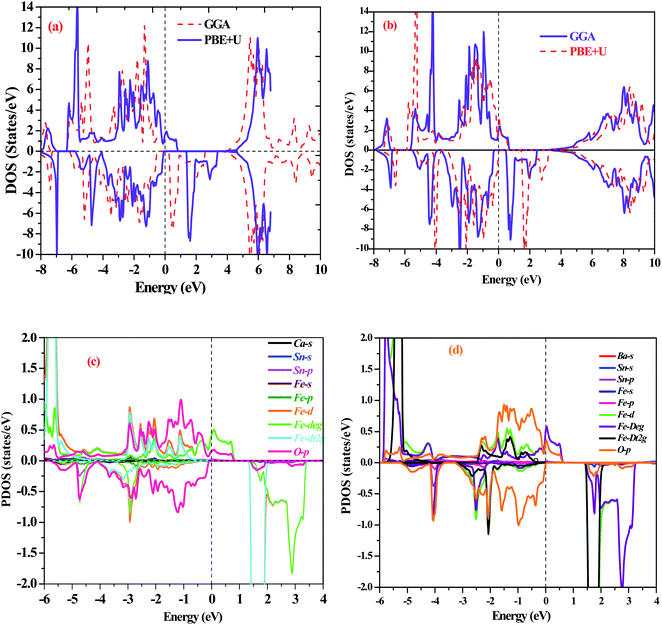 |
| | Fig. 5 (a and b) Graphical representation of the total density of states (TDOS) of (a) Ca2SnFeO6 and (b) Ba2SnFeO6 within the schemes of PBE-GGA and PBE + U. (c and d): Illustration of the half-metallic partial density of states (pDOS) of (c) Ca2SnFeO6 and (d) Ba2SnFeO6 within PBE + U functional schemes. | |
Table 5 Estimated atomic, interstitial, total magnetic moments and energy gap of the A2SnFeO6 (A = Ca, Ba) compounds
| Compounds |
Magnetic moment (μB) |
Energy gap (eV) |
| Ca/Ba |
Sn |
Fe |
O |
Interstitial |
Total |
| Ca2SnFeO6 |
| GGA |
0.00 |
0.02 |
3.28 |
0.07 |
0.23 |
4.00 |
0.81 |
| PBE + U |
0.00 |
0.01 |
3.60 |
0.02 |
0.22 |
4.00 |
1.51 |
| SOC |
0.00 |
0.01 |
3.61 |
0.03 |
0.20 |
4.00 |
— |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Ba2SnFeO6 |
| GGA |
0.00 |
0.02 |
3.27 |
0.07 |
0.26 |
4.00 |
0.81 |
| PBE + U |
0.00 |
0.01 |
3.69 |
0.01 |
0.21 |
4.00 |
1.44 |
| SOC |
0.00 |
0.01 |
3.71 |
0.03 |
0.17 |
4.00 |
— |
| Others40,41 |
|
|
|
|
|
4.00 |
|
3.4 Electron density analysis
DFT calculations for the charge density have been predominantly used to portray the charge distraction, as it acts as the indicator for the chemical bonding. However, it includes the effect of nonbonding states and gives the overall charge density. The chemical bonding associated with these layered A2SnFeO6 (A = Ca, Ba) perovskites has been configured from the charge density plots along the (111) planes, as displayed in Fig. 6. Here, the description of these plots conveys that the electrons by these perovskite materials are shared between the oxygen–iron atoms. Hence, a covalent character and ionic nature can be seen between the barium–oxygen atoms. The non-spherical shape of the transition atom indicates that the d states are partially filled. The overall charge density plots reflect that the polar chemical bonding is preserved within these crystal lattices.
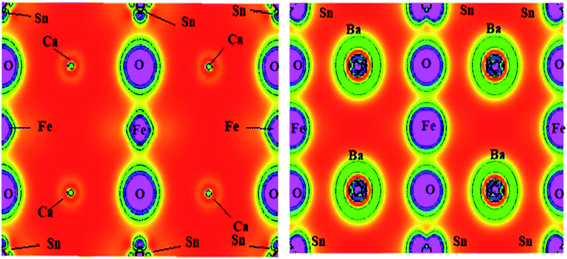 |
| | Fig. 6 Chemical bonding via charge density plots of A2SnFeO6 (A = Ca, Ba) in the (111) plane. | |
3.5 Thermoelectricity
The half-metallic nature characterized from their band structures and increased amount of density of states, along with the corresponding charge carriers around the Fermi level, prompted us to study the thermoelectric response of these materials. However, energy is in big demand nowadays, and one of the prime factors to resolve this critical need is due to its scarcity. Owing to the loss of heat released from automotive exhausts, industries have also become an another challenge for the material scientists that should be sorted. So, keeping these things in consideration, we have carried out this piece of work within the instructions of density functional theory, mainly focusing on determining the thermoelectric applicability of these materials, which could recapture the unwanted heat into useable electric power. Thermoelectric oxide materials that have potential to exchange the energy conversion have been extensively studied in terms of their efficiency, known as the figure of merit (ZT), which corresponds to its intrinsic properties and can be expressed as:| |
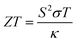 | (8) |
The terms in the commonly used equation describe ‘S’ as the Seebeck coefficient, σ as the electrical conductivity, T as the operational temperature and κ as the lattice thermal conductivity.42–51 So far, as A2SnFeO6 (A = Ca, Ba) alloys are concerned, the understanding of the transport mechanism within the semi-classical Boltzmann theory under constant relaxation time approximation has been properly addressed.52,53 Since both of these materials support the half-metallicity, as characterized from their band structures and density of states, the transport coefficients in two spin phases (spin-up/spin-down) are therefore assembled in single plots as designated in Fig. 7(a–f). These transport coefficients are calculated along the selected temperature range from “0 to 800” K at the constant chemical potential values 0.409 and 0.516 Ry respectively. Here, gaining insight towards the various temperature-dependent parameters by observing the Seebeck coefficient (S) first, we label the thermoelectric mechanism and thermoelectric sensitivity in response to the temperature gradient. The description from the graphic plot of S shown in Fig. 7(a) claims that the metallic behavior in the up-spin is due to the increasing value of the Seebeck coefficient against temperature. The increasing value of the Seebeck coefficient is seen in the spin-majority channel, which arises from a lower temperature value of 50 K having an approximate value of 1.23 μV K−1, and reaches its maximum along the selected temperatures up to a value of 7.43 μV K−1 at 800 K temperature. Meanwhile, for the down spin-minority channel, the decreasing trend is reflected at 50 K towards the high temperature of 800 K, followed by a value of −979.56 μV K−1 to −234.38 μV K−1, respectively. Similarly, for Ba2SnFeO6, the Seebeck coefficient shown in Fig. 7(b) follows the same trend, but the value increases from −5.67 μV K−1 at 50 K to −21.40 μV K−1 at 800 K in the spin-up channel. The negative sign indicates that the electrons are the major transporters for heat conduction. Meanwhile, in the spin-down semiconducting channel, S declines from 977.74 μV K−1 to 256.10 μV K−1 with linearly increasing temperature. The turnout value of the large S is due to the presence of a flat conduction band (CB) parallel to the Γ–X direction, as seen from all of the spin-minority band structures of both of these perovskite alloys. The thermoelectric behavior at 300 K in the spin-down channels of both perovskite alloys is estimated to be −343.35 μV K−1 and 354.56 μV K−1, respectively. However, the experimental results performed by others on the thermoelectric properties of Sr2RuYO6 and Sr2RuErO6 (ref. 54) at room temperature are consistent with the obtained values of both perovskite oxides. Next, we graphically plotted the electrical conductivity (σ/τ) over the relaxation time τ = (1.5 × 10−15) for Ca2SnFeO6 (Ba2SnFeO6), which portrays a decreasing pattern in both up-spin phases shown in Fig. 7(c and d). The decrease in the electrical conductivity is attributed to its metallic behaviour and the electron-scattering processes that describe an essential reason of decreasing the nature of electrical conductivity. The value eventually decreases from 2.14 × 1018 Ω−1 m−1 s−1 (6.45 × 1018 Ω−1 m−1 s−1) to 1.89 × 1018 Ω−1 m−1 s−1 (1.11 × 1018 Ω−1 m−1 s−1) along the above said temperatures. In addition, the increase in σ/τ is visualized within spin-down from a value of 1.11 × 1018 Ω−1 m−1 s−1 (1.09 × 1018 Ω−1 m−1 s−1) in Ca2SnFeO6 (Ba2SnFeO6) at higher temperatures, respectively. The increasing nature is due to the negative temperature coefficient of resistance, i.e., with the increase in temperature, the electrical conductivity increases. Hence, the overall investigation from the spin-dependent electrical conductivities in both spin phases confirms the occurrence of the perfect half-metallic nature. In addition, with the help of the two current models, we have calculated the total Seebeck coefficient for both oxide materials as shown graphically in Fig. 7(e), which aids the generation of thermopower given by the formula:
| |
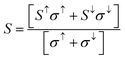 | (9) |
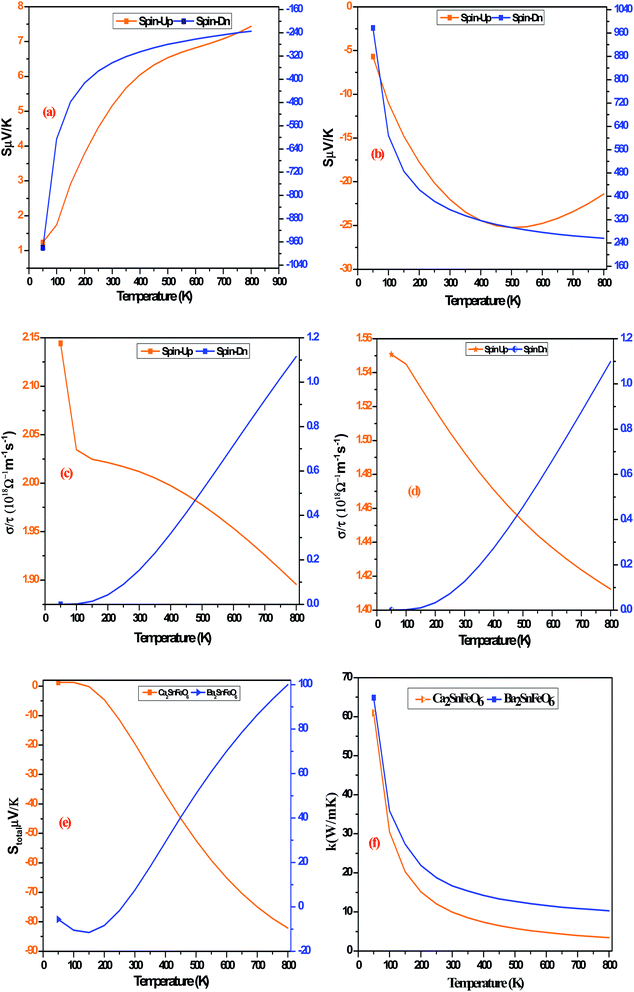 |
| | Fig. 7 (a and b) Graphical representation of the Seebeck coefficient (S) against temperature for A2SnFeO6 (A = Ca, Ba) double perovskites. (c and d) Graphical representation of the electrical conductivity (σ/τ) against temperature for A2SnFeO6 (A = Ca, Ba) double perovskites. (e and f) Graphical representation of the total Seebeck coefficient (S) and lattice thermal conductivity (κ) against temperature for A2SnFeO6 (A = Ca, Ba) double perovskites. | |
This model assumes the resistivities from two spin channels as parallel resistors, and are added as if no spin-flip process occurs. Therefore, the resulting average resistivity (ρ) and conductivity (σ) become:
| |
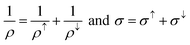 | (10) |
To see the lattice thermal conductivity (κl) displayed in Fig. 7(f), we have taken the use of Slack's method analytically,55,56 which accounts for the phonon vibrations containing these crystal lattices weighted as:
| |
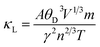 | (11) |
In the above equation, (A = 3.04 × 10−8, M, θD) in the numerator hand signifies the physical constant, average mass, and Debye temperature, respectively. The terms on the denominator side (γ, n, T) are the Grüneisen parameter, number of atoms in the primitive unit cell, and temperature, respectively. The graphical representation of the lattice thermal conductivity of Ca2SnFeO6 shows an exponential decreasing trend from a higher value of 60.95 κ (W m−1 K−1) at 50 K to 3.38 κ (W m−1 K−1) at 800 K. Similar results are reflected for Ba2SnFeO6 with a decreasing value of 40.30 κ (W m−1 K−1) to 2.34 κ (W m−1 K−1). The suppressed value of the lattice thermal conductivity (κl) of both of these alloys projects its imminent applications in thermoelectrics. Unfortunately, due to the lack of experimental results of the transport analysis of these materials, the accuracy and comparison of the overall quantified transport properties is not possible. However, these calculations may provide better support to forthcoming experimental verifications.
3.6 Thermodynamic stability
To describe the thermodynamic stability of these perovskites A2SnFeO6 (A = Ca, Ba), we have taken a quasi-harmonic approximation of the Debye model (QHM),57 which significantly describes the stability of these various quantities, inclusive of the specific heat at a constant volume (Cv), Grüneisen parameter (γ) and thermal expansion coefficient (α), in the temperature and pressure range of ‘0–800’ K and ‘0–25’ GPa, respectively. This kind of model is preferred and is considered to be good in establishing the results in such temperature and pressure range. However, remaining under (QHM) approximation, we have first portrayed the specific performance of both materials at constant volume (CV), which is one of the prime factors related to the dynamics of the material. The present oxides allow the greater capability of heat transport at room temperature upon T3 relation. The graphical variation of the specific performance of both compounds experiences a tendency towards the Dulong petit limit at higher temperatures, as shown in Fig. 8(a and b). The high-temperature limit suggests that the change is in accordance with the Delong–Petit's law.58
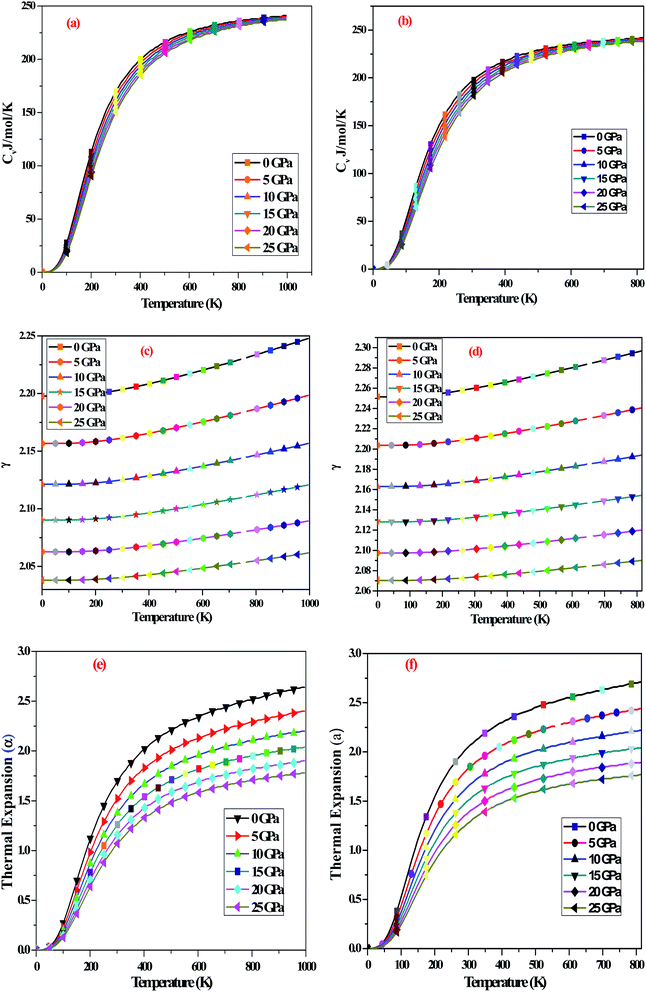 |
| | Fig. 8 (a and b) Variation of the specific heat (Cv) for A2SnFeO6 (A = Ca, Ba) with pressure and temperature. (c and d) Variation of the Grüneisen parameter (γ) for A2SnFeO6 (A = Ca, Ba) with pressure and temperature. (e and f) Variation of the thermal expansion (α) for A2SnFeO6 (A = Ca, Ba) with pressure and temperature. | |
Next, we have tried to figure out the Grüneisen parameter (γ), which labels the anharmonicity and provides a detailed description about the phonon frequency modes, as shown Fig. 8(c and d). The softly increasing exponential trend of the Grüneisen parameter (γ) at lower temperatures is observed, but remains almost constant at higher temperatures. However, the impact of pressure on (γ) has a negligible effect on it. The recorded value of the Grüneisen parameter at temperature 300 K and pressure 0 GPa is 2.20 and 2.25, respectively.
The thermal expansion (α), so far as theoretical, as well as the experimental point of view, predicts the thermodynamic equation of state. The graphical representation with regards to the temperature and pressure variation for both layered alloys is shown in Fig. 8(e and f). A fast increasing trend of (α) is observed at lower temperatures, while at high temperatures, the variation tends towards a constant value. The overall predicted thermodynamic quantities within the Debye approximation model certifies the stability of these oxides at high temperatures and pressures.
4 Conclusion
From the first-principles DFT ab initio calculations, we have successfully scrutinized the electronic, magnetic, mechanical stability and transport performance of the newly cation-modified magnetic perovskites A2SnFeO6 (A = Ca, Ba). The physical properties established are greatly affected by changing the ‘A’ cation site, and are strongly dependent on it. The lattice constants show a decreasing trend from Ca2SnFeO6 (7.99 Å) to Ba2SnFeO6 (7.85 Å) due to variation of the atomic size. In addition, the cohesive energy supports the structural stability of A2SnFeO6 (A = Ca, Ba) with its values, indicating the strong bonding forces among the constituent atoms. The robustness of the structural stability of these materials approves the cubic structure specifying the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry. The magnetic character, which surely depends upon there being unpaired electrons, comes out at 4 μB, showing its applicability towards spintronics. The analysis of the band structures, as well as density of states, corresponds to its half-metallic nature. The manipulation of the elastic constants yields the brittle character with their higher value bulk modulus, leading to its incompressible nature and also features a promising route towards various engineering applications. Furthermore, the Debye temperature of Ca2SnFeO6 is found to be larger than that of Ba2SnFeO6 due to its lower value of lattice thermal conductivity. The semiclassical theory integrated in BoltzTraP suggests the applicability of these materials in green energy sources. In addition, the thermodynamic potentials on the application of pressure and temperature describe the stability of these compounds at varying conditions. In a nutshell, the overall depiction of various essential properties projects their better standing in spintronics and thermoelectric device applications.
m symmetry. The magnetic character, which surely depends upon there being unpaired electrons, comes out at 4 μB, showing its applicability towards spintronics. The analysis of the band structures, as well as density of states, corresponds to its half-metallic nature. The manipulation of the elastic constants yields the brittle character with their higher value bulk modulus, leading to its incompressible nature and also features a promising route towards various engineering applications. Furthermore, the Debye temperature of Ca2SnFeO6 is found to be larger than that of Ba2SnFeO6 due to its lower value of lattice thermal conductivity. The semiclassical theory integrated in BoltzTraP suggests the applicability of these materials in green energy sources. In addition, the thermodynamic potentials on the application of pressure and temperature describe the stability of these compounds at varying conditions. In a nutshell, the overall depiction of various essential properties projects their better standing in spintronics and thermoelectric device applications.
Conflicts of interest
There are no conflicts to declare.
References
- Bo. Cai, Xi. Chen, M. Xie, S. Zhang, X. Liu, J. Yang, W. Zhou, S. Guoa and H. Zeng, Mater. Horiz., 2018, 5, 961 RSC.
- Y. H. Huang, R. I. Dass, Z. L. Xing and J. B. Goodenough, Science, 2006, 312, 34 Search PubMed.
- P. Roy, I. Bose and T. Maiti, Integr. Ferroelectr., 2016, 174, 34 CrossRef CAS.
- S. A. Khandy and D. C. Gupta, J. Magn. Magn. Mater., 2018, 458, 176 CrossRef CAS.
- T. Wu and P. Gao, Mat, 2018, 11, 999 Search PubMed.
- S. Vasala and M. Karppinen, Prog. Solid State Chem., 2015, 43, 1 CrossRef CAS.
- C. Wood, Rep. Prog. Phys., 1988, 51, 459 CrossRef CAS.
- B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto and D. Vashaee, Science, 2008, 320, 634 CrossRef CAS PubMed.
- V. L. Kuznetsov, L. A. Kuznetsova, A. E. Kaliazin and D. M. Rowe, J. Mater. Sci., 2002, 37, 2893 CrossRef CAS.
- K. Kadel, L. Kumari, W. Li, J. Y. Huang and P. P. Provencio, Nanoscale Res. Lett, 2011, 6, 1 Search PubMed.
- M. Scheele, N. Oeschler, K. Meier, A. Kornowski, C. Klinke and H. Weller, Adv. Funct. Mater., 2009, 19, 3476 CrossRef CAS.
- S. A. Khandy and D. C. Gupta, Mater. Chem. Phys., 2020, 239, 1219813 CrossRef.
- M. Faizan, G. Murtaza, S. H. Khan, A. Khan, A. Mehmood, R. Khenata and S. Hussain, Bull. Mater. Sci., 2016, 36, 1419 CrossRef.
- S. A. Mir and D. C. Gupta, Int. J. Energy Res., 2019, 43, 4783 CrossRef CAS.
- S. A. Dar, V. Srivastava and U. K. Sakalle, J. Magn. Magn. Mater., 2019, 484, 298 CrossRef CAS.
- M. U. Kahaly, K. Ozdogan and U. Schwingenschlögl, J. Mater. Chem. A, 2013, 1, 8406 RSC.
- O. Sahnoun, H. Bouhani-Benziane, M. Sahnoun and M. Driz, J. Alloys Compd., 2017, 714, 704 CrossRef CAS.
- R. Ramesh and N. A. Spaldin, Nat. Mater., 2007, 6, 21 CrossRef CAS PubMed.
- Z. Li, M. Yang, J. S. Park, S. H. Wei, J. J. Berry and K. Zhu, Chem. Mater., 2016, 28, 284 CrossRef CAS.
- Z. Cheng and J. Lin, CrystEngComm, 2010, 12, 2646 RSC.
- P. W. Barnis, Exploring Structural Changes and Distortions in Quaternary Perovskites and Defectpyrochlores Using Powder Diffraction Techniques, The Ohio State University, Ohio, Columbus, 2003 Search PubMed.
- Q. Wang, L. Ma, L. Wang and D. Wang, New J. Chem., 2019, 43, 3911 Search PubMed.
- M. Saxena, K. Tanwar and T. Maiti, Scr. Mater., 2017, 130, 205 CrossRef CAS.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, J. Luitz, WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties Karlheinz Schwarz, Techn. Universität Wien, Austria, ISBN 3-9501031-1-2, 2001 Search PubMed.
- P. Blaha, K. Schwarz and J. Luitz, Comput. Phys. Commun., 1990, 59, 399 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B, 1998, 57, 1505 CrossRef CAS.
- A. Jain, G. Hautier, S. P. Ong, C. J. Moore, C. C. Fischer, K. A. Persson and G. Ceder, Phys. Rev. B, 2011, 84, 045115 CrossRef.
- F. Brich, J. Appl. Phys., 1938, 9, 279 CrossRef.
- S. Singh and D. C. Gupta, Results Phys., 2019, 13, 102300 CrossRef.
- I. R. Shein, V. L. Kozhevnikov and A. L. Ivanovskii, Fiz. Tekhnika Poluprovodn., 2006, 40, 1295 Search PubMed.
- M. W. Mohamedi, A. Chahed, A. Amarl, H. Rozale, A. Lakdja, O. Benhelal and A. Sayede, Eur. Phys. J. B, 2016, 89, 26 CrossRef.
- K. Benkaddour, A. Chahed, A. Amar, H. Rozale, A. Lakdji, O. Benhelal and A. Sayede, J. Alloys Compd., 2016, 687, 211 CrossRef CAS.
- A. Iyigor and S. Ugur, Philos. Mag. Lett., 2014, 94, 708 CrossRef CAS.
- R. Hill, Proc. Phys. Soc. Lond., 1953, 65, 909 Search PubMed.
- W. Voigt, Ann. Phys., 1889, 38, 573 CrossRef.
- L. Hao, R. Khenata, X. Wang and T. Yang, J. Electron. Mater., 2018, 48, 6222 CrossRef.
- D. Pettifor, Mater. Sci. Technol., 1992, 8, 345 CrossRef CAS.
- K. Kaur, D. P. Rai, R. K. Thapa and S. Srivastava, J. Appl. Physiol., 2017, 122, 4891 Search PubMed.
- O. L. Anderson, J. Phys. Chem. Solids, 1963, 24, 909 CrossRef CAS.
- S. A. Khandy and D. C. Gupta, J. Magn. Magn. Mater., 2017, 441, 166 CrossRef CAS.
- S. A. Dar, V. Srivastava and U. K. Sakalle, J. Magn. Magn. Mater., 2019, 484, 298 CrossRef CAS.
- S. A. Khandy and D. C. Gupta, J. Phys. Chem. Solids, 2019, 135, 109079 CrossRef CAS.
- A. Quyoom Seh and D. C. Gupta, Int. J. Energy Res., 2019, 43, 8864 Search PubMed.
- S. Singh and D. C. Gupta, Results Phys., 2019, 13, 102300 CrossRef.
- M. Nabi and D. C. Gupta, Int. J. Energy Res., 2019, 43, 4229 CrossRef CAS.
- S. A. Sofi, S. Yousuf and D. C. Gupta, Cocom, 2019, 19, e00375 Search PubMed.
- T. M. Bhat and D. C. Gupta, J. Electron. Mater., 2016, 45, 6012 CrossRef CAS.
- S. A. Khandy and D. C. Gupta, RSC Adv., 2016, 6, 48009 RSC.
- S. A. Mir and D. C. Gupta, Int. J. Energy Res., 2019, 43, 4783 CrossRef CAS.
- D. C. Gupta and S. Ghosh, J. Supercond. Novel Magn., 2018, 31, 2465 CrossRef CAS.
- S. Yousuf and D. C. Gupta, J. Phys. Chem. Solids, 2017, 108, 109 CrossRef CAS.
- D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 1 Search PubMed.
- T. M. Bhat and D. C. Gupta, RSC Adv., 2016, 6, 80302 RSC.
- M. H. Aguirre, D. Logvinovich, L. Bocher, R. Robert, S. G. Ebbinghaus and A. Weidenkaff, Acta Mater., 2009, 57, 108 CrossRef CAS.
- S. Yousuf and D. C. Gupta, J. Electron. Mater., 2018, 47, 2468 CrossRef CAS.
- A. J. Hong, L. Li, R. He, J. J. Gong, Z. B. Yan, K. F. Wang, J. M. Lui and Z. F. Ren, Sci. Rep., 2016, 6, 22778 CrossRef CAS PubMed.
- E. Francisco, J. M. Rebico, M. A. Blanco, A. M. pendas and A. Costales, J. Phys. Chem., 1998, 102, 1595 CrossRef CAS.
- F. Peng, H. Z. Fu and X. L. Cheng, Phys. B, 2007, 400, 83 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Dinesh C. Gupta
and
Dinesh C. Gupta *
*
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, I4/m, and P4/nmc.23 The possibilities of tailoring the applications in such systems have increased the resurgent interests in these compounds with the advent of time. However, a large number of experimental and theoretical studies are going on to expand the properties of these compounds. Therefore, we have carried this piece of work to discuss the main highlights regarding the main theme of the present study. The survey of the literature reveals that the compositional analysis of both these materials belongs to the cubic unit cell structures, along with the space group orientation of Fm
m, I4/m, and P4/nmc.23 The possibilities of tailoring the applications in such systems have increased the resurgent interests in these compounds with the advent of time. However, a large number of experimental and theoretical studies are going on to expand the properties of these compounds. Therefore, we have carried this piece of work to discuss the main highlights regarding the main theme of the present study. The survey of the literature reveals that the compositional analysis of both these materials belongs to the cubic unit cell structures, along with the space group orientation of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with ferromagnetic parallel spin ordering. Similar prototype perovskites Sr2SnMnO6 and Sr2SnFeO6 were also predicted within the strict and rigorous DFT simulation techniques, showing a satisfactory thermoelectric and spintronic response. The present report is confined to explore the basic understandings of A2SnFeO6 (A = Ca, Ba) double perovskites above and beyond 100% spin polarization, which may be fruitful to meet the requirements in future situations.
m with ferromagnetic parallel spin ordering. Similar prototype perovskites Sr2SnMnO6 and Sr2SnFeO6 were also predicted within the strict and rigorous DFT simulation techniques, showing a satisfactory thermoelectric and spintronic response. The present report is confined to explore the basic understandings of A2SnFeO6 (A = Ca, Ba) double perovskites above and beyond 100% spin polarization, which may be fruitful to meet the requirements in future situations.
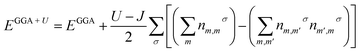
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225) with four distinct elements (A, B, B, and X) in the ratio of 2
m (225) with four distinct elements (A, B, B, and X) in the ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6. The constituents (atoms) occupy their positions at their corresponding cites. The position of the larger cation A (Ca, Ba) with 12-fold coordination resides at the body-centered cubic system having a Wyckoff site at (0.25, 0.25, 0.25). The remaining B and B′ (Fe) atoms are located in the centre having fractional coordinates (0.5, 0.5, 0.5). In addition, the B and B′ atoms are inside the cages surrounded by the O atoms having crystallographic site at the corner positions (0.25, 0, 0), forming alternate BO6 and B′O6 octahedrons, respectively, and are shown in Fig. 1. Furthermore, the accuracy of the relaxed lattice constants is well established from Birch Murnaghan's equation of state.28,29 From the literature survey and graphical plot as shown in Fig. 2, it is visualized that the lowest ground state energy from both alloys is released in the ferromagnetic phase, and is hence thermodynamically stable. However, the stability curve for both oxides displays essential parameters, including the lattice constant a0 (Å), volume in (a. u.3), bulk modulus (B), derivative of the bulk modulus (B′) and crystal-free minimum energy (Ry), as presented in Table 1. In addition, understanding the bond lengths shown in Table 2 describes a crucial role in defining the structural stability, as well as the tolerance factor (t) of these perovskites.19 The tolerance factor varies between crystal structures; henceforth, it is mentioned that if the value of t lies in the interval range of 0.9–1.0, this means that all of the atoms are ideally fit at individual positions, resulting in an ideal cubic structure. When t = 0.71–0.9, the 12-folded cation is so small that it cannot fit its position, resulting in an orthorhombic or rhombohedral structure. However, if t > 1, the A-site cations are oversized to fit their positions, resulting in hexagonal structures. For t < 0.71, different structures are formed. The present study reveals that A2SnFeO6 (A = Ca, Ba), with their tolerance factor values within the cubic range, defines the structural stability in the Fm
6. The constituents (atoms) occupy their positions at their corresponding cites. The position of the larger cation A (Ca, Ba) with 12-fold coordination resides at the body-centered cubic system having a Wyckoff site at (0.25, 0.25, 0.25). The remaining B and B′ (Fe) atoms are located in the centre having fractional coordinates (0.5, 0.5, 0.5). In addition, the B and B′ atoms are inside the cages surrounded by the O atoms having crystallographic site at the corner positions (0.25, 0, 0), forming alternate BO6 and B′O6 octahedrons, respectively, and are shown in Fig. 1. Furthermore, the accuracy of the relaxed lattice constants is well established from Birch Murnaghan's equation of state.28,29 From the literature survey and graphical plot as shown in Fig. 2, it is visualized that the lowest ground state energy from both alloys is released in the ferromagnetic phase, and is hence thermodynamically stable. However, the stability curve for both oxides displays essential parameters, including the lattice constant a0 (Å), volume in (a. u.3), bulk modulus (B), derivative of the bulk modulus (B′) and crystal-free minimum energy (Ry), as presented in Table 1. In addition, understanding the bond lengths shown in Table 2 describes a crucial role in defining the structural stability, as well as the tolerance factor (t) of these perovskites.19 The tolerance factor varies between crystal structures; henceforth, it is mentioned that if the value of t lies in the interval range of 0.9–1.0, this means that all of the atoms are ideally fit at individual positions, resulting in an ideal cubic structure. When t = 0.71–0.9, the 12-folded cation is so small that it cannot fit its position, resulting in an orthorhombic or rhombohedral structure. However, if t > 1, the A-site cations are oversized to fit their positions, resulting in hexagonal structures. For t < 0.71, different structures are formed. The present study reveals that A2SnFeO6 (A = Ca, Ba), with their tolerance factor values within the cubic range, defines the structural stability in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m lattice symmetry.
m lattice symmetry.

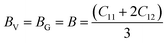
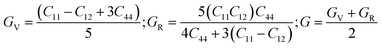
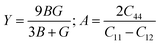
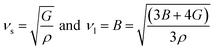
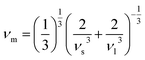
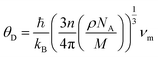
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
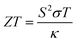
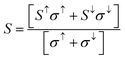
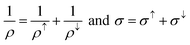
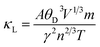
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry. The magnetic character, which surely depends upon there being unpaired electrons, comes out at 4 μB, showing its applicability towards spintronics. The analysis of the band structures, as well as density of states, corresponds to its half-metallic nature. The manipulation of the elastic constants yields the brittle character with their higher value bulk modulus, leading to its incompressible nature and also features a promising route towards various engineering applications. Furthermore, the Debye temperature of Ca2SnFeO6 is found to be larger than that of Ba2SnFeO6 due to its lower value of lattice thermal conductivity. The semiclassical theory integrated in BoltzTraP suggests the applicability of these materials in green energy sources. In addition, the thermodynamic potentials on the application of pressure and temperature describe the stability of these compounds at varying conditions. In a nutshell, the overall depiction of various essential properties projects their better standing in spintronics and thermoelectric device applications.
m symmetry. The magnetic character, which surely depends upon there being unpaired electrons, comes out at 4 μB, showing its applicability towards spintronics. The analysis of the band structures, as well as density of states, corresponds to its half-metallic nature. The manipulation of the elastic constants yields the brittle character with their higher value bulk modulus, leading to its incompressible nature and also features a promising route towards various engineering applications. Furthermore, the Debye temperature of Ca2SnFeO6 is found to be larger than that of Ba2SnFeO6 due to its lower value of lattice thermal conductivity. The semiclassical theory integrated in BoltzTraP suggests the applicability of these materials in green energy sources. In addition, the thermodynamic potentials on the application of pressure and temperature describe the stability of these compounds at varying conditions. In a nutshell, the overall depiction of various essential properties projects their better standing in spintronics and thermoelectric device applications.







