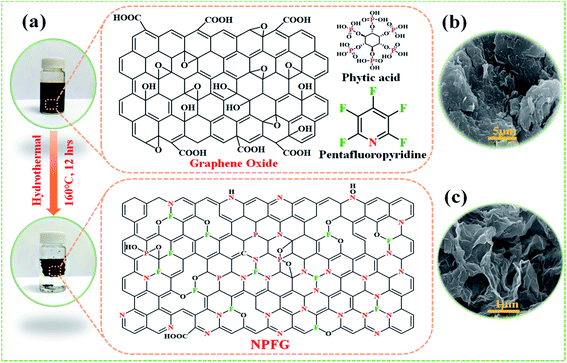
Open Access Article
Open Access ArticlePentafluoropyridine functionalized novel heteroatom-doped with hierarchical porous 3D cross-linked graphene for supercapacitor applications†
Amit Kumar ab,
Chih-Shan Tan
ab,
Chih-Shan Tan b,
Nagesh Kumarc,
Pragya Singhb,
Yogesh Sharma
b,
Nagesh Kumarc,
Pragya Singhb,
Yogesh Sharma c,
Jihperng Leua,
E.-Wen Huanga,
Tan Winied,
Kung-Hwa Wei
c,
Jihperng Leua,
E.-Wen Huanga,
Tan Winied,
Kung-Hwa Wei a and
Tseung Yuen Tseng
a and
Tseung Yuen Tseng *b
*b
aDepartment of Materials Science and Engineering, National Yang Ming Chiao Tung University, Hsinchu 300, Taiwan
bInstitute of Electronics, National Yang Ming Chiao Tung University, Hsinchu 300, Taiwan. E-mail: tseng@nctu.edu.tw
cCentre of Nanotechnology, I. I. T. Roorkee, Roorkee 247667, India
dFaculty of Applied Sciences, Universiti Teknologi MARA, 40450 Shah Alam, Selangor, Malaysia
First published on 6th August 2021
Abstract
The fabrication with high energy density and superior electrical/electrochemical properties of hierarchical porous 3D cross-linked graphene-based supercapacitors is one of the most urgent challenges for developing high-power energy supplies. We facilely synthesized a simple, eco-friendly, cost-effective heteroatoms (nitrogen, phosphorus, and fluorine) co-doped graphene oxide (NPFG) reduced by hydrothermal functionalization and freeze-drying approach with high specific surface areas and hierarchical pore structures. The effect of different heteroatoms doping on the energy storage performance of the synthesized reduced graphene oxide is investigated extensively. The electrochemical analysis performed in a three-electrode system via cyclic voltammetry (CV), galvanostatic charging–discharging (GCD), and electrochemical impedance spectroscopy (EIS) demonstrates that the nitrogen, phosphorous, and fluorine co-doped graphene (NPFG-0.3) synthesized with the optimum amount of pentafluoropyridine and phytic acid (PA) exhibits a notably enhanced specific capacitance (319 F g−1 at 0.5 A g−1), good rate capability, short relaxation time constant (τ = 28.4 ms), and higher diffusion coefficient of electrolytic cations (Dk+ = 8.8261 × 10−9 cm2 s−1) in 6 M KOH aqueous electrolyte. The density functional theory (DFT) calculation result indicates that the N, F, and P atomic replacement within the rGO model could increase the energy value (GT) from −673.79 eV to −643.26 eV, demonstrating how the atomic level energy could improve the electrochemical reactivity with the electrolyte. The improved performance of NPFG-0.3 over NFG, PG, and pure rGO is mainly ascribed to the fast-kinetic process owing to the well-balanced electron/ion transport phenomenon. A symmetric coin cell supercapacitor device fabricated using NPFG-0.3 as the anode and cathode material with 6 M KOH aqueous electrolyte exhibits maximum specific energy of 38 W h kg−1, a maximum specific power of 716 W kg−1, and ∼88.2% capacitance retention after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles. The facile synthesis approach and promising electrochemical results suggest this synthesized NPFG-0.3 material has high potential for future supercapacitor application.
000 cycles. The facile synthesis approach and promising electrochemical results suggest this synthesized NPFG-0.3 material has high potential for future supercapacitor application.
Introduction
For sustainable development and to reduce environment pollution, presently there is a huge demand for high performance energy storage devices for efficient utilization of green and clean energy.1,2 In recent years, supercapacitors have attracted growing research interest in the energy storage industry due to their high specific energy, quick charge/discharge rate, high operating temperature, and long-run cyclability.3–5 To fabricate a high-performance supercapacitor device, the active material plays a crucial role. In recent research, graphene-based materials are mostly used to fabricate energy storage devices due to their outstanding qualities such as high chemical and electrochemical stability, high specific power, high electrical conductivity, and abundant electrocatalytic active sites for various redox reactions.6,7 Moreover, graphene-based materials are cheaper, eco-friendly, and simpler to prepare than other materials, such as conductive polymers and metal oxides. These properties have promoted the commercial development of graphene-based supercapacitors.8 Many efforts are being made to improve the energy storage performances of the materials. Among them, heteroatoms doping into the carbon skeleton is found as one of the most effective ways to obtain graphene-based materials with high energy storage performance. There have been many reports suggesting incorporation of foreign atoms like boron,9 nitrogen,10 phosphorus,11 sulfur,12 fluorine,13 nitrogen/boron,14 nitrogen/sulfur,15 nitrogen/phosphorus16 increase the electrochemical performance of the graphene via induced pseudocapacitance effect. In particular, N-doping increases the n-type conductivity and free-charge carrier densities, and improves the activity of the carbon material in redox reactions.17,18 F atom has higher electronegative (4.0) than C atom (2.5) form C–F bonds which demonstrates ionic, semi-ionic and covalent bond characters.19 F-doping can not only tunes the physical and chemical properties of carbon materials but also influences their structure and morphology to improve specific surface area.13 Phosphorus exhibits stronger electron-donating ability than nitrogen and the incorporation of phosphorus in the carbon material improves the wettability of the electrode as a result electrolytic ions can quickly spread on the electrode surface.11 It has been observed that multi-heteroatom doped carbon materials show superior electrochemical performance in comparison to the single heteroatom-doped carbon because co-doping due to synergetic effect amplifies the effects caused by single doping.20 Therefore, it is highly desirable to find out a facile strategy to synthesize multi-heteroatom doped graphene for high performance supercapacitor applications. To the best of our knowledge, the multi-heteroatoms doped graphene samples, including nitrogen (N), phosphorus (P), and fluorine (F) atoms, have been studied very limited. Thus, a sustainable and green method for developing functionalized heteroatoms doped graphene with hierarchical parous 3D cross-linked network with enhanced electrochemical performance is urgently needed.In the present work, we introduce phytic acid (PA) as a phosphorus dopant which is an abundant natural product found in plants. Its contains six phosphate groups, which provides plentiful crosslinking sites that may stitch the graphene sheets to form a 3D microstructure.21 At present, most of the fluorine (F) doping reactions are relatively complex and uncontrollable, generally using toxic and expensive gaseous fluorine-containing reagents. Under consideration of the safety parameters, pentafluoropyridine organic compound is incorporated as the precursor for fluorine (F) and nitrogen (N) doping both, which serves and significantly improves the carbonization yield due to low-temperature functionalization process. The best-synthesized NPFG-0.3 presents a hierarchical porous 3D cross-linked network with a high specific surface area up to 518 m2 g−1. By the DFT results, the N, P, and F replace with C atoms within rGO atomic model, accompany with KOH molecule, could increase the Gibbs free energy (GT) of lattice from −673.79 eV to a more considerable value as −643.26 eV. According to our calculation and experiment result, the electrochemical performance of our best synthesized sample depends on the electrochemical reactivity and the electrochemical reactivity depends on the Gibbs free energy (GT) within the atomic level. Electrochemical results show, NPFG-0.3 exhibits excellent specific capacitance of 319 F g−1 at 0.5 A g−1 in 6 M KOH aqueous electrolyte, higher than several previous reported values. Our designed symmetrical supercapacitor device by using NPFG-0.3 as both anode and cathode demonstrates a high energy density of 38 W h kg−1 at the power density of 716 W h kg−1 in 1 M Na2SO4 aqueous electrolyte and 24 W h kg−1 at the power density of 499 W h kg−1 in 6 M KOH aqueous electrolyte.
Experimental
Materials
All the chemicals used in this study were pure analytical grade. Natural graphite fine powder (no. 15553, Riedel-de Haen), conducting carbon (Super-P, TIMCAL), N-methyl 2-pyrrolidone (NMP, Alfa Aesar), phytic acid (PA, 50 wt% aqueous solution), and potassium hydroxide (KOH, Sigma Aldrich) were received and used without further purification. All dispersions and solutions were prepared in DI water of resistivity at least 18 MΩ cm at 25 °C, obtained from Milli-Q water purification system (Milli-Q, USA).Preparation of graphene oxide (GO)
The precursor material, graphene oxide (GO) was synthesized by the strong chemical oxidation of graphite powders in the mixture (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) of H2SO4 and H3PO4.22 The obtained product (GO flakes) was vacuum dried at 45 °C to remove moisture.
1) of H2SO4 and H3PO4.22 The obtained product (GO flakes) was vacuum dried at 45 °C to remove moisture.
Synthesis of the NPFG, NFG, and PG
To synthesize NPFG, a calculated amount of GO flakes was suspended in DI water via intense sonication to prepare homogeneous GO dispersion of 5 mg mL−1. After that, 0.3 mL C5F5N (Alfa Aesar, 99%) was added into 35 mL prepared GO colloidal solution with continuous stirring for 30 min. An optimized amount of phytic acid was added into the above mixture with additional stirring for 30 min. The resultant mixture was sealed in a 50 mL Teflon-lined autoclave and maintained at a specific temperature of 160 °C for 12 h. Thus, the obtained product was washed with DI water several times until the pH became 7 and freeze-dried at −52 °C for 48 h. Finally, the collected freeze-dried sample was dried in a vacuum oven at 60 °C overnight. The schematic of the whole synthesis process is illustrated in Fig. 1. The fabricated NPFG with different C5F5N amounts, 0.1, 0.2, 0.3 0.5, and 0.7 mL, are denoted as NPFG-0.1, NPFG-0.2, NPFG-0.3, NPFG-0.5, and NPFG-0.7, respectively. For comparison, PG, NFG, and rGO were also prepared. PG and NFG were designed according to the same procedure of NPFG at 160 °C using phytic acid and C5F5N. Pure rGO has been synthesized via hydrothermal reduction of GO colloidal solution.Fabrication of working electrodes for electrochemical testing
The working electrodes for electrochemical measurements were prepared by mixing the active material, carbon black, and polyvinylidene fluoride (PVDF) binder with a mass ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 with an appropriate amount of N-methyl-2-pyrrolidone (NMP) solvent. Then, this slurry was uniformly coated onto the graphite carbon substrate current collectors (1 × 1 cm2 area) dried at 80 °C for 12 h. The weight of active material loaded on a graphite carbon substrate, as measured by the microbalance (PRECISA XR125M-FR) with an accuracy of ∼0.1 μg, was ∼1.2 mg. The synthesis process is shown in Fig. 1. The NPFG-0.3 electrodes-based symmetric supercapacitor was successfully designed in a two-electrode coin cell configuration using two circular NPFG-0.3 electrodes of equal weights, 6 M KOH aqueous electrolyte, and glass microfiber membrane separator (Whatman™). The total mass of active material in the device was ∼3.8 mg.
10 with an appropriate amount of N-methyl-2-pyrrolidone (NMP) solvent. Then, this slurry was uniformly coated onto the graphite carbon substrate current collectors (1 × 1 cm2 area) dried at 80 °C for 12 h. The weight of active material loaded on a graphite carbon substrate, as measured by the microbalance (PRECISA XR125M-FR) with an accuracy of ∼0.1 μg, was ∼1.2 mg. The synthesis process is shown in Fig. 1. The NPFG-0.3 electrodes-based symmetric supercapacitor was successfully designed in a two-electrode coin cell configuration using two circular NPFG-0.3 electrodes of equal weights, 6 M KOH aqueous electrolyte, and glass microfiber membrane separator (Whatman™). The total mass of active material in the device was ∼3.8 mg.
Physico-chemical characterizations and electrochemical testing
The prepared samples were carefully examined via X-ray diffractometer (XRD, BRUKER D2 PHASER) assembled with CuKα irradiation (λ = 1.54184 Å, 10 mA, and 30 kV), and field emission scanning electron microscope (FE-SEM, Hitachi SU8010) for performing crystalline and surface morphology analysis, respectively. Raman spectra measurement of the samples was carried out using 514.5 nm Ar laser, 40 mW (Horiba Jobin Yvon Labarm HR 800). The specific surface area (SSA) and pore size distribution (PSD) was measured on Micromeritics ASAP 2020 analyzer and calculated by the methods of Brunauer–Emmett–Teller (BET) and density functional theory (DFT), respectively.The electrochemical properties of all prepared samples were investigated by cyclic voltammetry (CV), galvanostatic charge/discharge (GCD), and electrochemical impedance spectroscopy (EIS) with an Autolab electrochemical analyzer (M204 and FRA32M module) at room temperature. A three electrodes configuration containing a saturated calomel reference electrode (SCE), platinum sheet as the counter electrode, and sample NPFG-0.3 as working electrode were utilized for these measurements of electrolyte 6 M KOH. The value of specific capacitance Cs (F g−1) was calculated from GCD curve using the following equation:
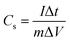 | (1) |
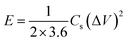 | (2) |
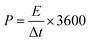 | (3) |
The electrochemical impedance spectroscopy (EIS) results are obtained by applying an ac amplitude of 5 mV in the frequency range 0.1 Hz to 100 kHz. The EIS data analysis provides the frequency-dependent characteristic of the supercapacitor electrode materials in terms of complex power as given below;
| S(ω) = P(ω) + iQ(ω) | (4) |
In terms of electrochemical impedance P(ω) and Q(ω) can be written as;
P(ω) = [ΔVrms2/|Z(ω)|]cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ ϕ
| (5) |
Q(ω) = [ΔVrms2/|Z(ω)|]sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ ϕ
| (6) |
Further, using EIS results, the diffusion coefficients (Da) of the electrolytic ions at the interfacial region can be determined using Randles plots eqn (7) given below;23,24
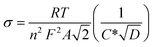 | (7) |
T is the absolute temperature, n is the charge-transfer number, R represents the gas constant, C* is the concentration of the electrolyte, and A represents the working electrode.
The coulombic efficiency (η), was also calculated by using eqn (8) given below.
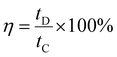 | (8) |
Density functional theory (DFT) calculation
Our calculation is based on a 72 carbons layer structure representing the rGO, and preplace the centered carbon atom as P, N, and F atoms, for further simulation of the experiment results. The GGA-PBE exchange–correlation functional is used to describe the interactions with a non-magnetic calculation using a plane wave cutoff energy of 400.000 eV.25 The electronic iterations convergence is 1.00 × 10−5 eV with k-spacing as 1 × 1 × 2 mesh. The k-mesh is forced to be centered on the gamma point, and we are using first-order Methfessel–Paxton smearing with a width of 0.2 eV for the whole slab free energy calculation.Results and discussion
The synthetic approach of nitrogen, phosphorus, and fluorine heteroatom doped graphene hydrogel (NPFG) is schematically illustrated in Fig. 1a. In brief, an aqueous dispersion of GO (5 mg mL−1) containing phytic acid (C6H18O24P6) and pentafluoropyridine (C5F5N) was hydrothermally functionalized at 160 °C for 12 h to obtain NPFG. More synthesis details can be found in the Experimental section. Moreover, the nitrogen and fluorine co-doped graphene (NFG), phosphorus-doped graphene (PG), and pure graphene hydrogel (rGO) were also synthesized as control samples using the same procedure with the addition of corresponding dopants as needs (see Experimental section). The microstructure of NPFG was characterized by scanning electron microscopy (SEM). As shown in Fig. 1b and c, morphology of pure graphene oxide and a highly crumples cross-linked 3D framework of functionalized graphene (NPFG).Structural and morphological characterizations
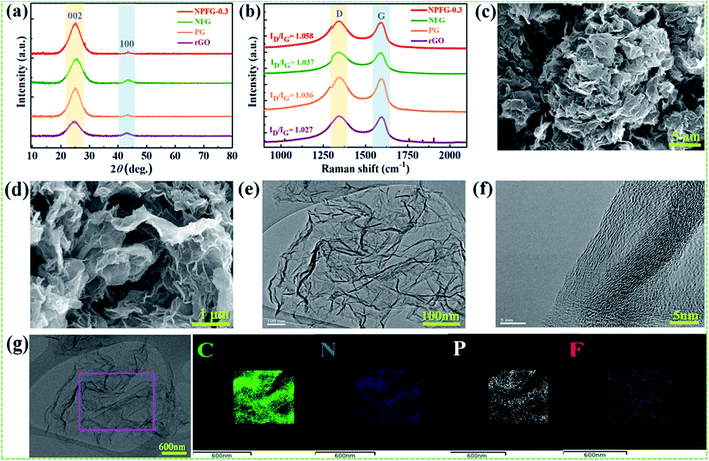
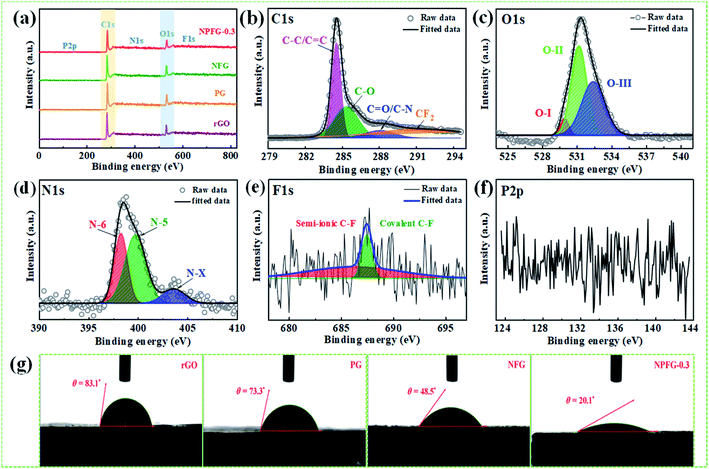
The structures of the samples rGO, PG, NFG, and NPFG-0.3 were detected by X-ray diffraction (XRD) analysis (Fig. 2a). The comprehensive characterization of XRD represents the deoxygenation of the as-prepared samples. The XRD pattern of GO (Fig. S1†) indicates that a sharp diffraction peak at 2θ = 10.5°, corresponds to the characteristic (001) diffraction of GO. This suggests larger interlayer spacing (d = 0.855 nm) of GO than that of graphite (∼0.34 nm) due to the introduction of oxygen-containing functional groups (e.g., epoxy and hydroxyl groups) adhered to the GO sheet surface.26,27 This GO peak entirely disappears after hydrothermal treatment due to the deoxygenation of oxygen functional groups of GO. Furthermore, a broad diffraction peak around 2θ = 24.8° has developed that corresponds to the (002) plane of graphene and represents the successful reduction of graphene oxide (GO) to reduced graphene oxide (rGO) nanosheets.28,29 In the case of PG, NFG, and NPFG-0.3 samples, the diffraction peaks appear at 2θ = 25°, 25.5° and 25.6° respectively, which are ascribed to (002) crystalline plane, suggesting the recovery of π-conjugate system from GO to some extent.30 The interlayer spacing of freeze-dried NPFG-0.3 is calculated to be 0.368 nm, which is much lower than that of GO precursor (∼0.855 nm) and slightly larger than that of rGO (∼0.356 nm). This enlargement in interlayer spacing of NPFG-0.3 compared with rGO is attributed to the introduction of heteroatoms (N, P, and F) doping via π–π interaction pentafluoropyridine and phytic acid assisted GO precursor. Besides, a weak peak observed at 2θ = 43.5° for rGO, PG, NFG, and NPFG-0.3 samples, corresponding to (100) plane. Raman spectra (Fig. 2b) are utilized to explore further the structures of rGO, PG, NFG, and NPFG-0.3 by the resulting characteristic G and D bands related to defects/disorder and graphitization respectively. To observe the defects presented in graphene-related materials, the intensity ratio (ID/IG) for the D band (at 1345 cm−1) and the G band (at 1590 cm−1) is generally used.31,32 The ID/IG ratio is 1.027, 1.036, 1.037, and 1.058 for rGO, PG, NFG, and NPFG-0.3, respectively, indicated that NPFG-0.3 had the highest degree of graphitization.33 It was observed that the lowest ID/IG ratio (0.96) of GO (Fig. S2†) would be associated with a lower disorder degree as compared with other samples.Subsequently, the ID/IG ratio of rGO is higher than that of GO, representing increased defects after the hydrothermal reduction process. Moreover, the ID/IG ratio value of PG and NFG rise to a different extent, implying that the phosphorus (P) doping modification with phytic acid and nitrogen (N), fluorine (F) co-doping with pentafluoropyridine both enhance the disorder of rGO after hydrothermal functionalization. Remarkably, the NPFG-0.3 shows the highest ID/IG ratio because of the interaction between phytic acid (P dopant) and the introduction of pentafluoropyridine (N, F co-dopant) via hydrothermal functionalization, resulting in more defects and disorder degree of rGO. To investigate the morphology of the NPFG-0.3 sample, we recorded field emission electron microscopy (FE-SEM) and transmission electron microscopy (TEM) images of the sample. As shown in Fig. 1b, the GO nanosheets are partially aggregated. When GO hydrothermally functionalized and freeze-dried, NPFG-0.3 as a highly crumpled cross-linked 3D interconnected framework is formed (Fig. 2c and d). The energy-dispersive X-ray spectroscopy (EDX) profile of NPFG-0.3 powder sample measured over a physical area shown in the inset of Fig. S3a.† In EDX profile, the x axis is the energy (keV) and the y axis represents the counts in arbitrary units. The EDX profile depicts the presence of C, O, N, F and P peaks, and there is no any impurity peak in the profile. The quantitative analyses of the C, O, N, F and P in the sample as estimated by EDX examination, are shown in the inset of Fig. S3b.† Additionally, the TEM image of the NPFG-0.3 displays a wrinkled few-layer sheet-like morphology with no obvious agglomerations (Fig. 2e). Furthermore, the (002) graphitic basal planes, revealed in the HRTEM image (Fig. 2f), indicate the graphitic structure within NPFG-0.3.34 The elemental mapping images of the NPFG-0.3 are shown in Fig. 2g, and the elements C, O, N, P, and F were distributed through the whole 3D graphene network. In addition, the HRTEM images (Fig. S4a and b†) show the existence of mesoporous and microporous structures uniformly distributed throughout the sample, graphene sheet wrinkling and carbon chain defects caused by the incorporation of N, P and F atoms into the graphene framework. Interestingly, the addition of pentafluoropyridine redox-active molecules on the conductive graphene nanosheets with a highly crumpled, cross-linked 3D interconnected framework is an excellent strategy for energy storage application since such a structure guarantees adequate exposure of the active site to the electrolyte and preserve its rich porous structure that can provide fast ion transport pathways through the pores.35,36 The surface chemistry about the elemental composition and chemical states of the samples' elements is studied using X-ray photoelectron spectroscopy (XPS) analysis as shown in Fig. 3. All the XPS peaks are identified with the help of reported data. The broad scan spectrum is shown in Fig. 3a illustrate sharp C 1s (at 283.5 eV) and O 1s (at 531.4 eV) peaks in pure rGO. After hydrothermal functionalization, the C 1s and O 1s peaks are comparatively weaker, whereas the spectra of NPFG-0.3 show the presence of heteroatoms N 1s (at 398.5 eV), F 1s (at 688.9 eV), and P 2p (at 131.2 eV), respectively. The high-resolution X-ray photoelectron spectrum (HRXPS) of individual elements C 1s, O 1s, N 1s, F 1s, and P 2p, for NPFG-0.3 sample, are shown in Fig. 3b–f, respectively. Fig. 3b exhibits the characteristic deconvoluted C 1s spectra of NPFG-0.3 into four peaks at binding energies of 284.6 eV (C–C/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 286.0 eV (C–O), 288.6 eV (C
C), 286.0 eV (C–O), 288.6 eV (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C–N) and 291.3 eV (CF2). The intensive peak at 284.6 eV is attributed to non-functionalized sp2 hybridized C atoms. The lower intensity peak at 286.0 eV is assigned to the C atoms connected to the residual O atoms with sp3 hybridization, indicating that most of the oxygen-containing functional groups are removed during the hydrothermal process. However, the peak at 288.6 eV in the C 1s spectra is overlapped by C
C/C–N) and 291.3 eV (CF2). The intensive peak at 284.6 eV is attributed to non-functionalized sp2 hybridized C atoms. The lower intensity peak at 286.0 eV is assigned to the C atoms connected to the residual O atoms with sp3 hybridization, indicating that most of the oxygen-containing functional groups are removed during the hydrothermal process. However, the peak at 288.6 eV in the C 1s spectra is overlapped by C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and C–N bond configurations. The peak at 291.3 eV in NPFG-0.3 indicates the covalent C–F bond with different configurations in which carbon atoms transform to sp3 hybridization.37–39 To check the oxygen content on the surface, the core O 1s spectrum is fitted in three Gaussian distributed peaks which belong to low, medium, and high binding energy were determined to correspond to the amount of oxygen in fully oxidized regions (OI), deficient regions (OII), and chemisorbed oxygen (OIII), respectively as shown in Fig. 3c. The high-resolution N 1s spectrum of the NPFG-0.3 (Fig. 3d) shows the typical three peaks assigned to N-6 (pyridinic-N) at 397.0 eV, N-5 (pyrrolic-N) at 400.0 eV, and N-X (graphitic-N) at 403.8 eV binding energy,40 respectively, which confirms that nitrogen is successfully incorporated into NPFG-0.3 during functionalization process. The high-resolution F 1s spectrum (Fig. 3e) is deconvoluted into two peaks at 685.5 eV (semi-ionic C–F bond) and 688.6 eV (covalent C–F bond), which confirms the fluorine has been successfully incorporated into the material. A large number of semi-ionic C–F and covalent C–F bonds support the rate capability and cycling stability of the active material.41 The weak peak intensity of P 2p spectrum is observed as depicted in Fig. 3f. The atomic percentage of individual elements in all samples are listed in Table 1. Furthermore, in aqueous electrolyte, electrode materials' high hydrophilicity supports the fast transport of electrolyte ions into the inner active surface and contributes extra electroactive sites for rapid adsorption/desorption of solvation electrolyte ions and thus accomplish improved electrochemical performance.42 The contact angle measurements further verified each synthesized sample's wettability for 6 M KOH electrolyte droplets on all the manufactured electrodes (Fig. 3g). As shown in Table 1, PG, NFG, and NPFG-0.3 electrodes were hydrophilic with contact angles of 73.3°, 48.5°, and 20.1°, respectively. However, a pure rGO electrode presented a large contact angle (∼83.1°) that tends to near hydrophobic behavior due to rather its clean surface. Owing to the presence of plentiful N, P, and F containing groups, NPFG-0.3 shows the smallest contact angle and excellent wettability.3,43 Combined with the XPS analysis, these results demonstrated that heteroatoms increase the material's wettability, resulting in a significant increase of electrolyte ions accessible surface area and plentiful active sites to generate pseudocapacitance via a reversible redox reaction. Surface area and pore-size distribution are essential for energy-related technologies. Surface area and pore-size distribution of freeze-dried rGO, PG, NFG and NPFG-0.3 were evaluated by Brunauer–Emmett–Teller (BET) and Horvath–Kawazoe (H–K) model density functional theory (DFT) methods, respectively. As shown in Fig. 4a, the N2 adsorption–desorption isotherms of rGO, PG, NFG, and NPFG-0.3 represents type-IV isotherms with mixed H2, H4 types hysteresis loop at 0.5–1.0 relative pressure range, indicating the existence of micropores as well as mesopores in all synthesized samples.44,45 Based on the evaluation of nitrogen sorption data, the BET, specific surface area of 518.2 m2 g−1, is obtained for the NPFG-0.3, which is significantly higher than the BET specific surface area values reported previously doped graphene synthesized via various methods.46–50 The incorporation of phytic acid (PA) and fluorination process via pentafluoropyridine lead to much more curls and wrinkles, which prevent the aggregation of adjacent graphene nanosheets and greatly enhances the specific surface area (SSA) of NPFG-0.3, NFG, and PG as compared to neat rGO.51–53 The higher specific surface area predicts the availability of more interfacial area between the electrolytic ions and the active electrode material and might provide better performance.54 As shown in Fig. 4b, the DFT pore size distribution curves of NPFG-0.3, NFG, PG, and rGO revels that all the samples have a wide range of pore size distribution extended from microporous (0.39–1 nm) to mesoporous (2–50 nm) regions. In such a structure, the micropores significantly increase the specific surface area. The mesopores afford effective ion transport pathways with a minimized resistance and strengthen the supercapacitor's
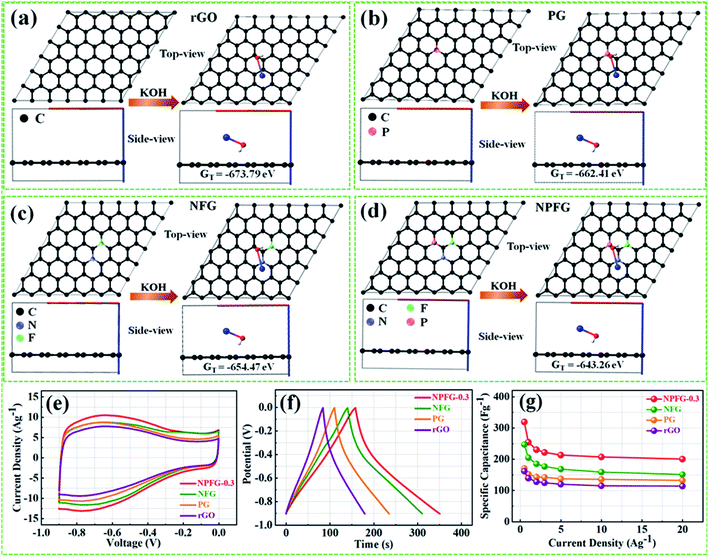
electrical double layer characteristics.34,35 The structure characterization parameters of N2 adsorption/desorption analyses in terms of BET specific surface area, BET average pore size, and total pore volume have been summarized in Table 1. To investigate the influence of heteroatoms on the electrochemical performance of NPFG, a first-principal calculation using density functional theory (DFT) was performed. Our DFT calculations were obtained the Gibbs free energy, i.e., useful energy produced by an electrochemical system is a state function and depends on the identity of the active electrode materials and the initial and final states of the related electrochemical reactions.55 Typically, the crystal structure with higher Gibbs free energy, within the whole system, is accompanied by better reactivity and instability.
O bond and C–N bond configurations. The peak at 291.3 eV in NPFG-0.3 indicates the covalent C–F bond with different configurations in which carbon atoms transform to sp3 hybridization.37–39 To check the oxygen content on the surface, the core O 1s spectrum is fitted in three Gaussian distributed peaks which belong to low, medium, and high binding energy were determined to correspond to the amount of oxygen in fully oxidized regions (OI), deficient regions (OII), and chemisorbed oxygen (OIII), respectively as shown in Fig. 3c. The high-resolution N 1s spectrum of the NPFG-0.3 (Fig. 3d) shows the typical three peaks assigned to N-6 (pyridinic-N) at 397.0 eV, N-5 (pyrrolic-N) at 400.0 eV, and N-X (graphitic-N) at 403.8 eV binding energy,40 respectively, which confirms that nitrogen is successfully incorporated into NPFG-0.3 during functionalization process. The high-resolution F 1s spectrum (Fig. 3e) is deconvoluted into two peaks at 685.5 eV (semi-ionic C–F bond) and 688.6 eV (covalent C–F bond), which confirms the fluorine has been successfully incorporated into the material. A large number of semi-ionic C–F and covalent C–F bonds support the rate capability and cycling stability of the active material.41 The weak peak intensity of P 2p spectrum is observed as depicted in Fig. 3f. The atomic percentage of individual elements in all samples are listed in Table 1. Furthermore, in aqueous electrolyte, electrode materials' high hydrophilicity supports the fast transport of electrolyte ions into the inner active surface and contributes extra electroactive sites for rapid adsorption/desorption of solvation electrolyte ions and thus accomplish improved electrochemical performance.42 The contact angle measurements further verified each synthesized sample's wettability for 6 M KOH electrolyte droplets on all the manufactured electrodes (Fig. 3g). As shown in Table 1, PG, NFG, and NPFG-0.3 electrodes were hydrophilic with contact angles of 73.3°, 48.5°, and 20.1°, respectively. However, a pure rGO electrode presented a large contact angle (∼83.1°) that tends to near hydrophobic behavior due to rather its clean surface. Owing to the presence of plentiful N, P, and F containing groups, NPFG-0.3 shows the smallest contact angle and excellent wettability.3,43 Combined with the XPS analysis, these results demonstrated that heteroatoms increase the material's wettability, resulting in a significant increase of electrolyte ions accessible surface area and plentiful active sites to generate pseudocapacitance via a reversible redox reaction. Surface area and pore-size distribution are essential for energy-related technologies. Surface area and pore-size distribution of freeze-dried rGO, PG, NFG and NPFG-0.3 were evaluated by Brunauer–Emmett–Teller (BET) and Horvath–Kawazoe (H–K) model density functional theory (DFT) methods, respectively. As shown in Fig. 4a, the N2 adsorption–desorption isotherms of rGO, PG, NFG, and NPFG-0.3 represents type-IV isotherms with mixed H2, H4 types hysteresis loop at 0.5–1.0 relative pressure range, indicating the existence of micropores as well as mesopores in all synthesized samples.44,45 Based on the evaluation of nitrogen sorption data, the BET, specific surface area of 518.2 m2 g−1, is obtained for the NPFG-0.3, which is significantly higher than the BET specific surface area values reported previously doped graphene synthesized via various methods.46–50 The incorporation of phytic acid (PA) and fluorination process via pentafluoropyridine lead to much more curls and wrinkles, which prevent the aggregation of adjacent graphene nanosheets and greatly enhances the specific surface area (SSA) of NPFG-0.3, NFG, and PG as compared to neat rGO.51–53 The higher specific surface area predicts the availability of more interfacial area between the electrolytic ions and the active electrode material and might provide better performance.54 As shown in Fig. 4b, the DFT pore size distribution curves of NPFG-0.3, NFG, PG, and rGO revels that all the samples have a wide range of pore size distribution extended from microporous (0.39–1 nm) to mesoporous (2–50 nm) regions. In such a structure, the micropores significantly increase the specific surface area. The mesopores afford effective ion transport pathways with a minimized resistance and strengthen the supercapacitor's
electrical double layer characteristics.34,35 The structure characterization parameters of N2 adsorption/desorption analyses in terms of BET specific surface area, BET average pore size, and total pore volume have been summarized in Table 1. To investigate the influence of heteroatoms on the electrochemical performance of NPFG, a first-principal calculation using density functional theory (DFT) was performed. Our DFT calculations were obtained the Gibbs free energy, i.e., useful energy produced by an electrochemical system is a state function and depends on the identity of the active electrode materials and the initial and final states of the related electrochemical reactions.55 Typically, the crystal structure with higher Gibbs free energy, within the whole system, is accompanied by better reactivity and instability.
| Sample | C (at%) | O (at%) | N (at%) | P (at%) | F (at%) | Contact angle (Deg.) | Specific surface area (SBET) (m2 g−1) | Total pore volume (Vt) (cm3 g−1) | Pore diameter (nm) |
|---|---|---|---|---|---|---|---|---|---|
| rGO | 86.76 | 13.24 | 0 | 0 | 0 | 83.1° | 277.5 | 0.193 | 1.27, 2.74 |
| PG | 84.94 | 14.31 | 0 | 0.75 | 0 | 73.3° | 328 | 0.296 | 1.28, 2.73 |
| NFG | 81.95 | 14.61 | 3.12 | 0 | 1.52 | 48.5° | 438 | 0.892 | 0.45, 2.72 |
| NFG-0.3 | 80.75 | 15.06 | 1.41 | 0.77 | 0.83 | 20.1° | 518.2 | 0.718 | 0.46, 2.93 |
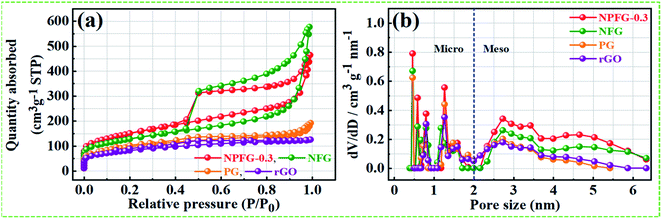 | ||
| Fig. 4 (a) and (b) N2 adsorption–desorption isotherm and DFT pore size distribution curves of rGO, PG, NFG and NPFG-0.3, respectively. | ||
Therefore, we have calculated the total Gibbs free energy (GT), by the DFT method, for KOH molecule combine with the rGO and rGO replace C atom within P, N, and F as the similar structures of rGO, PG, NFG, and NPFG-0.3, experimental samples. In our calculation results, the P atom replacement, N and F atoms replacement, and P, N, and F atoms replacement could increase the total free energy (GT), all. And, this result is could explain our PG, NFG, and NPFG-0.3 samples offering a better electrochemical performance as compared with pure rGO one. Indeed, those atomic models and calculations give us that the total free energy (GT) within the electrode could be the hint for the electrochemical charge storage mechanism of the supercapacitor. Finally, the total Gibbs free energy (GT) value of P, N, and F atoms replacement (GT = −643.26 eV) is the highest one, compare to other three models, and it could help us to explain our NPFG-0.3 sample has the best electrochemical performance than others. Higher the value of Gibbs free energy, more the supercapacitor system stored energy.56 The total amount of charge transferred during the electrochemical reaction has a strong relationship with the free energy through the relation, ΔG = −nFEcell, where “Ecell” is the cell potential, n is the number of electrons per mole of active material, F is Faraday constant, and the term nF is described as capacity/capacitance factor. These results will indicate that the heteroatom doped graphene (NPFG-0.3) electrode is a promising electrode in 6 M KOH electrolyte system. Furthermore, to verify these results, we studied the electrochemical performances of the NPFG-0.3, NFG, PG, and rGO as working electrodes via a three-electrode cell system in 6 M KOH electrolyte. Fig. 5e compares the CV curves of as-synthesized NPFG-0.3, NFG, PG, and rGO electrodes recorded at a scan rate of 25 mV s−1 in the potential range −0.9 to 0.0 V. Evidentially, in comparison to rGO, PG, and NFG, the CV curve of NPFG-0.3 occupies the larger area. It belongs to a quasi-rectangular shape with poorly defined broaden peaks at −0.75 to 0.4 V, implying the coexistence of both electrical double-layer capacitive (EDLC) behavior graphene sheet and pseudocapacitance arising from heteroatom doping into the graphene network during the hydrothermal functionalization process. Fig. 5f represents the GCD curves of all the samples recorded at 1 A g−1 in the potential range −0.9 to 0.0 V. The GCD curve of neat rGO showed a typical symmetrical triangle shape, corresponding to the electric double-layer capacitance (EDLC) behavior of carbon material. The curves of PG, NFG, and NPFG-0.3 indicate a deviation from an ideal linear shape, which further confirms the significant contribution of the pseudocapacitance arises from P and N, F containing functional groups. Comparison of specific capacitances versus different current densities shown in Fig. 5g. The electrical conductivity of energy storage materials is the crucial parameter to investigate electrochemical performance. The four-point probe measurements revealed that the ohmic resistances of rGO, PG, NFG, and NPFG-0.3 are 2.43, 2.12, 1.62, and 1.41 mΩ sq−1, respectively, (Fig. S5a†). The calculated electrical conductivity for rGO, PG, NFG, and NPFG-0.3 to be 55.7 × 10−2, 58.4 × 10−2, 82.9 × 10−2, and 88.7 × 10−2 S cm−1, respectively, as shown in Fig. S5b.† The higher electrical conductivity of NPFG-0.3, evidently proves the synergistic effect of heteroatoms doping with a well-preserved π-conjugated structure. This is in good agreement with the EIS analysis showing that the doping of foreign atoms into the graphene network induces a significant reduction of the semi-circle in the Nyquist plots.51,57,58
Application of NPFG-0.3 in a supercapacitor
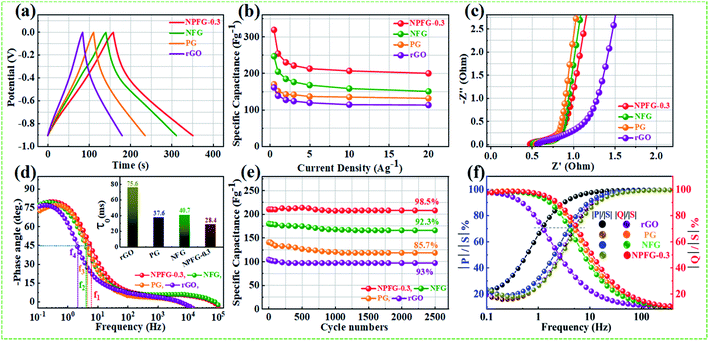
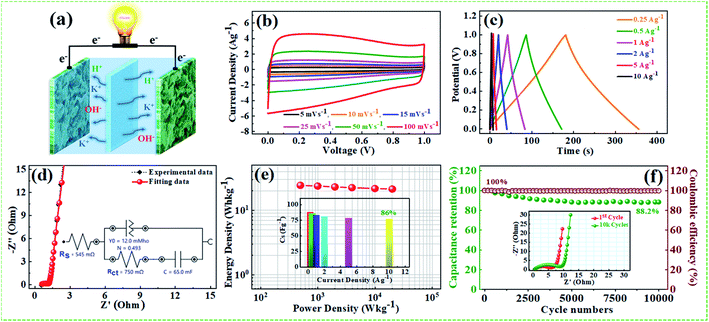
The supercapacitive performance comparisons of all synthesized samples in a three electrode cell system with 6 M KOH electrolyte as shown in Fig. 6. The galvanostatic charge/discharge curves (Fig. 6a) of all the samples recorded at 1 A g−1 in the potential range −0.9 to 0.0 V. The GCD curve of neat rGO showed a typical symmetrical triangle shape, corresponding to the electric double-layer capacitance (EDLC) behavior of carbon material. The curves of PG, NFG, and NPFG-0.3 indicate a deviation from an ideal linear shape, which further confirms the significant contribution of the pseudocapacitance arises from P and N, F containing functional groups. Here, it is clear that the NPFG-0.3 has a longer discharge time (Δt) significantly, and hence higher SC among the synthesized samples. There was no obvious IR drop at the discharge curve from all GCD profiles, indicating low internal resistance. The values of specific capacitances (SCs) calculated from the GCD curves using eqn (1) as a function of discharge current densities are shown in Fig. 6b. The NPFG-0.3 exhibits specific capacitance values of 319, 254.1, 230, 221.3, 212.8, 206.7, and 200 F g−1 at the current densities of 0.5, 1, 2, 3, 5, 10, and 20 A g−1, respectively. Moreover, all the synthesized samples' specific capacitance decreases with an increase in the current density because diffusion of electrolytic ions into the material becomes slower at higher current density values. Electrochemical impedance spectroscopy (EIS) is extremely used to address supercapacitor's electrochemical performance based on ion transfer and electrical conductivity. We conduct EIS measurements to obtain insight into the charge and ion transport properties of each sample. Fig. 6c shows the Nyquist plots of all the electrodes, indicating that with an introduction, the foreign atoms internal resistance starts to decrease. The internal resistance is the ohmic resistance, consisting of ionic resistance of the electrolyte, inherent resistance of substrate and active electrode material, and contact resistance at the active electrode material and substrate interface. NPFG-0.3 electrode performs the smallest internal resistance (0.47 Ω), while the internal resistances for rGO, PG, and NFG are found to be about 0.56, 0.54, and 0.5 Ω, respectively. The smaller value of internal resistance for NPFG-0.3 can be ascribed to the better contact and its higher electrical conductivity (see Fig. S5a and b†). Furthermore, the Bode phase plots can be utilized to determine the characteristic frequency (f0), also known as knee frequency at the intermediate-frequency region (Fig. 6d and the inset). This is the frequency at phase angle 45°, where capacitive and resistive impedances attain equal values, and below which pure capacitive behavior and most of the stored energy is accessible. The characteristic frequency (f0) is utilized to determine the relaxation time constant (τ0 = 1/2πf0), also known as the supercapacitor's dielectric relaxation time. A supercapacitor system's relaxation time is the minimum time it requires to discharge all the stored energy with at least ∼50% efficiency.59,60 The characteristic frequencies (f1–4) for rGO, PG, NFG, and NPFG-0.3 are found to be ∼2.1, 4.5, 3.85, and 5.95 Hz, respectively, which correspond to the relaxation times equal to 75.6, 37.6, 40.7, and 28.4 ms, respectively. The short relaxation time constant (τ0) value of NPFG-0.3, allow it to deliver the fast frequency response and affords fast energy charging/discharging velocity. Randles curves (real impedance Z′ vs. ω−1/2), plotted for NPFG-0.3 compared with rGO are shown in Fig. S6.† The calculated values of diffusion coefficients (Da), with the help of Randles plot using eqn (7), are found to be 2.1832 × 10−9 and 8.8261 × 10−9 cm2 s−1 for rGO and NPFG 0.3 samples, respectively, in 6 M KOH electrolyte. It can be seen that the short relaxation time constant and high diffusion coefficient of NPFG-0.3 electrode allow it to deliver stored energy quickly, and high specific capacitance makes it desirable for engineering high-power capacitors. Cycling stability is an important parameter from a practical point of view. As shown in Fig. 6e the cyclic stability performance of all the synthesized samples measured over successive 2500 charge/discharge cycles @ 2 A g−1. We observed that after adding functionalized groups, the cyclability of NPFG-0.3 electrode improved probably due to the incorporation of heteroatoms and forming of 3D cross-linked channels. After 2500 charge/discharge cycles, the rGO, PG, NFG, and NPFG-0.3 maintain ∼93%, 85%, 92.3%, and 98.5% of their initial capacitance values. To find the desired operating frequency of the prepared electrodes, particularly NPFG-0.3, graphs between normalized real component |P|/|S| and imaginary component |Q|/|S| of the complex power vs. frequency (in logarithmic scale) is plotted (Fig. 6f). The terms Q|/|S| and P|/|S| represent the reactive and active power dissipations in the supercapacitor system, respectively. At high frequency, values supercapacitor responds like a pure resistor, and all the power dissipated in the system is mainly active, i.e., P = 100%. |P|/|S| decreases as the frequency decreases and attains minimum value at a point where a normalized imaginary component of the power, i.e., reactive power (|Q|/|S|), is maximum. At this point, the supercapacitor acts like a pure capacitance, and the real part of the complex power P dissipated becomes zero (Φ = 90°) eqn (6). Therefore, both the curves |P|/|S| and |Q|/|S| exhibit contrary behavior with frequency and, when plotted in the same graph, intersect at some frequency value (f0), which is the characteristic frequency of a capacitor system and defines the frontier between the resistive and capacitive nature of an electrochemical capacitor.At this frequency, |P| = |Q|, i.e., Φ = 45° and |P|/|S| = |Q|/|S| = 1/√2 eqn (5) and (6). Evidently, for all the tested samples rGO, PG, NFG, and NPFG-0.3, both the |P|/|S| and |Q|/|S| curves act contrarily with frequency variation and cross each other at the resonance frequency (f0) as well. The electrochemical properties of all the synthesized samples are summarized in Table S1 (see in the ESI†).
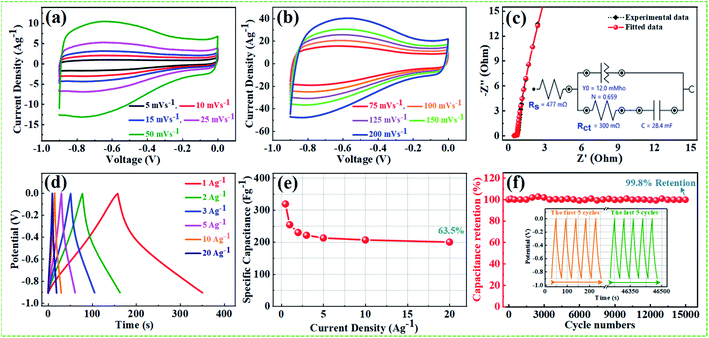
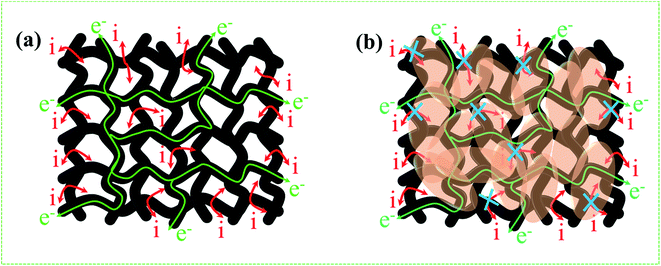
From the above results, NPFG-0.3 based supercapacitor electrode exhibits the best electrochemical properties among the synthesized NFG, PG, and neat rGO samples. Therefore, we investigate its electrochemical performance in detail. Fig. 7a and b indicates the CV curves of NPFG-0.3 from the scan rate 5 to 200 mV s−1 in the potential range −0.9 V to 0.0 V vs. Ag/AgCl reference electrode. The CV curves belong to quasi-rectangular shape with poorly defined broaden peaks at −0.75 to −0.65 V, implying the coexistence of both electrical double-layer capacitive (EDLC) behavior graphene sheet and pseudocapacitance arising from heteroatom doping into the graphene network during functionalization. A Nyquist plot of the NPFG-0.3 electrode as shown in Fig. 7c. In the high-frequency region indicated in the inset, it is found that the as-prepared sample presents an ideal semicircle and a small real axis intercept, implying small charge transfer resistance (Rct = 0.3 Ω), and low solution resistance (Rs = 0.47 Ω), respectively (inset in Fig. 7c). Furthermore, it also demonstrates that the introduction of heteroatoms atoms into the graphene oxide network enriches the internal structure and improves the contact ability between the electrode surface and the electrolyte, and reduces the internal resistance of the material. Fig. 7d represents the GCD curves of NPFG-0.3 evaluated at 0.5 to 20 A g−1 in −0.9 to 0.0 V. During the charge/discharge process, the corresponding curves also verify that the charging curve of NPFG-0.3 electrode displays an approximately triangular shape, and no distinct IR drop can be seen, further demonstrating a low charge transfer resistance and superior electrochemical kinetics. The values of specific capacitances (SCs) calculated from the GCD curves using eqn (1) as a function of discharge, current densities are shown in Fig. 7e. The NPFG-0.3 exhibits specific capacitance values of 319, 254.1, 230, 221.3, 212.8, 206.7, and 200 F g−1 at the current densities of 0.5, 1, 2, 3, 5, 10, and 20 A g−1, respectively. Moreover, the specific capacitance of the as prepared sample decreases with an increase in the current density because diffusion of electrolytic ions into the material becomes slower at higher current density values. The capacitance profile clearly shows that the NPFG-0.3 retains 63.5% of its initial capacitance value at current density 0.5 A g−1 up to 20 A g−1, performing a quite good rate capability. Furthermore, we have optimized pentafluoropyridine content as shown in Fig. S7a and b,† increasing the mass ratio of pentafluoropyridine to GO in the nanocomposite up to 0.3, the integrated area of the CV curves increased. By further increasing the pentafluoropyridine content up to 0.7 in the nanocomposite, the capacitance of the electrode starts to decrease, which can be attributed to either (1) disorganized conjugation of the pentafluoropyridine molecules on the rGO surface or (2) blockage of the pores, or a combination of above two. Besides, the long cycle stability of the NPFG-0.3 electrode was examined at the current density of 2 A g−1 over 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000th charge/discharge (Fig. 7f) cycles, and 99.8% of excellent capacitance retention was obtained. The inset Fig. 7f shows the first and last 5 charge/discharge cycles with unchanged shape, further verified its excellent durability. The observed capacitance of NPFG-0.3 electrode is higher than those of several recently reported doped graphene-based supercapacitor electrodes, as shown in Table S2 (see in the ESI†). Furthermore, we involve phytic acid (PA) as reducing and scaffolding molecules to prepare a PA-mediated graphene architecture via hydrothermal method accompanied by freeze-drying treatment. Phytic acid (PA), a great natural product found in plants, has six phosphate groups.61,62 These groups provide a great deal of feasible cross-linking sites that may stitch the graphene sheets to form a 3D cross-linked architecture as shown in Fig. 8 (schematic illustration of electron/ion transport). As shown in Fig. S8a and b,† the effect of PA content to GO up to 3 mL, the integrated area of the CV curve increases. By further increasing the PA content up to 5, the capacitance of the electrode starts to decrease. Therefore, according to the above discussion and the investigation of micromorphology and electron/ion transport behavior for NPFG-0.3 prepared with an optimized amount of PA achieves the best electrochemical performance can be illustrated in Fig. 8a. Owing to PA and 3D interconnected porous nanostructure's optimized content, the NPFG-0.3 achieves the well-balanced ionic (i) and electronic (e−) transport behaviors and the highest specific capacitance. In contrast, both the ionic and electronic transmissions are significantly obstructed with a large PA in the NPFG-0.3 electrode, resulting in the lowest electrochemical performance, as shown in Fig. 8b. Furthermore, the three-electrode system was employed to evaluate the possible charge storage mechanisms occurring in the NPFG-0.3 electrode at low scan rate, namely, diffusion-controlled faradic intercalation/de-intercalation of ions and capacitive mechanism, which combination of faradic surface redox reactions (pseudocapacitance) and non-faradic electric double layer (EDLC). Fig. 9a shows that the CV curves exhibit the quasi-rectangular-like shape, indicating that the capacitance of NPFG-0.3 dominantly arises from the electrical double layer capacitance (EDLC). Meanwhile, the poorly defined broaden peaks at −0.75 to −0.65 V implying the coexistence of both electrical double-layer capacitive (EDLC) behavior from the graphene sheet and pseudocapacitance arising from heteroatom doping into the graphene network.21,63,64
000th charge/discharge (Fig. 7f) cycles, and 99.8% of excellent capacitance retention was obtained. The inset Fig. 7f shows the first and last 5 charge/discharge cycles with unchanged shape, further verified its excellent durability. The observed capacitance of NPFG-0.3 electrode is higher than those of several recently reported doped graphene-based supercapacitor electrodes, as shown in Table S2 (see in the ESI†). Furthermore, we involve phytic acid (PA) as reducing and scaffolding molecules to prepare a PA-mediated graphene architecture via hydrothermal method accompanied by freeze-drying treatment. Phytic acid (PA), a great natural product found in plants, has six phosphate groups.61,62 These groups provide a great deal of feasible cross-linking sites that may stitch the graphene sheets to form a 3D cross-linked architecture as shown in Fig. 8 (schematic illustration of electron/ion transport). As shown in Fig. S8a and b,† the effect of PA content to GO up to 3 mL, the integrated area of the CV curve increases. By further increasing the PA content up to 5, the capacitance of the electrode starts to decrease. Therefore, according to the above discussion and the investigation of micromorphology and electron/ion transport behavior for NPFG-0.3 prepared with an optimized amount of PA achieves the best electrochemical performance can be illustrated in Fig. 8a. Owing to PA and 3D interconnected porous nanostructure's optimized content, the NPFG-0.3 achieves the well-balanced ionic (i) and electronic (e−) transport behaviors and the highest specific capacitance. In contrast, both the ionic and electronic transmissions are significantly obstructed with a large PA in the NPFG-0.3 electrode, resulting in the lowest electrochemical performance, as shown in Fig. 8b. Furthermore, the three-electrode system was employed to evaluate the possible charge storage mechanisms occurring in the NPFG-0.3 electrode at low scan rate, namely, diffusion-controlled faradic intercalation/de-intercalation of ions and capacitive mechanism, which combination of faradic surface redox reactions (pseudocapacitance) and non-faradic electric double layer (EDLC). Fig. 9a shows that the CV curves exhibit the quasi-rectangular-like shape, indicating that the capacitance of NPFG-0.3 dominantly arises from the electrical double layer capacitance (EDLC). Meanwhile, the poorly defined broaden peaks at −0.75 to −0.65 V implying the coexistence of both electrical double-layer capacitive (EDLC) behavior from the graphene sheet and pseudocapacitance arising from heteroatom doping into the graphene network.21,63,64
In general, the relationship between sweep rate (v) and peak current (ip) from the CV profile can be qualitatively represented as eqn (9) and (10), respectively.
| ip = kvb | (9) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ip = b ip = b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v + log(k) v + log(k)
| (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ip and log
ip and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v.
v.
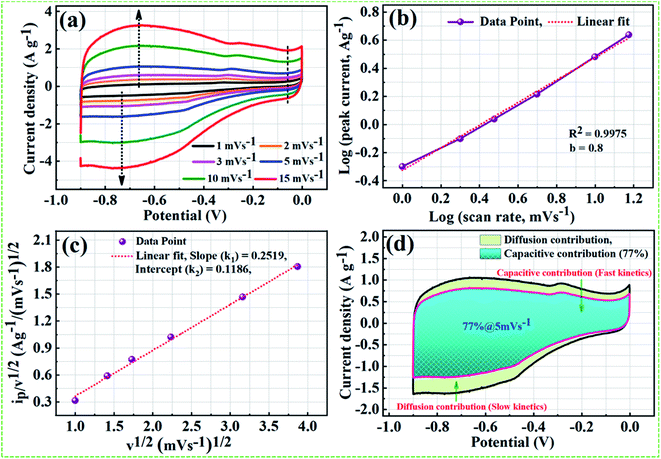
On the basis of theoretical claims, when b (power-low exponent) value is nearly equal to 0.5, the charge storage mechanism mainly involves the diffusion process, whereas b value close to 1 implies that the mechanism is dominated by the capacitive process.65 As shown in Fig. 9b, nearly a linear relationship between average peak current and the square root of the scanning rate with the anodic peak and cathodic peak around −0.65 V and −75 V, respectively. We found the b value from the fitted data is 0.8 and correlation coefficient R2 = 0.9975, indicating charge storage mechanism in the NPFG-0.3 sample is mainly capacitive with fast kinetics. Moreover, the Dunn procedure (eqn (11)) has been employed to quantify the contributions of currents caused by the EDLC and/or surface redox reactions and diffusion controlled redox reactions to the total current at a fixed potential.66,67
| ip = k1v + k1v1/2 | (11) |
For simple mathematical calculations eqn (11) can be transferred into eqn (12) by dividing v1/2, rearranged as below:
| ip/v1/2 = +k1v1/2 + k2 | (12) |
A relationship can be established between v1/2 vs. ip/v1/2 for a prominent anodic peak at −0.65 V as shown in Fig. 9c. From the slope and y-axis intercept of this curve, the value of variables k1 and k2 can be determined, which can further be used to determine the quantitative contribution of capacitive currents, and that of diffusion-controlled current in the total current at a specific voltage and sweep rate using eqn (11). In Fig. 9d, the aqua blue shaded region (k1v) shows the contribution of capacitive currents (fast kinetics), and the light green area (k2v1/2) represents the contribution of diffusive currents (slow kinetics) to the total current. Here, it can be observed that ∼77% of the total current for NPFG-0.3 electrode at the sweep rate of 5 mV s−1 is due to capacitive-controlled storage mechanism, which certainly demonstrates the dominance of fast kinetics even at a low (5 mV s−1) scan rate value. Thus, the results indicate that the energy storage capacity of NPFG-0.3 is controlled by the EDLC and faradaic pseudocapacitance on the surface, which is beneficial to the achievement of good rate capability.
Electrochemical performance of symmetrical supercapacitor
For the sake of the evaluation, the practical application of the NPFG-0.3 electrode, we made a symmetric coin-type cell (CR2032) supercapacitor using two NPFG-0.3 electrodes of identical weight separated by a glass microfiber membrane, and electrochemical measurements are conducted in 6 M KOH electrolyte. Fig. 10a depicts the schematic diagram of a symmetric supercapacitor device in which the K+ ions well-performed charge storage phenomenon. Fig. 10b manifests the symmetric device's CV profiles at the scan rates of 5, 10, 15, 25, 50, and 100 mV s−1. We can observe approximate identical rectangular shape CV curves are well maintained. Furthermore, the GCD curves as represented in Fig. 10c retain nearly symmetrical triangular shapes at different current densities of 0.25–10 A g−1. Moreover, the EIS studies on NPFG-0.3/KOH/NPFG-0.3 device shows smaller internal resistance (Rs = 0.54 Ω) and the diameter of the semicircle at the high-frequency region, which represents Rct, is also minimal (Rct = 0.75 Ω), which indicates fast reaction kinetics and excellent electrochemical activity in the supercapacitor (Fig. 10d). Energy and power densities are essential parameters to evaluate the supercapacitors. The as-fabricated symmetrical device exhibits a high energy density (W h kg−1) and power density (W kg−1) by using eqn (2) and (3). As shown in Fig. 10e the device exhibits maximum and minimum energy densities of 24.5 and 21.2 W h kg−1 at power densities of 498.6 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020.5 W kg−1, respectively. The calculated specific capacitance from GCD curve of the device (middle inset Fig. 10e) is 87.6 F g−1 at the current density of 0.25 A g−1. As can be seen, upon increasing the current density up to 10 A g−1, the device's specific capacitance maintains excellent retention (86%) of its initial capacitance value. Moreover, the symmetric device's long cycle performance (Fig. 10f) shows the retention of ∼88.2% with excellent coulombic efficiency of 100% after 10
020.5 W kg−1, respectively. The calculated specific capacitance from GCD curve of the device (middle inset Fig. 10e) is 87.6 F g−1 at the current density of 0.25 A g−1. As can be seen, upon increasing the current density up to 10 A g−1, the device's specific capacitance maintains excellent retention (86%) of its initial capacitance value. Moreover, the symmetric device's long cycle performance (Fig. 10f) shows the retention of ∼88.2% with excellent coulombic efficiency of 100% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 successive cycles. The excellent cyclability of the device can be ascribed to the electrochemical stability of the active electrode material.
000 successive cycles. The excellent cyclability of the device can be ascribed to the electrochemical stability of the active electrode material.
The middle inset Fig. 10f depicts the Nyquist plots of the device during 1st, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000th long cycles imply that the Warburg region in the middle frequency region is increasing with repeated cycles. Nyquist plot of the device and inset showing the corresponding equivalent circuit diagram after 10
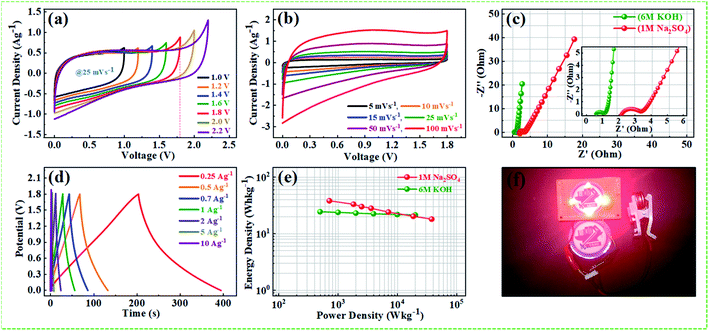
000th long cycles imply that the Warburg region in the middle frequency region is increasing with repeated cycles. Nyquist plot of the device and inset showing the corresponding equivalent circuit diagram after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000th charge/discharge long cycles are depicted in Fig. S9.† The solution resistance and the charge-transfer resistance of the device are increased after long cycling test from (Rs = 0.54 Ω) to (Rct = 0.75 Ω), and (Rs = 1.31 Ω) to (Rct = 4.2 Ω), respectively, which can be ascribed to the hindrance of charge transfer reaction at the electrode/electrolyte interface, and to the increased contact resistance between the NPFG-0.3 flakes and the current collector.68,69 Further, the reduced performance of the device after long cycle test can be attributed to the reduced accessibility of electroactive sites to the ions and to the slight electrolyte reducing during the cycling process. The supercapacitor NPFG-0.3//NPFG-0.3 was further examined in 1 M Na2SO4 aqueous electrolyte and the result is shown in Fig. 11. As mentioned in Fig. 11a, the CV curves maintain rectangular shape even the voltage window reached up to 1.8 V, however it appears a noticeable increase of anodic current when the voltage window up to 2.2 V, which is associated to water splitting. Fig. 11b manifests the symmetric device's CV profiles at the various scan rates in 1.8 V voltage window. We can observe approximate identical rectangular shape CV curves are well maintained. The Nyquist plots of NPFG-0.3//NPFG-0.3 symmetric supercapacitor in different electrolytes are shown in Fig. 11c. The device displays a typical characteristic of a semicircle at high frequency and a nearly vertical line at low frequency, that is related to ideal double-layer charge/discharge behavior. And the values of Rct are 0.6 Ω for KOH electrolyte and 2.03 Ω for Na2SO4 electrolyte. The smaller Rct in KOH electrolyte than that in Na2SO4 electrolyte could be attributed to high conductivity, small ionic radios, and abrupt ionic mobility of KOH electrolyte.70 The diameter of the semicircle in KOH is much smaller than that in Na2SO4, which is related to ionic mobility: OH− > SO42− > K+ > Na+.71 The Nyquist plots in the low-frequency region exhibits perfect electrical double layer capacitive properties. Furthermore, the GCD curves as represented in Fig. 11d retain nearly symmetrical triangular shapes at different current densities of 0.25–10 A g−1. Ragone plots of the NPFG-0.3//NPFG-0.3 symmetric supercapacitor using 6 M KOH and 1 M Na2SO4 as the electrolyte in terms of energy/power densities in different electrolytes are shown in Fig. 11e. The 1 M Na2SO4 electrolyte affords a maximum energy density of 38 W h kg−1 at a power density of 716 W kg−1, and it still maintains 18 W h kg−1 at 19
000th charge/discharge long cycles are depicted in Fig. S9.† The solution resistance and the charge-transfer resistance of the device are increased after long cycling test from (Rs = 0.54 Ω) to (Rct = 0.75 Ω), and (Rs = 1.31 Ω) to (Rct = 4.2 Ω), respectively, which can be ascribed to the hindrance of charge transfer reaction at the electrode/electrolyte interface, and to the increased contact resistance between the NPFG-0.3 flakes and the current collector.68,69 Further, the reduced performance of the device after long cycle test can be attributed to the reduced accessibility of electroactive sites to the ions and to the slight electrolyte reducing during the cycling process. The supercapacitor NPFG-0.3//NPFG-0.3 was further examined in 1 M Na2SO4 aqueous electrolyte and the result is shown in Fig. 11. As mentioned in Fig. 11a, the CV curves maintain rectangular shape even the voltage window reached up to 1.8 V, however it appears a noticeable increase of anodic current when the voltage window up to 2.2 V, which is associated to water splitting. Fig. 11b manifests the symmetric device's CV profiles at the various scan rates in 1.8 V voltage window. We can observe approximate identical rectangular shape CV curves are well maintained. The Nyquist plots of NPFG-0.3//NPFG-0.3 symmetric supercapacitor in different electrolytes are shown in Fig. 11c. The device displays a typical characteristic of a semicircle at high frequency and a nearly vertical line at low frequency, that is related to ideal double-layer charge/discharge behavior. And the values of Rct are 0.6 Ω for KOH electrolyte and 2.03 Ω for Na2SO4 electrolyte. The smaller Rct in KOH electrolyte than that in Na2SO4 electrolyte could be attributed to high conductivity, small ionic radios, and abrupt ionic mobility of KOH electrolyte.70 The diameter of the semicircle in KOH is much smaller than that in Na2SO4, which is related to ionic mobility: OH− > SO42− > K+ > Na+.71 The Nyquist plots in the low-frequency region exhibits perfect electrical double layer capacitive properties. Furthermore, the GCD curves as represented in Fig. 11d retain nearly symmetrical triangular shapes at different current densities of 0.25–10 A g−1. Ragone plots of the NPFG-0.3//NPFG-0.3 symmetric supercapacitor using 6 M KOH and 1 M Na2SO4 as the electrolyte in terms of energy/power densities in different electrolytes are shown in Fig. 11e. The 1 M Na2SO4 electrolyte affords a maximum energy density of 38 W h kg−1 at a power density of 716 W kg−1, and it still maintains 18 W h kg−1 at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 646 W kg−1. In 6 M KOH electrolyte, a high energy density of 24 W h kg−1 is achieved at a power density of 499 W kg−1. Our fabricated NPFG-0.3//NPFG-0.3 symmetric supercapacitor devices can light up four red LEDs in series as shown in Fig. 11f. The superior performance of the as-prepared NPFG-0.3 electrode can be ascribed to the synergistic effect of the N, P, and F heteroatom doping modification with hierarchical porous 3D cross-linked structure. The specific factors can be listed as follows: (1) N and F co-doping can create a large number of defects and thus provide more active sites for increasing the specific surface area, leading to improved specific capacitance. Also, N, F co-doping can offer more electrons to the π-conjugated system of rGO and therefore enhance the electronic conductivity of the material, resulting in the enhanced rate capability. (2) Phytic acid (PA) as the intercalator, the optimized amount can effectively overcome the aggregation and re-stack between rGO sheets and increase the specific surface, contributing to the enhancement of capacitive performance. Additionally, the material's hierarchical porous structure can not only afford more efficient paths for the rapid penetration of electrolyte ions and transport of electrons, which lead to the enhancement of rate performance but also accommodate the volume change in process, which results in the enhancement of cycling stability.
646 W kg−1. In 6 M KOH electrolyte, a high energy density of 24 W h kg−1 is achieved at a power density of 499 W kg−1. Our fabricated NPFG-0.3//NPFG-0.3 symmetric supercapacitor devices can light up four red LEDs in series as shown in Fig. 11f. The superior performance of the as-prepared NPFG-0.3 electrode can be ascribed to the synergistic effect of the N, P, and F heteroatom doping modification with hierarchical porous 3D cross-linked structure. The specific factors can be listed as follows: (1) N and F co-doping can create a large number of defects and thus provide more active sites for increasing the specific surface area, leading to improved specific capacitance. Also, N, F co-doping can offer more electrons to the π-conjugated system of rGO and therefore enhance the electronic conductivity of the material, resulting in the enhanced rate capability. (2) Phytic acid (PA) as the intercalator, the optimized amount can effectively overcome the aggregation and re-stack between rGO sheets and increase the specific surface, contributing to the enhancement of capacitive performance. Additionally, the material's hierarchical porous structure can not only afford more efficient paths for the rapid penetration of electrolyte ions and transport of electrons, which lead to the enhancement of rate performance but also accommodate the volume change in process, which results in the enhancement of cycling stability.
Conclusions
In summary, present work demonstrates the successful synthesis of heteroatoms (nitrogen, phosphorous, and fluorine) co-doped reduced graphene oxide using a simple, cost-effective, and ecofriendly hydrothermal functionalization approach. Several characterization techniques such as XRD, XPS, contact angle analysis, BET, FESEM, and HRTEM with EDX were employed to understand the structural, morphological, and elemental analysis of as-synthesized samples. The nitrogen, phosphorous, and fluorine co-doped graphene (NPFG-0.3) synthesized with the optimum amount of pentafluoropyridine and phytic acid (PA) demonstrates notably enhanced specific capacitance (319 F g−1 at 0.5 A g−1), excellent durability with 99.8% retention after 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 long cycle test, short relaxation time constant (∼28.4 ms), the higher diffusion coefficient of electrolytic cations (Dk+ = 8.8261 × 10−9 cm2 s−1). By the DFT results, the N, P, and F replace with C atoms within rGO atomic model, accompany with KOH molecule, could increase the Gibbs free energy (GT) of lattice from −673.79 eV to a more considerable value as −643.26 eV. According to our calculation and experiment results, the electrochemical performance of our best synthesized sample depends on the electrochemical reactivity while such electrochemical reactivity depends on the Gibbs free energy (GT) within the atomic level. The symmetric coin cell supercapacitor using NPFG-0.3 as both anode and cathode exhibits maximum energy density of 38 W h kg−1 at the power density of 716 W h kg−1 in 1 M Na2SO4 aqueous electrolyte and 24 W h kg−1 at the power density of 499 W h kg−1 in 6 M KOH aqueous electrolyte, respectively. Our symmetric cell demonstrates excellent retention of 88.2%, with coulombic efficiency of ∼100% after 10
000 long cycle test, short relaxation time constant (∼28.4 ms), the higher diffusion coefficient of electrolytic cations (Dk+ = 8.8261 × 10−9 cm2 s−1). By the DFT results, the N, P, and F replace with C atoms within rGO atomic model, accompany with KOH molecule, could increase the Gibbs free energy (GT) of lattice from −673.79 eV to a more considerable value as −643.26 eV. According to our calculation and experiment results, the electrochemical performance of our best synthesized sample depends on the electrochemical reactivity while such electrochemical reactivity depends on the Gibbs free energy (GT) within the atomic level. The symmetric coin cell supercapacitor using NPFG-0.3 as both anode and cathode exhibits maximum energy density of 38 W h kg−1 at the power density of 716 W h kg−1 in 1 M Na2SO4 aqueous electrolyte and 24 W h kg−1 at the power density of 499 W h kg−1 in 6 M KOH aqueous electrolyte, respectively. Our symmetric cell demonstrates excellent retention of 88.2%, with coulombic efficiency of ∼100% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 successive cycles at 1 A g−1. The improved supercapacitor performances stem from the synergistic effect of the unique structures. The covalently bonded pentafluoropyridine offers more electrons to the π-conjugated system of rGO and generates seamless ohmic contact between functional redox groups, therefore, enhance the electronic conductivity of the material resulting in the enhanced rate capability. Phytic acid (PA) prevents the aggregation of graphene sheets, increases available active sites. We believe that our current work can offer a promising strategy for designing and developing novel and high-performance 3D cross-linked heteroatom doped hydrogels for practical applications and appropriate for designing high capacitive energy storage (supercapacitors or Li-batteries) devices.
000 successive cycles at 1 A g−1. The improved supercapacitor performances stem from the synergistic effect of the unique structures. The covalently bonded pentafluoropyridine offers more electrons to the π-conjugated system of rGO and generates seamless ohmic contact between functional redox groups, therefore, enhance the electronic conductivity of the material resulting in the enhanced rate capability. Phytic acid (PA) prevents the aggregation of graphene sheets, increases available active sites. We believe that our current work can offer a promising strategy for designing and developing novel and high-performance 3D cross-linked heteroatom doped hydrogels for practical applications and appropriate for designing high capacitive energy storage (supercapacitors or Li-batteries) devices.
Author contributions
AK prepared the materials and drafted the manuscript. CST and TTY designed the work. AK, NK, PS, YS, EWH, TW, KHW and JL carried out the sample's structural analysis and electrochemical performance test. TTY approved the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank staff members of the Nano Facility Center of National Yang Ming Chiao Tung University for their kind support. This work financially supported by Ministry of Science and Technology of Taiwan under contract no. MOST 110-2636-E-009-020.Notes and references
- H. An, Y. Li, Y. Gao, C. Cao, J. Han, Y. Feng and W. Feng, Carbon, 2017, 116, 338–346 CrossRef CAS.
- G. Wang, L. Zhang and J. Zhang, Chem. Soc. Rev., 2012, 41, 797–828 RSC.
- K. Xia, Z. Huang, L. Zheng, B. Han, Q. Gao, C. Zhou, H. Wang and J. Wu, J. Power Sources, 2017, 365, 380–388 CrossRef CAS.
- Y. Huang, J. Liang and Y. Chen, Small, 2012, 8, 1805–1834 CrossRef CAS.
- J. Yan, Q. Wang, T. Wei and Z. Fan, Adv. Energy Mater., 2013, 4, 1300816 CrossRef.
- C. Singh, A. K. Mishra and A. Paul, J. Mater. Chem. A, 2015, 3, 18557–18563 RSC.
- C. Singh, S. Nikhil, A. Jana, A. K. Mishra and A. Paul, Chem. Commun., 2016, 52, 12661–12664 RSC.
- A. Borenstein, O. Hanna, R. Attias, S. Luski, T. Brousse and D. Aurbach, J. Mater. Chem. A, 2017, 5, 12653–12672 RSC.
- V. Thirumal, A. Pandurangan, R. Jayavel and R. Ilangovan, Synth. Met., 2016, 220, 524–532 CrossRef CAS.
- J. Lee, J. Choi, D. Kang, Y. Myung, S. M. Lee, H. J. Kim, Y. J. Ko, S. K. Kim and S. U. Son, ACS Sustainable Chem. Eng., 2018, 6, 3525–3532 CrossRef CAS.
- H. J. Denisa, A. M. Puziy, O. I. Poddubnaya, S. G. Fabian, J. M. D. Tascón and G. Q. Lu, J. Am. Chem. Soc., 2009, 131, 5026–5027 CrossRef PubMed.
- J. Lee, S. Noh, N. D. Pham and J. H. Shim, Electrochim. Acta, 2019, 313, 1–9 CrossRef CAS.
- T. Wang, X. Zang, X. Wang, X. Gu, Q. Shao and N. Cao, Energy Storage Mater., 2020, 30, 367–384 CrossRef.
- X. Chen, X. Duan, W. DaOh, P. H. Zhang, C. T. Guan, Y. A. Zhu and T. T. Lim, Appl. Catal., B, 2019, 253, 419–432 CrossRef CAS.
- Z. Lu, Y. Chen, Z. Liu, A. Li, D. Sun and K. Zhuo, RSC Adv., 2018, 8, 18966–18971 RSC.
- X. Sun, P. Cheng, H. Wang, H. Xu, L. Dang, Z. Liu and Z. Lei, Carbon, 2015, 92, 1–10 CrossRef CAS.
- N. Subramanian and B. Viswanathan, RSC Adv., 2015, 5, 63000–63011 RSC.
- M. Mirzaeian, Q. Abbas, D. Gibson and M. Mazur, Energy, 2019, 173, 809–819 CrossRef CAS.
- W. Na, J. Jun, J. W. Park, G. Lee and J. Jang, J. Mater. Chem. A, 2017, 5, 17379–17387 RSC.
- Y. Ma, D. Wu, T. Wang and D. Jia, ACS Appl. Energy Mater., 2020, 3, 957–969 CrossRef CAS.
- X. Song, Y. Chen, M. Rong, Z. Xie, T. Zhao, Y. Wang, X. Chen and O. S. Wolfbeis, Angew. Chem., Int. Ed., 2016, 55, 3936–3941 CrossRef CAS.
- D. Marcano, D. Kosynkin and J. Berlin, ACS Nano, 2010, 4, 4806–4814 CrossRef CAS.
- N. Kanaujiya, N. Kumar, A. K. Srivastava, Y. Sharma and G. D. Varma, J. Electroanal. Chem., 2018, 824, 226–237 CrossRef CAS.
- C. Wei, W. He, X. Zhang, S. Liu, C. Jin, S. Liu and Z. Huang, RSC Adv., 2015, 5, 28662–28669 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Yuan, L. Yang, L. Hou, J. Li, Y. Sun, X. Zhang, L. Shen, X. Lu, S. Xiong and X. W. Lou, Adv. Funct. Mater., 2012, 22, 2560–2566 CrossRef CAS.
- J. Che, L. Shen and Y. Xiao, J. Mater. Chem., 2010, 20, 1722 RSC.
- Y. Xu, Z. Lin, X. Huang, Y. Wang, Y. Huang and X. Duan, Adv. Mater., 2013, 25, 5779–5784 CrossRef CAS PubMed.
- B. Song, C. Sizemore, L. Li, X. Huang, Z. Lin, K. S. Moon and C. P. Wong, J. Mater. Chem. A, 2015, 3, 21789–21796 RSC.
- T. Wang, L. X. Wang, D. L. Wu, W. Xia and D. Z. Jia, Sci. Rep., 2015, 5, 1–9 Search PubMed.
- A. Kumar, N. Kumar, Y. Sharma, J. Leu and T. Y. Tseng, Nanoscale Res. Lett., 2019, 14, 1–17 CrossRef CAS.
- X. Gao and X. S. Tang, Carbon, 2014, 76, 133–140 CrossRef CAS.
- J. Hu, W. He, S. Qiu, W. Xu, Y. Mai and F. Guo, Appl. Surf. Sci., 2019, 496, 143643 CrossRef CAS.
- G. Du, Q. Bian, J. Zhang and X. Yang, RSC Adv., 2017, 7, 46329–46335 RSC.
- Y. Li, Q. Zhang, J. Zhang, L. Jin, X. Zhao and T. Xu, Sci. Rep., 2015, 5, 1–10 Search PubMed.
- Z. S. Wu, Y. Sun, Y. Z. Tan, S. Yang, X. Feng and K. Müllen, J. Am. Chem. Soc., 2012, 134, 19532–19535 CrossRef CAS PubMed.
- H. An, Y. Li, Y. Feng, Y. Cao, C. Cao, P. Long, S. Li and W. Feng, Chem. Commun., 2018, 54, 2727–2730 RSC.
- X. Wang, Y. Dai, J. Gao, J. Huang, B. Li, C. Fan, J. Yang and X. Liu, ACS Appl. Mater. Interfaces, 2013, 5, 8294–8299 CrossRef CAS.
- S. Zhou, S. D. Sherpa, D. W. Hess and A. Bongiorno, J. Phys. Chem. C, 2014, 118, 26402–26408 CrossRef CAS.
- Y. Sim, S. J. Kim, G. Janani, Y. Chae, S. Surendran, H. Kim, S. Yoo, D. C. Seok, Y. H. Jung, C. Jeon, J. Moon and U. Sim, Appl. Surf. Sci., 2020, 507, 145157 CrossRef CAS.
- M. Karuppannan, Y. Kim, Y. E. Sung and O. J. Kwon, J. Mater. Chem. A, 2018, 6, 7522–7531 RSC.
- D. Xue, D. Zhu, W. Xiong, T. Cao, Z. Wang, Y. Lv, L. Li, M. Liu and L. Gan, ACS Sustainable Chem. Eng., 2019, 7, 7024–7034 CrossRef CAS.
- L. Sun, G. Song, Y. Sun, Q. Fu and C. Pan, Electrochim. Acta, 2020, 333, 135496 CrossRef CAS.
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. W. Sing, Pure Appl. Chem., 2015, 87, 1051–1069 CAS.
- M. Thommes and K. A. Cychosz, Adsorption, 2014, 20, 233–250 CrossRef CAS.
- T. Jin, J. Chen, C. Wang, Y. Qian and L. Lu, J. Mater. Sci., 2020, 55, 12103–12113 CrossRef CAS.
- X. Zhou, T. Meng, F. Yi, D. Shu, D. Han, Z. Zhu, A. Gao, C. Liu, X. Li, K. Yang and H. Yi, J. Power Sources, 2020, 475, 228554 CrossRef CAS.
- T. He, X. Meng, J. Nie, Y. Tong and K. Cai, ACS Appl. Mater. Interfaces, 2016, 8, 13865–13870 CrossRef CAS PubMed.
- X. Q. Ma, Y. Q. Shan, M. Y. Wang, Z. A. Alothman, Z. X. Xu, P. G. Duan, J. Zhou and R. Luque, ACS Sustainable Chem. Eng., 2020, 8, 18810–18815 CrossRef CAS.
- Y. Zhang, G. Wen, S. Fan, Y. Chu, S. Li, B. Xu and J. Zhang, J. Power Sources, 2019, 435, 226799 CrossRef CAS.
- H. An, Y. Li, P. Long, Y. Gao, C. Qin, C. Cao, Y. Feng and W. Feng, J. Power Sources, 2016, 312, 146–155 CrossRef CAS.
- L. Sun, L. Wang, C. Tian, T. Tan, Y. Xie, K. Shi, M. Li and H. Fu, RSC Adv., 2012, 2, 4498–4506 RSC.
- Y. Yuanyuan, L. Ruiyi, L. Zaijun, L. Junkang, G. Zhiguo and W. Guangli, Electrochim. Acta, 2014, 125, 330–337 CrossRef.
- N. Kumar, M. Singh, A. Kumar, T. Y. Tseng and Y. Sharma, ACS Appl. Energy Mater., 2020, 3, 2450–2464 CrossRef CAS.
- M. Winter and R. J. Brodd, Chem. Rev., 2004, 104, 4245–4269 CrossRef CAS.
- B. E. Conway, Electrochemical supercapacitors: scientific fundamentals and technological applications, New York, 1999 Search PubMed.
- N. Kumar, A. Kumar, G. M. Huang, W. W. Wu and T. Y. Tseng, Appl. Surf. Sci., 2018, 433, 1100–1112 CrossRef CAS.
- Y. Li, D. Chen and R. A. Caruso, J. Mater. Chem. C, 2016, 4, 10500–10508 RSC.
- G. Xu, C. Zheng, Q. Zhang, J. Huang, M. Zhao, J. Nie, X. Wang and F. Wei, Nano Res., 2011, 4, 870–881 CrossRef CAS.
- J. Yan, L. Miao, H. Duan, D. Zhu, Y. Lv, W. Xiong, L. Li, L. Gan and M. Liu, Electrochim. Acta, 2020, 358, 136899 CrossRef CAS.
- P. L. Taberna, P. Simon and J. F. Fauvarque, J. Electrochem. Soc., 2003, 150, A292 CrossRef CAS.
- L. Pan, G. Yu, D. Zhai, H. R. Lee, W. Zhao, N. Liu, H. Wang, B. C. K. Tee, Y. Shi, Y. Cui and Z. Bao, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 9287–9292 CrossRef CAS.
- H. Jin, X. Feng, J. Li, M. Li, Y. Xia, Y. Yuan, C. Yang, B. Dai, Z. Lin, J. Wang, J. Lu and S. Wang, Angew. Chem., Int. Ed., 2019, 58, 2397–2401 CrossRef CAS.
- J. Chen, H. Wei, H. Chen, W. Yao, H. Lin and S. Han, Electrochim. Acta, 2018, 271, 49–57 CrossRef CAS.
- Y. Lu, J. Liang, S. Deng, Q. He, S. Deng, Y. Hu and D. Wang, Nano Energy, 2019, 65, 103993 CrossRef CAS.
- T. Liu, Z. Zhou, Y. Guo, D. Guo and G. Liu, Nat. Commun., 2019, 10, 1–10 CrossRef.
- X. Guo, T. Wang, T. X. Zheng, C. Xu, J. Zhang, Y. X. Zhang, X. Y. Liu and F. Dong, J. Mater. Chem. A, 2018, 6, 24717–24727 RSC.
- J. G. Kang, Y. D. Ko, J. G. Park and D. W. Kim, Nanoscale Res. Lett., 2008, 3, 390–394 CrossRef CAS.
- M. Arunkumar and A. Paul, ACS Omega, 2017, 11, 8039–8050 Search PubMed.
- X. Zhang, H. Li, B. Qin, Q. Wang, X. Xing, D. Yang, L. Jin and Q. Cao, J. Mater. Chem. A, 2019, 7, 3298–3306 RSC.
- X. Zhang, X. Wang, L. Jiang, H. Wu, C. Wu and J. Su, J. Power Sources, 2012, 216, 290–296 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra03911c |
| This journal is © The Royal Society of Chemistry 2021 |