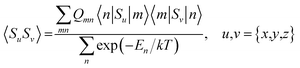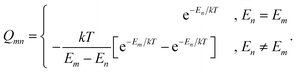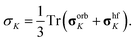Open Access Article
Open Access ArticleProton-detected fast-magic-angle spinning NMR of paramagnetic inorganic solids†
Jan Blahut a,
Ladislav Benda
a,
Ladislav Benda a,
Arthur L. Lejeune
a,
Arthur L. Lejeune ab,
Kevin J. Sandersa,
Benjamin Burcherb,
Erwann Jeanneau
ab,
Kevin J. Sandersa,
Benjamin Burcherb,
Erwann Jeanneau c,
David Proriol
c,
David Proriol b,
Leonor Catitab,
Pierre-Alain R. Breuil
b,
Leonor Catitab,
Pierre-Alain R. Breuil b,
Anne-Agathe Quoineaudb,
Andrew J. Pell
b,
Anne-Agathe Quoineaudb,
Andrew J. Pell ad and
Guido Pintacuda
ad and
Guido Pintacuda *a
*a
aUniversité de Lyon, Centre de RMN à Très Hauts Champs de Lyon (UMR 5082 – CNRS, ENS Lyon, UCB Lyon 1), 5 rue de la Doua, 69100 Villeurbanne, France. E-mail: guido.pintacuda@ens-lyon.fr
bIFP Energies Nouvelles, Rond-point de l'échangeur de Solaize, 69360 Solaize, France
cUniversité de Lyon, Centre de Diffractométrie Henri Longchambon (UCB Lyon 1), 5 rue de la Doua, 69100 Villeurbanne, France
dStockholm University, Department of Materials and Environmental Chemistry, Svante Arrhenius väg 16C, SE-106 91 Stockholm, Sweden
First published on 29th September 2021
Abstract
Fast (60 kHz) magic angle spinning solid-state NMR allows very sensitive proton detection in highly paramagnetic organometallic powders. We showcase this technique with the complete assignment of 1H and 13C resonances in a high-spin Fe(II) polymerisation catalyst with less than 2 mg of sample at natural abundance.
Introduction
Solid-state NMR has developed as a generally applicable characterization technique, capable of complementing X-ray crystallography, solution NMR and electron microscopy on a wide range of samples in chemistry, materials science and biology.1–3 1H-NMR spectroscopy is the most obvious avenue to fast routine characterization of chemical compounds and biomolecules due to the ubiquitous presence of 1H nuclei, their large gyromagnetic ratio γH and high natural abundance. Nonetheless, these same properties lead to a strong dipolar coupling network which prevents identification of the different 1H sites and limits the utility of the technique. In the case of paramagnetic samples, the hyperfine interaction of the high-γ 1H nuclei with the unpaired electrons of the paramagnetic center(s) further exacerbates the problem of acquisition and interpretation of the spectra.4A major step forward in solid-state NMR was the development of very fast magic-angle spinning (MAS) probes. Specifically, fast MAS weakens the 1H dipolar coupling networks and allows the direct detection of proton spectra, opening the door for the characterization of hydrogen environments.5 MAS rates of 60 kHz and above have allowed accelerated data acquisition for the atomic-level description of structure and dynamics of insoluble, non-crystalline or poorly-crystalline samples, from inorganic matrices6 to viral capsids7,8 and membrane proteins in lipid bilayers.9 The improvements associated with fast MAS are particularly evident in samples of paramagnetic molecules,10–12 where sensitivity and resolution experience a spectacular enhancement as compared to slower rates, allowing efficient detection of previously unobservable nuclei in close proximity to a metal center.13–15 Despite this impressive progress, however, the advantages of 1H detection remain largely unexplored on highly paramagnetic substances. In fully-protonated paramagnetic molecules, the massive paramagnetic shift anisotropies add to the large homonuclear dipolar couplings so that a significant number of sidebands are observed for some or all of the resonances even at very large spinning rates. Despite notable proofs of concept highlighting the possibility of the detection of 1H resonances,16–20 the resulting spectra failed to provide a sufficient level of detail necessary for the identification of individual 1H sites. The characterization of paramagnetic organometallic solids has therefore been mainly based on 13C detection techniques,21–23 for which sensitivity is optimal in larger MAS rotors (e.g. 1.9–2.5 mm) at intermediate spinning frequencies (e.g. 30–40 kHz). The low natural abundance of 13C causes a problem in particular in chemistry, where isotopic enrichment is not straightforward.
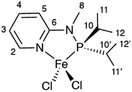
Here, we show that, by using MAS rates of 60 kHz, in combination with tailored RF irradiation schemes and modern computational approaches, it is possible to record and interpret resolved 1H NMR shifts in a powdered sample of a paramagnetic organometallic complex. Specifically, we characterize a tetracoordinated 14-valence-electron high-spin (S = 2) Fe(II) complex (1, Scheme 1), a newly-synthetized catalyst for unsaturated compound transformations such as olefin oligomerization and polymerization.
Experimental
Sample preparation
The ligand [N-(diisopropylphosphino)-N-methylpyridin-2-amine (py-NMe-PiPr2)] in compound 1 was synthetized as described by Gambarotta's group24 with yield of 86%. As a Fe(II) source we used FeCl2(THF)1.5 which reacts with 1.05 eq. of py-NMe-PiPr2 in toluene forming 1 in 91% yield as a white powder which was characterized by standard methods including single-crystal X-ray diffraction (see ESI† for details). The obtained XRD unit cell contains eight molecules, two molecules per asymmetric unit.Solid-state NMR
Solid-state NMR experiments were performed on a Bruker Avance III spectrometer operating at a magnetic field strength of 11.7 T (corresponding to 1H and 13C Larmor frequency of 500.1 and 125.7 MHz) using either a 2.5 mm or a 1.3 mm MAS probe. The sample was packed under inert atmosphere into either a 2.5 mm or a 1.3 mm zirconia rotor and sealed with Vespel rotor caps (estimated sample volume 10 and 2 μL, respectively). In order to improve the seal of the 1.3 mm rotor, FKM inserts were placed between the sample and the caps. Experiments were performed at 31.25 kHz (2.5 mm) or 60 kHz (1.3 mm) MAS (corresponding to a 32 μs and a 16.67 μs rotor period, respectively). The stator was cooled to a temperature of approximately 250 K (31.25 kHz MAS, 3.2 mm) and 260 K (60 kHz MAS, 1.3 mm) using a Bruker BCU XTreme cooling unit, which corresponds to 311.7 ± 0.5 K inside the sample due to frictional heating for the 1.3 mm rotor and similar temperature for the 2.5 mm rotor, as calibrated using δ(207Pb) in crystalline PbNO3,25 (see ESI†). Temperature variations within the sample were estimated to ±5 K by the same method. Nitrogen gas dried to a dew point of −80 °C was used for sample rotation and temperature regulation.For experiments in the 2.5 mm and the 1.3 mm probe, the π/2 1H pulse lengths used were 1.23 μs at 200 W and 1.1 μs at 30 W, corresponding to RF field strengths of 109 kHz and 227 kHz, respectively. Due to the large span of chemical shifts, short high-powered adiabatic tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h/tan pulses (SHAPs)26 were used to refocus the chemical shift evolution and invert nuclear spin populations. The adiabatic pulses swept through 5 MHz and were 33.33 μs and 32 μs long, with RF field strengths of 227 kHz and 200 kHz for 31.25 kHz MAS in the 2.5 mm rotor and 60 kHz MAS in the 1.3 mm rotor, respectively. Spectra were acquired with a rotor-synchronized double adiabatic echo experiment with a total double-echo time of 66.68 μs at 60 kHz MAS and 128 μs at 31.25 kHz MAS (four rotor periods). The 1H adiabatic magic angle turning (aMAT)14 experiment was performed using six adiabatic pulses.
h/tan pulses (SHAPs)26 were used to refocus the chemical shift evolution and invert nuclear spin populations. The adiabatic pulses swept through 5 MHz and were 33.33 μs and 32 μs long, with RF field strengths of 227 kHz and 200 kHz for 31.25 kHz MAS in the 2.5 mm rotor and 60 kHz MAS in the 1.3 mm rotor, respectively. Spectra were acquired with a rotor-synchronized double adiabatic echo experiment with a total double-echo time of 66.68 μs at 60 kHz MAS and 128 μs at 31.25 kHz MAS (four rotor periods). The 1H adiabatic magic angle turning (aMAT)14 experiment was performed using six adiabatic pulses.
The 13C-detected TEDOR was conducted as in ref. 11 (Fig. 3A), while the new 1H-detected HSQC-TEDOR follows the scheme illustrated in Fig. 3B (for details sequence Fig. S2A and B†).
Due to the requirement of a rotor-synchronized sampling of the indirect dimension (f1), the spectral width in the indirect 13C dimension is limited by the MAS frequency. In the states-TPPI f1 acquisition mode, this suppresses the spinning sidebands and removes line-shape distortions,27 but also produces folding of signals resonating outside this spectral window. The position of the folded resonances was identified by recording a second HSQC-TEDOR spectrum at 58 kHz MAS, i.e., with a 58 kHz 13C spectral widths in f1. Between the two experiments, any signal folded n-times is shifted by (n × ΔSW) Hz in the indirect dimension, where ΔSW = 2 kHz is the difference in spectral width between the two experiments. Here, a shift of 2 kHz and 4 kHz for the two C3 and C10 signals appearing respectively at δ(1H) = 44 and 265 ppm allowed to deduce the isotropic δ(13C) shifts of 570 and 1067 ppm, respectively, as illustrated in Fig. S3.†
Quantum chemistry calculations
The XRD structure of complex 1 was subjected to optimization of hydrogen atom positions while keeping all other atoms fixed, employing the hybrid Perdew–Burke–Ernzerhof functional PBE0,28,29 Grimme's D3 dispersion correction30 with Becke–Johnson damping,31 and a locally dense Gaussian basis set using def2-TZVP for Fe and def2-SVP for main group elements32 as implemented in the TURBOMOLE code.33 The NMR reference compound tetramethylsilane (TMS) was fully optimized on the same level. All DFT calculations for the Fe(II) complex 1 were done for a quintet ground state.Electron paramagnetic resonance (EPR) g- and D-tensors were obtained for the hydrogen-optimized XRD structure of complex 1, applying a strongly contracted variant of the N-electron valence-state perturbation theory of the second order (NEVPT2)34 to a state-averaged complete-active-space self-consistent-field reference wave-function35,36 with six electrons in five active 3d-orbitals of Fe(II) (SA-CASSCF(6,5)) as implemented in ORCA.37 The locally dense basis used in the DFT structure optimizations was enhanced with diffuse functions optimized for molecular property calculations38 thus employing def2-TZVPD and def2-SVPD bases for Fe and main group elements, respectively. Fermi-contact and spin-dipolar terms of EPR hyperfine coupling tensors for the 1H and 13C nuclei were calculated using a series of hybrid PBE functionals with the admixture of Hartree–Fock exchange ranging from 10 to 40%. GIAO orbital shielding tensors39 were calculated on the PBE0 level with GAUSSIAN.40 The hyperfine coupling and orbital shielding calculations employed the def2-TZVPD and IGLO-III41 atomic bases for Fe and main group elements, respectively. Spin–orbit terms of hyperfine coupling were calculated for all 1H and 13C nuclei using non-hybrid PBE functional and IGLO-II + def2-TZVPD (Fe) basis set. The associated paramagnetic NMR shift corrections were found negligible (Fig. S5,† panel D).
Paramagnetic NMR shift calculations
Hyperfine shielding tensors σhfK were calculated according to the theory of Kurland & McGarvey42 in its recent formulation by Vaara et al.43 where the hyperfine shielding tensor is expressed in terms of EPR property tensors,
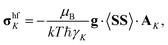 | (1) |
Isotropic paramagnetic NMR shielding was obtained as the isotropic value of the total (orbital plus hyperfine) shielding tensor,
Finally, paramagnetic NMR shifts were calculated as δK = σrefK − σK where the values of calculated reference shielding σrefK in TMS were 31.6 and 185.7 ppm for 1H and 13C nuclei, respectively.44 Intermolecular pseudo-contact shifts (PCS) in molecular crystal of complex 1 were included by periodically extending the XRD unit cell and collecting contributions from all paramagnetic Fe(II) centers within 40 Å from the central Fe(II) ion (645 contributions to each NMR shift).
Individual PCS contributions δpcK,i were calculated with a classical dipolar approximation
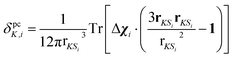 | (2) |
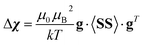 | (3) |
Results and discussion
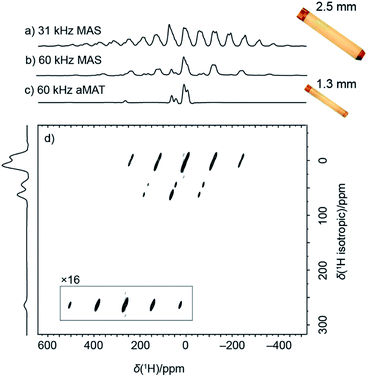
Fig. 1a shows a 1H spin–echo spectrum acquired under standard conditions for 13C detection, namely moderately fast MAS rate of 31.25 kHz, achievable with a 2.5 mm rotor. Due to the large anisotropy of the paramagnetic 1H shifts and of the 1H–1H dipolar couplings, the spectrum consists of broad isotropic resonances overlapping with spinning sidebands. The overlap of isotropic signals with spinning side bands is partially removed by spinning the sample at 60 kHz MAS in a smaller 1.3 mm rotor (Fig. 1b). Fast MAS suppresses the intensity and number of spinning sidebands, concentrating more intensity in the center band, and at the same time, allows to reduce the duration of the spin–echo required for the undistorted acquisition of the large spectrum.Altogether, in addition to the resolution improvement, this produces a sensitivity increase. Interestingly here, the signal intensity of the center-band signals is conserved despite a five-fold smaller sample volume (signal-to-noise ratio normalized by square root of number of scans is 16.7 and 14.9 for 2.5 mm and 1.3 mm rotors respectively, for the dominant center band at 10 ppm).
An additional effort is however still needed for the unambiguous identification of the individual isotropic 1H resonances. This is provided by a 2D sideband separation experiment such as the adiabatic Magic Angle Turning (aMAT) sequence,14 which uses a train of adiabatic refocusing pulses46 with unique timings in order to result in pure isotropic evolution in the indirect dimension. The experiment, originally developed for lower-γ nuclei in the context of energy storage materials,47–50 achieves a 2D spectrum correlating pure isotropic to anisotropic frequencies (Fig. 1d), with a projection along the indirect dimension (Fig. 1c) featuring greatly enhanced spectral resolution. Only 54 minutes were required for the acquisition of such correlation, and notably, despite linewidths of 5 to 9 kHz, several well-resolved resonances could be identified, distributed over a broad spectral range between 300 and −25 ppm.
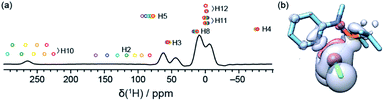
These resonances can be interpreted on the basis of the paramagnetic shifts predicted from the crystal structure of 1. Rigorous quantum chemistry prediction of paramagnetic shifts including the effects of spin–orbit coupling has been enabled by recent theory developments within the Kurland–McGarvey framework.42,43,51 Paramagnetic shifts are calculated with an uncertainty associated with the problem of density functional theory (DFT) with reliably quantifying contact hyperfine interactions.52 Adjusting the admixture of Hartree–Fock exchange (HFX) in hybrid DFT calculations offers a means to probe this uncertainty.53–56 In Fig. 2a, colored circles correspond to the shifts calculated with hybrid PBE functional with HFX percentage ranging from 10 to 40%. By comparing experimental 1H spectrum and predictions, some resonances (H3, H5, H10) can be readily assigned within the confidence intervals provided by the set of multiple-level calculations. Note that the predicted range of shifts is very narrow for some resonances (H8, H11, and H12), which allows a tentative assignment despite the crowding and overlap in that region. This result already demonstrates the possibility of an atomic-level characterization of such challenging samples at natural abundance.
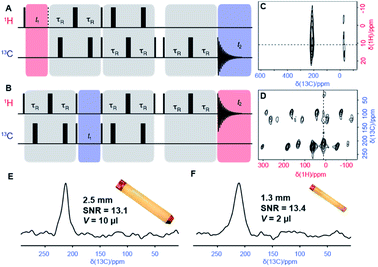 | ||
| Fig. 3 (A and B) Pulse sequences of the two-dimensional TEDOR experiment for correlating nearby 1H and 13C nuclei. The sequence in (A) is designed for 13C detection and referred to as TEDOR. It consists of a 1H excitation pulse followed by t1 evolution and a first recoupling block, then after a magnetization transfer, a second recoupling block is applied to refocus observable 13C coherences. A z-filtered echoed detection is used as described by Kervern et al.11 The 1H detected experiment is performed using the sequence shown in (B), and referred to as HSQC-TEDOR. The 13C evolution period is interleaved with two REDOR blocks used to refocus 1H coherences by reintroducing CH dipolar couplings. 1H coherences are detected after a z-filter and an echo. (C and D) Experimental TEDOR spectra with 13C detection (C), acquired at 31.25 kHz using a 2.5 mm rotor, and with 1H detection (D), acquired at 60 kHz using a 1.3 mm rotor. Both spectra were recorded in an external magnetic field of 11.7 T. Narrow and broad black rectangles denote π/2 and π pulses, respectively. Experimental times were about 13 h and 11 h respectively. (E and F) 13C slices from spectra shown in C and D extracted at δ1H = 11 ppm. | ||
The contrasting scale of response of different atoms to the variation of HFX admixture demonstrates the difficulty of the problem at hand. Propagation of unpaired electron density across several bonds from the metal to the ligand atoms (Fig. 2b) needs to be described very accurately for a reliable calculation of (Fermi-) contact hyperfine coupling. For example, high spin-density regions are visible for hydrogen atoms at position 10, which correspond to the largest 1H shift observed in the experiments. However, in the absence of a benchmark multi-reference ab initio method for hyperfine couplings we are limited to non-benchmarked, inherently single-reference DFT. The contrasting response of hyperfine shifts to the HFX admixture variation is thus not much surprising: unpaired electron density distribution obtained with a generic DFT functional not designed to capture such details may be differently sensitive to HFX admixtures in different parts of the molecule. We also note that, due to the described limitation, randomly trying out different DFT functionals would not be a useful approach. On the contrary, using a single, well-chosen DFT exchange and correlation functional removes one unnecessary degree of freedom that might otherwise obscure the view. PBE exchange and correlation functional used here is arguably the most robust choice for transition metal complexes at large.
Given the spectral overlap of the resonances H8, H11 and H12 (Fig. 2), however, a C–H correlation spectrum would clearly be beneficial for a more extensive characterization. A major step towards assignment of resonances in small to medium-sized paramagnetic complexes was the development of heteronuclear correlations.11 These experiments achieve transfer of polarization from protons to nearby hetero-nuclei via dipolar-recoupling sequences such as Transferred-Echo DOuble Resonance sequence (TEDOR)57 (Fig. 3a) that use short, high-powered RF pulses. Unlike cross-polarization transfer,58 this technique allows efficient magnetization transfer for nuclei exposed to strong paramagnetic shift and fast paramagnetic-induced relaxation.11
Here, the improved resolution at fast MAS enables the implementation of 1H-detected variants of TEDOR. Fig. 3b shows an example of pulse sequence for recording a 2D Dipolar Heteronuclear Single-Quantum Correlation through TEDOR recoupling (HSQC-TEDOR). This pulse sequence provides identical sensitivity to the 13C-detected spectrum acquired at slower MAS even though a five times larger sample volume was used in the latter case. This improvement is ascribed to the shorter recoupling times made possible with faster MAS, which is notably not efficient in the 30 kHz range.19
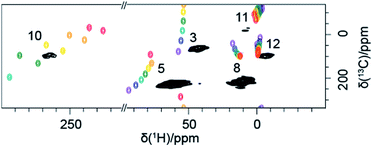
Finally, Fig. 4 shows the 2D H–C correlation spectrum of 1, exhibiting six correlations out of a total of eight H–C pairs (note that the non-symmetrical environment in the molecular crystal of 1 exposes each nucleus to different paramagnetic effects from several metal centres, making the two iPr moieties magnetically inequivalent and leading to peak doubling for C10 and C11, Fig. S4†). The spectral width in the indirect 13C dimension is limited by the MAS frequency in order to suppress the spinning sidebands and to remove line-shape distortions.27 This causes folding of the two most shifted signals (C3 and C10), whose position can however be easily deduced by recoding a second spectrum with a slightly different (±2 kHz) MAS rate (see ESI†). Overlaid with the experimental data are the computed shifts for each 1H–13C correlation, again calculated with a hybrid PBE functional with HFX percentage ranging from 10 to 40%. The overall agreement between calculated and experimental shifts permits a full assignment of all observed resonances (a summary of the calculated values and experimental shifts, together with the assignment, is given in Table S3†).
We note that the representation of calculated shifts in the form of a 2D “rainbow plot” on top of the experimental signals allows a direct, rapid and visual evaluation of the performance of the modelling approach chosen and guiding the choice of the most appropriate model. For example, here this graphic representation was used to systematically rate the importance of various secondary effects on the calculated shifts (see ESI, Fig. S5†). Molecular geometry is clearly an important underlying factor and an accurate, well-reasoned geometry treatment is indispensable. Here we compared the periodic X-ray structure with optimised hydrogens to a in vacuo fully-optimised structure, finding that the agreement of certain shifts is improved by full optimisation, while for other shifts the X-ray structure gives better agreement. This indicates that an even better prediction would possibly be achievable with a structure fully-optimised in a crystal lattice, on a dispersion-corrected hybrid DFT level. The contribution of inter-molecular PCS is also important, but only for the atoms in close proximity to the neighbouring FeII centres. Finally, calculations allow to estimate that the effect of a temperature variation comparable to the experimental variation (here ±5 K) is negligible.
Conclusion
In summary, the results above aim to establish the new state of the art in solid-state NMR spectroscopy applied to paramagnetic organometallic complexes. With the use of 60 kHz MAS, an experimental “toolkit” allowed to achieve (i) broadband acquisition of a 1H spectrum of a paramagnetic powdered complex, (ii) isotropic resolution by the removal of spinning sidebands, and (iii) broadband heteronuclear correlations. The combination of carefully-tuned pulse sequences and high MAS rates permits extensive experimental constraints for resonance assignment, and marked improvements in sensitivity and resolution, allowing a reduction in sample quantities and experiment time for obtaining NMR spectra of paramagnetic materials. We anticipate that the continued development of MAS probes capable of ever higher MAS rates and of the associated RF schemes will extend the horizons of experimental NMR and allow the study of even more complicated systems.Author contributions
Project design (JB, PAB, AAQ, AJP, GP), funding acquisition (PAB, AAQ, GP), design of NMR methodology (JB, ALL, KJS, AJP, LB, GP), sample preparation and characterization (BB, EJ, DP, PAB), NMR data acquisition and analysis (JB, LB, ALL, KJS), supervision and validation (LC, DP, PAB, AAQ, GP), writing – original draft (JB, LB, ALL, AJP, GP), writing – review & editing (all coauthors).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by the European Research Council (ERC-2015-CoG GA 648974), the Agence Nationale de la Recherche (ANR-15-CE29-0025 MrCAT), as well as by the CNRS (IR-RMN FR3050) and by IFP Energies nouvelles.Notes and references
- Y. C. Su, L. B. Andreas and R. G. Griffin, Annu. Rev. Biochem., 2015, 84, 465–497 CrossRef CAS PubMed.
- S. E. Ashbrook and P. Hodgkinson, J. Chem. Phys., 2018, 149, 040901–040914 CrossRef PubMed.
- B. F. Chmelka, J. Magn. Reson., 2019, 306, 91–97 CrossRef CAS PubMed.
- A. J. Pell, G. Pintacuda and C. P. Grey, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271 CrossRef CAS PubMed.
- Y. Ishii, J. P. Yesinowski and R. Tycko, J. Am. Chem. Soc., 2001, 123, 2921–2922 CrossRef CAS PubMed.
- T. Kobayashi, K. Mao, P. Paluch, A. Nowak-Krol, J. Sniechowska, Y. Nishiyama, D. T. Gryko, M. J. Potrzebowski and M. Pruski, Angew. Chem., Int. Ed., 2013, 52, 14108–14111 CrossRef CAS PubMed.
- L. B. Andreas, K. Jaudzems, J. Stanek, D. Lalli, A. Bertarello, T. Le Marchand, D. Cala-De Paepe, S. Kotelovica, I. Akopjana, B. Knott, S. Wegner, F. Engelke, A. Lesage, L. Emsley, K. Tars, T. Herrmann and G. Pintacuda, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 9187–9192 CrossRef CAS PubMed.
- J. Struppe, C. M. Quinn, M. Lu, M. Wang, G. Hou, X. Lu, J. Kraus, L. B. Andreas, J. Stanek, D. Lalli, A. Lesage, G. Pintacuda, W. Maas, A. M. Gronenborn and T. Polenova, Solid State Nucl. Magn. Reson., 2017, 87, 117–125 CrossRef CAS PubMed.
- T. Schubeis, T. Le Marchand, C. Daday, W. Kopec, K. T. Movellan, J. Stanek, T. S. Schwarzer, K. Castiglione, B. L. de Groot and L. B. Andreas, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21014–21021 CrossRef CAS PubMed.
- Y. Ishii, N. P. Wickramasinghe and S. Chimon, J. Am. Chem. Soc., 2003, 125, 3438–3439 CrossRef CAS PubMed.
- G. Kervern, G. Pintacuda, Y. Zhang, E. Oldfield, C. Roukoss, E. Kuntz, E. Herdtweck, J.-M. Basset, S. Cadars, A. Lesage, C. Copéret and L. Emsley, J. Am. Chem. Soc., 2006, 128, 13545–13552 CrossRef CAS PubMed.
- G. Kervern, A. D'Aléo, L. Toupet, O. Maury, L. Emsley and G. Pintacuda, Angew. Chem., Int. Ed., 2009, 48, 3082–3086 CrossRef CAS PubMed.
- I. Bertini, L. Emsley, M. Lelli, C. Luchinat, J. Mao and G. Pintacuda, J. Am. Chem. Soc., 2010, 132, 5558–5559 CrossRef CAS PubMed.
- R. J. Clement, A. J. Pell, D. S. Middlemiss, F. C. Strobridge, J. K. Miller, M. S. Whittingham, L. Emsley, C. P. Grey and G. Pintacuda, J. Am. Chem. Soc., 2012, 134, 17178–17185 CrossRef CAS PubMed.
- A. Bertarello, T. Schubeis, C. Fuccio, E. Ravera, M. Fragai, G. Parigi, L. Emsley, G. Pintacuda and C. Luchinat, Inorg. Chem., 2017, 56, 6624–6629 CrossRef CAS PubMed.
- N. P. Wickramasinghe, M. Shaibat and Y. Ishii, J. Am. Chem. Soc., 2005, 127, 5796–5797 CrossRef CAS PubMed.
- G. Kervern, S. Steuernagel, F. Engelke, G. Pintacuda and L. Emsley, J. Am. Chem. Soc., 2007, 129, 14118–14119 CrossRef CAS PubMed.
- N. P. Wickramasinghe, M. A. Shaibat, C. R. Jones, L. B. Casabianca, A. C. de Dios, J. S. Harwood and Y. Ishii, J. Chem. Phys., 2008, 128, 052210 CrossRef PubMed.
- S. K. Kumara Swamy, A. Karczmarska, M. Makowska-Janusik, A. Kassiba and J. Dittmer, ChemPhysChem, 2013, 14, 1864–1870 CrossRef CAS PubMed.
- K. Levin and S. Kroeker, Solid State Nucl. Magn. Reson., 2019, 101, 101–109 CrossRef CAS PubMed.
- D. M. Dawson, L. E. Jamieson, M. I. Mohideen, A. C. McKinlay, I. A. Smellie, R. Cadou, N. S. Keddie, R. E. Morris and S. E. Ashbrook, Phys. Chem. Chem. Phys., 2013, 15, 919–929 RSC.
- B. Burcher, K. J. Sanders, L. Benda, G. Pintacuda, E. Jeanneau, A. A. Danopoulos, P. Braunstein, H. Olivier-Bourbigou and P. R. Breuil, Organometallics, 2017, 36, 605–613 CrossRef CAS PubMed.
- D. M. Dawson, C. E. F. Sansome, L. N. McHugh, M. J. McPherson, L. J. McCormick McPherson, R. E. Morris and S. E. Ashbrook, Solid State Nucl. Magn. Reson., 2019, 101, 44–50 CrossRef CAS PubMed.
- Y. Yang, J. Gurnham, B. Liu, R. Duchateau, S. Gambarotta and I. Korobkov, Organometallics, 2014, 33, 5749–5757 CrossRef CAS.
- A. Bielecki and D. P. Burum, J. Magn. Reson., Ser. A, 1995, 116, 215–220 CrossRef CAS.
- A. J. Pell and G. Pintacuda, Prog. Nucl. Magn. Reson. Spectrosc., 2015, 84–85, 33–72 CrossRef CAS PubMed.
- R. Tycko, D. P. Weliky and A. E. Berger, J. Chem. Phys., 1996, 105, 7915 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- R. Ahlrichs, M. K. Armbruster, R. A. Bachorz, M. Bär, H.-P. Baron, R. Bauernschmitt, F. A. Bischoff, S. Böcker, N. Crawford, P. Deglmann, F. Della Sala, M. Diedenhofen, M. Ehrig, K. Eichkorn, S. Elliot, F. Furche, A. Glöβ, F. Haase, M. Häser, C. Hättig, A. Hellweg, S. Höfener, H. Horn, C. Huber, U. Huniar, M. Kattannek, W. Klopper, A. Köhn, C. Kölmel, M. Kollwitz, K. May, P. Nava, C. Ochsenfeld, H. Öhm, M. Pabst, H. Patzelt, D. Rappoport, O. Rubner, A. Schäfer, U. Schneider, M. Sierka, D. P. Tew, O. Treutler, B. Unterreiner, M. von Arnim, F. Weigend, P. Weis, H. Weiss and N. Winter, Turbomole 6.3.1, 2011 Search PubMed.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- B. O. Roos, P. R. Taylor and P. E. M. Sigbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- P.-Å. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision D.01, 2009 Search PubMed.
- W. Kutzelnigg, U. Fleischer and M. Schindler, in NMR - Basic Principles and Progress, Springer, Heidelberg, 1990, vol. 23, pp. 165–262 Search PubMed.
- R. J. Kurland and B. R. McGarvey, J. Magn. Reson., 1970, 2, 286–301 CAS.
- J. Vaara, S. A. Rouf and J. Mareš, J. Chem. Theory Comput., 2015, 11, 4840–4849 CrossRef CAS PubMed.
- A. Bertarello, L. Benda, K. J. Sanders, A. J. Pell, M. J. Knight, V. Pelmenschikov, L. Gonnelli, I. C. Felli, M. Kaupp, L. Emsley, R. Pierattelli and G. Pintacuda, J. Am. Chem. Soc., 2020, 142, 16757–16765 CrossRef CAS PubMed.
- L. Lang, E. Ravera, G. Parigi, C. Luchinat and F. Neese, J. Phys. Chem. Lett., 2020, 11, 8735–8744 CrossRef CAS PubMed.
- G. Kervern, G. Pintacuda and L. Emsley, Chem. Phys. Lett., 2007, 435, 157–162 CrossRef CAS.
- F. C. Strobridge, D. S. Middlemiss, A. J. Pell, M. Leskes, R. J. Clément, F. Pourpoint, Z. Lu, J. V. Hanna, G. Pintacuda, L. Emsley, A. Samosond and C. P. Grey, J. Mat. Chem. A, 2014, 2, 11948–11957 RSC.
- J. Xu, D. H. Lee, R. J. Clément, X. Yu, M. Leskes, A. J. Pell, G. Pintacuda, X.-Q. Yang, C. P. Grey and Y. S. Meng, Chem. Mater., 2014, 26, 1260–1269 CrossRef CAS.
- E. Mitoudi-Vagourdi, W. Papawassiliou, S. Müllner, A. Jaworski, A. J. Pell, P. Lemmens, R. K. Kremer and M. Johnsson, Inorg. Chem., 2018, 57, 4640–4648 CrossRef CAS PubMed.
- W. Papawassiliou, A. Jaworski, A. J. Pell, J. H. Jang, Y. Kim, S.-C. Lee, H. J. Kim, Y. Alwahedi, S. Alhassan, A. Subrati, M. Fardis, M. Karagianni, N. Panopoulos, J. Dolinšek and G. Papavassiliou, Nature Comm, 2020, 11, 1285 CrossRef CAS PubMed.
- W. Van den Heuvel and A. Soncini, Phys. Rev. Lett., 2012, 109, 073001 CrossRef PubMed.
- M. Munzarová and M. Kaupp, J. Phys. Chem. A, 1999, 103, 9966–9983 CrossRef.
- C. Remenyi, R. Reviakine and M. Kaupp, J. Phys. Chem. A, 2006, 110, 4021–4033 CrossRef CAS PubMed.
- C. Remenyi, R. Reviakine and M. Kaupp, J. Phys. Chem. B, 2007, 111, 8290–8304 CrossRef CAS PubMed.
- A. Mondal and M. Kaupp, J. Phys. Chem. Lett., 2018, 9, 1480–1484 CrossRef CAS PubMed.
- A. Mondal and M. Kaupp, J. Phys. Chem. C, 2019, 123, 8387–8405 CrossRef CAS.
- A. W. Hing, S. Vega and J. Schaefer, J. Magn. Reson., 1992, 96, 205–209 CAS.
- S. Li, J. Trébosc, O. Lafon, L. Zhou, M. Shen, F. Pourpoint, J.-P. Amoureux and F. Deng, J. Magn. Reson., 2015, 251, 36–42 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details on sample preparation, NMR spectroscopy; RF pulse sequence schemes; list of chemical shifts; calculation details. CCDC 2063303. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1ra04110j |
| This journal is © The Royal Society of Chemistry 2021 |