Open Access Article
Open Access ArticlePhysico-chemical properties of 4-(methylnitrosamino)-1-(3-pyridyl)-1-butanone (NNK) diazonium ion: a theoretical investigation†
Christos Deligkaris *a,
Evan Millam
*a,
Evan Millam b,
Edmir O. Wadeb,
Maverick L. Grayer*a and
David M. Wahl*a
b,
Edmir O. Wadeb,
Maverick L. Grayer*a and
David M. Wahl*a
aDepartment of Geology and Physics, University of Southern Indiana, 8600 University Blvd, Evansville, USA. E-mail: Dr.Deligkaris@usi.edu; Tel: +1-812-228-5056
bDepartment of Chemistry, University of Southern Indiana, 8600 University Blvd, Evansville, USA
First published on 5th August 2021
Abstract
We have explored the physico-chemical properties of NNK diazonium ion to gain insight into its shape, bonding, charge distribution, and ro-vibrational features. This information is essential if the chemical reactivity and physical properties of this important intermediate are to be understood. NNK diazonium ion is a well-known alkylating agent. Its enzymatic production, its reaction with DNA, and its role in mutagenesis/carcinogenesis have all received significant experimental study. Computational work on the ion, however, is lacking. The species is sufficiently small such that its properties may be probed using sophisticated model chemistries. We present the first in silico investigation of NNK diazonium ion. Kohn–Sham density functional theory (B3LYP/6-311G**) and coupled cluster theory (CCSD/6-31G*) were deployed to obtain energies, geometries, electrostatic potential surfaces, molecular orbitals, and vibrational analyses for several energy-minimized structures. To provide insight into the motion of NNK diazonium ion (NNKDI) in solution, molecular dynamics simulations on the solvated intermediate were undertaken. To explore the initial reactivity of this important electrophile, local Fukui indices and natural population analysis charges were predicted. Analogous ab initio work on propane diazonium ion was also performed. Our vibrational analyses suggest a relatively weak carbon–nitrogen bond and a robust nitrogen–nitrogen interaction. Our condensed Fukui indices show that the terminal nitrogen is a site of significant electrophilicity while our electrostatic predictions yield high values near the formally charged nitrogen and its α carbon.
1 Introduction
The diazonium ion metabolite of 4-(methylnitrosamino)-1-(3-pyridyl)-1-butanone (NNKDI, Fig. 1) is an International Agency for Research on Cancer (IARC) Group 1 carcinogen1 whose unmetabolized form (NNK) is abundantly found in tobacco smoke.2–4 NNKDI is an alkylating agent4–7 and is known to cause lung adenocarcinoma.4,8–10 Its reaction with DNA bases and phosphate groups produces pyridyloxobutyl (POB) adducts4–7,9,11–14 and is considered an important early step in carcinogenesis.15–17 Two specific POB adducts, O6-pob-dGuo and O2-pob-dThd, have known mutagenic properties-predominantly resulting in GC to AT and TA to AT mutations, respectively.17 PDI (1-propane diazonium ion, Fig. 1), a simplified analog of NNKDI, has been found to react with isolated DNA bases, single stranded DNA, and double stranded DNA.18 While previous experimental studies assumed that NNKDI damages DNA via an SN2 mechanism, Fishbein and coworkers found that reactions between PDI and DNA can proceed via either SN2 or SN1 mechanisms.18 Previous computational work has examined the physical interaction of NNKDI with exon 5 of TP53 and has proposed adduct formation sites.19 Both in vitro and in vivo POB adduct formation have received significant study.7,9 These previous investigations inferred the reactivity of NNKDI by examining either its interaction with DNA or the products of that interaction.Our understanding of the isolated ion, however, remains incomplete. The reactive nature of NNKDI as well as its size, has limited the investigation of its physico-chemical properties to computational studies of simplified analogs. For example, the reaction of methane diazonium ion (MDI) with DNA bases has been studied.20–22 Chemical properties, including electrophilicity and stability, of a variety of diazonium ion species have also been examined.23–26 While this work provides valuable insight into the characteristics of related species, NNKDI is relatively large and contains additional moieties that may impact its reactivity.
We examine the unabridged NNKDI structure and report the first in silico exploration of its electronic, vibrational, and rotational features; and we present the results of the first classical molecular dynamics simulations performed on the solvated ion. We compare these findings to additional ab initio work undertaken on 1-propane diazonium ion (PDI). We examine PDI's and NNKDI's role as electrophiles, comment on the differences between NNKDI and PDI properties, and observe the impact of solvation.
2 Methodology
2.1 Geometry optimizations
We obtained the NNK coordinates from a crystallographic study27 and used UCSF Chimera version 1.11 (ref. 28) to manually delete the methyl group and oxygen and adjust the N6–N5 distance to 1.15 Å. We then created six NNKDI conformations by manually rotating the C1–C3′ torsion by 60° increments. The six starting conformations were used as the initial geometries for sequential optimizations advancing from HF/3-21G*, to B3LYP29–33/3-21G*,34 to B3LYP/6-31G*35–37 and finally to B3LYP/6-311G**38 level of theory with NWChem.39 At each step, we examined the resulting structures and the lowest energy unique geometries were chosen as the initial structures for the subsequent optimizations. We subsequently generated structures by manually rotating the C2–C1 torsion every 60° and performed geometry optimizations as described previously. This process was followed for the torsions on the chain: C3–C2, C4–C3. We did not perform a rotation around the N5–C4 torsion because the angle C4–N5–N6 is very close to 180°. Frequency calculations were used to confirm that the optimized geometries corresponded to energy minima of the potential energy surface.We manually created a geometry for PDI using one of the NNKDI optimized geometries and UCSF Chimera.28 We performed geometry optimizations using four initial structures for PDI, with different C2–C3 torsional angles (0°, 60°, 120°, 180°). The calculations were performed similarly to the geometry optimizations of NNKDI.
2.2 Reactivity descriptors
We calculated the condensed Fukui functions and condensed dual descriptor using Psi4 (ref. 40) and Multiwfn.41 The natural population analysis was performed with NBO 6.0.42 We visualized the electrostatic potential (ESP) using ESP values on the 0.002 electrons per bohr3 isodensity contour.2.3 Coupled cluster optimization and frequency calculation
The GAMESS43–45 computational chemistry suite was used to perform all coupled cluster geometry optimizations and vibrational analyses. Initial Cartesian coordinates were taken from our NWChem, B3LYP/6-31G* results. Geometry optimizations and vibrational analyses were completed on PDI at the CCSD(T)46–48/cc-pVTZ49 level of theory, and on NNKDI at the CCSD/6-31G* level of theory.2.4 Force-field parameters
We calculated RESP50,51 charges for one of the NNKDI optimized geometries (TCTT) at the HF/6-31G* level of theory using NWChem and Multiwfn.41 We used ACPYPE52 to assign GAFF2.0 (ref. 53) parameters on all NNKDI atoms. A new atom type was created for the formally positively charged N5 atom. All parameters for this atom were taken from the similar GAFF2 atom type N1, with the exception of the equilibrium bond lengths C4–N5 and N5–N6 and equilibrium bond angles C4–N5–N6, C3–C4–N5, H41–C4–N5, H42–C4–N5. These parameters were taken from the B3LYP/6-311G** optimized structure TCTT.Using the refined equilibrium bond lengths and angles we performed energy minimizations starting from the quantum mechanically optimized structures to examine transferability of the GAFF2 dihedral parameters to NNKDI.
We used a python script in NWChem to alter the dihedral (0–180°, every 5°), and performed a geometry optimization at the B3LYP/6-311G** level of theory while keeping the dihedral fixed. Starting with the C1–C3′ torsion, the optimized structures were used as the initial geometries for force field energy minimizations with a criterion of a gradient less than 10−3 kcal mol−1 Å−1, an infinite nonbonded cutoff and harmonic restraint with a force constant of 1000 kcal per mol per degree2 on all dihedral terms of all flexible torsions.54,55 During the minimization, the dihedral terms that belong to the C1–C3′ torsion were assigned a force constant of 0. We found, with the NMinimize function of Wolfram Mathematica 12,56 the force constants of the C1–C3′ dihedral terms by minimizing the weighted Root-Mean-Square-Error (RMSE):
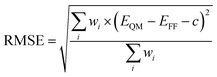 | (1) |
For torsion C3–C2 we used increased weights to capture the characteristics of the high energy minimum and the associated energy barrier on the potential energy surface, while modeling reasonably well the global energy minimum. Certain combinations of torsional angles produced an intramolecular reaction between the diazonio group and carbonyl moiety. This resulted in the loss of dinitrogen. Since our intent was to study NNK diazonium ion in its unreacted form, torsional angles were restricted to prevent this outcome. During the last iteration, all but the torsion being optimized were left unrestrained.
2.5 Molecular dynamics
NNKDI was placed in a dodecahedron periodic box with a minimum NNKDI-box distance of 1.5 nm. 1563 water molecules, 4 sodium and 5 chloride ions were added to solvate, to neutralize the charge of the system, and to more closely reflect cellular salt concentrations. Forces and interactions on particles were quickly evaluated using a combination of the Verlet cutoff-scheme57 and grid neighbor searching, with the neighbor list updating frequency set to 10. Long-range electrostatic interactions were calculated using fast smooth Particle Mesh Ewald electrostatics,58,59 with a cut-off distance of 1.2 nm and Fourier-spacing of 0.12 nm. We shifted the Lennard-Jones potential for the van der Waals interactions so that it is zero at the cutoff. All remaining parameters used the default settings in GROMACS.60 The energy of the system was minimized using a steepest descent algorithm with a maximum force less than 1000 kJ mol−1 nm−1.During equilibration, the structure of NNKDI was maintained with position restraints of 1000 kcal mol−1 Å−2. Every bond involving a hydrogen atom was converted to a constraint using the LINCS algorithm,61 and the TIP3P62 water molecules were kept rigid with SETTLE.63 These constraints allowed an integration time step of 2 fs.
NVT equilibration took place in 5 × 104 integration steps. Velocity rescaling, a time constant of 0.1 ps, and a reference temperature of 300 K were used to couple the temperature to the entire system. Initial velocities were generated according to a Maxwell distribution. During the 5 × 104 integration steps of NPT equilibration the Berendsen algorithm was used for isotropic pressure coupling.64 The reference pressure was set to 1.0 bar.
Four 1.5 μs production runs in the NPT ensemble were performed with independent solvation and equilibration. The temperature was kept at 300 K with the use of the Nosé–Hoover thermostat65,66 and a pressure of 1.0 bar was maintained using the Parrinello–Rahman barostat.67,68
2.6 Visualizations
We used MarvinSketch,69 UCSF Chimera,28 wxMcMolPlot,70 and WebMO,71 to make all figures in this paper.3 Results
3.1 PDI ab initio
Tables 1 and 2 give relative energies, absolute energies, and dihedral angles for the anti and gauche conformers of PDI. Results are presented for the B3LYP/6-311G** and CCSD(T)/cc-pVTZ levels of theory. Graphical representations of these minimum energy structures are found in the ESI.† Both models yielded analogous geometries, with DFT providing the most negative energies. Point group symmetry (Cs) in the anti structure locked both reported dihedral angles at their expected values. This symmetry was broken in the gauche conformer, however; and a small twist in C2–C3–N4–N5 was realized. At the same time, C1–C2–C3–C4 remained near its canonical quantity.Two energy minima were found for PDI (Table 1), one that corresponds to the anti conformation and one that corresponds to the gauche conformation. CCSD(T)/cc-pVTZ predicted the gauche conformation to be the lowest energy structure with the anti conformation just 0.16 kcal mol−1 higher. In contrast, the B3LYP/6-311G** level of theory predicted the anti conformation to be the lowest energy structure with the gauche conformation just 0.02 kcal mol−1 higher.
| Structure | Energy | Dihedrals [°] | ||
|---|---|---|---|---|
| [kcal mol−1] | [hartree] | a | b | |
| CCSD(T)/cc-pVTZ | ||||
| anti | 0.16 | −227.34677 | 180.00 | 0.00 |
| gauche | 0.00 | −227.34703 | −61.81 | −4.85 |
| B3LYP/6-311G** | ||||
| anti | 0.00 | −227.78917 | 180.00 | 0.00 |
| gauche | 0.02 | −227.78914 | −63.24 | −5.21 |
Table 2 provides bond lengths and bond angles for the PDI backbone. Starting at the diazonio group, we found an N4–N5 bond length of approximately 1.10 Å, a C3–N4 bond length of 1.48 to 1.51 Å, a C2–C3 bond length of 1.54 to 1.53 Å, and a C1–C2 bond length of 1.53 Å. Minor variations in bond distance were seen both between conformers and between levels of theory with the greatest differences realized in the C3–N4 bond. The C1–C2–C3 angle varied from 108° to 114° and was conformer-dependent. The C2–C3–N4 angle, on the other hand, was relatively constant varying from 109° to 110° depending upon the choice of model. The C3–N4–N5 angle was almost linear varying from 177° to 178° showing both model and conformer dependence.
| Property | B3LYP/6-311G** | CCSD(T)/cc-pVTZ | ||
|---|---|---|---|---|
| anti | gauche | anti | gauche | |
| C1–C2 | 1.534733 | 1.527646 | 1.532739 | 1.526579 |
| C2–C3 | 1.539448 | 1.537120 | 1.526982 | 1.525999 |
| C3–N4 | 1.478387 | 1.482949 | 1.502470 | 1.505324 |
| N4–N5 | 1.096464 | 1.096115 | 1.102609 | 1.102454 |
| C1–C2–C3 | 108.57 | 114.44 | 107.66 | 113.32 |
| C2–C3–N4 | 110.40 | 110.42 | 109.38 | 108.92 |
| C3–N4–N5 | 176.61 | 177.21 | 177.18 | 177.83 |
Vibrational analyses were performed on each optimized PDI structure. This was done to confirm that each geometry represented a local minimum on PDI's potential energy surface and to investigate vibration in or near the diazonium ion moiety. We were especially interested in changes in the C3–N4 and N4–N5 bond lengths. Additional normal modes are given in the ESI.† Two modes were found to yield significant, relevant geometric distortions: an approximately 610 to 670 cm−1 carbon–nitrogen stretch (with significant C1–C2–C3 angle deformation), and an approximately 2400 cm−1 nitrogen–nitrogen stretch. Table 3 gives the predicted frequency for each of these modes. The C3–N4 elongation shows some conformer-dependance.
| Mode | B3LYP/6-311G** | CCSD(T)/cc-pVTZ | ||
|---|---|---|---|---|
| anti | gauche | anti | gauche | |
| 13 | 669 | 613 | 669 | 614 |
| 29 | 2435 | 2437 | 2367 | 2369 |
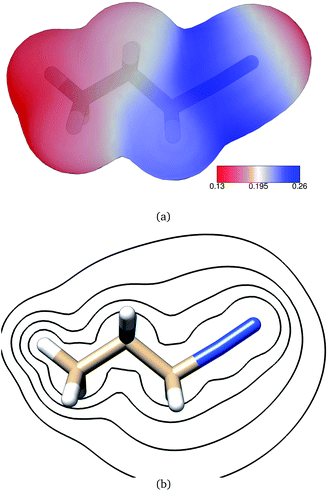
Frontier molecular orbitals and their energies are shown in Fig. 2. The HOMO was localized mainly on atoms C1, C2, and C3 whereas the LUMO was localized mainly on the diazonio group but with a significant density on all carbon atoms (Fig. 2). The LUMO+1 was only 0.92 kcal mol−1 higher (Fig. 2) and in contrast with the LUMO, this MO was localized on the diazonio group and carbon atom C3 (Fig. 2). The electron density contours showed a significant decrease in electron density between atoms C3 and N4 (Fig. 3).
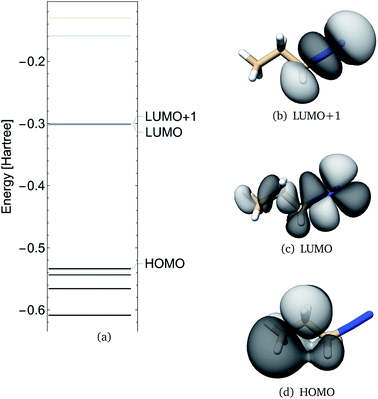 | ||
| Fig. 2 PDI anti molecular orbital energies (a), molecular orbital 19 (HOMO), 20 (LUMO) and 21 (LUMO+1) as calculated at the B3LYP/6-311G** level of theory. | ||
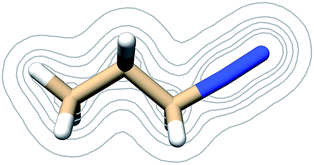 | ||
| Fig. 3 Contours of the PDI electron density as calculated at the B3LYP/6-311G** level of theory at contour levels 0.01, 0.05, 0.01, 0.2, 0.3 au. | ||
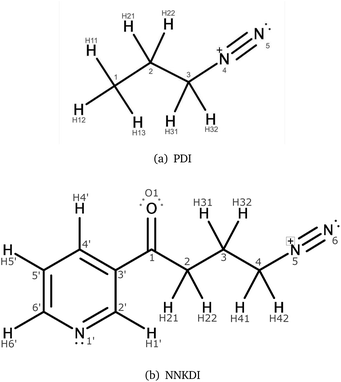
The electric potential on PDI's isodensity surface (Fig. 4) was overall positive, with higher values near atoms C3 and N4. Electrostatic equipotential contours (Fig. 4) did not reveal any local maxima or minima.
Condensed Fukui functions, dual descriptor, and NPA charges are shown in Table 4. PDI atom C1 had the largest condensed Fukui function for electrophilic attack and the most negative natural charge, whereas atom N5 had the largest condensed Fukui function for nucleophilic attack and the most positive charge (Table 4). Diazonio group atoms N4 and N5 had the most positive dual descriptor while atom C1 had the most negative dual descriptor (Table 4).
| Atom | f− | f+ | f+ − f− | NPA charge |
|---|---|---|---|---|
| C1 | 0.1428 | 0.0280 | −0.1148 | −0.58059 |
| C2 | 0.0992 | 0.0292 | −0.0700 | −0.38006 |
| C3 | 0.0266 | 0.0539 | +0.0273 | −0.21412 |
| N4 | 0.0062 | 0.2614 | +0.2552 | +0.16303 |
| N5 | 0.0885 | 0.3974 | +0.3089 | +0.33880 |
3.2 NNKDI ab initio
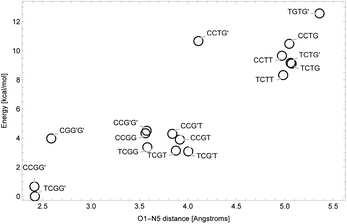
NNKDI in the singlet state had a lower energy than NNKDI in the triplet state (results not shown). Also, the energies of the restricted and unrestricted singlet calculation were similar. The frontier orbitals with spin α and β were practically indistinguishable in the unrestricted calculation (results not shown).We explored the rotational potential energy surface of NNKDI and located 19 energy minima. The results of this survey are summarized in Table 5. Conformer structures are shown in the SI. Rotation about the C3′–C1 bond produced 9 trans and 10 cis structures. Rotation about the C1–C2 bond produced 17 cis and 2 gauche structures. No trans or gauche′ structures were realized. For most conformers, the O1–C1–C2–C3 dihedral angle was small. The most notable exception to this trend was the TGTG′ structure, which was the highest energy conformer found. Rotation around the C2–C3 bond produced three minima. Seven trans, six gauche, and six gauche′ structures were found. No cis structures were observed. Rotation around the C3–C4 bond produced three minima. Six trans, six gauche, and seven gauche′ structures were found. No cis structures were observed. One expected minimum energy structure, TCG′G′, could not be located. Rotation about the C4–N5 bond defied categorization. The closer the diazonio group (atom N5 in particular) is to the carbonyl oxygen the lower the energy of NNKDI (Table 5 and Fig. 5). In a separate trend, conformations with the carbonyl oxygen near the ring's nitrogen (atom N1) tend to be lower in energy, but the global minimum is a notable exception and has a C2′–C3′–C1–O1 dihedral close to 180° (Table 5).
| B3LYP/6-311G** | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Structure | Energy | Dihedrals [°] | Distances [Å] | ||||||
| [kcal mol−1] | [hartree] | a | b | c | d | e | O1–N5 | O1–N1 | |
| TCTT | 8.3 | −588.28993 | −180.0 | 0.0 | −180.0 | −180.0 | 0.0 | 4.984 | 4.777 |
| TCG′T | 3.1 | −588.29828 | 178.8 | 12.4 | −58.7 | −171.7 | −62.1 | 4.004 | 4.770 |
| TCG′G | 0.0 | −588.30321 | 178.8 | 14.1 | −58.7 | 89.8 | 125.8 | 2.420 | 4.768 |
| TCGT | 3.1 | −588.29820 | −178.6 | −25.1 | 63.6 | −173.6 | 69.6 | 3.876 | 4.767 |
| TCGG′ | 0.0 | −588.30321 | −178.7 | −14.1 | 58.8 | −89.8 | −125.9 | 2.420 | 4.768 |
| TCGG | 3.4 | −588.29783 | −177.8 | −15.1 | 55.8 | 64.5 | −66.4 | 3.581 | 4.768 |
| TGTG′ | 12.6 | −588.28318 | 179.2 | 88.9 | −167.1 | −66.4 | −6.8 | 5.359 | 4.778 |
| TCTG′ | 9.2 | −588.28859 | 178.1 | 9.3 | −137.3 | −65.4 | −8.9 | 5.061 | 4.772 |
| TCTG | 9.1 | −588.28868 | −177.9 | −9.7 | 140.5 | 65.1 | 9.4 | 5.071 | 4.773 |
| CCTT | 9.7 | −588.28781 | −0.0 | −0.0 | 180.0 | −180.0 | −0.0 | 4.971 | 4.141 |
| CCGG′ | 0.7 | −588.30213 | 0.4 | −13.8 | 58.5 | −89.9 | −126.3 | 2.415 | 4.128 |
| CCGT | 3.9 | −588.29699 | 0.5 | −14.8 | 60.1 | −178.8 | 150.1 | 3.917 | 4.123 |
| CCGG | 4.3 | −588.29630 | 0.2 | −15.3 | 55.1 | 64.5 | −71.0 | 3.562 | 4.120 |
| CCTG′ | 10.7 | −588.28621 | 1.9 | −17.9 | 142.2 | −71.0 | −11.5 | 4.108 | 4.130 |
| CCTG | 10.5 | −588.28651 | 2.0 | −7.4 | 163.0 | 65.3 | 15.4 | 5.047 | 4.139 |
| CCG′T | 4.3 | −588.29636 | −3.3 | 30.6 | −64.1 | 170.2 | −75.6 | 3.839 | 4.113 |
| CCG′G′ | 4.5 | −588.29602 | −2.3 | 25.9 | −58.8 | −66.1 | 87.1 | 3.574 | 4.116 |
| CGG′G′ | 4.0 | −588.29687 | −0.3 | 42.3 | −37.3 | −48.1 | −96.4 | 2.589 | 4.114 |
| CCG′G | 0.7 | −588.30213 | −0.5 | 13.8 | −58.5 | 89.9 | 126.4 | 2.415 | 4.128 |
| CCSD/6-31G* with Cs symmetry | |||||||||
| TCTT | 0.0 | −586.39486 | 180.0 | 0.0 | 180.0 | 180.0 | 0.0 | 4.977 | 4.793 |
| CCTT | 1.4 | −586.39270 | 0.0 | 0.0 | 180.0 | 180.0 | 0.0 | 4.962 | 4.152 |
We have probed the geometry of the NNKDI backbone and carbonyl group using the B3LYP/6-311G** and CCSD/6-31G* models. The C2′–C3′–C1–O1 dihedral was manipulated to produce two conformers of Cs symmetry: one TCTT species and one CCTT structure. Table 6 reports bond lengths and bond angles for these ions. In the pyridine ring, our predicted C–N distances ranged from 1.33 to 1.34 Å. Moving away from the heteroatom, our C–C bond lengths varied from approximately 1.40 to 1.38 Å with the longest C–C bonds proximate to the side chain.
| Property | B3LYP/6-311G** | CCSD/6-31G* | ||
|---|---|---|---|---|
| TCTT | CCTT | TCTT | CCTT | |
| N1′–C2′ | 1.330802 | 1.328523 | 1.339693 | 1.337212 |
| C2′–C3′ | 1.401386 | 1.406516 | 1.401063 | 1.406012 |
| C3′–C4′ | 1.403119 | 1.400554 | 1.404161 | 1.401517 |
| C4′–C5′ | 1.384229 | 1.387447 | 1.389188 | 1.392451 |
| C5′–C6′ | 1.397423 | 1.395107 | 1.401336 | 1.398553 |
| C6′–N1′ | 1.336849 | 1.338066 | 1.341947 | 1.344052 |
| C3′–C1 | 1.481674 | 1.481301 | 1.486723 | 1.486537 |
| C1–O1 | 1.213711 | 1.213328 | 1.224112 | 1.223896 |
| C1–C2 | 1.544534 | 1.546557 | 1.535080 | 1.536258 |
| C2–C3 | 1.533612 | 1.533391 | 1.533112 | 1.533351 |
| C3–C4 | 1.534410 | 1.534490 | 1.527024 | 1.526975 |
| C4–N5 | 1.484650 | 1.484810 | 1.514204 | 1.514696 |
| N5–N6 | 1.096408 | 1.096636 | 1.110660 | 1.110684 |
| N1′–C2′–C3′ | 123.82 | 123.60 | 123.81 | 123.66 |
| C2′–C3′–C4′ | 117.86 | 117.82 | 118.32 | 118.26 |
| C3′–C4′–C5′ | 118.74 | 118.88 | 118.45 | 118.58 |
| C4′–C5′–C6′ | 118.53 | 118.42 | 118.59 | 118.51 |
| C5′–C6′–N1′ | 123.65 | 123.64 | 123.84 | 123.82 |
| C6′–N1′–C2′ | 117.40 | 117.64 | 116.99 | 117.18 |
| C2′–C3′–C1 | 123.32 | 118.16 | 122.86 | 118.16 |
| C4′–C3′–C1 | 118.82 | 124.02 | 118.83 | 123.58 |
| C3′–C1-O1 | 122.69 | 122.89 | 122.27 | 122.49 |
| C3′–C1-C2 | 118.57 | 118.53 | 119.01 | 118.97 |
| O1–C1–C2 | 118.74 | 118.58 | 118.71 | 118.54 |
| C1–C2–C3 | 108.97 | 108.74 | 108.91 | 108.64 |
| C2–C3–C4 | 109.07 | 109.35 | 108.50 | 108.78 |
| C3–C4–N5 | 109.40 | 109.28 | 108.67 | 108.56 |
| C4–N5–N6 | 176.05 | 175.64 | 177.54 | 177.45 |
Moving from C3′ to C4, we saw C–C bond lengths of 1.48 to 1.55 Å with the C3′–C1 distance being relatively short, the C1–C2 bond length being relatively long and the C2–C3 and C3–C4 distances tightly clustered around 1.53 Å. The carbonyl, C–N, and N–N bond lengths were all somewhat model-dependent ranging from 1.21 to 1.22 Å, 1.48 to 1.51 Å, and 1.10 to 1.11 Å, respectively.
Bond angles in the ring system varied from 124° for the C–C–N value to approximately 117° for the C–N–C angle. The C–C–C angles measured between 118 and 119° with the smallest angle centered on C3′. Moving to the side chain, conformer dependance was seen in the C1–C3′–C2′ (123°, 118°) and C1–C3′–C4′ (119°, 124°) angles. Rotation around the C3′–C1 bond approximately exchanged the values of these measurements. The carbonyl moiety showed a subtle tilt away from the ring system with the C3′–C1–O1 angle being 3 or 4° larger than both C2–C1–O1 and C3′–C1–C2 in each conformer. The rest of the side chain had C–C–C angles of 109°, a C3–C4–N5 angle of 109°, and a model-dependent C4–N5–N6 angle of 176 to 178°.
Vibrational analyses were performed on each optimized NNKDI structure. This was done to confirm that each geometry represented a local minimum on NNKDI's potential energy surface and to investigate vibration in or near the diazonio group. A single structure, CCTT CCSD/6-31G* was found to be a possible saddle point with a single negative frequency mode (−34 cm−1). Motion along this coordinate pulls the carbonyl group out of the plain of the ring system and breaks Cs symmetry. Additional normal modes are given in the ESI.† Two modes were found to yield significant, relevant geometric distortions: an approximately 660 cm−1 C4–N5 stretch and an approximately 2400 cm−1 N5–N6 stretch.
Comparing our PDI and NNKDI results, we found C–C and C–N bond lengths that were similar in both species with intermolecular variations of up to 0.02 Å near the carbonyl moiety. Likewise, the C1–C2–C3, C2–C3–C4, C3–C4–N5, and C4–N5–N6 angles in NNKDI were close to the C1–C2–C3, C2–C3–N4, and C3–N4–N5 angles found in PDI's anti conformation with intermolecular variations of about 1°. Vibrational analyses yielded C–N and N–N stretching frequencies that were consistent showing intermolecular variations of less than 100 cm−1 (Table 7).
| B3LYP/6-311G** | CCSD/6-31G* | |||
|---|---|---|---|---|
| Mode | TCTT | CCTT | TCTT | CCTT |
| C4–N5 stretch | 654 | 653 | 664 | 664 |
| N5–N6 stretch | 2433 | 2427 | 2443 | 2443 |
NNKDI frontier molecular orbitals are shown in Fig. 6. The HOMO of NNKDI was localized on the ring and carbonyl group, whereas the LUMO was localized on the diazonio group and carbon atoms C4, C3, and C2 (Fig. 6). The HOMO–LUMO energy gap was 41.54 kcal mol−1. The LUMO energy was only 0.81 kcal mol−1 lower than the next unoccupied molecular orbital which, in contrast with the LUMO, was localized only on the diazonio group and carbon atom C4 (Fig. 6). Similarly with PDI, the NNKDI electron density contours revealed a relatively smaller electron density between atoms C4 and N5 (Fig. 7).
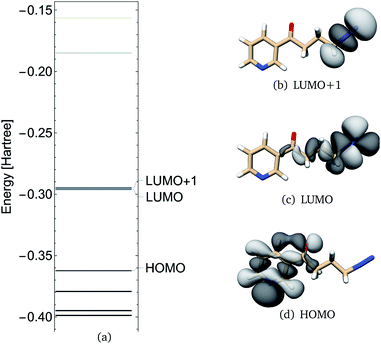 | ||
| Fig. 6 NNKDI TCTT molecular orbital energies (a), molecular orbitals 46 (HOMO), 47 (LUMO) and 48 (LUMO+1) as calculated at the B3LYP/6-311G** level of theory. | ||
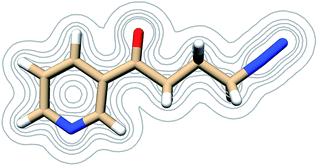 | ||
| Fig. 7 Contours of the NNKDI electron density as calculated at the B3LYP/6-311G** level of theory at contour levels 0.01, 0.05, 0.01, 0.2, 0.3 in atomic units. | ||
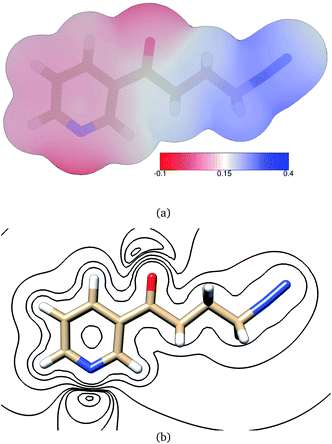
The electric potential on NNKDI's isodensity surface (Fig. 8) was overall positive, with higher values observed near atoms N5 and C4 and lower values near ring atom N1. In the extended TCTT conformation, the electrostatic equipotentials (Fig. 8) revealed two local minima, one near the carbonyl oxygen, atom O1, and one near the ring nitrogen, atom N1. The local minimum near the ring nitrogen was slightly negative and deeper than the one near the carbonyl oxygen which maintained always positive values.
NNKDI condensed Fukui functions and dual descriptor are shown in Table 8. The NNKDI ring nitrogen had the largest condensed Fukui function for electrophilic attack, followed by the carbonyl oxygen (Table 8). The two diazonio group nitrogen atoms had the largest Fukui function for nucleophilic attack (Table 8). A similar trend was observed with the dual descriptor, the ring nitrogen atom had the most negative value, whereas the two diazonio group nitrogens had the most positive values (Table 8). The carbonyl oxygen, ring nitrogen, and carbon atom C2 had large negative charges, whereas carbon atom C1 and the two nitrogen atoms of the diazonio group all had large positive charges.
| Atom | f− | f+ | f+ − f− | NPA charge |
|---|---|---|---|---|
| N1′ | 0.2327 | 0.0180 | −0.2147 | −0.43997 |
| C2′ | 0.0617 | 0.0079 | −0.0538 | +0.09223 |
| C3′ | 0.0453 | 0.0009 | −0.0444 | −0.20660 |
| C4′ | 0.0541 | 0.0150 | −0.0391 | −0.10596 |
| C5′ | 0.0605 | 0.0187 | −0.0417 | −0.22791 |
| C6′ | 0.0658 | 0.0296 | −0.0362 | +0.10694 |
| C1 | 0.0412 | 0.0177 | −0.0234 | +0.58990 |
| C2 | 0.0170 | 0.0146 | −0.0024 | −0.48391 |
| C3 | 0.0060 | 0.0206 | +0.0146 | −0.39264 |
| O1 | 0.1250 | 0.0204 | −0.1047 | −0.55216 |
| C4 | 0.0075 | 0.0476 | +0.0401 | −0.20431 |
| N5 | 0.0050 | 0.2344 | +0.2295 | +0.16275 |
| N6 | 0.0354 | 0.3558 | +0.3204 | +0.33720 |
3.3 NNKDI MD
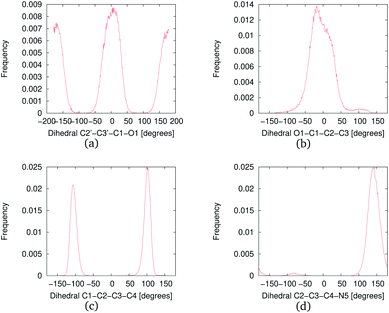
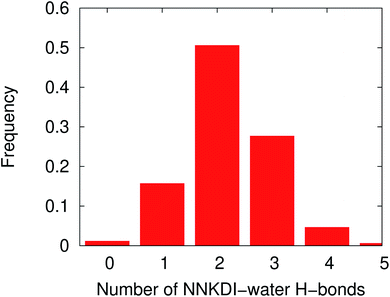
The MD simulations were performed with NNKDI in solution and with the presence of ions. We present the results from a single 1.5 μs MD simulation as the results from the other three MD simulations were similar. In solution, NNKDI spent about the same amount of time with its carbonyl oxygen in the cis and trans conformations (Fig. 9). Carbon atom C3 was almost always cis to the carbonyl oxygen, whereas carbon atom C4 was off the ring's plane almost all the time since the dihedral C1–C2–C3–C4 was rarely ever zero or 180° (Fig. 9). Atom N5 of the diazonio group was almost always trans to atom C2.NNKDI had most frequently two hydrogen bonds with the solvent, but that number ranged from none to five hydrogen bonds (Fig. 10). Nitrogen N6 of the diazonio group rarely participated in a hydrogen bond with water but nitrogen N1 and the carbonyl oxygen O1 had at least one hydrogen bond with water, most of the time (see ESI†).
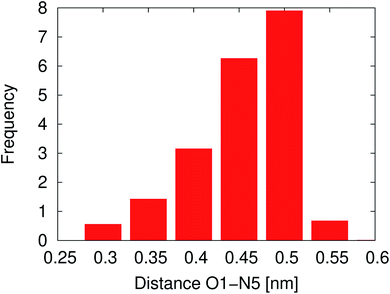
In solution, NNKDI rarely adopted a conformation with the diazonio group near the carbonyl oxygen, most of the time the aliphatic chain was in an extended conformation as the O1–N5 distance suggests (Fig. 11). Cluster analysis of the MD conformations resulted in four highly populated clusters. The center conformations of these clusters included the aliphatic chain in an extended conformation (see ESI†). The conformations that NNKDI adopted in solution allowed overall for the terminal nitrogen N6 of the diazonio group to be highly accessible. Atom N5 was less accessible, with the α carbon C4 and β carbon C3 even less accessible to the solvent. During the 1.5 μs MD simulation, the average solvent accessible surface area (SASA) of atom N5 was 0.093 nm2, the SASA of N6 was 0.63 nm2, the SASA of C4 0.030 nm2, and the SASA of C3 was 0.019 nm2.
4 Discussion
4.1 Geometries, frequencies and vibrational modes
We found significant variation, between conformers, in the C1–C2–C3 angle with the gauche conformer's prediction being approximately five degrees larger than that of the anti conformer. This is suggestive of steric repulsion between a C1 hydrogen and the diazonio group in the gauche conformation. Comparing these values to propane's experimentally determined C1–C2–C3 angle74 (112.4°), we find that the experimental value lies between our calculated values. This is consistent with free rotation around the C2–C3 bond. A weighted average of our predicted angles, approximately 113° for DFT and 112° for coupled-cluster, is comparable to propane's experimental value.
The C2–C3–N4 angle prediction (109° to 110°) is much smaller than the analogous value in ethylamine73 (115°). This is expected since the C3–N4–N5 angle is almost linear; thus, steric crowding should be less significant in the diazonium ion than in the amine. Comparing DFT and couple-cluster calculated bond angles, we find deviations of about one degree between the two models.
Our vibrational analyses show harmonic predictions for the nitrogen–nitrogen stretching frequency (2370 to 2440 cm−1) that are comparable to the experimental, harmonic value for dinitrogen (2358.57 cm−1). Our predicted carbon–nitrogen stretching frequency (610 to 670 cm−1), however, is significantly lower than the analogous predicted C–N and C–C stretching frequencies found in ethylamine (approximately 900 to 1100 cm−1). Thus, our vibrational analyses suggest that the C–N bond is relatively weak; and that the N–N interaction is robust. Comparing model chemistries, results of the vibrational analyses for the DFT and coupled-cluster levels of theory were remarkably similar varying by less than 100 cm−1 for the modes in question.
Looking at the C–N stretching frequency in the gauche and anti conformers, the difference in value (55 cm−1) may be significant; but, it should be noted that the modes in question are not perfectly parallel and are not pure stretching motions. The C–N deformation in the gauche structure is accompanied by a subtle CH2 rocking motion centered on C2. This movement is not found in the analogous vibrational mode in the anti structure. Likewise, the amount of C1–C2–C3 angle bending contaminating the C–N stretch varies between the conformers with less being seen in the anti structure. Thus, the frequency difference cannot be unambiguously assigned to changes in the C3–N4 bond.
Overall, the geometric data and vibrational results presented for the PDI system suggest that the ion's shape and normal modes are well modeled using either B3LYP/6-311G** or CCSD(T)/cc-pVTZ. Both levels of theory predict that the anti and gauche conformers are nearly degenerate. It is not clear from our results which conformer represents the global energy minimum.
Carbon–carbon and C–N bond lengths in the ring system are largely consistent with their pyridine analogs. NNKDI is less symmetric, however; and proximity to the side chain is somewhat impactful. Thus, our C–N distances varied from 1.33 to 1.34 Å with slightly shorter values found between N1′ and C2′. These are in near agreement with the 1.340 Å C–N bond length found in pyridine.76 Likewise, our C–C distances range from 1.38 to 1.41 Å with the largest values found proximate to the side chain. These results are like the 1.390 and 1.400 Å C–C distances in pyridine.76 In pyridine, however, proximity to the heteroatom produces the shortest C–C distances.76
Moving to the side chain, the C3′–C1 distance is somewhat model dependent, ranging from 1.48 to 1.49 Å, and is slightly smaller than the analogous bond in toluene (1.513 Å).77 Conjugation between the ring π system and the carbonyl group likely shortens this distance in NNKDI. The carbonyl bond length itself is somewhat model dependent, ranging from 1.21 to 1.22 Å, and is quite similar to that found in acetone (1.214 Å).78 Moving from C1–C2 to C2–C3 to C3–C4, our C–C distances contract varying from 1.55 to 1.53 Å and are like the value found in ethylamine (1.531 Å).73 The C4–N5 distance shows some model dependence ranging from 1.48 to 1.51 Å and is similar to the C–N distance found in ethylamine (1.475 Å);73 and the N5–N6 distance, though also somewhat model dependent (1.10 to 1.11 Å), is comparable to the dinitrogen experimental value (1.098 Å).72 Moving back to the ring system, our C–C–N, C–C–C, C–N–C angles (124°, 118 to 119°, 117°, respectively) are comparable to their experimental values in pyridine: 124°, 118.1° to 118.6°, and 116.7°, respectively.77 In both species the largest C–C–C angle is located spatially opposite the heteroatom.
We noted conformation dependent tilting of the side chain (relative to the ring). This likely reduces steric crowding between H21/H22 and either H1′ or H4′. We also found that the carbonyl moiety tilts slightly away from the ring system in either conformer. This may reduce steric crowding between O1's lone pair electrons and H1′ or H4′. Moving toward the diazonio group, we found C–C–C and C–C–N angles of 109° in reasonable agreement with C–C–C and C–C–N angles reported for the anti conformer PDI (Table 2). As was seen in PDI, our N–N and C–N stretching frequencies point to a weak C–N bond and a strong N–N interaction. The harmonic prediction for the nitrogen–nitrogen stretch (2443 cm−1) is comparable to the experimental, harmonic value for dinitrogen (2358.57 cm−1).79
Comparing the DFT and coupled-cluster models, bond lengths within the ring system are quite similar varying by about 0.1 Å. Bond lengths in the side chain show minor differences with DFT predicting a shorter C1–O1 length, a longer C1–C2 distance, a longer C3–C4 distance, a shorter C4–N5 length, and a shorter N5–N6 length. Bond angle data vary by less than one degree for all angles except C4–N5–N6. Results of the vibrational analyses for the DFT and coupled cluster levels of theory are remarkably similar varying by less than 10 cm−1. Overall, the geometric data and vibrational results presented for the NNKDI system suggest that the ion's shape and normal modes are well modeled using either level of theory.
In general, the relevant vibrational and geometric properties of PDI (anti conformer) were mirrored in NNKDI. Comparing analogous regions, bond lengths varied by approximately 0.01 Å and bond angles varied by about 1°. These differences were similar in magnitude to model-dependent variations noted in each structure near the diazonio group. While NNKDI's carbonyl moiety and pyridine ring may impact the reactivity of ion in other ways, they do not modify the backbone structure or stretching frequencies near the terminal nitrogen.
4.2 Interactions with nucleophiles
Our calculations offer insight about (i) the physical interaction between diazonium ions and approaching nucleophiles and (ii) the initial chemical reactivity of our substrates. Thus, we comment on the physical attraction between reactive species and the possibilities for electron reorganization.The ESP results on NNKDI suggest that atoms N5 and C4 have the highest electric potential on the isodensity contour. A similar conclusion can be drawn for PDI: the highest electric potential is near the formally charged nitrogen of the diazonio group. Thus, the strongest physical interaction between PDI or NNKDI and a nucleophile will likely occur near the diazonio group and its α carbon.
In contrast with PDI, two ESP local minima were found on NNKDI, one near the ring nitrogen (N1) due to the atom's lone electron pair, and another one near the carbonyl oxygen, also due to the atom's lone electron pairs. The local ESP minimum near the carbonyl oxygen is located close to the lone electron pair that is the furthest from the diazonio group as the potential there is less affected by the electron deficiency at N5 on the diazonio group.
Based on our NNKDI MD work, it should be noted that the terminal nitrogen N6 of the diazonio group is by far the most accessible atom, followed by atom N5, C4, and finally C3 with a much less accessible surface area. The presence of the carbonyl oxygen in close proximity to atom C3 prevents, to some extent, the solvent from approaching it.
Alkane diazonium ions are known to participate in substitution, elimination, and rearrangement reactions.81–84 Diazotization of n-butanamine, for example, yields products consistent with SN1 (2-butanol) and SN2 (1-butanol) substitution; products consistent with elimination (1-butene, trans-2-butene, cis-2-butene); and products consistent with rearrangement (2-butanol and diastereomeric cis and trans 2-butene).85,86 The diazonio moiety is recognized as one of the most stable leaving groups.86 Loss of N2 is thought to occur via a concerted process which leads to either primary alkylation or to rearrangement producing a secondary carbocation.87 This secondary cation, in turn, can undergo SN1, or elimination reactions.81–84 While the size of the alkyl chain can limit chemical outcomes somewhat (methane diazonium ion is restricted to SN2 reactions, for example), alkyl diazonium ions often participate in all the above chemistries.86
We generated frontier orbitals for both NNKDI and PDI to examine the ions' role as alkylating agents. Condensed Fukui indices were also predicted. Since we studied substrates, our results speak to initial reactivity. The canonical molecular orbital picture of second-order nucleophilic substitution begins with donation of electron density from the nucleophile into the substrate LUMO. This orbital is expected to have sigma antibonding character (along the C–N bond for our work). This facilitates the displacement of the leaving group (N2 for diazonium species). Alternately, the first-order analog of this reaction begins with the donation of electron density from the substrate HOMO to the leaving group LUMO. Here, the substrate HOMO is expected to have σ bonding character (along the C–N bond for our study).
Our results, while internally consistent, do not neatly support either of these frameworks. For example, both the NNKDI HOMO and PDI HOMO lack the C–N sigma bonding character expected for the SN1 pathway. Likewise, the NNKDI LUMO and PDI LUMO lack the C–N sigma antibonding character expected for the SN2 mechanism. Since orbital ordering may be approximate, we examined additional molecular orbitals similar in energy to the predicted HOMO and LUMO for both NNKDI and PDI to find candidates that would support SN1 or SN2 reactivity. The LUMO+1 orbital in both species has C–N σ antibonding character. Donation of electron density into this orbital by a nucleophile proximate to the diazonio α carbon is possible and is consistent with an SN2 mechanism. Our condensed Fukui indices suggest that nucleophilic attack will be initiated at the terminal nitrogen of either species (diazonio π system, NNKDI or PDI LUMO). In addition, our NBO analysis has shown that there is a stabilization energy of 8.23 kcal mol−1 due to the N6 lone pair → C4–N5 antibonding orbital delocalization. Thus, donation of electron density to the terminal nitrogen could impact the strength of carbon nitrogen bond. Alkylation at this nitrogen would produce azo products. While azo compounds are observed in experimental work on aryl diazonium ions88 they are not found in the experimental literature on NNKDI or PDI. Instead, alkylation at the carbon alpha (or beta) to the diazonio group has been seen; and significant evidence of an SN2-like and/or an SN1-like alkylation mechanism exists.9,18,85
When viewed within this experimental context, or Fukui indices suggest that bonding or coordination of a nucleophile to the terminal nitrogen is likely in both PDI and NNKDI. This may influence the initial reactivity of these species by occupying a site of significant electrophilicity. However, this interaction does not directly produce alkylation products; and a proximate nucleophile may attack elsewhere in either a subsequent or initial step. For example, in NNKDI, rotation around the C2–C3 torsion can bring C4 close to O1. In that conformation, there is the potential for spatial overlap between the NNKDI HOMO (ring/carbonyl π system) and the NNKDI LUMO+1 (C–N σ antibonding orbital) which may liberate N2 and form a new ring system (Fig. 6). This reactivity is consistent with the Fukui index of the carbonyl oxygen which is indicated as a site for electrophilic attack. The oxonium ion produced in this intramolecular reaction has been proposed previously.4 Our single point calculations suggest a significant rotational barrier for this chemistry (about 140 kJ mol−1, see ESI†). Classical MD simulations do not include any quantum mechanical effects, such as electron transfer, and in our case electron polarization as well. Thus, when the dihedral C1–C2–C3–C4 was approximately in between 30° and −30° (and the intramolecular process would be initiated), our MD simulations neglected these effects. But, given sufficient time and an absence of competing nucleophiles, this ion is likely to form. This species is an exciting target for future work on NNKDI. Likewise, mechanisms featuring initial attack at the terminal nitrogen should also be explored.
5 Conclusions
Static ab initio calculations reveal 19 minima on NNKDI's rotational potential energy surface. Vibrational analyses show an approximately 660 cm−1 C–N deformation and an approximately 2440 cm−1 N–N stretching mode in NNKDI. Geometric and vibrational results suggest strong similarities between PDI and NNKDI near the diazonio moiety. Orbital analyses and Fukui indices show that the terminal nitrogen in either species is a site of significant electrophilicity. While electrostatic potential findings, on the other hand, demonstrate a high electric potential on the formally charged nitrogen and its α carbon. Classical molecular dynamics simulations on NNKDI suggest that the solution-phase side chain will spend most of its time in a relatively extended configuration and that the presence of the carbonyl group limits the solvent accessibility of C4.Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. M., E. W., and C. D. thank the Pott College and the University of Southern Indiana for their support. D. W. and C. D. thank the USI Endeavor Program for their support. C. D. thanks the Indiana Academy of Science for their support via a Research Grant.Notes and references
- IARC Working Group on the Evaluation of Carcinogenic Risk to Humans, IARC Monographs on the Evaluation of carcinogenic Risks to Humans, Personal Habits and Indoor Combustions, International Agency for Research on Cancer, France, 2012, vol. 100E, https://monographs.iarc.fr/iarc-monographs-on-the-evaluation-of-carcinogenic-risks-to-humans-17/ Search PubMed.
- S. S. Hecht, Nat. Rev. Cancer, 2003, 3, 733–744 CrossRef CAS PubMed.
- G. P. Pfeifer, M. F. Denissenko, M. Olivier, N. Tretyakova, S. S. Hecht and P. Hainaut, Oncogene, 2002, 21, 7435–7451 CrossRef CAS PubMed.
- S. S. Hecht, Chem. Res. Toxicol., 1998, 11, 559–603 Search PubMed.
- S. S. Hecht, P. W. Villalta, S. J. Sturla, G. Cheng, N. Yu, P. Upadhyaya and M. Wang, Chem. Res. Toxicol., 2004, 17, 588–597 Search PubMed.
- V. P. Jasti, T. E. Spratt and A. K. Basu, Chem. Res. Toxicol., 2011, 24, 1833–1835 Search PubMed.
- E. S. Carlson, P. Upadhyaya, P. W. Villalta, B. Ma and S. S. Hecht, Chem. Res. Toxicol., 2018, 31, 358–370 Search PubMed.
- B. Chen, L. Liu, A. Castonguay, R. R. Maronpot, M. W. Anderson and M. You, Carcinogenesis, 1993, 14, 1603–1608 CrossRef CAS PubMed.
- S. S. Hecht, Mutat. Res., 1999, 424, 127–142 CrossRef CAS PubMed.
- M. J. Thun, C. A. Lally, E. E. Calle, J. Heath, W. Clark, J. T. Flannery and W. D. Flanders, J. Natl. Cancer Inst., 1997, 89, 1580–1586 CrossRef CAS.
- S. S. Hecht, T. E. Spratt and N. Trushin, Carcinogenesis, 1988, 9(1), 161–165 CrossRef CAS.
- R. S. Mijal, N. A. Loktionova, C. C. Vu, A. E. Pegg and L. A. Peterson, Chem. Res. Toxicol., 2005, 18, 1619–1625 Search PubMed.
- B. Ma, P. W. Villalta, A. T. Zarth, D. Kotandeniya, P. Upadhyaya, I. Stepanov and S. S. Hecht, Chem. Res. Toxicol., 2015, 28, 2151–2159 Search PubMed.
- J. Leng and Y. Wang, Anal. Chem., 2017, 89, 9124–9130 CrossRef CAS.
- N. Trushin, A. Rivenson and S. S. Hecht, Cancer Res., 1994, 54, 1205–1211 CAS.
- A. M. Urban, P. Upadhyaya, Q. Cao and L. A. Peterson, Chem. Res. Toxicol., 2012, 25, 2167–2178 Search PubMed.
- L. A. Peterson, Chem. Res. Toxicol., 2017, 30, 420–433 Search PubMed.
- X. Lu, J. M. Heilman, P. Blans and J. C. Fishbein, Chem. Res. Toxicol., 2005, 18, 1462–1470 Search PubMed.
- C. Deligkaris and E. Millam, Toxicol. Res., 2019, 8, 531–543 CrossRef CAS PubMed.
- K. S. Ekanayake and P. R. Lebreton, J. Comput. Chem., 2006, 27, 277–286 CrossRef CAS PubMed.
- K. S. Ekanayake and P. R. Lebreton, J. Comput. Chem., 2007, 28, 2352–2365 CrossRef CAS PubMed.
- K. Bhattacharjee and P. K. Shukla, Int. J. Quantum Chem., 2014, 114, 1637–1644 CrossRef CAS.
- R. Glaser and C. J. Horan, J. Org. Chem., 1995, 60, 7518–7528 CrossRef CAS.
- F. Doctorovich, N. Escola, C. Trápani, D. A. Estrin, M. C. González Lebrero and A. G. Turjanski, Organometallics, 2000, 19, 3810–3817 CrossRef CAS.
- P. Perez, J. Org. Chem., 2003, 68, 5886–5889 CrossRef CAS.
- B. F. Minaev, S. V. Bondarchuk and M. A. Girtu, J. Mol. Struct., 2009, 904, 14–20 CrossRef CAS.
- A. K. Katz, H. L. Carrell, C. E. Afshar, J. P. Glusker, D. Desai and S. Amin, Struct. Chem., 1999, 10, 439–443 CrossRef CAS.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. C. Slater, The Self-Consistent Field for Molecular and Solids, Quantum Theory of Molecular and Solids, McGraw-Hill, New York, 1974, vol. 4 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. F. Sousa, P. A. Fernandes and M. J. Ramos, J. Phys. Chem. A, 2007, 111, 10439–10452 CrossRef CAS PubMed.
- J. S. Binkley, J. A. Pople and W. J. Hehre, J. Am. Chem. Soc., 1980, 102 Search PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54 Search PubMed.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28 Search PubMed.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- E. Apra, E. J. Bylaska, W. A. de Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauet, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Fruchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Gotz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jonsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Martin del Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. Van Voorhis, A. Vazquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Wolinski, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102 CrossRef CAS PubMed.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 7.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2018 Search PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- M. S. Gordon and M. W. Schmidt, Theory and Applications of Computational Chemistry, Elsevier, Amsterdam, 2005, pp. 1167–1189 Search PubMed.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Wloch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102 CrossRef CAS.
- P. Piecuch, S. A. Kucharski, K. Kowalski and M. Musiał, Comput. Phys. Commun., 2002, 149, 71–96 CrossRef CAS.
- J. L. Bentz, R. M. Olson, M. S. Gordon, M. W. Schmidt and R. A. Kendall, Comput. Phys. Commun., 2007, 176, 589–600 CrossRef CAS.
- R. M. Olson, J. L. Bentz, R. A. Kendall, M. W. Schmidt and M. S. Gordon, J. Chem. Theory Comput., 2007, 3, 1312–1328 CrossRef.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- P. Cieplak, W. D. Cornell, C. Bayly and P. A. Kollman, J. Comput. Chem., 1995, 16, 1357–1377 CrossRef CAS.
- A. W. Sousa da Silva and W. F. Vranken, BMC Res. Notes, 2012, 5, 367 CrossRef.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS.
- O. Guvench and A. D. MacKerell, J. Mol. Model., 2008, 14, 667–679 CrossRef CAS PubMed.
- M. Zgarbova, M. Otyepka, J. Sponer, A. Mladek, P. Banas, T. E. Cheatham and P. Jurecka, J. Chem. Theory Comput., 2011, 7, 2886–2902 CrossRef CAS PubMed.
- W. R. Inc., Mathematica, Version 12.1, https://www.wolfram.com/mathematica, Champaign, IL, 2020 Search PubMed.
- S. Pall and B. Hess, Comput. Phys. Commun., 2013, 184, 2641–2650 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- S. Nose, J. Chem. Phys., 1984, 81, 511–519 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- S. Nose and M. Klein, Mol. Phys., 1983, 50, 1055–1076 CrossRef CAS.
- MarvinSketch 18.10, ChemAxon, https://www.chemaxon.com Search PubMed.
- B. Bode and M. Gordon, J. Mol. Graphics Modell., 1998, 16(3), 133–138 CrossRef CAS PubMed.
- J. Schmidt and W. Polik, WebMO Enterprise, WebMO LLC, https://www.webmo.net Search PubMed.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure: IV. Constants of Diatomic Molecules, Springer, Boston, MA, 1979 Search PubMed.
- Landolt-Bornstein: Group II: Atomic and Molecular Physics Volume 21: Structure Data of Free Polyatomic Molecules., ed. K. Kuchitsu, Springer-Verlag, Berlin, 1992 Search PubMed.
- Landolt-Bornstein: Group II: Atomic and Molecular Physics Volume 7: Structure Data of Free Polyatomic Molecules., ed. K. Hellwege and A. Hellwege, Springer-Verlag, Berlin, 1976 Search PubMed.
- G. J. Karabatsos and N. Hsi, J. Am. Chem. Soc., 1965, 87, 2864–2870 CrossRef CAS.
- G. Herzberg, Electronic Spectra and Electronic Structure of Polyatomic Molecules, Van Nostrand, New York, 1966 Search PubMed.
- V. Amir-Ebrahimi, A. Choplin, J. Demaison and G. Roussy, J. Mol. Spectrosc., 1981, 89, 42–52 CrossRef CAS.
- Structure of Free Polyatomic Molecules: Basic Data, ed. K. Kuchitsu, Springer, Berlin, Heidelberg, 1998 Search PubMed.
- K. K. Irikura, J. Phys. Chem. Ref. Data, 2007, 36, 389–397 CrossRef CAS.
- P. Politzer and J. S. Murray, in Molecular Electrostatic Potentials and Chemical Reactivity, John Wiley & Sons, Ltd, 1991, pp. 273–312 Search PubMed.
- T. E. Agnew, H.-J. Kim and J. C. Fishbein, J. Phys. Org. Chem., 2004, 17, 483–488 CrossRef CAS.
- L. A. Peterson, D. P. Predecki, N. M. Thomson, P. W. Villalta and E. E. Donaldson, Chem. Res. Toxicol., 2003, 16, 661–667 Search PubMed.
- S. G. Carmella, S. S. Kagan, T. E. Spratt and S. S. Hecht, Cancer Res., 1990, 50, 5453–5459 CAS.
- J. F. McGarrity and T. Smyth, J. Am. Chem. Soc., 1980, 102, 7303–7308 CrossRef CAS.
- D. Brosch and W. Kirmse, J. Org. Chem., 1991, 56, 907–908 CrossRef CAS.
- M. B. Smith and J. March, Aliphatic Substitution: Nucleophilic and Organometallic, John Wiley & Sons, Ltd, 2006, ch. 10, pp. 425–656 Search PubMed.
- F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry, Kluwer Academic/Plenum Pub., New York, 4th edn, 2000 Search PubMed.
- M. Stiborova, B. Asfaw, E. Frei, H. H. Schmeiser and M. Wiessler, Chem. Res. Toxicol., 1995, 8, 489–498 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra04343a |
| This journal is © The Royal Society of Chemistry 2021 |