Open Access Article
Open Access ArticleCoarse-grained molecular dynamics simulations of nanoplastics interacting with a hydrophobic environment in aqueous solution†
Lorenz F. Dettmann a,
Oliver Kühn
a,
Oliver Kühn ab and
Ashour A. Ahmed
ab and
Ashour A. Ahmed *ab
*ab
aUniversity of Rostock, Institute of Physics, Albert-Einstein-Str. 23-24, D-18059 Rostock, Germany. E-mail: ashour.ahmed@uni-rostock.de
bUniversity of Rostock, Department of Life, Light and Matter (LLM), Albert-Einstein-Str. 25, D-18059 Rostock, Germany
First published on 16th August 2021
Abstract
Nanoplastics (NPs) are emerging threats for marine and terrestrial ecosystems, but little is known about their fate in the environment at the molecular scale. In this work, coarse-grained molecular dynamics simulations were performed to investigate nature and strength of the interaction between NPs and hydrophobic environments. Specifically, NPs were simulated with different hydrophobic and hydrophilic polymers while carbon nanotubes (CNTs) were used to mimic surface and confinement effects of hydrophobic building blocks occurring in a soil environment. The hydrophobicity of CNTs was modified by introducing different hydrophobic and hydrophilic functional groups at their inner surfaces. The results show that hydrophobic polymers have a strong affinity to adsorb at the outer surface and to be captured inside the CNT. The accumulation within the CNT is even increased in presence of hydrophobic functional groups. This contribution is a first step towards a mechanistic understanding of a variety of processes connected to interaction of nanoscale material with environmental systems. Regarding the fate of NPs in soil, the results point to the critical role of the hydrophobicity of NPs and soil organic matter (SOM) as well as of the chemical nature of functionalized SOM cavities/voids in controlling the accumulation of NPs in soil. Moreover, the results can be related to water treatment technologies as it is shown that the hydrophobicity of CNTs and functionalization of their surfaces may play a crucial role in enhancing the adsorption capacity of CNTs with respect to organic compounds and thus their removal efficiency from wastewater.
1 Introduction
Plastics are synthetic or semi-synthetic organic materials that contain mostly polymers as the main component. They are lightweight, corrosion-resistant and inexpensive materials with a wide range of applications. The downside of their durability are the problems associated with plastic waste and plastic debris in the environment. Plastic debris can disintegrate into smaller particles, even under ambient conditions.1 Plastic particles that are smaller than a few millimeters in size are commonly known as microplastics and particles smaller than 1000 nm are known as nanoplastics (NPs).2 These particles are widespread in the environment, including the oceans3 and freshwater in Europe,4 North America,5 and Asia.6 In marine ecosystems, plastic waste do not only cause aesthetic problems, but it can be also digested by organisms that mistake it for food.7 80% of the plastics in the marine wastes come from land.8 It was estimated that there may be 4 to 23 times more microplastics on land than in the ocean and that soil alone may contain more microplastics than the oceans.9 In terrestrial systems, a primary entry point for microplastics is the agroecosystem, which is connected to the wide application of plastic mulch and sewage sludge.10–13In agricultural ecosystems, various noxious substances, like persistent organic pollutants, or heavy metals can be adsorbed on plastic particles. Thereby, plastic particles can act as vectors for such environmental contaminants.14 In general, transformations of NPs via homo- and hetero-aggregation could lead to advective flow transport, sedimentation, photo- and biodegradation, and/or sediment entrapment might occur.15,16
Estimation of NPs in the environment requires very sensitive and selective analytical techniques to detect the different types of NPs. These techniques would have to be sensitive towards particle sizes in the nanometer range and to concentrations down to nanograms per liter. Regarding the NPs investigation in soil, none of the published methods, such as vibrational spectroscopy or chromatography seems to be ideally suitable to detect these very small plastic particles. Regarding the spectroscopic measurements, the background fluorescence of organic matter or pigments of some polymers can strongly interfere with the spectra of interest, making them unidentifiable.17 Moreover, soil components can form relatively stable aggregates which may enclose plastic particles.18 Ongoing modifications and combinations of methods, however, may help to enhance the currently very limited data in this field of research.19
Carbon nanotubes (CNTs) are macromolecules formed by sheets of graphene. They are characterized by a very high surface area, low density, high mechanical resistance, strong hydrophobicity and severe biodegradation.20 Due to their unique physicochemical properties, CNTs have a wide range of technological applications.21 This includes their use in the fields of water treatment and agricultural sector. In agricultural ecosystems, CNTs were used as nanosensors for various tasks involving detection and release of toxic substances to regulate plant growth and also to increase the life of fruits after harvest.22–27 But also some toxic effects have been recorded for CNTs in soil and specifically in the agricultural sector.28,29
In a more fundamental study, Hyung and Kim30 investigated the adsorption behavior of standard humic and fulvic acids to multi-walled carbon nanotubes (MWCNTs). Based on the Freundlich model, they found that there is a positive linear correlation between adsorption capacity and amount of aromatic group content. Ateia et al.31 studied the adsorption process of the same humic and fulvic acids on MWCNTs and also found a linear correlation between adsorption constants and aromaticity (aromatic content) of a specific molecular system. In addition, they pointed to the dependence of the adsorption on the degree of oxidation and carboxylic acidity of the considered organic molecules. In a metastudy, Engel and Chefetz32 evaluated a large set of data to quantitatively validate the correlation between aromatic content of dissolved organic matter and its adsorption to CNTs. The result has been negative, i.e. no correlation was observed. This contradiction with earlier work on specific cases was explained by the complexity and heterogeneity of dissolved organic matter and different CNTs characteristics.
While there is a huge number of literature covering interactions between NPs33–35 or CNTs30,31,36–38 with organic compounds, no studies are addressing the interaction between NPs and CNTs, although both chemical compounds might coexist, especially in the terrestrial environment. Moreover, CNTs provide a simple model system for studying the interaction of NPs with hydrophobic surfaces and cavities, the latter being an abundant motif in macromolecular soil organic matter particles.39,40 Specific functional groups present in these macromolecules can easily be added to the CNTs and their effect, e.g., on NPs binding can be quantified. Therefore, our objective is to introduce a molecular level understanding for the interaction of NPs with CNTs, which not only addresses this particular system but it should also mimic aspects of the interaction of NPs with soil organic matter. It should be noted that polymers in confined environments were investigated extensively throughout the last years.41–47 Such models are not only a classical problem in polymer physics,48 but also of interest because of their connection to biological processes like DNA packing in capsids49 or chromosome separation during cell division.50 In most of the investigations, entropic effects, chain formation or segregation of multiple chains are in the main focus.
In the present contribution, coarse-grained molecular dynamics (CGMD) as an effective approach to describe polymers and CNTs51–54 will be used to model and simulate the behavior and interactions between NPs (unbranched polymer chains) and CNTs (bare and decorated with functional groups) in the presence of water. The overarching goals are (i) to introduce CGMD as an efficient tool for studying NP in the environmental context and (ii) to show the value of the generic model of functionalized CNTs, which captures essential aspects of the interaction of NPs with functional groups and hydrophobic cavities in situations where the actual atomistic information remains elusive due to complexity of composition and structural heterogeneity.
The rest of the paper is organized as follows. A detailed description of the modeling approach and computational details is presented in the next section. Then, the simulation results of different model systems are discussed. Finally, conclusions concerning the most important outcomes are presented.
2 Methods
2.1 Molecular modeling
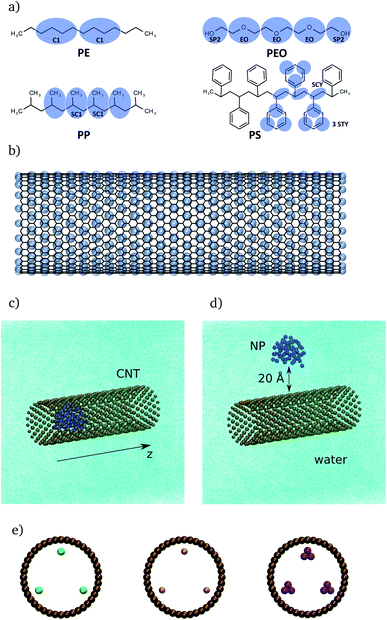
The present study focuses on three different model systems. First, NPs in water will be studied to establish a relation between the number of monomer units and the radius of gyration in absences of CNTs. Second, the CNT is included to investigate its interaction with the NPs. Third, the CNTs are functionalized with organic groups to investigate the effect of the modified hydrophobicity of CNTs on the interaction between NPs and CNTs.2.2 Computational details
MARTINI force field60 based coarse-grained molecular dynamics simulations were performed using the GROMACS software package (version 2019.04).72 The use of this coarse-graining approach has the advantages of accessing longer simulation times and larger system sizes compared with atomistic MD simulations. On the other hand, one has to be aware that this approach comes with the cost of reduced accuracy due to the lower resolution. Furthermore, the dynamics of the systems are accelerated due to the smoothed free energy surface. For further information about the coarse-grained approach, see Kmiecik et al.73 for a general overview and Marrink and Tieleman74 for a perspective on the MARTINI model. After energy minimization, an NPT simulation of 100 ns was done to adjust the box dimensions. In the latter step, the polymers were kept fixed at their initial position. Production runs were carried out with NVT molecular dynamics simulations for 500 ns for each setup. Here, the CNT was kept fixed at its initial position. The time step was set to 20 fs. In combination with the Verlet neighbor list scheme, a straight cutoff with a cutoff-distance of 11 Å was used. Furthermore, the temperature was controlled with the velocity-rescale thermostat75 using a coupling constant of 1 ps. To control the pressure in the NPT simulations, the Berendsen barostat with a coupling constant of 12 ps was applied. Furthermore, the compressibility of the system was set to 3 × 10−4 bar−1. Freezing of water is a common problem in coarse-grained simulations.60,76,77 To overcome this problem and decrease the probability of freezing, antifreeze (AF) particles with concentration of 15% with respect to water particles were considered. In addition, a temperature of 310 K was used for the simulations in the NPT and NVT ensembles. The issues related to water freezing and diffusion of water through CNTs with different lengths and diameters were considered in the ESI (see Section I involving Table S1, Fig. S1 and S2†).The radius of gyration, Rg, is defined as the mean-squared distance of the polymer beads to their center of mass, rG, i.e.
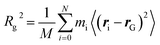 | (1) |
To characterize the strength of interaction/binding of NPs (polymers) to non-polar environment (CNT), interaction energies Eint between polymers and the rest of the system (CNT and water) were calculated as the sum of the Lennard–Jones interactions:
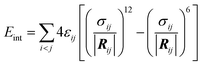 | (2) |
These energies were calculated via energy groups using GROMACS tools. The cutoff for the Lennard–Jones interaction was set to 11 Å, which is the standard cutoff used in the MARTINI force field. For the present models, no charged beads were applied. However, it should be emphasized that the electrostatic interactions are involved implicitly within the Lennard–Jones parameters and especially via the interaction strength ε.60 In principle, 10 different interaction levels among polar, non-polar, apolar and charged molecular systems or moieties could be defined based on the ε parameter. GROMACS tools were also used to calculate the partial density profiles of the NP particles along the z-dimension of the CNT (see Fig. 1c and d). Given the full density ρ(r), the partial density is defined as
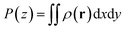 | (3) |
For a better comparison between the different polymer types, the resulting partial density distribution P(z) was normalized by its numerically calculated integral along the CNT:
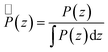 | (4) |
This quantity can be interpreted as a position probability density.
3 Results and discussion
The NPT equilibration simulations produced a density of around 0.86 g cm−3 for each investigated system. This deviation mainly comes from the usage of antifreeze-particles. It is a known effect and is caused by the stronger repulsion between antifreeze and water particles. It is assumed that models are still realistic enough to represent a system at nearly room temperature. It should be noted that all analyses are done with considering only the NVT production trajectories.3.1 NPs in water
The dependence of the radius of gyration, eqn (1), on the number of monomers N is shown in Fig. 2 for each polymer. Physical properties of the polymers such as hydrophobicity and hydrophilicity can be read off from Fig. 2. For PEO, Rg for a given chain length is larger than for the other polymers. This points to the PEO's hydrophilic nature leading to a more unfolded structure as compared to the hydrophobic PE, PP, and PS which tend to minimize their contact area with a polar solvent. However, one should not take the overall lowest Rg values for PP as an indication of its largest hydrophobicity. Instead, one should also take into account the relatively short bond length and a low mapping compared to e.g. PE (see Table S2 in the ESI†). PS, on the other hand, has also a comparable short bond length between beads of its backbone, but shows the largest Rg from the hydrophobic polymers. This is due to the phenyl groups, that increase the occupied volume of the folded PS chain and therefore raise Rg. The degree of hydrophobicity was estimated by calculating interaction energies and radial distribution functions between NPs and water (see Fig. S3 and S4 in the ESI†). From the interaction energy values, one can conclude that PE has the highest hydrophobicity, while PS has the lowest one among the considered hydrophobic polymers.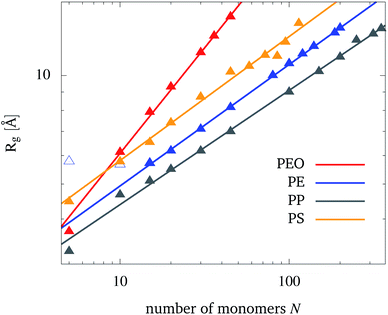 | ||
| Fig. 2 The dependence of the radius of gyration, Rg, on the number of monomers, N, for the polymers in water (symbols). Also shown is the fit to eqn (5) (straight lines). For PE, the first two data points are excluded from the fit. | ||
According to the Flory theory of polymers, Rg is proportional to the number of monomers to the power of the so-called Flory exponent ν.48 Therefore, the fit function
| Rg(N) = aNν | (5) |
| PEO | PE | PP | PS | |
|---|---|---|---|---|
| a [Å] | 1.58 | 2.27 | 2.11 | 2.63 |
| ν | 0.59 | 0.34 | 0.32 | 0.34 |
The Flory exponent makes a statement about the polymer–solvent interaction, especially whether the polymer is in a bad or good solvent. As water is polar, it is a good solvent for PEO and a bad solvent for PE, PP and PS. This can be observed from the calculated Flory exponents. According to the Flory theory for polymers, the Flory exponent is around 0.59, if a polymer is present in a good solvent, while it is around 0.33 if a polymer is present in a bad solvent. From the almost quantitative agreement observed in Table 1, one can conclude that the present coarse-grained model provides a reliable representation of the polymer–solvent interaction. There has been one previous study of PEO in water using the MARTINI force field by Grunewald et al.61 in which they obtained similar results (a = 1.81 and ν = 0.58). The larger value for a is likely due to the different temperature (298.15 K) and antifreeze particle concentration (AF = 10%) used by these authors.
Further, the reliability of the coarse-grained representation for the present modeled polymers in water was tested versus an atomistic representation. Specifically, 12 atomistic MD simulations based on the general CHARMM force field79,80 were performed considering all polymers (PE, PEO, PP and PS), each with three different chain lengths (10, 45 and 100 monomer units). For each case, about 20 ns MD simulation was carried out involving one polymer inside a water box with a density of about 1 g cm−3. The radii of gyration obtained by the CG simulation showed the same trend obtained by the atomistic simulation with a correlation having R2 = 0.99. Moreover, the CG representation showed a good correlation with the atomistic one for the interaction energy values (R2 = 0.95). This overall agreement between the results of both CG and atomistic representations refers to the validity and ability of the CG approach to simulate the present molecular models and especially the NPs interactions with water. For more details, see Section III in the ESI, Fig. S5, S6, Tables S3 and S4.†
3.2 NPs with CNTs in water
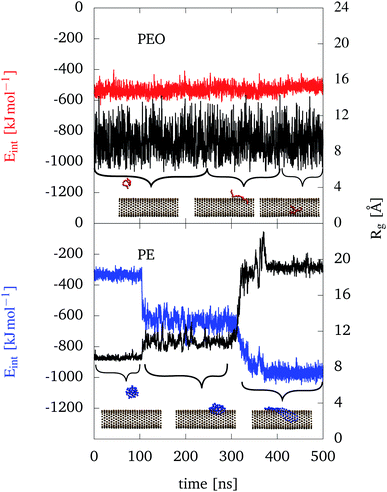
During the trajectory, PEO is in a relatively unfolded state (this holds for all Rg values used in this study) with an Rg value not much different from the solution case, see upper panel of Fig. 3. PEO partly sticks at the outer CNT wall (cf. middle snapshot), but frequently goes back into solution and returns. Once inside the CNT, PEO prefers to stay directly attached at the inner wall. Furthermore, some polymers go through every of the three introduced positions in one trajectory (in solution, outer walls, inside the CNT).
The interaction energies along the trajectory are shown in Fig. 3 as well. Notice that due to the cutoff for the Lennard–Jones potentials (11 Å) no interaction with the CNT would be observed when PEO is far away from the CNT in solution. However, from the red curve in the upper panel of Fig. 3 we notice that the interaction energy is nearly unchanged along the trajectory, no matter whether PEO is in solution or at the outer wall of the CNT. Once PEO is inside the CNT, the interaction is slightly decreased. Note that in this work, more negative Eint implies a stronger interaction. Thus we conclude that the interaction between PEO and the CNT is not much different than with water. The similarity of the two environments is also reflected in the almost unchanged radius of gyration which fluctuates around 9 Å. Of course, for the configurations inside the CNT once should note that Rg is much smaller than the CNT's diameter such that PEO does not have to make significant structural adjustments to go through the CNT.
The situation is rather different for the hydrophobic PE as shown in the lower panel of Fig. 3. In solution PE folds into a sphere like object. In contrast to PEO, once a PE chain adsorbs to the outer wall of the CNT, it stays there and does not go into solution again. Being at the outer wall, two configurations can be distinguished, i.e. a folded (A) and an unfolded one (B). The two configurations can be separated from one another by their different interaction energies and Rg values as seen in Fig. 3.
Regarding the interaction energy between PE and the rest of the system, the blue curve shows its course of time for sticking in an outer wall position. When the polymer is adsorbing at the CNT in the A configuration, the interaction energy drops to around −600 kJ mol−1. When the polymer is changing to configuration B, the interaction energy drops further by −350 kJ mol−1. This increased interaction is due to the increase of the contact area with the hydrophobic CNT as well as with the hydrophilic water in the unfolded state.
Compared to PEO, the interaction of PE with the CNT is much stronger and therefore leads to a more stable adsorbed configuration. Furthermore, the difference in positions (in solution or interacting with the CNT) are more pronounced for PE. As a consequence, PE doesn't change positions (solution, in/outside) in contrast to the hydrophilic PEO.
The differences between configuration A and B for PE are also visible in the time evolution of Rg in Fig. 3. For PE being in solution, Rg is around 9 Å. Then, after adsorbing at the CNT in configuration A, it is fluctuating around 11 Å and when the PE chain is unfolding itself into configuration B, Rg increases to around 19 Å. So, PE maximizes the contact area to the CNT, which significantly increases Rg and also the interaction energy, as discussed above.
Regarding the other two hydrophobic polymers, PP and PS, the following observations can be made from the trajectory data shown in Fig. S8 in the ESI.† Qualitatively, PP behaves like PE, e.g. there are similar configurations A and B although PP is slightly less unfolded in case B as compared with PE. In addition the energy drop when interacting with the CNT is generally weaker. In case of PS, there has been a difference insofar as it doesn't unfold once adsorbed at the outer wall of the CNT (see Fig. S8 in the ESI†). The increase of interaction upon adsorption is relatively modest only. This can be explained by the less flexible structure of PS such that a smaller part of the polymer can directly attach to the CNT (change of Rg is negligible small). PS shows a slight decrease in the interaction energy with the rest of the system, when being adsorbed at the CNT. This change is less pronounced, when compared to the other hydrophobic polymers PE and PP, but larger compared to PEO. This behavior also reflects the relative strong interaction energy of PS to water (see Fig. S3 in the ESI†), compared to the other hydrophobic polymers.
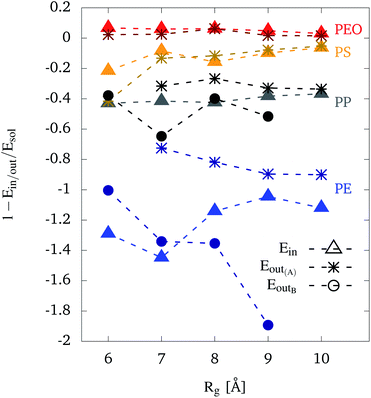
For the case of PEO, the relative interaction energies are above and close to zero for all chain lengths, no matter whether PEO is inside or adsorbed at the outer wall of the CNT. This confirms the conclusion drawn from Fig. 3, i.e. that there is no preference for PEO to be adsorbed at the CNT. The positive values indicate its hydrophilic character.
The other extreme is PE, which shows in particular noticeable differences with respect to the different configurations (cf. Fig. 3). Values for configuration A at the outer wall are around −0.8, slightly decreasing with increasing Rg. On the other hand, the relative interaction energies for configuration B are strongly decreasing with an increasing Rg. This clearly indicates that with increasing polymer length, the gain in interaction energy due to the higher contact area in the unfolded state outperforms the interaction with water which dominate for the shorter polymers. PE inside the CNT does not show a clear trend, except a minimum at Rg = 7 Å. PE (partly) unfolds inside the CNT. Given the size constraint due to the CNT, Rg = 7 Å is likely to present an optimum for unfolding and thus increasing the contact area. Compared to configuration B relative interaction energies for PE inside the CNT are lower or similar for a Rg up to Rg = 7 Å, but higher for longer polymer chains. All values for PE inside the CNT are lower than for configuration A. Hence, we can conclude that for shorter chain lengths an inside configuration is preferred, whereas long chains tend to unfold in an outer wall configuration.
The behavior of the other hydrophobic polymers, PP and PS, is intermediate between the cases of PEO and PE. Looking at the values for PP, relative interaction energies in configuration A and inside the CNT are approximately constant, around −0.3 and −0.4, respectively. For PP in configuration B, similar or lower values (e.g. for Rg = 7 Å) are observed, compared to the polymer being inside the CNT. Furthermore, configuration B results in lower values than configuration A. This result is similar to PE, although with a smaller gain in interaction energy. It agrees with the observations from the trajectories, namely that PP does not unfold itself that much when switching from configuration A to B, compared to PE.
Regarding the relative interaction energies for PS, the values are approximately constant around −0.2 to −0.1. Note that PS chains that were adsorbed at the CNT were observed in the folded A configuration only. An exception is the case Rg = 6 Å which could also have been counted as B configuration. This explains the deviation between interaction energies at this radius of gyration. Except for this case, all values for PS are higher than PP and lower than PEO.
3.3 NPs with functionalized CNTs in water
In the following, we will consider the influence of organic groups placed inside the CNT (as shown in Fig. 1e) on the binding of CNTs to NPs. The analysis will be performed in terms of the partial density![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (z) according to eqn (5). Partial densities for all polymers (with Rg = 7 Å) and different functionalizations are plotted in Fig. 5. Specifically, partial density profiles are calculated along the z axis of the CNT (see Fig. 1c). Here, z = 0 refers to the center of the CNT which the functional groups are placed as well. For each NP-CNT model with a specific functional group, only one simulation was performed by a starting conformation in which the polymer was placed at one CNT end (see Section 2.1.3). In principle, if the simulation started with a mirror configuration (i.e. the polymer was placed at the other CNT end), one would have a mirrored partial density profile. For this reason, in the following we are going to discuss the symmetrized partial density profiles, i.e. the normalized distribution (
(z) according to eqn (5). Partial densities for all polymers (with Rg = 7 Å) and different functionalizations are plotted in Fig. 5. Specifically, partial density profiles are calculated along the z axis of the CNT (see Fig. 1c). Here, z = 0 refers to the center of the CNT which the functional groups are placed as well. For each NP-CNT model with a specific functional group, only one simulation was performed by a starting conformation in which the polymer was placed at one CNT end (see Section 2.1.3). In principle, if the simulation started with a mirror configuration (i.e. the polymer was placed at the other CNT end), one would have a mirrored partial density profile. For this reason, in the following we are going to discuss the symmetrized partial density profiles, i.e. the normalized distribution (![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (z)+
(z)+![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (−z))/2 along |z|. The complete partial density profiles along both negative and positive z values are provided in Fig. S9 in the ESI.†
(−z))/2 along |z|. The complete partial density profiles along both negative and positive z values are provided in Fig. S9 in the ESI.†
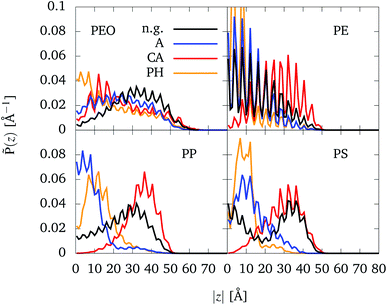 | ||
Fig. 5 Normalized partial densities, ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) (z), for different polymers being (mostly) inside the CNT (|z| < 50 Å), depending on the absolute value of the z-coordinate |z|. At z = 0 the functional groups are situated, cf. Fig. 1e). Four different cases are considered: no functional groups (black), alkane chains (blue), carboxylic acid groups (red), and phenyl groups (orange). Note that for PE-PH the two maxima which are out of the scale reach ∼0.16 Å−1. (z), for different polymers being (mostly) inside the CNT (|z| < 50 Å), depending on the absolute value of the z-coordinate |z|. At z = 0 the functional groups are situated, cf. Fig. 1e). Four different cases are considered: no functional groups (black), alkane chains (blue), carboxylic acid groups (red), and phenyl groups (orange). Note that for PE-PH the two maxima which are out of the scale reach ∼0.16 Å−1. | ||
The distributions show more or less pronounced periodic modulations with a period of about 4.1 Å. This can be explained with the structure of the CNT which consists of rings of beads separated by about 4.07 Å, see Fig. 1b. The beads of the polymers tend to be placed in between the CNT beads.
In case of PEO, no significant differences are visible between the different setups. There is a tendency that a small part of the chain leaves the CNT, which points to slight preference of PEO to be surrounded by water molecules. Moreover, in the cases of alkane and phenyl functionalization, the polymer chain passes z = 0 (see Fig. S9 in the ESI†). At first glance, it seems surprising that PEO accumulates at the phenyl groups. However, in the MARTINI force field the π electron density of the phenyl rings is represented by a higher ε value as compared to the alkane chain (2.66 vs. 2.53). Note that the interaction area with a phenyl group is also higher, because they are described by three beads. Further note that the interaction with the carboxylic acid groups is masked by the presence of water, attracted to that group.
The distributions for PE do not show significant differences with respect to the four setups. PE stays away from the center to avoid close contact with the hydrophilic carboxylic acid groups. In contrast the hydrophobic alkane chains and phenyl groups attract PE which therefore shows a higher density towards the middle of the CNT as compared to the bare CNT case. Since the bulky phenyl groups present an obstacle for PE it cannot easily penetrate through z = 0 and thus shows a higher density as compared with the case of alkane chains.
For the other hydrophobic polymers, PP and PS, the behavior concerning the hydrophilic carboxylic acid groups is similar to the case of PE. For PP and PS, one notices that the oscillations are less pronounced due to the shorter bond lengths (see Table S2 in the ESI†), i.e. its beads do not strictly fill out every of the spaces between the rings of the CNT. The same result can be obtained for PEO, also because it is less attracted by the CNT walls and therefore less influenced by its periodic potential. In absence of functional groups, PP and PS tend to stay closer to their initial positions as compared to PE. On the one hand side, this looks reasonable considering the different bulkiness, cf. Fig. 1a. On the other hand side, it could be that even the 500 ns trajectory doesn't fully sample the available configuration space.
In accordance with chemical intuition, the hydrophobic polymers have a preference for the hydrophobic functional groups and avoid hydrophilic ones. Water plays a role in controlling this behavior. Water particles are repelled by the hydrophobic functional groups, thus allowing the hydrophobic polymers to reach the region close the center more easily. On the other hand, water particles are attracted by carboxylic acid groups, making it harder for the hydrophobic polymers to access this region.
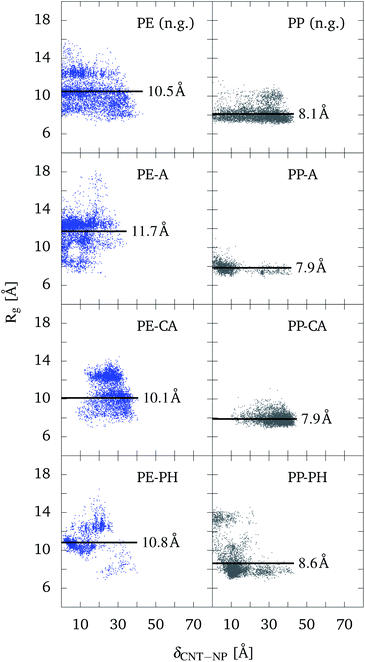
The structural changes of the polymers inside the functionalized CNT are addressed in Fig. 6. Here, Rg is plotted as a function of the distance between the CNT and polymer centers of masses. Only the cases PE and PP are considered here, which according to Fig. 5 show pronounced differences (for PEO and PS, see Fig. S10 in the ESI†).
For PE, the mean values of Rg (black lines) for the systems with alkane chains and phenyl groups are higher than for the carboxylic acid and bare CNT cases. This increase in Rg correlates with the attraction to the hydrophobic functional groups. Therefore, one can conclude that interaction with functional groups of similar (hydrophobic/hydrophilic) behavior leads to a slight unfolding of the polymers. In all cases, the polymer partly unfolds inside the CNT as compared to the solvated case (Rg = 7 Å). Concerning the spread of Rg values, the bare CNT and the case of alkane chains do not behave much different. For the system with the phenyl groups, data points are less spread. This comes due to an arrangement of PE to a ring structure (see Fig. S11 in the ESI†), in which it stays for more than the half of the simulation time. In this position, PE stays relatively fixed and close to the phenyl groups. It is the only case where such a special arrangement was observed. This might be only possible due to the phenyl groups occupying more space inside the CNT and therefore leading to a significant obstacle to the movement of the polymers. Also notable is the shift of the distribution towards larger δCNT-NP for the case of the carboxylic acid groups, which is caused by the repulsion of PE, or in general hydrophobic polymers (including PP) to the carboxylic acid groups. This can be observed as well in the distributions of Fig. 5.
Compared to PE, the distribution for PP is more compact. Also the pronounced tendency of PE to unfold inside the CNT is not observed for PP. This can be explained with the shorter bond length of PP in the coarse-grained picture, which allows it to stay more compact than PE. Regarding the atomistic picture, this comes due to the slightly more ramified structure caused by the methyl groups of PP. Notable changes are only observed for the system with phenyl groups. During the simulation, PP passes the phenyl groups to end up in a more stretched configuration leading to higher Rg values close to the center of the CNT.
Due to the final propagation time, one has to be careful with interpretation of the absolute numbers. Comparing the scenarios, however, the differences between functional groups and polymer types are becoming obvious. This holds in particular if one notes that PE and PP behave rather similar in water (cf. Fig. 2).
4 Conclusions
Coarse-grained molecular dynamics simulations were performed to address the interaction of NPs with hydrophobic parts of macromolecular organic soil constituents such as surfaces and functionalized cavities. NPs were modeled by four representative polymers, i.e. the hydrophilic PEO and the hydrophobic PE, PP, and PS. For the hydrophobic surfaces/functionalized cavities, a carbon nanotube model was taken.First, the behavior of the NPs in water was characterized by means of their radii of gyration. Results were found to be in agreement with Flory theory, thus validating the parametrization of the MARTINI force field for the particular models.
Next, the interaction of the polymers with a bare CNT in water was investigated. Based on the hydrophobicity/hydrophilicity of the polymers, different adsorption behaviors were observed. PEO as a hydrophilic polymer prefers solvation over adsorption either at the outer wall or inside, whereas the hydrophobic polymers stayed at the CNT, once adsorbed. In general, independent of the radius of gyration, PE showed the strongest interaction with the CNT, followed by PP and PS. For PE and PP, two configurations at the outer CNT wall were observed, which differ in the degree of unfolding. Unfolding increases the contact area with the CNT which leads to a more stable configuration.
The hydrophobicity of the CNT cavity was modified by introducing different hydrophilic and hydrophobic functional groups, i.e. alkane, phenyl and carboxylic acid groups. While PEO was not much influenced by the cavity and in fact it partly moved out during the simulation, a strong dependence of the behavior on the combination functional group/polymer was observed for the hydrophobic cases. Compared to the solution, PE shows the largest increase of the radius of gyration, followed by PP and PS. All three polymers tend to avoid the hydrophilic carboxylic acid groups. On the other hand, they are attracted by the hydrophobic groups and accumulate close to their positions inside the CNT.
Although these results are not unexpected, they can be viewed as a first step towards a mechanistic understanding of a variety of processes, e.g. in environmental soil chemistry, water treatment, and biochemistry. Correlating the present results to soil chemistry points to the critical role of the hydrophobicity in controlling the binding process of NPs in soil. In fact, the investigated models can be seen as capturing generic aspects of the interaction between NPs and soil organic matter (SOM). SOM is characterized by its overall hydrophobicity, apart from certain functional groups. The CNT in the present work acts as an effective hydrophobic environment for NPs. Due to the similarity of the chemical properties, conclusions can be made on how NPs might behave in SOM. Hydrophobic NPs could have a higher tendency to accumulate in soil and especially soil with high content of hydrophobic SOM. Furthermore, the results indicate that SOM cavities/voids could play an influential role in accumulation, i.e. immobilization, of NPs in soil. Moreover, the chemical nature of functional groups being present at SOM active surfaces and/or inside SOM cavities/voids plays a role by increasing/decreasing the extent of that accumulation. In a next step, refinement of the model can be envisioned, e.g. to include more complex SOM models such as macromolecules66,81,82 or to incorporate organic pollutants, heavy metals83,84 and other compounds85 bound to the NPs.
It is interesting to note that due to the well defined and unique physicochemical properties of CNTs, they have been used recently in water treatment technologies and especially to remove organic pollutants, e.g., dyes, pharmaceuticals/drugs, pesticides, phenols and aromatic amines. The present results are in accord with the literature in showing that the hydrophobicity of CNTs and modification/decoration of their surfaces with organic functional groups plays an important role in controlling the adsorption/binding/accumulation of organic compounds into outer and inner surfaces of CNTs.86–89 Therefore, fine tuning and modification for the hydrophobic character of CNTs with organic functional groups could enhance the adsorption capacity of CNTs to remove specific organic pollutants from aqueous solutions and waste water. Thus, the present contribution introduces a very fundamental model approaching the idea behind adsorption and removal of organic compounds by CNTs.
Conflicts of interest
There are no conflicts to declare.References
- K. N. Fotopoulou and H. K. Karapanagioti, The Handbook of Environmental Chemistry, Springer International Publishing, 2017, pp. 71–92 Search PubMed.
- J. Gigault, B. Pedrono, B. Maxit and A. T. Halle, Environ. Sci.: Nano, 2016, 3, 346–350 RSC.
- B. S. S. Ramasamy and S. Palanisamy, Environ. Sci. Pollut. Res., 2021 DOI:10.1007/s11356-021-14883-6.
- S. S. Sadri and R. C. Thompson, Mar. Pollut. Bull., 2014, 81, 55–60 CrossRef CAS PubMed.
- M. Zbyszewski, P. L. Corcoran and A. Hockin, J. Great Lakes Res., 2014, 40, 288–299 CrossRef CAS.
- C. M. Free, O. P. Jensen, S. A. Mason, M. Eriksen, N. J. Williamson and B. Boldgiv, Mar. Pollut. Bull., 2014, 85, 156–163 CrossRef CAS PubMed.
- M. R. Gregory, Philos. Trans. R. Soc., B, 2009, 364, 2013–2025 CrossRef PubMed.
- A. L. Andrady, Mar. Pollut. Bull., 2011, 62, 1596–1605 CrossRef CAS PubMed.
- A. A. de Souza Machado, W. Kloas, C. Zarfl, S. Hempel and M. C. Rillig, GCB Bioenergy, 2018, 24, 1405–1416 Search PubMed.
- M. C. Rillig, L. Ziersch and S. Hempel, Sci. Rep., 2017, 7, 1362 CrossRef PubMed.
- M. Bläsing and W. Amelung, Sci. Total Environ., 2018, 612, 422–435 CrossRef PubMed.
- A. A. Horton, A. Walton, D. J. Spurgeon, E. Lahive and C. Svendsen, Sci. Total Environ., 2017, 586, 127–141 CrossRef CAS PubMed.
- J. Wang, X. Liu, Y. Li, T. Powell, X. Wang, G. Wang and P. Zhang, Sci. Total Environ., 2019, 691, 848–857 CrossRef CAS PubMed.
- N. B. Hartmann, S. Rist, J. Bodin, L. H. Jensen, S. N. Schmidt, P. Mayer, A. Meibom and A. Baun, Integr. Environ. Assess. Manage., 2017, 13, 488–493 CrossRef PubMed.
- S. Wagner and T. Reemtsma, Nat. Nanotechnol., 2019, 14, 300–301 CrossRef CAS PubMed.
- O. S. Alimi, J. F. Budarz, L. M. Hernandez and N. Tufenkji, Environ. Sci. Technol., 2018, 52, 1704–1724 CrossRef CAS PubMed.
- A. Käppler, D. Fischer, S. Oberbeckmann, G. Schernewski, M. Labrenz, K.-J. Eichhorn and B. Voit, Anal. Bioanal. Chem., 2016, 408, 8377–8391 CrossRef PubMed.
- G. Zhang and Y. Liu, Sci. Total Environ., 2018, 642, 12–20 CrossRef CAS PubMed.
- J. N. Möller, M. G. J. Löder and C. Laforsch, Environ. Sci. Technol., 2020, 54, 2078–2090 CrossRef PubMed.
- K. Khosravi-Katuli, E. Prato, G. Lofrano, M. Guida, G. Vale and G. Libralato, Environ. Sci. Pollut. Res., 2017, 24, 17326–17346 CrossRef PubMed.
- M. F. L. De Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Science, 2013, 339, 535–539 CrossRef CAS PubMed.
- P.-H. Hermes, M.-P. Gabriela, V.-R. Ileana, C. Fusaro, L.-V. Fernando, M.-A. Mariana, C. Padilla-Rodríguez and F.-L. Fabián, Green Nanoparticles, ed. J. K. Patra, L. F. Fraceto, G. Das and E. V. R. Campos, Springer International Publishing, Cham, 2020, pp. 77–115 Search PubMed.
- W. Tang, T. Yan, F. Wang, J. Yang, J. Wu, J. Wang, T. Yue and Z. Li, Carbon, 2019, 147, 295–302 CrossRef CAS.
- V. Erady, R. J. Mascarenhas, A. K. Satpati, A. K. Bhakta, Z. Mekhalif, J. Delhalle and D. A, Microchem. J., 2019, 146, 73–82 CrossRef CAS.
- Y. Bakytkarim, S. Tursynbolat, Q. Zeng, J. Huang and L. Wang, J. Electroanal. Chem., 2019, 841, 45–50 CrossRef CAS.
- Y. Liu, S. Wang, W. Lan and W. Qin, Int. J. Biol. Macromol., 2019, 121, 1329–1336 CrossRef CAS PubMed.
- M. V. Khodakovskaya, B.-S. Kim, J. N. Kim, M. Alimohammadi, E. Dervishi, T. Mustafa and C. E. Cernigla, Small, 2012, 9, 115–123 CrossRef PubMed.
- X. Ma, J. Geiser-Lee, Y. Deng and A. Kolmakov, Sci. Total Environ., 2010, 408, 3053–3061 CrossRef CAS PubMed.
- P. Begum, R. Ikhtiari, B. Fugetsu, M. Matsuoka, T. Akasaka and F. Watari, Appl. Surf. Sci., 2012, 262, 120–124 CrossRef CAS.
- H. Hyung and J.-H. Kim, Environ. Sci. Technol., 2008, 42, 4416–4421 CrossRef CAS PubMed.
- M. Ateia, O. G. Apul, Y. Shimizu, A. Muflihah, C. Yoshimura and T. Karanfil, Environ. Sci. Technol., 2017, 51, 7101–7110 CrossRef CAS PubMed.
- M. Engel and B. Chefetz, Adv. Colloid Interface Sci., 2019, 271, 101993 CrossRef CAS PubMed.
- A. Bakir, S. J. Rowland and R. C. Thompson, Mar. Pollut. Bull., 2012, 64, 2782–2789 CrossRef CAS PubMed.
- T. Hüffer and T. Hofmann, Environ. Pollut., 2016, 214, 194–201 CrossRef PubMed.
- S. Seidensticker, P. Grathwohl, J. Lamprecht and C. Zarfl, Environ. Sci. Eur., 2018, 30, 30 CrossRef PubMed.
- K. Yang, L. Zhu and B. Xing, Environ. Sci. Technol., 2006, 40, 1855–1861 CrossRef CAS PubMed.
- C.-J. M. Chin, L.-C. Shih, H.-J. Tsai and T.-K. Liu, Carbon, 2007, 45, 1254–1260 CrossRef CAS.
- W. Chen, L. Duan, L. Wang and D. Zhu, Environ. Sci. Technol., 2008, 42, 6862–6868 CrossRef CAS PubMed.
- D. Petrov, D. Tunega, M. H. Gerzabek and C. Oostenbrink, Environ. Sci. Technol., 2017, 51, 5414–5424 CrossRef CAS PubMed.
- A. A. Ahmed, S. Thiele-Bruhn, S. G. Aziz, R. H. Hilal, S. A. Elroby, A. O. Al-Youbi, P. Leinweber and O. Kühn, Sci. Total Environ., 2015, 508, 276–287 CrossRef CAS PubMed.
- E. Slonkina and A. B. Kolomeisky, J. Chem. Phys., 2003, 118, 7112–7118 CrossRef CAS.
- H.-P. Hsu and P. Grassberger, J. Chem. Phys., 2004, 120, 2034–2041 CrossRef CAS PubMed.
- W. Reisner, K. J. Morton, R. Riehn, Y. M. Wang, Z. Yu, M. Rosen, J. C. Sturm, S. Y. Chou, E. Frey and R. H. Austin, Phys. Rev. Lett., 2005, 94, 196101 CrossRef PubMed.
- W. Sparreboom, A. van den Berg and J. C. T. Eijkel, Nat. Nanotechnol., 2009, 4, 713–720 CrossRef CAS PubMed.
- G. O. Ibáñez-García and P. Goldstein-Menache, Soft Matter, 2012, 8, 8666 RSC.
- B.-Y. Ha and Y. Jung, Soft Matter, 2015, 11, 2333–2352 RSC.
- M. P. Taylor, Macromolecules, 2017, 50, 6967–6976 CrossRef CAS.
- M. Rubinstein and R. Colby, Polymer Physics, OUP Oxford, 2003 Search PubMed.
- Q. Cao and M. Bachmann, Soft Matter, 2017, 13, 600–607 RSC.
- S. Jun and A. Wright, Nat. Rev. Microbiol., 2010, 8, 600–607 CrossRef CAS PubMed.
- F. Müller-Plathe, ChemPhysChem, 2002, 3, 754–769 CrossRef.
- J. Baschnagel, K. Binder, P. Doruker, A. A. Gusev, O. Hahn, K. Kremer, W. L. Mattice, F. Müller-Plathe, M. Murat, W. Paul, S. Santos, U. W. Suter and V. Tries, Viscoelasticity, Atomistic Models, Statistical Chemistry, Springer Berlin Heidelberg, Berlin, Heidelberg, 2000, vol. 152, pp. 41–156 Search PubMed.
- J. Zhao, J.-W. Jiang, L. Wang, W. Guo and T. Rabczuk, J. Mech. Phys. Solids, 2014, 71, 197–218 CrossRef CAS.
- S. Cranford and M. Buehler, Multiscale Modeling, ed. P. Derosa and T. Cagin, CRC Press, 2010, pp. 13–34 Search PubMed.
- R. Geyer, J. R. Jambeck and K. L. Law, Sci. Adv., 2017, 3, e1700782 CrossRef PubMed.
- S. Piehl, A. Leibner, M. G. J. Löder, R. Dris, C. Bogner and C. Laforsch, Sci. Rep., 2018, 8, 17950 CrossRef CAS PubMed.
- F. A. E. Lots, P. Behrens, M. G. Vijver, A. A. Horton and T. Bosker, Mar. Pollut. Bull., 2017, 123, 219–226 CrossRef CAS PubMed.
- D. He, Y. Luo, S. Lu, M. Liu, Y. Song and L. Lei, TrAC, Trends Anal. Chem., 2018, 109, 163–172 CrossRef CAS.
- J.-J. Guo, X.-P. Huang, L. Xiang, Y.-Z. Wang, Y.-W. Li, H. Li, Q.-Y. Cai, C.-H. Mo and M.-H. Wong, Environ. Int., 2020, 137, 105263 CrossRef CAS PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- F. Grunewald, G. Rossi, A. H. de Vries, S. J. Marrink and L. Monticelli, J. Phys. Chem. B, 2018, 122, 7436–7449 CrossRef CAS PubMed.
- E. Panizon, D. Bochicchio, L. Monticelli and G. Rossi, J. Phys. Chem. B, 2015, 119, 8209–8216 CrossRef CAS PubMed.
- G. Rossi, L. Monticelli, S. R. Puisto, I. Vattulainen and T. Ala-Nissila, Soft Matter, 2011, 7, 698–708 RSC.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- M. Vögele, J. Köfinger and G. Hummer, Faraday Discuss., 2018, 209, 341–358 RSC.
- H. R. Schulten and M. Schnitzer, Naturwissenschaften, 1993, 80, 29–30 CrossRef CAS.
- J. Kubicki and C. Trout, Geochemical and Hydrological Reactivity of Heavy Metals in Soils, ed. H. Magdi Selim and W. Kingery, CRC Press, 2003 Search PubMed.
- A. J. A. Aquino, D. Tunega, G. Haberhauer, M. H. Gerzabek and H. Lischka, Eur. J. Soil Sci., 2007, 58, 889–899 CrossRef CAS.
- A. J. A. Aquino, D. Tunega, H. Pašalić, G. E. Schaumann, G. Haberhauer, M. H. Gerzabek and H. Lischka, Environ. Sci. Technol., 2011, 45, 8411–8419 CrossRef CAS PubMed.
- A. A. Ahmed, O. Kühn and P. Leinweber, Sci. Total Environ., 2012, 441, 151–158 CrossRef CAS PubMed.
- A. A. Ahmed, O. Kühn, S. G. Aziz, R. H. Hilal and P. Leinweber, Sci. Total Environ., 2014, 476–477, 98–106 CrossRef CAS PubMed.
- E. Lindahl, M. J. Abraham, B. Hess and D. van der SpoelGROMACS 2020.3 Manual, Zenodo, 2020 Search PubMed.
- S. Kmiecik, D. Gront, M. Kolinski, L. Wieteska, A. E. Dawid and A. Kolinski, Chem. Rev., 2016, 116, 7898–7936 CrossRef CAS PubMed.
- S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801 RSC.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- S. J. Marrink, A. H. de Vries and A. E. Mark, J. Phys. Chem. B, 2004, 108, 750–760 CrossRef CAS.
- S. J. Marrink, X. Periole, D. P. Tieleman and A. H. de Vries, Phys. Chem. Chem. Phys., 2010, 12, 2254 RSC.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- J. Lee, X. Cheng, J. M. Swails, M. S. Yeom, P. K. Eastman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong, Y. Qi, S. Jo, V. S. Pande, D. A. Case, C. L. Brooks, A. D. MacKerell, J. B. Klauda and W. Im, J. Chem. Theory Comput., 2015, 12, 405–413 CrossRef PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell, J. Comput. Chem., 2010, 31, 671–690 CAS.
- H.-R. Schulten and P. Leinweber, Biol. Fertil. Soils, 2000, 30, 399–432 CrossRef CAS.
- H. Feng, H. Zhang, H. Cao, Y. Sun, A. Zhang and J. Fu, Environ. Sci. Technol., 2018, 52, 14228–14234 CrossRef CAS PubMed.
- J. Cheng, J. Liang, L. Dong, J. Chai, N. Zhao, S. Ullah, H. Wang, D. Zhang, S. Imtiaz, G. Shan and G. Zheng, RSC Adv., 2018, 8, 40813–40822 RSC.
- J. Liang, J. Li, X. Li, K. Liu, L. Wu and G. Shan, Sep. Purif. Technol., 2020, 230, 115874 CrossRef CAS.
- G. B. Braun, K. N. Sugahara, O. M. Yu, V. R. Kotamraju, T. Mölder, A. M. Lowy, E. Ruoslahti and T. Teesalu, J. Controlled Release, 2016, 232, 188–195 CrossRef CAS PubMed.
- V. K. Gupta, R. Kumar, A. Nayak, T. A. Saleh and M. Barakat, Adv. Colloid Interface Sci., 2013, 193–194, 24–34 CrossRef CAS PubMed.
- W. Wu, K. Yang, W. Chen, W. Wang, J. Zhang, D. Lin and B. Xing, Water Res., 2016, 88, 492–501 CrossRef CAS PubMed.
- J.-G. Yu, X.-H. Zhao, H. Yang, X.-H. Chen, Q. Yang, L.-Y. Yu, J.-H. Jiang and X.-Q. Chen, Sci. Total Environ., 2014, 482–483, 241–251 CrossRef CAS PubMed.
- X. Qu, P. J. Alvarez and Q. Li, Water Res., 2013, 47, 3931–3946 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra04439g |
| This journal is © The Royal Society of Chemistry 2021 |