Electronic properties of a two-dimensional van der Waals MoGe₂N₄/MoSi₂N₄ heterobilayer: effect of the insertion of a graphene layer and interlayer coupling

Abstract

van der Waals heterostructures (vdWHs) based on 2D layered materials with select properties are paving the way to integration at the atomic scale, and may give rise to new heterostructures exhibiting absolutely novel physics and versatility. Herein, we investigate the structural and contact types in a 2D vdW heterobilayer between MoGe₂N₄ and MoSi₂N₄ monolayers, and the monolayers in the presence of electrical graphene (GR) contact. In the ground state, the MoGe₂N₄/MoSi₂N₄ heterobilayer forms type-II band alignment, which effectively promotes the separation of electrons and holes and provides opportunity for further electrons and holes. Thus, the MoGe₂N₄/MoSi₂N₄ heterobilayer is promising for designing optoelectronic devices with significantly suppressed carrier-recombination. Interestingly, the insertion of the GR contact to a MoGe₂N₄/MoSi₂N₄ heterobilayer gives rise to the formation of a metal/semiconductor contact. Depending on the GR position relative to the MoGe₂N₄/MoSi₂N₄ heterobilayer, the GR-based heterostructure can form either an n-type or p-type Schottky contact. Intriguingly, the contact barriers in the GR contacted MoGe₂N₄/MoSi₂N₄ heterobilayer are significantly smaller than those in the GR contacted with MoGe₂N₄ or MoSi₂N₄ monolayers, suggesting that the GR/MoGe₂N₄/MoSi₂N₄ heterostructure offers an effective pathway to reduce the Schottky barrier, which is highly beneficial for improving the charge injection efficiency of the contact heterostructures. More interestingly, by controlling the interlayer coupling through stacking, both the Schottky barriers and contact types in the GR/MoGe₂N₄/MoSi₂N₄ heterostructure can be manipulated. Our findings could provide theoretical insight into the design of nanodevices based on a GR and MoGe₂N₄/MoSi₂N₄ heterobilayer.

---

1. Introduction

Two-dimensional (2D) materials^1–3 have received extensive interest owing to their intriguing physical and chemical properties and broad device application potential, including in electronics,^3,4 nanophotonics,⁵ optoelectronics^6,7 and spintronics.^8,9 A plethora of 2D materials, including graphene (GR),¹⁰ phosphorene,^11,12 transition metal dichalcogenides (TMDCs),^13,14 and graphitic carbon nitrides,^15–17 have been synthesized experimentally and predicted theoretically. These 2D materials exhibit outstanding properties and unique advantages over conventional bulk materials, and are particularly promising candidates for designing high-performance nanodevices, such as field-effect transistors¹⁸ and photodetectors.¹⁹

Very recently, Hong et al.²⁰ discovered a new family of 2D materials, namely MoSi₂N₄ monolayers, using chemical vapor deposition (CVD). The MoSi₂N₄ monolayer is a layered structure, which can be viewed as a MoN₂ layer sandwiched between two Si–N bilayers. The MoSi₂N₄ monolayer exhibits semiconducting characteristics with a band gap of about 1.94 eV, and possesses high carrier mobility up to 1200 cm² V⁻¹ s⁻¹. This monolayer is also stable and mechanically stronger than most other 2D semiconductors such as MoS₂ monolayers. The successful synthesis of MoSi₂N₄ monolayers has led to a new class of 2D materials with formula MA₂Z₄,²⁰ where M represents an early transition metal (Mo, W, Cr), A = Si or Ge, and Z = N, P, or As. Motivated by this finding, many theoretical investigations have been performed to explore the electronic, optical and transport properties of MA₂Z₄ monolayers. For instance, Guo et al.²¹ studied the electronic properties and transport coefficient of MoSi₂N₄ monolayers alongside the strain effect, and showed that band gap and Seebeck coefficient of such a monolayer are strain-tunable. Wu and colleagues²² also predicted that the band gap of MSi₂N₄ (M = Mo, W) monolayers can be altered by strain and electric field, which result in the transformation from indirect to direct band gap semiconductors. Furthermore, MoSi₂N₄, WSi₂N₄ and VSi₂N₄ monolayers are also predicted to be a potential valleytronic materials.^23,24 These ever expanding first-principle calculations of MA₂Z₄ have continually revealed the enormous potential of MA₂Z₄ monolayers for future high-performance device applications.

Currently, constructing 2D van der Waals (vdW) heterostructures between two or more 2D materials is known to be an effective strategy to explore more new properties and extend the potential applications of the corresponding 2D materials. These 2D vdW heterostructures have been predicted theoretically using first-principles calculations, and synthesized experimentally via several methods, such as CVD and mechanical exfoliation. In addition, 2D vdW heterostructures have new desirable properties which could be used for fabricating high-efficiency nanodevices experimentally, such as for solar cells, field-effect transistors (FFTs), and photodetectors. Recently, the combination between the layers of several MA₂Z₄ monolayers to form MA₂Z₄ bilayers,^22,25 and between the GR layer and MA₂Z₄ monolayers,^26,27 has received much attention from the scientific community. For instance, Zhong et al.²⁵ investigated the electronic features of MA₂Z₄ (M = Ti, Cr, Mo; A = Si and Z = N, P) bilayers under the strain effect. They predicted that the electronic properties of the MA₂Z₄ family are tunable with strain-induced transitions from semiconductor to metal. This finding makes the MA₂Z₄ family a potential candidate for fabricating electro-mechanical devices. Similarly, Wu and colleagues²² showed that applying an electric field can also tune the semiconductor-to-metal transition in both MoSi₂N₄ and WSi₂N₄ bilayers, they are therefore suitable for designing next generation nanoelectronics and optoelectronics. Nonetheless, the combination between MoSi₂N₄ and MoGe₂N₄ to form a heterobilayer, and between graphene and MoSi₂N₄/MoGe₂N₄ heterobilayer to form a GR/MoSi₂N₄/MoGe₂N₄ heterostructure, have not yet been explored thoroughly.

In this work, based on first-principles calculations, we investigate the electronic structures of the MoSi₂N₄/MoGe₂N₄ heterobilayer and explore its electronic properties and band alignment alongside the presence of the GR layer. Various combinations and stacking configurations of GR/MoSi₂N₄/MoGe₂N₄ heterostructures are investigated. Our results reveal that the MoSi₂N₄/MoGe₂N₄ heterobilayer exhibits an indirect band gap semiconductor and possesses type-II band alignment at the equilibrium state. With the presence of the GR layer in the MoSi₂N₄/MoGe₂N₄ heterobilayer, we see the formation of the Schottky contact with narrow barrier height of about 0.26 eV, which increases the carrier injection efficiency.

2. Computational details

In this work, all the calculations, including geometric optimization, electronic properties and band alignment of the MoSi₂N₄/MoGe₂N₄ heterobilayers and the heterostructures between GR and MoSi₂N₄/MoGe₂N₄ heterobilayer, were performed from first-principles calculations within density functional theory, which was implemented in Vienna Ab initio Simulation (VASP)²⁸ and Quantum Espresso^29,30 packages. The Perdew–Burke–Ernzerhof (PBE) in the framework of the generalized gradient approximation (GGA)³¹ was used to describe the exchange–correlation energy. The projector augmented wave (PAW)³² pseudopotentials were used to describe the electron-ion interaction. In addition, the DFT-D3 method of Grimme³³ was also selected for describing the presence of the weak vdW forces that always occur in layered vdW systems, including heterobilayers and heterostructures. Furthermore, it should be noted that the traditional DFT method always underestimates the band gap values of materials, especially 2D materials, we therefore used the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional to avoid this issue and obtain an accurate band gap of the considered materials. The Brillouin zone (BZ) was sampled using the Monkhorst-Pack scheme. A 12 × 12 × 1 (6 × 6 × 1) k-point mesh was used for all the calculations within the DFT-PBE (HSE06) method with a cutoff energy of 510 eV. To avoid the interactions between periodical slabs, we set a large vacuum thickness of 25 Å along the z direction. The geometric optimization was fully obtained with the convergence threshold for energy of 10⁻⁶ eV and for a force of 10⁻³ eV Å⁻¹. The spin–orbit coupling (SOC) was also taken into account for the electronic properties of the heterobilayer.

3. Results and discussion

3.1. Structural and electronic properties of MoGe₂N₄/MoSi₂N₄ heterobilayer

The relaxed atomic structures of the MoGe₂N₄/MoSi₂N₄ heterostructure for AA and AB stacking configurations are depicted in Fig. 1. In AA-stacking, both the Ge and N atoms in the MoGe₂N₄ layer are located directly above the Si and N atoms of the MoSi₂N₄ layer, as depicted in Fig. 1(a). Whereas, in AB-stacking, the Ge and N atoms in the MoGe₂N₄ layer are staggered with respect to the Si and N atoms of the MoSi₂N₄ layer, as depicted in Fig. 1(b). After geometric optimization, the interlayer spacings (D) between the MoGe₂N₄ and MoSi₂N₄ layers for the AA and AB stacking configurations are obtained as listed in Table 1. For the AA-stacking, the equilibrium interlayer spacing is 3.33 Å, and it is 3.35 Å for the AB-stacking configuration. For checking the structural stability of such a heterostructure, we further calculate the binding energy as: E_b = E_H − ΣE_Mi, where E_H is the total energy of the combined MoGe₂N₄/MoSi₂N₄ heterostructure. E_Mi is the total energy of the constituent MoGe₂N₄ and MoSi₂N₄ monolayers. The binding energy of the MoGe₂N₄/MoSi₂N₄ heterobilayer for AA and AB stacking configurations is calculated to be −0.11 and −0.16 eV, respectively. The negative binding energy confirms that the heterobilayer is dynamically stable. In addition, the binding energy of the MoGe₂N₄/MoSi₂N₄ heterobilayer for the AB stacking configuration is lower than that for the AA stacking configuration, suggesting that the AB stacking configuration can be considered as the most energetically favorable stacking configuration.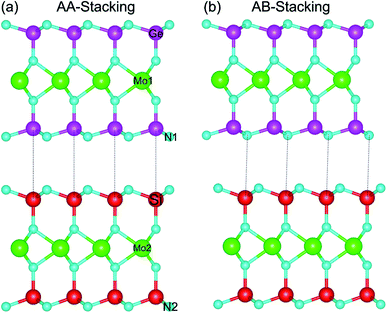

Fig. 1 Side view of the optimized atomic structures of the MoGe₂N₄/MoSi₂N₄ heterostructure for (a) AA-stacking and (b) AB-stacking.

Table 1 Optimized lattice constant a (Å), equilibrium interlayer spacing D (Å), binding energy E_b (eV), band gap E_g (eV) obtained from PBE, HSE and PBE + SOC and band alignment of MoGe₂N₄/MoSi₂N₄ heterostructures for different stacking configurations

	a	D	Eb	Eg			Band alignment
				PBE	HSE	PBE + SOC
AA-stacking	2.96	3.33	−0.11	0.88	1.29	0.87	Type-II
AB-stacking	2.96	3.35	−0.16	0.90	1.33	0.89	Type-II

---

The band structures of the MoGe₂N₄/MoSi₂N₄ heterostructure for different stacking configurations are displayed in Fig. 2. We used different methods, including PBE, HSE and PBE + SOC to calculate the band gaps of the considered heterostructure. The obtained band gaps for the MoGe₂N₄/MoSi₂N₄ heterostructure are listed in Table 1. For the AA-stacking, the band gaps of the MoGe₂N₄/MoSi₂N₄ heterostructure are calculated as 0.88 eV, 1.29 eV and 0.87 eV. It is clear that the HSE06 method gives rise to a larger band gap value than the PBE and PBE + SOC methods. However, all three methods predict the same characters of the MoGe₂N₄/MoSi₂N₄ heterostructure, which possesses the indirect band gap semiconductor. The valence band maximum (VBM) is located at the Γ point, while the conduction band minimum (CBM) is located at the M point. Interestingly, when the SOC effect is applied, it tends to split the valence bands at the M point of the MoGe₂N₄/MoSi₂N₄ heterostructure into two different parts, as depicted in Fig. 2(c). The energy of band splitting for the first and second valence bands of the AA-stacking is calculated to be 13.27 meV and 13.9 meV, respectively. However, the SOC effect splits only the valence bands at the M point, whereas the VBM of such heterostructure is located at the Γ point. Therefore, the SOC does not affect the band alignments of the heterostructures. Similar trends are also observed in the AB-stacking of the MoGe₂N₄/MoSi₂N₄ heterostructure. The PBE, HSE06 and PBE + SOC band gaps of the MoGe₂N₄/MoSi₂N₄ heterostructure for the AB-stacking are 0.90, 1.33 and 0.89 eV, respectively. The AB-stacking also predicts the indirect band gap semiconductor in the MoGe₂N₄/MoSi₂N₄ heterostructure with the VBM at the Γ point and the CBM at the M point, as depicted in Fig. 2(d–f). Furthermore, the band offset is also critical for the optoelectronic application, we therefore calculate the band offsets for valence bands (Δ_V) and for conduction bands (Δ_C). The band offsets Δ_V and Δ_C for the AA-stacking are calculated to be 0.43 eV and 0.47 eV, respectively. Whereas, these values for AB-stacking are 0.40 eV and 0.43 eV, respectively. In addition, comparing AA and AB stacking, the band structure and alignment seems to be almost unchanged. This is a very convenient behaviour for experimental fabrication since the electronic properties are less affected by stacking configurations.

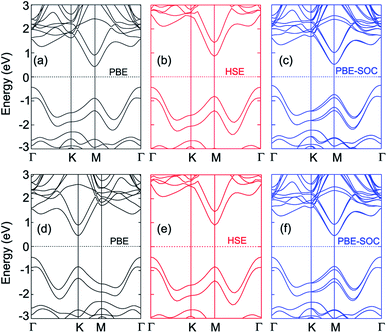Fig. 2 Band structures of the MoGe₂N₄/MoSi₂N₄ heterostructure calculated by (a, d) PBE, (b, e) HSE and (c, f) PBE + SOC methods for (a–c) AA-stacking and (d–f) AB-stacking.

More interestingly, device performance based on vdW heterostructures depends crucially on the band alignment, forming between two different 2D materials. Depending on the band edge positions of the constituent monolayers, vdW heterostructure can be divided into three different types of band alignment, including type-I (straddling gap), type-II (staggered gap) and type-III (broken gap). To investigate the band alignment, we further calculate weighted band structures of the MoGe₂N₄/MoSi₂N₄ heterostructure, as depicted in Fig. 3. For both the AA-stacking and AB-stacking, one can find that the CBM of the MoGe₂N₄/MoSi₂N₄ heterostructure is mainly contributed by the Mo-orbital states of the MoGe₂N₄ layer, as marked with green circles. Whereas, the VBM at the Γ point is mainly contributed by the Mo-orbital states of the MoSi₂N₄ layer, as marked by the violet circles. The contributions by the different monolayers to the VBM and CBM demonstrate that the MoGe₂N₄/MoSi₂N₄ heterostructure possesses type-II band alignment for both AA- and AB-stacking. The type-II band alignment promotes effective separation of electrons and holes and provides an opportunity for electrons and holes to separate in real space. Thus, the MoGe₂N₄/MoSi₂N₄ heterostructure is promising for designing optoelectronic devices with significantly suppressed carrier-recombination.

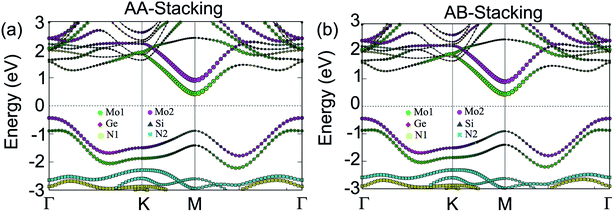Fig. 3 Weighted band structures of the MoGe₂N₄/MoSi₂N₄ heterostructure for (a) AA-stacking and (b) AB-stacking.

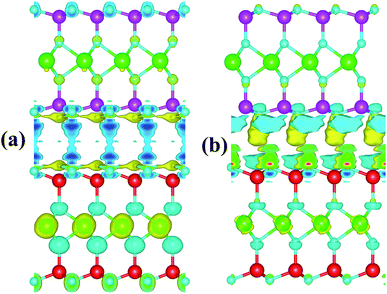
We further investigated the charge mechanism in the MoGe₂N₄/MoSi₂N₄ heterobilayer by calculating the charge density difference as follows: Δρ = ρ_HB − Σρ_Mi, where ρ_HB and ρ_Mi, respectively, are the charge density of the MoGe₂N₄/MoSi₂N₄ heterobilayer and the constituent MoGe₂N₄ and MoSi₂N₄ monolayers. The charge density difference of the MoGe₂N₄/MoSi₂N₄ heterobilayer for the AA- and AB stacking is illustrated in Fig. 4. The yellow and cyan regions represent the positive and negative charges, respectively. We find that the charges are mainly visualized at the interface. The yellow regions are located in the MoGe₂N₄ side, while the cyan regions are in the MoSi₂N₄ layer. This finding suggests that the charges are mainly accumulated in the MoGe₂N₄ layer and depleted in the MoSi₂N₄ layer.

Fig. 4 Charge density difference of the MoGe₂N₄/MoSi₂N₄ heterostructure for the (a) AA- and (b) AB-stacking configurations. Yellow and cyan regions represent the positive and negative charges, respectively. The isosurface value is set to be 2.35 e Å⁻³.

3.2. Electrical graphene contact to a MoGe₂N₄/MoSi₂N₄ heterobilayer

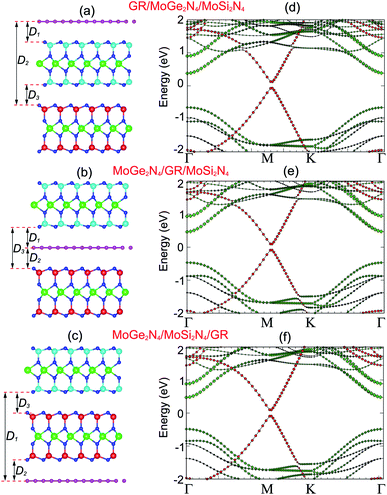
We now consider the formation of a triple-layered 2D-metal/2D-semiconductor heterostructure by including a graphene layer into the MoSi₂N₄/MoGe₂N₄ heterobilayer. The atomic structures of all vdW heterostructures between the GR and MoSi₂N₄/MoGe₂N₄ heterobilayer are depicted in Fig. 5(a–c). Three stacking sequences can be obtained: GR layer placed on top of the MoSi₂N₄ layer in the MoSi₂N₄/MoGe₂N₄ heterobilayer (Fig. 5(a)); GR layer between the MoSi₂N₄ and MoGe₂N₄ layers (Fig. 5(b)); and GR layer located below the MoGe₂N₄ layer in the MoSi₂N₄/MoGe₂N₄ heterobilayer (Fig. 5(c)). It is clear that the lattice constant of single-layer GR is calculated to be 2.46 Å, while the lattice constant of the MoSi₂N₄/MoGe₂N₄ heterobilayer is calculated to be 2.98 Å. Therefore, in order to avoid the effect of lattice mismatch, we use a supercell, consisting of (2 × 2) unit cells of GR and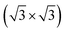 unit cells of MoSi₂N₄/MoGe₂N₄ heterobilayer to build the triple-layered 2D-metal/2D-semiconductors heterostructure. The lattice constant of the triple-layered 2D-metal/2D-semiconductors heterostructure is calculated to be 5.04 Å. Thus, the lattice mismatch between GR and the MoSi₂N₄/MoGe₂N₄ heterobilayer is 2.38%, which is reasonably small and does not affect the main results. The interlayer spacings between the GR, MoSi₂N₄ and MoGe₂N₄ are calculated and listed in Table 2. For the GR/MoSi₂N₄/MoGe₂N₄, the interlayer spacings D₁, D₂ and D₃ are calculated to be 3.58, 13.80 and 3.33 Å, respectively. These values indicate that the interactions between the GR, MoSi₂N₄ and MoGe₂N₄ are weak. In addition, we can see that the interlayer spacings of 3.33 Å and 3.58 Å are comparable with those in other 2D-layered heterostructures, which have typical vdW forces.^34–37 This finding suggests that the GR, MoSi₂N₄ and MoGe₂N₄ layers in their corresponding heterostructures are bonded together via weak vdW interactions. It should be noted that the systems that are characterized by the vdW interactions are feasible and thus they can be easily fabricated in experiments using several common strategies, such as mechanical exfoliation³⁸ and chemical vapor deposition (CVD).³⁹ Furthermore, considering the MoSi₂N₄/GR/MoGe₂N₄ and MoSi₂N₄/MoGe₂N₄/GR heterostructures, we also find that they are characterized by weak vdW forces. Furthermore, in order to guarantee stability, we also perform the ab initio molecular dynamics simulations of such heterostructures at room temperature of 300 K, as depicted in Fig. 6. We find that the heterostructures are stable at 300 K room temperature.

Fig. 5 Side view of the atomic structures of (a) GR/MoGe₂N₄/MoSi₂N₄, (b) MoGe₂N₄/GR/MoSi₂N₄ and (c) MoGe₂N₄/MoSi₂N₄/GR heterostructures. Weighted band structures of (d) GR/MoGe₂N₄/MoSi₂N₄, (e) MoGe₂N₄/GR/MoSi₂N₄ and (f) MoGe₂N₄/MoSi₂N₄/GR heterostructures. Red and green circles represent the contributions of semimetal graphene and semiconducting MoGe₂N₄/MoSi₂N₄ layers, respectively.

Fig. 6 The variation of the temperature of the considered heterostructures as a function of a time heating step by performing AIMD simulations. The insets represent snapshots of the heterostructures after heating for 4 ps.

Table 2 Calculated interlayer spacings between GR and MoSi₂N₄ (D₁), GR and MoGe₂N₄ (D₂) and between MoSi₂N₄ and MoGe₂N₄ (D₃), binding energy, Schottky barriers, band gap and contact types of vdW heterostructures, forming between the GR, MoSi₂N₄ and MoGe₂N₄ monolayers

Heterostructures	Interlayer spacings			Eb, meV per C atom	Φn, eV	Φp, eV	E^GRg, meV	Contact types
	D1, Å	D2, Å	D3, Å
GR/MoSi2N4 (ref. 27)	3.16	—	—	−49.14	1.49	0.96	17	p-type ShC
GR/MoGe2N4 (ref. 27)	—	3.38	—	−24.86	0.63	1.54	14	n-type ShC
GR/MoSi2N4/MoGe2N4	3.58	13.80	3.33	−67.66	0.33	0.61	42	n-type ShC
MoSi2N4/GR/MoGe2N4	3.70	3.67	7.37	−55.73	0.43	0.41	46	p-type ShC
MoSi2N4/MoGe2N4/GR	14.23	3.31	3.45	−65.35	0.47	0.46	45	p-type ShC

---

The projected band structures of the heterostructures combined between the GR and MoSi₂N₄/MoGe₂N₄ heterobilayer are depicted in Fig. 5(d–f). Red and green circles represent the contributions of the GR and MoSi₂N₄/MoGe₂N₄ layers, respectively. One can observe that the electronic band structures of these graphene-based heterostructures seem to be a combination between those of the constituent GR and MoSi₂N₄/MoGe₂N₄ heterobilayer. A Dirac cone with linear dispersion of the GR layer is well preserved and located at the M point. The physical mechanism of the shift in Dirac point from the K to M point is due to the size effects in the GR supercell.⁴⁰ The semiconducting feature of the MoSi₂N₄/MoGe₂N₄ heterobilayer is also maintained. The band gap of the MoSi₂N₄/MoGe₂N₄ heterobilayer contacted to the GR layer is about 0.84 eV, which is smaller than that of the freestanding MoSi₂N₄/MoGe₂N₄ heterobilayer. This finding suggests that the contact between GR and the MoSi₂N₄/MoGe₂N₄ heterobilayer tends to reduce the band gap of the MoSi₂N₄/MoGe₂N₄ heterobilayer semiconductor. This reduction gives rise to an enhancement in optical absorption of graphene-based heterostructures. Furthermore, the MoSi₂N₄/MoGe₂N₄ heterobilayer contacted with the GR layer possesses a direct band gap semiconductor with both the VBM and CBM at the Γ point, as depicted in Fig. 5(d–f). The nature of such a transformation from an indirect to direct band gap in the MoSi₂N₄/MoGe₂N₄ heterobilayer is due to a band folding effect. More interestingly, when GR contacts the MoSi₂N₄/MoGe₂N₄ heterobilayer, a band gap of about (17–46) meV is opened in the GR layer. It is clear that the mechanism of this band gap opening in the GR layer is due to symmetry breaking of the A and B sub-lattices in GR. This appearance was also observed in other GR-based heterostructures.^35–37

More interestingly, the contact between metallic GR and the semiconducting MoSi₂N₄/MoGe₂N₄ heterobilayer gives rise to the formation of a 2D metal/2D semiconductor interface. For the 2D metal/2D semiconductor interface, depending on the position of the Fermi level of metallic GR with respect to the band edges of the semiconductor, there is the formation of either Schottky contact (ShC) or Ohmic contact (OhC). One can find from the band structures in Fig. 5 that the Fermi level of the GR layer lies in the band gap region of the MoSi₂N₄/MoGe₂N₄ semiconductor, thus suggesting the formation of the ShC type in all three corresponding GR-based heterostructures. In addition, the Fermi level pinning is still weak in the heterostructures that are characterized by the weak vdW interactions. Therefore, we determine the contact barriers of such heterostructures using the Schottky–Mott rule.⁴¹ The n-type and p-type ShC, respectively, can be defined as Φ_n = E_C − E_F and Φ_p = E_F − E_V, where E_C, E_V and E_F, respectively, are the CBM, VBM and Fermi level of the GR-based heterostructure. The calculated Φ_n and Φ_p of the GR/MoGe₂N₄/MoSi₂N₄, MoGe₂N₄/GR/MoSi₂N₄ and MoGe₂N₄/MoSi₂N₄/GR heterostructures are listed in Table 2. We find that the Φ_n in the GR/MoGe₂N₄/MoSi₂N₄ heterostructure is still smaller than the Φ_p, indicating that it forms an n-type ShC at the equilibrium state. Whereas, for the MoGe₂N₄/GR/MoSi₂N₄ and MoGe₂N₄/MoSi₂N₄/GR heterostructures, the Φ_n is higher that the Φ_p, implying that they form the p-type ShC. The Φ_n of the MoGe₂N₄/GR/MoSi₂N₄ heterostructure is calculated to be 0.33 eV, which is smaller than that of the GR/MoGe₂N₄/MoSi₂N₄ and MoGe₂N₄/MoSi₂N₄/GR heterostructures, as illustrated in Fig. 7. The lower the contact barrier, the better the device performance. Intriguingly, the contact barriers in the GR contacted MoGe₂N₄/MoSi₂N₄ heterobilayer are significantly smaller than those in the GR contacted with MoGe₂N₄ and MoSi₂N₄ monolayers, as listed in Table 2. This suggests that the GR/MoGe₂N₄/MoSi₂N₄ heterostructure offers an effective pathway to reduce the Schottky barrier, which is highly beneficial for improving the charge injection efficiency of contact heterostructures.

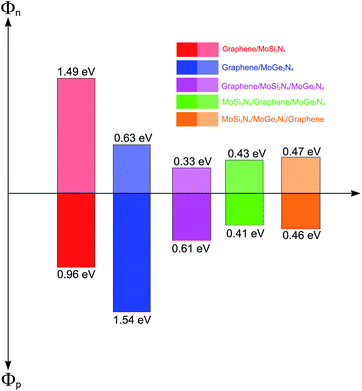Fig. 7 Histogram of the Schottky barrier height of the vdW heterostructures formed between graphene, MoSi₂N₄ and MoGe₂N₄ monolayers.

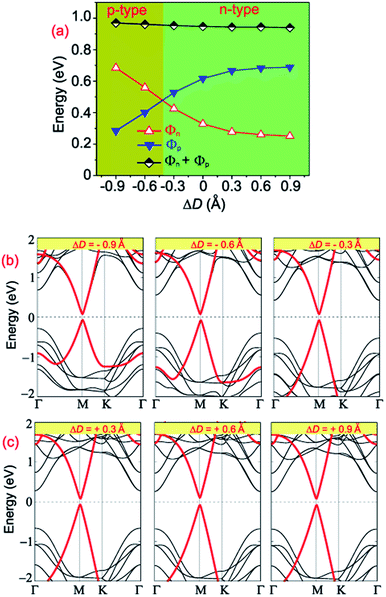
The tuning of the contact barriers and contact types in GR-based vdW heterostructures is an important factor of nanodevices based on the GR heterostructures. Controlling the interlayer coupling through stacking is one of the most efficient strategies in tuning both the contact barriers and contact types of GR-based heterostructures. The interlayer coupling can be manipulated by changing the interlayer spacings between the GR and semiconductors in their corresponding heterostructures. One can observe from Table 2 that the GR/MoGe₂N₄/MoSi₂N₄ has the lowest binding energy of −67.66 meV per C atom in comparison with that of other configurations, as it is the most stable configuration. Therefore, the effects of the interlayer couplings on the contact barriers and contact types of the GR/MoGe₂N₄/MoSi₂N₄ heterostructure are investigated as an illustrative example. The projected band structures of the GR/MoGe₂N₄/MoSi₂N₄ heterostructure as well as the variation in the contact barriers as functions of the interlayer couplings are displayed in Fig. 8. Red and black lines represent the contributions of the metallic GR and semiconducting MoGe₂N₄/MoSi₂N₄ heterobilayer, respectively.

Fig. 8 (a) The variation of the Schottky barriers of the GR/MoGe₂N₄/MoSi₂N₄ heterostructure as a function of the interlayer couplings. Projected band structures of the GR/MoGe₂N₄/MoSi₂N₄ heterostructure under (b) compressive and (c) tensile strains.

Interestingly, we find that changing interlayer couplings gives rise to a change not only in the Schottky barriers but also in the contact types of the GR/MoGe₂N₄/MoSi₂N₄ heterostructure. The changes in the Schottky barriers and contact types in the GR/MoGe₂N₄/MoSi₂N₄ heterostructure are illustrated in Fig. 8(a). The Φ_n decreases with increasing interlayer spacing, while the Φ_p increases accordingly. On the contrary, the Φ_n increases with decreasing the interlayer spacing, while the Φ_p decreases accordingly. When the ΔD is smaller than −0.45 Å, the Φ_n becomes larger than the Φ_p, leading to the transition from n-type ShC to p-type. The physical mechanism of such transitions can be described by analyzing the change in the Fermi level relative to the band edges of the semiconducting MoGe₂N₄/MoSi₂N₄ heterobilayer. With the applications of the compressive strain, i.e. ΔD < 0, the Fermi level of graphene moves towards the VBM of the semiconducting MoGe₂N₄/MoSi₂N₄ heterobilayer, thus resulting in an/a increase/decrease in the Φ_n/Φ_p. On the other hand, with the application of the tensile strain, i.e. ΔD > 0, the Fermi level of graphene shifts upwards from the VBM to the CBM of the semiconducting MoGe₂N₄/MoSi₂N₄ heterobilayer. Thus, the Φ_n is decreased and the Φ_p is increased accordingly. In this case, the heterostructure remains as n-type ShC. It can be concluded that with the application of different strains, both the Schottky barriers and contact types in the GR/MoGe₂N₄/MoSi₂N₄ heterostructure can be manipulated.

4. Conclusions

In summary, we have investigated the structural and contact types in a 2D vdW heterobilayer between MoGe₂N₄ and MoSi₂N₄ monolayers, as well as in the presence of electrical graphene. We found that the MoGe₂N₄/MoSi₂N₄ heterobilayer forms type-II band alignment, which effectively promotes the separation of electrons and holes, and provides an opportunity for further electrons and holes. Interestingly, the insertion of the electrical graphene contact to a MoGe₂N₄/MoSi₂N₄ heterobilayer gives rise to the formation of a metal/semiconductor contact, which is characterized by the contact type barriers. Depending on the graphene position relative to the MoGe₂N₄/MoSi₂N₄ heterobilayer, the graphene-based heterostructure can form either an n-type or p-type Schottky contact. The graphene/MoGe₂N₄/MoSi₂N₄ heterostructure exhibits an n-type Schottky contact, whereas the MoGe₂N₄/GR/MoSi₂N₄ and MoGe₂N₄/MoSi₂N₄/GR heterostructures form a p-type one. Intriguingly, the contact barriers in the GR contacted MoGe₂N₄/MoSi₂N₄ heterobilayer are significantly smaller than those in the GR contacted MoGe₂N₄ and MoSi₂N₄ monolayers, suggesting that the GR/MoGe₂N₄/MoSi₂N₄ heterostructure offers an effective pathway to reduce the Schottky barrier, which is highly beneficial for improving the charge injection efficiency of the contact heterostructures. More interesting, by controlling the interlayer coupling through stacking, both the Schottky barriers and contact types in the GR/MoGe₂N₄/MoSi₂N₄ heterostructure can be manipulated.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The author wishes to thank Prof. Yee Sin Ang (Singapore University of Technology and Design, Singapore) for critically reading the manuscript and helpful discussion.

References

1. S. Z. Butler, S. M. Hollen, L. Cao, Y. Cui, J. A. Gupta, H. R. Gutiérrez, T. F. Heinz, S. S. Hong, J. Huang and A. F. Ismach, et al., ACS Nano, 2013, 7, 2898.
2. P. Miró, M. Audiffred and T. Heine, Chem. Soc. Rev., 2014, 43, 6537.
3. G. Fiori, F. Bonaccorso, G. Iannaccone, T. Palacios, D. Neumaier, A. Seabaugh, S. K. Banerjee and L. Colombo, Nat. Nanotechnol., 2014, 9, 768.
4. X. Li, L. Tao, Z. Chen, H. Fang, X. Li, X. Wang, J.-B. Xu and H. Zhu, Appl. Phys. Rev., 2017, 4, 021306.
5. F. Xia, H. Wang, D. Xiao, M. Dubey and A. Ramasubramaniam, Nat. Photonics, 2014, 8, 899.
6. S. Lei, F. Wen, B. Li, Q. Wang, Y. Huang, Y. Gong, Y. He, P. Dong, J. Bellah and A. George, et al., Nano Lett., 2015, 15, 259.
7. J. S. Ponraj, Z.-Q. Xu, S. C. Dhanabalan, H. Mu, Y. Wang, J. Yuan, P. Li, S. Thakur, M. Ashrafi and K. Mccoubrey, et al., Nanotechnology, 2016, 27, 462001.
8. X. Li and X. Wu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 441.
9. Y. Liu, C. Zeng, J. Zhong, J. Ding, Z. M. Wang and Z. Liu, Nano-Micro Lett., 2020, 12, 1.
10. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
11. Y. Jing, X. Zhang and Z. Zhou, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 5.
12. A. Carvalho, M. Wang, X. Zhu, A. S. Rodin, H. Su and A. H. C. Neto, Nat. Rev. Mater., 2016, 1, 1.
13. S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, Nat. Rev. Mater., 2017, 2, 1.
14. W. Choi, N. Choudhary, G. H. Han, J. Park, D. Akinwande and Y. H. Lee, Mater. Today, 2017, 20, 116.
15. S. Yang, Y. Gong, J. Zhang, L. Zhan, L. Ma, Z. Fang, R. Vajtai, X. Wang and P. M. Ajayan, Adv. Mater., 2013, 25, 2452.
16. Q. Liang, Z. Li, Z.-H. Huang, F. Kang and Q.-H. Yang, Adv. Funct. Mater., 2015, 25, 6885.
17. L. Tan, C. Nie, Z. Ao, H. Sun, T. An and S. Wang, J. Mater. Chem. A, 2021, 9, 17.
18. C. Klinkert, Á. Szabó, C. Stieger, D. Campi, N. Marzari and M. Luisier, ACS Nano, 2020, 14, 8605.
19. F. Yan, Z. Wei, X. Wei, Q. Lv, W. Zhu and K. Wang, Small Methods, 2018, 2, 1700349.
20. Y.-L. Hong, Z. Liu, L. Wang, T. Zhou, W. Ma, C. Xu, S. Feng, L. Chen, M.-L. Chen and D.-M. Sun, et al., Science, 2020, 369, 670.
21. X.-S. Guo and S.-D. Guo, Chin. Phys. B, 2021, 30, 067102.
22. Q. Wu, L. Cao, Y. S. Ang and L. K. Ang, Appl. Phys. Lett., 2021, 118, 113102.
23. S. Li, W. Wu, X. Feng, S. Guan, W. Feng, Y. Yao and S. A. Yang, Phys. Rev. B, 2020, 102, 235435.
24. Q. Cui, Y. Zhu, J. Liang, P. Cui and H. Yang, Phys. Rev. B, 2021, 103, 085421.
25. H. Zhong, W. Xiong, P. Lv, J. Yu and S. Yuan, Phys. Rev. B, 2021, 103, 085124.
26. L. Cao, G. Zhou, Q. Wang, L. Ang and Y. S. Ang, Appl. Phys. Lett., 2021, 118, 013106.
27. K. D. Pham, C. Q. Nguyen, C. Nguyen, P. V. Cuong and N. V. Hieu, New J. Chem., 2021, 45, 5509.
28. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
29. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al., J. Phys.: Condens. Matter, 2009, 21, 395502.
30. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al., J. Phys.: Condens. Matter, 2017, 29, 465901.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
32. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758.
33. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
34. H. T. Nguyen, M. M. Obeid, A. Bafekry, M. Idrees, T. V. Vu, H. V. Phuc, N. N. Hieu, L. T. Hoa, B. Amin and C. V. Nguyen, Phys. Rev. B, 2020, 102, 075414.
35. S. Wang, J.-P. Chou, C. Ren, H. Tian, J. Yu, C. Sun, Y. Xu and M. Sun, Sci. Rep., 2019, 9, 1.
36. Z. Ben Aziza, H. Henck, D. Pierucci, M. G. Silly, E. Lhuillier, G. Patriarche, F. Sirotti, M. Eddrief and A. Ouerghi, ACS Nano, 2016, 10, 9679.
37. Z. B. Aziza, D. Pierucci, H. Henck, M. G. Silly, C. David, M. Yoon, F. Sirotti, K. Xiao, M. Eddrief and J.-C. Girard, et al., Phys. Rev. B, 2017, 96, 035407.
38. M. Velický, P. S. Toth, A. M. Rakowski, A. P. Rooney, A. Kozikov, C. R. Woods, A. Mishchenko, L. Fumagalli, J. Yin and V. Zólyomi, et al., Nat. Commun., 2017, 8, 1.
39. X. Zhou, X. Hu, J. Yu, S. Liu, Z. Shu, Q. Zhang, H. Li, Y. Ma, H. Xu and T. Zhai, Adv. Funct. Mater., 2018, 28, 1706587.
40. Y. Ren, X. Deng, Z. Qiao, C. Li, J. Jung, C. Zeng, Z. Zhang and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 245415.
41. J. Bardeen, Phys. Rev., 1947, 71, 717.

---