Open Access Article
Open Access ArticleTheoretical study of ternary silver fluorides AgMF4 (M = Cu, Ni, Co) formation at pressures up to 20 GPa†‡
Mateusz A. Domański*a,
Mariana Derzsi ab and
Wojciech Grochala
ab and
Wojciech Grochala *a
*a
aCentre of New Technologies, University of Warsaw, S. Banacha 2C, 02-097 Warsaw, Poland. E-mail: m.domanski@cent.uw.edu.pl; w.grochala@cent.uw.edu.pl
bAdvanced Technologies Research Institute, Faculty of Materials Science and Technology in Trnava, Slovak University of Technology in Bratislava, Trnava, 917 24, Slovakia
First published on 28th July 2021
Abstract
Only several compounds bearing the Ag(II) cation and other paramagnetic transition metal cations are known experimentally. Herein, we predict in silico stability and crystal structures of hypothetical ternary silver(II) fluorides with copper, nickel and cobalt in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry at a pressure range from 0 GPa up to 20 GPa employing the evolutionary algorithm in combination with DFT calculations. The calculations show that AgCoF4 could be synthesized already at ambient conditions but this compound would host diamagnetic Ag(I) and high-spin Co(III). Although none of the compounds bearing Ag(II) could be preferred over binary substrates at ambient conditions, at increased pressure ternary fluorides of Ag(II) featuring Cu(II) and Ni(II) could be synthesized, in the pressure windows of 7–14 and 8–15 GPa, respectively. All title compounds would be semiconducting and demonstrate magnetic ordering. Compounds featuring Ni(II) and particularly Co(II) should exhibit fundamental band gaps much reduced with respect to pristine AgF2. The presence of Cu(II) and Ni(II) does not lead to electronic doping to AgF2 layers, while Co(II) tends to reduce Ag(II) entirely to Ag(I).
1 stoichiometry at a pressure range from 0 GPa up to 20 GPa employing the evolutionary algorithm in combination with DFT calculations. The calculations show that AgCoF4 could be synthesized already at ambient conditions but this compound would host diamagnetic Ag(I) and high-spin Co(III). Although none of the compounds bearing Ag(II) could be preferred over binary substrates at ambient conditions, at increased pressure ternary fluorides of Ag(II) featuring Cu(II) and Ni(II) could be synthesized, in the pressure windows of 7–14 and 8–15 GPa, respectively. All title compounds would be semiconducting and demonstrate magnetic ordering. Compounds featuring Ni(II) and particularly Co(II) should exhibit fundamental band gaps much reduced with respect to pristine AgF2. The presence of Cu(II) and Ni(II) does not lead to electronic doping to AgF2 layers, while Co(II) tends to reduce Ag(II) entirely to Ag(I).
Introduction
Recent experimental and theoretical research on AgF2 demonstrated that this material mimics very closely the key structural and electronic properties of the well-known lanthanum oxocuprate La2CuO4 (ref. 1) – the prototype precursor of high-temperature oxocuprate superconductors – that are believed to be a necessary prerequisite for the unique behaviour of the latter. They account for strong antiferromagnetic coupling via a superexchange mechanism in two-dimensional sheets2 and substantial mixing of ligand and metal states in the top of the valence band. Superconductivity is reached in the oxocuprates via chemical doping and because of the striking similarities, not observed in any other known compound, it was suggested that superconductivity could be obtained also in the related silver(II) fluorides if proper chemical doping to AgF2 that would lead to metallization could be realized.1,3,4 It is therefore highly desirable to examine various possibilities to modify its electronic and magnetic properties via doping.Doping in essence is equivalent to the insertion of surplus holes or electrons into the chemical system. However, in contrast to cuprates, the bulk AgF2 has so far resisted all doping attempts. The hole doping of AgF2 could be introduced by F adatoms, but theoretical studies show that doping to this 001-type system via the addition of F atoms does not lead to a stable metallic phase.5 Partial oxidation of Ag(II) is also difficult, due to the immensely strong oxidative character of Ag(III); compounds of Ag(III) are even more difficult to synthesize and manipulate than Ag(II) compounds.
Therefore, our attention turned to electron doping, which could be introduced in two general ways. The first one is provided by vacancies at anionic sites (AgF2 → AgF2−δ). Similarly, as with additional F−, the study shows that the vacancies lead to clustering and phase separation without the prospect of obtaining a metallic phase.5 The second possibility, that we focus on here, is to modify AgF2 via substitution at the cationic site injecting the surplus electron. Early attempts to dope ternary silver fluorides (e.g. KAgF3) in a manner analogous to cuprates, i.e. substituting partially M(I) cations with M(II), failed. Recent theoretical investigations suggest that electron doping to AgF2 would not lead to a stable metallic phase due to a lattice polaronic effect and charge localization.6 Therefore the remaining way to achieve electron doping in AgF2 is to try partial isostructural substitution of Ag(II). By this, we mean to replace square planar Ag(II) in AgF2 with another redox-active metal cation, M(II), so that the layered structure is preserved but the electrons may partly flow from M(II) to Ag(II). This type of doping has not been yet achieved experimentally. Thus, in this study, we explored new ternary phases bearing Ag(II), especially isostructural to AgF2, to learn to what extent could the electronic structure of AgF2 sheets be altered by the presence of other metal cations.
The natural choice for the M element is a transition metal which also presents octahedral coordination featuring Jahn–Teller distortion like Ag(II). Accordingly, we considered diverse ternary fluoride stoichiometries which may host strongly coupled AgF2 sheets. Among ternary fluorides AgIIMxFy, many transition metal systems have been successfully prepared so far,3 i.e. for M = Au(III), Au(V), Nb(V), Ta(V), Ti(IV), Zr(IV), Hf(IV), Ru(V), Rh(IV), Ir(V), Pd(IV), Pt(IV), Pt(V), Mn(IV) and Cr(IV) (AgMnIVF6 (ref. 7) and AgCrIVF6 (ref. 8) structures not known). None of these fluorides host [AgF2] sheets or chains required for achieving strong antiferromagnetic coupling. Yet the great majority of these compounds contain closed-shell or low-spin cations which would not hold any magnetic interactions.
Late 3d-block transition metals, especially Cu, Ni and Co, seem to be promising candidates for electron doping due to their relative resistance towards oxidation in the fluoride environment while having partly filled d subshell. The redox potentials for the M3+/M2+ redox pairs decrease in the Cu > Ni > Co sequence. Experimentally, CoF3 and NiF3 (actually NiIINiIVF4 (ref. 9)) are moderately stable in an inert atmosphere, and they constitute strong fluorinating agents. On the other hand, CuF3 is quite unstable thermally and thermodynamically10 (even more than AgF3 (ref. 11)), thus minimizing the possibility of the intrinsic redox reaction between Ag(II) and Cu(II). Remarkably, such appealing synthesis has not been achieved experimentally yet, so no fluorides having Ag(II) and M(II) (M = Cu, Ni, Co) in any ratio are known, despite many similarities between these cations. There are, however, some examples of compounds with Ag(I) and M(III) valences. Among fluoride systems, only the Ag(I)Co(III) fluoride with Ag3CoF6 formula has been already described,12 suggesting that as yet unobserved Ag(II)Co(II) pair might be just beyond the border of intrinsic redox reaction. Silver fluorides with M = Cu or Ni are not known, thus the forms bearing Ag(II) and M(II) or Ag(I) and M(III) can not be excluded. Furthermore, there are known ternary oxide systems having Ag(I) and M(III) with AgMO2 formula (M = Cu, Ni, Co).13–17 Oxide and fluoride systems of silver tend to differ dramatically, thus the question about the nature of the late 3d ternary fluorides remains open.
The theoretical search for ternary systems bearing initially divalent cations has the aim of verification if it could possibly form a metallic phase with Ag(II). Since ternary oxides with Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M ratio of 1
M ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are known, here we decided to study ternary fluorides with the same ratio. To understand whether ternary fluorides bearing Ag(II) in combination with another transition metal (TM) constitute a viable synthetic target, we have examined here AgMF4 systems with Cu, Ni and Co using Density Functional Theory (DFT) methods in combination with evolutionary algorithms for crystal structures' prediction.
1 are known, here we decided to study ternary fluorides with the same ratio. To understand whether ternary fluorides bearing Ag(II) in combination with another transition metal (TM) constitute a viable synthetic target, we have examined here AgMF4 systems with Cu, Ni and Co using Density Functional Theory (DFT) methods in combination with evolutionary algorithms for crystal structures' prediction.
Preliminary results showed that such systems are very close in terms of energy to the sum of binary substrates but have lower volume, suggesting they could be obtained at elevated pressures. It is well-known that pressure may affect to a great extent both the crystal structures and stability of chemical compounds.19 High-pressure synthesis proved to be crucial in the synthesis of some transition metal compounds, e.g. copper oxyfluorides18 (and references therein), as well as for inducing metallization,19,20 the latter being not possible in pure AgF2.21 Thus, aside from variations of the chemical composition, we also study the impact of external pressure on crystal and electronic structure, and stability of AgMF4 systems with respect to the mixture of binary fluorides, AgF2 and MF2 (M = Cu, Ni, Co). Since both stability and electronic properties may depend on pressure, we have investigated the effect of external pressure on the formation and properties of the title AgMF4 compounds.
Computational methods
This theoretical study is based on periodic electronic-structure calculations for solids carried out with Vienna Ab initio Simulation Package 5.4.4 (VASP) software using projector-augmented wave method.22–24 We used the potentials set recommended by VASP with a 520 eV plane-wave energy cut-off. Energy calculations utilized collinearly spin-polarized DFT method using generalized gradient approximation functional PBEsol (i.e. solid-revised Perdew, Burke and Ernzerhof correlation–exchange functional25). The on-site electronic correlation was included with Hubbard and exchange repulsion terms (U and J) using Dudarev's approach.26,27 Geometry optimizations were done with k-spacing of 2π × 0.024 Å−1 (using the Monkhorst–Pack scheme) and conjugate-gradient algorithm for ionic relaxation with the criteria of 10−7 eV for electronic self-consistent-field convergence and 10−5 eV for ionic cycles convergence. In this approach effective Ueff = U − J, is considered, thus we used Ueff equal 4 eV (for Ag, Ni), 5 eV (Co) and 8 (Cu). These values were earlier used and validated in respective systems exhibiting +II oxidation state.2,28–30In our quest for the lowest-energy crystal structure of hypothetical compounds of AgCuF4, AgNiF4 and AgCoF4, we have initially tested various substitutions within the known crystal structure of AgF2. We have tested also various prototypical MIMIIIF4 structures, which allow for electron transfer between metal sites; notably, we presumed that electron-hungry Ag(II) could undergo reduction, with the concomitant 1 − e− oxidation of its neighbouring TM cations. The three scrutinized 3d elements, Cu, Ni and Co, differ in terms of redox properties, electron count, U-induced splitting of upper and lower Hubbard d-bands, and degree of tetragonal distortion of MF6 octahedra. All above-mentioned cations also have significantly smaller cationic radii than Ag(II). AgMF4 (M = Cu, Ni, Co) fluorides were modelled in the appropriate ABC4 structure types selected from the Inorganic Crystal Structure Database (ICSD). Furthermore, in each case, we have searched for the global minimum structure using evolutionary algorithms (EA) as implemented in the XtalOpt software33 for crystal structure prediction. The starting pool (i.e. 1st generation) for each XtalOpt run constituted 30 initial random structures containing 2 or 4 formula units in the unit cell. After the pool of structures is optimized by VASP, XtalOpt selects the best possible candidates for the next generation, employs such operators as strain, exchange, ripple, and crossover on the selected candidates, which form the next generation of structures. Such structure generation and optimization continue until the energy convergence is reached. The XtalOpt runs were performed for the three title stoichiometries of AgMF4, at 0 and 10 GPa considering unit cells containing 2 to 4 formula units. XtalOpt runs were done in combination with DFT calculations using VASP optimizer. A four-step optimization procedure of each structure was performed increasing accuracy at each step, using DFT for the first two and DFT+U (i.e. with Dudarev's approach) approach for the last two steps. These calculations were performed with reduced convergence criteria (5 × 10−7 eV and 5 × 10−5 eV for the electronic and ionic cycle, respectively) and k-point mesh (2π × 0.048 Å−1). For each system, we have obtained about optimized 500 structures (more in ESI, see Fig. S1 and S2‡). The selected lowest-energy EA structures were reoptimized with higher precision as described above. The XtalOpt is a robust tool that has been utilized more than sixty times in solid-state chemistry or physics applications.34
For selected systems, geometry optimization was additionally performed using the HSE06 hybrid functional35 with a coarser k-spacing (2π × 0.048 Å−1). For the chosen systems we calculated the electronic density of states (DOS) with tetrahedron method and Blöchl corrections, with both DFT+U and HSE06.
Dynamic stability was investigated in VASP by calculating Γ-point vibrational frequencies, using the density functional perturbation theory method and the DFT+U framework.
For visualization of crystal structures, VESTA36 software was used. Band structure plots were made using PyProcar library37 and AFLOW38 program.
Results and discussion
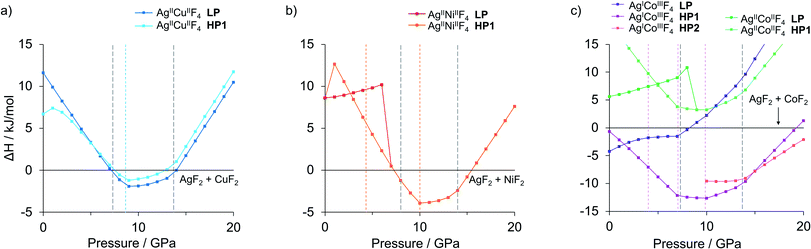
The idea of pressure study originates from preliminary results, as numerous low-volume polymorphs have already been identified in the XtalOpt quest at ambient pressure (Fig. S1a, c and e‡). Consequently, we have studied the AgMF4 phases in a range of hydrostatic pressure with the prospect of obtaining pressure-induced stability of AgMF4 (M = Cu, Ni and Co) in respect to binary substrates AgF2 and MF2, and to evaluate the possibility of high-pressure metallization of the ternary silver(II) fluorides. The formation enthalpy of the lowest-energy polymorphs from the substrates was investigated in the 0–20 GPa pressure range. The pressure evolution for AgMF4 systems with respect to the sum of those for the binary substrates in their most stable polymorphs is presented in Fig. 1. With our choice of Ueff we successfully confirmed the experimentally observed pressure-induced phase transitions of AgF2,21 CuF2,31 NiF2 (ref. 32) and CoF2 (ref. 28 and 32) up to 20 GPa (note in ESI, see also Table S1 and Fig. S3,‡ these phase transitions are marked in Fig. 1). The phase-transition sequences in the considered stoichiometries were calculated with the described DFT+U framework assuming hydrostatic conditions.Additional insight into pressure-induced effects on the enthalpy of formation of the ternary fluorides comes from pV term analysis (ESI, Fig. S4‡). Both for low pressure (<3 GPa) and high-pressure range (>9 GPa) the pV factor works against the formation of the studied ternary fluoride phases. Consequently, the ternary fluoride phases benefit from the pV term with respect to the substrates in the range 3–9 GPa; at higher pressures, binary substrates experience volume-reducing phase transitions which reduces this advantage. The crucial is the phase transition of constituent AgF2 at about 14 GPa into an unprecedented inorganic nanotube.21 This incredibly low-volume polymorph reduces the pV term of substrates and gradually destabilizes thermodynamically all proposed ternary fluorides at pressures approaching 20 GPa. These factors result in re-entrant instability of the ternary phases above certain characteristic pressure in each case.
The hypothetical mixed-cation AgMF4 fluorides from Fig. 1 are below described in the order of M = Cu, Ni, Co, in terms of their structure and stability, and then of the pressure effects. Finally, we investigate their electronic properties at ambient and elevated pressures.
Copper
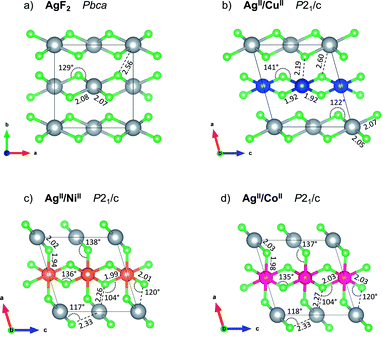
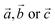 lattice vectors (cf. ESI, Fig. S5‡). Notably, these three diverse polymorphs were also found during EA search (see ESI, Fig. S1 and S2‡). We found that a monoclinic variant of the AgF2 type structure with metal alternation in the original b direction is the lowest-energy structure of AgCuF4 (marked here as low-pressure, LP, structure, Fig. 2b), as confirmed by evolutionary algorithm quest. This polymorph preserves the layered character of its binary constituents by separating Ag and Cu into distinct puckered [AgF4/2] and [CuF4/2] layers. Substantial axial elongation of both Ag(II) and Cu(II) octahedra is predicted (i.e. four shorter equatorial and two considerably longer axial Ag(Cu)–F distances (2 + 2) + 2 coordination), in agreement with the strong Jahn–Teller effect which is expected for d9 species in octahedral field. The rhombic distortion can be approximated to tetragonal distortion (4) + 2 in most cases. The ratio of axial to equatorial bond lengths R = dax/deq (dimensionless Jahn–Teller distortion parameter often used to describe such compounds40) equals 1.24 for the Ag(II) site and 1.14 for the Cu(II) one. The tetragonal distortion for both cations is similar as in the parent phases where this ratio equals 1.23 and 1.15, for AgF2 and CuF2, respectively (all geometry parameters are summarised in Table 1).
lattice vectors (cf. ESI, Fig. S5‡). Notably, these three diverse polymorphs were also found during EA search (see ESI, Fig. S1 and S2‡). We found that a monoclinic variant of the AgF2 type structure with metal alternation in the original b direction is the lowest-energy structure of AgCuF4 (marked here as low-pressure, LP, structure, Fig. 2b), as confirmed by evolutionary algorithm quest. This polymorph preserves the layered character of its binary constituents by separating Ag and Cu into distinct puckered [AgF4/2] and [CuF4/2] layers. Substantial axial elongation of both Ag(II) and Cu(II) octahedra is predicted (i.e. four shorter equatorial and two considerably longer axial Ag(Cu)–F distances (2 + 2) + 2 coordination), in agreement with the strong Jahn–Teller effect which is expected for d9 species in octahedral field. The rhombic distortion can be approximated to tetragonal distortion (4) + 2 in most cases. The ratio of axial to equatorial bond lengths R = dax/deq (dimensionless Jahn–Teller distortion parameter often used to describe such compounds40) equals 1.24 for the Ag(II) site and 1.14 for the Cu(II) one. The tetragonal distortion for both cations is similar as in the parent phases where this ratio equals 1.23 and 1.15, for AgF2 and CuF2, respectively (all geometry parameters are summarised in Table 1).
| System | Label | p (GPa) | Bond length (Å) | R | Bond length (Å) | R | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ag–F1 | Ag–F2 | Ag–F3 | M–F1 | M–F2 | M–F3 | |||||
| AgIIF2 | LP | 0 | 2.07 | 2.08 | 2.56 | 1.23 | — | — | — | — |
| HP1 | 10 | 2.06 | 2.06 | 2.37 | 1.15 | — | — | — | — | |
| AgIICuIIF4 | LP | 0 | 2.05 | 2.07 | 2.60 | 1.26 | 1.92 | 1.92 | 2.19 | 1.14 |
| HP1 | 10 | 2.03 | 2.10 | 2.38 | 1.15 | 1.85 | 1.91 | 2.15 | 1.14 | |
| AgIINiIIF4 | LP | 0 | 2.02 | 2.26 | 2.33 | 0.88 | 1.94 | 1.99 | 2.01 | 0.97 |
| HP1 | 10 | 2.02 | 2.11 | 2.43 | 1.18 | 1.93 | 1.94 | 1.95 | 0.99 | |
| AgIICoF4 | LP | 0 | 2.03 | 2.27 | 2.33 | 0.88 | 1.98 | 2.03 | 2.03 | 0.98 |
| HP1 | 10 | 2.01 | 2.18 | 2.33 | N.D. | 1.92 | 2.00 | 2.03 | 0.95 | |
Axial elongation suggests that in both cations d-hole occupies dx2−y2 orbital. Both constituent layers [AgF4/2] and [CuF4/2] of AgCuF4 preserve intra-sheet antiferromagnetic ordering.
The geometry within the puckered layers is reminiscent of those found in binary fluorides; the [AgF4/2] layers are more buckled than in pure AgF2 (the Ag–F–Ag angle is 122° vs. 129° in bulk AgF2), while [CuF4/2] layers are flattened (the corresponding angle is 141° vs. 132° in bulk CuF2). This feature stems from the difference in the ionic radii between Ag(II) and Cu(II). In order to form a segregated layer structure, the [AgF2] sheets must buckle and the [CuF2] sheets must simultaneously flatten; this accommodation is associated by bending of the crystallographic beta angle from 90° (for bulk AgF2) to 105°. We notice that two other models with mixed [(Ag,Cu)F4/2] layers (ESI, Fig. S5c and d‡), have energies higher by +6.4 and +7.3 kJ mol−1, respectively, as compared to the LP structure. We also found a crystal structure containing Ag–F–Cu bridges and exhibiting genuine 3D connectivity (Fig. S5b‡), characterized by much lower volume. Importantly, the most stable LP polymorph is computed to be +6.7 kJ mol−1 uphill in energy with respect to substrates:
| AgF2 + CuF2 → AgCuF4 | (1) |
Thus, if prepared, this ternary fluoride might be only metastable. However, its kinetic stability with respect to phase separation is indicated by our phonons calculations, yielding no imaginary frequencies for this polymorph (Appendix S4,‡ the same is true for all structures examined in this work).
 | ||
| Fig. 3 Crystal structures of (a) parent AgF2, and the lowest-energy predicted (b) AgCuF4, and (c) AgNiF4, and metastable (d) AgIICoIIF4 at 10 GPa (HP1 structure of each). The threshold for Ag–F bond drawing is 2.15 Å in all cases. Another view of these structures is shown in ESI, Fig. S6.‡ | ||
The HP1 polymorph is also based on the AgF2 type structure, but the fluorine bridges are now formed between the two chemically distinct metal cations (Ag–F–Cu) in contrary to the LP structure, where fluorine atoms bridge metal cations of the same type (Ag–F–Ag and Cu–F–Cu). One can think of the HP1 structure as the LP one with direct Jahn–Teller elongation taking place within the [AgF4/2] and [CuF4/2] layers (alternating along  ) instead of in the direction perpendicular to the layers (along
) instead of in the direction perpendicular to the layers (along  ). Consequently, the 2D connectivity within the [AgF4/2] and [CuF4/2] layers is broken and a 3D Ag–F–Cu one established with the cooperative Jahn–Teller mechanism. The HP1 form of AgCuF4 has a ferrimagnetic character with a small uncompensated spin (ca. 0.02 μB) due to opposite spin on Ag(II) and Cu(II) cations with slightly different magnetic moments on each type of TM cation. Like in the LP polymorph, here the Cu and Ag octahedra are both axially elongated, see Table 1.
). Consequently, the 2D connectivity within the [AgF4/2] and [CuF4/2] layers is broken and a 3D Ag–F–Cu one established with the cooperative Jahn–Teller mechanism. The HP1 form of AgCuF4 has a ferrimagnetic character with a small uncompensated spin (ca. 0.02 μB) due to opposite spin on Ag(II) and Cu(II) cations with slightly different magnetic moments on each type of TM cation. Like in the LP polymorph, here the Cu and Ag octahedra are both axially elongated, see Table 1.
Nickel
In contrast to AgCuF4, however, the HP1 AgIINiIIF4 structure emerges from the LP one while changing axial compression of Ag(II) cations to an elongation, taking place perpendicular to the [AgF4/2] layers and resulting in a hole in dx2−y2 orbital. Consequently, two-dimensional connectivity within the [AgF4/2] is established (Fig. 3c) in contrary to the situation in the LP form, where the Jahn–Teller distortion is responsible for no connectivity with the silver layers (Fig. 2c). Thus, the LP and HP1 AgIINiIIF4 structures differ topologically mainly by 2D Ag–F–Ag connectivity in the latter compared to no such connectivity in the former. The HP1 polymorph may be thought of as build from separate antiferromagnetic layers of [AgF4/2] and [NiF4/2] parallel to bc plane.
Cobalt
| AgF2 + CoF2 → AgF + CoF3 | (2) |
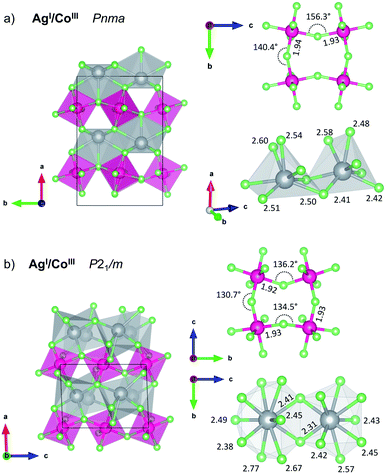
Importantly, it appears that the lowest-energy mixed-cation structure obtained in the cobalt system corresponds to the AgICoIIIF4 formulation, for which we also found the lowest-energy AgICoIIIF4 polymorph. Structure quests using evolutionary algorithms resulted in many similar layered AgICoIIIF4 structures, including KFeF4-HT polymorph (Z = 4, for others, see ESI, Fig. S1 and S2‡). Further modifications helped us finding the lowest-energy AgICoIIIF4 LP polymorph in the KFeF4-LT45 type structure (Z = 8, Fig. 4a). DFT+U calculations yield the energy of this structure to be −4.2 kJ mol−1 (or −24.8 kJ mol−1 at HSE06 level) with respect to the binary divalent metal fluorides. It also turns out that the energy for the Lewis acid–Lewis base reaction:
| AgF + CoF3 → AgICoIIIF4 | (3) |
The KFeF4-LT type structure comprises the puckered antiferromagnetic anionic sheets of [CoF4/2F2/1]− stoichiometry which features high-spin Co(III) cations, and diamagnetic Ag(I) counterions. While in parent CoF3 the octahedra are almost perfectly symmetric (with all bond lengths of 1.89 Å, the F–Co–F angles are distorted ±1.5° from 90°), in AgICoIIIF4 the CoF6 octahedra are markedly compressed with axial bond length 1.82 Å resulting in R ratio equal 0.94 (equatorial bonds are highlighted on Fig. 4a). Considering the coordination sphere of Ag(I), pristine AgF crystalizes in rock-salt structure with regular octahedra having 2.426 Å Ag–F bond lengths. In the case of AgCoF4, however, two types of Ag(I) can be distinguished, each with coordination number, CN = 7 within 2.65 Å radius, and both in the form of a bicapped tetragonal pyramid.
Likewise, at ambient pressure conditions, the intrinsic redox reaction in AgCoF4 system is favoured at elevated pressures. Here the lowest-energy mixed valence LP AgICoIIIF4 is predicted to undergo two subsequent high-pressure transitions at about 1 GPa (HP1) and 15 GPa (HP2), respectively while maintaining the metal oxidation states (Fig. 1c, magenta series). Both, HP1 and HP2 forms represent KMnF4 type structures similarly as the LP one but with reduced symmetry according to the sequence Pmna (LP) → P21/m (HP1) → C2/c (HP2). Apparently, it turns out that AgICoIIIF4 stability would increase under high pressure about threefold with respect to substrates at 10 GPa, up to −12.6 kJ mol−1.
The first AgICoIIIF4 high-pressure polymorph HP1 was found at 10 GPa using EA has a distorted monoclinic KMnF4 type structure (Fig. 4b). This polymorph of AgICoIIIF4 resembles the LP polymorph having antiferromagnetic puckered sheets of [CoF4/2F2/1]− stoichiometry with high-spin Co(III) cations and diamagnetic Ag(I) in between. Volume decrease of AgICoIIIF4 with respect to binary fluorides is mainly due to enhancement of [CoF4/2F2/1]− layers buckling and increase of Ag(I) coordination number. Antiferromagnetic sheets are built from CoF6 octahedra exhibiting axial bond compression with R ratio equal 0.92 (axial bonds are 1.78 Å, equatorial 1.92–1.93 Å, cf. Fig. 4b). The equatorial Co–F bonds form a layer parallel to the bc plane. The Ag(I) cation is found at 10 GPa in two distinct crystallographic sites which differ in their coordination number. Here, CN is either 9 or 10, with bond lengths varying from 2.31 up to 2.77 Å. For comparison, at the same pressure, parent AgF is found in the CsCl type structure with cubic coordination sphere (8 ligands) and Ag–F bond length of 2.47 Å. The second high pressure polymorph of AgICoIIIF4 AgICoIIIF4 also crystallizes in KMnF4 type structure (C2/c). It features higher CN for Ag(I) sites and more buckled [CoF4/2F2/1]− layers.
Electronic properties
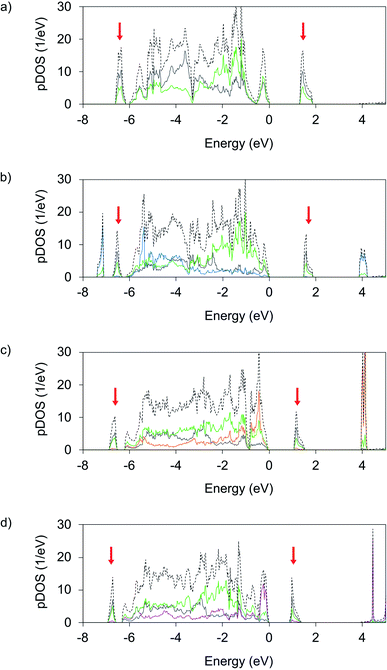
The main motivation behind studying novel ternary Ag(II) fluorides is to achieve appreciable changes in electronic structure that would result in facile metallization within the [AgF2] layers either at ambient or elevated pressures. To evaluate this possibility, we first discuss the electronic density of states (DOS) computed for AgF2 and the studied ternary AgMF4 fluorides at DFT+U level and zero pressure. Subsequently, we discuss the impact of pressure on their bandgaps.Analysis of the LP AgIICuIIF4 electronic DOS (Fig. 5b) shows that the formation of this compound does not lead to significant electronic changes within the [AgF4/2] layers with respect to pristine AgF2. The main difference is the presence of Cu 3d states. The Cu valence states show similar distribution as the valence Ag states, while the LHB (∼7.5 eV) and UHB (∼4 eV) of Cu display even larger separation than the Ag ones, which reflects the larger U at Cu(II) sites. Consequently, the nature of the bandgap of AgCuF4 is defined by the bandgap of the [AgF4/2] sublayer. It is only slightly broader than in the parent AgF2 (1.46 eV vs. 1.33 eV). Evidently, both the [AgF4/2] and [CuF4/2] layers in AgCuF4 are well electronically separated, preserving the nature of their respective substrates, i.e. insulating character associated with a ligand to metal CT gap.
More significant changes vs. AgF2 are observed in the DOS for AgNiF4 (Fig. 5c). Here, the additional Ni 3d states predominate the valence DOS at the highest energies below the Fermi level and on average above the F 2p valence states. This contrasts AgF2 and AgCuF4 DOS, where the metal states are on average shifted to lower energies relative to F 2p valence states. Due to the appearance of the Ni states at higher energies the position of the Ni LHB is positioned just below the Fermi level, while the conduction band preserves the character of the Ag UHB band level. This means that the CT character of the bandgap has changed. Now the charge transfer is realized between the valence states of dominant Ni and conduction states of dominant Ag character. The appearance of Ni 3d states above the F 2p states of valence DOS results in a noticeably narrower band gap (1.09 eV) than in parent AgF2 (1.33 e).
In the case of AgIICoIIF4, the Co 3d (Fig. 5d) valence states are shifted to even higher energies relative to the F 2p valence resulting in an even narrower bandgap of 0.90 eV. The Co LHB positioned just below the Fermi level has almost the entire Co character, meaning that charge transfer over the bandgap is now from Co(II) states to the UHB of Ag(II), and indicate the proximity of intrinsic redox reaction character.
Noticeably, the band gaps of AgIINiIIF4 and AgIICoIIF4 have an intervalence CT character, with Ni(II)/Co(II) serving as an electron donor, and Ag(II) as an acceptor, the intervalence CT being more pronounced in AgIICoIIF4. The picture of AgICoIIIF4 is reversed relative to both AgIICoIIF4 and AgIINiIIF4, here the top of the valence band mainly consists of filled 4d states of Ag(I) while the bottom of the conduction band corresponds to the UHB of Co(III) (Fig. S7a‡). Due to the intrinsic redox reaction discussed above band gap increases up to 2.02 eV, it is thus larger than that of AgF2, and of the AgIIMIIF4 analogues.
Clearly, the electronic structure of AgMF4 compounds in the series M = Cu, Ni, Co, changes together with the redox properties of M(II) cations. The gradual change of M bands contribution to the valence band is apparent on band structure plots, Fig. S8,‡ as well as in DOS (Fig. 5). For AgCuF4, with Cu(III) in fluoride environment is experimentally accessible with the greatest difficulty, AgCuF4 preserves Ag(II) and Cu(II) oxidation states and a ligand to metal CT insulator character. For AgNiF4, where Ni(III) forms easier, electronic DOS reveals moderate ease of intervalence CT between Ni(II) donor and Ag(II) acceptor, with the corresponding valence and conduction bands separated by a mere ∼1.1 eV. Finally, for AgICoIIIF4, where Co(III) is most accessible, a genuine redox reaction is seen which leads to “inverse” intervalence CT character, where Ag(I) serves as an electron donor, while Co(III) as an acceptor. Note that our hybrid DFT (HSE06) calculations yielded qualitatively similar results for the ambient pressure AgMF4 structures (Fig. S9‡).
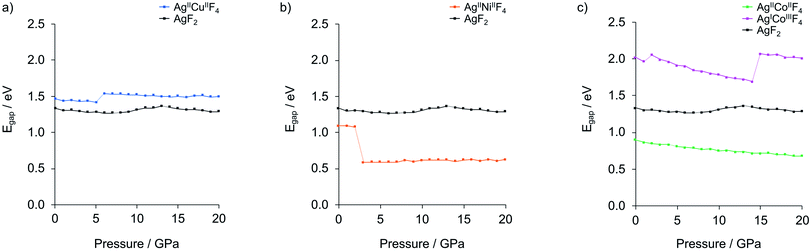 | ||
| Fig. 6 Electronic band gaps dependency on pressure elevation for the lowest-enthalpy structures of (a) AgCuF4, (b) AgNiF4 and (c) AgCoF4 (shown together with AgF2). Dotted lines connect values calculated for structures separated by phase transitions. Detailed data is provided in Table S3.‡ | ||
Conclusions
The silver(II) fluoride system is theoretically predicted to resist forming ternary fluorides with Cu, and Ni fluorides at ambient pressure conditions. The isostructural substitution is largely unfavoured at ambient pressure due to excessive differences in Ag(II) and M(II) bond lengths and in the extent of their tetragonal distortion. The energies of formation of AgIICuIIF4 and AgIINiIIF4 are positive but these compounds have real phonon frequencies, hence could be metastable if prepared. Both AgIICuIIF4 and AgIINiIIF4 are predicted to be semiconductors with a predominant charge-transfer character. There is a clear trend in electronic band gaps and character of the states at the top of the valence band as one moves from Cu, via Ni to Co. The AgCuF4 system has a comparable band gap with that of pristine AgF2 at ambient pressure (1.46 eV vs. 1.33 eV), while AgNiF4 system features a narrower band gap (1.09 eV).The cobalt(II) system displays many similarities to both nickel and copper structures while having an even smaller band gap (0.90 eV). However, AgIICoIIF4 configuration is predicted to be energetically unstable due to the potent oxidizing properties of Ag(II). The cobalt–silver fluoride system is thus quite different from the other two due to the intrinsic redox process resulting in a preference for as yet unknown AgICoIIIF4. The ambient-pressure KFeF4 type structure of this species is computed to be a ca. 2.02 eV band gap semiconductor, stable with respect to binaries and featuring antiferromagnetic sheets of [CoF4/2F2/1] stoichiometry.
Application of hydrostatic pressure in silico shows that there is a pressure range where the formation of ternary silver fluorides AgMF4 is favoured over binaries. The calculated range of stability is about 7–15 GPa for AgCuF4, 8–15 GPa for AgNiF4, and 0–22 GPa for AgICoIIIF4, meaning that in these conditions each system has a negative enthalpy of formation with respect to substrates. The nickel system appears to be interesting in terms of electronic structure because at 10 GPa it should form the separate layers polymorph with a narrow band gap of about 0.62 eV, less than half of that for AgF2. Regretfully, none of the system studied would be metallic or would feature electronically doped AgF2 sheets. The Co system is overdoped in that sense that Ag(II) becomes entirely reduced to Ag(I). Thus, doping to AgF2 remains a daunting target for the future studies.
Importantly, our study shows that in ternary fluorides of Ag and M (M = Ni, Cu), the AgIMIIIF4 formulation is not stable with respect to AgIIMIIF4, unlike in the known ternary oxides of these metals, AgMO2. Thus, Cu(II) and Ni(II) are expected to resist oxidizing power of Ag(II) both at ambient and elevated pressures while in the fluoride environment. Compounds with a formula AgIIMIIF4 might hold strong antiferromagnetic interactions due to the presence of strong spin-polarizer Ag(II) and second magnetic cation of 3d series. Scrutiny of the strength of magnetic interactions in these systems, especially a detailed description of superexchange coupling between Ag(II) and M(II) spins, will be performed in a forthcoming study.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Polish National Science Center (NCN) within Beethoven project (2016/23/G/ST5/04320). The research was carried out using supercomputers of Interdisciplinary Centre for Mathematical and Computational Modelling (ICM), University of Warsaw, under grant number GA76-19. Dr Derzsi acknowledges the ERDF, R&I Operational Program (ITMS2014+: 313011W085), Scientific Grant Agency of the Slovak Republic grant (VG 1/0223/19) and the Slovak Research and Development Agency grant (APVV-18-0168).Notes and references
- J. Gawraczyński, D. Kurzydłowski, R. A. Ewings, S. Bandaru, W. Gadomski, Z. Mazej, G. Ruani, I. Bergenti, T. Jaroń, A. Ozarowski, S. Hill, P. J. Leszczyński, K. Tokár, M. Derzsi, P. Barone, K. Wohlfeld, J. Lorenzana and W. Grochala, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 1495–1500 CrossRef PubMed.
- D. Kurzydłowski, M. Derzsi, P. Barone, A. Grzelak, V. Struzhkin, J. Lorenzana and W. Grochala, Chem. Commun., 2018, 54, 10252–10255 RSC.
- W. Grochala and R. Hoffmann, Angew. Chem., Int. Ed., 2001, 40, 2742–2781 CrossRef CAS PubMed.
- W. Grochala and Z. Mazej, Philos. Trans. R. Soc., A, 2015, 373, 20140179 CrossRef PubMed.
- A. Grzelak, M. Derzsi and W. Grochala, Inorg. Chem., 2021, 60, 1561–1570 CrossRef CAS PubMed.
- S. Bandaru, M. Derzsi, A. Grzelak, J. Lorenzana and W. Grochala, Phys. Rev. Mater., 2021, 5, 064801 CrossRef CAS.
- R. Hoppe and G. Siebert, Z. Anorg. Allg. Chem., 1970, 376, 261–267 CrossRef CAS.
- G. Stebert and R. Hoppe, Naturwissenschaften, 1971, 58, 95–96 CrossRef.
- C. Shen, L. C. Chacón, N. Rosov, S. H. Elder, J. C. Allman and N. Bartlett, C. R. Acad. Sci., Ser. IIc: Chim., 1999, 2, 557–563 CrossRef CAS.
- N. Bartlett, G. Lucier, C. Shen, W. J. Casteel, L. Chacon, J. Munzenberg and B. Žemva, J. Fluorine Chem., 1995, 71, 163–164 CrossRef CAS.
- B. Žemva, K. Lutar, A. Jesih, W. J. Casteel, A. P. Wilkinson, D. E. Cox, R. B. Von Dreele, H. Borrmann and N. Bartlett, J. Am. Chem. Soc., 1991, 113, 4192–4198 CrossRef.
- J. Grannec, A. Yacoubi, A. Tressaud and L. Rabardel, Solid State Commun., 1988, 68, 363–367 CrossRef CAS.
- J. Curda, W. Klein, H. Liu and M. Jansen, J. Alloys Compd., 2002, 338, 99–103 CrossRef CAS.
- Y. J. Shin, J. P. Doumerc, P. Dordor, C. Delmas, M. Pouchard and P. Hagenmuller, J. Solid State Chem., 1993, 107, 303–313 CrossRef CAS.
- T. Sörgel and M. Jansen, Z. Anorg. Allg. Chem., 2005, 631, 2970–2972 CrossRef.
- W. Stählin and H.-R. Oswald, Z. Anorg. Allg. Chem., 1969, 367, 206–208 CrossRef.
- H. Muguerra, C. Colin, M. Anne, M.-H. Julien and P. Strobel, J. Solid State Chem., 2008, 181, 2883–2888 CrossRef CAS.
- M. AI-Mamouri, P. P. Edwards, C. Greaves and M. Slaski, Nature, 1994, 369, 382–384 CrossRef.
- W. Grochala, R. Hoffmann, J. Feng and N. W. Ashcroft, Angew. Chem., Int. Ed., 2007, 46, 3620–3642 CrossRef CAS PubMed.
- Y. Liu-Xiang, Z. Jing-Geng, Y. Yong, L. Feng-Ying, Y. Ri-Cheng and J. Chang-Qing, Chin. Phys. Lett., 2006, 23, 426–427 CrossRef.
- A. Grzelak, J. Gawraczyński, T. Jaroń, D. Kurzydłowski, A. Budzianowski, Z. Mazej, P. J. Leszczyński, V. B. Prakapenka, M. Derzsi, V. V. Struzhkin and W. Grochala, Inorg. Chem., 2017, 56, 14651–14661 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245–8257 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- J. A. Barreda-Argüeso, S. López-Moreno, M. N. Sanz-Ortiz, F. Aguado, R. Valiente, J. González, F. Rodríguez, A. H. Romero, A. Muñoz, L. Nataf and F. Baudelet, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 214108 CrossRef.
- M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- C. Miller and A. S. Botana, Phys. Rev. B, 2020, 101, 195116 CrossRef CAS.
- D. Kurzydłowski, Crystals, 2018, 8, 140 CrossRef.
- L. C. Ming, M. H. Manghnani, T. Matsui and J. C. Jamieson, Phys. Earth Planet. Inter., 1980, 23, 276–285 CrossRef CAS.
- D. C. Lonie and E. Zurek, Comput. Phys. Commun., 2011, 182, 372–387 CrossRef CAS.
- XtalOpt – Publications, http://xtalopt.github.io/pub.html, accessed October 2, 2020 Search PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- U. Herath, P. Tavadze, X. He, E. Bousquet, S. Singh, F. Muñoz and A. H. Romero, Comput. Phys. Commun., 2020, 251, 107080 CrossRef CAS.
- W. Setyawan and S. Curtarolo, Comput. Mater. Sci., 2010, 49, 299–312 CrossRef.
- P. Fischer, D. Schwarzenbach and H. M. Rietveld, J. Phys. Chem. Solids, 1971, 32, 543–550 CrossRef CAS.
- W. Massa and D. Babel, Chem. Rev., 1988, 88, 275–296 CrossRef CAS.
- B. Žemva, K. Lutar, L. Chacon, M. Fele-Beuermann, J. Allman, C. Shen and N. Bartlett, J. Am. Chem. Soc., 1995, 117, 10025–10034 CrossRef.
- W. Grochala, Phys. Status Solidi B, 2006, 243, R81–R83 CrossRef CAS.
- In fact, during standard geometry optimization process a smooth transition between both HP1 and LP polymorphs occurred (i.e. optimization of HP1 polymorph at 0 GPa gave LP structure and also optimization of LP polymorph at 10 GPa led to HP1 structure).
- A. J. Bard, R. Parsons, J. Jordan and International Union of Pure and Applied Chemistry, Standard potentials in aqueous solution, M. Dekker, New York, 1985 Search PubMed.
- J. Lapasset, P. Sciau, J. Moret and N. Gros, Acta Crystallogr., Sect. B: Struct. Sci., 1986, 42, 258–262 CrossRef.
- J. Zaanen, G. A. Sawatzky and J. W. Allen, Phys. Rev. Lett., 1985, 55, 418–421 CrossRef CAS PubMed.
Footnotes |
| † This work is dedicated to Prof. Gary Schrobilgen at his 75th birthday. |
| ‡ Electronic supplementary information (ESI) available: Study of difluorides compression, detailed results of EA runs, electronic structure details at HP, crystal structures and vibration frequencies. See DOI: 10.1039/d1ra04970d |
| This journal is © The Royal Society of Chemistry 2021 |